量子信息导论第二章作业
- 格式:doc
- 大小:42.00 KB
- 文档页数:1

量子信息导论第一章作业(*标记者为选做题)1:计算二元对称信道的信道容量。
2:{}{}变换。
,试构造出该=,使得,则存在幺正变换、态中存在两组正交归一化空间U ~U U ~ii i i ψψψψH 3:{}{变换。
,并构造出该=,使得请证明,则存在=,有,它们满足:、中存在两组归一化态空间U ~U U ~~j i, ~ii j i j i i i ψψψψψψψψ∀H 4:对两比特态⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+=B B A B B A 121023121123021021φ i)求约化密度矩阵B A ρρ,;ii)求φ的Schmidt 分解形式。
5:对三粒子系统纯态ABC φ,在空间C B A H H H ⊗⊗中是否存在C B A H H H ,,中的正交基{}{}{}C B A i i i ,,,使得C B A ii ABC i i i p ⊗⊗=∑φ一定成立?给出理由。
6:设ψ为量子比特态,在Bloch 球面上均匀随机分布。
i) 随机地猜想一个态φ,求猜测态相对于ψ的平均保真度>=<2ψφF 。
ii) 对此量子态做正交测量{}I P P P P =+↓↑↓↑,,。
测量后系统被制备到:ψψψψρ↓↓↑↑+=P P P P ,求ρ与原来的态ψ的平均保真度。
(>=<ψρψF )7:123021,123021,0321--=+-==ψψψ。
现令i i i F ψψ32=,则{}3,2,1=a a F 构成二维空间中的POVM 。
现引入一个辅助的qubit ,试在扩展空间中实施一个正交测量,从而实现此POVM 。
8*:证明超算符仅在幺正条件下才是可逆的。
9:证明()011021-=-ψ在()()n U n U ,,ϑϑ⊗下是不变的。
10*:证明 ()()()()BC AC B A S S S S ρρρρ+≤+。
11:考虑2-qubit 系统--+⊗=ψψρ2181I I AB ,分别沿m n ,方向测A,B 粒子的自旋。


量子信息导论第二章作业1:Alice 和Bob 选择B92方案来建立量子密钥序列。
Alice 选择两种态:01=ψ,=2ψ )10(2/1+,分别以1/2的概率发送给Bob ,Bob 分别以1/2的几率选择基{}10和基)}10(2/110(2/1{-+对收到的态进行正交测量。
(1) 请论述Alice 和Bob 将遵从怎样的经典通信协议来建立密钥;(2)假定存在一个窃听者,该窃听者试图以概率克隆的方式对该密钥建立过程进行攻击。
则下列的几组克隆概率中,哪几组在理论上是可能的(括号中第一个数表示成功地克隆出1ψ的概率,第二个数表示成功地克隆出2ψ的概率)。
并给出证明。
,222,222⎪⎪⎭⎫ ⎝⎛--(1,0.1),(0.5,0.5),(0.7,0.7),(0.9,0.9)。
(3)窃听者如果克隆失败,他会随机发送1ψ或2ψ给Bob (分别以1/2的几率)。
如窃听者选择以上几组中最优的克隆方案进行攻击,则作为Alice 和Bob ,他们至少要公开对照多少组数据,均检验无误,才能确保该密钥的安全性达到99%以上?2:给出高维空间量子teleportation 的数学证明。
3:混合纠缠态()()14I I λρλλψψ--=-+⊗a) 求标准teleportation 的保真度,并且,当λ达到多少时,保真度将优于经典极限? (所谓经典极限是指:A 方随机选择一组测量基进行测量,并将测量结果通过经典 信道通知B ,B 根据A 的测量结果进行态制备。
)b) 计算()()()()()()Pr ()A A ob n m Tr E n E m ρλ↑↑=r r r r()E n r 是Alice 的比特投影到()n ↑r 上的投影子。


第二章定态薛定谔方程本章主要内容概要:1. 定态薛定谔方程与定态的性质:在势能不显含时间的情况下,含时薛定谔方程可以通过分离变量法来求解。
首先求解定态薛定谔方程(能量本征值方程)222.2d V E m dxψψψ-+= 求解时需考虑波函数的标准条件(连续、有限、单值等)。
能量本征函数n ψ具有正交归一性(分立谱)*()()m n mn x x dx ψψδ∞-∞=⎰或δ函数正交归一性(连续谱)'*'()()()q qx x dx q q ψψδ∞-∞=-⎰ 由能量本征函数n ψ可以得到定态波函数/(,)()niE t n n x t x eψ-ψ=定态波函数满足含时薛定谔方程。
对分立谱,定态是物理上可实现的态,粒子处在定态时,能量具有确定值n E ,其它力学量(不显含时间)的期待值不随时间变化。
对连续谱,定态不是物理上可实现的态(不可归一化),但是它们可以叠加成物理上可实现的态。
含时薛定谔方程的一般解可由定态解叠加而成,在分离谱情况下为(,)(,)n n nx t c x t ψ=ψ∑系数n c 由初始波函数确定(,0)()n n nx c x ψψ=∑ , *()(,0)n n c x x dx ψ∞-∞=ψ⎰由波函数(,)x t ψ的归一性,可以得到系数n c 的归一性21nnc=∑对(,)x t ψ态测量能量只能得到能量本征值,得到n E 的几率是2n c ,能量的期待值可由2n n nH c E =∑求出。
这种方法与用*ˆ(,)(,)H x t H x t dx∞-∞=ψψ⎰方法等价。
2. 一维典型例子:(a)一维无限深势阱(分立谱,束缚态)0, 0(),x aV x<<⎧=⎨∞⎩其它地方能量本征函数和能量本征值为2222(), 0;1,2,3,...2nnn xx x a nanEmaπψπ⎛⎫=<<=⎪⎝⎭=若0,(),a x aV x-<<⎧=⎨∞⎩其它地方则能量本征函数和能量本征值为2222()(), ;1,2,3,...22(2)nnnx x a a x a nanEm aπψπ⎛⎫=+-<<=⎪⎝⎭=1n=是基态(能量最低),2n=是第一激发态。




量子计算与量子信息原理第二卷一、引言随着科学技术的不断发展,量子计算和量子信息技术逐渐成为研究的热点。
量子理论的发展为计算和信息处理领域带来了全新的可能性和挑战。
而《量子计算与量子信息原理》第二卷正是针对这一领域的深入探讨和研究。
二、量子计算的基础原理1. 量子计算的基本概念量子计算是以量子理论为基础的一种全新的信息处理方法。
在量子计算中,信息以量子态的形式储存和处理,利用量子叠加和纠缠等特性进行计算操作,这使得量子计算具有比传统计算更强的计算能力和处理速度。
2. 量子位运算在量子计算中,量子位(qubit)是信息的基本单位。
与经典计算中的比特不同,量子位不仅可以处于0或1的叠加态,还可以利用量子纠缠来实现信息的同时处理和传输,为量子计算提供了更大的计算空间和灵活性。
3. 量子门操作量子门是用来改变量子位状态的操作,包括单量子门和多量子门操作。
单量子门可用于实现量子位的旋转和相位变换,而多量子门操作则可以实现量子态的纠缠和量子并行计算,是量子计算的重要基础。
三、量子信息的基础原理1. 量子通信量子通信是利用量子纠缠和量子隐形传态等量子特性进行信息传输和交换的一种全新通信方式。
量子通信具有绝对安全性和超高速度的特点,对信息传输安全和保密性有着重要意义。
2. 量子密钥分发量子密钥分发是基于量子纠缠的一种加密方法,可以实现安全的密钥分发和密钥认证。
与经典密钥分发方法相比,量子密钥分发具有抗窃听和攻击的能力,是未来信息安全领域的重要发展方向。
3. 量子信息处理量子信息处理是利用量子计算和量子通信等技术对信息进行处理和管理的一种新型信息处理方式。
通过量子计算和量子通信的结合,可以实现更高效的信息处理和传输,为信息技术的发展注入了新的动力。
四、量子计算与量子信息的应用前景1. 量子计算在密码学领域的应用量子计算可以对常用的非对称加密算法进行破解,从而对当前的信息安全体系造成冲击。
量子计算在密码学的研究和信息安全领域的应用具有重要意义,同时也提出了新的挑战。

2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
解: (1)bit x p x I x p i i i 170.4181log )(log )(18161616161)(=-=-==⨯+⨯=(2)bit x p x I x p i i i 170.5361log)(log )(3616161)(=-=-==⨯=(3)两个点数的排列如下: 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66共有21种组合:其中11,22,33,44,55,66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4)参考上面的两个点数的排列,可以得出两个点数求和的概率分布如下:symbolbit x p x p X H X P X ii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)bit x p x I x p i i i 710.13611log)(log )(3611116161)(=-=-==⨯⨯=2-42.6 掷两颗骰子,当其向上的面的小圆点之和是3时,该消息包含的信息量是多少?当小圆点之和是7时,该消息所包含的信息量又是多少? 解:1)因圆点之和为3的概率1()(1,2)(2,1)18p x p p =+=该消息自信息量()log ()log18 4.170I x p x bit =-== 2)因圆点之和为7的概率1()(1,6)(6,1)(2,5)(5,2)(3,4)(4,3)6p x p p p p p p =+++++=该消息自信息量()log ()log6 2.585I x p x bit =-==2.7 设有一离散无记忆信源,其概率空间为123401233/81/41/41/8X x x x x P ====⎛⎫⎛⎫=⎪ ⎪⎝⎭⎝⎭(1)求每个符号的自信息量(2)信源发出一消息符号序列为{202 120 130 213 001 203 210 110 321 010 021 032 011 223 210},求该序列的自信息量和平均每个符号携带的信息量 解:122118()log log 1.415()3I x bit p x === 同理可以求得233()2,()2,()3I x bit I x bit I x bit ===因为信源无记忆,所以此消息序列的信息量就等于该序列中各个符号的信息量之和 就有:123414()13()12()6()87.81I I x I x I x I x bit =+++= 平均每个符号携带的信息量为87.811.9545=bit/符号 2-9 “-” 用三个脉冲 “●”用一个脉冲(1) I(●)=Log 4()2= I(-)=Log 43⎛ ⎝⎫⎪⎭0.415=(2) H= 14Log 4()34Log 43⎛⎝⎫⎪⎭+0.811=2-10(2) P(黑/黑)= P(白/黑)=H(Y/黑)=(3) P(黑/白)= P(白/白)=H(Y/白)=(4) P(黑)= P(白)=H(Y)=2.11 有一个可以旋转的圆盘,盘面上被均匀的分成38份,用1,…,38的数字标示,其中有两份涂绿色,18份涂红色,18份涂黑色,圆盘停转后,盘面上的指针指向某一数字和颜色。
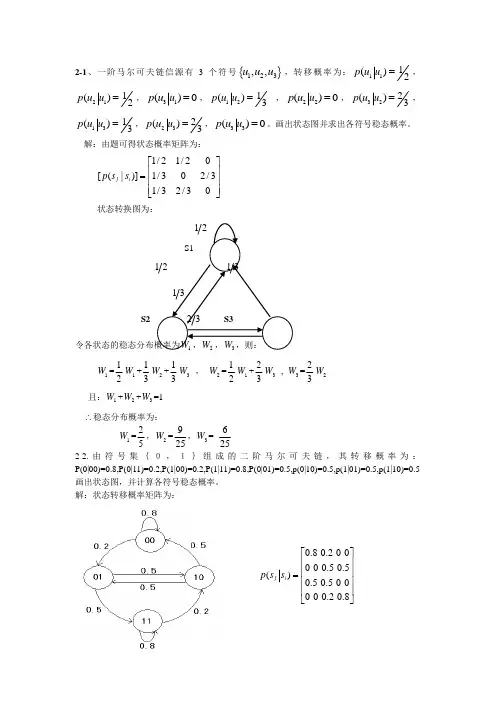
2-1、一阶马尔可夫链信源有3个符号{}123,,u u u ,转移概率为:1112()u p u=,2112()u p u =,31()0u p u =,1213()u p u = ,22()0u p u =,3223()u p u =,1313()u p u =,2323()u p u =,33()0u p u =。
画出状态图并求出各符号稳态概率。
解:由题可得状态概率矩阵为:1/21/20[(|)]1/302/31/32/30j i p s s ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦状态转换图为:12S112 13 13S2 23 S3 令各状态的稳态分布概率为1W ,2W ,3W ,则: 1W =121W +132W +133W , 2W=121W +233W , 3W =232W 且:1W +2W +3W =1∴稳态分布概率为:1W =25,2W =925,3W = 6252-2.由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:P(0|00)=0.8,P(0|11)=0.2,P(1|00)=0.2,P(1|11)=0.8,P(0|01)=0.5,p(0|10)=0.5,p(1|01)=0.5,p(1|10)=0.5画出状态图,并计算各符号稳态概率。
解:状态转移概率矩阵为:0.8 0.2 0 00 0 0.5 0.5()0.5 0.5 0 00 0 0.2 0.8j i p s s ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦令各状态的稳态分布概率为1w 、2w 、3w 、4w ,利用(2-1-17)可得方程组。
1111221331441132112222332442133113223333443244114224334444240.80.50.20.50.50.20.50.8w w p w p w p w p w w w w p w p w p w p w w w w p w p w p w p w w w w p w p w p w p w w =+++=+⎧⎪=+++=+⎪⎨=+++=+⎪⎪=+++=+⎩ 且12341w w w w +++=;解方程组得:12345141717514w w w w ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩ 即:5(00)141(01)71(10)75(11)14p p p p ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2-3、同时掷两个正常的骰子,也就是各面呈现的概率都是16,求:(1)、“3和5同时出现”事件的自信息量;(2)、“两个1同时出现”事件的自信息量; (3)、两个点数的各种组合的熵或平均信息量; (4)、两个点数之和的熵; (5)、两个点数中至少有一个是1的自信息量。
量子信息导论第一章作业(*标记者为选做题)1:计算二元对称信道的信道容量。
2:{}{}变换。
,试构造出该=,使得,则存在幺正变换、态中存在两组正交归一化空间U ~U U ~ii i i ψψψψH 3:{}{变换。
,并构造出该=,使得请证明,则存在=,有,它们满足:、中存在两组归一化态空间U ~U U ~~j i, ~ii j i j i i i ψψψψψψψψ∀H 4:对两比特态⎪⎪⎭⎫ ⎝⎛++⎪⎪⎭⎫ ⎝⎛+=B B A B B A 121023121123021021φ i)求约化密度矩阵B A ρρ,;ii)求φ的Schmidt 分解形式。
5:对三粒子系统纯态ABC φ,在空间C B A H H H ⊗⊗中是否存在C B A H H H ,,中的正交基{}{}{}C B A i i i ,,,使得C B A ii ABC i i i p ⊗⊗=∑φ一定成立?给出理由。
6:设ψ为量子比特态,在Bloch 球面上均匀随机分布。
i) 随机地猜想一个态φ,求猜测态相对于ψ的平均保真度>=<2ψφF 。
ii) 对此量子态做正交测量{}I P P P P =+↓↑↓↑,,。
测量后系统被制备到:ψψψψρ↓↓↑↑+=P P P P ,求ρ与原来的态ψ的平均保真度。
(>=<ψρψF )7:123021,123021,0321--=+-==ψψψ。
现令i i i F ψψ32=,则{}3,2,1=a a F 构成二维空间中的POVM 。
现引入一个辅助的qubit ,试在扩展空间中实施一个正交测量,从而实现此POVM 。
8*:证明超算符仅在幺正条件下才是可逆的。
9:证明()011021-=-ψ在()()n U n U ,,ϑϑ⊗下是不变的。
10*:证明 ()()()()BC AC B A S S S S ρρρρ+≤+。
11:考虑2-qubit 系统--+⊗=ψψρ2181I I AB ,分别沿m n ,方向测A,B 粒子的自旋。
量子信息导论第二章作业
1:Alice 和Bob 选择B92方案来建立量子密钥序列。
Alice 选择两种态:01=ψ,=2ψ )10(2/1+,分别以1/2的概率发送给Bob ,Bob 分别以1/2的几率选择基{}10和基)}10(2/1),10(2/1{-+对收到的态进行正交测量。
(1) 请论述Alice 和Bob 将遵从怎样的经典通信协议来建立密钥;
(2)假定存在一个窃听者,该窃听者试图以概率克隆的方式对该密钥建立过程进行攻击。
则下列的几组克隆概率中,哪几组在理论上是可能的(括号中第一个数表示成功地克隆出1ψ的概率,第二个数表示成功地克隆出2ψ的概率)。
并给出证明。
,222,222⎪⎪⎭
⎫ ⎝⎛--(1,0.1)
,(0.5,0.5),(0.7,0.7),(0.9,0.9)。
(3)窃听者如果克隆失败,他会随机发送1ψ或2ψ给Bob (分别以1/2的几率)。
如窃听者选择以上几组中最优的克隆方案进行攻击,则作为Alice 和Bob ,他们至少要公开对照多少组数据,均检验无误,才能确保该密钥的安全性达到99%以上?
2:给出高维空间量子teleportation 的数学证明。
3:混合纠缠态()()14I I λ
ρλλψψ--=-+⊗
a) 求标准teleportation 的保真度,并且,当λ达到多少时,保真度将优于经典极限? (所谓经典极限是指:A 方随机选择一组测量基进行测量,并将测量结果通过经典 信道通知B ,B 根据A 的测量结果进行态制备。
)
b) 计算()()()()()()Pr ()A A ob n m Tr E n E m ρλ↑↑=
()E n 是Alice 的比特投影到()n ↑上的投影子。