数学建模作业二:选课策略
- 格式:pdf
- 大小:148.44 KB
- 文档页数:4

数学建模选课策略问题推广数学建模作为一种实用的数学工具,已经广泛应用于各个领域。
在选课策略问题上,数学建模同样发挥着重要的作用。
本文将从不同角度探讨数学建模在选课策略中的应用。
数学建模可以帮助学生制定合理的选课计划。
在选课时,学生需要根据自己的兴趣、专业要求和个人能力来选择适合自己的课程。
数学建模可以通过分析历史数据和学术成绩,预测不同课程的难度和挑战程度,帮助学生做出明智的选择。
同时,数学建模还可以考虑到课程之间的关联性,避免选修了内容相似或冲突的课程,从而提高学习效果和学业成绩。
数学建模可以优化选课方案。
在大学选课中,学生通常会面临时间冲突、课程容量限制等问题。
数学建模可以通过建立数学模型,考虑到不同课程的时间安排和教室容量,找到最优的选课方案。
这样可以最大程度地满足学生的需求,避免时间冲突和选不上的情况,提高选课效率。
数学建模还可以考虑到学生的个体差异,制定个性化的选课策略。
每个学生都有自己的学习特点和目标,因此在选课时需要考虑到个体差异。
数学建模可以根据学生的学习能力、兴趣爱好和未来发展方向,制定个性化的选课策略。
通过分析学生的历史数据和学术成绩,预测不同课程的适应程度和发展前景,帮助学生做出更明智的选择。
在选课策略中,数学建模还可以考虑到学生的多样化需求。
随着社会的发展和人才需求的变化,学生对于课程的需求也在不断变化。
数学建模可以通过分析大量的数据和信息,预测不同课程的受欢迎程度和发展趋势,为学生提供更多元化的选课选择。
同时,数学建模还可以考虑到不同课程的培养目标和综合能力要求,帮助学生在选课时更好地发展自己的综合能力。
总的来说,数学建模在选课策略中的应用具有重要意义。
通过分析历史数据和学术成绩,制定合理的选课计划;通过建立数学模型,优化选课方案;考虑到学生的个体差异和多样化需求,制定个性化的选课策略。
这些都可以帮助学生更好地选择适合自己的课程,提高学习效果和学业成绩。
因此,数学建模在选课策略问题上的推广具有重要的意义。



数学建模选课分班问题
数学建模选课分班问题是指在学校的数学建模选修课程中,需要将学生分配到不同的班级中。
这个问题涉及到多个因素,包括学生的兴趣、能力水平、性别等,以及班级的容量和教师资源等。
在解决数学建模选课分班问题时,可以采用以下几种方法:
1.基于规则的分班方法:根据一些规则和标准,将学生分配到班级中。
例如,可以根据学生的兴趣和能力水平将他们分为不同的班级,以便更好地满足他们的学习需求。
2.基于优化算法的分班方法:利用数学建模中的优化算法,通过最小化某个目标函数来确定最佳的分班方案。
例如,可以将学生的分班问题建模为一个最小化总班级差异的问题,然后使用遗传算法或线性规划等方法求解最优解。
3.基于机器学习的分班方法:利用机器学习算法,通过学习历史数据和模式来预测学生在数学建模中的表现,并根据预测结果将学生分配到适合他们的班级。
这种方法可以根据学生的个性化需求和特点来进行分班。
在实际应用中,数学建模选课分班问题需要综合考虑多个因素,并进
行权衡和平衡。
例如,要避免班级之间的差异过大,同时也要注意班级容量和教师资源的合理分配。
为了更好地解决数学建模选课分班问题,可以采用多种方法的组合,例如先利用基于规则的方法进行初步分班,然后利用优化算法和机器学习算法进行微调和优化。
总之,数学建模选课分班问题是一个复杂的问题,需要综合考虑多个因素,并运用合适的方法进行求解。
通过合理的分班方案,可以更好地满足学生的学习需求,并提高数学建模课程的教学效果。

2013-2014第一学期数学建模课程设计题目:学生选课:金星班级:网络工程\2014年1月6日—1月10日一.模型摘要摘要:对于习惯了中小学课程(所有的课程由学校统一安排,而且科目从小学到高中有连续性)的大学新生来说,大学的课程多得令他们眼花缭乱,课程分类也比较复杂,因此选课对他们而言还是一件新鲜而陌生的事物。
但大学的学习与选课有莫大的关系,必须了解它,才能掌握主动权。
而要了解选课制,首先要对大学的课程设置有所认识。
大学的课程按大类来说一般分为必修课和选修课。
必修一般指学校或院系规定学生必须修习某课程,学校对必修课程一般有统一的要求和安排。
选修是指根据学生个人兴趣或专业需要自由选择修习某课程。
简言之,必修就是必须修读,选修就是选择性修读。
一般来说,基础性的知识都作为必修课程。
有些知识不是基础性的,与兴趣和研究方向有关,这部分知识可以选择。
这是大学与中学最大的不同之处。
本文针对关于大学生选课时所需要考虑到的问题,根据学校规定的要求达到的学分与每门课的学分多少,运用排列组合的知识建立模型,通过分析输出各种情况下所需的选课方案关键字:matlab,矩阵,排列组合二.问题重述某同学考虑下学期的选课,其中必修课只有一门(2学分),可供选修的限定选修课(限选课)有8门,任意选修课(任选课)有10门。
由于有些课程之间相按学校规定,学生每个学期选修的总学分数不能少于20学分,因此该同学必须在上述18门课中至少选修18个学分,学校还规定学生每学期选修任选课的比例不能少于所修总学分(包括2个必修学分)的1/6,也不能超过所修总学分的1/3。
学院也规定,课号为5,6,7,8的课程必须至少选一门。
1)为了达到学校和院系的规定,该同学下学期最少应该选几门课?应该选哪几门课?2)若考虑在选修最少学分的情况下,该同学最多可以选修几门课?选哪几门?三.模型假设(1)学生选修任何课程都是随机的,不存在主观意图。
实际生活中选课程是有主观意图的,但是本问题中不考虑这一点。

1.问题提出对于问题一,我们必须考虑在学校和院系的规定的条件下对同学选课最少进行求解。
所以我们先从已知条件入手,把他们转化为约束条件,然后建立0-1整数优化模型,利用LINGO软件对其进行求解。
对于问题二,我们同样考虑在选修学分最少的情况下对同学选课最多进行求解。
但两者不能同时都满足,所以我们必须把这个双优化模型转化为单优化模型,然后再利用LINGO对其进行求解。
问题三则是考虑了选修课程限选人数的问题,所以必须针对不同的学生类型设计相应的选择方案。
同时考虑到选修的课程能否如愿选上,需要在已只知不同课程限选人数的情况下,利用对不同目标加权的方法对问题进行优化。
2符号说明与模型假设2.1符号说明表2:符号说明表注:其它符号在文中另加说明2.2模型假设(1):各个同学在选修课程时不受其他因素影响,只受学分和选修课程门数影响。
(2):学生选课是独立的,相互之间不影响。
(3):选课的学生有两种类型,一类是对这门课真正感兴趣的,另一类是“混学分”的,且这两类各占选课学生人数的一半。
(4):学生的信息是不公开的。
(5):问题三中没有提到的课程表示人数没有限制。
3模型建立和求解3.1问题一的解决3.1.1模型的建立用xi表示选修表中按照编号顺序的18门课程的选择(i=1,2,…18),其中xi 取值为1或者0。
其定义如下:采用目标规划的方法,考虑到学校的各种约束条件,将约束条件用数学表达式表示为一下几点:1:要使选修课程的总学分数不少于18,既有下面的不等式:2:任选课程的比例不能少于所修总学分的1/6,也不能超过1/3:3:课程号为5、6、7、8的课程必须至少选一门:4:选修某些课程必须同时选修其他课程,可以表示为:在达到以上要求的情况下,只考虑选修课程最少的情况,相应的目标函数为:在Lingo[1]中可以对该目标函数进行优化,其中约束条件为①②③④,由于上述条件中有大于关系,可以在两边乘以—1将约束条件全部转换成小于关系,这样便于在Lingo中求解.最后本文建立了如下的优化模型3.1.2模型的求解利用LINGO软件求解可以得到3.1.3问题一的结果最后本文得到了在学校和院系的要求下选课最少是选五门,选择方案是选择课程1,2,6,10,14。

提高学生数学建模水平的教学策略在当今的教育环境中,培养学生的数学建模能力愈发重要。
数学建模不仅能够帮助学生更好地理解和应用数学知识,还能提升他们解决实际问题的能力和创新思维。
那么,如何提高学生的数学建模水平呢?以下是一些有效的教学策略。
一、激发学生的兴趣和积极性兴趣是最好的老师。
要提高学生的数学建模水平,首先要让他们对数学建模产生兴趣。
教师可以通过引入生动有趣的实际问题,如日常生活中的购物优惠计算、交通流量预测等,让学生感受到数学建模的实用性和趣味性。
同时,可以讲述一些数学建模在科学研究、工程技术等领域的成功应用案例,激发学生的好奇心和探索欲望。
例如,在讲解函数的概念时,可以以手机话费套餐的选择为例。
不同的套餐有不同的收费标准,让学生通过建立函数模型来分析哪种套餐更适合自己的通话和上网需求。
这样的例子贴近生活,能够让学生迅速进入建模的情境,从而提高他们的参与度和积极性。
二、夯实数学基础知识扎实的数学基础知识是进行数学建模的前提。
学生需要熟练掌握代数、几何、概率统计等方面的知识,才能在建模过程中灵活运用。
教师在教学中要注重知识的系统性和连贯性,帮助学生构建完整的数学知识体系。
比如,在学习线性规划问题时,学生需要掌握二元一次不等式组、直线的方程等基础知识。
教师可以通过有针对性的练习和讲解,让学生熟练掌握这些知识,为后续的建模活动打下坚实的基础。
三、培养学生的问题转化能力数学建模的关键在于将实际问题转化为数学问题。
教师要引导学生学会分析问题,提取关键信息,建立数学模型。
这需要培养学生的观察能力、逻辑思维能力和抽象概括能力。
以一个工厂生产安排的问题为例,教师可以引导学生思考:如何用数学语言描述生产过程中的限制条件(如原材料供应、设备工时、市场需求等)?如何定义目标函数(如利润最大化、成本最小化等)?通过这样的引导,让学生逐步掌握将实际问题转化为数学模型的方法。
四、开展小组合作学习小组合作学习在数学建模教学中具有重要作用。
选课问题声明:本人自做,仅作参考,不得商用,责任自负。
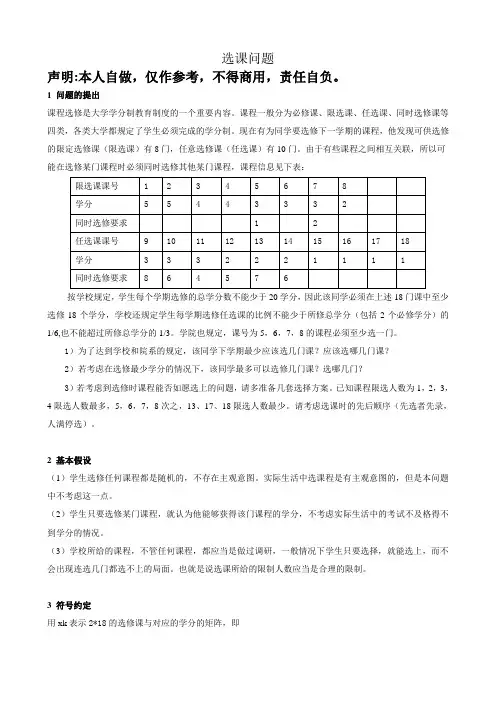
1 问题的提出课程选修是大学学分制教育制度的一个重要内容。
课程一般分为必修课、限选课、任选课、同时选修课等四类,各类大学都规定了学生必须完成的学分制。
现在有为同学要选修下一学期的课程,他发现可供选修的限定选修课(限选课)有8门,任意选修课(任选课)有10门。
由于有些课程之间相互关联,所以可能在选修某门课程时必须同时选修其他某门课程,课程信息见下表:按学校规定,学生每个学期选修的总学分数不能少于20学分,因此该同学必须在上述18门课中至少选修18个学分,学校还规定学生每学期选修任选课的比例不能少于所修总学分(包括2个必修学分)的1/6,也不能超过所修总学分的1/3。
学院也规定,课号为5,6,7,8的课程必须至少选一门。
1)为了达到学校和院系的规定,该同学下学期最少应该选几门课?应该选哪几门课?2)若考虑在选修最少学分的情况下,该同学最多可以选修几门课?选哪几门?3)若考虑到选修时课程能否如愿选上的问题,请多准备几套选择方案。
已知课程限选人数为1,2,3,4限选人数最多,5,6,7,8次之,13、17、18限选人数最少。
请考虑选课时的先后顺序(先选者先录,人满停选)。
2 基本假设(1)学生选修任何课程都是随机的,不存在主观意图。
实际生活中选课程是有主观意图的,但是本问题中不考虑这一点。
(2)学生只要选修某门课程,就认为他能够获得该门课程的学分,不考虑实际生活中的考试不及格得不到学分的情况。
(3)学校所给的课程,不管任何课程,都应当是做过调研,一般情况下学生只要选择,就能选上,而不会出现连选几门都选不上的局面。
也就是说选课所给的限制人数应当是合理的限制。
3 符号约定用xk表示2*18的选修课与对应的学分的矩阵,即⎥⎦⎤⎢⎣⎡111122233323334455181716151413121110987654321 用xk ()j i ,表示第i 行第j 列交叉点的元素。

数学建模论文题目生活中的数学建模问题学院理学院专业班级数学 111 班学生姓名张妍成绩2013年12月1 日摘要在日常生活中,我们会遇到各种各样的问题,其实许多问题都可以运用数学建模的知识来解决。
平时老师分派给我们任务时,为了尽快的去完成,我们同学之间分工合作,这就可以建立模型求解。
本文就是利用建立数学模型来解决生活中的几个实际问题。
其基本依据是建立数学模型,用LINGO软件来求解。
关键词:最优解,策略,LINGO正文模型1:给教室刷墙问题(目标规划)在校庆来临之前,学校准备给教室粉刷墙壁,现有3种类型的教室,分别用A,B,C 来表示3种不同的教室,具体相关数据如表所示。
某班同学承担了该任务,每天工作8小时,试问在一个星期内该班同学获得的最大利润。
基本模型如果用x1,x2,x3分别表示A,B,C三种教室粉刷的个数,一星期正常生产工时为56小时,则问题可以归结为下面的数序模型目标函数max=30*x1+50*x2+70*x3;约束条件x1<=30;x2<=20;x3<=10;2*x1+1.5*x2+x3<=56;x1>=0;x2>=0;x3>=0;模型求解max=30*x1+50*x2+70*x3;x1<=30;x2<=20;x3<=10;2*x1+1.5*x2+x3<=56;x1>=0;x2>=0;x3>=0;输入LINGO软件求得最优解如下:Optimal solution found at step: 0Objective value: 1940.000Variable Value Reduced CostX1 8.000000 0.0000000X2 20.00000 0.0000000X3 10.00000 0.0000000Row Slack or Surplus Dual Price1 1940.000 1.0000002 22.00000 0.00000003 0.0000000 27.500004 0.0000000 55.000005 0.0000000 15.000006 8.000000 0.00000007 20.00000 0.00000008 10.00000 0.0000000最优解由LINGO计算得到该班同学粉刷8间A教室,20间B教室,10间C教室获得的利润最大,最大利润为1940元。

数学建模案例_选修课问题某学校对某年级开设9门选修课,这些选修课之间可能存在学习先后顺序。
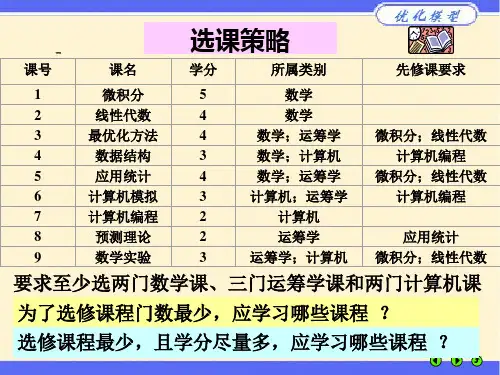
学校要求毕业前至少选两门数学课、三门运筹学课和两门计算机课。
在符合学校要求的条件下,考虑以下问题:(1)为了选修课程门数最少,应学习哪些课程?(2)选修课程少,且学分尽量多,应学习哪些课程?选修课程和限制条件如下:问题(1)分析:目标:最少的选课门数决策: 对是否选修某门课做出决策,选或不选.符号说明:对应9个0-1变量,设为i x ,选修第i 门课则取值为1,不选则取值为0.建立数学模型:目标函数明确为∑=91i i x min描述约束(翻译—建模)至少选两门数学课⇔254321≥++++x x x x x至少选三门运筹学课程⇔398653≥++++x x x x x至少选两门计算机课⇔29764≥+++x x x x最优化方法3的先修课程是微积分1⇔13x x ≤最优化方法3的先修课程是线性代数23x x ≤数据结构4的先修课程是计算机编程7⇔74x x ≤应用统计5的先修课程是微积分1,线性代数2;⇔1525,x x x x ≤≤ 计算机模拟6的先修课程是计算机编程7;⇔76x x ≤预测理论8的先修课程是应用统计5;⇔58x x ≤数学实验9的先修课程是微积分1和线性代数2;⇔1929,x x x x ≤≤第一问的数学模型:∑=91min i i x254321≥++++x x x x x398653≥++++x x x x x29764≥+++x x x x13x x ≤,23x x ≤,74x x ≤ 1525,x x x x ≤≤ 76x x ≤58x x ≤ 1929,x x x x ≤≤}1,0{∈i x使用lingo求解:model:sets:kecheng/1..9/:c,x; !c代表学分属性,x代表选或不选决策; endsetsdata:c=5 4 4 3 4 3 2 2 3;enddatamin=@sum(kecheng(i):x(i));x(1)+x(2)+x(3)+x(4)+x(5)>=2;x(3)+x(5)+x(6)+x(8)+x(9)>=3;x(4)+x(6)+x(7)+x(9)>=2;x(3)<=x(1);x(3)<=x(2);x(4)<=x(7);x(5)<=x(1);x(5)<=x(2);x(6)<=x(7);x(8)<=x(5);x(9)<=x(1);x(9)<=x(2);@for(kecheng(i):@bin(x(i)));zongfen=@sum(kecheng(i):c(i)*x(i));!zongfen代表此策略下总学分;end结果解释:满足所有选课限制条件的选课门数最少为6门(但不一定唯一),分别是第1,2,3,6,7,9门课;此时总学分21分。
数学建模与应用3规划模型的典型例题(1) 平板装货问题有七种规格的包装箱要装到两辆平板车上。
包装箱的宽和高是一样的,但厚度t (厘米)和重量w (公斤)是不同的。
下表给出了每种包装箱的厚度,重量以及数量。
每辆平板车有10.2米的地方可用来装包装箱(象面包片那样),载重为40吨。
由于地区货运的限制,对C5, C6, C7类包装箱的总数有一个特别的限制:这三类包装箱所占空间(厚度)不能超过302.7厘米。
问题要求:设计一种装车方案,使剩余的空间最小。
•首先找到已知的参量o各类型的包装的厚度: \small t_i(i=1\dots7) 。
o各类型的包装的重量: \small w_i(i=1\dots7) 。
o各类型包装的件数: \small n_i(i=1\dots7) 。
o平板车的空间: \small Space=1020cm 。
o平板车的载重: \small Weight=40000kg 。
o三类包装箱所占的空间上限: \smallLimit=302.7 。
•设出需要使用的变量:o第一辆车上装载的各类型包装的数量: \smallx_i(i=1\dots7)o第二辆车上装载的各类型包装的数量: \smally_i(i=1\dots7)•明确问题的要求:\min\{2\times Space-\displaystyle\sum^{7}_{i=1}t_ix_i- \displaystyle\sum^{7}_{i=1}t_iy_i\}\\x_i+y_i\leq n_i(i=1\dots7)\\ ~~\\ \displaystyle\sum^{7}_{i=1}w_i(x_i+y_i)\leq40000\\ ~~\\\displaystyle \sum^{7}_{i=1}t_ix_i\leq1020\\ ~~\\\displaystyle \sum^{7}_{i=1}t_iy_i\leq1020\\ ~~\\\displaystyle \sum^{7}_{i=5}t_i(x_i+y_i)\leq302.7\\\displaystyle \sum^{7}_{i=1}w_i(x_i+y_i)\leq40000\\\displaystyle \sum^{7}_{i=1}t_ix_i\leq1020\\\displaystyle \sum^{7}_{i=1}t_iy_i\leq1020\\\displaystyle \sum^{7}_{i=5}t_i(x_i+y_i)\leq302.7\\model:!程序由model开始,由end结束;sets:!sets开始设置变量,endsets结束变量设置;num/1..7/:t,w,n,x,y;!定义5个数组分别为t,w,n,x,yendsetsdata:!数据设置由data开始,由enddata结束;t=48.7,52.0,61.3,72.0,48.7,52.0,64.0;w=2000,3000,10 00,500,4000,2000,1000;n=8,7,9,6,6,4,8;enddatamin=(1020 -@sum(num:t*x))+(1020-@sum(num:t*y));!说明需要优化的为min;!以下是进行条件限制的量@sum(num:t*x)<=1020;@sum(num:t*y)<=1020;@sum(num:w*x)< =40000;@sum(num:w*y)<=40000;@for(num(i):x(i)+y(i)<=n(i ));@sum(num(i)|i#ge#5#and#i#le#7:(x(i)+y(i))*t(i))<=30 2.7;@for(num:@gin(x));@for(num:@gin(y));end(2) 选修课策略问题某学校规定,运筹学专业的学生毕业时必须至少学习过两门数学课、三门运筹学课和两门计算机课。
数学建模选修课策略
数学建模选修课的策略主要包括以下几个方面:
建立模型:首先,需要对实际问题进行深入理解,将其转化为数学模型。
这需要一定的数学基础和建模技巧,如概率论、统计学、线性代数等。
参数估计与调整:在建立模型后,需要根据实际数据对模型中的参数进行估计和调整,以使模型更好地拟合实际数据。
模型验证:在参数估计和调整后,需要对模型的预测能力和准确性进行验证。
这可以通过对比模型的预测结果和实际数据来进行。
优化模型:如果模型的预测结果和实际数据存在较大差异,需要对模型进行优化,以改进其预测能力和准确性。
这可能需要引入新的变量、改进模型结构或使用更复杂的模型。
应用模型:最后,可以将优化后的模型应用于实际问题中,以解决实际问题。
这可能需要一定的编程技能和对实际问题的深入理解。
以上是数学建模的一般步骤,具体实施时可以根据实际情况进行调整。
同时,数学建模也需要一定的实践经验,只有通过不断的实践才能提高建模能力和技巧。
数学建模的基本方法与策略总结数学建模是将实际问题抽象为数学模型,并利用数学方法对该模型进行分析和求解的过程。
在实际应用中,数学建模是解决问题、预测趋势和优化决策的有效工具。
本文将对数学建模的基本方法与策略进行总结,以帮助读者更好地理解和应用数学建模。
一、问题的理解与定义数学建模的第一步是充分理解和定义问题。
这包括对问题的背景、目标、限制条件和需求进行详细的分析。
通过对问题的深入了解,可以明确问题的关键变量和参数,为后续的建模过程提供基础。
二、问题的建模和抽象在对问题进行全面理解后,接下来是将问题抽象为数学模型。
数学模型应能准确描述问题的关键要素和关联关系,以便进行后续的数学分析。
常用的数学模型包括线性模型、非线性模型、随机模型等。
合适的模型选择与问题类型密切相关,需要根据具体情况进行判断。
三、数据的收集和处理在建立数学模型之前,需要对问题所涉及的数据进行收集和处理。
数据的质量和可靠性直接影响模型的准确性和可行性。
收集到的数据可以来自于实验、调查、统计等渠道。
在处理数据时,可以使用数据平滑、插值、拟合等方法,以消除数据中的噪声和误差,提高模型的精度。
四、模型的求解与分析根据建立的模型,使用适当的数学方法对模型进行求解和分析。
常用的方法包括解析解法、数值解法、优化算法等。
求解的结果应进行合理性和可行性的验证,以确保模型的准确性和可靠性。
如果模型复杂,可以采用近似方法、计算机仿真等手段来求解。
五、模型的评价和优化在完成模型的求解后,需要对模型的效果进行评价和优化。
评价指标可以根据具体问题而定,如模型的拟合程度、稳定性、鲁棒性等。
如果模型不满足要求,可以对模型进行优化,例如调整参数、引入约束条件等,以获得更好的结果。
六、模型的推广与应用当得到满意的模型后,可以将其推广应用到实际问题中。
这需要将数学模型与实际问题相结合,并针对具体情况进行调整和改进。
在应用过程中,需要不断收集反馈信息,对模型进行修正和完善,以适应实际应用的需求。
实验05 数学规划模型㈡(2学时)(第4章数学规划模型)1.(求解)汽车厂生产计划(LP,整数规划IP)p101~102(1) (LP)在模型窗口中输入以下线性规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3≥ 0并求解模型。
★(1) 给出输入模型和求解结果(见[101]):(2) (IP)在模型窗口中输入以下整数规划模型max z = 2x1 + 3x2 + 4x3s.t. 1.5x1 + 3x2 + 5x3≤ 600280x1 + 250x2 + 400x3≤ 60000x1, x2, x3均为非负整数并求解模型。
LINGO函数@gin见提示。
★(2) 给出输入模型和求解结果(见[102]模型、结果):2.(求解)原油采购与加工(非线性规划NLP ,LP 且IP )p104~107模型:已知 ⎪⎩⎪⎨⎧≤≤+≤≤+≤≤=)15001000(63000)1000500(81000)5000(10)(x x x x x xx c注:当500 ≤ x ≤ 1000时,c (x ) = 10 × 500 + 8( x – 500 ) = (10 – 8 ) × 500 + 8x112112221112212211112112122211122122max 4.8() 5.6()()500100015000.50.6,,,,0z x x x x c x x x x x x x x x x x x x x x x x x =+++-+≤++≤≤≥+≥+≥2.1解法1(NLP )p104~106将模型变换为以下的非线性规划模型:1121122212311122122111121121222123122312311122122max4.8()5.6()(1086)50010000.50.6(500)0(500)00,,500,,,,0z x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x =+++-+++≤++≤≥+≥+=++-=-=≤≤≥LINGO 软件设置:局部最优解,全局最优解,见提示。
选课策略一、 问题描述对于上述课程,要求至少选两门数学课、三门运筹学课和两门计算机课。
试讨论: (1)为了选修课程门数最少,应学习哪些课程 ?(2)选修课程最少,且学分尽量多,应学习哪些课程 ?二、 问题分析设 xi =1为选修课号i 的课程,xi =0 不选该门课程。
约束条件:⑴ 最少2门数学课,3门运筹学课,2门计算机课:254321≥++++x x x x x ;398653≥++++x x x x x ;29764≥+++x x x x 。
⑵先修课程要求:02213≤--x x x ;02215≤--x x x ;074≤-x x ;076≤-x x ;058≤-x x ;02219≤--x x x 。
目标函数:选修课程门数:∑==91i ixZ ,学分:987654321322343445x x x x x x x x x W ++++++++=。
对于(1)要使选修课程门数最少,应使∑==91i i x Z Min;对于(2)要使选修课程最少且学分尽量多,应使∑==91i i x Z Min,987654321322343445x x x x x x x x x W Max ++++++++=。
课号课名 学分 所属类别先修课要求1 微积分 5 数学2 线性代数 4 数学3 最优化方法4 数学;运筹学 微积分;线性代数4 数据结构 3 数学;计算机 计算机编程5 应用统计 4 数学;运筹学 微积分;线性代数6 计算机模拟 3 计算机;运筹学计算机编程7 计算机编程 2 计算机 8 预测理论 2 运筹学应用统计9数学实验3运筹学;计算机微积分;线性代数三、问题求解(1)可利用mathematica8中的Minimize()函数进行线性规划求解:(代码)Minimize[x1+x2+x3+x4+x5+x6+x7+x8+x9,{x1==1||x1==0,x2==1||x2==0,x2==1||x2==0,x3==1| |x3==0,x4==1||x4==0,x5==1||x5==0,x6==1||x6==0,x7==1||x7==0,x8==1||x8==0,x9==1||x9==0,x 1+x2+x3+x4+x5>=2,x3+x5+x6+x8+x9>=3,x4+x6+x7+x9>=2,2x3-x2-x1<=0,2x5-x1-x2<=0,x4-x 7<=0,x6-x7<=0,x8-x5<=0,2x9-x1-x2<=0},{x1,x2,x3,x4,x5,x6,x7,x8,x9}]结果为故最优解: x1 = x2 = x3 = x6 = x7 = x9 =1, 其它为0。