中考数学总复习知识点梳理第23讲及圆有关计算含考点分类汇编详解.doc
- 格式:doc
- 大小:92.52 KB
- 文档页数:1


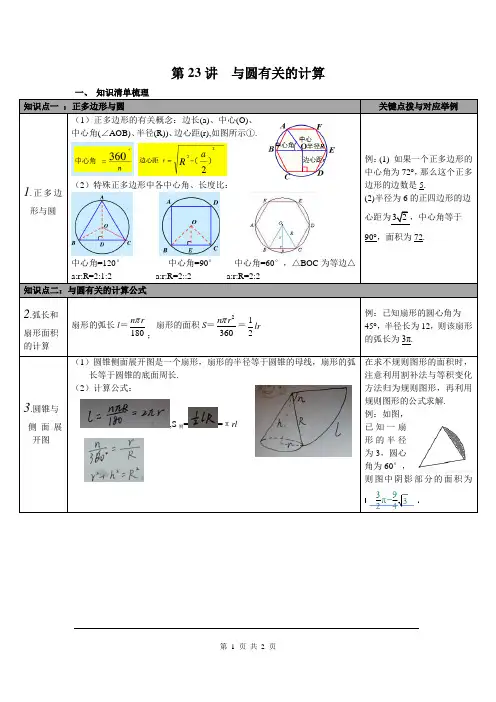
第23讲与圆有关的计算知识点一:正多边形与圆关键点拨与对应举例1.正多边形与圆(1)正多边形的有关概念:边长(a)、中心(O)、中心角(∠AOB)、半径(R))、边心距(r),如图所示①.(2)特殊正多边形中各中心角、长度比:中心角=120°中心角=90°中心角=60°,△BOC为等边△a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2例:(1) 如果一个正多边形的中心角为72°,那么这个正多边形的边数是5.(2)半径为6的正四边形的边心距为32,中心角等于90°,面积为72.知识点二:与圆有关的计算公式2.弧长和扇形面积的计算扇形的弧长l=180n rπ;扇形的面积S=2360n rπ=12lr例:已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为3π.3.圆锥与侧面展开图(1)圆锥侧面展开图是一个扇形,扇形的半径等于圆锥的母线,扇形的弧长等于圆锥的底面周长.(2)计算公式:,S侧==πrl在求不规则图形的面积时,注意利用割补法与等积变化方法归为规则图形,再利用规则图形的公式求解.例:如图,已知一扇形的半径为3,圆心角为60°,则图中阴影部分的面积为数学选择题解题技巧1、排除法。
是根据题设和有关知识,排除明显不正确选项,那么剩下唯一的选项,自然就是正确的选项,如果不能立即得到正确的选项,至少可以缩小选择范围,提高解题的准确率。
排除法是解选择题的间接方法,也是选择题的常用方法。
2、特殊值法。
即根据题目中的条件,选取某个符合条件的特殊值或作出特殊图形进行计算、推理的方法。
用特殊值法解题要注意所选取的值要符合条件,且易于计算。
此类问题通常具有一个共性:题干中给出一些一般性的条件,而要求得出某些特定的结论或数值。
在解决时可将问题提供的条件特殊化。
使之成为具有一般性的特殊图形或问题,而这些特殊图形或问题的答案往往就是原题的答案。


中考圆形知识点总结归纳圆形是中学数学中一个重要的几何概念,在中考中也是一个常见的考点。
本文将对中考中涉及到的圆形知识进行总结和归纳,帮助考生复习和掌握这一部分内容。
一、圆的基本概念圆是由平面上任意一点到另一点的距离都相等的点的集合。
其中,距离相等的这个固定值称为圆的半径,用字母r表示。
圆心是圆上任意两点的连线的垂直平分线的交点。
二、圆的性质1. 圆上任意两点之间的距离都等于圆的半径。
2. 圆心角的度数等于它所对的弧的度数,且圆心角所对的弧长等于圆的半径乘以圆心角的弧度值。
3. 相等弧所对的圆心角是相等的。
4. 圆的内切正多边形的中心与圆心重合。
三、弧1. 圆周角:圆周角是指以圆心为顶点的角,它的两边是相交于圆上的两条弧。
圆周角的度数等于它所对的弧的度数。
2. 弦:圆内部连接两点的线段称为弦。
弦分割出的两条弧叫做弦所对的弧。
3. 弧长:指圆上的一段弧所对应的圆周长度。
弧长等于圆心角的弧度值乘以圆的半径。
四、相交弦与切线的性质1. 相交弦定理:相交弦所对的弧相等,或者说两个相交弦所对应的圆心角相等。
2. 切线的性质:切线与半径的垂直分割线。
切线于半径的交点处所对应的圆心角为直角。
五、圆的面积和周长1. 圆的面积公式:S = πr²,其中S为圆的面积,r为圆的半径,π取近似值3.14。
2. 圆的周长公式:C = 2πr,其中C为圆的周长。
六、圆的应用1. 圆的切线与圆的性质:切线与切点间的弦相等,切线切割出的小圆与大圆相似。
2. 弧长与扇形面积:扇形面积等于扇形所对的圆心角的弧长所占整个圆的比例乘以圆的面积。
总结:通过对中考圆形知识点的总结和归纳,我们可以看到,圆形在中考中的考点比较多,涉及到圆的基本概念、性质、弧、相交弦与切线的性质、面积和周长以及应用等方面的内容。
对于考生而言,要牢固掌握圆的基本概念和性质,熟练运用相关公式和定理,灵活应用于解题过程中。
只有通过不断的实践和练习,才能在考试中熟练运用所学的圆形知识,取得好的成绩。


第23讲《圆的基本性质》要点梳理知识点1:主要概念1.圆:平面上到____的距离等于____的所有点组成的图形叫做圆.____叫做圆心,____叫做半径,以O为圆心的圆记作⊙O.2.弧和弦:圆上任意两点间的部分叫做___,连接圆上任意两点的线段叫做___,经过圆心的弦叫做直径,直径是最长的___.3.圆心角:顶点在____,角的两边与圆相交的角叫做圆心角.4.圆周角:顶点在____,角的两边与圆相交的角叫做圆周角.5.等弧:在__________中,能够完全____的弧叫做等弧.知识点2:圆的有关性质1.圆的对称性:①圆是______图形,其对称轴是________________.②圆是________图形,对称中心是_____.③旋转不变性,即圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.知识点3:垂径定理及推论1.垂径定理:垂直于弦的直径_______,并且____________________.2.垂径定理的推论:①平分弦(不是直径)的直径_________,并且_____________________;②弦的垂直平分线_______,并且平分弦所对的两条弧;③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.知识点4:弦、弧、圆心角的关系定理及推论①弦、弧、圆心角的关系:在同圆或等圆中,相等的圆心角所对的弧_____,所对的弦______.②推论:在同圆或等圆中,如果两个______、______、_______、__________中有一组量相等,那么它们所对应的其余各组量都分别相等.知识点5:圆周角定理及推论1.圆周角定理:一条弧所对的圆周角等于它所对圆心角的________.2.圆周角定理的推论:①同弧或等弧所对的圆周角相等;同圆或等圆中相等的圆周角所对的弧______.②半圆(或直径)所对的圆周角是_____;90°的圆周角所对的弦是_____.知识点6:点和圆的位置关系①点P在圆上⇔_______;②点P在圆内⇔______;③点P在圆外⇔_______.知识点7:过三点的圆①经过不在同一直线上的三点,有且只有一个圆.②经过三角形各顶点的圆叫做三角形的外接圆;外接圆的圆心叫做三角形的外心;三角形的外心是三边___________的交点,这个三角形叫做这个圆的内接三角形.锐角三角形的外心在三角形内部;直角三角形的外心在斜边中点处;钝角三角形的外心在三角形的外部.知识点8:圆内接四边形圆内接四边形的对角________常见的辅助线(1)有关弦的问题,如图1,常作其弦心距,构造以半径、弦的一半、弦心距为边的直角三角形,利用勾股定理知识求解;(2)有关直径的问题,如图2,常通过辅助线构造直径所对的圆周角是直角来进行证明或计算.(3)有等弧或证弧相等时,如图3,常连等弧所对的弦或作等(同)弧所对的圆周(心)角.图1 图2 图3命题点1:垂径定理1.(泸州)如图,AB是⊙O的直径,弦CD⊥AB于点E。




专题23 圆考点总结【思维导图】【知识要点】知识点一与圆有关的概念圆的概念:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆.这个固定的端点O叫做圆心,线段OA叫做半径.以O点为圆心的圆记作⊙O,读作圆O.特点:圆是在一个平面内,所有到一个定点的距离等于定长的点组成的图形.确定圆的条件:⑴圆心;⑵半径,⑶其中圆心确定圆的位置,半径长确定圆的大小.补充知识:1)圆心相同且半径相等的圆叫做同圆;2)圆心相同,半径不相等的两个圆叫做同心圆;3)半径相等的圆叫做等圆.弦的概念:连结圆上任意两点的线段叫做弦。
经过圆心的弦叫做直径,并且直径是同一圆中最长的弦.⏜,读作弧AB.在同圆或等弧的概念:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作AB圆中,能够重合的弧叫做等弧.圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.在一个圆中大于半圆的弧叫做优弧, 小于半圆的弧叫做劣弧.弦心距概念:从圆心到弦的距离叫做弦心距. 弦心距、半径、弦长的关系:(考点)圆心角概念:顶点在圆心的角叫做圆心角.圆周角概念:顶点在圆上,并且两边都和圆相交的角叫做圆周角. 三角形的外接圆1)经过三角形三个顶点的圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心,这个三角形叫做这个圆的内接三角形. 2)三角形外心的性质:①三角形的外心是指外接圆的圆心,它是三角形三边垂直平分线的交点,它到三角形各顶点的距离相等; ②三角形的外接圆有且只有一个,即对于给定的三角形,其外心是唯一的,但一个圆的内接三角形却有无数个,这些三角形的外心重合.3)锐角三角形外接圆的圆心在它的内部(如图1);直角三角形外接圆的圆心在斜边中点处(即直角三角形外接圆半径等于斜边的一半,如图2);钝角三角形外接圆的圆心在它的外部(如图3).圆内接四边形概念:如果一个四边形的所有顶点都在一个圆上,那么这个四边形叫做圆内接四边形。
第23讲与圆相关的计算
一、知识清单梳理
知识点一:正多边形与圆重点点拨与对应举例
(1)正多边形的相关观点 :
边长(a)、中心(O)、中心角
(∠AOB)、半径(R))、边心
距(r),如下图①.
(2)特别正多边形中各中心角、长度比: 例:(1)假如一个正多边形的中心角
1. 正
为72°,那么这个正多边形的边数是多边
5.
形与
(2)半径为6的正四边形的边心距为圆
32,中心角等于90°,面积为72.
中心角=120°中心角=90°
中心角=60°,△BOC为等边△
a:r:R=2:1:2 a:r:R=2::2
a:r:R=2:2
知识点二:与圆相关的计算公式
2
.弧
扇形的面积S=nr2
扇形的弧长l=nr
长和180;360例:已知扇形的圆心角为45°,半径
扇形=1lr
]长为12,则该扇形的弧长为3π.
2面积
的计
算
(1)圆锥侧面睁开图是一个扇形,扇形的在求不规则图形的面积时,注意利用半径等于圆锥的割补法与等积变化方法归为规则图
3.圆母线,扇形的弧长形,再利
用规则图形的
锥等于圆锥的底面公式求解.
与周长.例:如
图,已知一扇
侧面(2)计算公式:形的半
径为3,圆心
睁
开角为60°,则图中暗影部分的面积为图
,S侧==πrl。
2019-2020 年中考数学总复习知识点梳理:第23 讲与圆有关的计算含考点分
类汇编详解
一、知识清单梳理
知识点一:正多边形与圆
( 1)正多边形的有关概念:边长(a)、中心 (O) 、
中心角 (∠AOB) 、半径 (R)) 、边心距 (r), 如图所示① .
( 2)特殊正多边形中各中心角、长度比:
1.正多边
形与圆
中心角 =120 °中心角 =90°中心角 =60°,△ BOC 为等边△
a:r:R=2:1:2 a:r:R=2::2 a:r:R=2:2
知识点二:与圆有关的计算公式
2.弧长和
扇形的弧长 l=n r
扇形的面积 S=
n r 2
=
1
lr
扇形面积180 ;360 2
的计算
(1)圆锥侧面展开图是一个扇形,扇形的半径等于圆锥的母线,扇形的弧长等于圆锥的底面周长 .
(2)计算公式:
3
.圆锥与
侧面展,S 侧 = =π rl
开图
关键点拨与对应举例
例:(1) 如果一个正多边形的中心角为72°,那么这个正多边形的边数是 5.
(2)半径为 6 的正四边形的边心距为 3 2 ,中心角等于90°,面积为 72.
例:已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为3π.
在求不规则图形的面积时,
注意利用割补法与等积变化
方法归为规则图形,再利用
规则图形的公式求解 .
例:如图,
已知一扇
形的半径
为3,圆心
角为 60°,
则图中阴影部分的面积为。