104990_三角函数复习_万金圣[1]
- 格式:ppt
- 大小:749.50 KB
- 文档页数:23

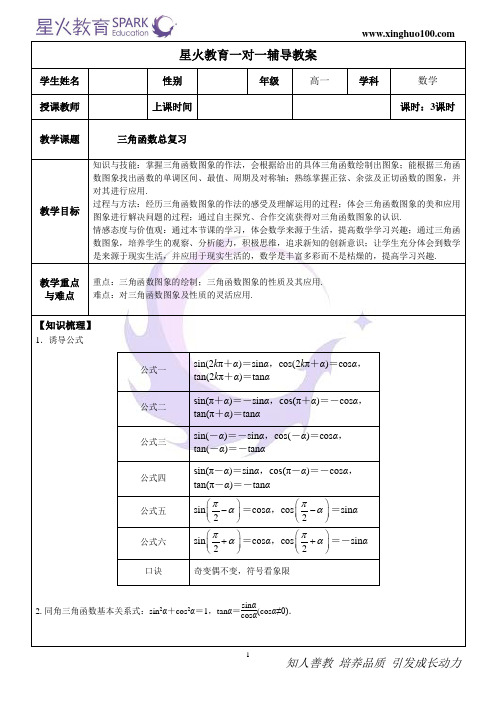
星火教育一对一辅导教案学生姓名 性别 年级 高一学科 数学 授课教师上课时间课时:3课时教学课题三角函数总复习教学目标知识与技能:掌握三角函数图象的作法,会根据给出的具体三角函数绘制出图象;能根据三角函数图象找出函数的单调区间、最值、周期及对称轴;熟练掌握正弦、余弦及正切函数的图象,并对其进行应用.过程与方法:经历三角函数图象的作法的感受及理解运用的过程;体会三角函数图象的美和应用图象进行解决问题的过程;通过自主探究、合作交流获得对三角函数图象的认识.情感态度与价值观:通过本节课的学习,体会数学来源于生活,提高数学学习兴趣;通过三角函数图象,培养学生的观察、分析能力,积极思维,追求新知的创新意识;让学生充分体会到数学是来源于现实生活,并应用于现实生活的,数学是丰富多彩而不是枯燥的,提高学习兴趣. 教学重点与难点重点:三角函数图象的绘制;三角函数图象的性质及其应用. 难点:对三角函数图象及性质的灵活应用.【知识梳理】1.诱导公式公式一sin(2k π+α)=sin α,cos(2k π+α)=cos α, tan(2k π+α)=tan α公式二sin(π+α)=-sin α,cos(π+α)=-cos α, tan(π+α)=tan α公式三sin(-α)=-sin α,cos(-α)=cos α, tan(-α)=-tan α公式四sin(π-α)=sin α,cos(π-α)=-cos α, tan(π-α)=-tan α公式五sin 2πα⎛⎫- ⎪⎝⎭=cos α,cos 2πα⎛⎫- ⎪⎝⎭=sin α 公式六 sin 2πα⎛⎫+ ⎪⎝⎭=cos α,cos 2πα⎛⎫+ ⎪⎝⎭=-sin α 口诀奇变偶不变,符号看象限2.同角三角函数基本关系式:sin 2α+cos 2α=1,tan α=sin αcos α(cos α≠0).3.正弦、余弦、正切函数的性质函数y =sin xy =cos xy =tan x单调性在[-π2+2k π,π2+2k π](k ∈Z )上递增在[π2+2k π,3π2+2k π](k ∈Z )上递减 在[-π+2k π,2k π](k ∈Z )上递增. 在[2k π,π+2k π](k ∈Z )上递减在(-π2+k π,π2+k π)(k ∈Z )上递增最值当x =π2+2k π,k ∈Z 时,y 取得最大值1.当x =-π2+2k π,k ∈Z 时,y 取得最小值-1当x =2k π,k ∈Z 时,y 取得最大值1. 当x =π+2k π,k ∈Z 时,y 取得最小值-1无最值对称性对称中心:(k π,0)(k ∈Z ).对称轴:x =π2+k π(k ∈Z )对称中心:(π2+k π,0)(k ∈Z ). 对称轴:x =k π(k ∈Z )对称中心:(k π2,0)(k ∈Z )4.)0(cos sin ≠+ab x b x a 变形为)sin(ϕ+x A 或者)cos(ϕ+x A 的形式,例如:22222222sin cos (sin cos )sin()a ba xb x a b x x a b a ba b x ϕ+=++++=++;其中辅助角ϕ由⎪⎪⎩⎪⎪⎨⎧+=+=2222sin cos b a b b a a ϕϕ确定,即辅助角ϕ的终边经过点(,)a b5.函数y =A sin(ωx +φ)的图象 (1)“五点法”作图设z =ωx +φ,令z =0、π2、π、3π2、2π,求出x 的值与相应的y 的值,描点连线可得.注意:1.正确区分正弦函数、余弦函数的奇偶性、单调区间、对称轴、对称中心. 2.先平移与先伸缩变换的区别.【典型例题】考点1.三角函数的图象变换【例1】已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2,x ∈R )的图象的一部分如图所示,则函数f (x )的解析式为________.【变式1】函数f(x )=Asin(ωx +φ)(其中A>0,ω>0,|φ|<)的图象如图所示,为了得到g(x)=sin3x 的图象,则只要将f(x)的图象( )A .向右平移π4个单位长度 B.向右平移π12个单位长度C.向左平移π4个单位长度D.向左平移π12个单位长度【变式2】已知函数f (x )=sin(ωx +φ)的部分图象如图所示,则f (π2)=( )A.-32 B .-22 C.32 D.22[方法规律总结]1.已知正弦型(或余弦型)函数的图象求其解析式时,用待定系数法求解.由图中的最大值或最小值确定A ,再由周期确定ω,由图象上特殊点的坐标来确定φ,只有限定φ的取值范围,才能得出唯一解,否则φ的值不确定,解析式也就不唯一.将点的坐标代入解析式时,要注意选择的点属于“五点法”中的哪一个点.“第一点”(即图象上升时与x 轴的交点)为ωx0+φ=0+2kπ(k ∈Z),其他依次类推即可.2.解答有关平移伸缩变换的题目时,向左(或右)平移m 个单位时,用x +m (或x -m )代替x ,向下(或上)平移n 个单位时,用y +n (或y -n )代替y ,横(或纵)坐标伸长或缩短到原来的k 倍,用x k 代替x (或yk 代替y ),即可获解.考点2.三角函数的性质【例2】已知函数f (x )=2-(3sin x -cos x )2. (1)求f (π4)的值和f (x )的最小正周期;(2)求函数f (x )在区间[-π6,π3]上的最大值和最小值.【变式1】已知函数f (x )=2sin(x +5π24)cos(x +5π24)-2cos 2(x +5π24)+1. (1)求f (x )的最小正周期; (2)求函数f (x )的单调递增区间.【变式2】已知f (x )=2sin(x -π4)cos(x -π4)+23cos 2(x -π4).(1)求f (x )的最大值及取到最大值时相应的x 的集合;(2)若函数y =f (x )-m 在区间[0,π2]上恰好有两个零点,求实数m 的取值范围.[方法规律总结]1.解答三角函数性质(单调性、周期性、最值等)问题时,通常是利用三角函数的有关公式,通过将三角函数化为只含一个函数名称且角度唯一,最高次数为一次(一角一函)的形式,再依正(余)弦型函数依次对所求问题作出解答.2.求三角函数的最值的方法: (1)化为正弦(余弦)型函数y =asinωx +bcosωx 型引入辅助角化为一角一函. (2)化为关于sinx(或cosx)的二次函数.考点3.数学思想方法在三角函数中的应用【例3】已知函数f (x )=2a sin(2x -π3)+b 的定义域为[0,π2],函数的最大值为1,最小值为-5,求a 和b 的值.【变式1】 已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)在一个周期内的图象如图所示.(1)求函数f (x )的解析式;(2)设0<x <π,且方程f (x )=m 有两个不同的实根根,求实数m 的取值范围以及这两个根的和.[方法规律总结]1.形如直线的斜率、直线的方程、圆与圆锥曲线方程形式的代数式或等式可考虑以形助数. 2.复数、向量中的最值问题或与模有关的问题常借助图形分析.3.三角函数问题中,求参数的取值范围(或恒成立)问题,图形的最高(低)点及对称,与其他曲线的交点等,常借助图象寻找关系.【练习巩固】1.下列四个函数中,以π为最小正周期,且在区间(π2,π)上为减函数的是( )A .y =sin2xB .y =2|cos x |C .y =cos x2 D .y =tan(-x )2.如果sin α=45,那么sin(α+π4)-22cos α等于( )A.225 B .-225 C.425 D .-4253.已知α∈R ,sin α+2cos α=102,则tan2α=( ) A.43 B.34 C .-34 D .-434.为了得到函数y =sin3x +cos3x 的图像,可以将函数y =2sin3x 的图像( ) A .向右平移π4个单位B .向左平移π4个单位C .向右平移π12个单位D .向左平移π12个单位5.将函数y =sin x 的图象向左平移π2个单位,得到函数y =f (x )的图象,则下列说法正确的是( )A .y =f (x )是奇函数B .y =f (x )的周期为πC .y =f (x )的图象关于直线x =π2对称D .y =f (x )的图象关于点(-π2,0)对称6.函数f (x )=sin(2x -π4)在区间[0,π2]上的最小值为( )A .-1B .-22 C.22D .0 7.用“五点法”画函数f (x )=A sin(ωx +φ)的简图时,若所得五个点的横坐标从小到大依次为x 1、x 2、x 3、x 4、x 5且x 1+x 5=3π2,则x 2+x 4( )A.π2 B .π C.3π2D .2π 8.设0<θ<π2,向量a =(sin2θ,cos θ),b =(1,-cos θ),若a ·b =0,则tan θ=________.9.函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图象如图所示,则f (x )=________.10.如果两个函数的图象平移后能够重合,那么称这两个函数为“互为生成”函数.给出下列四个函数: ①f (x )=sin x +cos x; ②f (x )=2(sin x +cos x );③f (x )=sin x; ④f (x )=2sin x + 2. 其中为“互为生成”函数的是________(填序号). 11.已知函数f (x )=(2cos 2 x -1)sin2x +12cos 4x .(1)求f (x )的最小正周期及最大值; (2)若α∈,2ππ⎛⎫⎪⎝⎭,且f (α)=22,求a 的值.【能力提升】1.若f (x )=2sin(ωx +φ)+m ,对任意实数t 都有f (π8+t )=f (π8-t ),且f (π8)=-3,则实数m 的值等于( )A .-1B .±5C .-5或-1D .5或12.(2013·浙江文,6)函数f (x )=sin x cos x +32cos2x 的最小正周期和振幅分别是( ) A .π,1 B .π,2 C .2π,1 D .2π,2 3.函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的图象关于直线x =π3对称,它的最小正周期为π,则函数f (x )图象的一个对称中心是( ) A .(π3,1) B .(π12,0) C .(5π12,0) D .(-π12,0)4.(2013·新课标Ⅱ文,16)函数y =cos(2x +φ)(-π≤φ<π)的图象向右平移π2个单位后,与函数y =sin(2x +π3)的图象重合,则φ=________.5.已知向量m =(sin 2x +1+cos2x 2,sin x ),n =(12cos2x -32sin2x,2sin x ),设函数f (x )=m ·n ,x ∈R .(1)求函数f (x )的最小正周期; (2)若x ∈[0,π2],求函数f (x )的值域.。


三角函数归纳整理复习一、基础知识定义1 角度制,把一周角360等分,每一等份为一度,弧度制:把等于半径长的圆弧所对的圆心角叫做一弧度。
360度=2π弧度。
若圆心角的弧长为L ,则其弧度数的绝对值rL=||α,其中r 是圆的半径。
定义2 三角函数,在直角坐标平面内,把角α的顶点放在原点,始边与x 轴的正半轴重合,在角的终边上任意取一个不同于原点的点P (x ,y ),到原点的距离为)(22y x r r +=,则正弦函数ry=αsin ,余弦函数r x =αcos ,正切函数xy =αtan . 定理1 同角三角函数的基本关系式:商数关系:,cos sin tan ααα=; 平方关系:1cos sin 22=+αα(变形:)cos 1)(cos 1(cos 1sin 22αααα-+=-=)定理2 诱导公式:(1)______________________________________________;(2)__________________________________________;(3)______________________________________; (4)__________________________________________; (5)_____________________________________; (6)___________________________________________(奇变偶不变,符号看象限)。
定理3 正弦函数的性质,根据图象可得y =s inx (x ∈R )的性质如下。
单调区间:在区间⎥⎦⎤⎢⎣⎡+-22,22ππππk k 上为增函数,在区间⎥⎦⎤⎢⎣⎡++ππππ232,22k k 上为减函数,最小正周期为2π. 奇偶数. 有界性:当且仅当x =2kx +2π时,y 取最大值1,当且仅当x =3k π-2π时, y 取最小值-1。


三角函数复习详细整理(原创)题型特征及分值:[1]高考中对三角函数的考查一般有四大类型:(1)利用三角函数的定义与三角变换求值(如2008年四川卷3题).(2)三角函数的图象、性质(单调性、奇偶性、周期性、对称性等)(如2008年四川卷5题);(3)三角形相关的三角函数(以正余弦定理的运用为主);(4)函数值域等综合问题(2008年四川卷17题).[2]近几年对三角函数的考察中对三角变换的考查要求有所降低,同时对三角函数的图像与性质的考查有所加强,近几年每套试卷中一般有1至3道填空题或选择题(以三角变换求值、三角函数性质、图象为主,如四川卷2007年16题)和一个解答题(12分)(如四川卷2007年17题),总分值在20-26分左右。
同时三角函数具有工具性作用,近年也常和其他章节§3.解斜三角形知识网络:§4.典型题型真题突破【例1】(2007年江西)若πtan 34α⎛⎫-= ⎪⎝⎭,则cot α等于( )A .2-B .12-C .12D .2解题思路:π1tan 3cot tan()tan[()]42445πππαααα-⎛⎫-=⇒=-=++= ⎪⎝⎭,选A.【例2】(2007年陕西)已知sin α=,则44sincos αα-的值为( )A .15-B .35-C .15D .35解题思路:44222222sin cos (sin cos )(sin cos )sin cos αααααααα-=-+=-=22sin 1α-=35-.选B.【例3】(2005年湖北) 若)20(tan cos sin παααα<<=+,则∈α( )A .(0,6π)B .(6π,4π)C .(4π,3π) D .(3π,2π)解题思路:sin cos tan cos ,2ααααα+=⇒=<<,故选C.【例4】(2007年浙江)已知11sin 225θ+=,且324θππ≤≤,则cos2θ的值是____. 解题思路:1sin cos 5θθ+=,两边平方得:11sin 225θ+=24sin 225θ-⇒=⇒cos 2θ=725-.【例5】(2007年江苏)若1cos()5αβ+=,3cos()5αβ-=,则tan tan αβ⋅=_____ 解题思路:1cos()cos cos sin sin 5αβαβαβ+==⋅-⋅①,3cos()5αβ-==cos cos sin sin αβαβ⋅+⋅②. ②-①得:1sin sin 5αβ⋅=③, ②+①得:2cos cos 5αβ⋅=.④,③④:tan tan αβ⋅=12. 【例6】(2006年重庆)已知()33,,,sin ,45παβπαβ⎛⎫∈+=- ⎪⎝⎭12sin()413πβ-=,则cos()4πα+=____. 解题思路:cos()cos[()]cos(cos )444πππααββαββ+=+--=+--)()( 56sin(sin )465παββ+-=-)(.【例7】(2005年重庆)已知α、β均为锐角,且αβαβαtan ),sin()cos(则-=+= 解题思路:cos()sin()cos()cos()2παβαβαβαβ+=-⇒+=--,2παβαβ++--=0,4πα=,tan 1α=.【例8】(1996年全国)tan 20tan 4020tan 40+⋅。
三角函数公式三角函数是数学中属于初等函数中的超越函数的一类函数。
它们的本质是任何角的集合与一个比值的集合的变量之间的映射。
通常的三角函数是在平面直角坐标系中定义的。
其定义城为整个实数城。
另一种定义是在直角三角形中,但并不完全。
现代数学把它们描述成无穷敖列的极限和方程的解,将其定义扩展到复数系。
公式分类1.锐角三角函数公式sin α=∠α的对边/ 斜边cos α=∠α的邻边/ 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边2.其他非重点三角函数csc(a) = 1/sin(a)sec(a) = 1/cos(a)3.倍角公式:sin(2α)=2sinα²cosα=2/(tanα+cotα)cos(2α)=(cosα)^2-(sinα)^2=2(cosα)^2-1=1-2(sinα)^2tan(2α)=2tanα/(1-tan^2α)cot(2α)=(cot^2α-1)/(2cotα)sec(2α)=sec^2α/(1-tan^2α)csc(2α)=1/2*secα²cscα4.三倍角公式:sin(3α) = 3sinα-4sin^3α= 4sinα²sin(60°+α)sin(60°-α)cos(3α) = 4cos^3α-3cosα= 4cosα²cos(60°+α)cos(60°-α)tan(3α) = (3tanα-tan^3α)/(1-3tan^2α) = tanαtan(π/3+α)tan(π/3-α)cot(3α)=(cot^3α-3cotα)/(3cot^2α-1)5.三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina=2sina(1-sin²a)+(1-2sin²a)sina=3sina-4sin³acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos²a-1)cosa-2(1-cos²a)cosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina(3/4-sin²a)=4sina[(√3/2)²-sin²a]=4sina(sin²60°-sin²a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos³a-3cosa=4cosa(cos²a-3/4)=4cosa[cos²a-(√3/2)²]=4cosa(cos²a-cos²30°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)6.半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))sec(α/2)=±√((2secα/(secα+1))csc(α/2)=±√((2secα/(secα-1))7.n倍角公式:sin(nα)=ncos^(n-1)α²sinα-C(n,3)cos^(n-3)α²sin^3α+C(n,5)cos^(n-5)α²sin^5α-…cos(nα)=cos^nα-C(n,2)cos^(n-2)α²sin^2α+C(n,4)cos^(n-4)α²sin^4α-…8.两角和与差的三角函数sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinBtan(A+B) = (tanA+tanB)/(1-tanAtanB)tan(A-B) = (tanA-tanB)/(1+tanAtanB)cot(A+B) = (cotAcotB-1)/(cotB+cotA)cot(A-B) = (cotAcotB+1)/(cotB-cotA)9.和差化积sinθ+sinφ = 2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ = 2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ = 2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ = -2 sin[(θ+φ)/2] sin[(θ-φ)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)10.积化和差sinαsinβ = [cos(α-β)-cos(α+β)] /2cosαcosβ = [cos(α+β)+cos(α-β)]/2sinαcosβ = [sin(α+β)+sin(α-β)]/2cosαsinβ = [sin(α+β)-sin(α-β)]/211.辅助角公式:12.万能公式13.三角和的三角函数:sin(α+β+γ)=sinα²cosβ²cosγ+cosα²sinβ²cosγ+cosα²cosβ²sinγ-sinα²sin β²sinγcos(α+β+γ)=cosα²cosβ²cosγ-cosα²sinβ²sinγ-sinα²cosβ²sinγ-sinα²sin β²cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα²tanβ²tanγ)/(1-tanα²tanβ-tanβ²tanγ-tan γ²tanα)14.诱导公式sin(-α) = -sinαcos(-α) = cosαtan (-α)=-tanαsin(π/2-α) = cosαcos(π/2-α) = sinαsin(π/2+α) = cosαcos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinαcos(π+α) = -cosαtanA= sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍:奇变偶不变,符号看象限15.双曲函数sinh(a) = [e^a-e^(-a)]/2cosh(a) = [e^a+e^(-a)]/2tanh(a) = sin h(a)/cos h(a)◆公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)= sinαtan(2kπ+α)= tanαcot(2kπ+α)= cotα◆公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)= -sinαcos(π+α)= -cosαtan(π+α)= tanαcot(π+α)= cotα◆公式三:任意角α与-α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα◆公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα◆公式五:利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanαcot(2π-α)= -cotα◆公式六:π/2±α及3π/2±α与α的三角函数值之间的关系:sin(π/2+α)= cosαcos(π/2+α)= -sinαtan(π/2+α)= -cotαcot(π/2+α)= -tanαsin(π/2-α)= cosαcos(π/2-α)= sinαtan(π/2-α)= cotαcot(π/2-α)= tanαsin(3π/2+α)= -cosαtan(3π/2+α)= -cotαcot(3π/2+α)= -tanαsin(3π/2-α)= -cosαcos(3π/2-α)= -sinαtan(3π/2-α)= cotαcot(3π/2-α)= tanα(以上k∈Z)A·sin(ωt+θ)+ B·sin(ωt+φ) =√{(A^2 +B^2 +2ABcos(θ-φ)} • sin{ωt + arcsin[ (A•sinθ+B•sinφ) / √{A^2 +B^2; +2ABcos(θ-φ)} }★√表示根号,包括{……}中的内容16.降幂公式sin^2α=(1-cos(2α))/2=versin(2α)/2cos^2α=(1+cos(2α))/2=covers(2α)/2tan^2α=(1-cos(2α))/(1+cos(2α))17.推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^21+sin(a)=(sin(a/2)+cos(a/2))^2 1-sin(a)=(sin(a/2)-cos(a/2))^2csc(a)=1/sin(a) sec(a)=1/cos(a)cos30=sin60sin30=cos6018.推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=[sin(α/2)+cos(α/2)]^2(1) (sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC。
.....三角函数专题(知识归纳/记忆技巧/典型真题题剖析)一、三角函数的概念(1) 角的概念:终边相同角的集合:所有与α终边相同的角,连同α在内,可构成集合{}0|360,k k Z ββα=⋅+∈或{}|2,k k Z ββπα=+∈(2) 象限角:第一象限角的集合|22,2x k x k k Z πππ⎧⎫<<+∈⎨⎬⎩⎭第二象限角的集合|22,2x k x k k Z ππππ⎧⎫+<<+∈⎨⎬⎩⎭第三象限角的集合|22,2x k x k k Z ππππ⎧⎫-<<-∈⎨⎬⎩⎭第四象限角的集合|22,2x k x k k Z πππ⎧⎫-<<∈⎨⎬⎩⎭(3) 轴线角:终边在x 轴上角的集合{}|,k k Z ααπ=∈,终边在y 轴上角的集合|,2k k Z πααπ⎧⎫=+∈⎨⎬⎩⎭,终边在坐标轴上角的集合|,2k k Z παα⎧⎫=∈⎨⎬⎩⎭(4) 角度、弧度的换算关系:(1)3602rad π=,1180rad π=,1801rad π⎛⎫= ⎪⎝⎭(2)扇形的弧长、面积公式:设扇形的弧长为l ,圆心角为()rad α,半径为r ,则l r α=⋅,扇形的面积21122S lr r α==⋅ 3、三角函数定义: 若(),P x y 是角θ终边上任意异于O 的一点,O 为坐标原点,OP r =,则sin ,cos ,tan ,cot y x y x r r x yθθθθ==== 4、三角函数在各象限的符号规律:口诀“一全正, 二正弦,三正切,四余弦.sin α cos α tan α(cot α)二、同角三角函数的基本关系与诱导公式1、同角三角函数的基本关系式(1)倒数关系:tan cot 1αα⋅=(2)商的关系:sin cos tan ,cot .cos sin αααααα== (3)平方关系:22sin 1cos αα+=sin αcot αtan α+ + ——+ + + + ————sin αcos α-cot αtan αtan αcot α±注意:(1)诱导公式可概括为2k α⋅±的各三角函数值的化简公式。
高中数学高考三角函数复习专题三角函数复专题一、核心知识点归纳:1、正弦函数、余弦函数和正切函数的图象与性质:函数性质:y=sinx y=cosx y=tanx图象定义域 R R R\{kπ+π/2|k∈Z}值域 [-1,1] [-1,1] R最值y_max=1 (when x=2kπ) y_max=1 (when x=2kπ+π/2) 无最大值y_min=-1 (when x=2kπ-π) y_min=-1 (when x=2kπ) 无最小值周期性2π 2π π奇偶性奇函数偶函数奇函数单调性在[2kπ-π/2,2kπ+π/2](k∈Z)上是增函数;在[2kπ+π/2,2kπ+3π/2](k∈Z)上是减函数。
在[kπ,kπ+π](k∈Z)上是减函数。
在[kπ-π/2,kπ+π/2](k∈Z)上是增函数;在[kπ+π/2,kπ+3π/2](k∈Z)上是减函数。
对称中心(kπ,0)(k∈Z) 对称中心(kπ+π/2,0)(k∈Z) 无对称中心对称性奇对称偶对称无对称轴对称轴x=kπ+π/2 (k∈Z) 对称轴x=kπ (k∈Z) 无对称轴2.正、余弦定理:在△ABC中有:①正弦定理:a/sinA=b/sinB=c/sinC=2R(R为△ABC外接圆半径)注意变形应用:sinA=2R/asinB=2R/bsinC=2R/c②面积公式:S△ABC=1/2absinC=1/2acsinB=1/2bcsinA ③余弦定理:b²=c²+a²-2accosBc²=a²+b²-2abcosCa²=b²+c²-2bccosA三、例题集锦:考点一:三角函数的概念1.如图,设A是单位圆和x轴正半轴的交点,P、Q是单位圆上的两点,O是坐标原点,∠AOP=π/6,∠AOQ=α,α∈[0,π)。
若Q(√3/2,y),求cos(α-π/6)。
三角函数知识点整理复习三角函数是初等数学的重要分支,是描述直角三角形中各个角的函数关系。
在几何、力学、电磁学等学科中都有广泛的应用。
下面是对三角函数常识的整理和复习。
1. 正弦函数(sin):正弦函数是一个周期性的函数,其定义域为所有实数,值域为[-1,1]。
根据单位圆的定义,正弦函数可以表示为一些角的斜边长度与半径长度之比。
在单位圆上,角度为θ时,正弦函数的值等于斜边长度(垂直边)与半径长度之比。
2. 余弦函数(cos):余弦函数也是一个周期性函数,其定义域为所有实数,值域也是[-1,1]。
余弦函数可以表示为一些角的直角边长度与半径长度之比。
在单位圆上,角度为θ时,余弦函数的值等于直角边长度(底边)与半径长度之比。
3. 正切函数(tan):正切函数也是一个周期性函数,其定义域为所有实数,值域为整个实数集。
正切函数可以表示为一些角的直角边长度的比值。
在单位圆上,角度为θ时,正切函数的值等于直角边长度(垂直边)与直角边长度(底边)之比。
4. 余切函数(cot):余切函数也是一个周期性函数,其定义域为所有实数,值域为整个实数集。
余切函数可以表示为一些角的直角边长度的比值。
在单位圆上,角度为θ时,余切函数的值等于直角边长度(底边)与直角边长度(垂直边)之比。
5.正弦函数和余弦函数的关系:正弦函数和余弦函数是互为余弦的关系,即sin(θ) = cos(π/2 - θ) 和cos(θ) = sin(π/2 - θ)。
这意味着两个角的正弦值相等,当且仅当这两个角互为余弦。
6.正切函数和余切函数的关系:正切函数和余切函数是互为余切的关系,即tan(θ) = cot(π/2 - θ) 和cot(θ) = tan(π/2 - θ)。
这意味着两个角的正切值相等,当且仅当这两个角互为余切。
7.正弦函数和余切函数的关系:正弦函数和余切函数是互为正弦的关系,即sin(θ) = 1/csc(θ) 和csc(θ) = 1/sin(θ)。