2平面任意力系习题

第一章静力学的基本概念和公理一，填空题1，力对物体的作用效果取决于力的，，，这三者称为力的三要素。

力的外效应是指力使物体的发生改变，力的内效应是指力使物体的发生改变。

力是物体间的相互作用，它可以使物体的_____________发生改变，或使物体产生___________。

2，物体的平衡是指物体相对于地球保持或状态。

3，在力的作用下和都保持不变的的物体称为刚体。

4，对物体的运动或运动趋势起限制作用的各种装置称为。

5，常见的铰链约束有和。

约束反力恒与约束所能限制的物体运动（趋势）方向。

6，刚体受到两个力作用而平衡，其充要条件是这两个力的大小，作用线。

7，作用力和反作用力是两个物体间的相互作用力，它们一定，，分别作用在。

作用在刚体上的力可沿其作用线任意移动,而_______________力对刚体的作用效果.所以,在静力学中,力是________________的矢量.9力对物体的作用效果一般分为__________效应和___________效应.10对非自由体的运动所预加的限制条件为_____________;约束反力的方向总是与约束所能阻止的物体的运动趋势的方向_____________;约束反力由_____力引起,且随_______________力的改变而改变.9柔性约束对物体只有沿_________的___________力。

10，铰链约束分为_________和_________。

11，光滑面约束力必过_________沿_________并指向______________的物体。

12，活动铰链的约束反力必通过___________并与___________相垂直。

表示一个力对物体转动效果的度量称为_________，其数学表达式为_________。

14、力偶是指______________________________________________________。

15，力偶对物体的转动效应取决于_______________、________________、 _______________三要素。

平面任意力系习题及答案平面任意力系习题及答案力学是物理学的一个重要分支，研究物体受力的作用和运动规律。

平面任意力系是力学中的一个重要概念，它涉及到多个力在平面内的作用和平衡问题。

在本文中，我们将探讨一些关于平面任意力系的习题，并提供相应的答案。

1. 问题描述：一个物体受到三个力的作用，力的大小和方向分别为F1=10N，θ1=30°；F2=15N，θ2=120°；F3=8N，θ3=210°。

求物体所受合力的大小和方向。

解答：首先，我们需要将力的分量计算出来。

根据三角函数的定义，我们可以得到F1x=F1*cosθ1=10*cos30°=8.66N，F1y=F1*sinθ1=10*sin30°=5N；F2x=F2*cosθ2=15*cos120°=-7.5N，F2y=F2*sinθ2=15*sin120°=12.99N；F3x=F3*cosθ3=8*cos210°=-6.93N，F3y=F3*sinθ3=8*sin210°=-4N。

然后，我们将分量相加，得到合力的分量。

Fx=F1x+F2x+F3x=8.66N-7.5N-6.93N=-5.77N，Fy=F1y+F2y+F3y=5N+12.99N-4N=13.99N。

最后，我们可以利用勾股定理计算合力的大小和方向。

合力的大小为F=sqrt(Fx^2+Fy^2)=sqrt((-5.77N)^2+(13.99N)^2)=15.16N，合力的方向为θ=arctan(Fy/Fx)=arctan(13.99N/-5.77N)=-68.6°。

因此，物体所受合力的大小为15.16N，方向为-68.6°。

2. 问题描述：一个物体受到四个力的作用，力的大小和方向分别为F1=8N，θ1=30°；F2=12N，θ2=120°；F3=10N，θ3=210°；F4=6N，θ4=300°。

第三章 平面任意力系[习题3-1] x 轴与y 轴斜交成α角，如图3-23所示。

设一力系在xy 平面内，对y 轴和x 轴上的A 、B 两点有0=∑iA M ，0=∑iB M ，且0=∑iy F ，0≠∑ix F 。

已知a OA =，求B 点在x 轴上的位置。

解：因为0==∑iA A M M ，但0≠∑ix F ，即0≠R F ，根据平面力系简化结果的讨论（2）可知，力系向A 点简化的结果是：R F 是原力系的合力，合力R F 的作用线通过简化中心A 。

又因为0==∑iB B M M ，但0≠∑ix F ，即0≠R F ，根据平面力系简化结果的讨论（2）可知，力系向B 点简化的结果是：R F 是原力系的合力，合力R F 的作用线通过简化中心B 。

一个力系的主矢量是一个常数，与简化中心的位置无关。

因此，合力R F 的作用线同时能过A 、B 两点。

又因为0==∑iy Ry F F ，所以合力R F 与y 轴垂直。

即AB 与y 垂直。

由直角三角形OAB 可知，B 点离O 点的距离为： αcos ab =[习题3-2] 如图3-24所示，一平面力系(在oxy 平面内)中的各力在x 轴上投影之代数和等于零，对A 、B 两点的主矩分别为m kN M A ⋅=12，m kN M B ⋅=15，A 、B 两点的坐标分别为（2，3）、（4，8），试求该力系的合力(坐标值的单位为ｍ)。

解：由公式（3-5）可知：)(212R O O O F M M M +=)(R B A B F M M M +=)()(Ry B Rx B A B F M F M M M ++=依题意0=Rx F ，故有：)(Ry B A B F M M M +=)24(1215-⨯+=Ry F 32=Ry F )(5.1kN F Ry = kN F F Ry R 5.1==)(85.112m F M a R A ===故C 点的水平坐标为：m x 6-=。

平面任意力系习题答案平面任意力系是指作用在物体上的力不满足平面力偶系或平面共面力系的条件，即力的作用线不在同一平面上，也不互相平行。

解决这类问题通常需要应用静力学的基本原理，如力的平衡条件、力矩平衡等。

习题1：已知一平面任意力系作用在刚体上，力F1=50N，方向为水平向右；力F2=30N，方向为竖直向上；力F3=40N，方向为与水平面成30度角斜向上。

求力系的合力。

答案：首先，将力F3分解为水平分量和竖直分量：- 水平分量：F3x = F3 * cos(30°) = 40 * (√3/2) = 20√3 N- 竖直分量：F3y = F3 * sin(30°) = 40 * (1/2) = 20 N然后，计算合力的水平分量和竖直分量：- 水平合力：Fx = F1 + F3x = 50 + 20√3 N- 竖直合力：Fy = F2 + F3y = 30 + 20 N最后，计算合力的大小和方向：- 合力大小：F = √(Fx^2 + Fy^2) = √((50 + 20√3)^2 + (30 + 20)^2) N- 方向：与水平面夹角θ满足tan(θ) = Fy / Fx习题2：一个平面任意力系作用在刚体上，已知力F1=60N，作用点A；力F2=40N，作用点B；力F3=50N，作用点C。

A、B、C三点不共线。

求力系的合力矩。

答案：首先，计算各力对任意一点（如A点）的力矩：- 力矩M1 = 0（因为力F1作用在A点，力矩为0）- 力矩M2 = F2 * (B到A的距离)- 力矩M3 = F3 * (C到A的距离)然后，计算合力矩：- 合力矩M = M1 + M2 + M3由于题目没有给出具体的距离，我们无法计算出具体的数值。

但是，上述步骤提供了计算合力矩的方法。

习题3：已知一平面任意力系作用在刚体上，力F1和F2的合力为100N，方向与F1相反，求F1和F2的大小。

答案：设F1的大小为xN，F2的大小为yN。

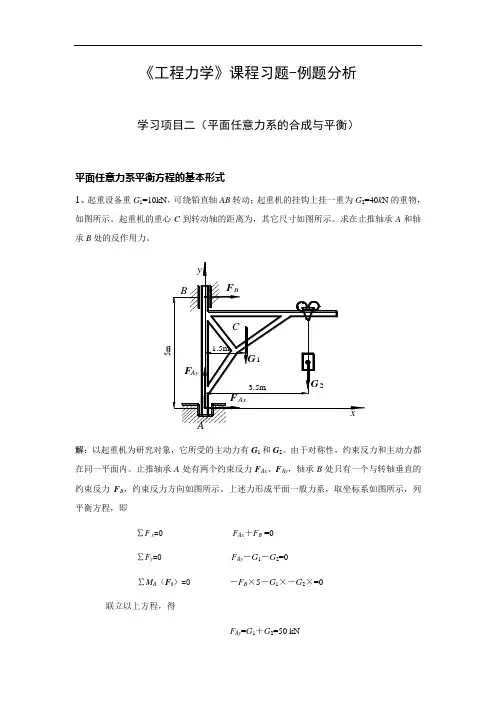
《工程力学》课程习题-例题分析学习项目二（平面任意力系的合成与平衡）平面任意力系平衡方程的基本形式1、起重设备重G1=10kN，可绕铅直轴AB转动；起重机的挂钩上挂一重为G2=40k N的重物，如图所示。

起重机的重心C到转动轴的距离为，其它尺寸如图所示。

求在止推轴承A和轴承B处的反作用力。

解：以起重机为研究对象，它所受的主动力有G1和G2。

由于对称性，约束反力和主动力都在同一平面内。

止推轴承A处有两个约束反力F Ax、F Ay，轴承B处只有一个与转轴垂直的约束反力F B，约束反力方向如图所示。

上述力形成平面一般力系，取坐标系如图所示，列平衡方程，即∑F x=0 F Ax＋F B =0∑F y=0 F Ay－G1－G2=0∑M A（F i）=0 －F B×5－G1×－G2×=0联立以上方程，得F Ay=G1＋G2=50 kNF B =－－=－31kNF Ax =－F B =31kNF B 为负值，说明其方向与假设的方向相反，即应指向左。

2、防洪用弧形闸门有对称的两个支架和铰链支座。

已知闸门重G =1100kN ，静水总压力2P 2G B V A (F i )=0 B V ×2G×=0得 V B = kN 取x 、y 轴方向如图b ，列投影方程由∑F x =0 05531sin 25531sin 21='︒-'︒+-G V R P B得 R 1=由∑F y =0 05531c 25531cos 2='︒-'︒+os G V R B得R2=反力的方向如图b所示。

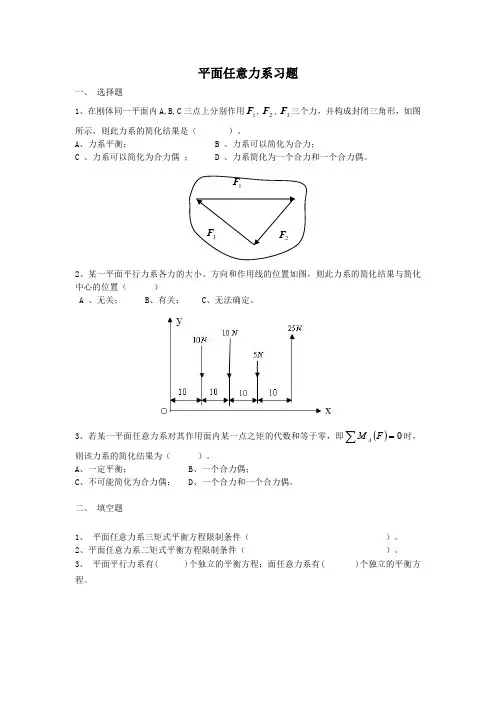
平面任意力系习题
一、选择题
1、在刚体同一平面内A,B,C 三点上分别作用1F ,2F ,3F 三个力，并构成封闭三角形，如图所示，则此力系的简化结果是（
）。

A、力系平衡；
B 、力系可以简化为合力；
C 、力系可以简化为合力偶；
D 、力系简化为一个合力和一个合力偶。

1
F 2
F 3F 2、某一平面平行力系各力的大小、方向和作用线的位置如图，则此力系的简化结果与简化中心的位置（）
A 、无关；B、有关；C、无法确定。

3、若某一平面任意力系对其作用面内某一点之矩的代数和等于零，即
()∑=0F M A 时，则该力系的简化结果为（
）。

A、一定平衡；
B、一个合力偶；
C、不可能简化为合力偶；
D、一个合力和一个合力偶。

二、填空题
1、平面任意力系三矩式平衡方程限制条件（
）。

2、平面任意力系二矩式平衡方程限制条件（
）。

3、平面平行力系有(
)个独立的平衡方程；面任意力系有()个独立的平衡方
程。

三、计算题
1、已知：F、M、q、L，各杆自重不计，试求A、C处约束反力。

2、求图示组合梁支座的约束反力。

由直角三角形OAB 可知，B 点离0点的距离为:a- COSPt第三章平面任意力系[习题3-1] x 轴与y 轴斜交成a 角，如图3-23所示。

设一力系在xy 平面内，对y轴和x 轴上的A 、B 两点有送M jA =0，送M jB = 0 ,且送F iy =0, 2 F i^ 0。

已知0A = a ，求B 点在x 轴上的位置。

解:因为M A =2 M iA =0，但S F ix H 0 ,即卩F^Q ，根据平面力系简化结果的 讨论（2）可知，力系向A 点简化的结果是：F R 是原力系的合力，合力F R 的作 用线通过简化中心A 。

又因为M B =S M iB=0，但送F ix^O ，即卩F R HQ ，根据平面力系简化结果的讨论（2）可知，力系向B 点简化的结果是：F R是原力系的合力，合力F R的 作用线通过简化中心B 0一个力系的主矢量是一个常数，与简化中心的位置无关。

因此，合力F R 的作用线同时能过A 、B 两点。

又因为F Ry =5： F iy =0，所以合力F R 与y 轴垂直。

即AB 与y 垂直。

图 3-23500［习题3-2］如图3-24所示，一平面力系（在oxy 平面内）中的各力在X 轴上投影之代数和等于零，对A 、B 两点的主矩分别为 M A =12kN .m, M B =15kN ”m，A 、B 两 点的坐标分别为（2, 3）、（4, 8）,试求该力系的合力（坐标值的单位为m ）。

解：由公式（3-5）可知: MO2 =M O1 中 M O2(F R ) M B =M A +M B (F R ) F RM B =M A +M B (F RX )+ M B (F Ry ) 依题意F RX =0，故有: k*---- C(-6,3)a =8mM B =M A +M B (F Ry ) 15 =12+F Ry>q 4-2) 2F Ry =3F Ry =1.5(kN) F R =F Ry =1.5kNF R 1.5故C 点的水平坐标为：X = -6m 。

工程力学练习册学校学院专业学号教师姓名第一章静力学基础1-1 画出下列各图中物体A，构件AB，BC或ABC的受力图，未标重力的物体的重量不计，所有接触处均为光滑接触。

（a）（b）（c）（d）（e）（f）（g）1-2 试画出图示各题中AC杆（带销钉）和BC杆的受力图（a）（b）（c）（a）1-3 画出图中指定物体的受力图。

所有摩擦均不计，各物自重除图中已画出的外均不计。

（a）（b）（c）（d）（e）（f）（g）第二章 平面力系2-1 电动机重P=5000N ，放在水平梁AC 的中央，如图所示。

梁的A 端以铰链固定，另一端以撑杆BC 支持，撑杆与水平梁的夹角为30 0。

如忽略撑杆与梁的重量，求绞支座A 、B 处的约束反力。

题2-1图解得: N P F F B A 5000===2-2 物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在绞车D 上，如图所示。

转动绞车，物体便能升起。

设滑轮的大小及轴承的摩擦略去不计，杆重不计，A 、B 、C 三处均为铰链连接。

当物体处于平衡状态时，求拉杆AB 和支杆BC 所受的力。

题2-2图解得: P F PF AB BC 732.2732.3=-=2-3 如图所示，输电线ACB 架在两电线杆之间，形成一下垂线，下垂距离CD =f =1m ，两电线杆间距离AB =40m 。

电线ACB 段重P=400N ，可近视认为沿AB 直线均匀分布，求电线的中点和两端的拉力。

题2-3图以AC 段电线为研究对象，三力汇交2-4 图示为一拔桩装置。

在木桩的点A 上系一绳，将绳的另一端固定在点C ，在绳的点B 系另一绳BE ，将它的另一端固定在点E 。

然后在绳的点D 用力向下拉，并使绳BD 段水平，AB 段铅直；DE 段与水平线、CB 段与铅直线成等角α=0.1rad （弧度）（当α很小时，tan α≈α）。

如向下的拉力F=800N ，求绳AB 作用于桩上的拉力。

题2-4图作BD 两节点的受力图 联合解得：kN F F F A 80100tan 2=≈=α 2-5 在四连杆机构ABCD 的铰链B 和C 上分别作用有力F 1和F 2，，机构在图示位置平衡。

平面任意力系习题答案平面任意力系习题答案在学习物理学的过程中，平面任意力系习题是非常重要的一部分。

通过解答这些习题，我们可以更好地理解和应用力学原理，提高我们的分析和解决问题的能力。

在本文中，我将为大家提供一些平面任意力系习题的答案，希望能对大家的学习有所帮助。

1. 题目：一个物体受到三个力的作用，分别是F1 = 10N，F2 = 15N，F3 = 20N，方向分别为水平向右、竖直向上和水平向左。

求物体所受合力的大小和方向。

解答：首先，我们需要将这三个力进行向量叠加。

由于F1和F3的方向相反，所以它们可以相互抵消，只需要计算F2的向量和即可。

设物体所受合力为F，根据力的平衡条件，有F + F2 = 0。

由此可得F = -F2 = -15N。

根据向量的定义，我们可以知道F的方向是竖直向下。

综上所述，物体所受合力的大小为15N，方向为竖直向下。

2. 题目：一个物体受到两个力的作用，分别是F1 = 20N，F2 = 30N，方向分别为水平向右和竖直向上。

已知物体所受合力的大小为40N，方向与F1的方向夹角为60°，求F2的大小和方向。

解答：设F2的大小为F，根据三角函数的定义，我们可以得到F1的水平分量为F1x = F1 * cos60° = 20N * 0.5 = 10N，F1的竖直分量为F1y = F1 * sin60° =20N * 0.866 = 17.32N。

根据力的平衡条件，我们可以得到F1x + F2 = 0，F1y + F = 0。

根据这两个方程可以解得F2 = -F1x = -10N，F = -F1y = -17.32N。

根据向量的定义，我们可以知道F2的方向是水平向左，F的方向是竖直向下。

综上所述，F2的大小为10N，方向为水平向左。

3. 题目：一个物体受到两个力的作用，分别是F1 = 15N，F2 = 25N，方向分别为水平向右和竖直向上。

已知物体所受合力的大小为30N，方向与F1的方向夹角为45°，求F2的大小和方向。

工程力学学习参考资料第一章静力学基础一、判断题1-1．如物体相对于地面保持静止或匀速运动状态,则物体处于平衡。

（）1-2．作用在同一刚体上的两个力,使物体处于平衡的必要和充分条件是：这两个力大小相等、方向相反、沿同一条直线。

( ) 1-3．静力学公理中,二力平衡公理和加减平衡力系公理仅适用于刚体。

( ) 1-4．二力构件是指两端用铰链连接并且指受两个力作用的构件。

( ) 1-5．对刚体而言，力是滑移矢量，可沿其作用线移动。

（）1-6．对非自由体的约束反力的方向总是与约束所能阻止的物体的运动趋势的方向相反。

（）1-7．作用在同一刚体的五个力构成的力多边形自行封闭，则此刚体一定处于平衡状态。

（）1-8．只要两个力偶的力偶矩相等，则此两力偶就是等效力偶。

（）二、单项选择题1-1．刚体受三力作用而处于平衡状态,则此三力的作用线( )。

A、必汇交于一点B、必互相平行C、必都为零D、必位于同一平面内1-2．力的可传性（）。

A、适用于同一刚体B、适用于刚体和变形体C、适用于刚体系统D、既适用于单个刚体，又适用于刚体系统1-3．如果力F R是F1、F2二力的合力,且F1、F2不同向，用矢量方程表示为F R= F1+ F2，则三力大小之间的关系为()。

A、必有F R= F1+ F2B、不可能有F R= F1+ F2C、必有F R＞F1, F R＞F2D、必有F R＜F1, F R＜F21-4．作用在刚体上的一个力偶，若使其在作用面内转移，其结果是（）。

A、使刚体转动B、使刚体平移C、不改变对刚体的作用效果D、将改变力偶矩的大小三、计算题1-1．已知：F1=2000N，F2=150N，F3=200N，F4=100N，各力的方向如图1-1所示。

试求各力在x、y轴上的投影。

解题提示F x= + F cosαF y= + F sinα注意：力的投影为代数量；式中：F x、F y的“+”的选取由力F的指向来确定；α为力F与x轴所夹的锐角。