第二章 2.3 第2课时
- 格式:pptx
- 大小:5.78 MB
- 文档页数:2

第二章 2.3 第2课时A 组·素养自测一、选择题1.若不等式x 2+mx +m2>0的解集为R ,则实数m 的取值X 围为( D )A .m >2B .m <2C .m <0,或m >2D .0<m <2[解析] 由Δ=m 2-4×m2=m 2-2m <0可得.2.已知不等式x 2+ax +4<0的解集为空集,则a 的取值X 围是( A ) A .-4≤a ≤4 B .-4<a <4 C .a ≤-4,或a ≥4D .a <-4,或a >4[解析] 由Δ=a 2-4×4≤0可得.3.若存在x 0∈R ,使得x 20+2x 0+m <0成立,则实数m 的取值X 围是( B ) A .m ≤1 B .m <1 C .m >1D .m ≥1[解析] 由题意可得Δ=4-4m >0,∴m <1.4.已知关于x 的不等式x 2-ax -b <0的解集是{x |2<x <3},则a +b 的值是( C ) A .-11 B .11 C .-1D .1[解析] 由已知可得2,3是方程x 2-ax -b =0的根,故a =5,b =-6,∴a +b =-1,故选C .5.如果ax 2+bx +c >0的解集为{x |x <-2,或x >4},那么对于函数f (x )=ax 2+bx +c ,应有( D )A .f (5)<f (2)<f (-1)B .f (2)<f (5)<f (-1)C .f (-1)<f (2)<f (5)D .f (2)<f (-1)<f (5)[解析] 由条件知a >0,且⎩⎪⎨⎪⎧-ba=-2+4,ca =-2×4,解得⎩⎪⎨⎪⎧b =-2a ,c =-8a ,所以f (x )=ax 2-2ax -8a =a [(x -1)2-9], 则f (-1)=-5a ,f (2)=-8a ,f (5)=7a . 又因为a >0,所以f (2)<f (-1)<f (5).6.如果方程x 2+(m -1)x +m 2-2=0的两个实根一个小于-1,另一个大于1,那么实数m 的取值X 围是( D )A .-2<m < 2B .-2<m <0C .-2<m <1D .0<m <1[解析] 令f (x )=x 2+(m -1)x +m 2-2,则⎩⎪⎨⎪⎧f 1=m 2+m -2<0,f -1=m 2-m <0,解得0<m <1,故选D .二、填空题7.若不等式x 2-ax -a ≤-3的解集为空集,则实数a 的取值X 围是__{a |-6<a <2}__. [解析] 不等式x 2-ax -a ≤-3可化为x 2-ax -a +3≤0,由不等式x 2-ax -a ≤-3的解集为空集,得Δ=(-a )2-4(-a +3)<0, 即a 2+4a -12<0,解得-6<a <2,则实数a 的取值X 围是{a |-6<a <2}. 8.若关于x 的不等式x -ax +1>0的解集为{x |x <-1或x >4},则实数a =__4__. [解析] 不等式x -ax +1>0等价于(x -a )(x +1)>0, 因为不等式x -ax +1>0的解集为{x |x <-1或x >4},所以a =4. 9.若不等式x 2+2x +2>|a -2|对于一切实数x 均成立,则实数a 的取值X 围是__{a |1<a <3}__.[解析]∵x 2+2x +2=(x +1)2+1≥1,∴当x =-1时,x 2+2x +2有最小值,最小值为1, 由不等式x 2+2x +2>|a -2|对于一切实数x 均成立, 得|a -2|<1,解得1<a <3, ∴实数a 的取值X 围是{a |1<a <3}. 三、解答题10.关于x 的不等式E :ax 2+ax -2≤0,其中a ∈R . (1)当a =1时,求不等式E 的解集;(2)若不等式E 在R 上恒成立,某某数a 的取值X 围.[解析] (1)当a =1时,不等式E :ax 2+ax -2≤0可化为x 2+x -2≤0, 即(x +2)(x -1)≤0,方程(x +2)(x -1)=0的两根为x 1=-2,x 2=1, 则不等式x 2+x -2≤0的解集是{x |-2≤x ≤1}, ∴当a =1时,不等式E 的解集为{x |-2≤x ≤1}.(2)当a =0时,不等式E 化为0·x 2+0·x -2≤0,对x ∈R 恒成立,即a =0满足题意. 当a ≠0时,由题意得⎩⎪⎨⎪⎧a <0,Δ=a 2-4a-2≤0⇒⎩⎪⎨⎪⎧a <0,-8≤a ≤0,解得-8≤a <0.综上可知,a 的取值X 围为{a |-8≤a ≤0}.11.汽车在行驶中,由于惯性的作用,刹车后还要继续向前滑行一段距离才能停止,我们称这段距离为“刹车距离”.刹车距离是分析事故的一个重要因素.在一个限速为40 km/h 的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事后现场勘查测得甲车的刹车距离略超过12 m ,乙车的刹车距离略超过10 m .已知甲、乙两种车型的刹车距离s (m)与车速x (km/h)之间分别有如下关系:s 甲=0.1x +0.01x 2,s 乙=0.05x +0.005x 2.问:甲、乙两车有无超速现象?[解析] 由题意知,对于甲车,有0.1x +0.01x 2>12,即x 2+10x -1 200>0,解得x >30或x <-40(不符合实际意义,舍去),这表明甲车的车速超过30 km/h.但根据题意知刹车距离略超过12 m ,由此估计甲车的车速不会超过限速40 km/h. 对于乙车,有0.05x +0.005x 2>10,即x 2+10x -2000>0,解得x >40或x <-50(不符合实际意义,舍去),这表明乙车的车速超过40 km/h ,即超过规定限速.B 组·素养提升一、选择题1.不等式组⎩⎪⎨⎪⎧x x +2>0,|x |<1的解集为( C )A .{x |-1<x <0}B .{x |-2<x <-1}C .{x |0<x <1}D .{x |x >1}[解析] 由x (x +2)>0,得x >0或x <-2.又由|x |<1,得-1<x <1,所以不等式组⎩⎪⎨⎪⎧x x +2>0,|x |<1的解集为{x |0<x <1}.2.不等式x 2-2x -2x 2+x +1<2的解集为( A )A .{x |x ≠-2}B .RC .∅D .{x |x <-2或x >2}[解析]∵x 2+x +1>0恒成立,∴原不等式⇔x 2-2x -2<2x 2+2x +2⇔x 2+4x +4>0⇔(x +2)2>0, ∴x ≠-2,∴不等式的解集为{x |x ≠-2}.3.(多选题)不等式x 2+ax +b ≤0(a ,b ∈R )的解集为{x |x 1≤x ≤x 2},且|x 1|+|x 2|≤2,其中错误的命题为( ACD )A .|a |≥1B .b ≤1C .|a +2b |≥2D .|a +2b |≤2[解析] 由题意知x 1x 2=b ,|x 1|+|x 2|≤2,不妨令a =-1,b =0,则x 1=0,x 2=1,但|a +2b |=1,所以C 不正确;令a =2,b =1,则x 1=x 2=1,但|a +2b |=4,所以D 不正确;令a =0,b =-1,则x 1=-1,x 2=1,但|a |=0,故A 不正确;b =x 1x 2≤(x 1+x 22)2≤⎝⎛⎭⎪⎫|x 1|+|x 2|22≤1,所以B 正确,故选ACD .4.(多选题)已知关于x 的方程x 2+(m -3)x +m =0,下列结论正确的是( BCD ) A .方程x 2+(m -3)x +m =0有实数根的充要条件是m ∈{m |m <1或m >9} B .方程x 2+(m -3)x +m =0有一正一负根的充要条件是m ∈{m |m <0} C .方程x 2+(m -3)x +m =0有两正实数根的充要条件是m ∈{m |0<m ≤1} D .方程x 2+(m -3)x +m =0无实数根的必要条件是m ∈{m |m >1}[解析] 在A 中,由Δ=(m -3)2-4m ≥0得m ≤1或m ≥9,故A 错误;在B 中,当x =0时,函数y =x 2+(m -3)x +m 的值为m ,由二次函数的图象知,方程有一正一负根的充要条件是m ∈{m |m <0},故B 正确;在C 中,由题意得⎩⎪⎨⎪⎧Δ=m -32-4m ≥0,3-m >0,m >0,解得0<m ≤1,故C 正确;在D 中,由Δ=(m -3)2-4m <0得1<m <9,又{m |1<m <9}⊆{m |m >1},故D 正确,故选BCD .二、填空题5.若对任意实数x ,不等式2kx 2+kx -3<0恒成立,则实数k 的取值X 围是__{k |-24<k ≤0}__.[解析] 当k =0时,不等式为-3<0,不等式恒成立;当k ≠0时,若不等式恒成立,则⎩⎪⎨⎪⎧k <0,Δ<0,解得-24<k <0.综上所述,-24<k ≤0.6.关于x 的方程x 2-(k +1)x +2k -1=0的根一个大于4,另一个小于4,则实数k 的取值X 围是__⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫k ⎪⎪⎪k >112__. [解析] 令f (x )=x 2-(k +1)x +2k -1,则f (4)<0,即42-4(k +1)+2k -1<0,整理有2k -11>0,解得k >112.7.若不等式x 2+ax +1≥0对一切x ∈{x |0<x ≤12}成立,则a 的最小值为__-52__.[解析]∵x 2+ax +1≥0对一切x ∈{x |0<x ≤12}成立,∴a ≥-(x +1x )在x ∈{x |0<x ≤12}上恒成立.令g (x )=-(x +1x ),则g (x )在{x |0<x ≤12}上为增函数.∴g (x )max =g (12)=-52.∴a ≥-52.∴a 的最小值为-52.三、解答题8.如图,有一长AM =30米,宽AN =20米的矩形地块,物业计划将其中的矩形ABCD 建为仓库,要求顶点C 在地块的对角线MN 上,B ,D 分别在边AM ,AN 上,其他地方建停车场和路,设AB =x 米.(1)求矩形ABCD 的面积S 关于x 的函数解析式;(2)若要求仓库占地面积不小于144平方米,求x 的取值X 围.[解析] (1)由题意知,△NDC ∽△NAM ,则DC AM =ND NA ,即x 30=20-AD 20,解得AD =20-23x .所以矩形ABCD 的面积S 关于x 的函数解析式为S =20x -23x 2(0<x <30).(2)由题意得20x -23x 2≥144,即x 2-30x +216≤0,解得12≤x ≤18.故x 的取值X 围是{x |12≤x ≤18}.。


第2课时 一元二次不等式的应用学习目标 1.经历从实际情境中抽象出一元二次不等式的过程.了解一元二次不等式的现实意义.2.能够构建一元二次函数模型,解决实际问题.知识点一 简单的分式不等式的解法 分式不等式的解法:思考x -3x +2>0与(x -3)(x +2)>0等价吗?x -3x +2≥0与(x -3)(x +2)≥0等价吗? 答案x -3x +2>0与(x -3)(x +2)>0等价;x -3x +2≥0与(x -3)(x +2)≥0不等价,前者的解集中没有-2,后者的解集中有-2.知识点二 一元二次不等式恒成立问题 1.转化为一元二次不等式解集为R 的情况,即 ax 2+bx +c >0(a ≠0)恒成立⇔⎩⎪⎨⎪⎧ a >0,Δ<0;ax 2+bx +c <0(a ≠0)恒成立⇔⎩⎪⎨⎪⎧a <0,Δ<0.2.分离参数,将恒成立问题转化为求最值问题. 知识点三 利用不等式解决实际问题的一般步骤 1.选取合适的字母表示题目中的未知数.2.由题目中给出的不等关系,列出关于未知数的不等式(组). 3.求解所列出的不等式(组). 4.结合题目的实际意义确定答案.思考 解一元二次不等式应用题的关键是什么?答案 解一元二次不等式应用题的关键在于构造一元二次不等式模型,选择其中起关键作用的未知量为x ,用x 来表示其他未知量,根据题意,列出不等关系再求解.1.不等式x -2x -1<0的解集为________.答案 {x |1<x <2}解析 原不等式⇔(x -1)(x -2)<0,∴1<x <2. 2.不等式1x ≤1的解集为________.答案 {x |x ≥1或x <0}解析 ∵1x ≤1,∴x -1x ≥0,∴⎩⎪⎨⎪⎧x (x -1)≥0,x ≠0,∴x ≥1或x <0.3.若方程x 2+ax +1=0的解集是∅,则实数a 的取值范围是________. 答案 -2<a <2解析 由题意可得a 2-4<0,所以-2<a <2.4.对∀x ∈R ,不等式x 2+2x +m >0恒成立,则实数m 的取值范围是________. 答案 m >1解析 由题意可得22-4m <0,所以m >1.一、简单的分式不等式的解法 例1 解下列不等式: (1)x +12x -1<0; (2)1-x 3x +5≥0; (3)x -1x +2>1. 解 (1)原不等式可化为(x +1)(2x -1)<0, ∴-1<x <12,故原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪-1<x <12.(2)原不等式可化为x -13x +5≤0,∴⎩⎪⎨⎪⎧(x -1)(3x +5)≤0,3x +5≠0,∴⎩⎨⎧-53≤x ≤1,x ≠-53,即-53<x ≤1.故原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪-53<x ≤1. (3)原不等式可化为x -1x +2-1>0,∴x -1-(x +2)x +2>0,-3x +2>0,则x <-2.故原不等式的解集为{x |x <-2}. (学生)反思感悟 分式不等式的解法(1)对于比较简单的分式不等式,可直接转化为一元二次不等式或一元一次不等式组求解,但要注意等价变形,保证分母不为零.(2)对于不等号右边不为零的较复杂的分式不等式,先移项再通分(不要去分母),使之转化为不等号右边为零,然后再用上述方法求解. 跟踪训练1 解下列不等式: (1)x +1x -3≥0;(2)5x +1x +1<3. 解 (1)不等式x +1x -3≥0可转化成不等式组⎩⎨⎧(x +1)(x -3)≥0,x ≠3.解这个不等式组,可得x ≤-1或x >3.即知原不等式的解集为{x |x ≤-1或x >3}. (2)不等式5x +1x +1<3可改写为5x +1x +1-3<0,即2(x -1)x +1<0.可将这个不等式转化成2(x -1)(x +1)<0, 解得-1<x <1.所以,原不等式的解集为{x |-1<x <1}. 二、不等式的恒成立问题例2 对∀x ∈R ,不等式mx 2-mx -1<0,求m 的取值范围. 解 若m =0,显然-1<0恒成立;若m ≠0,则⎩⎪⎨⎪⎧m <0,Δ=m 2+4m <0⇒解得-4<m <0.综上,m 的取值范围为{m |-4<m ≤0}. (教师) 延伸探究1.在本例中,是否存在m ∈R ,使得∀x ∈R ,不等式mx 2-mx -1>0,若存在,求m 的取值范围;若不存在,说明理由. 解 显然m =0时不等式不成立;由题意可得⎩⎪⎨⎪⎧m >0,Δ=m 2+4m <0,解得m ∈∅,所以不存在m ∈R ,使得∀x ∈R ,不等式mx 2-mx -1>0.2.在本例中,把条件“∀x ∈R ”改为“x ∈{x |2≤x ≤3}”,其余不变,求m 的取值范围. 解 由不等式mx 2-mx -1<0得m (x 2-x )<1, 因为x ∈{x |2≤x ≤3},所以x 2-x >0, 所以m (x 2-x )<1可化为m <1x 2-x, 因为x 2-x =⎝⎛⎭⎫x -122-14≤6, 所以1x 2-x ≥16,所以m <16.即m 的取值范围是⎩⎨⎧⎭⎬⎫m ⎪⎪m <16. (学生)反思感悟 一元二次不等式恒成立问题的解法(1)转化为对应的二次函数图象与x 轴的交点问题,考虑两个方面:x 2的系数和对应方程的判别式的符号.(2)转化为二次函数的最值问题:分离参数后,求相应二次函数的最值,使参数大于(小于)这个最值.跟踪训练2 若关于x 的不等式(k -1)x 2+(k -1)x -1<0恒成立,则实数k 的取值范围是________. 答案 {k |-3<k ≤1}解析 当k =1时,-1<0恒成立;当k ≠1时,由题意得⎩⎪⎨⎪⎧k -1<0,(k -1)2+4(k -1)<0,解得-3<k <1,因此实数k 的取值范围为{k |-3<k ≤1}. 三、一元二次不等式的实际应用例3 某农贸公司按每担200元的价格收购某农产品,并每100元纳税10元(又称征税率,为10个百分点),计划可收购a 万担.政府为了鼓励收购公司多收购这种农产品,决定将征税率降低x (x >0)个百分点,预测收购量可增加2x 个百分点. (1)写出降税后税收y (万元)与x 的关系式;(2)要使此项税收在税率调节后,不少于原计划税收的83.2%,试确定x 的取值范围. 解 (1)降低税率后的税率为(10-x )%,农产品的收购量为a (1+2x %)万担, 收购总金额为200a (1+2x %)万元. 依题意得y =200a (1+2x %)(10-x )% =150a (100+2x )(10-x )(0<x <10). (2)原计划税收为200a ×10%=20a (万元). 依题意得150a (100+2x )(10-x )≥20a ×83.2%,化简得x 2+40x -84≤0,解得-42≤x ≤2. 又因为0<x <10,所以0<x ≤2. 即x 的取值范围为{x |0<x ≤2}. (学生)反思感悟 解不等式应用题的步骤跟踪训练3 某农家院有客房20间,日常每间客房日租金为80元,每天都客满.该农家院欲提高档次,并提高租金,经市场调研,每间客房日租金每增加10元,客房出租数就会减少1间.每间客房日租金不得超过130元,要使每天客房的租金总收入不低于1 800元,该农家院每间客房日租金提高的空间有多大?解 设每间客房日租金提高x 个10元,即每间客房日租金提高到(80+10x )元,则客房出租数减少x 间,此时客房的租金总收入为(80+10x )(20-x )元.因为每天客房的租金总收入不低于1 800元,所以(80+10x )(20-x )≥1 800. 化简,得x 2-12x +20≤0.解得2≤x ≤10,所以20≤10x ≤100. 又由题意可知80+10x ≤130,所以10x ≤50.因此,该农家院每间客房日租金提高的空间是20~50元.1.不等式1+x1-x ≥0的解集为( )A .{x |-1<x ≤1}B .{x |-1≤x <1}C .{x |-1≤x ≤1}D .{x |-1<x <1}答案 B解析 原不等式⇔⎩⎪⎨⎪⎧(x +1)(x -1)≤0,x -1≠0,∴-1≤x <1.2.若集合A ={x |-1≤2x +1≤3},B =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪x -2x ≤0,则A ∩B 等于( )A .{x |-1≤x <0}B .{x |0<x ≤1}C .{x |0≤x <2}D .{x |0≤x ≤1}答案 B解析 ∵A ={x |-1≤x ≤1},B ={x |0<x ≤2}, ∴A ∩B ={x |0<x ≤1}.3.不等式x +1x≥5的解集是________.答案 ⎩⎨⎧⎭⎬⎫x ⎪⎪0<x ≤14 解析 原不等式⇔x +1x -5≥0⇔4x -1x ≤0⇔⎩⎪⎨⎪⎧x (4x -1)≤0,x ≠0,解得0<x ≤14.4.不等式x 2+ax +4<0的解集不是空集,则实数a 的取值范围是________. 答案 a >4或a <-4解析 ∵x 2+ax +4<0的解集不是空集, 即不等式x 2+ax +4<0有解,∴Δ=a 2-4×1×4>0,解得a >4或a <-4.5.某商品在最近30天内的价格y 1与时间t (单位:天)的关系式是y 1=t +10(0<t ≤30,t ∈N );销售量y 2与时间t 的关系式是y 2=-t +35(0<t ≤30,t ∈N ),则使这种商品日销售金额z 不小于500元的t 的取值范围为________. 答案 {t |10≤t ≤15,t ∈N } 解析 z =(t +10)(-t +35), 依题意有(t +10)·(-t +35)≥500,解得10≤t ≤15,t ∈N ,所以解集为{t |10≤t ≤15,t ∈N }.1.知识清单:(1)简单的分式不等式的解法. (2)不等式的恒成立问题. (3)一元二次不等式的实际应用. 2.方法归纳:转化、恒等变形.3.常见误区:(1)解分式不等式要等价变形.(2)利用一元二次不等式解决实际问题时,应注意实际意义.1.不等式x -2x +1≤0的解集是( )A .{x |x <-1或-1<x ≤2}B .{x |-1≤x ≤2}C .{x |x <-1或x ≥2}D .{x |-1<x ≤2} 答案 D解析 此不等式等价于⎩⎪⎨⎪⎧(x -2)(x +1)≤0,x +1≠0,∴-1<x ≤2.2.不等式3x -12-x≥1的解集是( )A.⎩⎨⎧⎭⎬⎫x ⎪⎪34≤x ≤2 B.⎩⎨⎧⎭⎬⎫x ⎪⎪34≤x <2 C.⎩⎨⎧⎭⎬⎫x ⎪⎪ x >2或x ≤34 D.⎩⎨⎧⎭⎬⎫x ⎪⎪x ≥34 答案 B解析 不等式3x -12-x ≥1,移项得3x -12-x -1≥0,即x -34x -2≤0,可化为⎩⎪⎨⎪⎧⎝⎛⎭⎫x -34(x -2)≤0,x -2≠0,解得34≤x <2,则原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪34≤x <2. 3.若关于x 的不等式ax -b >0的解集为{x |x >1},则关于x 的不等式ax +bx -2>0的解集为( )A .{x |x >1或x <-2}B .{x |1<x <2}C .{x |x >2或x <-1}D .{x |-1<x <2}答案 C解析 x =1为ax -b =0的根,∴a -b =0,即a =b , ∵ax -b >0的解集为{x |x >1},∴a >0, 故ax +b x -2=a (x +1)x -2>0,等价为(x +1)(x -2)>0. ∴x >2或x <-1.4.已知不等式-x 2+4x ≥a 2-3a 在R 上有解,则实数a 的取值范围为( ) A .{a |-1≤a ≤4} B .{a |-1<a <4} C .{a |a ≥4或a ≤-1} D .{a |-4≤a ≤1}答案 A解析 由题意知,原不等式可化为-(x -2)2+4≥a 2-3a 在R 上有解, ∴a 2-3a ≤4,即(a -4)(a +1)≤0,∴-1≤a ≤4.5.某地每年销售木材约20万立方米,每立方米价格为2 400元,为了减少木材消耗,决定按销售收入的t %征收木材税,这样每年的木材销售量减少52t 万立方米.为了既减少木材消耗又保证税金收入每年不少于900万元,则t 的取值范围是( ) A .{t |1≤t ≤3} B .{t |3≤t ≤5} C .{t |2≤t ≤4} D .{t |4≤t ≤6} 答案 B解析 设按销售收入的t %征收木材税时,税金收入为y 万元, 则y =2 400⎝⎛⎭⎫20-52t ×t %=60(8t -t 2). 令y ≥900,即60(8t -t 2)≥900.解得3≤t ≤5. 6.不等式x +5x -2>0的解集为________.答案 {x |x <-5或x >2} 解析x +5x -2>0⇔(x +5)(x -2)>0⇔x <-5或x >2. 7.不等式1x -1≥-1的解集是________.答案 {x |x ≤0或x >1}解析1x -1≥-1⇔1x -1+1≥0⇔x x -1≥0 ⇔⎩⎪⎨⎪⎧x (x -1)≥0,x -1≠0,∴不等式的解集是{x |x ≤0或x >1}.8.若实数a ,b 满足a +b <0,则不等式x +a b -x <0的解集为________.答案 {x |x >-a 或x <b }解析 原不等式等价于(x +a )(b -x )<0⇔(x -b )(x +a )>0. 因为a +b <0,所以b <-a .所以原不等式的解集为{x |x >-a 或x <b }. 9.解下列不等式: (1)2x -5x +4<0;(2)x +12x -3≤1. 解 (1)2x -5x +4<0⇔(2x -5)(x +4)<0⇔-4<x <52,∴原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪-4<x <52. (2)∵x +12x -3≤1,∴x +12x -3-1≤0,∴-x +42x -3≤0,即x -4x -32≥0.此不等式等价于(x -4)⎝⎛⎭⎫x -32≥0且x -32≠0, 解得x <32或x ≥4,∴原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <32或x ≥4. 10.某汽车厂上年度生产汽车的投入成本为10万元/辆,出厂价为12万元/辆,年销售量为10 000辆.本年度为适应市场需求,计划提高产品质量,适度增加投入成本.若每辆车投入成本增加的比例为x (0<x <1),则出厂价相应地提高比例为0.75x ,同时预计年销售量增加的比例为0.6x ,已知年利润=(出厂价-投入成本)×年销售量.(1)写出本年度预计的年利润y 与投入成本增加的比例x 的关系式;(2)为使本年度的年利润比上年度有所增加,则投入成本增加的比例x 应在什么范围内? 解 (1)由题意得y =[12(1+0.75x )-10(1+x )]×10 000×(1+0.6x )(0<x <1),整理得y =-6 000x 2+2 000x +20 000(0<x <1).(2)要保证本年度的年利润比上年度有所增加,必须有⎩⎪⎨⎪⎧ y -(12-10)×10 000>0,0<x <1,即⎩⎪⎨⎪⎧-6 000x 2+2 000x >0,0<x <1,解得0<x <13, 所以投入成本增加的比例x 应在0<x <13的范围内.11.二次不等式ax 2+bx +c <0的解集为全体实数的条件是( )A.⎩⎪⎨⎪⎧ a >0,Δ>0B.⎩⎪⎨⎪⎧ a >0,Δ<0C.⎩⎪⎨⎪⎧ a <0,Δ>0D.⎩⎪⎨⎪⎧a <0,Δ<0 答案 D解析 二次不等式ax 2+bx +c <0的解集为全体实数等价于二次函数y =ax 2+bx +c 的图象全部在x 轴下方,需要开口向下,且与x 轴无交点,故需要⎩⎨⎧ a <0,Δ<0.12.若a >0,b >0,则不等式-b <1x<a 的解集为( ) A.⎩⎨⎧⎭⎬⎫x ⎪⎪ x <-1b 或x >1a B.⎩⎨⎧⎭⎬⎫x ⎪⎪ -1a <x <1b C.⎩⎨⎧⎭⎬⎫x ⎪⎪ x <-1a 或x >1b D.⎩⎨⎧⎭⎬⎫x ⎪⎪-1b <x <0或0<x <1a 答案 A解析 原不等式可化为⎩⎨⎧ 1x >-b ,1x <a ,即⎩⎪⎨⎪⎧ bx +1x >0,ax -1x >0, 可得⎩⎨⎧ x <-1b 或x >0,x <0或x >1a , 故不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪ x <-1b 或x >1a . 13.设x 2-2x +a -8≤0对于任意x ∈{x |1≤x ≤3}恒成立,则a 的取值范围是________. 答案 {a |a ≤5}解析 原不等式x 2-2x +a -8≤0转化为a ≤-x 2+2x +8对任意x ∈{x |1≤x ≤3}恒成立,设y =-x 2+2x +8,易知y 在{x |1≤x ≤3}上的最小值为5.∴a ≤5.14.在一个限速40 km/h 的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是相碰了.事发后现场测得甲车的刹车距离略超过12 m ,乙车的刹车距离略超过10 m .又知甲、乙两种车型的刹车距离s m 与车速x km /h 之间分别有如下关系:s 甲=0.1x +0.01x 2, s 乙=0.05x +0.005x 2.则这次事故的主要责任方为________.答案 乙车解析 由题意列出不等式s 甲=0.1x +0.01x 2>12,s 乙=0.05x +0.005x 2>10.分别求解,得x 甲<-40或x 甲>30,x 乙<-50或x 乙>40.由于x >0,从而得x 甲>30 km /h ,x 乙>40 km/h.经比较知乙车超过限速,应负主要责任.15.不等式x 2+8y 2≥λy (x +y )对于任意的x ,y ∈R 恒成立,则实数λ的取值范围为________. 答案 -8≤λ≤4解析 因为x 2+8y 2≥λy (x +y )对于任意的x ,y ∈R 恒成立,所以x 2+8y 2-λy (x +y )≥0对于任意的x ,y ∈R 恒成立,即x 2-λyx +(8-λ)y 2≥0恒成立,由二次不等式的性质可得,Δ=λ2y2+4(λ-8)y2=y2(λ2+4λ-32)≤0,所以(λ+8)(λ-4)≤0,解得-8≤λ≤4.16.某热带风暴中心B位于海港城市A南偏东60°的方向,与A市相距400 km.该热带风暴中心B以40 km/h的速度向正北方向移动,影响范围的半径是350 km.问:从此时起,经多少时间后A市将受热带风暴影响,大约受影响多长时间?解如图,以A市为原点,正东方向为x轴建立直角坐标系.∵AB=400,∠BAx=30°,∴台风中心B的坐标为(2003,-200),x h后台风中心B到达点P(2003,40x-200)处.由已知,A市受台风影响时,有AP≤350,即(2003)2+(40x-200)2≤3502,整理得16x2-160x+375≤0,解这个不等式得,3.75≤x≤6.25,A市受台风影响的时间为6.25-3.75=2.5(h).故在3.75 h后,A市会受到台风的影响,时间长达2.5 h.。


2.3.1乘方第1课时有理数的乘方运算课时目标1.经历探索有理数乘方的意义的过程,体会转化的数学思想方法,培养学生的运算能力.2.理解乘方的意义,了解乘方与幂的关系,能识别指数和底数,掌握幂的符号法则,会进行乘方运算.3.经历发现问题、提出问题、分析问题和解决问题的过程,培养学生科学的思考问题的方法.学习重点乘方的意义以及幂的符号法则.学习难点幂、底数、指数的概念.课时活动设计情境引入问题1:如果一个正方形的边长为2,那么该正方形的面积是多少?问题2:如果一个正方体的棱长为2,那么该正方体的体积是多少?解:该正方形的面积为2×2,该正方体的体积为2×2×2.设计意图:创设情境,引入新课,为本节课的学习作铺垫.探究新知探究1有理数的乘方在上一教学活动中,所列的两个式子有什么特殊之处?你还能写出几个具有上述特征的式子吗?学生自主交流,独立完成,教师适时给予点拨.根据你发现的特征,完成下面的填空.(1)5×5×5记作53,读作5的3次方.(2)5×5×5×5记作54,读作5的4次方.(3)5×5×5×5×5记作55,读作5的5次方.⏟(4)5×5×5×…×5×5记作5n,读作5的n次方.n个5请你根据上面的内容,自己总结发现的规律.,记作a n,读作“a的n次方”.⏟总结:一般地,n个相同的乘数a相乘,即a·a·…·an个求n个相同乘数的积的运算,叫作乘方,乘方的结果叫作幂.在a n中,a叫作底数,n叫作指数,当a n看作a的n次方的结果时,也可读作“a的n次幂”.例如,在94中,底数是9,指数是4,94读作“9的4次方”,或“9的4次幂”.一个数可以看作这个数本身的1次方.例如,5就是51.指数1通常省略不写.因为a n就是n个a相乘,所以可以利用有理数的乘法运算来进行有理数的乘方运算.探究2幂的符号法则思考:(1)-26的底数是多少?它与(-2)6表示的意义相同吗?(2)计算,并将下表补充完整.思考:上表中的计算结果的符号有什么规律?学生归纳总结.总结:正数的任何次幂都是正数,负数的奇次幂是负数,负数的偶次幂是正数. 0的任何正整数次幂都是0.设计意图:通过探究引导学生思考有理数乘方的意义,区分-a n 与(-a )n ,通过让学生计算乘方,发现幂的符号规律,并总结出幂的符号法则.典例精讲 例1 计算:(1)(-4)3; (2)(-2)4; (3)(-23)3. 解:(1)(-4)3=(-4)×(-4)×(-4)=-64. (2)(-2)4=(-2)×(-2)×(-2)×(-2)=16. (3)(-23)3=(-23)×(-23)×(-23)=-827. 例2 用计算器计算(-8)5和(-3)6. 解:用带符号键的计算器.显示结果为-32 768.显示结果为729.因此,(-8)5=-32 768,(-3)6=729.设计意图:通过例题练习和讲解,提高学生的运算能力,并学会用计算器计算有理数的乘方运算,提高对新知识的应用能力.巩固训练1.(-2)3等于( C )A.-6B.6C.-8D.82.下列各组数中,运算结果相等的是( A )A.-53与(-5)3B.34与43C.-22与(-2)2D.(45)2与4253.计算3×3×…×32+2+⋯+2⏞ m 个3⏟ n 个2的结果为( A ) A.3m2nB.3m2nC.3mn 2D.m 32n4.(-2)5的底数是 -2 ,指数是 5 ,表示的意义是 5个-2相乘的积 ,即(-2)5= -32 .5.计算:(1)(-3)3; (2)(-5)4; (3)(-13)3; (4)0.23; (5)-72. 解:(1)(-3)3=(-3)×(-3)×(-3)=-27. (2)(-5)4=(-5)×(-5)×(-5)×(-5)=625. (3)(-13)3=(-13)×(-13)×(-13)=-127. (4)0.23=0.2×0.2×0.2=0.008. (5)-72=-(7×7)=-49.学生自主完成,教师订正并给予评价.设计意图:通过设置不同层次的练习,不仅能使学生的新知得到及时巩固,也能使学生的思维能力得到有效提高,能更好地将知识学以致用.最后针对练习结果进行统一订正,并对同学们的表现作出及时评价,体现课程评价在课堂中的合理运用.课堂小结1.乘方中的底数、指数和幂的概念,会求有理数的正整数指数幂,掌握乘方运算与乘法运算的关系,会进行有理数的乘方运算.2.强调有理数乘方的符号规律.3.负数的奇次幂是负数,负数的偶次幂是正数;正数的任何次幂都是正数;0的任何正整数次幂都是0.设计意图:学生通过自主反思,可加深对有理数乘方意义的理解,通过反思数学思想方法与活动经验,培养学生的数学思维品质,让学生学会学习,学会思考,使学生真正深入数学的学习过程中,抓住数学思维的内在实质.课堂8分钟.1.教材第52页练习第1,2,3题,第56页习题2.3第1,2题.2.七彩作业.教学反思第2课时有理数的混合运算课时目标1.能确定有理数加、减、乘、除、乘方混合运算的运算顺序,会进行有理数的混合运算,培养学生的运算能力.2.在进行有理数混合运算的过程中,能合理地使用运算律进行简化运算.学习重点掌握有理数混合运算的运算顺序,会进行有理数的混合运算.学习难点熟练合理使用运算律进行混合运算.课时活动设计情境引入计算:1. (1)-32; (2)(-3)2; (3)-16; (4)(-1)6. 2. -3÷25×52.3. 18-32÷8+(-2)2×5.问题:先计算,再思考上述运算中有几种运算?分别是什么?结合经验你能说说混合运算的运算顺序吗?设计意图:通过有理数的混合运算,让学生先独立思考运算顺序,然后谈一谈自己的理解,加深学生对运算顺序的理解.探究新知探究 有理数的混合运算问题:如何计算18-32÷8+(-2)2×5呢?分几步运算? 学生先独立思考,分解计算步骤.教师给出下述计算过程. 18-32÷8+(-2)2×5 ① ① ①所以原式=①-①+①=18-4+20=34.由此可知,有理数混合运算顺序:先算乘方,再算乘除,最后算加减.如果有括号,要先算括号内的.总结:有理数的加、减、乘、除、乘方混合运算的运算顺序为 1.先乘方,再乘除,最后加减; 2.同级运算,从左到右进行;3.如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行. 设计意图:通过探究,让学生确定有理数的加、减、乘、除、乘方混合运算的运算顺序,会进行有理数的混合运算,培养学生的运算能力.典例精讲 例1 计算:(1)2×(-3)3-4×(-3)+15;(2)(-2)3+(-3)×(-42+2)-(-3)2÷(-2).解:(1)原式=2×(-27)-(-12)+15=-54+12+15=-27.(2)原式=-8+(-3)×(-16+2)-9÷(-2)=-8+(-3)×(-14)-(-4.5)=-8+42+4.5=38.5. 例2 观察下面三行数: -2,4,-8,16,-32,64,…;① 0, 6, -6, 18, -30, 66, …; ① -1, 2, -4, 8, -16, 32, …. ①(1)第①行中的数可以看成按什么规律排列? (2)第①①行中的数与第①行中的数分别有什么关系? (3)取每行中的第10个数,计算这三个数的和.分析:观察第①行中的数,发现各数均为2的倍数,联系数的乘方,从符号和绝对值两方面考虑,可以发现排列的规律.解:(1)第①行中的数可以看成按如下规律排列:-2,(-2)2,(-2)3,(-2)4,….(2)对比第①①两行中位置对应的数,可以发现:第①行中的数是第①行中相应的数加2,即-2+2,(-2)2+2,(-2)3+2,(-2)4+2,…;对比第①①两行中位置对应的数,可以发现:第①行中的数是第①行中相应数的12,即(-2)×12,(-2)2×12,(-2)3×12,(-2)4×12,….(3)每行中的第10个数的和是(-2)10+[(-2)10+2]+(-2)10×12=1 024+(1 024+2)+1 024×12=1 024+1 026+512=2 562.设计意图:通过例1让学生得以练习,提高对有理数混合运顺序的应用能力;通过例2引导学生解决简单的规律性问题.巩固训练 计算:(1)(-1)8×3+(-2)4÷4; (2)(-3)3+(-12)3×16; (3)78×(23-12)×37÷54.解:(1)原式=1×3+16÷4=3+4=7. (2)原式=-27+(-18)×16=-27-2=-29. (3)原式=78×16×37×45=120.设计意图:通过设置练习,不仅能使学生的新知得到巩固,也能使学生的思维能力得到有效提高.课堂小结1.有理数混合运算顺序: 先乘方,再乘除,最后加减; 同级运算,从左到右进行;如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行. 2.探究简单的规律性问题.设计意图:回顾本节课内容,加深学生对本节课知识的理解,提高学生归纳总结及表达的能力.课堂8分钟.1.教材第54页练习,第56页习题2.3第3,11题. 2.七彩作业.教学反思2.3.2科学记数法课时目标1.借助身边熟悉的事物体会大数,发展学生的好奇心、想象力及创新意识.2.通过用科学记数法表示大数的学习,让学生从多种角度感受大数,促使学生重视大数的现实意义,以发展学生的数感.学习重点正确使用科学记数法表示大于10的数.学习难点正确掌握10n的特征以及科学记数法中n与数位的关系.课时活动设计情境引入地球距离月球表面约为384 000 000米.这样大的数,读写都有一定的困难.这节课我们就来学习表示大数的一种方法——科学记数法.设计意图:通过实际问题引入本节课的内容,激发学生的学习兴趣.探究新知探究科学记数法观察10的乘方,102=100,103=1 000,104=10 000,….问题1:等号左边10的指数与右边整数中0的个数有什么关系?教师引导学生得到左边10的指数与右边整数中0的个数相同,即10的n次幂等于10…0(在1的后面有n个0),因此可以利用10的乘方表示一些大数,例如,696 000=6.96×105,读作“6.96乘10的5次方(幂)”.像上面这样,把一个大于10的数表示成a×10n的形式(其中a大于或等于1,且a小于10,n是正整数),使用的是科学记数法.问题2:对于小于-10的数能否也用类似的方法表示呢?-567 000 000用这种方法应该怎样表示?学生分小组探究交流,教师将正确答案进行板书.解:-567 000 000=-5.67×108.设计意图:让学生经历用科学记数法表示数的探索过程,提高学生分析问题和解决问题的能力,增强学生的思维能力.典例精讲例用科学记数法表示下列各数:1 000 000,57 000 000,-123 000 000 000.解:1 000 000=1×106.57 000 000=5.7×107.-123 000 000 000=-1.23×1011.设计意图:通过例题讲解,让学生对科学记数法的表示得以运用,提高学生的运用能力.巩固训练1.用科学记数法表示下列各数:(1)352 000 000;(2)167 560 000;(3)602 000 000 000.解:(1)352 000 000=3.52×108.(2)167 560 000=1.675 6×108.(3)602 000 000 000=6.02×1011.2.下列用科学记数法表示的数,原来各是什么数?1×107,1.9×103,2.06×106.解:1×107=10 000 000,1.9×103=1 900,2.06×106=2 060 000.设计意图:通过练习,让学生巩固所学知识,加深对科学记数法的理解,提高学生的运算能力.课堂小结1.本节课主要学习用科学记数法表示大数的方法.应该注意:任意一个大于10的数表示成a×10n的形式,其中10的指数n应等于整数位数减1,1≤a<10,n是正整数.2.思考现实中还有哪些比较大的数,并用科学记数法表示出来.设计意图:学生通过反思,可进一步加深对科学记数法的理解,通过归纳总结,培养学生的数学思维品质,让学生学会学习,学会思考.课堂8分钟.1.教材第56页练习第1,2,3题,第56页习题2.3第4,5,9题.2.七彩作业.2.3.2科学记数法把一个大于10的数表示成a×10n的形式(其中a大于或等于1,且a小于10,n 是正整数),即为科学记数法.教学反思2.3.3近似数课时目标1.了解和掌握近似数的概念,能准确确定一个近似数的精确度.2.能根据要求用四舍五入法取近似数.学习重点近似数、精确度的概念.学习难点由给出的近似数求其精确度.课时活动设计回顾引入回顾什么是四舍五入法.设计意图:通过回顾旧知,引入本节课的学习.探究新知探究近似数和准确数1.宇宙的年龄约为138亿年,长江约长6 300千米,圆周率π约为3.14,每个三角形都有3个内角,某中学七年级共有10个班.上面语句中出现的数字中,哪些是与实际相符的?哪些是与实际相近的?学生分小组交流讨论.教师随后给出近似数和准确数的概念.准确数:与实际相符的数.近似数:与实际相近的数,通过测量或估计得到.2.小明和小颖分别测量了同一片树叶的长度,他们所用的直尺的最小单位是不同的,分别是厘米和毫米.问题:根据小明的测量,这片树叶的长度约为多少米?根据小颖的测量呢?谁的测量结果会更准确一些?学生自主探究.教师给出:近似数与准确数的接近程度,可以用精确度表示.追问:小明、小颖的测量分别精确到什么单位?解:分别精确到了十分位和百分位.按四舍五入法对圆周率π取近似数时,有π≈3(精确到个位),π≈3.1(精确到0.1,或叫作精确到十分位),π≈3.14(精确到0.01,或叫作精确到百分位),π≈3.142(精确到0.001,或叫作精确到千分位),π≈3.141 6(精确到0.000 1,或叫作精确到万分位),……设计意图:让学生通过实际情境理解近似数与准确数及精确度的概念.典例精讲例按括号内的要求,用四舍五入法对下列各数取近似数:(1)0.015 8(精确到0.001);(2)304.35(精确到个位);(3)1.804(精确到0.1);(4)1.804(精确到百分位).解:(1)0.015 8≈0.016.(2)304.35≈304.(3)1.804≈1.8.(4)1.804≈1.80.设计意图:通过例题让学生体会运用四舍五入法求近似数的方法.巩固训练用四舍五入法对下列各数取近似数:(1)0.012 36(精确到0.000 1);(2)688.753 2(精确到个位);(3)2.597 43(精确到0.01);(4)0.085 6(精确到千分位).解:(1)0.012 36≈0.012 4.(2)688.753 2≈689.(3)2.597 43≈2.60.(4)0.085 6≈0.086.设计意图:通过设置练习,不仅能使学生的新知得到巩固,也能使学生的思维能力得到有效提高.课堂小结1.本节课主要学习近似数的概念,并能按要求取近似数.2.通过这节课的学习,还有哪些收获呢?设计意图:学生通过反思,可进一步加深对近似数的理解.通过归纳总结,培养学生的数学思维品质,让学生学会学习,学会思考.课堂8分钟.1.教材第56页练习第4题,第56页习题2.3第6题.2.七彩作业.2.3.3近似数1.准确数和近似数.2.用四舍五入法求近似数.教学反思。


第三节水圈和水循环第二课时洋流【明确考点】洋流的概念、分类及分布规律。
洋流的地理意义。
【课堂互动】知识点一:洋流及分布规律自主学习1.洋流概念:海水沿相对稳定的____作______运动的现象。
2.洋流的形成因素:________是海洋水体运动的主要动力;________及________力能改变洋流的方向。
3.洋流的分类(1)按水温状况寒流:从______的海区流向______的海区的洋流。
暖流:从______的海区流向______的海区的洋流。
(2)按形成的主导因素:可分为____流、____流和____流三种类型;4.洋流的分布规律(1)以副热带为中心的大洋环流流向:北半球__时针,南半球__时针。
性质:大洋东部为____,西部为____。
(2)以副极地为中心的大洋环流(北半球)流向:__时针。
性质:大洋东部为__流,西部为__流。
(3)南半球中高纬海区:形成全球性的环流________。
(4)北印度洋海区受____的影响,形成季风洋流。
合作探究读教材图2-3-7“世界表层洋流分布”,回答下列问题。
(1)北太平洋中低纬度海区大洋环流的流向如何?南半球中低纬度海区大洋环流流向是怎样的?(2)南北半球中低纬度大洋环流东西两侧洋流性质有何差异?典例剖析例在世界洋流模式图中,A、B、C、D分别代表四个不同的大洋环流。
读图解答:(1)环流、呈顺时针方向流动。
(2)环流、流经大陆西岸时应为寒流。
(3)在环流B的都是形成大渔场的理想海区。
假如该图为大西洋,此处应是渔场。
(4)假如该图为大西洋,环流B的西部洋流名称是;环流C的南部洋流名称为。
解析:本题主要考查对世界大洋洋流模式图的识记和理解能力。
B、C是以副热带为中心的大洋环流,B在北半球为顺时针方向,C在南半球为逆时针方向;环流BC在大洋的东岸是由高纬流向低纬,属于寒流,在大洋的西岸是由低纬流向高纬,属暖流。
A、D属于分布在中高纬度以副极地为中心的大洋环流,在北半球为逆时针方向,在南半球为顺时针方向;环流AD在大洋的东岸是由低纬流向高纬,属暖流;在大洋东岸是由高纬流向低纬,属寒流。


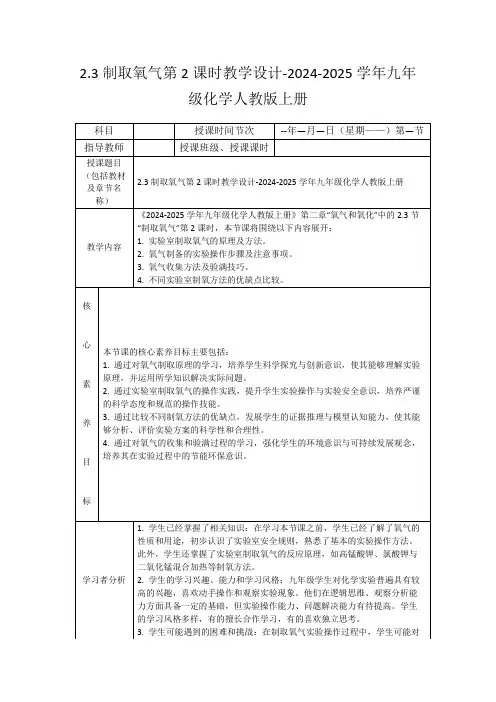

1.(2012·高考山东卷)圆(x +2)2+y 2=4与圆(x -2)2+(y -1)2=9的位置关系为( )A .内切B .相交C .外切D .相离解析:选B.两圆的圆心距离为17,两圆的半径之差为1、半径之和为5,而1<17<5,所以两圆相交.2.两圆x 2+y 2-4x +2y +1=0与x 2+y 2+4x -4y -1=0的公切线有( )A .1条B .2条C .3条D .4条解析:选C.∵两圆标准方程为(x -2)2+(y +1)2=4,(x +2)2+(y -2)2=9,∴圆心距d =(2+2)2+(-1-2)2=5,r 1=2,r 2=3.∴d =r 1+r 2,∴两圆外切,∴公切线有3条.3.过圆x 2+y 2+6x +4y =0与圆x 2+y 2+4x +2y -4=0的交点的直线方程是( )A .x +y +2=0B .x +y -2=0C .5x +3y -2=0D .不存在解析:选A.两圆方程相减即得.4.两圆交于A (1,3)及B (m ,-1),两圆的圆心均在直线x -y +n =0上,则m +n 的值为( )A .1B .3C .-3D .-1解析:选 B.由题意可知,k AB =-1且AB 的中点在直线x -y +n =0上,则⎩⎪⎨⎪⎧ -1-3m -1=-1,1+m 2-3-12+n =0,解得⎩⎪⎨⎪⎧m =5,n =-2, ∴m +n =3.5.点P 在圆x 2+y 2-8x -4y +11=0上,点Q 在圆:x 2+y 2+4x +2y +1=0上,则|PQ |的最小值是( )A .5B .0C .35-5D .5-3 5解析:选C.∵(x -4)2+(y -2)2=9的圆心为C 1(4,2),半径r 1=3,(x +2)2+(y +1)2=4的圆心为C 2(-2,-1),半径r 2=2,∴|C 1C 2|=35>r 1+r 2=5,∴两圆相离,∴|PQ |min =|C 1C 2|-r 1-r 2=35-5,故选C.6.已知圆(x -2)2+(y +3)2=13和圆(x -3)2+y 2=9交于A ,B 两点,则弦AB 的垂直平分线的方程是________.解析:弦AB 的垂直平分线也就是两圆连心线,因为两圆圆心分别是(2,-3)和(3,0).由两点式得y -3=x -32-3,即3x -y -9=0. 答案:3x -y -9=07.过两圆C 1:x 2+y 2-4x +2y +1=0与C 2:x 2+y 2-6x =0的交点,且过点(2,-2)的圆的方程为________.解析:设圆的方程为:x 2+y 2-4x +2y +1+λ(x 2+y 2-6x )=0,(λ≠-1)由于圆过(2,-2),可得22+(-2)2-4×2+2×(-2)+1+λ[22+(-2)2-6×2]=0,得λ=-34, 所以,所求圆的方程为x 2+y 2+2x +8y +4=0.答案:x 2+y 2+2x +8y +4=08.若⊙O :x 2+y 2=5与⊙O 1:(x -m )2+y 2=20(m ∈R )相交于A 、B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是________.解析:如图所示,在Rt △OO 1A 中,|OA |=5,|O 1A |=25,∴|OO 1|=5,∴|AC |=5×255=2, ∴|AB |=4.答案:49.求圆心在直线x +y =0上,且过圆x 2+y 2-2x +10y -24=0与圆x 2+y 2+2x +2y -8=0的交点的圆的方程.解:设圆的方程为x 2+y 2-2x +10y -24+λ(x 2+y 2+2x +2y -8)=0(λ≠-1),即x 2+y 2+2(λ-1)λ+1x +2(5+λ)λ+1y -8(λ+3)λ+1=0(λ≠-1). 圆心(1-λλ+1,-5+λλ+1),∴1-λλ+1-5+λλ+1=0, 解得λ=-2.故所求圆的方程为x 2+y 2-2x +10y -24-2(x 2+y 2+2x +2y -8)=0,即x 2+y 2+6x -6y +8=0.10.如图所示,在单位圆O 上任取C 点为圆心,作一圆与圆O 的直径AB 相切于点D ,圆C 与圆O 交于点E ,F ,求证:EF 平分CD .证明:取圆O 的直径AB 所在的直线为x 轴,圆心O 为坐标原点,建立平面直角坐标系,如图所示,则圆O 的方程为x 2+y 2=1.①设EF 与CD 相交于H ,令C (x 1,y 1),则可得圆C 的方程(x -x 1)2+(y -y 1)2=y 21,即x 2+y 2-2x 1x -2y 1y +x 21=0.②①-②得2x 1x +2y 1y -1-x 21=0,③③式就是直线EF 的方程.设CD 的中点为H ′,其坐标为(x 1,y 12),将H ′的坐标代入③式,得2x 21+2y 1·y 12-1-x 21=x 21+y 21-1=0,即H ′在EF 上,∴EF 平分CD .1.两圆x 2+y 2=16及(x -4)2+(y +3)2=R 2(R >0)在交点处的切线互相垂直,则R 等于( )A .3B .4C .5D .6解析:选A.由题意知两圆交点与两圆圆心构成直角三角形,可知(42+32)2=52=R 2+16,∴R =3.2.若实数x ,y 满足x 2+y 2=1,则y -2x -1的最小值等于________. 解析:y -2x -1表示圆上的点与定点(1,2)连线的斜率,令k =y -2x -1,画出图形,可知定点(1,2)与圆上的点的连线的倾斜角均小于90°,则当直线与圆在圆的上方相切时,斜率最小,直线方程可设为y -2=k (x -1),即kx -y -k +2=0.∴d =|-k +2|k 2+1=1,解得k =34. 答案:343.如图,圆C 与圆C 1:x 2+y 2-2x =0相外切,并且与直线l :x +3y =0相切于点P (3,-3),求此圆C 的方程.解:设所求圆的圆心为C (a ,b ),半径长为r .因为C (a ,b )在过点P 且与l 垂直的直线上, 所以b +3a -3= 3.① 又因为圆C 与l 相切于点P , 所以r =|a +3b |2.② 因为圆C 与C 1相外切,所以(a -1)2+b 2=|a +3b |2+1.③ 由①得3a -b -43=0,将其代入③得4a 2-26a +49=|2a -6|+1,解得⎩⎪⎨⎪⎧ a =4b =0或⎩⎨⎧a =0b =-43,此时r =2或r =6,所以所求圆C的方程为(x-4)2+y2=4或x2+(y+43)2=36.4.已知圆M:x2+y2-2mx-2ny+m2-1=0与圆N:x2+y2+2x+2y-2=0交于A、B 两点,且这两点平分圆N的圆周,求圆M的圆心的轨迹方程,并求其半径最小时,圆M的方程.解:两圆方程相减得公共弦AB所在直线的方程为2(m+1)x+2(n+1)y-m2-1=0.由于A、B两点平分圆N的圆周,∴AB为圆N的直径,即直线AB经过圆N的圆心.而N(-1,-1),∴-2(m+1)-2(n+1)-m2-1=0,即m2+2m+2n+5=0,即(m+1)2=-2(n+2)(n≤-2).由于圆M的圆心坐标为(m,n),从而可知圆M的圆心轨迹方程为(x+1)2=-2(y+2).又圆M的半径r=n2+1≥5(n≤-2).当且仅当n=-2,m=-1时取等号.故半径的最小值为5,此时圆M的方程为x2+y2+2x+4y=0.。
第2课时 等差数列前n 项和的性质及应用A 级:基础巩固练一、选择题1.S n 是等差数列{a n }的前n 项和,且S 9=9S 3,则{a n }的通项公式可能是( ) A .a n =4n -2 B .a n =4n -1 C .a n =4n +1 D .a n =4n +2 答案 A解析 设等差数列{a n }的公差为d ,则由S 9=9S 3得9a 1+36d =9(3a 1+3d ),化简得d =2a 1,若a n =4n -2,则d =4,a 1=2,适合题意,B ,C ,D 均不适合,故选A.2.等差数列{a n }的前n 项和为S n ,若S 3=-6,S 18-S 15=18,则S 18等于( ) A .36 B .18 C .72 D .9 答案 A解析 由S 3,S 6-S 3,…,S 18-S 15成等差数列,可知:S 18=S 3+(S 6-S 3)+(S 9-S 6)+…+(S 18-S 15)=6×-6+182=36.3.等差数列{a n }的前n 项和为S n ,若m >1,且a m -1+a m +1-a 2m =0,S 2m -1=38,则m 等于( ) A .38 B .20 C .10 D .9 答案 C解析 因为a m -1+a m +1-a 2m =0,所以a m -1+a m +1=a 2m .根据等差数列的性质得2a m =a 2m ,显然a m ≠0,所以a m =2.又因为S 2m -1=38,所以S 2m -1=2m -1a 1+a 2m -12=(2m -1)a m .将a m =2代入可得(2m -1)×2=38,解得m =10.故选C.4.设S n 是公差为d (d ≠0)的无穷等差数列{a n }的前n 项和,则下列命题错误的是( ) A .若d <0,则数列{S n }有最大项 B .若数列{S n }有最大项,则d <0C .若数列{S n }是递增数列,则对任意n ∈N *,均有S n >0 D .若对任意n ∈N *,均有S n >0,则数列{S n }是递增数列 答案 C解析 设{a n }的首项为a 1,则S n =na 1+12n (n -1)d =d 2n 2+⎝⎛⎭⎪⎫a 1-d 2n .由二次函数性质知S n有最大值时,则d <0,故A 、B 正确;因为{S n }为递增数列,则d >0,不妨设a 1=-1,d =2,显然{S n }是递增数列,但S 1=-1<0,故C 错误;对任意n ∈N *,S n 均大于0时,a 1>0,d >0,{S n }必是递增数列,D 正确.二、填空题5.已知四个数成等差数列,S 4=32,a 2∶a 3=1∶3,则公差d =________. 答案 8解析 设首项为a 1,公差为d ,则由a 2∶a 3=1∶3得a 1+d a 1+2d =13,∴d =-2a 1,又S 4=4a 1+4×32d =-8a 1=32,∴a 1=-4,d =8. 6.在等差数列{a n }中,a n =4n -52,a 1+a 2+…+a n =an 2+bn (n ∈N *),其中a ,b 均为常数,则ab =________.答案 -1解析 ∵a n =4n -52,∴a 1=32.设等差数列{a n }的公差为d ,则d =a n +1-a n =4.∴an 2+bn=a 1+a 2+…+a n =32n +nn -12×4=2n 2-12n .∴a =2,b =-12,故ab =-1.7.在等差数列{a n }中,a 1+a 2+a 3=15,a n +a n -1+a n -2=78,S n =155,则n =________. 答案 10解析 (a 1+a 2+a 3)+(a n +a n -1+a n -2) =3(a 1+a n )=15+78,∴a 1+a n =31. 又S n =n a 1+a n2=155,∴31n2=155⇒n =10.三、解答题8.在等差数列{a n }中,a 10=18,前5项的和S 5=-15, (1)求数列{a n }的通项公式;(2)求数列{a n }的前n 项和的最小值,并指出何时取得最小值. 解 (1)设{a n }的首项,公差分别为a 1,d .则⎩⎪⎨⎪⎧a 1+9d =18,5a 1+52×4×d =-15,解得a 1=-9,d =3, ∴a n =3n -12. (2)S n =n a 1+a n2=12(3n 2-21n ) =32⎝ ⎛⎭⎪⎫n -722-1478,∴当n =3或4时,前n 项的和取得最小值为-18.9.已知函数f (x )=x 2-2(n +1)x +n 2+5n -7,n ∈N *.(1)设函数y =f (x )的图象的顶点的纵坐标构成数列{a n },求证:{a n }为等差数列; (2)设函数y =f (x )的图象的顶点到x 轴的距离构成数列{b n },求{b n }的前n 项和S n . 解 (1)证明:因为f (x )=x 2-2(n +1)x +n 2+5n -7 =[x -(n +1)]2+3n -8, 所以a n =3n -8,因为a n +1-a n =3(n +1)-8-(3n -8)=3, 所以数列{a n }为等差数列. (2)由题意知,b n =|a n |=|3n -8|, 所以当1≤n ≤2时,b n =8-3n ,S n =b 1+b 2+…+b n =n b 1+b n 2=n [5+8-3n ]2=13n -3n 22,当n ≥3时,b n =3n -8,S n =b 1+b 2+b 3+…+b n =5+2+1+…+(3n -8)=7+n -2[1+3n -8]2=3n 2-13n +282.所以S n=⎩⎪⎨⎪⎧13n -3n 22,1≤n ≤2,n ∈N *,3n 2-13n +282,n ≥3,n ∈N *.10.已知数列{a n }的前n 项和为S n ,a n >0,且满足:(a n +2)2=4S n +4n +1,n ∈N *. (1)求a 1及通项公式a n ;(2)若b n =(-1)na n ,求数列{b n }的前n 项和T n . 解 (1)对于(a n +2)2=4S n +4n +1, ①n =1时,(a 1+2)2=4a 1+5,a 21=1,而a n >0,则a 1=1.又(a n +1+2)2=4S n +1+4(n +1)+1, ② 由②-①可得(a n +1+2)2-(a n +2)2=4a n +1+4,a 2n +1=(a n +2)2,而a n >0,∴a n +1=a n +2,即a n +1-a n =2.∴{a n }是等差数列,即a n =1+2(n -1)=2n -1.(2)∵b n =(-1)n·(2n -1),∴T n =-1+3-5+7+…+(-1)n(2n -1),当n 为偶数时,T n ==n ;当n 为奇数时,T n =-(2n -1)=-n .综上所述,T n =(-1)n·n .B 级:能力提升练1.一个凸多边形的内角成等差数列,其中最小的内角为120°,公差为5°,那么这个多边形的边数n 等于( )A .12B .16C .9D .16或9 答案 C解析 a n =120+5(n -1)=5n +115,由a n <180,得n <13且n ∈N *, 由n 边形内角和定理得,(n -2)×180=n ×120+n n -12×5,解得n =16或n =9.∵n <13,∴n =9.2.已知数列{a n }的前n 项和为S n ,点⎝ ⎛⎭⎪⎫n ,S n n 在直线y =12x +112上.数列{b n }满足b n +2-2b n +1+b n =0(n ∈N *),b 3=11,且其前9项和为153.(1)求数列{a n },{b n }的通项公式; (2)设=32a n -112b n -1,数列{}的前n 项和为T n ,求使不等式T n >k57对一切n ∈N *都成立的最大正整数k 的值.解 (1)由已知得S n n =12n +112,∴S n =12n 2+112n .当n ≥2时,a n =S n -S n -1=12n 2+112n -12(n -1)2-112(n -1)=n +5.当n =1时,a 1=S 1=6也符合上式, ∴a n =n +5(n ∈N *).由b n +2-2b n +1+b n =0(n ∈N *)知{b n }是等差数列. 由{b n }的前9项和为153, 可得9b 1+b 92=9b 5=153,得b 5=17,又∵b 3=11,∴{b n }的公差d =b 5-b 32=3.∵b 3=b 1+2d ,∴b 1=5.∴b n =3n +2. (2)=32n -16n +3=12⎝ ⎛⎭⎪⎫12n -1-12n +1,∴T n =12⎝ ⎛⎭⎪⎫1-13+13-15+…+12n -1-12n +1=12⎝⎛⎭⎪⎫1-12n +1.∵n 增大时,T n 增大,∴{T n }是递增数列. ∴T n ≥T 1=13.若T n >k57对一切n ∈N *都成立,只要T 1=13>k57,∴k <19,则k max =18.。