可见,保守力的功可写为
A保 F保 dr E pa E pb ( E pb E pa )
a
b
定义:Epa是系统在位置a的势能; Epb是系统在位置b的势能。
21
A保 F保 dr E pa E பைடு நூலகம்b ( E pb E pa )
a
b
上式的意义是: 保守力的功等于势能增量的负值。 若取b点为零势点,则由式我们得到系统在位置a 的势能为
a a
b
b
A1 A2 An
即:合力对某质点所作的功,等于在同一过程中各 分力所作功的代数和。 在直角坐标系中有
A ( Fx dx Fy dy Fz dz )
a
b
即:合力所作的功等于其直角分量所作功的代数和。 4
二、功率
单位时间内所作的功称功率,用P表示,单位, W(瓦特,瓦).
Mm Aab fds cos G 2 dr a ra r 1 1 GMm( ) ra rb
b rb
b rb
ds
dr m
r f
上式中的G是引力常数。 由式可见,万有引力的功也只与质 点始末位置有关,而与质点所经过的 实际路径形状无关。
M
ra
17
a
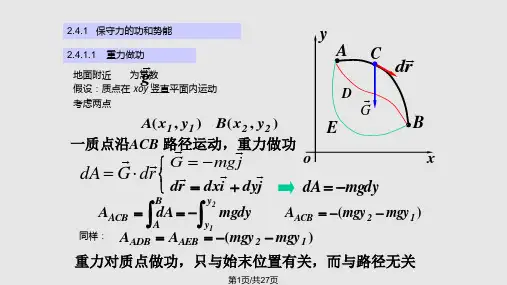
重力的功 设质量为m的质点沿一曲线L从a点运动到b点(高度 分别为ha和hb),如图所示;重力对质点m作的功为
25
§2-4 机械能守恒定律
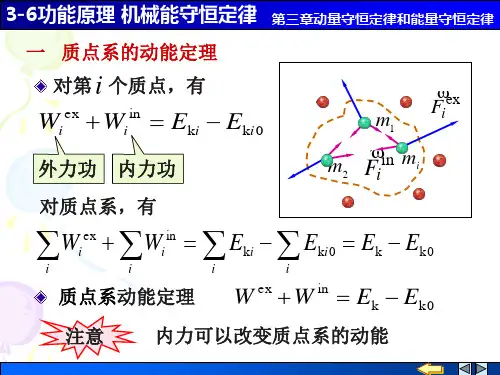
1.质点系动能定理 设系统由n个质点组成, 对mi 应用动能定理,有 1 1 2 2 Ai Ai内 Ai外 mii mii 0 2 2 式中:i=1,2,3,……。对上式求和得 1 1 2 2 Ai Ai内 Ai外 2mii 2mii0 i i i i i 写成: