第2章机构自由度的计算 共29页

第2章平面机构运动简图及机构自由度的计算机构由构件组成，各构件之间具有确定的相对运动。

然而，把构件任意拼凑起来不一定能运动；即使能够运动，也不一定具有确定的相对运动。

那么构件应如何组合才能运动？在什么条件下才具有确定的相对运动？这对分析现有机构或创新机构很重要。

所有构件的运动平面都相互平行的机构称为平面机构，否则称为空间机构。

本章仅讨论平面机构的情况，因为在生活和生产中，平面机构应用最多。

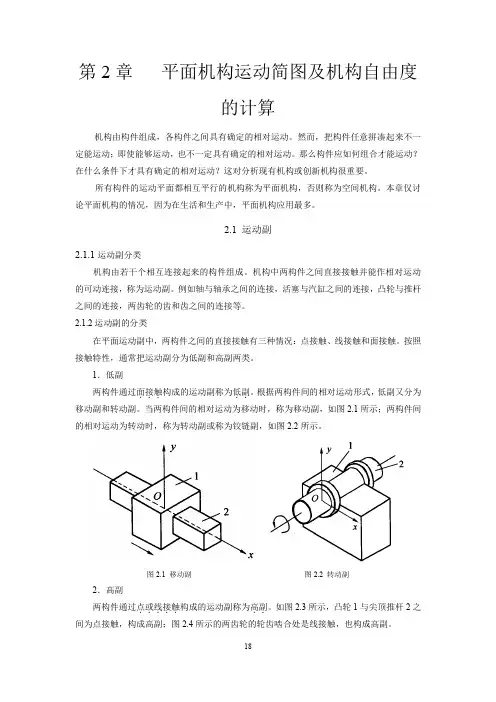
2.1 运动副2.1.1运动副分类机构由若干个相互连接起来的构件组成。

机构中两构件之间直接接触并能作相对运动的可动连接，称为运动副。

例如轴与轴承之间的连接，活塞与汽缸之间的连接，凸轮与推杆之间的连接，两齿轮的齿和齿之间的连接等。

2.1.2运动副的分类在平面运动副中，两构件之间的直接接触有三种情况：点接触、线接触和面接触。

按照接触特性，通常把运动副分为低副和高副两类。

1．低副两构件通过面接触．．。

根据两构件间的相对运动形式，低副又分为．．．构成的运动副称为低副移动副和转动副。

当两构件间的相对运动为移动时，称为移动副，如图2.1所示；两构件间的相对运动为转动时，称为转动副或称为铰链副，如图2.2所示。

图2.1 移动副图2.2 转动副2．高副两构件通过点或线接触．．．．．构成的运动副称为高副．．。

如图2.3所示，凸轮1与尖顶推杆2之间为点接触，构成高副；图2.4所示的两齿轮的轮齿啮合处是线接触，也构成高副。

图2.3 凸轮高副图2.4 齿轮高副低副因通过面接触而构成运动副，故其接触处的压强小，承载能力大，耐磨损，寿命长，且因其形状简单，所以容易制造。

低副的两构件之间只能作相对滑动；而高副的两构件之间则可作相对滑动或滚动，或两者并存。

2.2 机构运动简图实际构件的外形和结构往往很复杂，在研究机构运动时，为了突出与运动有关的因素，将那些无关的因素删减掉，保留与运动有关的外形，用规定的符号来代表构件和运动副，并按一定的比例表示各种运动副的相对位置。

机构自由度计算原理和方法机构自由度计算那可是相当重要哇！这就好比是给机构做一次全面的体检，能让我们清楚地了解机构的运动能力和灵活性。

那到底啥是机构自由度呢？简单来说，就是机构具有独立运动的数目。

计算机构自由度的步骤那可得仔细说说。

首先，要确定机构中的活动构件数目。

这就像是数数一样，把那些能运动的部分都找出来。

然后呢，计算低副和高副的数目。

低副就像是两个构件之间的紧密连接，比如转动副、移动副啥的。

高副呢，就是点接触或者线接触的地方，比如凸轮和从动件之间的接触。

接着，就可以用公式F = 3n - 2PL - PH 来计算自由度啦。

这里的n 是活动构件数目，PL 是低副数目，PH 是高副数目。

在计算过程中有啥注意事项呢？哎呀，那可不少呢！首先得正确判断活动构件和固定构件，可不能搞错了。

还有啊，对于复杂的机构，要仔细分析各个部分的连接关系，别漏算或者多算了低副和高副。

这就好比做饭的时候，要是调料放错了，那味道可就全变啦！那在这个过程中安全性和稳定性又咋体现呢？如果机构的自由度计算不准确，就可能导致设计出的机构在运动过程中出现不稳定的情况。

比如说，自由度太多了，机构可能会变得过于灵活，甚至出现乱动的情况，这多吓人啊！相反，如果自由度太少，机构可能就无法按照预期的方式运动，那不是白忙活了嘛。

所以啊，准确计算机构自由度对于保证机构的安全性和稳定性至关重要。

机构自由度计算的应用场景那可多了去了。

在机械设计中，它可以帮助设计师确定机构的运动方案，选择合适的构件和连接方式。

在机器人领域，更是离不开自由度的计算，只有准确知道机器人的自由度，才能让它完成各种复杂的动作。

这就像给机器人装上了一双灵活的手脚，让它能在各种环境中大展身手。

它的优势也是显而易见的。

通过计算自由度，可以快速评估机构的性能，节省设计时间和成本。

而且，还能提前发现潜在的问题，避免在实际生产中出现故障。

这不是一举两得嘛！咱再来看看实际案例。

比如说汽车的发动机，里面就有很多复杂的机构。

机构的自由度计算公式一、机构自由度的基本概念。

1. 定义。

- 机构的自由度是指机构具有的独立运动的数目。

它是衡量机构运动灵活性的一个重要指标。

例如，一个平面机构能够在平面内进行独立运动的方式数量就是它的自由度。

二、平面机构自由度的计算公式。

1. 一般公式。

- 对于平面机构，自由度计算公式为F = 3n - 2P_L-P_H。

- 其中，n为机构中活动构件的数目。

这里的活动构件是指能够相对运动的构件，例如在一个简单的曲柄滑块机构中，曲柄、连杆和滑块都是活动构件。

- P_L为低副的数目。

低副是指两构件之间以面接触而构成的运动副，常见的低副有转动副（如轴与轴承之间的连接，允许相对转动）和移动副（如滑块与导轨之间的连接，允许相对移动）。

- P_H为高副的数目。

高副是指两构件之间以点或线接触而构成的运动副，例如齿轮的啮合（轮齿之间为线接触）、凸轮与从动件之间的接触（点或线接触）。

2. 计算示例。

- 以曲柄滑块机构为例，它有3个活动构件（n = 3），4个低副（P_L=4，包括曲柄与机架之间的转动副、连杆与曲柄之间的转动副、连杆与滑块之间的转动副、滑块与导轨之间的移动副），没有高副（P_H = 0）。

- 根据自由度计算公式F=3n - 2P_L-P_H，可得F = 3×3-2×4 - 0=9 - 8=1，这表明曲柄滑块机构具有1个自由度，即它只有一种独立的运动方式。

3. 特殊情况说明。

- 当计算出的自由度F≤slant0时，机构一般不能运动或者是具有特殊的结构约束情况。

例如，如果F = 0，机构就成为一个刚性桁架结构，各构件之间相对位置固定，不能产生相对运动。

- 在计算自由度时，要准确判断活动构件、低副和高副的数量，有时可能存在虚约束的情况。

虚约束是一种对机构运动不起实际约束作用的约束，在计算自由度时需要去除虚约束的影响，否则会得出错误的自由度结果。

例如，在平行四边形机构中，如果存在一些对运动不起实际限制作用的约束，在计算自由度时需要正确识别并处理这些虚约束。

第二章机构的组成及其自由度的计算一、学习要求1.搞清构件、运动副、约束、自由度及运动链等重要概念。

2.能绘制比较简单的机械的机构运动简图。

3.能正确计算平面机构的自由度并能判断其是否具有确定的运动。

4.对虚约束对机构工作性能的影响有所认识。

二、本章重点及难点本章的重点是构件、运动副、运动链等的概念,机构运动简图的绘制,机构具有确定运动的条件及机构自由度的计算。

本章的难点是机构中虚约束的判定问题。

三、思考题1．何谓构件?构件与零件有何区别?2．何谓高副?何谓低副?在平面机构中高副和低副一般各带入几个约束?齿轮副的约束数应如何确定?3．何谓运动链?运动链与机构有何联系和区别?4．何谓机构运动简图?它与机构示意图有何区别?绘制机构运动简图的目的和意义是什么?绘制机构运动简图的主要步骤如何?5．何谓机构的自由度?在计算平面机构的自由度时应注意哪些问题?6．什么是虚约束?虚约束对机构有哪些重要影响?7．机构具有确定运动的条件是什么?该条件是在什么前提下获得的?若不满足这一条件,机构将会出现什么情况?四、练习题2-1 试画出图2-1所示泵机构的机构运动简图,并计算其自由度。

2-2 试画出图2-2所示冲压机构的机构运动简图,并判断其是否有确定的相对运动。

2-3 试计算图2-3所示凸轮-连杆组合机构的自由度。

2-4 试确定图2-4所示机构的自由度。

图2-1 图2-2图2-3图2-42-5 图2-5所示为一小型压力机，试绘制其机构运动简图，并计算其自由度。

图2-52-6 试计算图2-6中所示两种压力机的自由度。

图2-62-7 试计算图2－7中所示凸轮－连杆组合机构的自由度。

图2-72-8 试计算图2-8中所示各平面高副机构的自由度。

a) b)图2-13。

机构自由度计算方法机构自由度的计算例子机械原理机构自由度的计算是机构的结构分析的重要内容。

任何一个机构设计好以后，需要做的第一件事情就是计算机构的自由度。

机构自由度的计算公式是：F=3n-2p l-p h。

公式本身简单，只需要数出活动构件的数目n，低副的数目p l，高副的数目p h,则自由度就很容易计算了。

使用该公式有一个前提，就是要先判断出一些特殊情况：复合铰链，局部自由度和虚约束，在把这些情况都弄清楚后，再用上述公式计算，才可以得到正确的结果。

下面举一个例子，说明机构自由度的计算方法。

计算图示机构的自由度，并判断该机构是否具有确定运动。

如有复合铰链、局部自由度、虚约束，请直接在题图中标出。

拿到该机构以后，第一步就是找到凸轮M，发现推杆DB尖端有一个滚子，此滚子就是局部自由度。

局部自由度几乎永远出现在滚子推杆的凸轮机构中。

对于该局部自由度，处理方法是把该滚子B与BD杆焊接在一起，成为一个整体。

接着考察虚约束。

虚约束中最常见的就是某一个构件和机架之间有导路重合或者平行的移动副。

这里FH构件就在F,G,H三个地方有三个移动副与机架相联，而这三个移动副导路重合。

此时只有一个起作用，其它的就是虚约束。

对于虚约束，只保留其中一个，其它的全部拿掉。

最后考虑复合铰链。

复合铰链出现在转动副的地方，如果在转动副处有2个以上的构件相联，则该铰链就是复合铰链。

从上图可以看出，J点有三个构件IJ,KJ,JL相连，所以J 是复合铰链。

对于复合铰链，在计算转动副的数目时，在此处留心即可，注意这里的转动副数目等于相连的构件数目减1.综上所述，把局部自由度，虚约束，复合铰链表示出来的结果见下图这样，把滚子B和BD焊接在一起，从而去掉局部自由度；而去掉G，H这两个虚约束；J点有两个转动副。

下面进入公式的计算。

活动构件：齿轮A，齿轮M，连杆IJ,连杆KJ，连杆JL，滑块L，连杆BD(焊接了滚子B)，连杆DE，连杆FH。

共计9个。