专题：小船渡河及绳子末端速度的分解问题(学校学案)

素养提升课(一) 小船渡河与关联速度问题1．进一步理解合运动与分运动，掌握运动合成与分解的方法。

2．能利用运动的合成与分解的知识，分析小船渡河问题和关联速度问题。

小船渡河问题1．运动分析：小船渡河时，同时参与了两个分运动：一个是船相对水的运动(即船在静水中的运动)，一个是船随水漂流的运动。

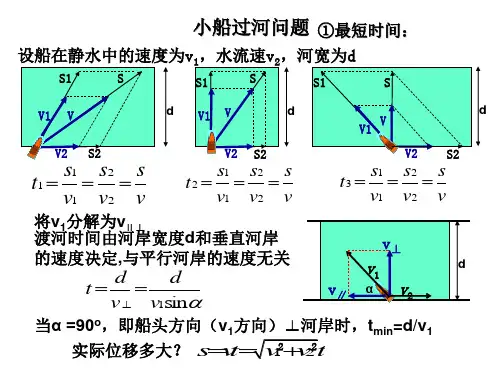
2．两类常见问题 (1)渡河时间问题①渡河时间t 取决于河宽d 及船沿垂直河岸方向上的速度大小，即t ＝dv ⊥。

②若要渡河时间最短，只要使船头垂直于河岸航行即可，如图所示，此时t ＝dv 船。

(2)最短位移问题①若v 水<v 船，如图甲所示，最短的位移为河宽d ，船头与上游河岸夹角满足cos θ＝v 水v 船。

②若v 水>v 船，如图乙所示，从出发点A 开始作矢量v 水，再以v 水末端为圆心，以v 船的大小为半径画圆弧，自出发点A 向圆弧作切线即为船位移最小时的合运动的方向。

这时船头与河岸夹角θ满足cos θ＝v 船v 水，最短位移x 短＝dcos θ。

【典例1】 一小船渡河，河宽d ＝180 m ，水流速度v 1＝2.5 m/s ，船在静水中的速度为v 2＝5 m/s ，则：(1)欲使船在最短的时间内渡河，船头应朝什么方向？用多长时间？位移是多少？ (2)欲使船渡河的航程最短，船头应朝什么方向？用多长时间？位移是多少？(3)如果其他条件不变，水流速度变为6 m/s 。

船过河的最短时间和最小位移是多少？[思路点拨] 求解小船渡河问题应理清以下问题： (1)船头指向是小船在静水中的速度的方向。

(2)小船实际运动的方向是合速度的方向。

(3)v 水＞v 船时，小船不能垂直河岸渡河。

[解析] (1)欲使船在最短时间内渡河，船头应朝垂直河岸方向，当船头垂直河岸时，如图甲所示。

时间t ＝d v 2＝1805s ＝36 sv 合＝√v 12+v 22＝5√52m/s位移为x ＝v 合t ＝90√5 m 。

C．小船在垂直于河岸方向的速度会随水流速度的变化而变化D．小船沿直线到达对岸[例4](多选)下列图中实线为河岸，河水的流动方向如图v的箭头所示，虚线为小船从河岸M驶向对岸N的实际航线．则其中可能正确的是()[例5]小船匀速横渡一条河流，当船头垂直对岸方向航行时，在出发后10 min到达对岸下游120 m处；若船头保持与河岸成θ角向上游航行，则在出发后12.5min到达正对岸，求：(1)水流速度大小v1；(2)船在静水中的速度大小v2；(3)河的宽度；(4)船头与河岸的夹角θ。

【关联速度】1、如图，人拉绳的速度为v，求船在静水中前进速度为多少？2、如图所示，汽车在岸上用轻绳拉船，若汽车行进速度为v，拉船的绳与水平方向夹角为π6，则船速度为（）A．33v B．3v C．233v D．32v3、如图所示，在水平力F作用下，物体B沿水平面向右运动，物体A恰匀速上升，以下说法正确的是（）A．物体B正向右做匀减速运动B．物体B正向右做加速运动C．地面对B的摩擦力减小D．斜绳与水平方向成30o时，v A ：v B=3꞉ 24、A、B两物体通过一根跨过光滑轻质定滑轮的不可伸长的轻绳相连放在水平面上，现物体A 以v1的速度向右匀速运动，当绳被拉成与水平面夹角分别是α、β时，如图所示，物体B的运动速度v B为(绳始终有拉力)( )A.v1sin αsin βB.v1cos αsin βC.v1sin αcos βD.v1cos αcos β5、如图所示，沿竖直杆以速度v匀速下滑的物体A通过轻质细绳拉光滑水平面上的物体B，细绳与竖直杆间的夹角为θ，则以下说法正确的是（）A．物体B向右匀速运动B．物体B向右先加速运动，后减速运动C．物体B向右减速运动D．物体B向右加速运动。

第2节运动的合成与分解第2课时小船渡河问题【学习目标】1．能运用合成和分解的思想分析“小船渡河”模型。

【知识梳理】一、小船渡河1．船的合运动与分运动(1)船的合运动：小船在河流中实际的运动，即相对岸边(地面)的速度v(2)船的分运动：①船相对水的运动，即船在静水中的运动v，它的方向与船身的指向相同；船，它的方向与河岸平行。

②船随水漂流的运动，即速度等于水的流速v水2．两类最值问题v<v时，船头斜向上游，【学习过程】[例1]已知某船在静水中的速度为v1＝4 m/s，现让船渡过某条河，假设这条河的两岸是理想的平行线，河宽为d＝100 m，水流速度为v2＝3 m/s，方向与河岸平行．(1)欲使船以最短时间渡河，航向怎样？最短时间是多少？船发生的位移有多大？(2)欲使船以最小位移渡河，航向又怎样？渡河所用时间是多少？答案：(1)船头垂直于河岸渡河t＝25 s x＝125 m(2)船头斜指向上游河对岸，且与河岸所成夹角为θ，cosθ＝34t＝10077s[变式训练1-1]一小船在静水中的速度为3 m/s，它在一条河宽为150 m，水流速度为4 m/s的河流中渡河，则该小船()．A．能到达正对岸B．渡河的时间可能少于50 sC．以最短时间渡河时，它沿水流方向的位移大小为200 mD．以最短位移渡河时，位移大小为150 m答案：C[变式训练1-2]船在静水中的速度与时间的关系如图甲所示，河水的流速随离一侧河岸的距离的变化关系如图乙所示，经过一段时间该船以最短时间成功渡河，下列对该船渡河的说法错误的是()A．船在河水中的最大速度是5 m/sB．船渡河的时间是150 sC．船在行驶过程中，船头必须始终与河岸垂直D．船渡河的位移是13×102 m答案：B【巩固训练】1．一条小船正在以5 m/s的速度且船头指向对岸渡河，水流速度为3 m/s，若河宽为200 m，试分析计算：(1)船能否到达出发点的正对岸？(2)船员登陆的地点离船出发点正对岸的距离是多少．2．小船在静水中的速度一定，今小船要渡过一条河，渡河时小船垂直指向河岸，若越靠近河中间，水流速度越大，则下列对小船运动分析正确的是( ) A．小船渡河时间不变B．小船能够垂直到达对岸C．小船在垂直于河岸方向的速度会随水流速度的变化而变化D．小船沿直线到达对岸3．如图所示，河水由西向东流，河宽为800 m，河中各点的水流速度大小为v水，各点到较近河岸的距离为x，v水与x的关系为v水＝3400x(m/s)(x的单位为m)，让小船船头垂直河岸由南向北渡河，小船划水速度大小恒为v船＝4 m/s，则下列说法正确的是()A．小船渡河的轨迹为直线B．小船在河水中的最大速度是5 m/sC．小船在距南岸200 m处的速度小于在距北岸200 m处的速度D．小船渡河的时间是160 s4．(多选)下列图中实线为河岸，河水的流动方向如图v的箭头所示，虚线为小船从河岸M驶向对岸N的实际航线．则其中可能正确的是()．5．如图所示，甲、乙两同学从河中O点出发，分别沿直线游到A点和B点后，立即沿原路线返回到O点，OA、OB分别与水流方向平行和垂直，且OA＝OB．若水流速度不变，两人在静水中游速相等，则他们所用时间t甲、t乙的大小关系为()．A．t甲<t乙B．t甲＝t乙C．t甲>t乙D．无法确定6．小船匀速横渡一条河流，当船头垂直对岸方向航行时，在出发后10 min到达对岸下游120 m处；若船头保持与河岸成θ角向上游航行，则在出发后12.5min到达正对岸，求：(1)水流速度大小v1；(2)船在静水中的速度大小v2；(3)河的宽度；(4)船头与河岸的夹角θ。

小船渡河与关联速度问题 习题课一【前提测评】限时2.5分钟1．合运动和分运动：一个物体同时参与两种运动时，这两种运动是____运动，而物体的实际运动叫做___运动．2．位移的合成与分解：一个物体同时发生两个方向的分位移与这个物体的合位移的效果可以相互____．由分位移求合位移叫做位移的_____；由合位移求分位移叫做位移的____．位移的合成与分解遵循矢量合成的_______定则．3．速度的合成与分解：物体同时发生的两个方向上的分速度与这个物体的合速度的效果也可以相互___，速度的合成与分解也遵循____________定则．4.小船渡河的最短时间：5.小船渡河的最短位移：（1）船速大于水速： （2）船速小于水速：6.关联速度可分解为： 和二【学习目标】1. 准确说出小船渡河和关联速度的相关要点前测。

2. 通过解决问题，总结解题的注意事项．三 【围标】例题1 .(2019·山西平遥中学高一下期中)在抗洪抢险中，战士驾驶摩托艇救人，假设江岸是平直的，洪水沿江向下游流去，水流速度为v 1，摩托艇在静水中的航速为v 2，战士救人的地点A 离岸边最近处O 的距离为d ，若战士想在最短时间内将人送上岸，则摩托艇登陆的地点离O 点的距离为( ) A.d v 2v 22－v 21 B .0 C.d v 1v2 D.d v 2v 12 .(多选)(2019·山东省实验中学高一下期中)如图2，河水由西向东流，河宽为800 m ，河中各点的水流速度大小为v 水，各点到较近河岸的距离为x ，v 水与x 的关系为v 水＝3400x (m /s)，让小船船头垂直河岸由南向北渡河，小船在静水中的速度大小恒为v 船＝4 m/s ，下列说法正确的是( )A.小船渡河的轨迹为直线B.小船在河水中的最大速度是5 m/sC.小船渡河的时间是200 sD.小船在距南岸200 m 处的速度小于距北岸200 m 处的速度3.(2019·眉山高中下学期期末质检)如图8所示，人用轻绳通过定滑轮拉穿在光滑竖直杆上的物块A ，人以速度v 0向左匀速拉绳，某一时刻，绳与竖直杆的夹角为θ，与水平面的夹角为α，此时物块A 的速度v 1为( )A.v 1＝v 0sin αcos θB.v 1＝v 0sin αsin θC.v 1＝v 0cos αcos θD.v 1＝v 0cos αcos θ4.如图10所示，河宽d ＝120 m ，设小船在静水中的速度为v 1，河水的流速为v 2.小船从A 点出发，若船头指向河对岸上游的B 点，经过10 min ，小船恰好到达河正对岸的C 点；若船头指向河正对岸的C 点，经过8 min ，小船到达C 点下游的D 点.求： (1)小船在静水中的速度v 1的大小；(2)河水的流速v 2的大小；(3)在第二次渡河中小船被冲向下游的距离s CD .5.一辆车通过一根跨过光滑轻质定滑轮的轻绳提升一个质量为m 的重物，开始车在滑轮的正下方，绳子的端点离滑轮的距离是H.车由静止开始向左做匀加速直线运动，经过时间t绳子与水平方向的夹角为θ，如图11所示.试求：(1)车向左运动的加速度的大小；(2)重物m在t时刻速度的大小.（一）【自主学习】限时：4分钟自学指导：1 能准确找到被分解的合速度（即实际速度）。

专题拓展课一小船过河与关联速度问题【学习目标要求】 1.通过实例分析进一步理解运动的合成与分解的原理。

2.会用运动合成与分解的理论分析小船过河问题。

3.会分析实际运动中的关联速度问题。

拓展点1小船过河问题1.小船参与的两个分运动(1)船相对水的运动(即船在静水中的运动)，它的方向与船头的指向相同。

(2)船随水漂流的运动，它的方向与河岸平行。

2.区别三个速度：水流速度v水、船在静水中的速度v船、船的实际速度(即船的合速度)v合。

3.两类最值问题(1)渡河时间最短问题由于水流速度始终沿河道方向，不能提供指向河对岸的分速度。

因此若要渡河时间最短，只要使船头垂直于河岸航行即可。

由图甲可知，t短＝dv船，此时船渡河的位移x＝dsin θ，位移方向满足tan θ＝v船v水。

甲(2)渡河位移最短问题①v水＜v船最短的位移为河宽d，此时渡河所用时间t＝dv船sin θ，船头与上游河岸夹角θ满足cos θ＝v水v船，如图乙所示。

乙②若v水>v船，如图丙所示，从出发点A开始作矢量v水，再以v水末端为圆心，以v船的大小为半径画圆弧，自出发点A向圆弧作切线即为船位移最小时的合运动的方向。

这时船头与上游河岸夹角θ满足cos θ＝v船v水，最短位移x短＝dcos θ，而渡河所用时间仍用t＝dv船sin θ计算。

丙【例1】(2020·黑龙江哈尔滨三中高一月考)某人以一定的速度使船头垂直于河岸向对岸划船，当水流匀速时，对于他过河所需时间、发生的位移与水速的关系描述正确的是()A.水速小时，位移小，时间短B.水速大时，位移大，时间长C.水速大时，位移大，时间不变D.位移、时间与水速无关解析由分运动和合运动具有独立性和等时性可知，水流速度对过河时间没有影响，水速大时，合速度较大，位移较大，故只有C项正确。

答案 C【例2】已知某船在静水中的速度为v1＝5 m/s，现让船渡过某条河，假设这条河的两岸是理想的平行线，河宽为d＝100 m，水流速度为v2＝3 m/s，方向与河岸平行，(1)欲使船以最短时间渡河，渡河所用时间是多少？位移的大小是多少；(2)欲使船以最小位移渡河，渡河所用时间是多少？(3)若水流速度为v2′＝6 m/s，船在静水中的速度为v1＝5 m/s不变，船能否垂直河岸渡河？解析(1)由题意知，当船在垂直于河岸方向上的分速度最大时，渡河所用时间最短，河水流速平行于河岸，不影响渡河时间，所以当船头垂直于河岸渡河时，所用时间最短，最短时间为t＝dv1＝1005s＝20 s。

小船渡河问题分析(1)船的实际运动是水流的运动和船相对静水的运动的合运动． (2)三种速度：v 1(船在静水中的速度)、v 2(水流速度)、v (船的实际速度)． (3)三种情景①过河时间最短：船头正对河岸时，渡河时间最短，t 短＝dv 1(d 为河宽)．②过河路径最短(v 2<v 1时)：合速度垂直于河岸时，航程最短，s 短＝d .船头指向上游与河岸夹角为α，cos α＝v 2v 1.③过河路径最短(v 2>v 1时)：合速度不可能垂直于河岸，无法垂直渡河．确定方法如下：如图所示，以v 2矢量末端为圆心，以v 1矢量的大小为半径画弧，从v 2矢量的始端向圆弧作切线，则合速度沿此切线方向航程最短．由图可知：cos α＝v 1v 2，最短航程：s 短＝dcos α＝v 2v 1d .两类问题、三种情景题型一v 船>v 水1．（2019·四川·成都七中实验学校高一期末）金马河流经温江后河宽逐渐增大，由300米扩至1200米，是温江的一张名片。

如图所示，一条小船位于400m 宽的河中央A 点处，从这里向下游处有一危险的急流区，当时水流速度恒定为4m/s ，为使小船避开危险区沿直线到达对岸；小船在静水中的速度至少为（ ）Am/s B ．2m/s Cm/s D ．4m/s2．（2021·四川·成都七中高一期中）一船在静水中的速度大小恒定为v 1，水流速度的方向沿着河岸向右且大小恒定为v 2，且v 1>v 2，河岸宽度恒定为d 。

小船从O 点开始渡河，图中OB 垂直于河岸，AB =BC =L 。

已知当小船划行方向垂直于河岸时，小船正好航行到C 点。

下列说法中正确的是（ ）A ．12v L v d=B ．若小船改变划行方向，最终到达对岸A 点，则从O 点到A 点所用时间等于小船航行到C 点所用时间C ．若小船的划行方向沿OA 方向，则小船最终会航行到BC 之间的某一点D ．若小船改变划行方向，最终到达对岸B 点，则从O 点到B3．（2021·辽宁·沈阳市第一二〇中学高一阶段练习）如图所示，一条小河河宽d =60 m ，水速v 1=3 m/s 。