化工热力学各章小结
- 格式:doc
- 大小:521.00 KB
- 文档页数:20
化工热力学总结一、单选/填空1. 逸度与逸度系数纯物质逸度i f :用逸度f 来表示实际气体的压力的函数真实气体i f RT G ln d d =,理想气体p f i =逸度与压力单位相同,不可测量,只能计算,可视为矫正的压力。
物理意义:表征体系的逃逸趋势。
逸度系数:物质逸度与其压力之比p f i2. 偏摩尔性质定义:在恒温恒压下,物质的广度性质随某种组分i 摩尔数的变化率,叫做组份i 的偏摩尔性质。
公式:ij n p T i i n nM M ≠⎥⎦⎤⎢⎣⎡∂∂=,,)( 物理意义:在恒温恒压下,物系中某组分i 摩尔数的变化所引起物系一系列热力学性质的变化。
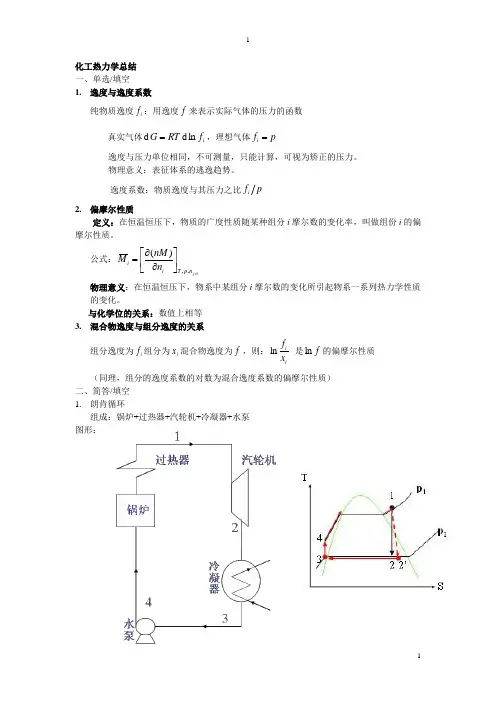
与化学位的关系:数值上相等3. 混合物逸度与组分逸度的关系组分逸度为i f 组分为i x 混合物逸度为f ,则:ii x f ln 是f ln 的偏摩尔性质 (同理,组分的逸度系数的对数为混合逸度系数的偏摩尔性质)二、简答/填空1. 朗肯循环组成:锅炉+过热器+汽轮机+冷凝器+水泵图形:过程:1-2:汽轮机中工质做等熵膨胀2-3:蒸汽在冷凝器中等压等温冷凝3-4:饱和水在水泵中做可逆绝热压缩4-1:水在锅炉中等压升温和等压汽化 不足之处:可逆程度低、热效率不高,不能完全转换;改进办法:1)提高过热器出口蒸汽压力与温度。
2)降低排汽压力。
3)改进热力循环方式,如采用回热循环,热电循环等2、卡诺循环过程:1→2 11,T p 水蒸汽在汽轮机内作等熵膨胀,变成湿蒸汽(乏汽)2,同时对外作输出轴功S W2→3 乏汽在冷凝器内等压、等温冷凝,放出汽化潜热,放出的热量3→4 冷凝水在水泵中等熵压缩,升压至1p 进至锅炉4→1 水在锅炉中吸收热量,变化到状态1,完成一个循环。
不足:(1)湿蒸汽对汽轮机和水泵有浸蚀作用,汽轮机带水量不得超过10%,水泵不能带入蒸汽进泵;(2)绝热可逆过程实际上难以实现。
3、相平衡三大判据1)体系自由焓(吉布斯自由能)为0 即0d =G2)各组分在各相中化学位相等3)各组分在各相中分逸度相等4、活度系数法定义:根据溶液热力学理论,将液相中组分的逸度于组分的活度系数相联系 基本式:P164()N i RT p p V p x py i i ii i i i i ,,2,1,)(exp ˆS L S S V=⎥⎦⎤⎢⎣⎡-=ϕγϕ 举例:已知体系压力p 与液相组成i x ,求泡点温度与汽相组成y6、状态方程法定义:是以各组分逸度系数与气液两相均实用的状态方程和混合规则相联系基本式:()N i x y i i i i ,,2,1 ˆˆLV =⋅=⋅ϕϕ 举例:已知有N 个组分的混合物,压力为p ,液相组成为i x ,求平衡温度与汽相组成i y7、节流膨胀特点:节流前后流体焓不变作用:改变流体的温度(其熵增加)理想流体节流后温度不变节流膨胀与绝热膨胀的比较:降温程度:做外功的绝热膨胀比节流大,且可回收功降温条件:节流膨胀需要条件,对于氢等需预冷才能获得冷效应。


第一章1.化工热力学的作用地位:化工热力学是将热力学原理应用于化学工程技术领域。
它的主要任务是以热力学第一、第二定律为基础,研究化工过程中各种能量的相互转化及其有效利用,研究各种物理和化学变化过程达到平衡的理论极限、条件和状态。
化工热力学是化学工程学的重要组成部分,是化工过程研究、开发与设计的理论基础。
2.热力学第零定律:当两个物体分别与第三个物体处于热平衡时,则这两个物体彼此之间也必定处于热平衡。
这是经验的叙述,称热平衡定律,又称热力学第零定律。
热力学第一定律即能量守恒定律:在任何过程中能量不能创造也不能消灭,只能按照严格的当量从一种形式转变为另一种形式。
热力学第二定律:任何体系都是自动地趋向平衡状态,一切自动过程都是不可逆的3.相律定义:'2R R K F--+-=π式中F 称为自由度,也就是独立的强度性质的数目,π、R 和'R 分别是相数、独立的化学反应数和其它的强度性质的限制数。
4.热力学基本方程 对于均相系统,热力学基本方程一共有四个,它们是:∑∑==++-=Ki ii L l l l dn dY X pdV TdS dU 11μ,∑∑==+++=Ki i i Ll l l dn dY X Vdp TdS dH 11μ∑∑==++--=Ki i i Ll l l dn dY X pdV SdT dA 11μ,∑∑==+++-=Ki i i Ll l l dn dY X Vdp SdT dG 11μ),,,(),,,(),,,(),,,(i l i l i l i l n Y P T G TS H G n Y V T A TS U A n Y P S H PV U H n Y V S U U =-==-==+==这四个基本方程可由热力学第一和第二定律导得。
推导前需要一个有关状态或平衡态的基本假定:对于一个均相系统,如果不考虑除压力以外的其它广义力,为了确定平衡态,除了系统中每一种物质的数量外,还需确定两个独立的状态函数。

化工热力学总结(1)写出多相系统的热力学方程;(2)二组分溶液,若已知一组分的逸度和组分含量,如何求另一组分的逸度? (3)低压下,由气液相平衡关系测得{P ,y ,x ,T },如何由提供的这些数据算出活度系数。
(4)GE> 0,属于正负偏差溶液?为什么?(5)真实溶液在反应器中,经过绝热变化后,系统熵变∆S= - 13000 J ,判断此过程的可能性。
(6)二组分溶液,其超额Gibbs 自由能满足:GE/RT=150-45x1-5x13,求各组分的活度系数r1, r2Gibbs 函数(G 函数) 应用反映真实气体与理想气体性质之差,称之为剩余G 函数。
与逸度或逸度系数的关系:反映真实溶液和理想溶液性质之差,称为过量Gibbs 函数。
与活度或活度系数的关系为:实验数据的热力学一致性检验 相平衡和化学平衡 有效能的综合利用:理想功与有效能也是一种Gibbs 函数。
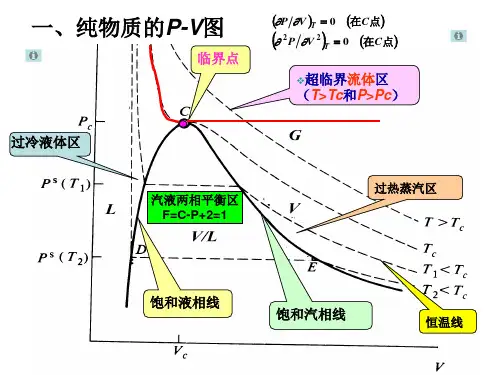
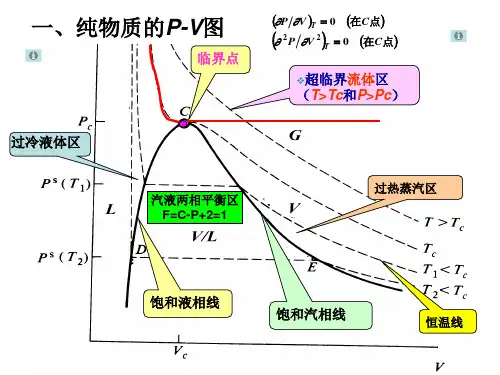
理想功: 有效能: 第二章 流体的 P-V-T 关系2.1 纯物质的P-V-T 关系 2.2 气体的状态方程 2.3 对比态原理及其应用2.4 真实气体混合物的P-V-T 关系 2.5 液体的P-V-T 性质 理想气体方程TSH G -=RTTS H RT G RR R pf -===ϕln )ln(0ˆ(/)ln()ln ii i j iE f i f x i T p n nG RT n γ≠⎡⎤∂==⎢⎥∂⎣⎦、、0G T p ∆=、恒定id 00()W H T S G T p T =-∆+∆=∆,,X 00000()()(,,)E H H T S S G T p T p =--+-=∆,PV RTZ PVRT===11 在较低压力和较高温度下可用理想气体方程进行计算。
2 为真实气体状态方程计算提供初始值。
3 判断真实气体状态方程的极限情况的正确程度,当 或者 时,任何的状态方程都还原为理想气体方程。
立方型状态方程立方型状态方程可以展开成为 V 的三次方形式。


![化工热力学各章总结[1].](https://uimg.taocdn.com/4c647d3277232f60ddcca174.webp)
⑶掌握蒸汽动力循环流程原理图与T ①流程原理图与T-S图热力计算:②热力计算:各过程的能量关系分析③提高效率的途径⑷掌握制冷循环流程原理图与T ①流程原理图与T-S图热力计算:②热力计算:各过程的能量关系分析③实现更低温度的制冷途径吸收式制冷特点;④吸收式制冷特点;热泵林德循环与克劳德循环的循环与克劳德循环的特点和差异⑸林德循环与克劳德循环的特点和差异EXIT
第七章复习题 1、节流膨胀和等熵膨胀有何不同? 2、画出朗肯循环原理图和T-S图,并分别以过程中的每个设备及整套装置为系统进行热力分析,写出能量方程并对各相应系统进行方程简化处理。
3、循环的特点是什么?写出热效率与制冷系数的定义式。
5、提高蒸气动力循环热效率有哪些方法?在朗肯循环基础上进行改进的循环有哪些循环?它们分别通过采取什么措施来提高热效率或扩大应用范围的?
6、画出单级蒸汽制冷循环原理图和T-S图,并分别以过程中的每个设备及整套装置为系统进行热力分析,写出能量方程并对各相应系统进行方程简化。
7、为达到获得
较低的制冷温度,而能耗不增加的目的可采用什么制冷循环?吸收式制冷有何特点?热泵与制冷有什么区别? 8、林德循环与克劳特循环的特点和差异是什么?。


化工热力学专业知识点总结一、物质的热力学性质1.热力学状态方程:描述热力学系统状态的方程,可以通过实验数据拟合得到,常见的有理想气体状态方程、范德华方程等。
2.热力学过程:系统经历的状态变化过程,包括等温过程、等容过程、绝热过程等,这些过程可以通过热力学定律进行定量描述和分析。
3.热力学势函数:用来描述系统稳定状态的函数,常见的有焓、内能、吉布斯函数等。
4.相变热力学性质:液相、气相、固相之间的相互转化过程,包括液气平衡、固液平衡等。
5.热力学平衡条件:系统达到热力学平衡的条件,包括热平衡、力学平衡、相平衡等。
二、热力学定律1.热力学第一定律:能量守恒定律,即能量既不会凭空消失,也不会凭空产生,只会在不同形式之间进行转化。
2.热力学第二定律:热不能自发地从低温物体传递到高温物体,这是宇宙中熵增加的基本规律。
3.热力学第三定律:当温度趋近于绝对零度时,系统的熵趋于常数,这是绝对零度不可能实现的热力学定律。
化工热力学不仅包含了上述物质的热力学性质和热力学定律,还涉及到一些实际的应用技术和工程问题。
例如,化工过程中的热力学分析、热力学循环、热能利用、燃烧热力学等内容。
下面我们来重点介绍一些与化工工程实际相关的热力学知识点。
三、热力学循环1.卡诺循环:理想可逆循环过程,由等温膨胀、绝热膨胀、等温压缩和绝热压缩四个过程组成,是热机效率的理论极限。
2.汽轮机循环:以水蒸气为工质的循环,包括理想朗肯循环、实际朗肯循环、再热朗肯循环等。
3.制冷循环:以制冷剂为工质的循环,包括制冷机、空调机、冷冻机等。
四、燃烧热力学1.燃烧过程:燃烧是一种复杂的热力学过程,包括燃烧反应机理、燃料燃烧热值、燃烧平衡等内容。
2.燃烧产物:燃料燃烧的产物包括二氧化碳、水蒸汽、一氧化碳、氨气、硫化物等,这些产物的生成与燃烧条件密切相关。
3.燃烧效率:燃料的利用效率,可以通过燃烧反应焓变来计算。
五、化工热力学应用1.热力学分析:化工反应器设计、炼油装置设计、化工装备热力计算等都需要进行热力学分析。
化工热力学知识点总结思维导图化工工程是涉及化学反应、热传递、质量转移等许多学科的交叉学科。
在这个复杂的过程中,热力学是一个非常重要的学科,它研究了化学反应、物质转化过程中的能量关系。
热力学在化工工程中有着广泛的应用,涉及到反应过程的热力学性质、热力学分析和计算等方面。
本文将对化工热力学知识点进行总结,并提供一份简洁的思维导图。
第一部分:基本概念1.1 热力学系统定义:热力学所研究的任何物体或物质都称为系统。
分类:封闭系统、开放系统、孤立系统。
1.2 状态量定义:用于描述系统状态的量,如压力、温度、体积、物质的量等。
分类:广延量、强度量、定量量、自由量、参量等。
1.3 热力学过程定义:由一个状态变化到另一个状态的过程称为热力学过程。
分类:可逆过程、不可逆过程、等压过程等。
1.4 热力学第一定律定义:能量守恒定律。
公式:ΔU=Q-W解释:U代表系统内能,Q代表热量,W代表功。
第二部分:热力学计算2.1 热力学平衡定义:系统属性、热力学状态处于平衡状态的条件称为热力学平衡。
条件:熵最大、内能最小。
2.2 热力学计算公式:ΔG=ΔH-TΔS解释:G代表吉泽自由能,H代表焓,S代表熵。
2.3 热力学逆过程定义:系统在平衡状态下,由外界施加的微小变化。
公式:dS/dt=Q/T第三部分:化学反应3.1 化学反应热力学性质定义:化学反应在热力学上可以由焓和熵来描述。
公式:ΔH=ΔHp-ΔHr解释:Hp代表生成热,Hr代表反应热。
3.2 变温变压等热力学性质计算公式:(ΔG/ΔT)p=ΔH/ΔT-V(ΔS/ΔT)(ΔG/ΔP)p=V(ΔS/ΔP)-ΔV/ΔP解释:ΔG代表自由能变化量,ΔH代表焓变化量,ΔS代表熵变化量,ΔV代表体积变化量。
第四部分:区域综合4.1 热力学循环定义:通过吸收和放出热量,沿固定的轨迹完成气态、液态和固态之间的相互转换的过程。
条件:热机循环和制冷循环。
4.2 活动热力学定义:在非平衡状态下,化学势是描述物质转移的最适宜量。
《化工热力学》学习体会报告近期,我在大学的研究生课程中学习了化工热力学。
通过这门课程,我对热力学原理和其在化工领域的应用有了更深入的理解。
在学习的过程中,我积累了一些体会和经验,下面将进行总结和分享。
首先,在学习过程中,我深刻认识到了热力学在化工领域的重要性。
热力学不仅是构建化学过程模型的基础,也是实际操作和优化过程的关键。
通过学习热力学,我们能够了解物质的热力学性质,例如熵、焓、自由能等,并能够通过热力学原理分析反应过程的可行性和优化条件。
只有通过深入了解热力学,我们才能更好地设计和操作化学工艺。
其次,在学习过程中,我学会了热力学的基本概念和计算方法。
热力学的基础概念包括热力学系统、状态函数、热力学平衡等。
通过学习,我了解了状态函数的定义和性质,以及熵增原理和放热放热原理等基本定律。
在计算方法方面,我学会了利用热力学数据手册计算热力学性质的方法,以及通过方程和计算提供准确结果的方法。
这些基本概念和计算方法的学习为我更深入地理解和应用热力学打下了坚实的基础。
此外,学习过程中,我也注意到了热力学在实际应用中的一些挑战。
虽然热力学提供了分析和优化化学工艺的理论基础,但在实际应用中,我们还需要考虑到实际操作的限制和实验数据的可靠性。
化工过程往往涉及多为反应和相变等复杂的物理过程,因此在实际应用中,我们需要确定热力学模型的适用范围,并考虑到操作条件和实验数据的误差。
此外,热力学数据的获取和准确性也是一个挑战,因为很多化学反应或物质性质的热力学数据并不总是容易获取。
所以,在应用热力学原理进行实际工程设计时,需要充分考虑这些挑战。
最后,通过学习《化工热力学》,我也认识到了学习的重要性和持续努力的必要性。
热力学是一个广阔而复杂的领域,仅通过一门课程是难以掌握所有知识的。
因此,我意识到需要不断学习和阅读相关文献,以加深对热力学的理解和应用。
在实际的工程设计和优化中,深入研究热力学对于解决问题和提高工艺效率是至关重要的。
第2章流体的P-V-T关系基本要求1.掌握状态方程式和用三参数对应态原理计算PVT性质的方法。
2.了解偏心因子的概念,掌握有关图表及计算方法。
1.状态方程:在题意要求时使用该法。
①范德华方程:常用于公式证明和推导中。
②R—K 方程:③维里方程:2.普遍化法:使用条件:在不清楚用何种状态方程的情况下使用。
三参数法:①普遍化压缩因子法②普遍化第二维里系数法第3章纯物质的热力学性质本章要求1.掌握热力学性质间的基本关系式,并能用P-V-T关系计算有关热力学性质。
2.了解热力学性质图、表的制作原理,学会工程上常用热力学图表的使用。
重点弄清剩余性质的概念,并能计算。
3.1 热力学性质间的关系dU TdS pdV =- H=U+PV dH TdS Vdp =+A=U-TS d A S d T p =--G=H-TS d G S d T V =-+Maxwell 关系式S V T P V S ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭ S PT V P S ∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭V TP S T V ∂∂⎛⎫⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭P TV S T P ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭推荐记忆法:T → V↑↓顺②P → S 逆①其中,顺②=逆①时,S P ∂⎛⎫ ⎪∂⎝⎭带“-”号要求:根据热力学第一定律,结合状态函数和数学知识,推导得出有关热力学性质之间的关系式。
推导H ∆和S ∆的计算公式的一般步骤:1.任意设关系。
------依题意,根据经验得出一推导简便的关系式2.利用全微分性质的公式过渡。
3.用Maxwell 关系式或热力学第一定律进行变换。
4.根据不同情况,运用数学知识变换。
此时有两条经验:①下标为P.V 的U ∂⎛⎫ ⎪⎝⎭,H ∂⎛⎫ ⎪⎝⎭,S ∂⎛⎫⎪⎝⎭的偏导数,常与pC ,Cv 有关。
②下标为H ,U ,S ,A ,G 的偏导数,一般应先利用偏微分转换公式换去下标为H ,U ,S ,A ,G 的偏导式,然后再进行推导。
转换公式:1Z X YX Y Z Y Z X ∂∂∂⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭3.2计算H ∆和S ∆的方法 1.状态方程法: P P V d H C d T V T d PT ⎡⎤∂⎛⎫=+- ⎪⎢⎥∂⎝⎭⎣⎦P PC V dS dT dP T T ∂⎛⎫=- ⎪∂⎝⎭2.剩余性质法:①普遍化压缩因子图()()1R R RTC C CH H HRT RT RT ω=+()()1R R R TS S S RRRω=+②普遍化的第二维里系数方法0101R T r r r C r r H dB dB P B T B T RT dT dT ω⎡⎤⎛⎫=-+-⎢⎥ ⎪⎝⎭⎣⎦01R T r rr S dB dB P R dT dT ω⎛⎫=-+ ⎪⎝⎭0 1.60.4220.083r B T =-1 4.20.1720.139r B T =-导出:0 2.60.675r rdB dT T =1 5.20.772r rdB dT T =3.3热力学性质图、表要求:了解热力学性质图、表的制作原理,掌握用图表进行计算的方法。
第4章 均相混合物热力学性质本章要求1. 正确理解偏摩尔性质,化学位,逸度,活度,混合变量,超额性质及标准态等概念。
2. 掌握均相混合物热力学性质关系式,偏摩尔性质的相关公式,特别是Gibbs-Duhem 方程及其应用,超额性质与活度系数关系式,了解逸度系数的计算方法。
4.1变组成系统的热力学关系()()1CdU Td nS Pd nV dn t i ii μ=-+∑= ()()()t i iidH d nH Td nS nV dP dn μ==++∑ ()()()t i iidA d nA nS dT Pd nV dn μ==--+∑()()()t i iidG d nG nS dT nV dP dn μ==--+∑化学势iμ的表达形式根据性质不同,可以写成下列四个式子:{}{}{}{},,,,,,,,t t t t iiiittttiiiiiS V n S p n T V n T V n U H A G n n n nμ≠≠≠≠⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂∂==== ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭ 4.2 偏摩尔性质定义式:{},,it i i T P n M M n ≠⎛⎫∂= ⎪∂⎝⎭ (M=V , U, H, S, A, G , C v ,C P ,……)①偏导数下标一定要是T, p, jn ,否则就不是偏摩尔性质.②由偏摩尔性质的定义式可知: 偏摩尔性质是一个强度性质,它是温度T 、压力P 与体系组成的函数.④用偏摩尔性质表达摩尔性质: 偏摩尔性质i M 和总性质tM 的关系:即:1Nt i ii M nM n M ===∑(4-16)(11N Nt iii i i i M n M M x M n n =====∑∑ 液相 等稳、等压条件)对于纯系统,偏摩尔性质就等于摩尔性质即1lim i iix MM →=。
lim i i ix M M ∞→=⑤用摩尔性质表达偏摩尔性质:各组分偏摩尔性质与摩尔性质之间的关系:在T ,p 一定时,对于二元系统有 :()1111dM M M x dx =+-211dM M M x dx =-⑦根据偏摩尔性质的定义可知,当化学位用下式表示时:,,jtiiiT P n G G nμ⎛⎫∂== ⎪∂⎝⎭ 我们就称化学位为偏摩尔自由焓。
⑧G —D 方程:条件:恒T ,恒P 下,表示了所有物质的偏摩尔性质有其内在联系。
1,0N i i i T px d M =⎛⎫= ⎪⎝⎭∑常用形式: 对于二元:121212dMdM x x dxdx =它的作用有两个:ⅰ 已知组分1的1M 的表达式,可得出组分2的2M 的表达式;ⅱ 判断实验数据或实验确定的iM 的方程式是否符合热力学一致性的唯一检验标准。
iM 的求法:⑴ 从iM 的定义式出发求iM ,使用条件是必须知道tM 与in 的关系式,否则无法求出。
⑵ 由G —D 方程可知,只要知道了除i 组分以外的组分的i M ,就可求出iM 。
⑶ 截距法:已知条件:M ——ix 数据或方程式。
()1111dM M M x dx =+-211dM M M x dx =-4.3 混合过程性质变化1. 定义: ()iii iiM M M x M M x M∆=-=-=∆∑∑混合后混合前2. 求法:()122M M M x x ∂∆⎡⎤∆=∆-⎢⎥∂⎣⎦()211M M M x x ∂∆⎡⎤∆=∆-⎢⎥∂⎣⎦4.4逸度和逸度系数纯气体逸度和逸度系数的定义,fP φ=lim1.0p fp→=()0ln 1PdPZ Pφ=-⎰对于理想气体:f P =, 1φ=;对于真实气体:1φ≠。
4.5 理想混合物(溶液)对于理想溶液,满足以下几个公式:id i i if x f =ln id i iG RT x x ∆=∑ln id i iS R x x ∆=-∑0id V ∆=0idH ∆= 0idU∆=4.6 活度和活度系数对液体混合物而言:ii ia r x =()ˆln i i i i i G x G G RT x a∆=-=∑∑ ① 纯液体 1ia= ∴ 1ir = ② 理想溶液 1ir =③ ir ﹥1 正偏差; ir ﹤1 负偏差4.6.3 超额性质定义:真实溶液与理想溶液的摩尔性质之差称为超额性质。
即E ididM M MM MM =-=∆-∆=∆EidEi i i iM M M M =-=∆ , 当M=V ,H 时,EVV=∆E H H=∆ln E i i G RT x γ=∑ln E i i G RT γ= 二元溶液G -D方程:121212,,ln ln T P T Px x x x γγ⎛⎫⎛⎫∂∂= ⎪ ⎪∂∂⎝⎭⎝⎭4.7活度系数模型 4.7.1正规溶液(Wohl 方程) ①二元Margules 方程: ()2112211212ln 2A A A x x γ=+-⎡⎤⎣⎦ ()2221122121ln 2A AA x x γ=+-⎡⎤⎣⎦②二元van Laar 方程:2212112121212ln A x A A x A x γ⎛⎫= ⎪+⎝⎭2121221121212ln A x A A x A x γ⎛⎫= ⎪+⎝⎭A 12、A 21的计算方法:①111120lim ln ln x A γγ∞→==,222210lim ln ln x A γγ∞→== ②根据恒沸点的汽液平衡数据,由下式求出:22212111ln ln 1ln x A x γγγ⎛⎫=+ ⎪⎝⎭ (4—155 a )21121222ln ln 1ln x A x γγγ⎛⎫=+ ⎪⎝⎭(4—155b )③由部分浓度或全浓度范围内的汽液平衡数据,通过数据处理得出。
4.7.4无热溶液(Wilson 方程) 常见二元系统的Wilson 方程:()122111122211222211ln ln x x x x x x x γ⎛⎫ΛΛ=-+Λ+- ⎪+Λ+Λ⎝⎭ ()211222211122111122ln ln x x x x x x x γ⎛⎫ΛΛ=-+Λ+- ⎪+Λ+Λ⎝⎭式中:1211l 212l 1V V RTeλλ--Λ=和2122l 121l 2V V RTeλλ--Λ=第5章 相平衡本章要求(1)掌握完全互溶体系在中低压下汽液平衡的计算方法;(2)会应用活度系数和液相组成的关联式,对活度系数与液相组成关联式的推导不作要求。
5.1相平衡判据达平衡态时:,T T T P P P αβαβ====== ⑴ 用化学位表示相平衡判据:iiαβμμ=⑵ 用逸度表示的相平衡态判据:i if f αβ= 5.1互溶系统的汽液平衡关系式汽液平衡问题: V lii i i iy P r x f φ=——此式是低压和加压汽液平衡最普遍且严格的一个热力学方程。
有四种汽液平衡体系,其中要求掌握的是低压体系。
低压体系:汽相:理想气体的混合物 iiP y P =液相:非理想溶液Llii iif r x f = 相平衡时li i i iy P r x f =工程上:大多数体系可采用此法计算。
计算二元体系汽液平衡数据时,根据已知条件不同,采用不同的方法。
1111S y P r x P = 2222Sy P r x P = 12111222S SP P P r x P r x P ∴=+=+一、若已知i r 和组成关系,则可以计算: 1)已知恒T ,ix ,求P 和iy 。
因为温度恒定,故SiP 已知,求得P ,再由Si i i i r x P y p=求得iy 。