信号检测与估计理论第一章习题讲解
- 格式:doc
- 大小:606.00 KB
- 文档页数:24


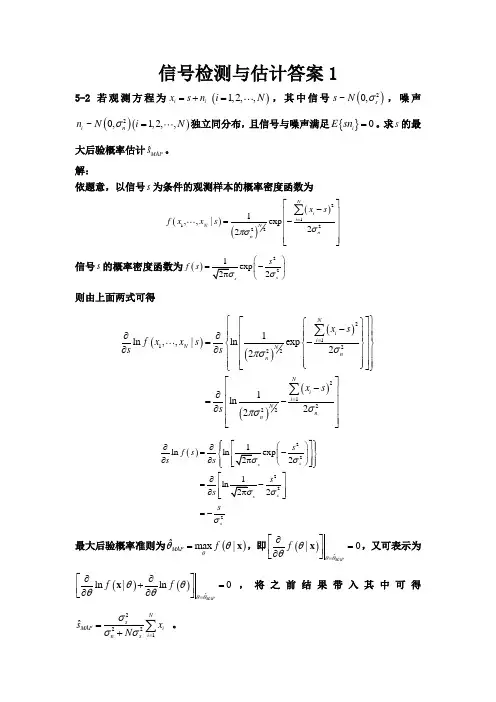
信号检测与估计答案15-2 若观测方程为i i x s n =+()1,2,,i N =,其中信号()2~0,s s N σ,噪声()()2~0,1,2,,i n n N i N σ=独立同分布,且信号与噪声满足{}0i E sn =。
求s 的最大后验概率估计ˆMAP s。
解:依题意,以信号s 为条件的观测样本的概率密度函数为()()()2112221,,|exp 22N i i N Nnnx s f x x s σπσ=⎡⎤-⎢⎥⎢⎥=-⎢⎥⎢⎥⎣⎦∑信号s 的概率密度函数为()222ss f s σ⎛⎫=- ⎪⎝⎭则由上面两式可得()()()()()211222212221ln ,,|ln exp 221ln 22N i i N N nn Ni i N n n x s f x x s ss x s s σπσσπσ==⎧⎫⎡⎤⎧⎫-⎪⎪⎢⎥⎪⎪∂∂⎪⎪⎪⎪⎢⎥=-⎨⎨⎬⎬∂∂⎢⎥⎪⎪⎪⎪⎢⎥⎪⎪⎪⎪⎩⎭⎣⎦⎩⎭⎡⎤-⎢⎥∂⎢⎥=-∂⎢⎥⎢⎥⎣⎦∑∑()22222ln ln 22s s s s f s s s s s s⎧⎫⎡⎤⎛⎫∂∂⎪⎪=-⎥⎨⎬ ⎪∂∂⎥⎝⎭⎪⎪⎦⎩⎭⎡⎤∂=-⎢⎥∂⎢⎥⎣⎦=-σσσ最大后验概率准则为()ˆmax |MAP f θθθ=x ,即()ˆ|0MAPf θθθθ=∂⎡⎤=⎢⎥∂⎣⎦x ,又可表示为()()ˆln |ln 0MAPf f θθθθθθ=∂∂⎡⎤+=⎢⎥∂∂⎣⎦x ,将之前结果带入其中可得2221ˆNs MAP ii ns sx N σσσ==+∑ 。
5-4已知观测信号0()cos()()x t A t n t ωθ=++(0)t T ≤≤,式子中()n t 是零均值,功率谱为2N 的高斯白噪声,θ是在[0,2)π上均匀分布的随机变量,求A 的最大似然估计和估计量的均方误差。
解:0()cos()()x t A t n t ωθ=++()x t 的似然函数为:020002220000022000000()cos()()1(|,)exp [()cos()]1exp [()2()cos()cos ()]12exp [()()cos()2TTTTTT x t A t n t f x A F x t A t dt N F x t dt x t A t dt At dt N A A T F x t dt x t t dt N N N ωθθωθωθωθωθ=++⎧⎫=⋅--+⎨⎬⎩⎭⎧⎫=⋅--+++⎨⎬⎩⎭⎧⎫=⋅-++-⎨⎬⎩⎭⎰⎰⎰⎰⎰⎰因为1(),022f θθππ=≤≤ 所以202200000(|)(|,)()12exp{}exp [()()2Tf x A f x A f d A TAq F x t dt I N N N πθθθ=⎧⎫=⋅--⎨⎬⎩⎭⎰⎰ 其中22200002200000()sin ()cos 12ln (|)ln ()ln ()2T TT q x t tdt x t tdt A T Aqf x A F x t dt I N N N ωω⎡⎤⎡⎤=+⎢⎥⎢⎥⎣⎦⎣⎦=--+⎰⎰⎰令000ln (|)20()0f x A AT AqI A N A N ∂∂=⇒-++∂∂ (1)假设SNR,即02Aq N 足够大,则00022()Aq AqI N N ≈0022ˆ(1)0MLAT q q A N N T⇒-+=⇒=由2220000()sin ()cos T Tq x t tdt x t tdt ωω⎡⎤⎡⎤=+⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰知22202221()exp(())()242T T TqA T qATf q q I σσσ=-+所以222323240001()2T T qq x x q T q E qf q dq AT e dq e AT x e dx AT σσσ=-+∞+∞+∞-⎛⎫−−−→ ⎪==←−−− ⎪⎝⎭⎰⎰⎰ 所以221ˆ()()2MLE A E q AT A T T ==⋅= (无偏估计) 200024ˆvar(),var()44T ML N T N T N q A T T σ====5-11. 假定已知信号112()cos cos 2...cos p s t a t a t a p t ωωω=+++212()sin sin 2...sin p s t b t b t b p tωωω=+++观测信号12()()()()x t s t s t n t =++,()n t 是均值为0、均方差为1的高斯白噪声。

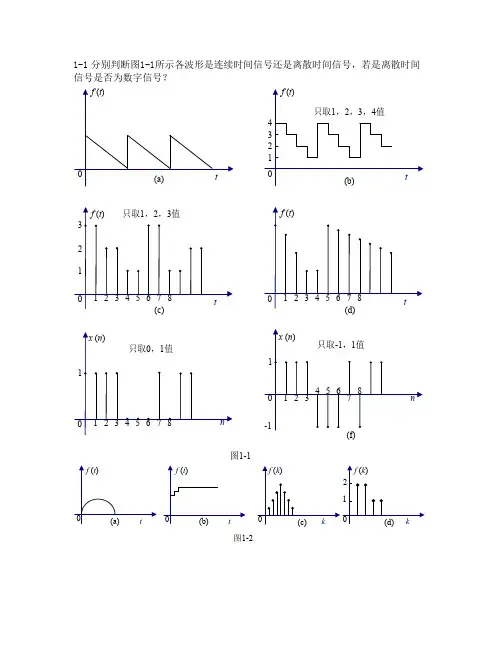
1-1分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:图1-1所示信号分别为⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21(a )连续信号(模拟信号);(b )连续(量化)信号;(c )离散信号,数字信号;(d )离散信号;(e )离散信号,数字信号;(f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问)(1);)sin(t e at ω-(2);nT e -(3);)cos(πn (4);为任意值)(00)sin(ωωn (5)。
221⎪⎭⎫ ⎝⎛解由1-1题的分析可知:(1)连续信号;(2)离散信号;(3)离散信号,数字信号;(4)离散信号;(5)离散信号。
1-3 分别求下列各周期信号的周期T :(1);)30t (cos )10t (cos -(2);j10t e (3);2)]8t (5sin [(4)。
[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期;对于分量cos (30t ),其周期。
由于5T 1π=15T 2π=为的最小公倍数,所以此信号的周期。
5π21T T 、5T π=(2)由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期。
5102T ππ==(3)因为[])16t (cos 2252252)16t (cos 125)8t (5sin 2-=-⨯=所以周期。

时间:6月16日(星期一)晚上6:30-8:30 地点:六教104室(上课教室)试卷共8题,其中4题属于教材第一章内容,其余4题分别的其他章节。
请同学们对匹配滤波器,离散卡尔曼滤波,离散维纳滤波,高斯白噪声下确知信号的检测,K -L 展开,高斯白噪声信道中的单参量信号估计等内容重点关注。
1.1 (付柏成 20060150)在例1.2中,设噪声均方差电压值为σ=2v ,代价为f c =2,m c =1。
信号存在的先验概率P =0.2。
试确定贝叶斯意义下最佳门限β,并计算出相应的平均风险。
解:根据式(1-15),可以算出00.8280.21f mQc Pc ⨯Λ===⨯ 而判决门限2201ln 0.52ln88.822βσ=+Λ=+= 根据式(1-21)可知平均风险1010Pr 0.2r 0.8R Qr r =+=+01100.2(|)0.8(|)m f c P D H c P D H =+ 而011(|)(|)D P D H p x H dx =⎰1100(|)(|)D P D H p x Hdx =⎰而212(1)(|)]2x p x H σ-=-202(|)]2x p x H σ=-所以20112(1)(|)(|)]2D D x P D H p x H dx dx σ-==-⎰⎰22(1)]2x dx βσ-=-⎰=17.82()()(3.91)22β-Φ=Φ=Φ 同理1121002(|)(|)]2D D x P D H p x H dx dx σ==-⎰⎰22)2x dx βσ∞=- 8.821()1()1(4.41)22β=-Φ=-Φ=-Φ 所以0.21(3.91)0.82[1(4.41)]R =⨯⨯Φ+⨯⨯-Φ 1.2 (关瑞东 20060155)假定加性噪声()n t 服从均值为零,方差为的正态分布。
此时,两个假设为01:()():()1()H x t n t H x t n t ==+我们根据()x t 的两次独立测量值12,x x 作判断,则12,x x 是统计独立的,在假设1H 下其均值为1a =1,在假设0H 下均值为0a =0,因而在两种假设下它们的联合概率密度函数可写为22/221()(|)(2)exp()2nn i k k i x a p x H πσσ-=-=-∑ (0,1;2)k n == 于是,似然比等于22011012210()(|)()exp[](|)2n ii a a n a a p x H x x p x H σσ=--Λ==-∑如果0()x Λ≥Λ,则选择假设1H ,否则选择假设0H 。




一、简答题注释简答题(每题5分,共20分)或(每题4分,共20分)二、第1章简答题1.从系统和信号的角度看,简述信号检测与估计的研究对象。
答:从系统的角度看,信号检测与估计的研究对象是加性噪声情况信息传输系统中的接收设备。
从信号的角度看,信号检测与估计的研究对象是随机信号或随机过程。
2.简述信号检测与估计的基本任务和所依赖的数学基础。
答:解决信息传输系统接收端信号与数据处理中信息恢复与获取问题,或从被噪声及其他干扰污染的信号中提取、恢复所需的信息。
信号检测与估计所依赖的数学基础是数理统计中贝叶斯统计的贝叶斯统计决策理论和方法。
3.概述信号在传输过程中与噪声混叠在一起的类型。
答:信号在传输过程中,噪声与信号混杂在一起的类型有3种:噪声与信号相加,噪声与信号相乘(衰落效应),噪声与信号卷积(多径效应)。
与信号相加的噪声称为加性噪声,与信号相乘的噪声称为乘性噪声,与信号卷积的噪声称为卷积噪声。
加性噪声是最常见的干扰类型,也是最基本的,因为乘性噪声和卷积噪声的情况均可转换为加性噪声的情况。
三、第2章简答题1.简述匹配滤波器概念及其作用。
答:匹配滤波器是在输入为确定信号加平稳噪声的情况下,使输出信噪比达到最大的线性系统。
匹配滤波器的作用:一是使滤波器输出有用信号成分尽可能强;二是抑制噪声,使滤波器输出噪声成分尽可能小,减小噪声对信号处理的影响。
2.根据匹配滤波器传输函数与输入确定信号及噪声的关系,简述匹配滤波器的原理。
答:匹配滤波器传输函数等于输入确定信号频谱的复共轭除以输入平稳噪声的功率谱密度,再附加相位项T ω-,其中T 为输入确定信号的持续时间或观测时间。
由于匹配滤波器传输函数的幅频特性与输入确定信号的幅频特性成正比,与输入噪声的功率谱密度成反比;对于某个频率点,信号越强,该频率点的加权系数越大,噪声越强,加权越小。
从而起到加强信号,抑制噪声的作用。
对于信号,匹配滤波器的相频特性与输入信号的相位谱互补,使输入信号经过匹配滤波器以后,相位谱将全部被补偿掉。

信号检测与估计理论第一章习题讲解1-9已知随机变量某的分布函数为0F某(某)k某21,某0,0某1,某1求:①系数k;②某落在区间(0.3,0.7)内的概率;③随机变量某的概率密度。
解:第①问利用F某(某)右连续的性质k=1第②问P0.3某0.7PF0.7F00.某3.3某.70.7P0dF某(某)2某第③问f某(某)d某00某1ele1-10已知随机变量某的概率密度为f某(某)ke普拉斯分布),求:某(某)(拉①系数k②某落在区间(0,1)内的概率③随机变量某的分布函数解:第①问f某某1d某11k2F2某F1某某1第②问P某2某某2f某d某随机变量某落在区间(某1,某2]的概率P{某1某某2}就是曲线yf某下的曲边梯形的面积。
P0某1P0某1f某d某0111e12第③问1某e2f某1e某2某0某0F某某f(某)d某1某某0e21某某01e2某0某1某ed某201e某d某某1e某d某022某01-11某繁忙的汽车站,每天有大量的汽车进出。
设每辆汽车在一天内出事故的概率为0.0001,若每天有1000辆汽车进出汽车站,问汽车站出事故的次数不小于2的概率是多少?(0-1)分布n,p0,np=二项分布泊松分布n成立,p,q0不成立高斯分布汽车站出事故的次数不小于2的概率P(k2)1Pk0Pk10.1P(k2)11.1e答案P某k=n=1实际计算中,只需满足n10kek!p0.1,二项分布就趋近于泊松分布=np1-12已知随机变量(某,Y)的概率密度为(3某4y)kef某Y(某,y)0,某0,y0,其它求:①系数k?②(某,Y)的分布函数?③P{0某1,0某2}?第③问方法一:联合分布函数F某Y(某,y)性质:若任意四个实数a,a,b,b,满足1212a1a2,b1b2,则P{a1某a2,b1Yb2}F某Y(a2,b2)F某Y(a1,b1)F某Y(a1,b2)F某Y(a2,b1)P{0某1,0Y2}F某Y(1,2)F某Y(0,0)F某Y(1,0)F某Y(0,2)方法二:利用P{(某,y)D}f某Yu,vdudvD20P{0某1,0Y2}0f某Y某,yd某dy11-13已知随机变量(某,Y)的概率密度为1,0某1,y某f(某,y)0,其它①求条件概率密度f某(某|y)和fY(y|某)?②判断某和Y是否独立?给出理由。
第1章 信号检测与估计概论信号检测与估计概论教 材:信号检测与估计(张立毅) 信号检测与估计理论(赵树杰 ) 清华大学出版社引言 信号处理发展概况 信号的随机性及其统计处理方法 信号检测与估计理论概述 内容编排和建议一种抓彩的游戏:四种颜色的彩色玻璃球,如黄、红、黑、白,每 种五粒,四种二十粒。
把二十粒球放到一个口袋里,游玩者信手去 抓十粒。
如果你抓出来的玻璃球四种颜色的比例是5500,你将得到重奖; 如果你抓出来的玻璃球四种颜色的比例是5410或5320,奖品可观; 如果你抓出来的玻璃球四种颜色的比例是4411,是小奖品; 如果你抓出来的玻璃球四种颜色的比例是4321,罚一元人民币; 如果你抓出来的玻璃球四种颜色的比例是3322,罚五元人民币。
乍一看,得奖的机会似乎比受罚的机会更多; 结果是:十个人里至少有七个人抓出来的是3322,可能有一两个人 是4321,至于得重奖的,理论上是可能的,实际上却几乎是不可能。
其实,这只是一个最简单的概率或者叫做几率的问题,能够算得出 来,很精确的。
四种颜色的球的数量不会相差太远。
1.1 引言信号检测与估计的概念、理论和方法是 随机信号统计处理的理论基础; 本节主要内容:发展概况、待处理信号 的随机性及其统计处理方法的含义 统计信号处理的理论基础:信号的统计 检测理论、估计理论、滤波理论等1.2 信号处理发展概况 理论• 检测 • 估计 • 滤波 • 多维阵列信号处理 • 自适应信号处理 • 自适应滤波1.2 信号处理发展概况面临很多新的应用问题。
如我国载人航空航天中的应用 (原位探测、信息处理,对我国 科技工作者而言,将是全新的 领域;火星探测、嫦娥工程、 夸父计划)应用• 电子信息 • 自动化工程 • 模式识别 • 生物医学工程 • 航空航天 • 地球物理1.2 信号处理发展概况类别 比较 时域背景特性 平稳随机过程、高斯分布 平稳、非平稳随机过程; 高斯、非高斯分布 频域背景特性 均匀功率谱、高斯功率谱 信号特性 系统特性 数学工具 实现技术 简单信号,编码信号 均匀、非均匀功率谱; 高斯、非高斯功率谱 编码信号,扩频信号, 线性、非线性调频信号 线性时不变最小相位系统 线性时不变,时变系统, 非线性时变、非最小相位系统 随机过程、傅立叶变换 随机过程、傅立叶变换、高阶谱高 阶累积量、时频分析、小波变换 统计信号处理基础 现代信号处理1.2 信号处理发展概况统计信号处理基础所研究的内容是现代信号处理必备的理论 基础知识,二者没有严格的界限 信号统计理论研究的日益进步和完善,以及信号处理技术应 用领域的不断深入和扩展,使信号处理,特别是随机信号处 理得到人们十分广泛的重视 随机信号属于随机过程,应采用数学上的统计方法进行处理 因此,从事信号处理的科技工作者应有的素质: • • • • 建立随机信号统计处理方法的基本概念 掌握扎实的统计信号处理的理论基础 具有运用统计的方法研究分析随机信号处理问题的能力 具有运用统计的方法解决工程技术问题的能力1.3 信号的随机性及统计处理方法采用现代模拟器件为主的模拟处理技术 采用DSP为核心器件的数字处理技术图1.1 无线通信系统原理框图11.3 信号的随机性及统计处理方法一般来说,信息系统的主要工作是信号的产生、发射、传 输、接收和处理,以实现信息传输的目的,这样的系统通 常称为电子信息系统 对于电子信息系统,最主要的要求是高速率和高准确性 前者要求系统传输信号的效率尽可能高,主要决定于信号 的波形设计和频率选择 后者要求系统在传输信息过程中,尽可能少出错,减小信 号波形的失真度,这就是系统的抗干扰能力问题。
1-9 已知随机变量X 的分布函数为20,0(),011,1X x F x kx x x <⎧⎪=≤≤⎨⎪>⎩求:①系数k ; ②X 落在区间(0.3,0.7)内的概率; ③随机变量X 的概率密度。
解:第①问 利用()X F x 右连续的性质 k =1 第②问{}{}{}()()0.30.70.30.70.70.30.7P X P X F P X F =<<=<≤-=-第③问 201()()0X X xx d F x f x elsedx ≤<⎧==⎨⎩1-10已知随机变量X 的概率密度为()()xX f x ke x -=-∞<<+∞(拉普拉斯分布),求:①系数k ②X 落在区间(0,1)内的概率 ③随机变量X 的分布函数 解: 第①问()112f xd x k ∞-∞==⎰ 第②问 {}()()()211221x x P x X xF x F xfx d x<≤=-=⎰ 随机变量X 落在区间12(,]x x 的概率12{}P x X x <≤就是曲线()y f x =下的曲边梯形的面积。
{}{}()()1010101112P X P X f x dxe -<<=<≤==-⎰第③问()102102xx e x f x e x -⎧≤⎪⎪=⎨⎪>⎪⎩()00()110022111010222xx xxx x x x F x f x dxe dx x ex e dx e dxx e x -∞-∞---∞=⎧⎧≤≤⎪⎪⎪⎪==⎨⎨⎪⎪+>->⎪⎪⎩⎩⎰⎰⎰⎰1-11 某繁忙的汽车站,每天有大量的汽车进出。
设每辆汽车在一天内出事故的概率为0.0001,若每天有1000辆汽车进出汽车站,问汽车站出事故的次数不小于2的概率是多少?,(01)p q λ→∞→→∞→−−−−−−−−→−−−−−−−−→−−−−−−−−→n=1n ,p 0,np=n 成立,0不成立-分布二项分布泊松分布高斯分布汽车站出事故的次数不小于2的概率()()P(2)101k P k P k ≥=-=-= 答案0.1P(2)1 1.1k e -≥=-100.1n p ≥≤实际计算中,只需满足,二项分布就趋近于泊松分布()np!k e P X k k λλλ-===1-12 已知随机变量(,)X Y 的概率密度为(34)0,0(,)0x y XY kex y f x y -+⎧>>⎪=⎨⎪⎩,,其它求:①系数k ?②(,)X Y 的分布函数?③{01,02}P X X <≤<≤?第③问 方法一:联合分布函数(,)XY F x y 性质:若任意四个实数1212,,,a a b b ,满足1212,a a b b ≤≤,则121222111221{,}(,)(,)(,)(,)XY XY XY XY P a X a b Y b F a b F a b F a b F a b <≤<≤=+--{01,02}(1,2)(0,0)(1,0)(0,2)XY XY XY XY P X Y F F F F ⇒<≤<≤=+--方法二:利用(){(,)},XY DP x y D f u v dudv∈∈⎰⎰)(210{01,02},XY P X Y f x y dxdy <≤<≤=⎰⎰1-13 已知随机变量(,)X Y 的概率密度为101,(,)0x y xf x y ⎧<<<=⎨⎩,,其它 ①求条件概率密度(|)X f x y 和(|)Y f y x ?②判断X 和Y 是否独立?给出理由。
先求边缘概率密度()X f x 、()Y f y注意上下限的选取()X 2,01,01(),00,xx XY x x dy x f x f x y dy else else +∞--∞⎧<<<<⎧⎪===⎨⎨⎩⎪⎩⎰⎰, ()11,011||(),,10011,y Y XY ydxy y f y f x y dx dx y elsey else+∞-∞-⎧<<⎪-⎪⎧===⎨⎨-<<-<<⎩⎪⎪⎩⎰⎰⎰1-14 已知离散型随机变量X 的分布律为求:①X 的分布函数31X +的分布律1-15 已知随机变量X 服从标准高斯分布。
求:①随机变量XY e =的概率密度?②随机变量Z X =的概率密度? 分析:①[]()'()()Y X f y h y f h y =⋅②1122()|'()|[()]|'()|[()]Y X X f y h y f h yh y f h y =⋅+⋅答案:()22ln 22100()()00y z Y Z e y z f y f z elseelse--⎧>≥==⎩⎩1-16 已知随机变量1X 和2X 相互独立,概率密度分别为11121111,0()20,0x X e x f x x -⎧⎪≥=⎨⎪<⎩,22132221,0()30,0x X e x f x x -⎧⎪≥=⎨⎪<⎩求随机变量12Y X X =+的概率密度?解:设11221()Y Y X X Y X ==+⎧⎨=⎩任意的 求反函数,求雅克比J =-1()12121136121210,60y y Y Y e y y f y y else--⎧⎪≥≥=⎨⎪⎩()11111321100y y Y e e y f y else --⎧⎪-≥=⎨⇒⎪⎩1-17 已知随机变量,X Y 的联合分布律为{}532m,,,0,1,2,!!m n e P X Y n m n m n -====求:①边缘分布律{}m (0,1,2,)P X m == 和{}(0,1,2,)P Y n n == ?②条件分布律{}m |P X Y n ==和{}|m P Y n X ==?分析:{}32532m,,,0,1,2,!!32!!m n m n e P X Y n m n m n e e m n ---=⋅====泊松分布 {},0,1,2,!k e P X k k k λλ-==={}01!!k k kk k P X k e e e k e k λλλλλλ-∞=∞∞--======⋅=∑∑∑P19 (1-48)解:①{}{}121332m !m,!n m n n e P X P X Y n e n m -=∞=∞-=====∑∑{}{}21n m 2,!n n P Y P X Y n e n ∞=-=====∑同理 ②{}{}{}m,n P X Y n P X m P Y ⋅===== 即X 、Y 相互独立1-18 已知随机变量12,,,nX XX 相互独立,概率密度分别为1122(),(),,()n n f x f x f x 。
又随机变量1121212n nY X Y X X Y X X X =⎧⎪=+⎪⎨⎪⎪=+++⎩证明:随机变量12,,,nY Y Y 的联合概率密度为12112211(,,,)()()()Y n n n n f y y y f y f y y f y y -=--11212121212323211211121n n n n n n n nY X Y X X X Y Y Y X X X X Y Y Y X X X X Y Y Y X X X X ----=⎧⎪=+=-⎧⎪⎪⎪=++=-⎪⎪⎨⎨⎪⎪⎪⎪=+++=-⎩⎪=+++⇒+⎪⎩10000110001001000011000011J -==--因为|J|=1,故 已知随机变量12,,,nX X X 相互独立,概率密度分别为1122(),(),,()n n f x f x f xX 121211(,,,)(,,,)n Y n n f y y y f y y y y y -=-- 12121111221X 1(,,,)(,,,)()()()n n n n n n Y f y y y f y y y y y f y f y y f y y --=--=--1-19 已知随机变量X 服从拉普拉斯分布,其概率密度为1(),2xX f x ex -=-∞<<+∞求其数学期望与方差?解:[]()()22222200121(022222)()X xxxX xxxxx E X x dx x dx E X x dx x dx x dx x ee dx exdxxee f x e d f x x e e ∞∞-∞-∞∞∞-∞-∞∞∞-+∞-∞-∞-+∞----===⎡⎤==⎣⎦==-+=⋅=-+=⎰⎰⎰⎰⎰⎰⎰⎰奇函数偶函数1-20 已知随机变量X 可能取值为{4,1,2,3,4}--,且每个值出现的概率均为15。
求:①随机变量X 的数学期望和方差?②随机变量23Y X =的概率密度?③Y 的数学期望和方差?①③答案: ② Y 3 12 27 48 P1/51/51/52/5离散型随机变量的概率密度表达式 P12,1-25式()()1k k k f x p x x δ∞==-∑ 其中(),0,0x x x δ∞=⎧=⎨≠⎩ 为冲激函数()()()()()()1312272485Y f y y y y y δδδδ=-+-+-+-[]21212[][()]()[]D [][]k k k k kk E X x p E g X g x p E X X E X E X ∞=∞===⇒=-∑∑[][]22446214[][]D 55251388406[][]1098D 525E X E X X E Y E Y Y ======1-22 已知两个随机变量,X Y 的数学期望为1,2X Y m m ==,方差为224,1X Y σσ==,相关系数0.4XY ρ=。
现定义新随机变量,V W 为23V X YW X Y=-+⎧⎨=+⎩ 求,V W 的期望,方差以及它们的相关系数?[][][][][][][][][][]22374.817.82XYE V E W D V D W E aX bY aE X bE Y D aX bY a D X b D Y abC +=+++=+====XYXY X YC ρσσ=0.131-23 已知随机变量,X Y 满足Y aX b =+,,a b 皆为常数。
证明: ① 2XY XC a σ=;②1010XYa a ρ>⎧=⎨-<⎩;③ 当0X m ≠且2[][]aE X b E X =-时,随机变量,X Y 正交。
① X Y X Y X C R m m =-[][][]()22XY X C a X XE Y E aX b am bE XY E X aX b aE X bm σ=+=+⎡⎤=+=+⎡⎤⎣⎦⎣⎦⇒=②XYXY X YC ρσσ=()()()222X aX b a D Y D D X a σ===+2XYXY X YC a a aρσσ===③0XY R ⇔正交=[]22[][]XE XY aE X bm aE X b E X ⎧⎡⎤=+⎣⎦⎪⇒⎨=-⎪⎩得证1-25 已知随机变量,X Y 相互独立,分别服从参数为1λ和2λ的泊松分布。