2016年四年级希望杯100题
- 格式:pdf
- 大小:365.31 KB
- 文档页数:7

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 17C. 20D. 214. 1千米等于多少米?A. 100米B. 1000米C. 10,000米D. 100,000米5. 下列哪个图形是三维图形?A. 正方形B. 圆形C. 立方体D. 三角形二、判断题(每题1分,共5分)1. 1+1=3 ()2. 长方形是一种特殊的正方形。
()3. 0是最小的自然数。
()4. 圆的周长等于直径的两倍。
()5. 任何数乘以0都等于0。
()三、填空题(每题1分,共5分)1. 1+2+3+4+5=_____2. 一个长方形的长是10厘米,宽是5厘米,那么它的面积是____平方厘米。
3. 100的因数有____个。
4. 9是____的倍数。
5. 一个正方体的体积是27立方厘米,那么它的边长是____厘米。
四、简答题(每题2分,共10分)1. 请列举出前五个质数。
2. 请解释什么是因数和倍数。
3. 请简述平行四边形的特征。
4. 请解释什么是周长和面积。
5. 请列举出三种不同的三维图形。
五、应用题(每题2分,共10分)1. 一个长方形的长是8厘米,宽是4厘米,求它的周长和面积。
2. 一个数加上20后等于30,这个数是多少?3. 一个正方形的周长是24厘米,求它的边长。
4. 两个数相乘等于18,这两个数可能是什么?5. 一个立方体的体积是64立方厘米,求它的边长。
六、分析题(每题5分,共10分)1. 小明有10个苹果,他吃了一些后,还剩下6个苹果。
请问他吃了多少个苹果?2. 一个长方形的长是10厘米,宽是5厘米,求它的对角线长度。
七、实践操作题(每题5分,共10分)1. 请用纸和剪刀制作一个正方形。

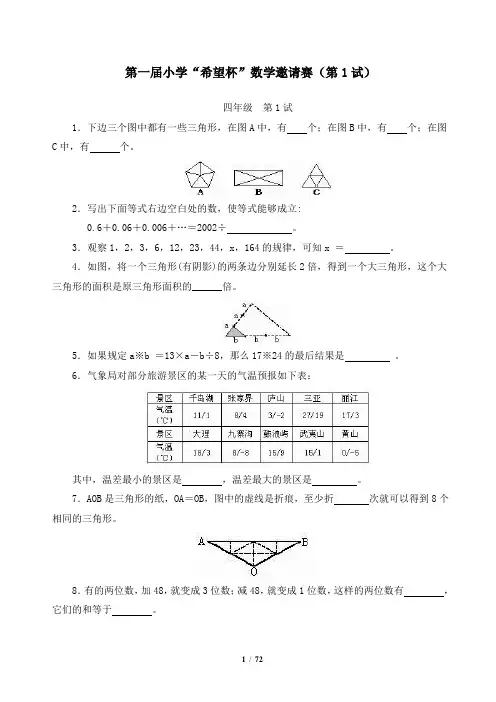
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
第一届小学“希望杯”数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。

第希望杯考前训练题四年级HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第16届希望杯考前训练100题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训,主要学习内容有:1.整数的四则运算,运算定律,简便运算。
2.基本图形,图形的拼组(分、合、移、补),图形的变换,折叠与展开。
3.角的概念与度量,长方形、正方形的周长和面积,平行四边形、梯形的概念和周长计算。
4.整除概念,数的整除特征,带余数除法,平均数。
5.几何计数(数图形),找规律,归纳,统计,可能性。
6.数谜,分析推理能力,数位,十进制表示法。
7.生活数学(钟表,时间,人民币,位置与方向,长度,质量的单位)。
8.应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。
考前100题选讲1.计算:8×27×25。
2.计算:9+98+987+9876。
3.计算:2-4+6-8+10-12+…-48+50。
4.计算:2017×2016+2016×2014-2015×2016-2015X2017。
5.计算:15÷7+68÷14。
6.已知999999÷(a÷2)=142857,求a7.某数被27除,商是8,余数是5,求这个数。
8.定义:A*B=(A+3)×(B-2),求15*17。
9.除法算式△÷7=12……□中,余数最大是多少?10.有5个连续偶数之和恰好等于4个连续奇数之和,如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11.将36表示成三个大于1的自然数的乘积(不考虑三个自然数的相乘顺序)。
共有几种不同的表示方法?12.用数字2,0,1,7可以组成多少个不重复的三位数?13.用2295除以一个两位数,丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了,得到的结果是45,则正确的结果应该是多少?14.如果把某个除法算式的被除数152写成125,则商会比原来的结果小3,且余数不发生变化,求余数?和某个小于100的自然数的和正好等于两个连续自然数之积,求这个小于100的自然数。

四年级希望杯奥数试卷【含答案】专业课原理概述部分一、选择题(每题1分,共5分)1. 下列哪个数字是偶数?A. 3B. 4C. 5D. 62. 一个正方形的四条边长相等,那么它的周长是?A. 边长的两倍B. 边长的三倍C. 边长的四倍D. 边长的五倍3. 下列哪个数字是质数?A. 12B. 13C. 15D. 184. 一个长方形的长是10厘米,宽是5厘米,那么它的面积是?A. 50平方厘米B. 60平方厘米C. 70平方厘米D. 80平方厘米5. 下列哪个数字是最大的两位数?A. 90B. 91C. 92D. 93二、判断题(每题1分,共5分)1. 1+1=3 ()2. 9乘以9等于81 ()3. 2加2等于4 ()4. 10减去5等于7 ()5. 8除以2等于4 ()三、填空题(每题1分,共5分)1. 5加5等于______。
2. 20减去10等于______。
3. 6乘以6等于______。
4. 49除以7等于______。
5. 100减去25等于______。
四、简答题(每题2分,共10分)1. 请写出5个两位数。
2. 请写出5个三位数。
3. 请写出5个两位数的和。
4. 请写出5个两位数的差。
5. 请写出5个两位数的积。
五、应用题(每题2分,共10分)1. 小明有10个苹果,他吃掉了3个,还剩下几个苹果?2. 小红有20个糖果,她给了小华5个糖果,还剩下几个糖果?3. 一个长方形的长是8厘米,宽是4厘米,求这个长方形的面积。
4. 一个正方形的边长是6厘米,求这个正方形的周长。
5. 两个数的和是15,其中一个数是7,另一个数是多少?六、分析题(每题5分,共10分)1. 请用两种方法计算24加36的和。
2. 请用两种方法计算56减去28的差。
七、实践操作题(每题5分,共10分)1. 请用纸和剪刀剪出一个正方形,边长为10厘米,然后计算这个正方形的面积。
2. 请用纸和剪刀剪出一个长方形,长为12厘米,宽为8厘米,然后计算这个长方形的周长。

江西省南昌市2015-2016学年度第一学期期末试卷(江西师大附中使用)高三理科数学分析一、整体解读试卷紧扣教材和考试说明,从考生熟悉的基础知识入手,多角度、多层次地考查了学生的数学理性思维能力及对数学本质的理解能力,立足基础,先易后难,难易适中,强调应用,不偏不怪,达到了“考基础、考能力、考素质”的目标。
试卷所涉及的知识内容都在考试大纲的范围内,几乎覆盖了高中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的大部分知识点均有涉及,其中应用题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学生感受到了数学的育才价值,所有这些题目的设计都回归教材和中学教学实际,操作性强。
2.适当设置题目难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较大,学生不仅要有较强的分析问题和解决问题的能力,以及扎实深厚的数学基本功,而且还要掌握必须的数学思想与方法,否则在有限的时间内,很难完成。
3.布局合理,考查全面,着重数学方法和数学思想的考察在选择题,填空题,解答题和三选一问题中,试卷均对高中数学中的重点内容进行了反复考查。
包括函数,三角函数,数列、立体几何、概率统计、解析几何、导数等几大版块问题。
这些问题都是以知识为载体,立意于能力,让数学思想方法和数学思维方式贯穿于整个试题的解答过程之中。
二、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满足AB AC →→=,则AB AC →→⋅的最小值为( )A .14-B .12-C .34-D .1-【考查方向】本题主要考查了平面向量的线性运算及向量的数量积等知识,是向量与三角的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确用OA ,OB ,OC 表示其它向量。
2.找不出OB 与OA 的夹角和OB 与OC 的夹角的倍数关系。

第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。
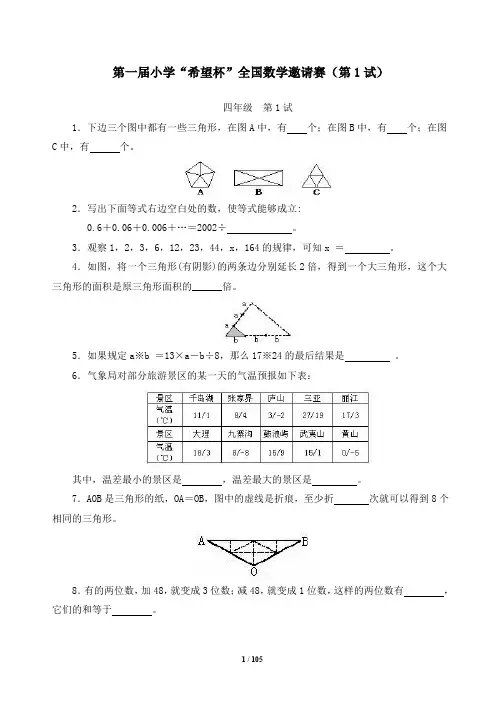
第一届小学“希望杯”全国数学邀请赛(第1试)四年级第1试1.下边三个图中都有一些三角形,在图A中,有个;在图B中,有个;在图C中,有个。
2.写出下面等式右边空白处的数,使等式能够成立:0.6+0.06+0.006+…=2002÷。
3.观察1,2,3,6,12,23,44,x,164的规律,可知x =。
4.如图,将一个三角形(有阴影)的两条边分别延长2倍,得到一个大三角形,这个大三角形的面积是原三角形面积的______倍。
5.如果规定a※b =13×a-b÷8,那么17※24的最后结果是。
6.气象局对部分旅游景区的某一天的气温预报如下表:其中,温差最小的景区是,温差最大的景区是。
7.AOB是三角形的纸,OA=OB,图中的虚线是折痕,至少折次就可以得到8个相同的三角形。
8.有的两位数,加48,就变成3位数;减48,就变成1位数,这样的两位数有,它们的和等于。
9.甲、乙、丙、丁四个学习小组共有图书280本,班主任老师提议让四个组的书一样多,得到拥护,于是从甲调14本给乙,从乙调15本给丙,从丙调17本给丁,从丁调18本给甲。
这时四个组的书一样多。
这说明甲组原来有书本。
10.幼儿园老师给几组小朋友分苹果,每组分7个,少3个;每组分6个,则多4个,苹果有个,小朋友共组。
11.在 a=20032003×2002和 b=20022003×2003中,较大的数是,它比较小的数大。
12.小明的家离学校2千米,小光的家离学校3千米,小明和小光的家相距千米。
13.甲、乙、丙三人中只有1人会开汽车。
甲说:“我会开。
”乙说:“我不会开。
”丙说:“甲不会开。
”三人的话只有一句是真话。
会开车的是。
14.为了支援西部,1班班长小明和2班班长小光带了同样多的钱买了同一种书44本,钱全部用完,小明要了26本书,小光要了18本书。
回校后,小明补给小光28元。
小明、小光各带了元,每本书价元。

2016年第14届小学“希望杯”全国数学邀请赛四年级第2试模拟试题(1)(时间:90分钟;满分120分)一、填空题。
(每小题5分,共60分) 1.计算:3333×3333+11111 = 。
【难度】:★★【考点】:积不变性质,乘法分配律 【答案】:11120000 【解析】: 3333×3333+11111 =9999×1111+11111 =(9999+1)×1111+10000 =10000×1111+10000 =11110000+10000 =111200002.计算:20162017×2015-20152015×2016= 。
【难度】:★★ 【考点】:重叠数 【答案】:2015 【解析】:20162017×2015-20152015×2016 =20162016×2015-20152015×2016+2015 =2016×10001×2015-2015×10001×2016+2015 =0+2015 =20153.如果a △b=a+b-6,a ☆b=2a+2b+ab 。
计算()[]84822÷☆☆△=。
【难度】:★★ 【考点】:定义新运算 【答案】:25 【解析】:2☆82△3632☆4200÷8=25=2×2+2×8+2×8 =2+36-6 =2×32+2×4+4×32=4+16+16 =32 =64+8+128=36 =2004.9个自然数从小到大排列,相邻两个数的差是2.其中最大的数与第二大的数之和是中间数的3倍,那么这9个自然数的和是。
【难度】:★★★【考点】:等差数列【答案】:126【解析】:把9个数从小到大依次排列、表示出来:①②③④⑤⑥⑦⑧⑨a a+2 a+4 a+6 a+8把中间数表示为a,则第二大的数为a+6,最大的数为a+8由此,题意可以翻译为:(a+8)+(a+6)=3×a 可以算出a=14和=中间数×项数=14×9=1265.在一次慈善义卖中,丹丹自制的蛋挞和布丁共卖了200个,收入479元。

第16届希望杯考前训练100题学前知识点梳理主要针对“希望杯”全国数学邀请赛进行考前特训,主要学习内容有:1.整数的四则运算,运算定律,简便运算。
2.基本图形,图形的拼组(分、合、移、补),图形的变换,折叠与展开。
3.角的概念与度量,长方形、正方形的周长和面积,平行四边形、梯形的概念和周长计算。
4.整除概念,数的整除特征,带余数除法,平均数。
5.几何计数(数图形),找规律,归纳,统计,可能性。
6.数谜,分析推理能力,数位,十进制表示法。
7.生活数学(钟表,时间,人民币,位置与方向,长度,质量的单位)。
8.应用题(植树问题、年龄问题、鸡兔同笼、盈亏问题、行程问题)。
考前100题选讲1.计算:8×27×25。
2.计算:9+98+987+9876。
3.计算:2-4+6-8+10-12+…-48+50。
4.计算:2017×2016+2016×2014-2015×2016-2015X2017。
5.计算:15÷7+68÷14。
6.已知999999÷(a÷2)=142857,求a7.某数被27除,商是8,余数是5,求这个数。
8.定义:A*B=(A+3)×(B-2),求15*17。
9.除法算式△÷7=12……□中,余数最大是多少?10.有5个连续偶数之和恰好等于4个连续奇数之和,如4+6+8+10+12=7+9+11+13。
请写出一个符合要求的式子。
11.将36表示成三个大于1的自然数的乘积(不考虑三个自然数的相乘顺序)。
共有几种不同的表示方法?12.用数字2,0,1,7可以组成多少个不重复的三位数?13.用2295除以一个两位数,丽丽在计算的时候错把这个两位数的十位数字和个位数字写反了,得到的结果是45,则正确的结果应该是多少?14.如果把某个除法算式的被除数152写成125,则商会比原来的结果小3,且余数不发生变化,求余数?15.2017和某个小于100的自然数的和正好等于两个连续自然数之积,求这个小于100的自然数。
