浦东新区2015学年第二学期预备年级数学期末试卷

A B OA O BB O AB O A浦东新区2013学年度第二学期期末质量测试六 年 级（预备年级）数 学（完卷时间：90分钟 满分：100分） 2014.6一、 选择题（本大题共6题，每小题3分，满分18分）（每题只有一个选项正确） 1．在数轴上点A 、点B 所表示的数分别是a 、b ，那么能够判断b a <的是…………（ ）（A ）； （B ）； （C ）； （D ）．2．下面的变形正确的是…………………………………………………………………（ ） （A ）由137=-x ，得713-=x ； （B ）由845+=x x ，得845=+x x ；（C ）由121=x ，得21=x ； （D ）由2372+=-x x ，得7232+=-x x ．3．某商场促销，小鱼将促销信息告诉了妈妈，小鱼妈妈假设某一商品的定价为x ，并列出不等式为()100010027.0<-⨯x ，那么小鱼告诉妈妈的信息是……………………（ ）（A ）买两件等值的商品可减100元，再打3折，最后不到1000元；（B ）买两件等值的商品可打3折，再减100元，最后不到1000元； （C ）买两件等值的商品可减100元，再打7折，最后不到1000元； （D ）买两件等值的商品可打7折，再减100元，最后不到1000元．题 号 一 二 三 四 五 总 分得 分4．小明某天记录的支出如图所示，不小心饼干的支出金额被墨水污染了，如果小明原来有30元，每包饼干的售价为1.3元，那么小明剩下的钱数不可能是……………………………（ ） （A ）0.1元； （B ）0.8元； （C ）1.4元； （D ）2.7元． 5．下列说法中，正确的是……………………………………………………………………（ ） （A ）联结两点的线段叫做两点之间的距离；（B ）用度量法和叠合法都可以比较两个角的大小；（C ）六个面、十二条棱和八个顶点组成的图形都是长方体； （D ）空间两条直线间的位置关系只有相交和平行两种．6．只利用一副（两块）三角尺不能直接拼出的角度是…………………………………（ ）（A ）75°；（B ）105°；（C ）150°；（D ）165°．二、 填空题（本大题共12题，每小题2分，满分24分）7．52-的相反数是 ．8．计算：()835.3-- ． 9．每年5月18日是国际博物馆日，2014年5月18日上海中国航海博物馆一上午参观者达9 000人，全天超过16 000人，将16 000用科学记数法表示为 ． 10．当0<a ，b 0时，0<ab ．（填“＞”“＜”或“＝”） 11．二元一次方程1525=+y x 的正整数解是 ．12．a 、b 表示两个有理数，规定新运算“*”为：a *b =b ma 2+（其中 m 为有理数），如果1*2=5，那么m 的值为 ．13．在线段AB 延长线上顺次截取BC =CD =2AB ，如果AB =2，那么AD = ． 14．如图，OP 、OQ 分别是∠AOB 、∠BOC 的平分线，如果∠POQ =52°26′，那么∠AOC = （结果用度、分、秒表示）．15．一个角的补角一定比它的余角大 度．（第14题图）QPCB OA项目 支出金额（元）早餐 4 午餐 7 晚餐 15 饼干16．在长方体ABCD －EFGH 中，与平面ABCD 和平面ABFE 都平行的棱是 ．17．在长方体ABCD －EFGH 中，既与平面ADHE 垂直，又与平面EFGH 平行的平面是 ．18．如果一根铁丝可以折成长6分米，宽4分米，高2分米的长方体框架模型，那么用这根铁丝折成一个正方体框架模型，它的棱长是 分米．三、 简答题（本大题共6题，每小题6分，满分36分）19．计算：()⎪⎭⎫ ⎝⎛-÷-+-⨯⎪⎭⎫ ⎝⎛-3131337972．解：20．解方程：12135x x +--=．解：21．解不等式：x 15≥()246233--x ，并把它的解集在数轴上表示出来． 解：22．解不等式组：⎪⎩⎪⎨⎧->+>．，－31221302x x x解：ABCD EFGH（第16、17题图）① ②23．解方程组：⎩⎨⎧=-+=--．，0243053y x y x解： 24．解方程组：⎪⎩⎪⎨⎧=++=-+=+-．，，223243223z y x z y x z y x 解：四、作图题（本大题6分）25．线段AB 与射线AP 有一公共端点A ．（1） 用直尺和圆规作出线段AB 的中点M ；（不写作图方法） （2） 用直尺和圆规作出以点B 为顶点的∠ABQ ，使∠ABQ ＝∠P AB ，且BQ 与AP 相交于点C ．（不写作图方法） （3） 联结CM ，用量角器测量∠AMC 和∠BMC 的度数，你认为∠AMC 和∠BMC 的大小关系如何？ ①②PBA第25题①②③五、解答题（本大题共2题，26题7分，27题9分，满分16分）26．学校“六一节”活动，设计了一个飞镖游戏，飞镖游戏的规则如下：如图，掷到A区和B 区的得分不同，A区为小圆内部分，B区为大圆内小圆外部分（A区、B区均不含边界，如果掷到边界上重新投掷，投掷在大圆以外的无效）．现在将投掷有效的每次位置用一个点标注，统计出小红，小华和小明的有效成绩情况如下：如果小红得了65分，小华得了71分，求：（1）掷中A区、B区一次各得多少分？（2）按照这样的记分方法，小明得了多少分？解：27．小红，小华和小明准备用透明胶和66张大小相同的正方形硬纸板制作一些长方体纸盒，如图1，三人分别将正方形硬纸板按各自方案裁剪，然后各取两张制作成一个长方体纸盒，现在需要你的帮忙：（1）制作前，要画出长方体纸盒的直观图，小明只画了一部分（如图2），请你帮他画完整（不写画法）；（2）如果按照设计的方案全部用完可以做成几个完整的长方体纸盒？（3）制作过程中，小明少裁剪了几张正方形硬纸板，这几张正方形硬纸板由小红和小华分别按各自的方案裁剪完，裁剪出的长方形硬纸板正好可以全部做成与（2）大小相同的无盖盒子，请问小明少裁剪了几张硬纸板？解：小明小华小红（第27题图1）（第27题图2）浦东新区2013学年度第二学期期末质量测试 六年级（预备年级）数学参考答案及评分说明一、选择题（本大题共6题，每小题3分，满分18分）（每题只有一个选项正确） 1．B ； 2．D ； 3．C ； 4．B ； 5．B ； 6．D ．二、填空题（本大题共12题，每小题2分，满分24分）7．52； 8．831-； 9．4106.1⨯； 10．>； 11．⎩⎨⎧==．5,1y x 12．１；13．10； 14．104°52′； 15．90； 16．HG ； 17．ABCD ； 18．4．三、简答题（本大题共6题，每小题6分，满分36分）19．解：原式=()331992197-⨯+⨯⎪⎭⎫⎝⎛-．…………………………………………………（3分）=3319914⨯-⨯-． =114--．……………………………………………………………………（2分）=15-．…………………………………………………………………………（1分）20．解：()()152315=--+x x ．…………………………………………………………（2分）156355=+-+x x ．…………………………………………………………（2分）42=x ．2=x ．……………………………………………………………（2分）∴原方程的解为2=x ．21．解：x 15≥481233+-x ．……………………………………………………………（2分） x 27≥81．x ≥3．…………………………………………………………………………（2分）所以，这个不等式的解集在数轴上表示为：……………………………………（2分）22．解：由①，得 2<x ．…………………………………………………………………（2分）由②，得 ()()122133->+x x ．2439->+x x ．55->x ．1->x ．………………………………………………………（3分） 所以，原不等式组的解集是21<<-x ．………………………………………（1分）23．解：由①，得 53+=y x ． …………………………………………………（1分）把③代入由②，得 024159=-++y y ． 1313-=y ．1-=y ．…………………………………（2分） 把1-=y 代入③，得 2=x ．……………………………………………………（2分）所以，原方程组的解是⎩⎨⎧-==．，12y x …………………………………………………（1分）24．解：由①＋③，得 2433=+z x ．8=+z x ． ④………………………………………………（1分）由①＋②×3，得 1410=-z x ． ⑤…………………………………………（1分） 由④＋⑤，得 2211=x ．2=x ．………………………………………………………（1分） 把2=x 代入④，得 6=z ．……………………………………………………（1分） 把2=x ，6=z 代入②，得 4=y ．……………………………………………（1分）所以，原方程组的解是⎪⎩⎪⎨⎧===．，，642z y x …………………………………………………（1分）四、作图题（本大题6分） 25．（1）作图略．……………………………………………………………………………（2分） （2）作图略．……………………………………………………………………………（2分）（3）∠AMC =∠BMC =ο90．……………………………………………………………（2分）③五、解答题（本大题共2题，26题7分，27题9分，满分16分） 26．解：（1）设掷中A 区得x 分，掷中B 区y 分．根据题意，得方程组⎩⎨⎧=+=+．，71356553y x y x ………………………………………………………………（2分）解这个方程组，得⎩⎨⎧==．，710y x …………………………………………………（2分）答：掷中A 区得10分，掷中B 区7分．（2）小明得分为：6276102=⨯+⨯（分）．…………………………………（3分） 答：按照这样的记分方法，小明得了62分．27．解：（1）图略．…………………………………………………………………………（2分） （2）设可以做成x 个完整的长方体纸盒．根据题意，得方程66332=++xx x ．……………………………………………………………（2分） 解这个方程，得33=x ．……………………………………………………（1分） 答：可以做成33个完整的长方体纸盒．（3）设可以做成y 个完整的长方体纸盒．根据题意，得方程66632=++y y y ．……………………………………………………………（2分）解这个方程，得36=y ．……………………………………………………（1分）小明少裁剪的硬纸板数是5336333=-（张）．……………………………（1分） 答：小明少裁剪了5张硬纸板． （注：其他做法请相应给分）。

浦东新区2015学年度第二学期期末质量抽测初一数学题号一二三四总分得分（完卷时间：90分钟满分：100分）2016.6一、选择题（本大题共6题，每题2分，满分12分）（每题只有一个选项正确）1．下列关于无理数的说法，错误的是……………………………………………………（）（A）无理数是实数；（B）无理数是无限不循环小数；（C）无理数是无限小数；（D）无理数是带根号的数．2．如图，线段AB将边长为1个单位长度的正方形分割为两个等腰直角三角形，以A为圆心、AB的长为半径画弧交数轴于点C，那么点C在数轴上表示的实数是………………（）（A）1+2；（B）2；（C）2-1；（D）1．3．如图，直线l1∥l2，∠1=110°，∠2=130°，那么∠3的度数是………………………………（）（A）40°；（B）50°；（C）60°；（D）70°．4．下列说法：①任意三角形的内角和都是180°；②三角形的一个外角大于任何一个内角；③三角形的中线、角平分线和高线都是线段；④三角形的三条高线必在三角形内．其中正确的是……………………………………………………………………………………（）（第5题图）（第2题图）（第3题图）（A）①②；（B）①③；（C）②③；（D）③④．5．如图，已知两个三角形全等，那么∠1的度数是…………………………………………（）（A）72°；（B）60°；（C）50°；（D）58°．6．在直角坐标平面内，已知在y轴与直线x=3之间有一点M(a，3)，如果该点关于直线x=3的对称点M'的坐标为(5，3)，那么a的值为…………………………………………（）（A）4；（B）3；（C）2；（D）1．二、填空题（本大题共12题，每题3分，满分36分）7．计算：9=．8．据上海市统计局最新发布的统计公报显示，2015年末上海市常住人口总数约为24 152 700人，用科学记数法将24 152 700保留三个有效数字是．9．如图，∠2的同旁内角是．10．如图，已知BC∥DE，∠ABC=120°，那么直线AB、DE的夹角是°．11．已知三角形的三边长分别为3cm、x cm和7cm，那么x的取值范围是．（第9题图）（第10题图）（第12题图）12．如图，在等腰△ABC中，AB=AC，点O是△ABC内一点，且OB=OC．联结AO并延长交边BC于点D．如果BD=6，那么BC的值为．13．如图，已知点A、B、C、F在同一条直线上，AD∥EF，∠D=40°，∠F=30°，那么∠ACD 的度数是．14．如图，将△ABC沿射线BA方向平移得到△DEF，AB=4，AE=3，那么DA的长度是．15．如图，在四边形ABCD中，AD∥BC，要使△ABD≌△CDB，可添加一个条件为．16．在平面直角坐标系中，如果点M（-1，a-1）在第三象限，那么a的取值范围是．17．如图，将边长为1个单位长度的正方形ABCD置于平面直角坐标系内，如果BC与x轴平行，且点A的坐标是（2，2），那么点C的坐标为．18．在等腰△ABC中，如果过顶角的顶点A的一条直线AD将△ABC分割成两个等腰三角形，那么∠BAC= °．（第15题图）（第14题图）（第17题图）（第13题图）（第21题图）三、简答题（本大题共4题，第19题，每小题3分；第20题，每小题2分；第21题6分，第22题5分，满分21分）19．计算（写出计算过程）：（1）()62623-+； （2）521135÷⨯．解： 解：20．利用幂的性质计算（写出计算过程，结果表示为含幂的形式）：（1）212193⨯；（2）342331010-⎛⎫÷ ⎪ ⎪⎝⎭．解：解：21．如图，已知直线AB 、CD 被直线EF 所截，FG 平分∠EFD ，∠1=∠2=80°，求∠BGF的度数．解：因为∠1=∠2=80°（已知），所以AB ∥CD （ ）．所以∠BGF +∠3=180°（ ）． 因为∠2+∠EFD =180°（邻补角的意义）， 所以∠EFD = °（等式性质）． 因为FG 平分∠EFD （已知），所以∠3=∠EFD （角平分线的意义）． 所以∠3= °（等式性质）． 所以∠BGF = °（等式性质）．22．如图，在△ABC 中，AD ⊥BC ，垂足为点D ，∠C =2∠1，∠2=32∠1，求∠B 的度数．四、解答题（本大题共4题，第23题6分，第24题7分，第25题8分，第26题10分，满分31分）23．如图，已知AB =AC ，BD ⊥AC ，CE ⊥AB ，垂足分别为点D 、E ．说明△ABD 与△ACE全等的理由．24．如图，点E 是等边△ABC 外一点，点D 是BC 边上一点，AD =BE ，∠CAD =∠CBE ，联结ED 、EC ．（1）试说明△ADC 与△BEC 全等的理由； （2）试判断△DCE 的形状，并说明理由．（第22题图）（第23题图）25．如图，在直角坐标平面内，已知点A (8，0)，点B 的横坐标是2，△AOB 的面积为12．（1）求点B 的坐标；（2）如果P 是直角坐标平面内的点，那么点P 在什么位置时，S △AOP =2S △AOB ？26．如图1，以AB 为腰向两侧分别作全等的等腰△ABC 和△ABD ，过顶角的顶点A 作∠MAN ，使MAN BAC α∠=∠=（060α︒<<︒），将∠MAN 的边AM 与AC 叠合，绕点A 按逆时针方向旋转，与射线CB 、BD 分别交于点E 、F ，设旋转角度为β．（1）如图1，当0βα︒<<时，线段BE 与DF 相等吗？请说明理由．（第25题图）（2）当2αβα<<时，线段CE 、FD 与线段BD 具有怎样的数量关系？请在图2中画出图形并说明理由．（3）联结EF ，在∠MAN 绕点A 逆时针旋转过程中(02βα︒<<)，当线段AD ⊥EF 时，请用含α的代数式直接表示出∠CEA 的度数．（第26题图3）（第26题图2）浦东新区2015学年度第二学期期末质量测试初一数学参考答案一、选择题：（本大题共6题，每小题2分，满分12分）（每题只有一个选项正确） 1．D ． 2．A ． 3．C ． 4．B ． 5．C ． 6．D ．二、填空题：（本大题共12题，每题3分，满分36分） 7．3． 8．72.4210⨯． 9．∠4． 10．60． 11．4<x <10． 12．12． 13．110°． 14．1． 15．略．16．1<a ．17．（3，1）．18．90或108．三、简答题（本大题共4题，第19、20题，每题3分；第20题，每小题2分；第21题6分，第22题5分，满分21分）19．（1）解：原式=62262-+………………………………………………………（1分） =226+………………………………………………………………（2分）（2）解：原式（1分）=25⨯⨯（1分）=…………………………………………………………………（1分） 20．（1）解：原式=1233⨯…………………………………………………………………（1分） =323………………………………………………………………………（1分）（2）解：原式=32310-⎛⎫ ⎪ ⎪⎝⎭……………………………………………………………………（1分）=210-…………………………………………………………………………（1分）21．同位角相等，两直线平行………………………………………………………………（1分） 两直线平行，同旁内角互补……………………………………………………………（1分） 100…………………………………………………………………………………………（1分）12…………………………………………………………………………………………（1分）50…………………………………………………………………………………………（1分） 130…………………………………………………………………………………………（1分）22．解：因为AD ⊥BC （已知），所以∠ADC=90°（垂直的意义）． …………………（1分）因为∠C+∠1+∠ADC =180°（三角形内角和性质），∠C =2∠1（已知），……（1分） 所以3∠1+90°=180°（等量代换）， 所以∠1=30°．……………………………………………………………………（1分） 因为∠2=32∠1，所以∠2=45°……………………………………………………（1分） 因为∠C+∠1+∠2+∠B =180°（三角形内角和性质），所以∠B =45°．………（1分）四、解答题（本大题共4题，第23题6分，第24题7分，第25题8分，第26题10分，满分31分）23．因为BD ⊥AC ，CE ⊥AB （已知），所以∠ADB =∠AEC =90°（垂直的意义）．…（2分）在△ABD 和△ACE 中，⎪⎩⎪⎨⎧=∠=∠∠=∠，（已知）（公共角），，（已证）AC AB A A AEC ADB …………………………………………………………（3分） 所以△ABD ≌△ACE （A ．A ．S ）．…………………………………………… （1分）24．解：（1）因为等边△ABC （已知），所以AC =BC ，∠ACB =60°（等边三角形的性质）．…………………………（2分） 在△ADC 和△BEC 中，⎪⎩⎪⎨⎧=∠=∠=，（已知）（已知），（已证）BE AD CBE CAD BC AC ,…………………………………………………………（1分） 所以△ACE ≌△DBF （S ．A ．S ）．…………………………………………… （1分）（2）因为△ACE ≌△DBF （已证），所以∠ACD =∠BCE =60°.（全等三角形对应角相等），………………………… （1分） DC =EC （全等三角形对应边相等），………………………………………… （1分） 即△DCE 是等腰三角形．所以△DCE 是等边三角形．(有一个内角等于60°的等腰三角形是等边三角形)…（1分） 25．解：（1）设点B 的纵坐标为y ，因为A (8，0)，所以OA =8； ………………………………………………………（1分） 因为S △AOB =12OA ·|y |=12×8|y |=12，所以y =±3， ………………………………（2分） 所以点B 的坐标为(2，3)或(2，-3)．………………………………………………（1分）（2）设点P 的纵坐标为h ，因为S △AOP =2S △AOB ，所以S △AOP =12OA ·|h |=12×8|h |=24，所以h =±6，………（2分）所以点P 在直线y =6或直线y =-6．………………………………………………………（2分）26．解：（1）BE =DF ．………………………………………………………………………（1分） 因为等腰△ABC 和△ABD 全等所以AB =AC =AD ，∠C =∠ABC =∠ABD =∠D ，（全等三角形、等腰三角形的性质）∠BAC =∠BAD （全等三角形的对应角相等） ………………………………………（1分）因为MAN BAC α∠=∠=（已知），所以MAN BAD α∠=∠=（等量代换），所以∠MAN -∠BAN =∠BAD -∠BAN （等式性质），即∠EAB =∠F AD.… …………………… …………………………………………………（1分）在△AEB 和△AFD 中ABE D AB AD EAB FAD ∠=∠⎧⎪=⎨⎪∠=∠⎩（已证）（已证）（已证） 所以△AEB ≌△AFD （A ．S ．A ），………………………………………………………（1分） 所以BE =DF ．（全等三角形的对应边相等）（2）CE -FD =BD . …………………………………………………………………………（1分）图形正确. ……………………………………………………………………………………（1分） 因为MAN BAD α∠=∠=（等量代换），所以∠MAN -∠EAD =∠BAD -∠EAD （等式性质），即∠DAF =∠BAE ．因为∠ABC =∠ADB （已证），所以180°-∠ABC =180°-∠ADB ，即∠ABE =∠ADF ．在△AEB 和△AFD 中ABE ADF AB AD BAE DAF ∠=∠⎧⎪=⎨⎪∠=∠⎩（已证）（已证）（已证）所以△AEB≌△AFD（A．S．A），………………………………………………………（1分）所以BE=DF（全等三角形的对应边相等），所以CE-FD=CB+BE-DF=CB（等量代换）．因为等腰△ABC与等腰△ABD全等，所以BC=BD（全等三角形的对应边相等），所以CE-FD=BD（等量代换）．……………………………………………………………（1分）（3）90°-α．………………………………………………………………………………（2分）。

浦东新区2015学年度第二学期期末质量抽测初一数学题号一二三四总分得分（完卷时间：90分钟满分：100分）2016.6一、选择题（本大题共6题，每题2分，满分12分）（每题只有一个选项正确）1．下列关于无理数的说法，错误的是……………………………………………………（）（A）无理数是实数；（B）无理数是无限不循环小数；（C）无理数是无限小数；（D）无理数是带根号的数．2．如图，线段AB将边长为1个单位长度的正方形分割为两个等腰直角三角形，以A为圆心、AB的长为半径画弧交数轴于点C，那么点C在数轴上表示的实数是………………（）（A）1+2；（B）2；（C）2-1；（D）1．3．如图，直线l1∥l2，∠1=110°，∠2=130°，那么∠3的度数是………………………………（）（A）40°；（B）50°；（C）60°；（D）70°．4．下列说法：①任意三角形的角和都是180°；②三角形的一个外角大于任何一个角；③三角形的中线、角平分线和高线都是线段；④三角形的三条高线必在三角形．其中正确的是……………………………………………………………………………………（）（A）①②；（B）①③；（C）②③；（D）③④．5．如图，已知两个三角形全等，那么∠1的度数是…………………………………………（）（A）72°；（B）60°；（C）50°；（D）58°．6．在直角坐标平面，已知在y轴与直线x=3之间有一点M(a，3)，如果该点关于直线x=3的对称点M'的坐标为(5，3)，那么a的值为…………………………………………（）（A）4；（B）3；（C）2；（D）1．二、填空题（本大题共12题，每题3分，满分36分）（第5题图）（第2题图）（第3题图）7．计算：9= ．8．据市统计局最新发布的统计公报显示，2015年末市常住人口总数约为24 152 700人，用科学记数法将24 152 700保留三个有效数字是 ． 9．如图，∠2的同旁角是 ．10．如图，已知BC ∥DE ，∠ABC =120°，那么直线AB 、DE 的夹角是 °． 11．已知三角形的三边长分别为3cm 、x cm 和7cm ，那么x 的取值围是 ．12．如图，在等腰△ABC 中，AB =AC ，点O 是△ABC 一点，且OB =OC ．联结AO 并延长交边BC于点D ．如果BD =6，那么BC 的值为 ．13．如图，已知点A 、B 、C 、F 在同一条直线上，AD ∥EF ，∠D=40°，∠F =30°，那么∠ACD的度数是 ．14．如图，将△ABC 沿射线BA 方向平移得到△DEF ，AB =4，AE =3，那么DA 的长度是 ． 15．如图，在四边形ABCD 中，AD ∥BC ，要使△ABD ≌△CDB ，可添加一个条件为 ． 16．在平面直角坐标系中，如果点M （-1，a -1）在第三象限，那么a 的取值围是 ． 17．如图，将边长为1个单位长度的正方形ABCD 置于平面直角坐标系，如果BC 与x 轴平行，且点A 的坐标是（2，2），那么点C 的坐标为 ．18．在等腰△ABC 中，如果过顶角的顶点A 的一条直线AD 将△ABC 分割成两个等腰三角形，那么∠BAC = °．三、简答题（本大题共4题，第19题，每小题3分；第20题，每小题2分；第21题6分，第22题5分，满分21分） 19．计算（写出计算过程）：（第15题图）（第9题图）（第14题图）（第10题图）（第17题图）（第12题图）（第13题图）（第21题图）（1）()62623-+； （2）521135÷⨯．解： 解：20．利用幂的性质计算（写出计算过程，结果表示为含幂的形式）：（1）212193⨯；（2）342331010-⎛⎫÷ ⎪ ⎪⎝⎭．解：解：21．如图，已知直线AB 、CD 被直线EF 所截，FG 平分∠EFD ，∠1=∠2=80°，求∠BGF 的度数．解：因为∠1=∠2=80°（已知），所以AB ∥CD （ ）．所以∠BGF +∠3=180°（ ）． 因为∠2+∠EFD =180°（邻补角的意义）， 所以∠EFD = °（等式性质）． 因为FG 平分∠EFD （已知），所以∠3= ∠EFD （角平分线的意义）． 所以∠3= °（等式性质）． 所以∠BGF = °（等式性质）．22．如图，在△ABC 中，AD ⊥BC ，垂足为点D ，∠C =2∠1，∠2=32∠1，求∠B 的度数．四、解答题（本大题共4题，第23题6分，第24题7分，第25题8分，第26题10分，满分31分）23．如图，已知AB=AC，BD⊥AC，CE⊥AB，垂足分别为点D、E．说明△ABD与△ACE全等的理由．24．如图，点E是等边△ABC外一点，点D是BC边上一点，AD=BE，∠CAD=∠CBE，联结ED、EC．（1）试说明△ADC与△BEC全等的理由；（2）试判断△DCE的形状，并说明理由．25．如图，在直角坐标平面，已知点A(8，0)，点B的横坐标是2，△AOB的面积为12．（1）求点B的坐标；（2）如果P是直角坐标平面的点，那么点P在什么位置时，S△AOP=2S△AOB？（第24题图）（第23题图）26．如图1，以AB 为腰向两侧分别作全等的等腰△ABC 和△ABD ，过顶角的顶点A 作∠MAN ，使MAN BAC α∠=∠=（060α︒<<︒），将∠MAN 的边AM 与AC 叠合，绕点A 按逆时针方向旋转，与射线CB 、BD 分别交于点E 、F ，设旋转角度为β． （1）如图1，当0βα︒<<时，线段BE 与DF 相等吗？请说明理由．（2）当2αβα<<时，线段CE 、FD 与线段BD 具有怎样的数量关系？请在图2中画出图形并说明理由．（第26题图1）（第26题图2）（第25题图）（3）联结EF ，在∠MAN 绕点A 逆时针旋转过程中(02βα︒<<)，当线段AD ⊥EF 时，请用含α的代数式直接表示出∠CEA 的度数．（第26题图3）浦东新区2015学年度第二学期期末质量测试初一数学参考答案一、选择题：（本大题共6题，每小题2分，满分12分）（每题只有一个选项正确） 1．D ． 2．A ． 3．C ． 4．B ． 5．C ． 6．D ．二、填空题：（本大题共12题，每题3分，满分36分） 7．3． 8．72.4210⨯． 9．∠4． 10．60． 11．4<x <10． 12．12． 13．110°． 14．1． 15．略．16．1<a ．17．（3，1）．18．90或108．三、简答题（本大题共4题，第19、20题，每题3分；第20题，每小题2分；第21题6分，第22题5分，满分21分） 19．（1）解：原式=62262-+………………………………………………………（1分） =226+………………………………………………………………（2分）（2）解：原式1分）=25⨯⨯（1分）=…………………………………………………………………（1分） 20．（1）解：原式=1233⨯…………………………………………………………………（1分） =323………………………………………………………………………（1分）（2）解：原式=32310-⎛⎫ ⎪ ⎪⎝⎭……………………………………………………………………（1分） =210-…………………………………………………………………………（1分）21．同位角相等，两直线平行………………………………………………………………（1分） 两直线平行，同旁角互补……………………………………………………………（1分） 100…………………………………………………………………………………………（1分）12…………………………………………………………………………………………（1分）50…………………………………………………………………………………………（1分） 130…………………………………………………………………………………………（1分）22．解：因为AD ⊥BC （已知），所以∠ADC=90°（垂直的意义）． …………………（1分）因为∠C+∠1+∠ADC =180°（三角形角和性质），∠C =2∠1（已知），……（1分） 所以3∠1+90°=180°（等量代换）， 所以∠1=30°．……………………………………………………………………（1分）因为∠2=32∠1，所以∠2=45°……………………………………………………（1分）因为∠C+∠1+∠2+∠B =180°（三角形角和性质），所以∠B =45°．………（1分）四、解答题（本大题共4题，第23题6分，第24题7分，第25题8分，第26题10分，满分31分）23．因为BD ⊥AC ，CE ⊥AB （已知），所以∠ADB =∠AEC =90°（垂直的意义）．…（2分） 在△ABD 和△ACE 中，⎪⎩⎪⎨⎧=∠=∠∠=∠，（已知）（公共角），，（已证）AC AB A A AEC ADB …………………………………………………………（3分） 所以△ABD ≌△ACE （A ．A ．S ）．…………………………………………… （1分）24．解：（1）因为等边△ABC （已知），所以AC =BC ，∠ACB =60°（等边三角形的性质）．…………………………（2分） 在△ADC 和△BEC 中，⎪⎩⎪⎨⎧=∠=∠=，（已知）（已知），（已证）BE AD CBE CAD BC AC ,…………………………………………………………（1分） 所以△ACE ≌△DBF （S ．A ．S ）．…………………………………………… （1分）（2）因为△ACE ≌△DBF （已证），所以∠ACD =∠BCE =60°.（全等三角形对应角相等），………………………… （1分） DC =EC （全等三角形对应边相等），………………………………………… （1分） 即△DCE 是等腰三角形．所以△DCE 是等边三角形．(有一个角等于60°的等腰三角形是等边三角形)…（1分） 25．解：（1）设点B 的纵坐标为y ，因为A (8，0)，所以OA =8； ………………………………………………………（1分） 因为S △AOB =12OA ·|y |=12×8|y |=12，所以y =±3， ………………………………（2分） 所以点B 的坐标为(2，3)或(2，-3)．………………………………………………（1分）（2）设点P 的纵坐标为h ，因为S △AOP =2S △AOB ，所以S △AOP =12OA ·|h |=12×8|h |=24，所以h =±6，………（2分） 所以点P 在直线y =6或直线y =-6．………………………………………………………（2分）26．解：（1）BE =DF ．………………………………………………………………………（1分） 因为等腰△ABC 和△ABD 全等 所以AB =AC =AD ，∠C =∠ABC =∠ABD =∠D ，（全等三角形、等腰三角形的性质）∠BAC =∠BAD （全等三角形的对应角相等） ………………………………………（1分） 因为MAN BAC α∠=∠=（已知），所以MAN BAD α∠=∠=（等量代换）， 所以∠MAN -∠BAN =∠BAD -∠BAN （等式性质），即∠EAB =∠FAD .… …………………… …………………………………………………（1分） 在△AEB 和△AFD 中ABE D AB AD EAB FAD ∠=∠⎧⎪=⎨⎪∠=∠⎩（已证）（已证）（已证）所以△AEB ≌△AFD （A ．S ．A ），………………………………………………………（1分） 所以BE =DF ．（全等三角形的对应边相等）（2）CE -FD =BD . …………………………………………………………………………（1分） 图形正确. ……………………………………………………………………………………（1分） 因为MAN BAD α∠=∠=（等量代换）， 所以∠MAN -∠EAD =∠BAD -∠EAD （等式性质）， 即∠DAF =∠BAE ．因为∠ABC =∠ADB （已证），所以180°-∠ABC =180°-∠ADB ， 即∠ABE =∠ADF ． 在△AEB 和△AFD 中ABE ADFAB AD BAE DAF ∠=∠⎧⎪=⎨⎪∠=∠⎩（已证）（已证）（已证）所以△AEB ≌△AFD （A ．S ．A ），………………………………………………………（1分） 所以BE =DF （全等三角形的对应边相等）， 所以CE -FD =CB +BE -DF =CB （等量代换）． 因为等腰△ABC 与等腰△ABD 全等， 所以BC =BD （全等三角形的对应边相等），所以CE -FD =BD （等量代换）．……………………………………………………………（1分） （3）90°-α ． ………………………………………………………………………………（2分）。

上海市浦东新区2015-2016学年七年级（下）期末数学试卷(解析版)一、选择题（本大题共6小题，每题2分，满分12分）1．下列关于无理数的说法，错误的是（）A．无理数是实数 B．无理数是无限不循环小数C．无理数是无限小数 D．无理数是带根号的数2．如图，线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形，以A为圆心，AB的长为半径画弧交数轴于点C，那么点C在数轴上表示的实数是（）A．1+B．C．D．13．如图，直线l1∥l2，∠1=110°，∠2=130°，那么∠3的度数是（）A．40°B．50°C．60°D．70°4．下列说法：①任意三角形的内角和都是180°；②三角形的一个外角大于任何一个内角；③三角形的中线、角平分线和高线都是线段；④三角形的三条高线必在三角形内，其中正确的是（）A．①②B．①③C．②③D．③④5．已知如图所示的两个三角形全等，则∠α的度数是（）A．72°B．60°C．50°D．58°6．在直角坐标平面内，已知在y轴与直线x=3之间有一点M（a，3），如果该点关于直线x=3的对称点M的坐标为（5，3），那么a的值为（）A．4 B．3 C．2 D．1二、填空题（本大题共12题，每题3分，满分36分）7．=．8．据上海市统计局最新发布的统计公报显示，2015年末上海市常住人口总数约为24152700人，用科学记数法将24152700保留三个有效数字是．9．如图，∠2的同旁内角是．10．如图，已知BC∥DE，∠ABC=120°，那么直线AB、DE的夹角是．11．已知三角形的三边长分别为3cm，xcm和7cm，那么x的取值范围是．12．如图，在等腰△ABC中，AB=AC，点O是△ABC内一点，且OB=OC，联结AO并延长交边BC于点D，如果BD=6，那么BC的值为．13．如图，已知点A、B、C、F在同一条直线上，AD∥EF，∠D=40°，∠F=30°，那么∠ACD 的度数是．14．如图，将△ABC沿射线BA方向平移得到△DEF，AB=4，AE=3，那么DA的长度是．15．如图，在四边形ABCD中，AD∥BC，要使△ABD≌△CDB，可添加一个条件为．16．在平面直角坐标系中，如果点M（﹣1，a﹣1）在第三象限，那么a的取值范围是．17．如图，将边长为1个单位长度的正方形ABCD置于平面直角坐标系内，如果BC与x轴平行，且点A的坐标是（2，2），那么点C的坐标为．18．在等腰△ABC中，如果过顶角的顶点A的一条直线AD将△ABC分别割成两个等腰三角形，那么∠BAC=．三、解答题（本大题共8小题，第19题，每小题6分；第20题，每小题6分；第21题6分；第22题5分，第23题6分，第24题7分，第25题8分，第26题10分）19．（6分）计算（写出计算过程）：（1）2+（）0﹣；（2）×．20．（4分）利用幂的性质计算（写出计算过程，结果表示为含幂的形式）：（1）3×；（2）（10÷10）﹣3．21．（6分）如图，已知直线AB、CD被直线EF所截，FG平分∠EFD，∠1=∠2=80°，求∠BGF的度数．解：因为∠1=∠2=80°（已知），所以AB∥CD（）所以∠BGF+∠3=180°（）因为∠2+∠EFD=180°（邻补角的意义）．所以∠EFD=．（等式性质）．因为FG平分∠EFD（已知）．所以∠3=∠EFD（角平分线的意义）．所以∠3=．（等式性质）．所以∠BGF=．（等式性质）．22．（5分）如图，在△ABC中，AD⊥BC，垂足为点D，∠C=2∠1，∠2=∠1，求∠B 的度数．23．（6分）如图，已知AB=AC，BD⊥AC，CE⊥AB，垂足分别为点D，E，说明△ABD 与△ACE全等的理由．24．（7分）如图，点E 是等边△ABC 外一点，点D 是BC 边上一点，AD=BE ，∠CAD=∠CBE ，连结ED ，EC ．（1）试说明△ADC 与△BEC 全等的理由；（2）试判断△DCE 的形状，并说明理由．25．（8分）如图，在直角坐标平面内，已知点A （8，0），点B 的横坐标是2，△AOB 的面积为12．（1）求点B 的坐标；（2）如果P 是直角坐标平面内的点，那么点P 在什么位置时，S △AOP =2S △AOB ？26．（10分）如图1，以AB 为腰向两侧分别作全等的等腰△ABC 和△ABD ，过点A 作∠MAN ，使∠MAN=∠BAC=α（0°＜α＜60°），将∠MAN 的边AM 与AC 叠合，绕点A 按逆时针方向旋转，与射线CB ，BD 分别交于点E ，F ，设旋转角度为β．（1）如图1，当0°＜β＜α时，线段BE与DF相等吗？请说明理由．（2）当α＜β＜2α时，线段CE，FD与线段BD具有怎样的数量关系？请在图2中画出图形并说明理由．（3）联结EF，在∠MAN绕点A逆时针旋转过程中（0°＜β＜2α），当线段AD⊥EF时，请用含α的代数式直接表示出∠CEA的度数．2015-2016学年上海市浦东新区七年级（下）期末数学试卷参考答案与试题解析一、选择题（本大题共6小题，每题2分，满分12分）1．下列关于无理数的说法，错误的是（）A．无理数是实数 B．无理数是无限不循环小数C．无理数是无限小数 D．无理数是带根号的数【考点】无理数．【分析】依据无理数的定义以及无理数常见类型进行解答即可．【解答】解：A、实数包括无理数和有理数，故A正确，与要求不符；B、无理数是无限不循环小数，正确，与要求不符；C、无理数是无限小数，正确，与要求不符；D、无理数是带根号的数，错误，如=3是有理数，与要求相符．故选：D．【点评】本题主要考查的是无理数的认识，掌握无理数的定义以及常见类型是解题的关键．2．如图，线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形，以A为圆心，AB的长为半径画弧交数轴于点C，那么点C在数轴上表示的实数是（）A．1+B．C．D．1【考点】实数与数轴；勾股定理．【分析】先根据勾股定理求出直角三角形的斜边，即可得出选项．【解答】解：C点表示的数是： +1=+1=1+，故选A．【点评】本题考查了数轴和实数，勾股定理的应用，能读懂图象是解此题的关键．3．如图，直线l1∥l2，∠1=110°，∠2=130°，那么∠3的度数是（）A．40°B．50°C．60°D．70°【考点】平行线的性质．【分析】延长AC交FB的延长线于点D得到∠4，根据两直线平行，同旁内角互补得到∠4=180°﹣∠1，再根据三角形外角性质可得∠3=∠2﹣∠4，代入数据计算即可．【解答】解：如图，延长AC交FB的延长线于点D，∵AE∥BF，∴∠4=180°﹣∠1=70°，∴∠3=∠2﹣∠4=60°．故选：C．【点评】主要考查两直线平行，同旁内角互补的性质，作辅助线和运用三角形的一个外角等于和它不相邻的两个内角的和也非常重要．4．下列说法：①任意三角形的内角和都是180°；②三角形的一个外角大于任何一个内角；③三角形的中线、角平分线和高线都是线段；④三角形的三条高线必在三角形内，其中正确的是（）A．①②B．①③C．②③D．③④【考点】三角形内角和定理；三角形的角平分线、中线和高；三角形的外角性质．【分析】分别根据三角形外角的性质、三角形的分类及三角形的内角和定理对各选项进行逐一分析即可．【解答】解：任意三角形的内角和都是180°，故①正确；三角形的一个外角大于任何一个和它不相邻的内角，故②错误；三角形的中线、角平分线、高线都是线段，故③正确；只有锐角三角形的三条高线在三角形内，故④错误；故选B．【点评】本题考查的是三角形外角的性质，三角形的高、中线、角平分线的概念；三角形的内角和定理及其推论；三角形的分类即三角形的外角大于任何一个与之不相邻的内角．5．已知如图所示的两个三角形全等，则∠α的度数是（）A．72°B．60°C．50°D．58°【考点】全等三角形的性质．【分析】根据全等三角形对应角相等解答即可．【解答】解：∵两个三角形全等，∴α=50°，故选：C．【点评】本题考查了全等三角形的性质，熟记性质并准确识图，确定出对应角是解题的关键．6．在直角坐标平面内，已知在y轴与直线x=3之间有一点M（a，3），如果该点关于直线x=3的对称点M的坐标为（5，3），那么a的值为（）A．4 B．3 C．2 D．1【考点】坐标与图形变化-对称．【分析】根据题意得出对称点到直线x=3的距离为2，再利用对称点的性质得出答案．【解答】解：∵该点关于直线x=3的对称点N的坐标为（5，3），∴对称点到直线x=3的距离为2，∵点M（a，3）到直线x=3的距离为2，∴a=1，故选：D．【点评】此题主要考查了坐标与图形的性质，根据题意得出对称点到直线x=3的距离是解题关键．二、填空题（本大题共12题，每题3分，满分36分）7．=3．【考点】算术平方根．【分析】根据算术平方根的概念直接解答即可【解答】解：=3．故答案为：3．【点评】本题主要考查了开平方的能力，比较简单．8．据上海市统计局最新发布的统计公报显示，2015年末上海市常住人口总数约为24152700人，用科学记数法将24152700保留三个有效数字是 2.42×107．【考点】科学记数法与有效数字．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值是易错点，由于24152700有8位，所以可以确定n=8﹣1=1．有效数字的计算方法是：从左边第一个不是0的数字起，后面所有的数字都是有效数字．用科学记数法表示的数的有效数字只与前面的a有关，与10的多少次方无关．【解答】解：用科学记数法将24152700保留三个有效数字是2.42×107．故答案为：2.42×107．【点评】本题考查科学记数法的表示方法，正确确定出a和n的值是解题的关键．9．如图，∠2的同旁内角是∠4．【考点】同位角、内错角、同旁内角．【分析】根据同旁内角：两条直线被第三条直线所截形成的角中，若两个角都在两直线的之间，并且在第三条直线（截线）的同旁，则这样一对角叫做同旁内角进行分析即可．【解答】解：∠2的同旁内角是∠4，故答案为：∠4．【点评】此题主要考查了同旁内角，关键是掌握同旁内角的边构成“U”形．10．如图，已知BC∥DE，∠ABC=120°，那么直线AB、DE的夹角是120°或60°．【考点】平行线的性质．【分析】根据平行线的性质得出∠AOE=∠ABC=120°，即可得出答案．【解答】解：∵BC∥DE，∠ABC=120°，∴∠AOE=∠ABC=120°，∴∠EOB=180°﹣120°=60°，即直线AB、DE的夹角是120°或60°，故答案为：120°或60°．【点评】本题考查了平行线的性质的应用，能根据平行线的性质得出∠AOE=∠ABC=120°是解此题的关键，注意：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补．11．已知三角形的三边长分别为3cm，xcm和7cm，那么x的取值范围是4cm＜x＜10cm．【考点】三角形三边关系．【分析】根据三角形任意两边之和大于第三边，任意两边之差小于第三边可得：4＜x＜10．【解答】解：∵三角形的三边长分别是3，7，x，根据三角形三边关系：x＜7+3，x＞7﹣3，∴x的取值范围是4cm＜x＜10cm．故答案为：4cm＜x＜10cm．【点评】考查了三角形的三边关系，解答此题的关键是熟知三角形的三边关系，即任意两边之和大于第三边，任意两边之差小于第三边．12．如图，在等腰△ABC中，AB=AC，点O是△ABC内一点，且OB=OC，联结AO并延长交边BC于点D，如果BD=6，那么BC的值为12．【考点】等腰三角形的性质．【分析】根据AB=AC，OB=OC，可知直线AO是线段BC的垂直平分线，由AO与BC交于点D，BD=6，从而可以得到BC的长，本题得以解决．【解答】解：∵AB=AC，OB=OC，∴点A，点O在线段BC的垂直平分线上，∴直线AO是线段BC的垂直平分线，∵AO与BC交于点D，∴BD=CD，∵BD=6，∴BC=2BD=12，故答案为：12．【点评】本题考查等腰三角形的性质，解题的关键是明确题意，利用线段垂直平分线的性质解答问题．13．如图，已知点A、B、C、F在同一条直线上，AD∥EF，∠D=40°，∠F=30°，那么∠ACD 的度数是110°．【考点】平行线的性质．【分析】根据两直线平行，内错角相等可求∠A的度数，再根据三角形内角和定理即可得到∠ACD的度数，从而求解．【解答】解：∵AD∥EF，∴∠A=∠F=30°，∵∠D=40°，∴∠ACD=180°﹣30°﹣40°=110°．故答案为：110°．【点评】此题主要考查了平行线的性质及三角形内角和定理等知识点．本题的关键是求得∠A的度数．14．如图，将△ABC沿射线BA方向平移得到△DEF，AB=4，AE=3，那么DA的长度是1．【考点】平移的性质．【分析】根据平移的性质得到AD=BE，从而求解．【解答】解：∵将△ABC沿射线BA方向平移得到△DEF，AB=4，AE=3，∴DA=BE=AB﹣AE=4﹣3=1，故答案为：1．【点评】本题考查平移的基本性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．15．如图，在四边形ABCD中，AD∥BC，要使△ABD≌△CDB，可添加一个条件为∠A=∠C．【考点】全等三角形的判定．【分析】先根据平行线的性质得∠CBD=∠ADB，加上公共边BD，所以根据“AAS”判断△ABD≌△CDB时，可添加∠A=∠C．【解答】解：∵AD∥BC，∴∠CBD=∠ADB，而BD=DB，∴当添加∠A=∠C时，可根据“AAS”判断△ABD≌△CDB．故答案为：∠A=∠C【点评】本题考查了全等三角形的判定，全等三角形的判定方法的选择，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边，或两角的夹边；若已知一边一角，则找另一组角，或找这个角的另一边．16．在平面直角坐标系中，如果点M（﹣1，a﹣1）在第三象限，那么a的取值范围是a ＜1．【考点】解一元一次不等式；点的坐标．【分析】利用各个象限点的特点，第三象限，纵坐标和横坐标都小于零列出不等式求解即可．【解答】解：∵点M（﹣1，a﹣1）在第三象限，∴a﹣1＜0，∴a＜1，故答案为a＜1【点评】此题是解一元一次不等式，主要考查了象限点的特点求解，解本题的关键是掌握象限点的特点，是中考常考的常规题．17．如图，将边长为1个单位长度的正方形ABCD置于平面直角坐标系内，如果BC与x轴平行，且点A的坐标是（2，2），那么点C的坐标为（3，1）．【考点】坐标与图形性质．【分析】根据点A的坐标是（2，2），BC∥x轴、AB=BC=1即可得．【解答】解：∵点A的坐标是（2，2），BC∥x轴，且AB=1，∴点B坐标为（2，1），又BC=1，∴点C的坐标为（3，1），故答案为：（3，1）．【点评】本题主要考查坐标与图形性质，点到坐标轴的距离与这个点的坐标是有区别的，表现在两个方面：①到x轴的距离与纵坐标有关，到y轴的距离与横坐标有关；②距离都是非负数，而坐标可以是负数，在由距离求坐标时，需要加上恰当的符号．18．在等腰△ABC中，如果过顶角的顶点A的一条直线AD将△ABC分别割成两个等腰三角形，那么∠BAC=90°或108°．【考点】等腰三角形的性质．【分析】根据题意画出图形，分类讨论，利用三角形的内角和定理和等腰三角形的性质可得结论．【解答】解：①当BD=CD，CD=AD时，如图①所示，∵AB=AC，∴∠B=∠C，设∠B=∠C=x，∵BD=CD，CD=AD，∴∠BAD=∠B=x，∠CAD=∠C=x，∴4x=180°，∴x=45°，∴∠BAC=2x=45°×2=90°；②当AD=BD，AC=CD时，如图②所示，∵AB=AC，∴∠B=∠C设∠B=∠C=x，∵AD=BD，AC=CD，∴∠BAD=∠B=x，∠CAD=，∴=180°﹣2x，解得：x=36°，∴∠BAC=180°﹣2x=180°﹣2×36°=108°，故答案为：90°或108°．【点评】本题主要考查了等腰三角形的性质，根据题意画出图形分类讨论，利用三角形的内角和定理是解答此题的关键．三、解答题（本大题共8小题，第19题，每小题6分；第20题，每小题6分；第21题6分；第22题5分，第23题6分，第24题7分，第25题8分，第26题10分）19．计算（写出计算过程）：（1）2+（）0﹣；（2）×．【考点】二次根式的混合运算；零指数幂．【分析】（1）计算出0指数的值，然后合并同类二次根式即可；（2）把除法化成乘法，然后按乘法的交换律计算即可．【解答】解：（1）原式=2+1﹣=+1；（2）原式=××2=10×=10．【点评】本题考查了二次根式的混合运算，熟练掌握运算顺序和运算律是解题的关键．20．利用幂的性质计算（写出计算过程，结果表示为含幂的形式）：（1）3×；（2）（10÷10）﹣3．【考点】实数的运算；分数指数幂；负整数指数幂．【分析】（1）原式利用二次根式性质法则计算即可得到结果；（2）原式利用同底数幂的除法，以及幂的乘方运算法则计算即可得到结果．【解答】解：（1）原式=3×3=3；（2）原式=（10）﹣3=10﹣2．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．21．如图，已知直线AB、CD被直线EF所截，FG平分∠EFD，∠1=∠2=80°，求∠BGF 的度数．解：因为∠1=∠2=80°（已知），所以AB∥CD（同位角相等，两直线平行）所以∠BGF+∠3=180°（两直线平行，同旁内角互补）因为∠2+∠EFD=180°（邻补角的意义）．所以∠EFD=100°．（等式性质）．因为FG平分∠EFD（已知）．所以∠3=∠EFD（角平分线的意义）．所以∠3=50°．（等式性质）．所以∠BGF=130°．（等式性质）．【考点】平行线的判定；角平分线的定义；对顶角、邻补角．【分析】根据平行显得判定及性质求角的过程，一步步把求解的过程补充完整即可．【解答】解：因为∠1=∠2=80°（已知），所以AB∥CD（同位角相等，两直线平行），所以∠BGF+∠3=180°（两直线平行，同旁内角互补）．因为∠2+∠EFD=180°（邻补角的意义）．所以∠EFD=100°．（等式性质）．因为FG平分∠EFD（已知）．所以∠3=∠EFD（角平分线的意义）．所以∠3=50°．（等式性质）．所以∠BGF=130°．（等式性质）．故答案为：同位角相等，两直线平行；两直线平行，同旁内角互补；100°；；50°；130°．【点评】本题考查了平行线的判定及性质、角平分线的定义以及邻补角，解题的关键是把解题的过程补充完整．本题属于基础题，难度不大，解决该题型题目时，熟悉利用平行线的性质解决问题的过程．22．如图，在△ABC中，AD⊥BC，垂足为点D，∠C=2∠1，∠2=∠1，求∠B的度数．【考点】三角形内角和定理．【分析】根据垂直的定义和三角形内角和定理计算即可．【解答】解：∵AD⊥BC，∴∠ADC=90°，∴∠C+∠1=90°，又∠C=2∠1，∴∠C=60°，∠1=30°，∴∠2=∠1=45°，∴∠B=45°．【点评】本题考查的是三角形内角和定理，掌握三角形的内角和等于180°是解题的关键．23．如图，已知AB=AC，BD⊥AC，CE⊥AB，垂足分别为点D，E，说明△ABD与△ACE 全等的理由．【考点】全等三角形的判定．【分析】根据垂直定义得出∠ADB=∠AEC=90°，根据全等三角形的判定定理AAS推出即可．【解答】解：∵BD⊥AC，CE⊥AB，∴∠ADB=∠AEC=90°，在△ABD和△ACE中∴△ABD≌△ACE（AAS）．【点评】本题考查了全等三角形的判定定理的应用，能熟记全等三角形的判定定理的内容是解此题的关键，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．24．如图，点E是等边△ABC外一点，点D是BC边上一点，AD=BE，∠CAD=∠CBE，连结ED，EC．（1）试说明△ADC与△BEC全等的理由；（2）试判断△DCE的形状，并说明理由．【考点】全等三角形的判定与性质；等边三角形的判定与性质．【分析】（1）由等边三角形的性质得出AC=BC ，∠ACB=60°，由SAS 证明△ADC ≌△BEC 即可；（2）由全等三角形的性质得出∠ACD=∠BCE=60°，DC=EC ，即可得出结论．【解答】（1）证明：∵△ABC 是等边三角形，∴AC=BC ，∠ACB=60°，在△ADC 和△BEC 中，， ∴△ADC ≌△BEC （SAS ）；（2）解：△DCE 是等边三角形；理由如下：∵△ADC ≌△BEC ，∴∠ACD=∠BCE=60°，DC=EC ，即△DCE 是等腰三角形，∴△DCE 是等边三角形．【点评】本题考查了等腰三角形的判定定理，直角三角形的性质，熟记等腰三角形的判定是解题的关键．25．如图，在直角坐标平面内，已知点A （8，0），点B 的横坐标是2，△AOB 的面积为12．（1）求点B 的坐标；（2）如果P 是直角坐标平面内的点，那么点P 在什么位置时，S △AOP =2S △AOB ？【考点】坐标与图形性质．【分析】（1）设点B的纵坐标为y，根据△AOB的面积为12列等式求出y的值，写出点B的坐标；（2）设点P的纵坐标为h，先求出△AOP的面积，再列等式求出h的值，因为横坐标没有说明，所以点P在直线y=6或直线y=﹣6上．【解答】解：（1）设点B的纵坐标为y，因为A（8，0），所以OA=8，=OA•|y|=12，则S△AOB∴y=±3，∴点B的坐标为（2，3）或（2，﹣3）；（2）设点P的纵坐标为h，S△AOP=2S△AOB=2×12=24，∴OA•|h|=24，×8|h|=24，h=±6，所以点P在直线y=6或直线y=﹣6上．【点评】本题是坐标与图形的性质，要明确一个点的坐标到两坐标轴的距离：到x轴的距离与纵坐标有关，到y轴的距离与横坐标有关；其次是根据面积公式列等式求解．26．（10分）（2016春•浦东新区期末）如图1，以AB为腰向两侧分别作全等的等腰△ABC 和△ABD，过点A作∠MAN，使∠MAN=∠BAC=α（0°＜α＜60°），将∠MAN的边AM 与AC叠合，绕点A按逆时针方向旋转，与射线CB，BD分别交于点E，F，设旋转角度为β．（1）如图1，当0°＜β＜α时，线段BE与DF相等吗？请说明理由．（2）当α＜β＜2α时，线段CE，FD与线段BD具有怎样的数量关系？请在图2中画出图形并说明理由．（3）联结EF，在∠MAN绕点A逆时针旋转过程中（0°＜β＜2α），当线段AD⊥EF时，请用含α的代数式直接表示出∠CEA的度数．【考点】三角形综合题．【分析】（1）结论：BE=DF．只要证明△AEB≌△AFD即可．（2）结论：CE﹣FD=BD，由△AEB≌△AFD，得BE=DF，由此即可证明．（3）结论：90°﹣α．只要证明∠AOB=∠AOF=90°即可解决问题．【解答】解：（1）结论：BE=DF．理由：如图1中，∵等腰△ABC和△ABD全等，∴AB=AC=AD，∠C=∠ABC=∠ABD=∠D，∠BAC=∠BAD，∵∠MAN=∠BAC=α，∴∠MAN=∠BAD=α，∴∠EAB=∠FAD，在△AEB和△AFD中，，∴△AEB≌△AFD，∴BE=DF．（2）结论：CE﹣FD=BD．理由：如图2中所示，∵∠MAN=∠BAD，∴∠DAF=∠BAE，∵∠ABC=∠ADB，∴∠ABE=∠ADF，在△ABE和△ADF中，，∴△AEB≌△AFD，∴BE=DF，∵BC=BD，∴CE﹣FD=CE﹣BE=BC=BD．（3）结论：90°﹣α．理由：如图3中，AE交BD于点O．∵AD⊥EF，∴∠DAF+∠AFE=90°，∵∠DAF=∠BAE，∠ABD=∠AFE，∴∠OAB+∠OBA=90°，∴∠AOB=∠AOF=90°，∴∠AFD=90°﹣∠EAF=90°﹣α，∵∠CEA=∠AFD，∴∠CEA=90°﹣α．【点评】本题考查三角形综合题、全等三角形的判定和性质，解题的关键是熟练掌握全等三角形的判定和性质，正确寻找全等三角形，属于中考常考题型．。

2015-2016学年某某市浦东新区高二（下）期末数学试卷一、填空题（共12小题，每小题3分，满分36分）1．抛物线x2=﹣8y的准线方程为．2．如果直线ax+y+1=0与直线3x﹣y﹣2=0垂直，则系数a=．3．双曲线9x2﹣4y2=﹣36的渐近线方程是．4．已知复数z=（3+i）2（i为虚数单位），则|z|=．5．已知点A（﹣4，﹣5），B（6，﹣1），则以线段AB为直径的圆的方程为．6．设复数z（2﹣i）=11+7i（i为虚数单位），则z=．7．若椭圆C的焦点和顶点分别是双曲线的顶点和焦点，则椭圆C的方程是．8．一动点在圆x2+y2=1上移动时，它与定点B（3，0）连线的中点轨迹方程是．9．若复数z满足|z+3i|=5（i是虚数单位），则|z+4|的最大值=．10．设F1和F2是双曲线﹣y2=1的两个焦点，点P在双曲线上，且满足∠F1PF2=90°，则△F1PF2的面积是．11．已知抛物线型拱桥的顶点距离水面2米时，测量水的宽为8米，当水面上升米后，水面的宽度是米．12．已知圆x2+y2+2x﹣4y+a=0关于直线y=2x+b成轴对称，则a﹣b的取值X围是．二、选择题（共4小题，每小题3分，满分12分）13．直线倾斜角的X围是（）A．（0，]B．[0，]C．[0，π） D．[0，π]14．平面内有两定点A、B及动点P，设命题甲：“|PA|+|PB|是定值”，命题乙：“点P的轨迹是以A、B为焦点的椭圆”，则甲是乙的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件15．若1+i是关于x的实系数方程x2+bx+c=0的一个复数根，则（）A．b=2，c=3 B．b=﹣2，c=3 C．b=﹣2，c=﹣1 D．b=2，c=﹣116．对于抛物线C：y2=4x，我们称满足y02＜4x0的点M（x0，y0）在抛物线的内部．若点M（x0，y0）在抛物线内部，则直线l：y0y=2（x+x0）与曲线C （）A．恰有一个公共点B．恰有2个公共点C．可能有一个公共点，也可能有两个公共点D．没有公共点三、解答题（共5小题，满分52分）17．已知直线l平行于直线3x+4y﹣7=0，并且与两坐标轴围成的三角形的面积为24，求直线l的方程．18．设复数z满足|z|=1，且（3+4i）•z是纯虚数，求．19．已知圆C和y轴相切，圆心在直线x﹣3y=0上，且被直线y=x截得的弦长为，求圆C的方程．20．已知F1，F2为椭圆C： +=1（a＞b＞0）的左右焦点，O是坐标原点，过F2作垂直于x轴的直线MF2交椭圆于M，设|MF2|=d．（1）证明：b2=ad；（2）若M的坐标为（，1），求椭圆C的方程．21．已知双曲线C1：．（1）求与双曲线C1有相同焦点，且过点P（4，）的双曲线C2的标准方程；（2）直线l：y=x+m分别交双曲线C1的两条渐近线于A、B两点．当•=3时，某某数m 的值．2015-2016学年某某市浦东新区高二（下）期末数学试卷参考答案与试题解析一、填空题（共12小题，每小题3分，满分36分）1．抛物线x2=﹣8y的准线方程为y=2 ．【考点】抛物线的简单性质．【分析】由于抛物线x2=﹣2py的准线方程为y=，则抛物线x2=﹣8y的准线方程即可得到．【解答】解：由于抛物线x2=﹣2py的准线方程为y=，则有抛物线x2=﹣8y的准线方程为y=2．故答案为：y=2．2．如果直线ax+y+1=0与直线3x﹣y﹣2=0垂直，则系数a=．【考点】直线的一般式方程与直线的垂直关系．【分析】利用相互垂直的直线的斜率之间关系即可得出．【解答】解：由ax+y+1=0得y=﹣ax﹣1，直线3x﹣y﹣2=0得到y=3x﹣2，又直线ax+y+1=0与直线3x﹣y﹣2=0垂直，∴﹣a•3=﹣1，∴a=，故答案为：3．双曲线9x2﹣4y2=﹣36的渐近线方程是y=±x ．【考点】双曲线的简单性质．【分析】求出双曲线的标准方程，结合双曲线渐近线的方程进行求解即可．【解答】解：双曲线的标准方程为﹣=1，则双曲线的渐近线方程为y=±x，故答案为：y=±x4．已知复数z=（3+i）2（i为虚数单位），则|z|= 10 ．【考点】复数求模；复数代数形式的乘除运算．【分析】利用复数的模的平方等于复数的模的乘积，直接计算即可．【解答】解：复数z=（3+i）2（i为虚数单位），则|z|=|3+i||3+i|==10．故答案为：10．5．已知点A（﹣4，﹣5），B（6，﹣1），则以线段AB为直径的圆的方程为（x﹣1）2+（y+3）2=29 ．【考点】圆的标准方程．【分析】由点A和点B的坐标，利用中点坐标公式求出线段AB的中点C的坐标，因为线段AB为所求圆的直径，所以求出的中点C的坐标即为圆心坐标，然后由圆心C的坐标和点A 的坐标，利用两点间的距离公式求出|AC|的长即为圆的半径，根据圆心和半径写出圆的标准方程即可．【解答】解：由中点坐标公式得线段AB的中点坐标为C（1，﹣3），即圆心的坐标为C（1，﹣3）；，故所求圆的方程为：（x﹣1）2+（y+3）2=29．故答案为：（x﹣1）2+（y+3）2=29．6．设复数z（2﹣i）=11+7i（i为虚数单位），则z= 3+5i ．【考点】复数代数形式的乘除运算．【分析】等式两边同乘2+i，然后化简，即可求出复数z．【解答】解：因为z（2﹣i）=11+7i（i为虚数单位），所以z（2﹣i）（2+i）=（11+7i）（2+i），即5z=15+25i，z=3+5i．故答案为：3+5i．7．若椭圆C的焦点和顶点分别是双曲线的顶点和焦点，则椭圆C的方程是．【考点】椭圆的标准方程；双曲线的简单性质．【分析】先确定双曲线的顶点和焦点坐标，可得椭圆C的焦点和顶点坐标，从而可得椭圆C 的方程【解答】解：双曲线的顶点和焦点坐标分别为（±，0）、（±3，0）∵椭圆C的焦点和顶点分别是双曲线的顶点和焦点，∴椭圆C的焦点和顶点坐标分别为（±，0）、（±3，0）∴a=3，c=∴∴椭圆C的方程是故答案为：8．一动点在圆x2+y2=1上移动时，它与定点B（3，0）连线的中点轨迹方程是x2+y2﹣3x+2=0 ．【考点】轨迹方程；中点坐标公式．【分析】设出中点坐标，利用中点坐标公式求出与之有关的圆上的动点坐标，将圆上的动点坐标代入圆的方程，求出中点轨迹方程．【解答】解：设中点坐标为（x，y），则圆上的动点坐标为（2x﹣3，2y）所以（2x﹣3）2+（2y）2=1即x2+y2﹣3x+2=0故答案为：x2+y2﹣3x+2=09．若复数z满足|z+3i|=5（i是虚数单位），则|z+4|的最大值= 10 ．【考点】复数求模．【分析】由复数模的几何意义可得复数z对应的点在以（0，﹣3）为圆心，以5为半径的圆周上，由此可得|z+4|的最大值是点（0，﹣3）与点（﹣4，0）的距离加上半径 5．【解答】解：由|z+3i|=5，所以复数z对应的点在以（0，﹣3）为圆心，以5为半径的圆周上，所以|z+4|的最大值是点（0，﹣3）与点（﹣4，0）的距离加上半径5，点（0，﹣3）与点（﹣4，0）的距离： =5．|z+4|的最大值：5+5=10故答案为：10．10．设F1和F2是双曲线﹣y2=1的两个焦点，点P在双曲线上，且满足∠F1PF2=90°，则△F1PF2的面积是 1 ．【考点】双曲线的应用；双曲线的简单性质．【分析】设|PF1|=x，|PF2|=y，根据根据双曲线性质可知x﹣y的值，再根据∠F1PF2=90°，求得x2+y2的值，进而根据2xy=x2+y2﹣（x﹣y）2求得xy，进而可求得△F1PF2的面积．【解答】解：设|PF1|=x，|PF2|=y，（x＞y）根据双曲线性质可知x﹣y=4，∵∠F1PF2=90°，∴x2+y2=20∴2xy=x2+y2﹣（x﹣y）2=4∴xy=2∴△F1PF2的面积为xy=1故答案为：1．11．已知抛物线型拱桥的顶点距离水面2米时，测量水的宽为8米，当水面上升米后，水面的宽度是4米．【考点】双曲线的标准方程．【分析】以拱顶为坐标原点，拱的对称轴为y轴，水平轴为x轴建立平面直角坐标系，设抛物线方程为：x2=ay，由x=4，y=﹣2，解得a=﹣8，由此能求出当水面上升米后，水面的宽度．【解答】解：以拱顶为坐标原点，拱的对称轴为y轴，水平轴为x轴建立平面直角坐标系，设抛物线方程为：x2=ay，由x=4，y=﹣2，解得a=﹣8，当水面上升米后，y=﹣2+=﹣，x2=（﹣8）•（﹣）=12．解得x=2，或x=﹣2，∴水面宽为4（米）．故答案为：4．12．已知圆x2+y2+2x﹣4y+a=0关于直线y=2x+b成轴对称，则a﹣b的取值X围是（﹣∞，1）．【考点】直线与圆相交的性质．【分析】求出圆的圆心，由题意圆心在直线上，求出a，b的关系，然后确定a﹣b的X围．【解答】解：圆的方程变为（x+1）2+（y﹣2）2=5﹣a，∴其圆心为（﹣1，2），且5﹣a＞0，即a＜5．又圆关于直线y=2x+b成轴对称，∴2=﹣2+b，∴b=4．∴a﹣b=a﹣4＜1．故答案为：（﹣∞，1）二、选择题（共4小题，每小题3分，满分12分）13．直线倾斜角的X围是（）A．（0，]B．[0，]C．[0，π） D．[0，π]【考点】直线的倾斜角．【分析】根据直线倾斜角的定义判断即可．【解答】解：直线倾斜角的X围是：[0，π），故选：C．14．平面内有两定点A、B及动点P，设命题甲：“|PA|+|PB|是定值”，命题乙：“点P的轨迹是以A、B为焦点的椭圆”，则甲是乙的（）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】结合椭圆的定义，利用充分条件和必要条件的定义进行判断．【解答】解：若点P的轨迹是以A、B为焦点的椭圆，则根据椭圆的定义可知动点P到两定点A，B的距离之和|PA|+|PB|=2a （a＞0，且a为常数）成立是定值．若动点P到两定点A，B的距离之和|PA|+|PB|=2a （a＞0，且a为常数），当2a≤|AB|，此时的轨迹不是椭圆．∴甲是乙的必要不充分条件．故选：B．15．若1+i是关于x的实系数方程x2+bx+c=0的一个复数根，则（）A．b=2，c=3 B．b=﹣2，c=3 C．b=﹣2，c=﹣1 D．b=2，c=﹣1【考点】复数相等的充要条件．【分析】由题意，将根代入实系数方程x2+bx+c=0整理后根据得数相等的充要条件得到关于实数a，b的方程组，解方程得出a，b的值即可选出正确选项【解答】解：由题意1+i是关于x的实系数方程x2+bx+c=0∴1+2i﹣2+b+bi+c=0∴，解得b=﹣2，c=3故选B16．对于抛物线C：y2=4x，我们称满足y02＜4x0的点M（x0，y0）在抛物线的内部．若点M（x0，y0）在抛物线内部，则直线l：y0y=2（x+x0）与曲线C （）A．恰有一个公共点B．恰有2个公共点C．可能有一个公共点，也可能有两个公共点D．没有公共点【考点】抛物线的简单性质．【分析】先把直线与抛物线方程联立消去y，进而根据y02＜4x0判断出判别式小于0进而判定直线与抛物线无交点．【解答】解：由y2=4x与y0y=2（x+x0）联立，消去x，得y2﹣2y0y+4x0=0，∴△=4y02﹣4×4x0=4（y02﹣4x0）．∵y02＜4x0，∴△＜0，直线和抛物线无公共点．故选D三、解答题（共5小题，满分52分）17．已知直线l平行于直线3x+4y﹣7=0，并且与两坐标轴围成的三角形的面积为24，求直线l的方程．【考点】直线的一般式方程与直线的平行关系．【分析】设直线l的方程为：3x+4y+m=0，分别令x=0，解得y=﹣；y=0，x=﹣．利用l 与两坐标轴围成的三角形的面积为24，可得=24，解得m即可．【解答】解：设直线l的方程为：3x+4y+m=0，分别令x=0，解得y=﹣；y=0，x=﹣．∵l与两坐标轴围成的三角形的面积为24，∴=24，解得m=±24．∴直线l的方程为3x+4y±24=0．18．设复数z满足|z|=1，且（3+4i）•z是纯虚数，求．【考点】复数的基本概念；复数求模．【分析】设出复数z，|z|=1可得一个方程，化简（3+4i）•z是纯虚数，又得到一个方程，求得z，然后求．【解答】解：设z=a+bi，（a，b∈R），由|z|=1得；（3+4i）•z=（3+4i）（a+bi）=3a﹣4b+（4a+3b）i是纯虚数，则3a﹣4b=0，，．19．已知圆C和y轴相切，圆心在直线x﹣3y=0上，且被直线y=x截得的弦长为，求圆C的方程．【考点】圆的标准方程；直线与圆的位置关系．【分析】由圆心在直线x﹣3y=0上，设出圆心坐标，再根据圆与y轴相切，得到圆心到y轴的距离即圆心横坐标的绝对值等于圆的半径，表示出半径r，然后过圆心作出弦的垂线，根据垂径定理得到垂足为弦的中点，利用点到直线的距离公式求出圆心到直线y=x的距离d，由弦长的一半，圆的半径r及表示出的d利用勾股定理列出关于t的方程，求出方程的解得到t的值，从而得到圆心坐标和半径，根据圆心和半径写出圆的方程即可．【解答】解：设圆心为（3t，t），半径为r=|3t|，则圆心到直线y=x的距离d==|t|，由勾股定理及垂径定理得：（）2=r2﹣d2，即9t2﹣2t2=7，解得：t=±1，∴圆心坐标为（3，1），半径为3；圆心坐标为（﹣3，﹣1），半径为3，则（x﹣3）2+（y﹣1）2=9或（x+3）2+（y+1）2=9．20．已知F1，F2为椭圆C： +=1（a＞b＞0）的左右焦点，O是坐标原点，过F2作垂直于x轴的直线MF2交椭圆于M，设|MF2|=d．（1）证明：b2=ad；（2）若M的坐标为（，1），求椭圆C的方程．【考点】椭圆的简单性质．【分析】（1）x=c代入椭圆方程求得y，进而求得d，可知d×a=b2，原式得证；（2）由M坐标可得c，再把M再把代入椭圆方程求得a和b的关系，结合隐含条件得到a 和b的方程组，求得a，b，则椭圆的方程可求．【解答】（1）证明：把x=c代入椭圆方程： +=1，得，则d=|y|=，∴d×a=b2，即b2=ad；（2）解：∵M的坐标为（，1），∴c=，则，解得b2=2，a2=4．故椭圆的方程为．21．已知双曲线C1：．（1）求与双曲线C1有相同焦点，且过点P（4，）的双曲线C2的标准方程；（2）直线l：y=x+m分别交双曲线C1的两条渐近线于A、B两点．当•=3时，某某数m 的值．【考点】直线与圆锥曲线的综合问题；双曲线的标准方程．【分析】（1）先确定双曲线C1：的焦点坐标，根据双曲线C2与双曲线C1有相同焦点，且过点P（4，），建立方程组，从而可求双曲线C2的标准方程；（2）直线方程与双曲线C1的两条渐近线联立，求出A、B两点的坐标用坐标，利用数量积，即可求得实数m的值．【解答】解：（1）∵双曲线C1：，∴焦点坐标为（，0），（，0）设双曲线C2的标准方程为（a＞0，b＞0），∵双曲线C2与双曲线C1有相同焦点，且过点P（4，）∴，解得∴双曲线C2的标准方程为（2）双曲线C1的两条渐近线为y=2x，y=﹣2x由，可得x=m，y=2m，∴A（m，2m）由，可得x=﹣m，y=m，∴B（﹣m， m）∴∵∴m2=3∴。

第1页（共12页）2015-2016学年上海市浦东新区八年级（下）期末数学试卷一、选择题（本大题共6题，每题3分，满分18分）（每题只有一个选择正确1．下列直线中，与直线y=﹣3x +2平行的是（ ）A ．y=﹣2x +3B ．y=2x +2C ．y=﹣3x +3D ．y=3x ﹣22．已知一次函数y=kx +b （k 、b 为常数）的图象如图所示，那么关于x 的不等式kx +b ＞0的解集是（ ）A ．x ＞3B ．x ＞4C ．x ＜3D ．x ＜43．下列说法中，正确的是（ ）A ．方程=4的根是x=±16B ．方程=﹣x 的根是x 1=0，x 2=3C ．方程+1=0没有实数根D ．方程3﹣的根是x 1=2，x 2=64．如图，将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分，利用这两部分不能拼成的图形是（ ）A ．直角三角形B ．平行四边形C ．菱形D ．等腰梯形5．下列等式正确的是（ ）A ． +=+B ．﹣=C ． +﹣=D ． ++=6．在平行四边形、矩形、菱形、等腰梯形这个四个图形中任选一个图形，那么下列事件是不可能事件的是（ ）A ．这个图形既是轴对称图形又是中心对称图形B ．这个图形既不是轴对称图形又不是中心对称图形C ．这个图形是轴对称图形D ．这个图形是中心对称图形二、填空题（本大题共12题，每题3分，满分36分）7．一次函数y=2x ﹣5的图象在y 轴上的截距是______．8．已知一次函数y=kx +b 的图象不经过第二象限，那么函数值y 随自变量x 的值增大而______（填“增大”或“减小”）．9．如果关于x 的方程（m +2）x=8无解，那么m 的取值范围是______．10．方程x 3﹣8=0的根是______．11．已知关于x 的方程+=，如果设=y ，那么原方程化为关于y 的方程是______．12．某企业的年产值在三年内从1000万元增加到1331万元，如果这三年中每年的增长率相同，设为x ，那么可以列出关于x 的方程是______．13．如果多边形的每个外角都是40°，那么这个多边形的边数是______．14．已知点E 、F 、G 、H 分别是凸四边形ABCD 各边AB 、BC 、CD 、DA 的中点，如果对角线AC=BD=4，那么四边形EFGH 的周长是______．15．在梯形的一条底边长为5，中位线长为7，那么另一条底边的长为______．16．将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，设菱形中较小的角为α度，平行四边形中较大的角为β度，那么β可以用含α的代数式表示为______．17．如图，平行四边形ABCD 中，∠B=60°，AB=8cm ，AD=10cm ，点P 在边BC 上从B 向C 运动，点Q 在边DA 上从D 向A 运动，如果P ，Q 运动的速度都为每秒1cm ，那么当运动时间t=______秒时，四边形ABPQ 是直角梯形．18．已知边长为4的正方形ABCD ，点E 、F 分别在CA 、AC 的延长线上，且∠BED=∠BFD=45°，那么四边形EBFD 的面积是______．三、解答题（本题共4题，每题5分，满分20分）19．解方程组：．20．布袋里有一个红球两个黄球，它们除了颜色外其他都相同．（1）任意摸出一个球恰好是红球的概率是______；（2）摸出一个球再放回袋中，搅匀后再摸出一个球，请利用树形图求事件“摸到一红一黄两球”的概率P．21．已知弹簧在一定限度内，它的长度y（厘米）与所挂重物质量x（千克）是一次函数关系．表中记录的是两次挂不同重量重物的质量（在弹性限度内）与相对应的弹簧长度．所挂重物质量x（千克） 2.5 5弹簧长度y（厘米） 7.5 9求不挂重物时弹簧的长度．22．如图，点E在平行四边形ABCD的对角线BD的延长线上．（1）填空： +=______.﹣=______；（2）求作： +（不写作法，保留作图痕迹，写出结果）四、解答题（本题共3题，第23题7分，第24题9分，第25题10分，满分26分）23．如图，已知矩形ABCD中，点E是CD边上的一点，连结BE，过点A作AF⊥BE．垂足为点F，且AF=BE，过点F作MN∥BC，与AB、CD边分别交于点M、N，求证：四边形AMND为正方形．24．已知：如图，平面直角坐标系中有一个等腰梯形ABCD，且AD∥BC，AB=CD，点A在y轴正半轴上，点B、C在x轴上（点B在点C的左侧），点D在第一象限，AD=3，BC=11，梯形的高为2，双曲线y=经过点D，直线y=kx+b经过A、B两点．（1）求点A、B、C、D的坐标；（2）求双曲线y=和直线y=kx+b的解析式；（3）点M在双曲线上，点N在y轴上，如果四边形ABMN是平行四边形，求点N的坐标．25．已知：如图，在矩形ABCD中，AB=2，BC=5，点P是边AD上一点，连接CP，将四边形ABCP沿CP所在直线翻折，落在四边形EFCP的位置，点A、B的对应点分别为点E，F，边CF与边AD的交点为点G．（1）当AP=2时，求PG的值；（2）如果AP=x，FG=y，求y关于x的函数解析式，并写出它的定义域；（3）连结BP并延长与线段CF交于点M，当△PGM是以MG为腰的等腰三角形时，求AP的长．2015-2016学年上海市浦东新区八年级（下）期末数学试卷参考答案与试题解析一、选择题（本大题共6题，每题3分，满分18分）（每题只有一个选择正确1．下列直线中，与直线y=﹣3x+2平行的是（）A．y=﹣2x+3 B．y=2x+2 C．y=﹣3x+3 D．y=3x﹣2【考点】两条直线相交或平行问题．【分析】根据两直线平行k相同即可解决．【解答】解：根据两直线平行k相同，∵直线y=﹣3x+2，∴k=﹣3，故选C．2．已知一次函数y=kx+b（k、b为常数）的图象如图所示，那么关于x的不等式kx+b＞0的解集是（）A．x＞3 B．x＞4 C．x＜3 D．x＜4第2页（共12页）第3页（共12页）【考点】一次函数与一元一次不等式．【分析】从图象上得到函数的增减性及与x 轴的交点的横坐标，即能求得不等式kx +b ＞0的解集．【解答】解：函数y=kx +b 的图象经过点（4，0），并且函数值y 随x 的增大而减小，所以当x ＜4时，函数值大于0，即关于x 的不等式kx +b ＞0的解集是x ＜4．故选D ．3．下列说法中，正确的是（ ）A ．方程=4的根是x=±16B ．方程=﹣x 的根是x 1=0，x 2=3C ．方程+1=0没有实数根D ．方程3﹣的根是x 1=2，x 2=6【考点】无理方程．【分析】根据各个选项，错误的选项说明错在哪，正确的选项进行说明，即可判断出哪个选项是正确的．【解答】解：当x=﹣16时，没有意义，故选项A 错误；当x=3时， ==3，而﹣x=﹣3，3≠﹣3，故选项B 错误； ∵≥0，则+1≥1，故选项C 正确；3﹣不是方程，故选项D 错误．故选C ．4．如图，将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分，利用这两部分不能拼成的图形是（ ）A ．直角三角形B ．平行四边形C ．菱形D ．等腰梯形【考点】图形的剪拼．【分析】将剪开的△ABE 绕E 点旋转180°，EC 与EB 重合，得到直角三角形；把△ABE 平移，使AB 与DC 重合，则得到平行四边形；把△ABE 的顶点E 与C 重合，B 与D 重合，与四边形AECD 不重叠拼在一起，组成等腰梯形；不能得到菱形；即可得出结论．【解答】解：将△ABE 绕E 点旋转180°，EC 与EB 重合，得到直角三角形，故选项A 正确；把△ABE 平移，使AB 与DC 重合，则得到平行四边形，故选项B 正确；把△ABE 的顶点E 与C 重合，B 与D 重合，与四边形AECD 不重叠拼在一起，组成等腰梯形，故选项D 正确； 不能得到菱形，故选项C 错误．故选C ．5．下列等式正确的是（ ）A ． +=+B ．﹣=C ． +﹣=D ． ++=【考点】*平面向量．【分析】直接利用三角形法则求解即可求得答案．注意掌握排除法在选择题中的应用．【解答】解：A 、∵+=， +=， ∴+=﹣（+）；故本选项错误；B 、+=；故本选项错误；C 、∵+=， ∴+﹣=；故本选项正确；D 、∵+=， ∴++=+=；故本选项错误．故选C ．6．在平行四边形、矩形、菱形、等腰梯形这个四个图形中任选一个图形，那么下列事件是不可能事件的是（ ）A ．这个图形既是轴对称图形又是中心对称图形B ．这个图形既不是轴对称图形又不是中心对称图形C．这个图形是轴对称图形D．这个图形是中心对称图形【考点】随机事件．【分析】根据确定事件的定义，结合轴对称以及中心对称的定义即可判断．【解答】解：A、4个图形中有3个是轴对称图形，有3个是中心对称图形，所以任选一个图形既是轴对称图形又是中心对称图形，可能发生，也可能不发生，是随机事件；B、一定不会发生，是不可能事件；C、4个图形中有3个是轴对称图形，所以任选一个图形是轴对称图形，可能发生，也可能不发生，是随机事件；D、4个图形中有3个是中心对称图形，所以任选一个图形是中心对称图形，可能发生，也可能不发生，是随机事件．故选B．二、填空题（本大题共12题，每题3分，满分36分）7．一次函数y=2x﹣5的图象在y轴上的截距是﹣5 ．【考点】一次函数图象上点的坐标特征．【分析】令x=0，则y=﹣5，即一次函数与y轴交点为（0，﹣5），即可得出答案．【解答】解：由y=2x﹣5，令x=0，则y=﹣5，即一次函数与y轴交点为（0，﹣5），∴一次函数在y轴上的截距为：﹣5．故答案为：﹣5．8．已知一次函数y=kx+b的图象不经过第二象限，那么函数值y随自变量x的值增大而增大（填“增大”或“减小”）．【考点】一次函数图象与系数的关系．【分析】直接根据一次函数的图象与系数的关系即可得出结论．【解答】解：∵一次函数y=kx+b的图象不经过第二象限，∴k＞0，b＜0．所以函数值y随自变量x的值增大而增大，故答案为：增大；9．如果关于x的方程（m+2）x=8无解，那么m的取值范围是m=﹣2 ．【考点】一元一次方程的解．【分析】根据一元一次方程无解，则m+2=0，即可解答．【解答】解∵关于x的方程（m+2）x=8无解，∴m+2=0，∴m=﹣2，故答案为：m=﹣2．10．方程x3﹣8=0的根是x=2 ．【考点】立方根．【分析】首先整理方程得出x3=8，进而利用立方根的性质求出x的值．【解答】解：x3﹣8=0，x3=8，解得：x=2．故答案为：x=2．11．已知关于x的方程+=，如果设=y，那么原方程化为关于y的方程是3y+=．第4页（共12页）【考点】换元法解分式方程．【分析】先根据=y 得到，再代入原方程进行换元即可．【解答】解：由=y ，可得∴原方程化为3y +=故答案为：3y +=12．某企业的年产值在三年内从1000万元增加到1331万元，如果这三年中每年的增长率相同，设为x，那么可以列出关于x 的方程是1000（1+x）2=1331 ．【考点】由实际问题抽象出一元二次方程．【分析】根据某企业的年产值在三年内从1000万元增加到1331万元，这三年中每年的增长率相同，设为x，可知第一年为1000万，第三年为1331万，从而可以列出相应的方程．【解答】解：∵某企业的年产值在三年内从1000万元增加到1331万元，这三年中每年的增长率相同，设为x，∴1000（1+x）2=1331，故答案为：1000（1+x）2=1331．13．如果多边形的每个外角都是40°，那么这个多边形的边数是9 ．【考点】多边形内角与外角．【分析】根据多边形的外角和是360度即可求得外角的个数，即多边形的边数．【解答】解：多边形的边数是： =9，故答案为：9．14．已知点E、F、G、H分别是凸四边形ABCD各边AB、BC、CD、DA的中点，如果对角线AC=BD=4，那么四边形EFGH的周长是8 ．【考点】中点四边形．【分析】根据三角形中位线定理分别求出EF+FG+GH+HE的长，根据四边形的周长公式计算即可．【解答】解：∵E、F、G、H分别是AB、BC、CD、DA的中点，∴EF、FG、GH、HF分别是△ABC、△BCD、△CDA、△DAB的中位线，∴EF=AC=2，FG=BD=2，GH=AC=2，HE=BD=2，∴四边形EFGH的周长=EF+FG+GH+HE=8．故答案为：8．15．在梯形的一条底边长为5，中位线长为7，那么另一条底边的长为9 ．【考点】梯形中位线定理．【分析】此题只需根据梯形的中位线等于梯形两底和的一半进行计算即可．【解答】解：设另一条底边为x，则5+x=2×7，解得x=9．即另一条底边的长为9．故答案为：9．第5页（共12页）16．将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，设菱形中较小的角为α度，平行四边形中较大的角为β度，那么β可以用含α的代数式表示为β=．【考点】菱形的性质；平行四边形的性质．【分析】由将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，可求得∠1与∠2的度数，再利用周角的定义，即可求得答案．【解答】解：如图，∵是几个全等的平行四边形和全等的菱形镶嵌而成，∴∠2=α°，∠1=180°﹣β°，∵2∠2+4∠1=360°，∴2α+4=360，∴β=．故答案为：β=．17．如图，平行四边形ABCD中，∠B=60°，AB=8cm，AD=10cm，点P在边BC上从B向C运动，点Q在边DA上从D向A运动，如果P，Q运动的速度都为每秒1cm，那么当运动时间t= 7 秒时，四边形ABPQ是直角梯形．【考点】直角梯形；平行四边形的性质．【分析】过点A作AE⊥BC于E，因为AD∥BC，所以当AE∥QP时，则四边形ABPQ是直角梯形，利用已知条件和路程与速度的关系式即可求出时间t的值．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，过点A作AE⊥BC于E，∴当AE∥QP时，则四边形ABPQ是直角梯形，∵∠B=60°，AB=8cm，∴BE=4cm，∵P，Q运动的速度都为每秒1cm，∴AQ=10﹣t，AP=t，∵BE=4，∴EP=t﹣4，∵AE⊥BC，AQ∥EP，AE∥QP，∴QP⊥BC，AQ⊥AD，∴四边形AEPQ是矩形，∴AQ=EP，即10﹣t=t﹣4，解得t=7，故答案为：7．18．已知边长为4的正方形ABCD，点E、F分别在CA、AC的延长线上，且∠BED=∠BFD=45°，那么四边形EBFD 的面积是16+16．【考点】正方形的性质．【分析】连接BD交AC于O，首先证明四边形EBFD是菱形，根据菱形的面积等于对角线乘积的一半即可解决问题．【解答】解：如图连接BD交AC于O．∵四边形ABCD是正方形，第6页（共12页）∴AB=BC=CD=AD=4，∠CAD=∠CAB=45°，∴∠EAD=∠EAB=135°，在△EAB和△EAD中，，∴△EAB≌△EAD，∴∠AEB=∠AED=22.5°，EB=ED，∴∠ADE=180°﹣∠EAD﹣∠AED=22.5°，∴∠AED=∠ADE=22.5°，∴AE=AD=4，同理证明∠DFC=22.5°，FD=FB，∴∠DEF=∠DFE，∴DE=DF，∴ED=EB=FB=FD，∴四边形EBFD的面积=•BD•EF=×4（（4+8）=16+16．故答案为16+16．三、解答题（本题共4题，每题5分，满分20分）19．解方程组：．【考点】高次方程．【分析】先由②得x+y=0或x﹣2y=0，再把原方程组可变形为：或，然后解这两个方程组即可．【解答】解：，由②得：（x+y）（x﹣2y）=0，x+y=0或x﹣2y=0，原方程组可变形为：或，解得：，．20．布袋里有一个红球两个黄球，它们除了颜色外其他都相同．（1）任意摸出一个球恰好是红球的概率是；（2）摸出一个球再放回袋中，搅匀后再摸出一个球，请利用树形图求事件“摸到一红一黄两球”的概率P．【考点】列表法与树状图法．【分析】（1）根据题意可得到任意摸出一个球恰好是红球的概率；第7页（共12页）（2）根据题意可以画出树状图，从而可以求出∴“摸到一红一黄两球”的概率．【解答】解：（1）由题意可得，任意摸出一个球恰好是红球的概率是，故答案为：；（2）由题意可得，∴“摸到一红一黄两球”的概率P=．21．已知弹簧在一定限度内，它的长度y（厘米）与所挂重物质量x（千克）是一次函数关系．表中记录的是两次挂不同重量重物的质量（在弹性限度内）与相对应的弹簧长度．所挂重物质量x（千克） 2.5 5弹簧长度y（厘米） 7.5 9求不挂重物时弹簧的长度．【考点】一次函数的应用．【分析】弹簧总长y=挂上xkg的重物时弹簧伸长的长度+弹簧原来的长度，把相关数值代入即可．【解答】解：设长度y（厘米）与所挂重物质量x（千克）的一次函数关系式是：y=kx+b（k≠0）将表格中数据分别代入为：，解得：，∴y=x+6，当x=0时，y=6．答：不挂重物时弹簧的长度为6厘米．22．如图，点E在平行四边形ABCD的对角线BD的延长线上．（1）填空： += .﹣= ；（2）求作： +（不写作法，保留作图痕迹，写出结果）【考点】*平面向量；平行四边形的性质．【分析】（1）根据向量的平行四边形法则写出+即可，根据平行四边形的对边平行且相等可得=，然后根据向量的三角形法则求解即可；（2）根据平行四边形的对边平行且相等可得=，然后根据向量的平行四边形法则作出以DC、DE为邻边的平行四边形，其对角线即为所求．【解答】解：（1）+=，∵=，∴﹣=﹣=；故答案为：；．（2）如图，即为所求+．四、解答题（本题共3题，第23题7分，第24题9分，第25题10分，满分26分）23．如图，已知矩形ABCD中，点E是CD边上的一点，连结BE，过点A作AF⊥BE．垂足为点F，且AF=BE，过点F作MN∥BC，与AB、CD边分别交于点M、N，求证：四边形AMND为正方形．【考点】正方形的判定；矩形的性质．第8页（共12页）【分析】由四边形ABCD是矩形，得到两组对边平行，四个角为直角，对角线相等，根据MN与BC平行，得到MN 与AD平行，可得出四边形AMND是平行四边形，由一个角为直角的平行四边形是矩形得到AMND是矩形，得到∠AMN=90°，根据AF与BE垂直，得到一对直角相等，利用AAS得到三角形AFM与三角形BEC全等，利用全等三角形对应边相等得到AM=BC，根据AD=BC，得到AM=AD，利用邻边相等的矩形是正方形即可得证．【解答】证明：∵四边形ABCD是矩形，∴AD∥BC，AB∥CD，∠BAD=∠C=∠ABC=90°，BC=AD，∵MN∥BC，∴MN∥AD，又∵AB∥CD，∴四边形AMND是平行四边形，又∵∠BAD=90°，∴四边形AMND是矩形，∴∠AMN=90°，∵AF⊥BE，∴∠AFB=90°，∵∠AFB+∠ABF+∠BAF=180°，∴∠ABF+∠BAF=90°，又∵∠ABC=∠ABF+∠EBC=90°，∴∠BAF=∠EBC，在△AFM和△BEC中，，∴△AFM≌△BEC（AAS），∴AM=BC，又∵AD=BC，∴AM=AD，又∵四边形AMND是矩形，∴四边形AMND是正方形．24．已知：如图，平面直角坐标系中有一个等腰梯形ABCD，且AD∥BC，AB=CD，点A在y轴正半轴上，点B、C在x轴上（点B在点C的左侧），点D在第一象限，AD=3，BC=11，梯形的高为2，双曲线y=经过点D，直线y=kx+b经过A、B两点．（1）求点A、B、C、D的坐标；（2）求双曲线y=和直线y=kx+b的解析式；（3）点M在双曲线上，点N在y轴上，如果四边形ABMN是平行四边形，求点N的坐标．【考点】反比例函数综合题．【分析】（1）首先过点D作DH⊥x轴于点H，由AD∥BC，AB=CD，易得四边形AOHD是矩形，证得Rt△ABO≌Rt△DCH，又由AD=3，BC=11，梯形的高为2，即可求得答案；（2）由双曲线y=过点D，直线y=kx+b过点A，B，直接利用待定系数法求解即可求得答案；（3）由四边形ABMN是平行四边形，可得点M的横坐标为﹣4，继而求得点M的坐标，又由AN=BM，求得答案．【解答】解：（1）如图1，过点D作DH⊥x轴于点H．第9页（共12页）∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∵AO⊥x轴，∴四边形AOHD是矩形，∴AO=DH，AD=OH，∠AOB=∠DHC=90°，在Rt△ABO和Rt△DCH中，，∴Rt△ABO≌Rt△DCH（HL）．∴BO=CH，∵梯形的高为2，∴AO=DH=2．∵AD=3，BC=11，∴BO=4，OC=7．∴A（0，2），B（﹣4，0），C（7，0），D（3，2）；（2）∵双曲线y=经过点D（3，2），∴m=xy=6．∴双曲线的解析式为：y=，∵直线y=kx+b经过A（0，2）、B（﹣4，0）两点，得：，∴解得：．∴直线的解析式为：y=x+2；（3）如图2，∵四边形ABMN是平行四边形．∴BM∥AN且BM=AN．∵点N在y轴上，∴过点B作x轴的垂线与双曲线y=的交点即为点M．∴点M的坐标为M（﹣4，﹣），∴BM=．∴AN=BM=，∴ON=OA﹣AN=，∴点N的坐标为N（0，）．第10页（共12页）25．已知：如图，在矩形ABCD中，AB=2，BC=5，点P是边AD上一点，连接CP，将四边形ABCP沿CP所在直线翻折，落在四边形EFCP的位置，点A、B的对应点分别为点E，F，边CF与边AD的交点为点G．（1）当AP=2时，求PG的值；（2）如果AP=x，FG=y，求y关于x的函数解析式，并写出它的定义域；（3）连结BP并延长与线段CF交于点M，当△PGM是以MG为腰的等腰三角形时，求AP的长．【考点】四边形综合题．【分析】（1）设PG=a，则在RT△DGC中，CG=a，DG=3﹣a，CD=2，利用勾股定理即可解决问题．（2）在RT△DGC中，CD2+DG2=CG2，得到（y﹣x）2+22=（5﹣y）2，由此即可解决问题．（3）如图1中，分两种情形讨论即可，①MG=MP，只要证明△APB≌△DGC，得到AP=DG，列出方程即可，②MG=PG，只要证明△ABP，△DPC，△BPC均为直角三角形，根据AP2+AB2+DP2+CD2=BC2，列出方程即可．【解答】（1）由题意得：四边形ABCP与四边形EFCP全等．∴∠BCP=∠FCP．∵四边形ABCD是矩形，∴AD∥BC，∴∠BCP=∠DPC，∴∠DCP=∠FCP，∴PG=CG，设PG=a，则在RT△DGC中，CG=a，DG=3﹣a，CD=2，且CD2+DG2=CG2，∴22+（3﹣a）2=a2，解得：a=，即PG=．（2）由题意得：CF=BC=5，∴CG=5﹣y，∴PG=5﹣y，∴DG=5﹣（5﹣y）﹣x=y﹣x，∵在RT△DGC中，CD2+DG2=CG2，∴（y﹣x）2+22=（5﹣y）2，∴y=，∴y关于x的函数解析式为：y=，（0≤x≤3）（3）∵△PGM是以MG为腰的等腰三角形，∴MG=MP或MG=PG，如图1中，①当MG=MP时，∵∠MPG=∠MGC，∵∠APB=∠MPG，∠MGP=∠DGC，∴∠APB=∠DGC，在△APB和△DGC中，第11页（共12页），∴△APB≌△DGC，∴AP=DG，∴y=2x，∴=2x，化简整理得：3x2﹣20x+21=0，解得：x=，∵x=＞3不符合题意舍去，∴x=．②当MG=PG时，∵∠MPG=∠PMG，∵∠MPG=∠MBC，∴∠MBC=∠PMC，∴CM=CB，（即点M与点F重合）．又∵∠BCP=∠MCP，∴CP⊥BP，∴△ABP，△DPC，△BPC均为直角三角形．∴AP2+AB2+DP2+CD2=BC2，即x2+22+（5﹣x）2+22=52，化简整理得：x2﹣5x+4=0，解得：x=1或4．∵x=4＞3不符合题意舍弃，∴x=1．综上所述：当△PGM是以MG腰的等腰三角形时，AP=或1．第12页（共12页）。

预备年级第二学期数学期末考试试卷 （满分100分 附加分20分 时间100分钟）姓名： 得分：一 二 三 四 五 六 总 分一、填空题（每小题2分，共28分）1. 已知a 的倒数是-5，则a=2. 计算：121535⎛⎫⨯-⎪⎝⎭= 3. 计算：()22--=4.125x y-=，化为用x 的式子表示y= 5. 我国国土面积约为960万平方千米，用科学记数法可表示为 平方千米 6. 已知32(1)1a a -->-，化简482a a ---=7. 若2423435m n m n xy+-+--=-是二元一次方程，那么()2011n m -=8. 不等式组1x ax >⎧⎨<-⎩无解，则a 的取值范围是9. 点C 在线段AB 的延长线上，AB=4cm ，AC=6cm ，M 、N 分别是线段AC 、AB 的中点，则MN=10. 如果一个角和它的余角的比是2:3，那么这个角的补角是 度11. 小明从O 点出发向北偏西40°走了500米到达A 点，小方从O 点出发向南偏东40°走了150米到达B 点，这时A 、B 两点的距离是 米 12. 在长方体ABCD-EFGH 中，与棱EF 异面的棱有 条13. 某商场出售某种文具，每件可盈利2元，为了支援贫困山区，现在按原价的7折出售给一山区学校，结果每件盈利0.2元，问该文具每件进货价是 元 14. 如图，将两块三角板的直角顶点重合后重叠在一起，如果∠1=45°18ˊ30〞，那么∠2=二、选择题（每小题3分，共12分）15. 方程x x -=-20082008 的解的个数是（ ） A ．1个 B ．2个 C ．3个 D ．无穷多个 16. 下列解关于x 的不等式中正确的是（ ）A. 3ax >，则3x a >B. 23x ->，则32x >- C. 132x <-，则6x >- D. 132x >，则6x >17. 下列说法正确的有（ ）个① 两点之间，直线最短；②如果点M 到线段AB 两个端点的距离相等，即MA=MB ，那么点M 一定是线段AB的中点；③平分一个角的射线叫做这个角的平分线；④联结两点的线段叫做两点间的距离；⑤两个相等的角不可能互余； ⑥一个锐角的余角比这个角的补角小︒90 A. 1个 B. 2个 C. 3个 D.4个18. 如图，点C 是线段AB 的中点，点D 是线段CB 上任意一点，则下列表示线段关系的式子不正确的是( ) （A ）AC AB 2= （B ）AB DB CD AC =++ （C ）AB AD CD 21-= （D ）)(21AB CD AD += 三、简答题(每小题5分，共25分)19.计算：3212(0.51)5(3)3⎡⎤---÷⨯--⎣⎦ 20. 解方程：1.5 1.50.50.62x x--=21. 解方程组2313424575615u v u v ⎧+=⎪⎪⎨⎪+=⎪⎩ 22. 解不等式：72244x x +<+并把它的解集在数轴上表示出来。

浦东新区2012学年第⼆学期预初年级数学期末卷和答案浦东新区2012学年度第⼆学期期末质量抽测预备年级数学试卷1．本试卷含四个⼤题，共30题；2．除第⼀、⼆⼤题外，其余各题都必须写出解题的主要步骤．⼀、选择题（本⼤题共6题，每题2分，满分12分）1．下列各数中，互为相反数的是………………………………………………（）（A ）2和21；（B ）32-和32；（C ）32-和32-；（D ）32-和23-． 2．有下列四个等式：①3x =0；②x -2y =0；③2+3=5；④2y -(y +2)=6.其中⼀元⼀次⽅程有……………………………………………………………………………………………（）（A ）1个；（B ）2个；（C ）3个；（D ）4个． 3．下列说法正确的是…………………………………………………………………（）（A ）⽅程y=x 不是⼆元⼀次⽅程；（B ）⽅程xy =1是⼆元⼀次⽅程；（C ）⽅程10057=+y x 的正整数解有⽆数个；（D ）任何⼀个⼆元⼀次⽅程都有⽆数个解． 4．如图，从景点甲到景点⼄有1、2、3、4共4条线路可⾛，其中最近的⼀条线路是……………………（）（A ）第1条；（B ）第2条；（C ）第3条；（D ）第4条． 5．已知∠A =38°15′，∠B =38.15°，则∠A 与∠B 的⼤⼩关系是……………（）（A ）∠A >∠B ；（B ）∠A <∠B ；（C ）∠A =∠B ；（D ）不能确定⼤⼩． 6．⼀个长⽅体的棱长之和为48cm ，长为5cm ，宽为3cm ，则这个长⽅体的⾼为的（）（A ）1cm ；（B ）2cm ；（C ）4cm ；（D ）6cm. ⼆、填空题（本⼤题共12题，每题2分，满分24分）7．计算：()()2422-÷-= ．8. 绝对值⼩于2.3的整数是 .9.有三个连续整数，中间⼀个数位x ，它们的和为18，则x +2= .10.不等式组?->-≥-1,32x x 的解集是 .11.已知线段AB =36cm ，点C 在AB 上，D 和E 分别是AC 、CB 的中点，则DE = cm .12.看图⽤⽅向⾓填空：射线OA 表⽰的⽅向是；射线OB 表⽰的⽅向是 .第4题图⼄景点甲13.如图，∠AOB =∠COD .则∠AOC ∠BOD ；∠BOC ∠AOC.（填“>”“=”“<”）14. 如图，若∠AOC =∠BOD ，∠COD =20°，∠BOC =2∠COD ，则∠AOC = °15.补画图形，使之成为长⽅体的直观图（虚线表⽰遮住部分）. 16.如图，在长⽅体ABCD-EFGH 中，棱AE 与棱CG 的位置关系是；棱AD 与棱HG 的位置关系是．17. 如图，在长⽅体ABCD-EFGH 中，与平⾯AEHD 平⾏的平⾯有；与平⾯ABFE 垂直的平⾯有（只写⼀个平⾯即可） .18.四个棱长为1的正⽅体叠在⼀起，成为⼀个长⽅体，则这个长⽅体的表⾯积为 .三、简答题（本⼤题共6题，每题4分，满分24分）19．解不等式：4385183+<+x x ，并把它的解集在数轴上表⽰出来.20．解⽅程：285216++=x x .21．学⽣课桌装备车间共有⽊⼯10⼈，每个⽊⼯⼀天能装备双⼈课桌3张或单⼈椅9把，如果安排⼀部分⽊⼯装备课桌，另⼀部分⽊⼯装备单⼈椅，怎样分配才能使⼀天装配的课桌椅配套.第13、14题图第15题图A东西南北第12题图G F E D C B A第16、17题图第19题图x3210-3-2-122.如图，（1）分别作∠A 、∠B 的平分线，并作出它们的交点O ；（2）量⼀量∠AOB = °． 23．⼀个⾓的补⾓⽐它的余⾓的2倍⼤25°，求这个⾓的度数. 24．在长⽅体ABCD-EFGH 中，（1）哪些棱与⾯ABFE 垂直？（2）哪些⾯与棱BC 垂直？四、解答题（本⼤题共6题，25-28题，每题6分，29、30题，每题8分，满分40分）25．计算：????--??? ??-+-875.487163425.2.26．解不等式组：-≥-->-.3415,623425x x xx27．解⽅程组：=--=+.1536,152y x y x第22题图D C BA第24题图A B CDE FG28.甲⼄两⼈从相距42千⽶的两地同时相向出发，3⼩时30分钟后相遇.如果⼄先出发6⼩时，那么在甲出发1⼩时后与⼄相遇，求甲⼄两⼈的速度.29．解⽅程组：??=++-=--=++.11523,1332,122z y x z y x z y x30．⾜球⽐赛的记分规则为：胜⼀场得3分，平⼀场得1分，输⼀场得0分.⼀⽀⾜球队在某个赛季中共需⽐赛14场，现已⽐赛8场，输了1场，得15分.请问：（1）这⽀球队打满14场⽐赛，最⾼能得多少分？（2）前8场⽐赛中，这⽀球队共胜了多少场？（3）有甲、⼄两球迷对这⽀球队打满14场⽐赛后的最后得分作了⼀个预测：甲预计得27分，⼄预计得32分. 根据⽬前的情况，请你对两位的预测作⼀个判断，若有可能，则剩下6场的胜负情况将是怎样的？若没有可能，请说明理由.浦东新区2012学年度第⼆学期期末质量抽测预备年级数学参考答案及评分说明⼀、选择题：（本⼤题共6题，每题2分，满分12分） 1．C ； 2．B ； 3．D ； 4．B ； 5.A ； 6.C. ⼆、填空题：（本⼤题共12题，每题2分，满分24分） 7．-4； 8．-2,-1,0,1,2； 9．8； 10．-123； 11．18； 12．北偏西30°南偏东70°； 13．=、< ； 14．60； 15．略，每画对两条棱给1分； 16．平⾏、异⾯； 17．平⾯BFGC 、平⾯EFGH （或平⾯ABCD ，或平⾯BCGF ,或平⾯AEHD ）； 18．16或18. 三、简答题：（本⼤题共6题，每题4分，满分24分）19．解：去分母，得6583+<+x x ………………………………（1分）移项、化简，得 22-<-x ………………………………（1分）两边同除以x 的系数-2，得 x >1. ………………………………（1分）在数轴上表⽰，略.………………………………………………（1分）20．解：去分母，得32)52(2++=x x ……………………………（1分）去括号，得 32104++=x x ………………………………（1分）移项、化简，得 423-=x ………………………………（1分）两边同除以x 的系数3，得 x =-14.……………………………（1分）21．解：设装备课桌的⽊⼯x ⼈，装备椅⼦的y ⼈，依题意，可列⽅程组： ?==+.932,10y x y x …………………………………………………………（2分）解之，得 ??==.4,6y x ………………………………………………………（1分）答：安排6⼈装备课桌，4⼈装备单⼈椅可使⼀天装配的课桌椅配套. ……（1分） 22．解：（1）作图略…………………………………………………（3分）（2）∠AOB =90 °．（87°~93°均给满分）……………（1分）23．解：设这个⾓的度数为x 度．则有180-x =2(90-x )+25……………………………………………（2分）解之，得x =25.……………………………………………………（1分）答：这个⾓为25度. ………………………………………………（1分）24. 解：（1）FG 、EH 、AD 、BC ………………………………………（2分）（2）⾯ABFE 、⾯DCGH ………………………………………（2分）四、解答题：（本⼤题满分40分）25．解：原式=??+-+-44349…………………………………（3分）44349+--=………………………………………（1分） =4412+-……………………………………………（1分） =1 ……………………………………………………（1分）26．解：由①得 .29<x …………………………………………（3分）由②得 2-≥x . …………………………………………（2分）所以，原不等式组的解为：292<≤-x .……………………（1分）27．解：①×3-②，得 1818-=y ………………………………（2分）解之，得 y =-1. ………………………………………………（1分）将y =-1代⼊①式，得 2x -5=-1.解之，得 x =2. …………………………………………………（2分）所以，原⽅程组的解为??-==.1,2y x ………………………………（1分）28．解：设甲的速度为x 千⽶/⼩时，⼄的速度为y 千⽶/⼩时，依题意，有()?=+=+.427,425.3y x y x ………………………………………（3分）解之，得 ??==.5,7y x ………………………………………（2分）答：甲的速度为7千⽶/⼩时，⼄的速度为5千⽶/⼩时. ……（1分） 29．解：由①+②，得1223-=-z x ④…………………………（2分）由②+③，得.224-=+z x ⑤…………………………（2分）由④+⑤，得 7x =-14，解之，得 x =-2. ……………………………………………………（1分）将x =-2代⼊④，得 -6-2z =-12，解之，得 z =3. ……………………………………………………（1分）将 x =-2,z =3代⼊①，得 y =1.…………………………………（1分）所以，原⽅程组的解为??==-=.3,1,2z y x …………………………………（1分）30．解：（1）如果后6场⽐赛全胜，得分最⾼，最⾼能得15+3×6=33(分).………………………………………（1分）（2）设前8场⽐赛中，这⽀球队胜了x 场，平了y 场，则由题意，得=+=+.153,7y x y x ………………………………………（2分）解之，得 ??==.3,4y x ………………………………………（2分）所以前8场⽐赛中，这⽀球队共赢了4场. ………………… …………（1分）（3）设后6场⽐赛中，这⽀球队胜了x 场，平了y 场，根据甲的预测，只需在后6场⽐赛中得12分即可.则由题意，有123=+y x .这个⽅程的⾮负整数解为：?==========.0,4;3,3;6,2;8,1;12,0y x y x y x y x y x ⼜因为x+y ≤6,所以有两组解：??====.0,4;3,3y x y x 即胜3场、平3场或胜4场、输2场时可以达到甲预测的分数. ………………………………………（1分）根据⼄的预测，可得⽅程：173=+y x .其⾮负整数解为：============.2,5;5,4;8,3;11,2;14,1;17,0y x y x y x y x y x y x ⼜因为x+y 要⼩于等于6，故没有符合条件的整数解.即该球队不可能得32分，⼄的预测是不可能实现的. ………………………………………（1分）。

A B OA O BB O AB O A浦东新区2013学年度第二学期期末质量测试六 年 级（预备年级）数 学（完卷时间：90分钟 满分：100分） 2014.6一、 选择题（本大题共6题，每小题3分，满分18分）（每题只有一个选项正确） 1．在数轴上点A 、点B 所表示的数分别是a 、b ，那么能够判断b a <的是…………（ ）（A ）； （B ）； （C ）； （D ）．2．下面的变形正确的是…………………………………………………………………（ ） （A ）由137=-x ，得713-=x ； （B ）由845+=x x ，得845=+x x ；（C ）由121=x ，得21=x ； （D ）由2372+=-x x ，得7232+=-x x ．3．某商场促销，小鱼将促销信息告诉了妈妈，小鱼妈妈假设某一商品的定价为x ，并列出不等式为()100010027.0<-⨯x ，那么小鱼告诉妈妈的信息是……………………（ ）（A ）买两件等值的商品可减100元，再打3折，最后不到1000元；（B ）买两件等值的商品可打3折，再减100元，最后不到1000元； （C ）买两件等值的商品可减100元，再打7折，最后不到1000元； （D ）买两件等值的商品可打7折，再减100元，最后不到1000元．4．小明某天记录的支出如图所示，不小心饼干的支出金额被墨水污染了，如果小明原来有30元，每包饼干的售价为1.3元，那么小明剩下的钱数不可能是……………………………（ ）题 号 一 二 三 四 五 总 分 得 分项目 支出金额（元）早餐 4 午餐 7 晚餐 15 饼干（A ）0.1元； （B ）0.8元； （C ）1.4元； （D ）2.7元．5．下列说法中，正确的是……………………………………………………………………（ ） （A ）联结两点的线段叫做两点之间的距离；（B ）用度量法和叠合法都可以比较两个角的大小；（C ）六个面、十二条棱和八个顶点组成的图形都是长方体； （D ）空间两条直线间的位置关系只有相交和平行两种． 6．只利用一副（两块）三角尺不能直接拼出的角度是…………………………………（ ）（A ）75°；（B ）105°；（C ）150°；（D ）165°．二、 填空题（本大题共12题，每小题2分，满分24分）7．52-的相反数是 ．8．计算：()835.3-- ． 9．每年5月18日是国际博物馆日，2014年5月18日上海中国航海博物馆一上午参观者达9 000人，全天超过16 000人，将16 000用科学记数法表示为 ． 10．当0<a ，b 0时，0<ab ．（填“＞”“＜”或“＝”） 11．二元一次方程1525=+y x 的正整数解是 ．12．a 、b 表示两个有理数，规定新运算“*”为：a *b =b ma 2+（其中 m 为有理数），如果1*2=5，那么m 的值为 ．13．在线段AB 延长线上顺次截取BC =CD =2AB ，如果AB =2，那么AD = ． 14．如图，OP 、OQ 分别是∠AOB 、∠BOC 的平分线，如果∠POQ =52°26′，那么∠AOC = （结果用度、分、秒表示）．15．一个角的补角一定比它的余角大 度． 16．在长方体ABCD －EFGH 中，与平面ABCD 和平面ABFE都平行的棱是 ．AB C D EFGH （第16、17题图）（第14题图）QPCB OA17．在长方体ABCD －EFGH 中，既与平面ADHE 垂直，又与平面EFGH 平行的平面是 ．18．如果一根铁丝可以折成长6分米，宽4分米，高2分米的长方体框架模型，那么用这根铁丝折成一个正方体框架模型，它的棱长是 分米．三、 简答题（本大题共6题，每小题6分，满分36分）19．计算：()⎪⎭⎫ ⎝⎛-÷-+-⨯⎪⎭⎫ ⎝⎛-3131337972．解：20．解方程：12135x x +--=．解：21．解不等式：x 15≥()246233--x ，并把它的解集在数轴上表示出来． 解：22．解不等式组：⎪⎩⎪⎨⎧->+>．，－31221302x x x解：① ②23．解方程组：⎩⎨⎧=-+=--．，0243053y x y x解： 24．解方程组：⎪⎩⎪⎨⎧=++=-+=+-．，，223243223z y x z y x z y x 解：四、作图题（本大题6分）25．线段AB 与射线AP 有一公共端点A ．（1） 用直尺和圆规作出线段AB 的中点M ；（不写作图方法） （2） 用直尺和圆规作出以点B 为顶点的∠ABQ ，使∠ABQ ＝∠P AB ，且BQ 与AP 相交于点C ．（不写作图方法） （3） 联结CM ，用量角器测量∠AMC 和∠BMC 的度数，你认为∠AMC 和∠BMC 的大小关系如何？①②PBA第25题①②③五、解答题（本大题共2题，26题7分，27题9分，满分16分）26．学校“六一节”活动，设计了一个飞镖游戏，飞镖游戏的规则如下：如图，掷到A区和B 区的得分不同，A区为小圆内部分，B区为大圆内小圆外部分（A区、B区均不含边界，如果掷到边界上重新投掷，投掷在大圆以外的无效）．现在将投掷有效的每次位置用一个点标注，统计出小红，小华和小明的有效成绩情况如下：如果小红得了65分，小华得了71分，求：（1）掷中A区、B区一次各得多少分？（2）按照这样的记分方法，小明得了多少分？解：27．小红，小华和小明准备用透明胶和66张大小相同的正方形硬纸板制作一些长方体纸盒，如图1，三人分别将正方形硬纸板按各自方案裁剪，然后各取两张制作成一个长方体纸盒，现在需要你的帮忙：（1）制作前，要画出长方体纸盒的直观图，小明只画了一部分（如图2），请你帮他画完整（不写画法）；（2）如果按照设计的方案全部用完可以做成几个完整的长方体纸盒？（3）制作过程中，小明少裁剪了几张正方形硬纸板，这几张正方形硬纸板由小红和小华分别按各自的方案裁剪完，裁剪出的长方形硬纸板正好可以全部做成与（2）大小相同的无盖盒子，请问小明少裁剪了几张硬纸板？解：小明小华小红（第27题图1）（第27题图2）浦东新区2013学年度第二学期期末质量测试 六年级（预备年级）数学参考答案及评分说明一、选择题（本大题共6题，每小题3分，满分18分）（每题只有一个选项正确） 1．B ； 2．D ； 3．C ； 4．B ； 5．B ； 6．D ．二、填空题（本大题共12题，每小题2分，满分24分）7．52； 8．831-； 9．4106.1⨯； 10．>； 11．⎩⎨⎧==．5,1y x 12．１；13．10； 14．104°52′； 15．90； 16．HG ； 17．ABCD ； 18．4．三、简答题（本大题共6题，每小题6分，满分36分）19．解：原式=()331992197-⨯+⨯⎪⎭⎫⎝⎛-．…………………………………………………（3分）=3319914⨯-⨯-． =114--．……………………………………………………………………（2分）=15-．…………………………………………………………………………（1分）20．解：()()152315=--+x x ．…………………………………………………………（2分）156355=+-+x x ．…………………………………………………………（2分）42=x ．2=x ．……………………………………………………………（2分）∴原方程的解为2=x ．21．解：x 15≥481233+-x ．……………………………………………………………（2分） x 27≥81．x ≥3．…………………………………………………………………………（2分）所以，这个不等式的解集在数轴上表示为：……………………………………（2分）22．解：由①，得 2<x ．…………………………………………………………………（2分）由②，得 ()()122133->+x x ．2439->+x x ．55->x ．1->x ．………………………………………………………（3分） 所以，原不等式组的解集是21<<-x ．………………………………………（1分）23．解：由①，得 53+=y x ． …………………………………………………（1分）把③代入由②，得 024159=-++y y ． 1313-=y ．1-=y ．…………………………………（2分） 把1-=y 代入③，得 2=x ．……………………………………………………（2分）所以，原方程组的解是⎩⎨⎧-==．，12y x …………………………………………………（1分）24．解：由①＋③，得 2433=+z x ．8=+z x ． ④………………………………………………（1分）由①＋②×3，得 1410=-z x ． ⑤…………………………………………（1分） 由④＋⑤，得 2211=x ．2=x ．………………………………………………………（1分） 把2=x 代入④，得 6=z ．……………………………………………………（1分） 把2=x ，6=z 代入②，得 4=y ．……………………………………………（1分）所以，原方程组的解是⎪⎩⎪⎨⎧===．，，642z y x …………………………………………………（1分）四、作图题（本大题6分） 25．（1）作图略．……………………………………………………………………………（2分） （2）作图略．……………………………………………………………………………（2分）（3）∠AMC =∠BMC = 90．……………………………………………………………（2分）③五、解答题（本大题共2题，26题7分，27题9分，满分16分） 26．解：（1）设掷中A 区得x 分，掷中B 区y 分．根据题意，得方程组⎩⎨⎧=+=+．，71356553y x y x ………………………………………………………………（2分）解这个方程组，得⎩⎨⎧==．，710y x …………………………………………………（2分）答：掷中A 区得10分，掷中B 区7分．（2）小明得分为：6276102=⨯+⨯（分）．…………………………………（3分） 答：按照这样的记分方法，小明得了62分．27．解：（1）图略．…………………………………………………………………………（2分） （2）设可以做成x 个完整的长方体纸盒．根据题意，得方程66332=++xx x ．……………………………………………………………（2分） 解这个方程，得33=x ．……………………………………………………（1分） 答：可以做成33个完整的长方体纸盒．（3）设可以做成y 个完整的长方体纸盒．根据题意，得方程66632=++y y y ．……………………………………………………………（2分）解这个方程，得36=y ．……………………………………………………（1分）小明少裁剪的硬纸板数是5336333=-（张）．……………………………（1分） 答：小明少裁剪了5张硬纸板． （注：其他做法请相应给分）。

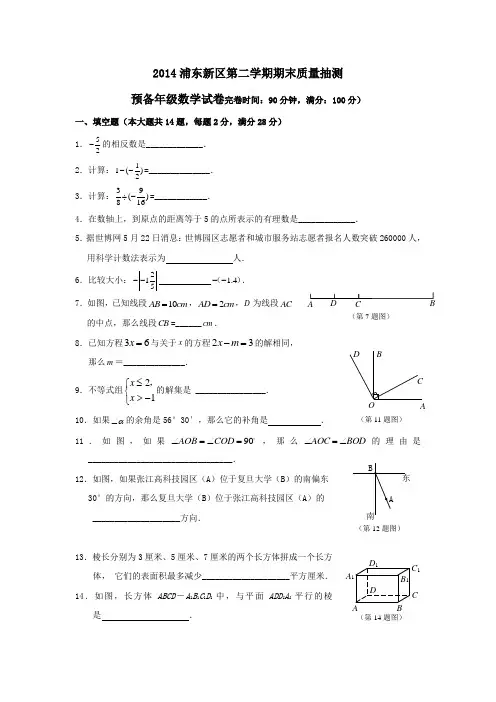
2014浦东新区第二学期期末质量抽测 预备年级数学试卷完卷时间：90分钟，满分：100分）一、填空题（本大题共14题，每题2分，满分28分） 1．52-的相反数是_____________． 2．计算：11()2--=______________． 3．计算：39()816÷-=____________．4．在数轴上，到原点的距离等于5的点所表示的有理数是_____________．5．据世博网5月22日消息：世博园区志愿者和城市服务站志愿者报名人数突破260000人，用科学计数法表示为人．6．比较大小：215-- 1.4--（）． 7．如图，已知线段10AB cm =，2AD cm =，D 为线段AC 的中点，那么线段CB =______cm ．8．已知方程36x =与关于x 的方程23x m -=的解相同， 那么m ＝______________．9．不等式组⎩⎨⎧->≤12x x ，的解集是 ________________．10．如果α∠的余角是56°30′，那么它的补角是 ．11．如图，如果90AOB COD ∠=∠=o ，那么AOC BOD ∠=∠的理由是_________________________________．12．如图，如果张江高科技园区（A ）位于复旦大学（B ）的南偏东 30°的方向，那么复旦大学（B ）位于张江高科技园区（A ）的____________________方向．13．棱长分别为3厘米、5厘米、7厘米的两个长方体拼成一个长方体， 它们的表面积最多减少____________________平方厘米． 14．如图，长方体ABCD －A 1B 1C 1D 1中，与平面ADD 1A 1平行的棱是 ．A D C（第7题图）A（第11题图）OCBD（第12题图）A BCDA 1B 1C 1D 1（第14题图）二、选择题（本大题共4题，每题3分，满分12分）（每题只有一个选项正确）15．关于x 的不等式2x －a ≤－1的解集如图所示，那么a 的值是………………………（ ） （A ）0； （B ）－1； （C ）－2； （D ）－3．16．如果a b >，那么下列不等式中正确．．的是……………………………………………（ ） （A ）0a b -<； （B ）33a b +<-； （C ）22ac bc >； （D ）77a b-<-．17．如图所示，已知线段m n >，求作一线段m n -．作法：画射线AM ，在射线AM 上截取AB m =，在线段AB 上截取BC n =，那么所求的线段是………………（ ） （A ）AC ； （B ）BC ； （C ）AB ； （D ）BM ．18．如图所示,与棱AD 异面的棱有…………………（ ）（A ）2条； （B ）3条； （C ）4条； （D ） 5条．三、解答题（本大题共有6题，每题6分，满分36分） 19．计算：22)31(1853-⨯--+- 20．解方程：612141+=--x x 解： 解：21．解不等式：732444x x +≤+， 22．解不等式组：513(1)131722x x x x +>-⎧⎪⎨-≤-⎪⎩ 并把它的解集在数轴上表示出来.解： 解：-3-2-1543210① ②（第15题图）mn AMC（第17题图）ABC DA 1B 1C 1D 1 （第18题图）23．解方程组：341239x y y x -=-⎧⎨-=⎩ 24．解方程组：2021324x y z x y z x y z -+=⎧⎪+-=⎨⎪+-=⎩解： 解：四（本大题8分）25．（1）下面四个图分别由六个相同的正方形拼接而成，其中不能．．折成正方体的是（ ）．（2）用斜二侧画法补画下面的图形，使之成为长方体的直观图（虚线表示被遮住的线段；只要在已有图形基础上画出长方体，不必写画法步骤）．（3）在这一长方体中，从同一个顶点出发的三个面的面积之比是5:7:2，其中最大的比最小的面积大260cm ,求这个长方体的表面积． ABC D① ② ①②③五、应用题（本大题共2题，第26题7分，第27题9分）26．由于最近受甲型H1N1流感的影响，猪肉价格下降比较明显，由原来的每千克20元下降了10%；海鲜类价格有所上升，如河虾由原来的每千克46元上调至50元．某饭店到市场分别购进猪肉和河虾共 180千克，发现调价前后的总价格仍然不变，问饭店购进猪肉和河虾各多少千克？解：27．为了2010年世博会，上海市准备对黄浦江边的某工程进行改造．若请甲工程队单独做此项工程需3个月完成，每月耗资12万元；若请乙工程队单独做此项工程需6个月完成，每月耗资5万元．（1）请问甲、乙两工程队合作需几个月完成？耗资多少万元？（2）因其它原因，要求最迟4个月完成此项工程即可，请你设计一种方案，既保证完成任务，又最大限度节省资金．（时间按整数月计算）解：。

2015-2016学年上海市浦东新区八年级（下）期末数学试卷1836（每题只有一个选择正确一、选择题（本大题共分，满分题，每题分）1y=3x2 ）﹣平行的是（+．下列直线中，与直线Ay=2x3 By=2x2 Cy=3x3 Dy=3x2﹣++﹣+．．．﹣．2y=kxbkbxkxb0＞+的不等式（为常数）的图象如图所示，那么关于、+．已知一次函数）的解集是（Ax3 Bx4 Cx3 Dx4 ＜．＜＞＞．．．3 ）．下列说法中，正确的是（=4x=16 A±．方程的根是=xx=0xB=3 ，﹣的根是．方程211=0 C没有实数根．方程+x=23x=6D，﹣．方程的根是214．如图，将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部）分，利用这两部分不能拼成的图形是（A B C D ．等腰梯形．平行四边形．菱形．直角三角形5 ）．下列等式正确的是（=C== BA ﹣．+﹣． ++．D= +． +6．在平行四边形、矩形、菱形、等腰梯形这个四个图形中任选一个图形，那么下列事件是）不可能事件的是（A ．这个图形既是轴对称图形又是中心对称图形B ．这个图形既不是轴对称图形又不是中心对称图形C ．这个图形是轴对称图形D ．这个图形是中心对称图形36312分）二、填空题（本大题共分，满分题，每题7y=2x5y______ ．的图象在轴上的截距是．一次函数﹣8y=kxbyx______的值增大而．已知一次函数那么函数值+随自变量的图象不经过第二象限，””““．增大或）（填减小9xm2x=8m______ ．）+无解，那么的取值范围是．如果关于的方程（38=0______ x10．的根是﹣．方程=yx=11，+的方程．已知关于，如果设y______ ．那么原方程化为关于的方程是1210001331万元，某企业的年产值在三年内从如果这三年中每年的增长率相万元增加到．xx______ ．，那么可以列出关于同，设为的方程是1340______ °．，那么这个多边形的边数是．如果多边形的每个外角都是14EFGHABCDABBCCDDA的中点，如果对各边．已知点、、、、、、分别是凸四边形AC=BD=4EFGH______ ．角线的周长是，那么四边形1557______ ．．在梯形的一条底边长为，那么另一条底边的长为，中位线长为16α设菱形中较小的角为．将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，______ αββ．可以用含度，那么度，平行四边形中较大的角为的代数式表示为17ABCDB=60AB=8cmAD=10cmPBCB°向，点，中，∠在边，．如图，平行四边形上从CQDADAPQ1cm，那么当运上从，向运动的速度都为每秒运动，点在边运动，如果t=______ABPQ 是直角梯形．秒时，四边形动时间18FCAAC4ABCDEBED=BFD=45°，、的延长线上，已知边长为且∠的正方形，点．分别在∠、EBFD______ ．那么四边形的面积是2054分）三、解答题（本题共分，满分题，每题19．．解方程组：20 ．布袋里有一个红球两个黄球，它们除了颜色外其他都相同．1______ ；）任意摸出一个球恰好是红球的概率是（2“摸到一红一黄两请利用树形图求事件）摸出一个球再放回袋中，搅匀后再摸出一个球，（P ”．的概率球．21yx（千克）是一次函数关（厘米）与所挂重物质量．已知弹簧在一定限度内，它的长度系．表中记录的是两次挂不同重量重物的质量（在弹性限度内）与相对应的弹簧长度．x 5 2.5 （千克）所挂重物质量y 7.5 9 （厘米）弹簧长度求不挂重物时弹簧的长度．22EABCDBD 的延长线上．在平行四边形．如图，点的对角线1=______=______. ﹣；）填空：（ +2（不写作法，保留作图痕迹，写出结果））求作：（ +2610925323724分）四、解答题（本题共分，第题，第分，满分题题分，第题23ABCDECDBEAAFBE．垂，过点．如图，已知矩形⊥中，点作是边上的一点，连结FAF=BEFMNBCABCDMN，求证：四边，过点作、∥、足为点，与，且边分别交于点AMND 为正方形．形24ABCDADBCAB=CDA，点．已知：如图，平面直角坐标系中有一个等腰梯形∥，且，CxAD=3BC=11yBBCD在第一象限，，（点轴上点，在点，在轴正半轴上，点的左侧）、在y=Dy=kxbAB 2两点．经过点经过，双曲线，直线、梯形的高为+1ABCD 的坐标；、）求点、、（y=y=kxb2 的解析式；和直线（）求双曲线+ 3MNyABMNN的坐标．求点点（）点在双曲线上，在轴上，如果四边形是平行四边形，25ABCDAB=2BC=5PADCP，将四，是边，点．已知：如图，在矩形上一点，连接中，ABCPCPEFCPABE，点边形的对应点分别为点沿、所在直线翻折，落在四边形的位置，FCFADG ．与边，边的交点为点1AP=2PG 的值；（时，求）当2AP=xFG=yyx 的函数解析式，并写出它的定义域；，求（关于）如果，3BPCFMPGMMG为腰的等腰三角形时，求交于点，当△是以（）连结并延长与线段AP 的长．2015-2016学年上海市浦东新区八年级（下）期末数学试卷参考答案与试题解析1836（每题只有一个选择正确一、选择题（本大题共分，满分题，每题分）1y=3x2 ）﹣平行的是（+．下列直线中，与直线Ay=2x3 By=2x2 Cy=3x3 Dy=3x2 ﹣++﹣．．．﹣．+两条直线相交或平行问题．【考点】k 相同即可解决．根据两直线平行【分析】k 相同，解：根据两直线平行【解答】y=3x2 ，﹣+∵直线k=3 ，∴﹣C ．故选2y=kxbkbxkxb0＞（、的不等式为常数）的图象如图所示，那么关于．已知一次函数++）的解集是（Ax3 Bx4 Cx3 Dx4＜＞＜．．＞．．一次函数与一元一次不等式．【考点】xkxb0＞【分析】从图象上得到函数的增减性及与+轴的交点的横坐标，即能求得不等式的解集．y=kxb40yx 的增大而减小，，【解答】解：函数随+）的图象经过点（，并且函数值x40xkxb0x4 ．，即关于的解集是的不等式时，函数值大于＞所以当+＜＜D ．故选3 ）．下列说法中，正确的是（=4x=A16 ±．方程的根是=xx=0xB=3 ，的根是．方程﹣211=0C 没有实数根．方程+x=2x=63D，．方程﹣的根是21无理方程．【考点】【分析】根据各个选项，错误的选项说明错在哪，正确的选项进行说明，即可判断出哪个选项是正确的．A x=16错误；【解答】解：当时，﹣没有意义，故选项x=3 333Bx= ==3时，，≠﹣﹣当，故选项错误；，而﹣11C 0正确；，故选项≥+，则≥∵．D 3错误．﹣不是方程，故选项C ．故选4．如图，将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部）分，利用这两部分不能拼成的图形是（A B C D ．等腰梯形．菱形．直角三角形．平行四边形图形的剪拼．【考点】ABEE180ECEBABE°重合，得到直角三角形；把△【分析】将剪开的△，绕与点旋转ABDCABEECBD重合，与与重合，则得到平行四边形；把△与的顶点重合，平移，使AECD 不重叠拼在一起，组成等腰梯形；不能得到菱形；即可得出结论．与四边形ABEE180ECEBA°正确；故选项点旋转重合，，得到直角三角形，【解答】解：将△与绕ABEABDCB 正确；把△与平移，使重合，则得到平行四边形，故选项ABEECBDAECD不重叠拼在一起，组成等腰梯与与与四边形重合，把△重合，的顶点D 正确；形，故选项C 错误．不能得到菱形，故选项C ．故选5 ）．下列等式正确的是（= B C==A﹣．﹣ +．+． += D+ +．*平面向量．【考点】直接利用三角形法则求解即可求得答案．注意掌握排除法在选择题中的应用．【分析】=A=，、∵，+解：【解答】 +=；故本选项错误；）﹣（+∴+B=；故本选项错误；+、C=，、∵+=﹣∴；故本选项正确；+=D，、∵+==；故本选项错误．∴+++C ．故选6．在平行四边形、矩形、菱形、等腰梯形这个四个图形中任选一个图形，那么下列事件是）不可能事件的是（．A ．这个图形既是轴对称图形又是中心对称图形B ．这个图形既不是轴对称图形又不是中心对称图形C ．这个图形是轴对称图形D ．这个图形是中心对称图形随机事件．【考点】根据确定事件的定义，结合轴对称以及中心对称的定义即可判断．【分析】A433个是中心对称图形，所以任选一个解：个是轴对称图形，有、个图形中有【解答】图形既是轴对称图形又是中心对称图形，可能发生，也可能不发生，是随机事件；B 、一定不会发生，是不可能事件；C43个是轴对称图形，所以任选一个图形是轴对称图形，可能发生，也可能个图形中有、不发生，是随机事件；D43个是中心对称图形，所以任选一个图形是中心对称图形，可能发生，也个图形中有、可能不发生，是随机事件．B ．故选36123分）题，每题分，满分二、填空题（本大题共7y=2x5y5 ．．一次函数轴上的截距是﹣的图象在﹣一次函数图象上点的坐标特征．【考点】x=0y=5y05 ，即可得出答案．，则﹣，﹣，即一次函数与）【分析】令轴交点为（y=2x5x=0y=5 ，﹣，则解：由，令﹣【解答】y05 ，，﹣即一次函数与）轴交点为（y5 ．轴上的截距为：﹣∴一次函数在5 ．故答案为：﹣8y=kxbyx的值增大而随自变量的图象不经过第二象限，那么函数值增．已知一次函数+””““．或）减小大（填增大一次函数图象与系数的关系．【考点】直接根据一次函数的图象与系数的关系即可得出结论．【分析】y=kxb 的图象不经过第二象限，【解答】解：∵一次函数+k0b0 ．，∴＜＞yx 的值增大而增大，所以函数值随自变量故答案为：增大；9xm2x=8mm=2 ．无解，那么﹣．如果关于的取值范围是的方程（+ ）一元一次方程的解．【考点】m2=0 ，即可解答．【分析】根据一元一次方程无解，则+xm2x=8 无解，+【解答】解∵关于）的方程（m2=0 ，∴+m=2 ，﹣∴m=2 ．故答案为：﹣38=0x=210x ．．方程﹣的根是立方根．【考点】3=8xx 的值．，进而利用立方根的性质求出首先整理方程得出【分析】．3 8=0x，解：﹣【解答】3 x=8，x=2．解得：x=2．故答案为：=y11x=，+，如果设的方程．已知关于=3y+y．那么原方程化为关于的方程是换元法解分式方程．【考点】=y，再代入原方程进行换元即得到【分析】先根据可．=y，可得【解答】解：由=3y+∴原方程化为=3y+故答案为：1210001331万元，如果这三年中每年的增长率相万元增加到．某企业的年产值在三年内从2=13311+x xx1000．）同，设为（，那么可以列出关于的方程是由实际问题抽象出一元二次方程．【考点】10001331万元，万元增加到【分析】根据某企业的年产值在三年内从这三年中每年的增长x10001331 万，从而可以列出相应的方程．，可知第一年为万，第三年为率相同，设为10001331万元，∵某企业的年产值在三年内从解：这三年中每年的增万元增加到【解答】x ，长率相同，设为2=1331 10001x，（∴）+2=1331 1x1000．+（）故答案为：13409 °．，那么这个多边形的边数是．如果多边形的每个外角都是多边形内角与外角．【考点】360 度即可求得外角的个数，即多边形的边数．根据多边形的外角和是【分析】=9 ，【解答】解：多边形的边数是：9 ．故答案为：14EFGHABCDABBCCDDA的中点，如果对、分别是凸四边形、各边、、．已知点、、AC=BD=4EFGH8 ．角线，那么四边形的周长是中点四边形．【考点】．HEGHEFFG的长，根据四边形的周长公式计+【分析】根据三角形中位线定理分别求出++算即可．BCCDDAGEFHAB的中点，、分别是、、、、、【解答】解：∵CDADABFGEFGHHFABCBCD 的中位线，、、△、、△分别是△∴、△、GH=AC=2BD=2EF=AC=2HE=FG=BD=2，，∴，，EFGH=EFFGGHHE=8．+的周长+∴四边形+ 8．故答案为：975 15．，那么另一条底边的长为．在梯形的一条底边长为，中位线长为梯形中位线定理．【考点】此题只需根据梯形的中位线等于梯形两底和的一半进行计算即可．【分析】x5x=27 ，【解答】解：设另一条底边为+，则×x=9 ．解得9 ．即另一条底边的长为9 ．故答案为：16α设菱形中较小的角为将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，．ββα的代数式表示为可以用含度，平行四边形中较大的角为度，那么=β．菱形的性质；平行四边形的性质．【考点】1与∠由将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，可求得∠【分析】2 的度数，再利用周角的定义，即可求得答案．解：如图，∵是几个全等的平行四边形和全等的菱形镶嵌而成，【解答】2=1=180 β°α°°，∴∠，∠﹣2241=360 °，∵∠∠+24=360 α，+∴= β．∴=β．故答案为：BAD=10cmPBC17ABCDB=60AB=8cm°向，点，．如图，平行四边形上从中，∠，在边1cmAPQCQDAD，那么当运运动，如果运动的速度都为每秒运动，点向在边，上从ABPQt=7是直角梯形．动时间秒时，四边形直角梯形；平行四边形的性质．【考点】ABPQQPADBCAEAAEBCE是【分析】过点∥作时，则四边形⊥，所以当于∥，因为t的值．直角梯形，利用已知条件和路程与速度的关系式即可求出时间解：【解答】ABCD是平行四边形，∵四边形BCAD，∴∥EAEBCA，⊥作过点于QPABPQAE是直角梯形，时，则四边形∥∴当B=60AB=8cm°，∵∠，BE=4cm，∴Q1cmP，，∵运动的速度都为每秒tAP=tAQ=10，﹣∴，BE=4，∵4EP=t，﹣∴QPEPAEBCAEAQ，，∥∵∥⊥，AQBCADQP，，⊥∴⊥AEPQ是矩形，∴四边形AQ=EP，∴4t=t10，﹣即﹣t=7，解得7．故答案为：BFD=45BED=4ACABCDECA18F°，∠、且∠点．分别在、的延长线上，已知边长为的正方形，EBFD16+16 ．的面积是那么四边形．正方形的性质．【考点】BDACOEBFD是菱形，根据菱形的面积等于对角线【分析】连接于交，首先证明四边形乘积的一半即可解决问题．BDACO ．【解答】解：如图连接于交ABCD 是正方形，∵四边形AB=BC=CD=AD=4CAD=CAB=45 °，，∠∴∠EAD=EAB=135 °，∠∴∠EABEAD 中，在△和△，EABEAD ，∴△≌△AEB=AED=22.5EB=ED °，∠∴∠，ADE=180EADAED=22.5 °°，﹣∠﹣∠∴∠AED=ADE=22.5 °，∠∴∠AE=AD=4 ，∴DFC=22.5FD=FB °，同理证明∠，DEF=DFE ，∴∠∠DE=DF ，∴ED=EB=FB=FD ，∴=164EF=4816BDEBFD=??．×的面积+）+（（∴四边形1616．+故答案为2045分）题，每题三、解答题（本题共分，满分19．．解方程组：高次方程．【考点】．2y=0xxy=0②或﹣先由【分析】或得再把原方程组可变形为：+，，然后解这两个方程组即可．，【解答】解：yx2y=0x②，）（得：（）+由﹣2y=0y=0xx，或+﹣，或原方程组可变形为：．解得：，20．布袋里有一个红球两个黄球，它们除了颜色外其他都相同．1；（）任意摸出一个球恰好是红球的概率是2“摸到一红一黄两请利用树形图求事件）摸出一个球再放回袋中，（搅匀后再摸出一个球，P ”．的概率球列表法与树状图法．【考点】1 ）根据题意可得到任意摸出一个球恰好是红球的概率；【分析】（2 ”“的概率．）根据题意可以画出树状图，从而可以求出∴（摸到一红一黄两球1 ）由题意可得，（【解答】解：，任意摸出一个球恰好是红球的概率是；故答案为：2 ）由题意可得，（P= ”“．∴的概率摸到一红一黄两球21yx（千克）是一次函数关．已知弹簧在一定限度内，它的长度（厘米）与所挂重物质量系．表中记录的是两次挂不同重量重物的质量（在弹性限度内）与相对应的弹簧长度．x 5 2.5 （千克）所挂重物质量y 7.5 9 （厘米）弹簧长度求不挂重物时弹簧的长度．一次函数的应用．【考点】xkgy=把相关数值代入弹簧原来的长度，【分析】弹簧总长的重物时弹簧伸长的长度挂上+即可．ky=kxbyx（解：设长度（千克）的一次函数关系式是：（厘米）与所挂重物质量+【解答】0）≠，将表格中数据分别代入为：，解得：x6y=，∴+ y=6x=0．当时，6厘米．答：不挂重物时弹簧的长度为BD22EABCD的延长线上．．如图，点的对角线在平行四边形.= =1；）填空： + （﹣2 （不写作法，保留作图痕迹，写出结果） +）求作：（* 平面向量；平行四边形的性质．【考点】1）根据向量的平行四边形法则写出+即可，根据平行四边形的对边平【分析】（= ，然后根据向量的三角形法则求解即可；行且相等可得=2）根据平行四边形的对边平行且相等可得（，然后根据向量的平行四边形法DCDE 为邻边的平行四边形，其对角线即为所求．则作出以、=1 ，+解：（）【解答】= ，∵== ；﹣∴﹣．；故答案为：2 ．即为所求+（）如图，2610972425323分）分，第题题分，第四、解答题（本题共分，满分题，第题23ABCDECDBEAAFBE．垂，过点⊥．如图，已知矩形中，点作是边上的一点，连结FAF=BEFMNBCABCDMN，求证：四边、足为点，且，过点作∥，与、边分别交于点AMND 为正方形．形．正方形的判定；矩形的性质．【考点】ABCD是矩形，得到两组对边平行，四个角为直角，对角线相等，根据【分析】由四边形MNBCMNADAMND是平行四边形，由一个角为平行，得到平行，可得出四边形与与AMNDAMN=90AFBE°垂直，得与是矩形，得到∠直角的平行四边形是矩形得到，根据AASAFMBEC全等，利用全等三角形对应边到一对直角相等，利用与三角形得到三角形AM=BCAD=BCAM=AD，利用邻边相等的矩形是正方形即可得证．相等得到，得到，根据ABCD 是矩形，证明：∵四边形【解答】ADBCABCDBAD=C=ABC=90BC=AD °，，∠，∴∥∥∠，∠MNBC ，∵∥MNAD ，∴∥ABCD ，又∵∥AMND 是平行四边形，∴四边形BAD=90 °，又∵∠AMND 是矩形，∴四边形AMN=90 °，∴∠AFBE ，⊥∵AFB=90 °，∴∠AFBABFBAF=180 °，+∠∠∵∠+ABFBAF=90 °，+∴∠∠ABC=ABFEBC=90 °，+∠又∵∠∠BAF=EBC ，∴∠∠AFMBEC 中，在△和△，AFMBECAAS ，（∴△）≌△AM=BC ，∴AD=BC ，又∵AM=AD ，∴AMND 是矩形，又∵四边形AMND 是正方形．∴四边形24ABCDADBCAB=CDA，点∥，且．已知：如图，平面直角坐标系中有一个等腰梯形，CxAD=3BC=11yBBCD在第一象限，，、（点的左侧）在轴上在点，，在点轴正半轴上，点y=Dy=kxbAB2 两点．，直线+经过点、梯形的高为，双曲线经过1ABCD 的坐标；、、、）求点（．y=y=kxb 2的解析式；+）求双曲线（和直线3MNyABMNN的坐标．是平行四边形，轴上，（如果四边形）点在双曲线上，点求点在反比例函数综合题．【考点】1DDHxHADBCAB=CDAOHD，易得四边形作∥⊥，由轴于点【分析】（，）首先过点RtABORtDCHAD=3BC=112 ，即可求得答案；≌，△△，梯形的高为是矩形，证得，又由y=Dy=kxbAB2，直接利用待定系数法求解即可求得+过点，，直线（过点）由双曲线答案；3ABMNM4M的坐标，（的横坐标为﹣）由四边形，继而求得点是平行四边形，可得点AN=BM ，求得答案．又由11DDHxH ．，过点⊥作【解答】解：（轴于点）如图ADBCAB=CD ，∵，∥ABCD 是等腰梯形，∴四边形AOx 轴，⊥∵AOHD 是矩形，∴四边形AO=DHAD=OHAOB=DHC=90 °，，∠，∴∠RtABORtDCH 中，和△在△，RtABORtDCHHL ．∴△△）≌（BO=CH ，∴2 ，∵梯形的高为AO=DH=2 ．∴AD=3BC=11 ，∵，BO=4OC=7 ．，∴A02B40C70D32 ；（（，，∴）（，，），（﹣），），y=D322 ，（，经过点（）∵双曲线）m=xy=6．∴y=，∴双曲线的解析式为：y=kxbA02B40 ）两点，，（﹣、），（经过+∵直线，得：．∴解得：y=x2 ；∴直线的解析式为：+32ABMN 是平行四边形．（，∵四边形）如图BMANBM=AN ．∴且∥Ny 轴上，∵点在y=M Bx的交点即为点∴过点轴的垂线与双曲线作．MM4，（﹣，﹣∴点）的坐标为BM=．∴AN=BM=，∴AN=ON=OA，﹣∴0NN．∴点的坐标为（），25ABCDAB=2BC=5PADCP，将四，是边．已知：如图，在矩形，点中，上一点，连接ABCPCPEFCPABE，的位置，边形点沿的对应点分别为点所在直线翻折，落在四边形、FCFADG ．与边，边的交点为点1AP=2PG 的值；）当（时，求2AP=xFG=yyx 的函数解析式，并写出它的定义域；（，求）如果关于，3BPCFMPGMMG为腰的等腰三角形时，求（交于点）连结是以并延长与线段，当△AP 的长．四边形综合题．【考点】1PG=aRTDGCCG=aDG=3aCD=2，利用勾股定理即可△﹣中，【分析】（，）设，，则在解决问题．222222y5yx= 2RTDGCCDDG2=CG，由此即可解决问题．，得到（﹣（﹣）在（△）中，）++MG=MP31APBDGCAP=DG①，只要证明△，≌△，（得到）如图分两种情形讨论即可，中，MG=PGABPDPCBPC②均为直角三角形，根据，只要证明△，△列出方程即可，，△22222 DPAP=BCABCD，列出方程即可．+++1ABCPEFCP 全等．）由题意得：四边形【解答】（与四边形BCP=FCP ．∴∠∠ABCD 是矩形，∵四边形ADBC ，∥∴BCP=DPC ，∠∴∠DCP=FCP ，∴∠∠PG=CG ，∴PG=a ，设222 DGaDGCCG=aDG=3CD=2CD=CGRT，中，，，且﹣，则在△+222a==aa23 ，﹣），解得：∴+（PG=．即2CF=BC=5 ，）由题意得：（．CG=5y ，﹣∴PG=5y ，﹣∴DG=55yx=yx ，﹣﹣∴）﹣﹣（222 DGCCD=CGDGRT，中，△∵在+222 52y=yx，+﹣）（）∴（﹣y= ，∴y=0xx3 y）的函数解析式为：≤关于≤，∴（3PGMMG 为腰的等腰三角形，）∵△是以（MG=MPMG=PG1 中，或，如图∴MG=MP ①时，当MPG=MGC ，∵∠∠APB=MPGMGP=DGC ，∵∠，∠∠∠APB=DGC ，∴∠∠APBDGC 中，和△在△，APBDGC ，≌△∴△AP=DG ，∴y=2x ，∴2x=21=020x=2x3x ，∴，解得：，化简整理得：﹣+3x=不符合题意舍去，＞∵x=．∴MG=PG②时，当PMGMPG=，∠∵∠MBCMPG=，∠∵∠MBC=PMC，∴∠∠CM=CBMF．，（即点重合）与点∴BCP=MCP，∠又∵∠CPBP，⊥∴BPCDPCABP均为直角三角形．，△，△∴△2222222222 =5xAPABDPCD2=BCx25，），即﹣+∴+++++（2 4x=1x5x4=0．+或化简整理得：，解得：﹣x=43不符合题意舍弃，∵＞x=1．∴．AP=1PGMMG ．或是以综上所述：当△腰的等腰三角形时，。

浦东新区2015学年度第二学期期末质量抽测八年级（初二年级）数学2016．6一、选择题：（本大题共6题，每题3分，满分18分）（每题只有一个选项正确）1．下列直线中，与直线23+-=xy平行的是……………………………………………（ ） （A ）32+-=x y ； （B ）22y x =+； （C ）33+-=x y ； （D ）23-=x y ． 2．已知一次函数b kx y +=（k 、b x 的不等式0>+b kx 的解集是…………………………………（ （A ）3>x ； （B ）4>x ； （C ）3<x ； （D ）4<x ．3．下列说法中，正确的是…………………………………………（ （A ）方程4=x 的根是16±=x ；（B ）方程x x -=3的根是01=x ，32=x ； （C ）方程011=++x 没有实数根；（D ）方程x x =--323的根是21=x ，62=x ．4．如图，将一张正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分，利用这两部分不能拼成的图形是…………………………………………………………（ ） （A ）直角三角形； （B ）平行四边形； （C ）菱形； （D ）等腰梯形． 5．下列等式正确的是…………………………………………………………………………（ ） （A ）BA CB BC AB +=+； （B ）AC BC AB =-； （C ）0=-+AC BC AB ；（D ）DA CD BC AB =++．6．在平行四边形、矩形、菱形、等腰梯形这四个图形中任选一个图形，那么下列事件是不可能事件的是……………………………………………………………………………… （ ） （A ）这个图形既是轴对称图形又是中心对称图形； （B ）这个图形既不是轴对称图形又不是中心对称图形； （C ）这个图形是轴对称图形； （D ）这个图形是中心对称图形．二、填空题：（本大题共12题，每题3分，满分36分）7．一次函数52-=x y 的图像在y 轴上的截距是 ．8．已知一次函数b kx y +=的图像不经过第二象限，那么函数值y 随自变量x 的值增大而 ．（填“增大”或“减小”）9．如果关于x 的方程()82=+x m 无解，那么m 的取值范围是 ． 10．方程083=-x 的根是 ．11．已知关于x 的方程2511322=-+-x x x x ，如果设y x x =-12，那么原方程化为关于y 的方程是 ．12．某企业的年产值在三年内从1 000万元增加到1 331万元，如果这三年中每年的增长率相同，设为x ，那么可以列出关于x 的方程是 ． 13．如果多边形的每个外角都是40°，那么这个多边形的边数是 ．14．已知点E 、F 、G 、H 分别是凸四边形ABCD 各边AB 、BC 、CD 、DA 的中点，如果对角线AC =BD =4，那么四边形EFGH 的周长是 ．15．梯形的一条底边长为5，中位线长为7，那么另一条底边的长是 ．16．将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，设菱形中较小的角为α度，平行四边形中较大的角为β度，那么β可以用含α的代数式表示为 ． 17．如图，平行四边形ABCD 中，∠B =60°，AB=8cm ，AD=10cm ，点P 在边BC 上从B 向C运动，点Q 在边DA 上从D 向A 运动，如果P 、Q 运动的速度都为每秒1cm ，那么当运动时间t= 秒时，四边形ABPQ 是直角梯形.18．已知边长为1的正方形ABCD ，点E 、F 分别在CA 、AC 的延长线上，且∠BED =∠BFD =45°，那么四边形EBFD 的面积是 ．（第18题图） FEDCBA（第17题图）（第16题图）αβ三、简答题（本大题共4题，每题5分，满分20分） 19． 解方程组：⎩⎨⎧=---=-．，02222y xy x y x（1）任意摸出一个球恰好是红球的概率是 ；（2）摸出一个球再放回袋中，搅匀后再摸出一个球，请利用树形图求事件“摸到一红一黄两球”的概率P ．21．已知弹簧在一定限度内，它的长度y （厘米）与所挂重物质量x （千克）是一次函数关系．求不挂重物时弹簧的长度．①②22．如图，点E 在平行四边形ABCD 的对角线BD 的延长线上． （1）填空：=+DC DA ；=-BC AE ； （2）求作：DE AB +．（不写作法，保留作图痕迹，写出结果）．四、解答题（本大题共3题，第23题7分，第24题9分，第25题10分，满分26分） 23．如图，已知矩形ABCD 中，点E 是CD 边上的一点，联结BE ，过点A 作AF ⊥BE ，垂足为点F ，且AF =BE ，过点F 作MN ∥BC ，与AB 、CD 边分别交于点M 、N ． 求证：四边形AMND 为正方形．（第21题图）E AB CD（第23题图）N M FABCDE24．已知：如图，平面直角坐标系中有一个等腰梯形ABCD ，且AD ∥BC ，AB =CD ，点A在y 轴正半轴上，点B 、C 在x 轴上（点B 在点C 的左侧），点D 在第一象限，AD =3，BC =11，梯形的高为2．双曲线xmy =经过点D ，直线b kx y +=经过A 、B 两点． （1）求点A 、B 、C 、D 的坐标；（2）求双曲线xmy =和直线b kx y +=的解析式； （3）点M 在双曲线上，点 N 在y 轴上，如果四边形ABMN 是平行四边形， 求点N 的坐标．（第24题图）25．已知：如图，在矩形ABCD中，AB=2，BC=5．点P是边AD上一点，联结CP，将四边形ABCP沿CP所在直线翻折，落在四边形EFCP的位置，点A、B的对应点分别为点E、F，边CF与边AD的交点为点G．（1）当AP=2时，求PG的值；（2）如果AP=x，FG=y，求y关于x的函数解析式，并写出它的定义域；（3）联结BP并延长与线段CF交于点M，当△PGM是以MG为腰的等腰三角形时，求AP的长．（第25题图）（第25题备用图）浦东新区2015学年度第二学期期末质量抽测 八年级数学试卷参考答案及评分标准（供参考）一、选择题：（本大题共6题，每题3分，满分18分）（每题只有一个选项正确） 1．C ； 2．D ； 3．C ； 4．C ； 5．C ； 6．B ．二、填空题：（本大题共12题，每题3分，满分36分） 7．5-； 8．增大； 9．2-=m ；10．2=x ； 11．2513=+y y ；12．()1331110003=+x ； 13．9； 14．8； 15．9； 16．2180αβ+=； 17．7； 18．12+．三、简答题（本大题共4题，每题5分，满分20分） 19．解：（方法一）由②得0))(2(=+-y x y x ， ……………………………………………………（1分）∴02=-y x 或0=+y x ．原方程组可化为⎩⎨⎧=--=-；，022y x y x ⎩⎨⎧=+-=-.02y x y x ，……………………………………（2分）解这两个方程组得 ⎩⎨⎧-=-=;2,411y x ⎩⎨⎧=-=.1,122y x∴原方程组的解是⎩⎨⎧-=-=;2,411y x⎩⎨⎧=-=.1,122y x …………………………………………（2分） （方法二）由①得 2-=y x ． ③ …………………………………………………………（1分） 将③代入②得 ()()022222=----y y y y ．整理，得022=-+y y ． ………………………………………………（1分）解这个方程，得 21-=y ，12=y ．…………………………………………（1分）将21-=y 代入③，得 41-=x ；将12=y 代入③，得12-=x ．………………（1分）∴原方程组的解是⎩⎨⎧-=-=;2,411y x ⎩⎨⎧=-=.1,122y x ……………………………………………（1分）20．（1）31；………………………………………（2分）（2）正确画出树形图.…………………………（2分）可得：94=P . ………………………………（1分）21．解：设长度y （厘米）与所挂重物质量x （千克）的一次函数关系式是：b kx y +=（0≠k ）将表格中数据分别代入为：⎩⎨⎧=+=+.95,5.75.2b k b k ………………………………………（2分）解得：⎪⎩⎪⎨⎧==.6,53b k ∴653+=x y .……………………………………………………（2分） 当0=x 时，6=y .答：不挂重物时弹簧的长度为6厘米．………………………………………………（1分）22. （1）DB ；DE .………………………………………………………………………（各1分） （2）图略. ……………………………………………（正确画图2分，写出正确结论1分）四、解答题（本大题共3题，第23题7分，第24题9分，第25题10分，满分26分） 23．证明：∵四边形ABCD 是矩形，∴AD ∥BC ，AB ∥CD ，︒=∠=∠=∠90ABC C BAD ，AD BC =. ∵MN ∥BC ，∴MN ∥AD .………………………………………………………………………（1分） 又∵AB ∥CD ，∴四边形AMND 是平行四边形. …………………………………………………（1分） 又∵︒=∠90BAD ，∴四边形AMND 是矩形. …………………………………………………………（1分） ∴︒=∠90AMN .∵BE AF ⊥，∴︒=∠90AFB .∵︒=∠+∠+∠180BAF ABF AFB ， ∴︒=∠+∠90BAF ABF .又∵︒=∠+∠=∠90EBC ABF ABC ，∴EBC BAF ∠=∠.…………………………………………………………………（1分） 在AFM △和BEC △中，EBC FAM ∠=∠，︒=∠=∠90C AMF ，BE AF =，∴AFM △≌BEC △.………………………………………………………………（1分） ∴BC AM =. 又∵BC AD =，∴AD AM =.………………………………………………………………………（1分） 又∵四边形AMND 是矩形，∴四边形AMND 是正方形. ………………………………………………………（1分） 备注：其他证法类比得分. 24．（1）过点D 作x DH ⊥轴于点H ．由x AO ⊥轴，四边形ABCD 是等腰梯形，可证得四边形AOHD 是矩形，ABO △Rt ≌DCH △Rt ． ∴CH BO =，OH AD =，DH AO =． ∵梯形的高为2， ∴2==DH AO ． ∵3=AD ，11=BC ， ∴4=BO ，7=OC ．∴()2,0A ，()0,4-B ，()0,7C ，()2,3D ．…………………………………………（4分） （2）∵双曲线xm y =经过点()2,3D ，∴6=m ．∴x y 6=．………………………（1分）∵直线b kx y +=经过()3,0A 、()0,4-B 两点，∴43=k ，3=b ．∴221+=x y ．………………………………………………（1分） （3）∵四边形ABMN 是平行四边形.∴BM ∥AN 且AN BM =. ∵点N 在y 轴上，∴过点B 作x 轴的垂线与双曲线xmy =的交点即为点M ． ∴点M 的坐标为⎪⎭⎫ ⎝⎛--23,4M ．…………………………………………………（1分）∴23=BM ．（或又∵AB ∥MN ，∴直线MN 的解析式为：2121+=x y ．…（1分） ∴点N 的坐标为⎪⎭⎫⎝⎛21,0N ．………………………………………………………（1分）25．（1）由题意得：四边形ABCP 与四边形EFCP 全等．∴FCP BCP ∠=∠．∵四边形ABCD 是矩形，∴AD ∥BC .∴DPC BCP ∠=∠．∴FCP DPC ∠=∠．∴CG PG =．………………………………………………（1分） 设a PG =，则在DGC △Rt 中，a CG =，a DG -=3，2=CD ，且222CG DG CD =+．（1分） ∴()22232a a =-+．解得：613=a ． 即613=PG ．………………………………………………………………………（1分） （2）由题意得：5==BC CF ．∴y CG -=5．∴y PG -=5．∴()x y x y DG -=---=55．…………………………………（1分） ∵在DGC △Rt 中，222CG DG CD =+．∴()()22252y x y -=+-．…………（1分）∴y 关于x 的函数解析式为：xx y 210212--=．定义域为：0≤x ≤3．…………（1分）（3）∵PGM △是以MG 为腰的等腰三角形，∴MP MG =或PG MG =．①MP MG =，∴MGC MPG ∠=∠．∴DGC APB ∠=∠．又∵D A ∠=∠，CD AB =，∴APB △≌DCG △．∴DG AP =．∴x y 2=．…………………………………………………………（1分）∴x xx 2210212=--．化简整理得：0212032=+-x x ．解得：33710±=x ． ∵333710>+=x 不符合题意舍去，∴33710-=x ．………………………（1分） ②PG MG =，∴PMG MPG ∠=∠．∵MBC MPG ∠=∠，PMC MBC ∠=∠．∴BC CM =（即点M 与点F 重合）． 又∵MCP BCP ∠=∠，∴BP CP ⊥．∴ABP △、DPC △、BPC △均为直角三角形．∴22222BC CD DP AB AP =+++．即()222225252=+-++x x ．……………（1分）化简整理得：0452=+-x x ．解得：1=x 或4=x ．∵34>=x 不符合题意舍去，∴1=x ．…………………………………………（1分） 综上：当PGM △是以MG 为腰的等腰三角形时，33710-=AP 或1=AP ．。

2015-2016学年上海市浦东新区八年级（下）期末数学试卷一、选择题（本大题共6题，每题3分，满分18分）（每题只有一个选择正确1．下列直线中，与直线y=﹣3x+2平行的是（）A．y=﹣2x+3 B．y=2x+2 C．y=﹣3x+3 D．y=3x﹣22．已知一次函数y=kx+b（k、b为常数）的图象如图所示，那么关于x的不等式kx+b＞0的解集是（）A．x＞3 B．x＞4 C．x＜3 D．x＜43．下列说法中，正确的是（）A．方程=4的根是x=±16B．方程=﹣x的根是x1=0，x2=3C．方程+1=0没有实数根D．方程3﹣的根是x1=2，x2=64．如图，将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分，利用这两部分不能拼成的图形是（）A．直角三角形B．平行四边形C．菱形 D．等腰梯形5．下列等式正确的是（）A． +=+B．﹣=C． +﹣=D． ++=6．在平行四边形、矩形、菱形、等腰梯形这个四个图形中任选一个图形，那么下列事件是不可能事件的是（）A．这个图形既是轴对称图形又是中心对称图形B．这个图形既不是轴对称图形又不是中心对称图形C．这个图形是轴对称图形D．这个图形是中心对称图形二、填空题（本大题共12题，每题3分，满分36分）7．一次函数y=2x﹣5的图象在y轴上的截距是______．8．已知一次函数y=kx+b的图象不经过第二象限，那么函数值y随自变量x的值增大而______（填“增大”或“减小”）．9．如果关于x的方程（m+2）x=8无解，那么m的取值范围是______．10．方程x3﹣8=0的根是______．11．已知关于x的方程+=，如果设=y，那么原方程化为关于y的方程是______．12．某企业的年产值在三年内从1000万元增加到1331万元，如果这三年中每年的增长率相同，设为x，那么可以列出关于x的方程是______．13．如果多边形的每个外角都是40°，那么这个多边形的边数是______．14．已知点E、F、G、H分别是凸四边形ABCD各边AB、BC、CD、DA的中点，如果对角线AC=BD=4，那么四边形EFGH的周长是______．15．在梯形的一条底边长为5，中位线长为7，那么另一条底边的长为______．16．将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，设菱形中较小的角为α度，平行四边形中较大的角为β度，那么β可以用含α的代数式表示为______．17．如图，平行四边形ABCD中，∠B=60°，AB=8cm，AD=10cm，点P在边BC上从B向C运动，点Q在边DA上从D向A运动，如果P，Q运动的速度都为每秒1cm，那么当运动时间t=______秒时，四边形ABPQ是直角梯形．18．已知边长为4的正方形ABCD，点E、F分别在CA、AC的延长线上，且∠BED=∠BFD=45°，那么四边形EBFD的面积是______．三、解答题（本题共4题，每题5分，满分20分）19．解方程组：．20．布袋里有一个红球两个黄球，它们除了颜色外其他都相同．（1）任意摸出一个球恰好是红球的概率是______；（2）摸出一个球再放回袋中，搅匀后再摸出一个球，请利用树形图求事件“摸到一红一黄两球”的概率P．21．已知弹簧在一定限度内，它的长度y（厘米）与所挂重物质量x（千克）是一次函数关系．表中记录的是两次挂不同重量重物的质量（在弹性限度内）与相对应的弹簧长度．所挂重物质量x（千克） 2.5 5弹簧长度y（厘米）7.5 9求不挂重物时弹簧的长度．22．如图，点E在平行四边形ABCD的对角线BD的延长线上．（1）填空： +=______.﹣=______；（2）求作： +（不写作法，保留作图痕迹，写出结果）四、解答题（本题共3题，第23题7分，第24题9分，第25题10分，满分26分）23．如图，已知矩形ABCD中，点E是CD边上的一点，连结BE，过点A作AF⊥BE．垂足为点F，且AF=BE，过点F作MN∥BC，与AB、CD边分别交于点M、N，求证：四边形AMND为正方形．24．已知：如图，平面直角坐标系中有一个等腰梯形ABCD，且AD∥BC，AB=CD，点A 在y轴正半轴上，点B、C在x轴上（点B在点C的左侧），点D在第一象限，AD=3，BC=11，梯形的高为2，双曲线y=经过点D，直线y=kx+b经过A、B两点．（1）求点A、B、C、D的坐标；（2）求双曲线y=和直线y=kx+b的解析式；（3）点M在双曲线上，点N在y轴上，如果四边形ABMN是平行四边形，求点N的坐标．25．已知：如图，在矩形ABCD中，AB=2，BC=5，点P是边AD上一点，连接CP，将四边形ABCP沿CP所在直线翻折，落在四边形EFCP的位置，点A、B的对应点分别为点E，F，边CF与边AD的交点为点G．（1）当AP=2时，求PG的值；（2）如果AP=x，FG=y，求y关于x的函数解析式，并写出它的定义域；（3）连结BP并延长与线段CF交于点M，当△PGM是以MG为腰的等腰三角形时，求AP的长．2015-2016学年上海市浦东新区八年级（下）期末数学试卷参考答案与试题解析一、选择题（本大题共6题，每题3分，满分18分）（每题只有一个选择正确1．下列直线中，与直线y=﹣3x+2平行的是（）A．y=﹣2x+3 B．y=2x+2 C．y=﹣3x+3 D．y=3x﹣2【考点】两条直线相交或平行问题．【分析】根据两直线平行k相同即可解决．【解答】解：根据两直线平行k相同，∵直线y=﹣3x+2，∴k=﹣3，故选C．2．已知一次函数y=kx+b（k、b为常数）的图象如图所示，那么关于x的不等式kx+b＞0的解集是（）A．x＞3 B．x＞4 C．x＜3 D．x＜4【考点】一次函数与一元一次不等式．【分析】从图象上得到函数的增减性及与x轴的交点的横坐标，即能求得不等式kx+b＞0的解集．【解答】解：函数y=kx+b的图象经过点（4，0），并且函数值y随x的增大而减小，所以当x＜4时，函数值大于0，即关于x的不等式kx+b＞0的解集是x＜4．故选D．3．下列说法中，正确的是（）A．方程=4的根是x=±16B．方程=﹣x的根是x1=0，x2=3C．方程+1=0没有实数根D．方程3﹣的根是x1=2，x2=6【考点】无理方程．【分析】根据各个选项，错误的选项说明错在哪，正确的选项进行说明，即可判断出哪个选项是正确的．【解答】解：当x=﹣16时，没有意义，故选项A错误；当x=3时，==3，而﹣x=﹣3，3≠﹣3，故选项B错误；∵≥0，则+1≥1，故选项C正确；3﹣不是方程，故选项D错误．故选C．4．如图，将一种正方形的纸片沿着过一边中点的虚线剪成形状分别为三角形和梯形的两部分，利用这两部分不能拼成的图形是（）A．直角三角形B．平行四边形C．菱形 D．等腰梯形【考点】图形的剪拼．【分析】将剪开的△ABE绕E点旋转180°，EC与EB重合，得到直角三角形；把△ABE平移，使AB与DC重合，则得到平行四边形；把△ABE的顶点E与C重合，B与D重合，与四边形AECD不重叠拼在一起，组成等腰梯形；不能得到菱形；即可得出结论．【解答】解：将△ABE绕E点旋转180°，EC与EB重合，得到直角三角形，故选项A正确；把△ABE平移，使AB与DC重合，则得到平行四边形，故选项B正确；把△ABE的顶点E与C重合，B与D重合，与四边形AECD不重叠拼在一起，组成等腰梯形，故选项D正确；不能得到菱形，故选项C错误．故选C．5．下列等式正确的是（）A． +=+B．﹣=C． +﹣=D． ++=【考点】*平面向量．【分析】直接利用三角形法则求解即可求得答案．注意掌握排除法在选择题中的应用．【解答】解：A、∵+=， +=，∴+=﹣（+）；故本选项错误；B、+=；故本选项错误；C、∵+=，∴+﹣=；故本选项正确；D、∵+=，∴++=+=；故本选项错误．故选C．6．在平行四边形、矩形、菱形、等腰梯形这个四个图形中任选一个图形，那么下列事件是不可能事件的是（）A．这个图形既是轴对称图形又是中心对称图形B．这个图形既不是轴对称图形又不是中心对称图形C．这个图形是轴对称图形D．这个图形是中心对称图形【考点】随机事件．【分析】根据确定事件的定义，结合轴对称以及中心对称的定义即可判断．【解答】解：A、4个图形中有3个是轴对称图形，有3个是中心对称图形，所以任选一个图形既是轴对称图形又是中心对称图形，可能发生，也可能不发生，是随机事件；B、一定不会发生，是不可能事件；C、4个图形中有3个是轴对称图形，所以任选一个图形是轴对称图形，可能发生，也可能不发生，是随机事件；D、4个图形中有3个是中心对称图形，所以任选一个图形是中心对称图形，可能发生，也可能不发生，是随机事件．故选B．二、填空题（本大题共12题，每题3分，满分36分）7．一次函数y=2x﹣5的图象在y轴上的截距是﹣5．【考点】一次函数图象上点的坐标特征．【分析】令x=0，则y=﹣5，即一次函数与y轴交点为（0，﹣5），即可得出答案．【解答】解：由y=2x﹣5，令x=0，则y=﹣5，即一次函数与y轴交点为（0，﹣5），∴一次函数在y轴上的截距为：﹣5．故答案为：﹣5．8．已知一次函数y=kx+b的图象不经过第二象限，那么函数值y随自变量x的值增大而增大（填“增大”或“减小”）．【考点】一次函数图象与系数的关系．【分析】直接根据一次函数的图象与系数的关系即可得出结论．【解答】解：∵一次函数y=kx+b的图象不经过第二象限，∴k＞0，b＜0．所以函数值y随自变量x的值增大而增大，故答案为：增大；9．如果关于x的方程（m+2）x=8无解，那么m的取值范围是m=﹣2．【考点】一元一次方程的解．【分析】根据一元一次方程无解，则m+2=0，即可解答．【解答】解∵关于x的方程（m+2）x=8无解，∴m+2=0，∴m=﹣2，故答案为：m=﹣2．10．方程x3﹣8=0的根是x=2．【考点】立方根．【分析】首先整理方程得出x3=8，进而利用立方根的性质求出x的值．【解答】解：x3﹣8=0，x3=8，解得：x=2．故答案为：x=2．11．已知关于x的方程+=，如果设=y，那么原方程化为关于y的方程是3y+=．【考点】换元法解分式方程．【分析】先根据=y得到，再代入原方程进行换元即可．【解答】解：由=y，可得∴原方程化为3y+=故答案为：3y+=12．某企业的年产值在三年内从1000万元增加到1331万元，如果这三年中每年的增长率相同，设为x，那么可以列出关于x的方程是1000（1+x）2=1331．【考点】由实际问题抽象出一元二次方程．【分析】根据某企业的年产值在三年内从1000万元增加到1331万元，这三年中每年的增长率相同，设为x，可知第一年为1000万，第三年为1331万，从而可以列出相应的方程．【解答】解：∵某企业的年产值在三年内从1000万元增加到1331万元，这三年中每年的增长率相同，设为x，∴1000（1+x）2=1331，故答案为：1000（1+x）2=1331．13．如果多边形的每个外角都是40°，那么这个多边形的边数是9．【考点】多边形内角与外角．【分析】根据多边形的外角和是360度即可求得外角的个数，即多边形的边数．【解答】解：多边形的边数是：=9，故答案为：9．14．已知点E、F、G、H分别是凸四边形ABCD各边AB、BC、CD、DA的中点，如果对角线AC=BD=4，那么四边形EFGH的周长是8．【考点】中点四边形．【分析】根据三角形中位线定理分别求出EF+FG+GH+HE的长，根据四边形的周长公式计算即可．【解答】解：∵E、F、G、H分别是AB、BC、CD、DA的中点，∴EF、FG、GH、HF分别是△ABC、△BCD、△CDA、△DAB的中位线，∴EF=AC=2，FG=BD=2，GH=AC=2，HE=BD=2，∴四边形EFGH的周长=EF+FG+GH+HE=8．故答案为：8．15．在梯形的一条底边长为5，中位线长为7，那么另一条底边的长为9．【考点】梯形中位线定理．【分析】此题只需根据梯形的中位线等于梯形两底和的一半进行计算即可．【解答】解：设另一条底边为x，则5+x=2×7，解得x=9．即另一条底边的长为9．故答案为：9．16．将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，设菱形中较小的角为α度，平行四边形中较大的角为β度，那么β可以用含α的代数式表示为β=．【考点】菱形的性质；平行四边形的性质．【分析】由将几个全等的平行四边形和全等的菱形镶嵌成如图所示的图案，可求得∠1与∠2的度数，再利用周角的定义，即可求得答案．【解答】解：如图，∵是几个全等的平行四边形和全等的菱形镶嵌而成，∴∠2=α°，∠1=180°﹣β°，∵2∠2+4∠1=360°，∴2α+4=360，∴β=．故答案为：β=．17．如图，平行四边形ABCD中，∠B=60°，AB=8cm，AD=10cm，点P在边BC上从B向C运动，点Q在边DA上从D向A运动，如果P，Q运动的速度都为每秒1cm，那么当运动时间t=7秒时，四边形ABPQ是直角梯形．【考点】直角梯形；平行四边形的性质．【分析】过点A作AE⊥BC于E，因为AD∥BC，所以当AE∥QP时，则四边形ABPQ是直角梯形，利用已知条件和路程与速度的关系式即可求出时间t的值．【解答】解：∵四边形ABCD是平行四边形，∴AD∥BC，过点A作AE⊥BC于E，∴当AE∥QP时，则四边形ABPQ是直角梯形，∵∠B=60°，AB=8cm，∴BE=4cm，∵P，Q运动的速度都为每秒1cm，∴AQ=10﹣t，AP=t，∵BE=4，∴EP=t﹣4，∵AE⊥BC，AQ∥EP，AE∥QP，∴QP⊥BC，AQ⊥AD，∴四边形AEPQ是矩形，∴AQ=EP，即10﹣t=t﹣4，解得t=7，故答案为：7．18．已知边长为4的正方形ABCD，点E、F分别在CA、AC的延长线上，且∠BED=∠BFD=45°，那么四边形EBFD的面积是16+16．【考点】正方形的性质．【分析】连接BD交AC于O，首先证明四边形EBFD是菱形，根据菱形的面积等于对角线乘积的一半即可解决问题．【解答】解：如图连接BD交AC于O．∵四边形ABCD是正方形，∴AB=BC=CD=AD=4，∠CAD=∠CAB=45°，∴∠EAD=∠EAB=135°，在△EAB和△EAD中，，∴△EAB≌△EAD，∴∠AEB=∠AED=22.5°，EB=ED，∴∠ADE=180°﹣∠EAD﹣∠AED=22.5°，∴∠AED=∠ADE=22.5°，∴AE=AD=4，同理证明∠DFC=22.5°，FD=FB，∴∠DEF=∠DFE，∴DE=DF，∴ED=EB=FB=FD，∴四边形EBFD的面积=•BD•EF=×4（（4+8）=16+16．故答案为16+16．三、解答题（本题共4题，每题5分，满分20分）19．解方程组：．【考点】高次方程．【分析】先由②得x+y=0或x﹣2y=0，再把原方程组可变形为：或，然后解这两个方程组即可．【解答】解：，由②得：（x+y）（x﹣2y）=0，x+y=0或x﹣2y=0，原方程组可变形为：或，解得：，．20．布袋里有一个红球两个黄球，它们除了颜色外其他都相同．（1）任意摸出一个球恰好是红球的概率是；（2）摸出一个球再放回袋中，搅匀后再摸出一个球，请利用树形图求事件“摸到一红一黄两球”的概率P．【考点】列表法与树状图法．【分析】（1）根据题意可得到任意摸出一个球恰好是红球的概率；（2）根据题意可以画出树状图，从而可以求出∴“摸到一红一黄两球”的概率．【解答】解：（1）由题意可得，任意摸出一个球恰好是红球的概率是，故答案为：；（2）由题意可得，∴“摸到一红一黄两球”的概率P=．21．已知弹簧在一定限度内，它的长度y（厘米）与所挂重物质量x（千克）是一次函数关系．表中记录的是两次挂不同重量重物的质量（在弹性限度内）与相对应的弹簧长度．所挂重物质量x（千克） 2.5 5弹簧长度y（厘米）7.5 9求不挂重物时弹簧的长度．【考点】一次函数的应用．【分析】弹簧总长y=挂上xkg的重物时弹簧伸长的长度+弹簧原来的长度，把相关数值代入即可．【解答】解：设长度y（厘米）与所挂重物质量x（千克）的一次函数关系式是：y=kx+b（k ≠0）将表格中数据分别代入为：，解得：，∴y=x+6，当x=0时，y=6．答：不挂重物时弹簧的长度为6厘米．22．如图，点E在平行四边形ABCD的对角线BD的延长线上．（1）填空： +=.﹣=；（2）求作： +（不写作法，保留作图痕迹，写出结果）【考点】*平面向量；平行四边形的性质．【分析】（1）根据向量的平行四边形法则写出+即可，根据平行四边形的对边平行且相等可得=，然后根据向量的三角形法则求解即可；（2）根据平行四边形的对边平行且相等可得=，然后根据向量的平行四边形法则作出以DC、DE为邻边的平行四边形，其对角线即为所求．【解答】解：（1）+=，∵=，∴﹣=﹣=；故答案为：；．（2）如图，即为所求+．四、解答题（本题共3题，第23题7分，第24题9分，第25题10分，满分26分）23．如图，已知矩形ABCD中，点E是CD边上的一点，连结BE，过点A作AF⊥BE．垂足为点F，且AF=BE，过点F作MN∥BC，与AB、CD边分别交于点M、N，求证：四边形AMND为正方形．【考点】正方形的判定；矩形的性质．【分析】由四边形ABCD是矩形，得到两组对边平行，四个角为直角，对角线相等，根据MN与BC平行，得到MN与AD平行，可得出四边形AMND是平行四边形，由一个角为直角的平行四边形是矩形得到AMND是矩形，得到∠AMN=90°，根据AF与BE垂直，得到一对直角相等，利用AAS得到三角形AFM与三角形BEC全等，利用全等三角形对应边相等得到AM=BC，根据AD=BC，得到AM=AD，利用邻边相等的矩形是正方形即可得证．【解答】证明：∵四边形ABCD是矩形，∴AD∥BC，AB∥CD，∠BAD=∠C=∠ABC=90°，BC=AD，∵MN∥BC，∴MN∥AD，又∵AB∥CD，∴四边形AMND是平行四边形，又∵∠BAD=90°，∴四边形AMND是矩形，∴∠AMN=90°，∵AF⊥BE，∴∠AFB=90°，∵∠AFB+∠ABF+∠BAF=180°，∴∠ABF+∠BAF=90°，又∵∠ABC=∠ABF+∠EBC=90°，∴∠BAF=∠EBC，在△AFM和△BEC中，，∴△AFM≌△BEC（AAS），∴AM=BC，又∵AD=BC，∴AM=AD，又∵四边形AMND是矩形，∴四边形AMND是正方形．24．已知：如图，平面直角坐标系中有一个等腰梯形ABCD，且AD∥BC，AB=CD，点A 在y轴正半轴上，点B、C在x轴上（点B在点C的左侧），点D在第一象限，AD=3，BC=11，梯形的高为2，双曲线y=经过点D，直线y=kx+b经过A、B两点．（1）求点A、B、C、D的坐标；（2）求双曲线y=和直线y=kx+b的解析式；（3）点M在双曲线上，点N在y轴上，如果四边形ABMN是平行四边形，求点N的坐标．【考点】反比例函数综合题．【分析】（1）首先过点D作DH⊥x轴于点H，由AD∥BC，AB=CD，易得四边形AOHD 是矩形，证得Rt△ABO≌Rt△DCH，又由AD=3，BC=11，梯形的高为2，即可求得答案；（2）由双曲线y=过点D，直线y=kx+b过点A，B，直接利用待定系数法求解即可求得答案；（3）由四边形ABMN是平行四边形，可得点M的横坐标为﹣4，继而求得点M的坐标，又由AN=BM，求得答案．【解答】解：（1）如图1，过点D作DH⊥x轴于点H．∵AD∥BC，AB=CD，∴四边形ABCD是等腰梯形，∵AO⊥x轴，∴四边形AOHD是矩形，∴AO=DH，AD=OH，∠AOB=∠DHC=90°，在Rt△ABO和Rt△DCH中，，∴Rt△ABO≌Rt△DCH（HL）．∴BO=CH，∵梯形的高为2，∴AO=DH=2．∵AD=3，BC=11，∴BO=4，OC=7．∴A（0，2），B（﹣4，0），C（7，0），D（3，2）；（2）∵双曲线y=经过点D（3，2），∴m=xy=6．∴双曲线的解析式为：y=，∵直线y=kx+b经过A（0，2）、B（﹣4，0）两点，得：，∴解得：．∴直线的解析式为：y=x+2；（3）如图2，∵四边形ABMN是平行四边形．∴BM∥AN且BM=AN．∵点N在y轴上，∴过点B作x轴的垂线与双曲线y=的交点即为点M．∴点M的坐标为M（﹣4，﹣），∴BM=．∴AN=BM=，∴ON=OA﹣AN=，∴点N的坐标为N（0，）．25．已知：如图，在矩形ABCD中，AB=2，BC=5，点P是边AD上一点，连接CP，将四边形ABCP沿CP所在直线翻折，落在四边形EFCP的位置，点A、B的对应点分别为点E，F，边CF与边AD的交点为点G．（1）当AP=2时，求PG的值；（2）如果AP=x，FG=y，求y关于x的函数解析式，并写出它的定义域；（3）连结BP并延长与线段CF交于点M，当△PGM是以MG为腰的等腰三角形时，求AP的长．【考点】四边形综合题．【分析】（1）设PG=a，则在RT△DGC中，CG=a，DG=3﹣a，CD=2，利用勾股定理即可解决问题．（2）在RT△DGC中，CD2+DG2=CG2，得到（y﹣x）2+22=（5﹣y）2，由此即可解决问题．（3）如图1中，分两种情形讨论即可，①MG=MP，只要证明△APB≌△DGC，得到AP=DG，列出方程即可，②MG=PG，只要证明△ABP，△DPC，△BPC均为直角三角形，根据AP2+AB2+DP2+CD2=BC2，列出方程即可．【解答】（1）由题意得：四边形ABCP与四边形EFCP全等．∴∠BCP=∠FCP．∵四边形ABCD是矩形，∴AD∥BC，∴∠BCP=∠DPC，∴∠DCP=∠FCP，∴PG=CG，设PG=a，则在RT△DGC中，CG=a，DG=3﹣a，CD=2，且CD2+DG2=CG2，∴22+（3﹣a）2=a2，解得：a=，即PG=．（2）由题意得：CF=BC=5，∴CG=5﹣y，∴PG=5﹣y，∴DG=5﹣（5﹣y）﹣x=y﹣x，∵在RT△DGC中，CD2+DG2=CG2，∴（y﹣x）2+22=（5﹣y）2，∴y=，∴y关于x的函数解析式为：y=，（0≤x≤3）（3）∵△PGM是以MG为腰的等腰三角形，∴MG=MP或MG=PG，如图1中，①当MG=MP时，∵∠MPG=∠MGC，∵∠APB=∠MPG，∠MGP=∠DGC，∴∠APB=∠DGC，在△APB和△DGC中，，∴△APB≌△DGC，∴AP=DG，∴y=2x，∴=2x，化简整理得：3x2﹣20x+21=0，解得：x=，∵x=＞3不符合题意舍去，∴x=．②当MG=PG时，∵∠MPG=∠PMG，∵∠MPG=∠MBC，∴∠MBC=∠PMC，∴CM=CB，（即点M与点F重合）．又∵∠BCP=∠MCP，∴CP⊥BP，∴△ABP，△DPC，△BPC均为直角三角形．∴AP2+AB2+DP2+CD2=BC2，即x2+22+（5﹣x）2+22=52，化简整理得：x2﹣5x+4=0，解得：x=1或4．∵x=4＞3不符合题意舍弃，∴x=1．综上所述：当△PGM是以MG腰的等腰三角形时，AP=或1．2016年9月25日。

浦东新区2015学年度第二学期期末质量抽测初一数学（完卷时间：90分钟 满分：100分） 2016.6一、选择题（本大题共6题，每题2分，满分12分）（每题只有一个选项正确）1．下列关于无理数的说法，错误的是…………………………………………………… （ ）（A ）无理数是实数；（B ）无理数是无限不循环小数； （C ）无理数是无限小数；（D ）无理数是带根号的数．2．如图，线段AB 将边长为1个单位长度的正方形分割为两个等腰直角三角形，以A 为圆心、AB 的长为半径画弧交数轴于点C ，那么点C 在数轴上表示的实数是………………（ ） （A ）2 （B 2； （C 2-1； （D ）1．3．如图，直线l 1∥l 2，∠1=110°，∠2=130°，那么∠3的度数是………………………………（ ）（A ）40°；（B ）50°；（C ）60°；（D ）70°．4．下列说法：①任意三角形的内角和都是180°；②三角形的一个外角大于任何一个内角；③三角形的中线、角平分线和高线都是线段；④三角形的三条高线必在三角形内．其中正确的是……………………………………………………………………………………（ ） （A ）①②；（B ）①③；（C ）②③；（D ）③④．5．如图，已知两个三角形全等，那么∠1的度数是…………………………………………（ ）（A ）72°；（B ）60°；（C ）50°；（D ）58°．6．在直角坐标平面内，已知在y 轴与直线x =3之间有一点M (a，3)，如果该点关于直线x =3的对称点M'的坐标为(5，3)，那么a 的值为…………………………………………（ ）（A ）4； （B ）3； （C ）2； （D ）1． 二、填空题（本大题共12题，每题3分，满分36分）（第5题图）（第2题图）（第3题图）7．计算：9= ．8．据上海市统计局最新发布的统计公报显示，2015年末上海市常住人口总数约为24 152 700人，用科学记数法将24 152 700保留三个有效数字是 ． 9．如图，∠2的同旁内角是 ．10．如图，已知BC ∥DE ，∠ABC =120°，那么直线AB 、DE 的夹角是 °． 11．已知三角形的三边长分别为3cm 、x cm 和7cm ，那么x 的取值范围是 ．12．如图，在等腰△ABC 中，AB =AC ，点O 是△ABC 内一点，且OB =OC ．联结AO 并延长交边BC 于点D ．如果BD =6，那么BC 的值为 ．13．如图，已知点A 、B 、C 、F 在同一条直线上，AD ∥EF ，∠D=40°，∠F =30°，那么∠ACD 的度数是 ．14．如图，将△ABC 沿射线BA 方向平移得到△DEF ，AB =4，AE =3，那么DA 的长度是 ． 15．如图，在四边形ABCD 中，AD ∥BC ，要使△ABD ≌△CDB ，可添加一个条件为 ． 16．在平面直角坐标系中，如果点M （-1，a -1）在第三象限，那么a 的取值范围是 ． 17．如图，将边长为1个单位长度的正方形ABCD 置于平面直角坐标系内，如果BC 与x 轴平行，且点A 的坐标是（2，2），那么点C 的坐标为 ．18．在等腰△ABC 中，如果过顶角的顶点A 的一条直线AD 将△ABC 分割成两个等腰三角形，那么∠BAC = °．三、简答题（本大题共4题，第19题，每小题3分；第20题，每小题2分；第21题6分，第22题5分，满分21分） 19．计算（写出计算过程）：（1）()62623-+； （2）521135÷⨯．解：解：（第15题图）（第9题图）（第14题图）（第10题图）（第17题图）（第12题图）（第13题图）（第21题图）20．利用幂的性质计算（写出计算过程，结果表示为含幂的形式）：（1）212193⨯；（2）342331010-⎛⎫÷ ⎪ ⎪⎝⎭．解：解：21．如图，已知直线AB 、CD 被直线EF 所截，FG 平分∠EFD ，∠1=∠2=80°，求∠BGF 的度数．解：因为∠1=∠2=80°（已知），所以AB ∥CD （ ）．所以∠BGF +∠3=180°（ ）． 因为∠2+∠EFD =180°（邻补角的意义）， 所以∠EFD = °（等式性质）． 因为FG 平分∠EFD （已知），所以∠3= ∠EFD （角平分线的意义）． 所以∠3= °（等式性质）． 所以∠BGF = °（等式性质）．22．如图，在△ABC 中，AD ⊥BC ，垂足为点D ，∠C =2∠1，∠2=32∠1，求∠B 的度数．（第22题图）四、解答题（本大题共4题，第23题6分，第24题7分，第25题8分，第26题10分，满分31分）23．如图，已知AB =AC ，BD ⊥AC ，CE ⊥AB ，垂足分别为点D 、E ．说明△ABD 与△ACE 全等的理由．24．如图，点E 是等边△ABC 外一点，点D 是BC 边上一点，AD =BE ，∠CAD =∠CBE ，联结ED 、EC ．（1）试说明△ADC 与△BEC 全等的理由； （2）试判断△DCE 的形状，并说明理由．25．如图，在直角坐标平面内，已知点A (8，0)，点B 的横坐标是2，△AOB 的面积为12．（1）求点B 的坐标；（2）如果P 是直角坐标平面内的点，那么点P 在什么位置时，S △AOP =2S △AOB ？（第24题图）（第25题图）（第23题图）26．如图1，以AB 为腰向两侧分别作全等的等腰△ABC 和△ABD ，过顶角的顶点A 作∠MAN ，使MAN BAC α∠=∠=（060α︒<<︒），将∠MAN 的边AM 与AC 叠合，绕点A 按逆时针方向旋转，与射线CB 、BD 分别交于点E 、F ，设旋转角度为β．（1）如图1，当0βα︒<<时，线段BE 与DF 相等吗？请说明理由．（2）当2αβα<<时，线段CE 、FD 与线段BD 具有怎样的数量关系？请在图2中画出图形并说明理由．（3）联结EF ，在∠MAN 绕点A 逆时针旋转过程中(02βα︒<<)，当线段AD ⊥EF 时，请用含α的代数式直接表示出∠CEA 的度数．（第26题图3）（第26题图1）（第26题图2）浦东新区2015学年度第二学期期末质量测试初一数学参考答案一、选择题：（本大题共6题，每小题2分，满分12分）（每题只有一个选项正确） 1．D ． 2．A ． 3．C ． 4．B ． 5．C ． 6．D ．二、填空题：（本大题共12题，每题3分，满分36分） 7．3． 8．72.4210⨯． 9．∠4． 10．60． 11．4<x <10． 12．12． 13．110°． 14．1． 15．略．16．1<a ．17．（3，1）．18．90或108．三、简答题（本大题共4题，第19、20题，每题3分；第20题，每小题2分；第21题6分，第22题5分，满分21分） 19．（1）解：原式=62262-+………………………………………………………（1分） =226+………………………………………………………………（2分）（2）解：原式………………………………………………………（1分）=25⨯（1分） =1013…………………………………………………………………（1分） 20．（1）解：原式=1233⨯…………………………………………………………………（1分） =323………………………………………………………………………（1分）（2）解：原式=32310-⎛⎫ ⎪ ⎪⎝⎭……………………………………………………………………（1分）=210-…………………………………………………………………………（1分）21．同位角相等，两直线平行………………………………………………………………（1分） 两直线平行，同旁内角互补……………………………………………………………（1分） 100…………………………………………………………………………………………（1分）12…………………………………………………………………………………………（1分） 50…………………………………………………………………………………………（1分） 130…………………………………………………………………………………………（1分）22．解：因为AD ⊥BC （已知），所以∠ADC=90°（垂直的意义）． …………………（1分）因为∠C+∠1+∠ADC =180°（三角形内角和性质），∠C =2∠1（已知），……（1分） 所以3∠1+90°=180°（等量代换）， 所以∠1=30°．……………………………………………………………………（1分）因为∠2=32∠1，所以∠2=45°……………………………………………………（1分） 因为∠C+∠1+∠2+∠B =180°（三角形内角和性质），所以∠B =45°．………（1分）四、解答题（本大题共4题，第23题6分，第24题7分，第25题8分，第26题10分，满分31分） 23．因为BD ⊥AC ，CE ⊥AB （已知），所以∠ADB =∠AEC =90°（垂直的意义）．…（2分）在△ABD 和△ACE 中，⎪⎩⎪⎨⎧=∠=∠∠=∠，（已知）（公共角），，（已证）AC AB A A AEC ADB …………………………………………………………（3分） 所以△ABD ≌△ACE （A ．A ．S ）．…………………………………………… （1分）24．解：（1）因为等边△ABC （已知），所以AC =BC ，∠ACB =60°（等边三角形的性质）．…………………………（2分） 在△ADC 和△BEC 中，⎪⎩⎪⎨⎧=∠=∠=，（已知）（已知），（已证）BE AD CBE CAD BC AC ,…………………………………………………………（1分） 所以△ACE ≌△DBF （S ．A ．S ）．…………………………………………… （1分）（2）因为△ACE ≌△DBF （已证），所以∠ACD =∠BCE =60°.（全等三角形对应角相等），………………………… （1分） DC =EC （全等三角形对应边相等），………………………………………… （1分） 即△DCE 是等腰三角形．所以△DCE 是等边三角形．(有一个内角等于60°的等腰三角形是等边三角形)…（1分） 25．解：（1）设点B 的纵坐标为y ，因为A (8，0)，所以OA =8； ………………………………………………………（1分） 因为S △AOB =12OA ·|y |=12×8|y |=12，所以y =±3， ………………………………（2分） 所以点B 的坐标为(2，3)或(2，-3)．………………………………………………（1分）（2）设点P 的纵坐标为h ，因为S △AOP =2S △AOB ，所以S △AOP =12OA ·|h |=12×8|h |=24，所以h =±6，………（2分） 所以点P 在直线y =6或直线y =-6．………………………………………………………（2分）26．解：（1）BE =DF ．………………………………………………………………………（1分） 因为等腰△ABC 和△ABD 全等 所以AB =AC =AD ，∠C =∠ABC =∠ABD =∠D ，（全等三角形、等腰三角形的性质）∠BAC =∠BAD （全等三角形的对应角相等） ………………………………………（1分） 因为MAN BAC α∠=∠=（已知）， 所以MAN BAD α∠=∠=（等量代换），所以∠MAN -∠BAN =∠BAD -∠BAN （等式性质），即∠EAB =∠F AD .… …………………… …………………………………………………（1分） 在△AEB 和△AFD 中ABE DAB AD EAB FAD ∠=∠⎧⎪=⎨⎪∠=∠⎩（已证）（已证）（已证）所以△AEB ≌△AFD （A ．S ．A ），………………………………………………………（1分） 所以BE =DF ．（全等三角形的对应边相等）（2）CE -FD =BD . …………………………………………………………………………（1分） 图形正确. ……………………………………………………………………………………（1分） 因为MAN BAD α∠=∠=（等量代换），所以∠MAN -∠EAD =∠BAD -∠EAD （等式性质）， 即∠DAF =∠BAE ．因为∠ABC =∠ADB （已证），所以180°-∠ABC =180°-∠ADB ， 即∠ABE =∠ADF ． 在△AEB 和△AFD 中ABE ADFAB AD BAE DAF ∠=∠⎧⎪=⎨⎪∠=∠⎩（已证）（已证）（已证）所以△AEB ≌△AFD （A ．S ．A ），………………………………………………………（1分） 所以BE =DF （全等三角形的对应边相等）， 所以CE -FD =CB +BE -DF =CB （等量代换）． 因为等腰△ABC 与等腰△ABD 全等， 所以BC =BD （全等三角形的对应边相等），所以CE -FD =BD （等量代换）．……………………………………………………………（1分） （3）90°-α ． ………………………………………………………………………………（2分）。