第6章 材料的介电性能-3

第一章无机材料的受力形变1 简述正应力与剪切应力的定义2 各向异性虎克定律的物理意义3 影响弹性模量的因素有哪些？4 试以两相串并联为模型推导复相材料弹性模量的上限与下限值。

5 什么是应力松弛与应变松弛？6 应力松弛时间与应变松弛时间的物理意义是什么？7 产生晶面滑移的条件是什么？并简述其原因。

8 什么是滑移系统？并举例说明。

9 比较金属与非金属晶体滑移的难易程度。

10 晶体塑性形变的机理是什么？11 试从晶体的势能曲线分析在外力作用下塑性形变的位错运动理论。

12 影响晶体应变速率的因素有哪些？13 玻璃是无序网络结构，不可能有滑移系统，呈脆性，但在高温时又能变形，为什么？14 影响塑性形变的因素有哪些？并对其进行说明。

15 为什么常温下大多数陶瓷材料不能产生塑性变形、而呈现脆性断裂？16 高温蠕变的机理有哪些？17 影响蠕变的因素有哪些？为什么？18 粘滞流动的模型有几种？19 影响粘度的因素有哪些？第二章无机材料的脆性断裂与强度1 试比较材料的理论强度、从应力集中观点出发和能量观点出发的微裂纹强度。

2 断裂能包括哪些内容？3 举例说明裂纹的形成？4 位错运动对材料有哪两方面的作用？5 影响强度的因素有哪些？6 Griffith关于裂纹扩展的能量判据是什么？7 试比较应力与应力强度因子。

8 有一构件，实际使用应力为1.30GPa,有下列两种钢供选：甲钢：sf =1.95GPa, K1c =45Mpa·m 1\2乙钢：sf =1.56GPa, K1c =75Mpa·m 1\2试根据经典强度理论与断裂强度理论进行选择，并对结果进行说明。

9 结构不连续区域有哪些特点？10 什么是亚临界裂纹扩展？其机理有哪几种？11 介质的作用(应力腐蚀)引起裂纹的扩展、塑性效应引起裂纹的扩展、扩散过程、热激活键撕裂作用引起裂纹扩展。

12 什么是裂纹的快速扩展？13 影响断裂韧性的因素有哪些？14 材料的脆性有哪些特点？通过哪些数据可以判断材料的脆性？15 克服材料脆性和改善其强度的关键是什么？16 克服材料的脆性途径有哪些？17 影响氧化锆相变的因素有哪些？18 氧化锆颗粒粒度大小及分布对增韧材料有哪些影响？19. 比较测定静抗折强度的三点弯曲法和四点弯曲法，哪一种方法更可靠，为什么？20. 有下列一组抗折强度测定结果，计算它的weibull模数，并对该测定数据的精度做出评价。

材料介电性能
材料的介电性能是指材料在电场作用下的响应能力，是材料的一项重要物理性质。

介电性能的好坏直接影响着材料在电子器件、电力设备等领域的应用。

因此，研究和了解材料的介电性能对于材料科学和工程技术具有重要意义。

首先，介电常数是衡量材料介电性能的重要参数之一。

介电常数是指材料在外电场作用下的极化能力，它反映了材料对电场的响应程度。

介电常数越大，表示材料对外电场的响应能力越强，极化程度越高。

介电常数的大小直接影响着材料的绝缘性能和电容性能。

因此，提高材料的介电常数是提高材料介电性能的重要途径之一。

其次，介电损耗是另一个重要的介电性能指标。

介电损耗是指材料在电场作用下吸收和释放能量的能力。

介电损耗越小，表示材料对外电场的能量损耗越小，电能的传输和存储效率越高。

因此，降低材料的介电损耗是提高材料介电性能的关键之一。

此外，介电强度也是衡量材料介电性能的重要参数之一。

介电强度是指材料在外电场作用下的耐受能力，它反映了材料在电场作用下的抗击穿能力。

介电强度越大，表示材料在外电场作用下的耐受能力越强，抗击穿能力越高。

因此，提高材料的介电强度是提高材料介电性能的重要途径之一。

总之，材料的介电性能是材料科学和工程技术领域中的一个重要研究方向。

通过研究和了解材料的介电性能，可以为材料的设计、制备和应用提供重要的理论指导和技术支持。

希望通过不断的研究和探索，能够进一步提高材料的介电性能，推动材料科学和工程技术的发展。

材料物理习题集第一章 固体中电子能量结构和状态（量子力学基础）1. 一电子通过5400V 电位差的电场，（1）计算它的德布罗意波长；（2）计算它的波数；（3）计算它对Ni 晶体（111）面（面间距d =2.04×10-10m ）的布拉格衍射角。

（P5）12341311921111o '(2)6.610 =(29.1105400 1.610)=1.67102K 3.7610sin sin 2182hh pmE md dλπλθλλθθ----=⨯⨯⨯⨯⨯⨯⨯=⨯==⇒=解：（1）=（2）波数=（3）22. 有两种原子，基态电子壳层是这样填充的;;s s s s s s s 2262322626102610（1）1、22p 、33p （2）1、22p 、33p 3d 、44p 4d ，请分别写出n=3的所有电子的四个量子数的可能组态。

（非书上内容）3. 如电子占据某一能级的几率是1/4，另一能级被占据的几率为3/4，分别计算两个能级的能量比费米能级高出多少k T ？（P15）1()exp[]11ln[1]()()1/4ln 3()3/4ln 3FF F F f E E E kT E E kT f E f E E E kT f E E E kT=-+⇒-=-=-=⋅=-=-⋅解：由将代入得将代入得4. 已知Cu 的密度为8.5×103kg/m 3，计算其E 0F 。

（P16） 2203234262333118(3/8)2(6.6310)8.510 =(3 6.0210/8)291063.5=1.0910 6.83Fh E n m J eVππ---=⨯⨯⨯⨯⨯⨯⨯⨯=解：由5. 计算Na 在0K 时自由电子的平均动能。

（Na 的摩尔质量M=22.99，.0ρ⨯33=11310kg/m ）（P16）22323426233311900(3/8)2(6.6310) 1.01310 =(3 6.0210/8)291022.99=5.2110 3.253 1.085F F h E n mJ eVE E eVππ---=⨯⨯⨯⨯⨯⨯⨯⨯===解：由由 6. 若自由电子矢量K 满足以为晶格周期性边界条件x x L ψψ+()=()和定态薛定谔方程。

材料物理习题集第一章 固体中电子能量结构和状态（量子力学基础）1. 一电子通过5400V 电位差的电场，（1）计算它的德布罗意波长；（2）计算它的波数；（3）计算它对Ni 晶体（111）面（面间距d =2.04×10-10m ）的布拉格衍射角。

（P5）12341311921111o '(2)6.610 =(29.1105400 1.610)=1.67102K 3.7610sin sin 2182hh pmE m d dλπλθλλθθ----=⨯⨯⨯⨯⨯⨯⨯=⨯==⇒=解：（1）=（2）波数=（3）22. 有两种原子，基态电子壳层是这样填充的;;s s s s s s s 2262322626102610（1）1、22p 、33p （2）1、22p 、33p 3d 、44p 4d ，请分别写出n=3的所有电子的四个量子数的可能组态。

（非书上内容）3. 如电子占据某一能级的几率是1/4，另一能级被占据的几率为3/4，分别计算两个能级的能量比费米能级高出多少k T ？（P15）1()exp[]11ln[1]()()1/4ln 3()3/4ln 3FF F F f E E E kT E E kT f E f E E E kT f E E E kT=-+⇒-=-=-=⋅=-=-⋅解：由将代入得将代入得4. 已知Cu 的密度为8.5×103kg/m 3，计算其E 0F 。

（P16）2203234262333118(3/8)2(6.6310)8.510 =(3 6.0210/8)291063.5=1.0910 6.83Fh E n m J eVππ---=⨯⨯⨯⨯⨯⨯⨯⨯=解：由5. 计算Na 在0K 时自由电子的平均动能。

（Na 的摩尔质量M=22.99，.0ρ⨯33=11310kg/m ）（P16）220323426233311900(3/8)2(6.6310) 1.01310 =(3 6.0210/8)291022.99=5.2110 3.253 1.085FF h E n mJ eVE E eVππ---=⨯⨯⨯⨯⨯⨯⨯⨯===解：由由 6. 若自由电子矢量K 满足以为晶格周期性边界条件x x L ψψ+()=()和定态薛定谔方程。

材料物理习题集第一章 固体中电子能量结构和状态（量子力学基础）1. 一电子通过5400V 电位差的电场，（1）计算它的xxxx 波长；（2）计算它的波数；（3）计算它对Ni 晶体（111）面（面间距d=2.04×10-10m ）的布拉格衍射角。

（P5）12341311921111o '(2)6.610 =(29.1105400 1.610) =1.67102K 3.7610sin sin 2182h h p mE m d d λπλθλλθθ----=⨯⨯⨯⨯⨯⨯⨯=⨯==⇒=解：（1）=（2）波数=（3）2 2. 有两种原子，基态电子壳层是这样填充的，请分别写出n=3的所有电子的四个量子数的可能组态。

（非书上内容）3. 如电子占据某一能级的几率是1/4，另一能级被占据的几率为3/4，分别计算两个能级的能量比费米能级高出多少kT ？（P15）4. 已知Cu 的密度为8.5×103kg/m3，计算其（P16）5. 计算Na 在0K 时自由电子的平均动能。

（Na 的摩尔质量M=22.99，）（P16）6. 若自由电子矢量K 满足以为晶格周期性边界条件和定态xx 方程。

试证明下式成立：eiKL=17.d h r K K cos r /2θϕ=*hkl *hkl 已知晶面间距为，晶面指数为（ k l ）的平行晶面的倒易矢量为，一电子波与该晶面系成角入射，试证明产生布拉格反射的临界波矢量的轨迹满足方程。

8. 试用布拉格反射定律说明晶体电子能谱中禁带产生的原因。

（P20）9. 试用晶体能带理论说明元素的导体、半导体、绝缘体的导电性质。

答： （画出典型的能带结构图，然后分别说明）10. 过渡族金属物理性质的特殊性与电子能带结构有何联系？（P28）答：过渡族金属的d 带不满，且能级低而密，可xx 较多的电子，夺取较高的s 带中的电子，降低费米能级。

补充习题1. 为什么镜子颠倒了左右而没有颠倒上下？2.只考虑xx 力学，试计算在不损害人体安全的情况下，加速到光速需要多少时间？ 3. 已知下列条件，试计算空间两个电子的电斥力和万有引力的比值4. 画出原子间引力、斥力、能量随原子间距变化的关系图。

材料物理习题集第一章固体中电子能量结构和状态（量子力学基础）1.一电子通过5400V 电位差的电场，（1）计算它的德布罗意波长；（2）计算它的波数；（3） 计算它对Ni 晶体（111 ）面（面间距d =x 10-10m 的布拉格衍射角。

（P5）解：(1) =h —咕P(2mE)2= 6.6 10 34= 1 (2 9.1 10 31 5400 1.6 10 19尸 =1.67 10 11m (2)波数 K = — 3.76 1011 (3) 2d sin sin2o 18'2d2. 有两种原子，基态电子壳层是这样填充的子数的可能组态。

（非书上内容）3.如电子占据某一能级的几率是 1/4 ,另一能级被占据的几率为3/4，分别计算两个能级的能量比费米能级高出多少k T ?（ P15）解：由f （E ）将f (E) 1/4代入得 E E F ln3 kT 将f (E) 3/ 4代入得 E E Fln3 kT4. 已知Cu 的密度为x 103kg/m 3,计算其E ；。

（P16）(1) 1s 2、2s 22p 6、3s 23p 3;(2) 1s 2、2s 22p 6、3s 23p 63d 10、4 24 64d 10，请分别写出 4s 4p 4d ;n=3的所有电子的四个量E E FkT ln[1f(E)解:h 22由E F —(3n/8 )32m(6.63 10 34)" 8.5 106 = 3i (3 - 2 9 10 63.5 =1.09 10 18J 6.83eV试证明下式成立：e iKL =1解：由于满足薛定谔定态方程Kx(x) Ae又Q 满足周期性边界条件(x L) Ae iK(x L) Ae iKx c p iKL (x) Ae iKxe iKL 17.已知晶面间距为d ,晶面指数为(h k l )的平行晶面 的倒易矢量为爲，一电子波与该晶面系成角入射，试证明产生布拉格反射的临界波矢量K 的轨迹满足方程K cos r hki /2。

练习题第一章材料物理基本知识简介1.一电子通过5 400 V电位差的电场。

-11m)；(1)计算它的德布罗意波波长(1.67×10(2)计算它的波数；?10m)的布拉格衍射角(2°18面(111)(面间距′)。

(3)计算它对Ni晶体102.04?d?226232262310、2s3p2s2p2p3d、3s3p、；(2)1s3s、2.有两种原子，基态电子壳层是这样填充的(1)1s、2610。

请分别写出的所有电子的四个量子数的可能组态。

4d4s 4p3n?3.如电子占据某一能级的几率为1/4，另一能级被占据的几率为3/4。

(1)分别计算两个能级的能量比费密能高出多少kT?(2)应用你计算的结果说明费密分布函数的特点。

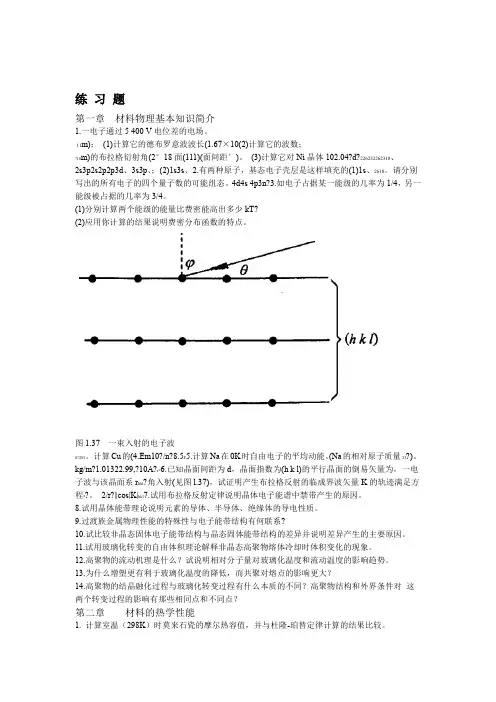
图1.37 一束入射的电子波0?283。

计算Cu的(4.Em10?/n?8.5F5.计算Na在0K时自由电子的平均动能。

(Na的相对原子质量33?)。

kg/m?1.01322.99,?10A?r*6.已知晶面间距为d，晶面指数为(h k l)的平行晶面的倒易矢量为，一电子波与该晶面系r hkl?角入射(见图l.37)，试证明产生布拉格反射的临成界波矢量K的轨迹满足方程*?。

2/r?||cos|K|hkl7.试用布拉格反射定律说明晶体电子能谱中禁带产生的原因。

8.试用晶体能带理论说明元素的导体、半导体、绝缘体的导电性质。

9.过渡族金属物理性能的特殊性与电子能带结构有何联系?10.试比较非晶态固体电子能带结构与晶态固体能带结构的差异并说明差异产生的主要原因。

11.试用玻璃化转变的自由体积理论解释非晶态高聚物熔体冷却时体积变化的现象。

12.高聚物的流动机理是什么？试说明相对分子量对玻璃化温度和流动温度的影响趋势。

13.为什么增塑更有利于玻璃化温度的降低，而共聚对熔点的影响更大？14.高聚物的结晶融化过程与玻璃化转变过程有什么本质的不同？高聚物结构和外界条件对这两个转变过程的影响有那些相同点和不同点？第二章材料的热学性能1. 计算室温（298K）时莫来石瓷的摩尔热容值，并与杜隆-珀替定律计算的结果比较。

《材料物理性能》第一章材料的力学性能1-1一圆杆的直径为2.5 mm 、长度为25cm 并受到4500N 的轴向拉力，若直径拉细至2.4mm ，且拉伸变形后圆杆的体积不变,求在此拉力下的真应力、真应变、名义应力和名义应变，并比较讨论这些计算结果。

解：由计算结果可知：真应力大于名义应力，真应变小于名义应变。

1-5一陶瓷含体积百分比为95%的Al 2O 3 (E = 380 GPa)和5%的玻璃相(E = 84 GPa)，试计算其上限和下限弹性模量。

若该陶瓷含有5 %的气孔，再估算其上限和下限弹性模量。

解：令E 1=380GPa,E 2=84GPa,V 1=0.95,V 2=0.05。

则有当该陶瓷含有5%的气孔时，将P=0.05代入经验计算公式E=E 0(1-1.9P+0.9P 2)可得，其上、下限弹性模量分别变为331.3 GPa 和293.1 GPa 。

1-6试分别画出应力松弛和应变蠕变与时间的关系示意图，并算出t = 0,t = ∞ 和t = τ时的纵坐标表达式。

解：Maxwell 模型可以较好地模拟应力松弛过程：V oigt 模型可以较好地模拟应变蠕变过程：).1()()(0)0()1)(()1()(100//0----==∞=-∞=-=e E E e e E t t t στεσεεεσεττ；；则有：其蠕变曲线方程为：./)0()(;0)();0()0((0)e (t)-t/e στσσσσσστ==∞==则有：：其应力松弛曲线方程为以上两种模型所描述的是最简单的情况，事实上由于材料力学性能的复杂性，我们会用到用多个弹簧和多个黏壶通过串并联组合而成的复杂模型。

如采用四元件模型来表示线性高聚物的蠕变过程等。

1-11一圆柱形Al 2O 3晶体受轴向拉力F ，若其临界抗剪强度τf 为135 MPa,求沿图中所示之方向的滑移系统产生滑移时需要的最小拉力值，并求滑移面的法向应力。

解：第二章 脆性断裂和强度2-1 求融熔石英的结合强度，设估计的表面能力为1.75J/m 2; Si-O 的平衡原子间距为1.6*10-8cm;弹性模量从60到75Gpaa E th γσ==GPa 64.28~62.2510*6.175.1*10*)75~60(109=- 2-2 融熔石英玻璃的性能参数为：E=73 Gpa ；γ=1.56 J/m 2；理论强度σth=28 Gpa 。

第六章高聚物的电学性能¾交变电场¾弱电场¾强电场¾发生在聚合表面¾光导电¾压电¾热电（焦电）¾热释电¾驻极体等在外电场F 作用下，诱导偶极矩µ1为由取向极化引起的偶极矩µ2在外电场作用下所产生的偶极矩µ为αe ——电子极化率αa ——原子极化率αo ——取向极化率µ0——永久（固有）偶极矩E ——材料内部的场强，又称为局域场强E ≠F高聚物的有效偶极矩（单体单元偶极矩）与所带基团的偶极矩不完全一致，结构对称性会导致偶极矩部分或全部相互抵消介电系数：表征材料介电性能的主要参数（ε）含有该材料的电容器之电容C 与其在真空下的电容C 0之比值物理意义是电介质电容器储电能力的大小，在微观上则是电介质的极化能力式中，ε0为直流电场中的静电介电常数；M为高聚物的相对分子质量；ρ为密度；P为摩尔极化度；为阿伏加德罗常数。

克劳修斯-莫索提（Clausius-Mossotti）公式宏观的介电系数（ε）和微观的分子极化率（α）均反映了电介质材料的极化能力对于极性高聚物德拜（Debye）方程N~在高频电场下（>1014Hz），即极化时间为10-14s时，取向极化和原子极化都不容易发生，记这时的介电系数为ε（光频介电系数）∞对于非极性介质，介电系数ε与介质的光折射率n的平方相等介电损耗一个理想电容器的外电场作用下能储存电能，当外电场移去时，所储存的电能又全部释放出来，形成电源，没有能量损耗对于交变电压V=V 0e iwt ，理想电容器的电流I 理想和电压有90º相位差，ε1为介电系数，ε2为介电损耗因子，决定电介质内电能转变成热能的损耗程度对于高聚物电介质，在每一周期内所放出的能量就不等于所储存的能量，因为完成高聚物电介质偶极取向需要克服分子间相互作用而消耗一部分电能，这时，介电损耗介电损耗：电介质在交变电场中，由于消耗一部分电能使介质本身发热的现象产生介电损耗的原因：1. 电导损耗：电介质中含有能导电的载流子在外加电场的作用下，产生电导电流，消耗一部分电能转化为热能。

材料的介电性能
材料的介电性能是指材料在电场作用下的响应能力，包括介电常数、介电损耗、击穿强度等指标。

介电性能对于材料在电子、通信、能源等领域的应用具有重要意义。

本文将对材料的介电性能进行探讨，以期为相关领域的研究和应用提供参考。

首先，介电常数是衡量材料在电场中响应能力的重要参数。

介电常数越大，材
料在电场中的极化效应越明显，从而具有更好的电绝缘性能。

常见的高介电常数材料包括氧化铁、氧化铌、氧化锆等。

这些材料在电子器件和电容器中得到广泛应用，能够提高器件的性能和稳定性。

其次，介电损耗是材料在电场中能量损耗的指标。

介电损耗越小，材料在高频
电子器件中的性能就越好。

常见的低介电损耗材料包括氧化铝、氮化硅、聚四氟乙烯等。

这些材料被广泛应用于微波器件、通信设备等领域，能够提高设备的传输效率和稳定性。

最后，击穿强度是衡量材料在电场中耐受电压的能力。

击穿强度越大，材料在
高压电器设备中的安全性就越高。

常见的高击穿强度材料包括氧化铝陶瓷、硅橡胶、聚乙烯等。

这些材料在电力系统、电子设备中得到广泛应用，能够提高设备的可靠性和安全性。

综上所述，材料的介电性能对于电子、通信、能源等领域的应用具有重要意义。

通过对介电常数、介电损耗、击穿强度等指标的研究，能够为材料的设计和应用提供重要参考，推动相关领域的技术进步和产业发展。

希望本文的内容能够对相关领域的研究人员和工程师有所帮助，促进材料的创新和应用。

材料物理材料介电性能材料物理是研究物质的结构、性质和行为的学科领域。

材料的介电性能是指材料对电场的响应能力，包括介电常数、介电损耗、电容率等电学参数。

这些参数直接影响着材料在电子器件、能源存储和传输等领域的应用。

首先，介电常数是介电性能的重要参数之一、它描述了材料在电场作用下的极化能力。

介电常数大的材料意味着材料在电场作用下更容易极化，从而使得材料可以存储更多的电荷。

一些常见的高介电常数材料包括铁电体和铁电薄膜。

这些材料在电子器件中被广泛应用，例如电容器和存储器件。

其次，介电损耗是材料介电性能的另一个关键参数。

它描述了材料在电场作用下吸收能量的能力。

也就是说，当电场作用下，部分电能会被转化为热能而损耗掉。

介电损耗大的材料会导致电能的浪费，从而降低电子器件的效率。

因此，在设计和选择材料时，介电损耗的降低是一个重要的考虑因素。

最后，电容率是衡量材料存储能量的指标。

它与介电常数和材料的体积有关。

当介电常数和电容率高时，材料可以存储更多的电荷，从而提高电容器的性能。

这对于能源存储和传输领域尤为重要，例如电动车的电池和太阳能电池的电容器。

除了介电常数、介电损耗和电容率之外，还有其他一些介电性能的重要参数。

例如，介电强度是指材料可以承受的最大电场强度。

当电场强度超过介电强度时，材料会发生击穿现象。

因此，了解材料的介电强度可以帮助我们设计更可靠和安全的电子器件。

总之，材料的介电性能对于电子器件、能源存储和传输等领域的应用至关重要。

通过研究和了解材料的介电常数、介电损耗、电容率和介电强度等参数，我们可以优化材料的性能，提高电子器件的效率和可靠性。

对于未来的材料科学和工程领域的发展，介电性能的研究和探索仍然是一个重要的方向。

解:&) 4.909x10 《材料物理馅能》第一章材料的力学性能1.1 一圆杆的直径为2.5 mm、长度为25cm并受到4500N的轴向拉力，若直径拉细至2.4mm ,且拉伸变形后圆杆的体积不变，求在此拉力下的真应力、真应变、名义应力和名义应变，并比较讨论这些计算结果。

F 4500 、—= ---------------- =995( MPa)A 4.524x1()2真应变勺=In上=In色=In 7 = 0.0816 1° A 2.42名义应力a = — = —- =917 (MP。

) —o名义应变 ^ = - = —-1=0.0851/。

A山计算结果町知：真应力大于名义应力，真应变小于名义应变。

1- 5 —陶瓷含体积百分比为95%的A12O3(E = 380 GPa)和5%的玻璃相(E = 84 GPa),试计算其上限和下限弹性模量。

若该陶瓷含有5 %的气孔，再估算其上限和下限弹性模量。

解：令Ei=380GPa,E2=84GPa,Vi=0.95,V2=0.05。

则有上限弹性模量=E}V{ +E2V2 = 380 X 0.95 +84 X 0.05 =365.2(GF Q)下限弹性模量曲=(4 +生尸=(性 + 些广=323.1(。

「。

)E] E2 380 84当该陶瓷含有5%的气孔时，将P=0. 05代入经验计算公式E=E o(l-1.9P+O. 9P2)可得，其上、下限弹性模量分别变为331.3 GPa和293. 1 GPa。

1-11 一圆柱形MO]晶体受轴向拉力F,若其临界抗剪强度弓为135 MPa,求沿图中所示之方向的滑移系统产生滑移时需要的最小拉力值，并求滑移面的法向应力。

解：由题意得图示方向滑移系统的剪切强度可表示为:Feos 53。

T = -------- ；— x cos 600.00152〃r f xO.00152^- 2nFmin = ---------------- = 3.17 x 103 (N)m,n cos 53° X cos 60°此拉力下的法向应力为：(7 =317xI0_xcos60° = L12xl08(P€/) = 112(A/P6Z) 0.00152^/cos 60°0.0 应变蠕变曲线 =25.62 〜28.64GF“ 1-6试分别画出应力松弛利应变蠕变与时间的关系示意图,并算出t 二0, t=g 和L 二T 时的纵 坐标表达式。