最优化运输问题
- 格式:doc
- 大小:61.00 KB
- 文档页数:6


最优化问题[知识要点]结合实际,联系生活。
通过列举、计算、对比等手段,选择最佳方法。
有些问题,从部分思考,再全面解决问题,得到最佳对策。
[例题解析]例1 甲地有59吨货物要运到乙地。
大货车的载重量是7吨,小货车的载重量是4吨,大货车运一次耗油14升,小货车运一次耗油9升。
运完这批货物至少耗油多少升?解:14÷7=2(升/吨) 9÷4=2.25(升/吨)2<2.25 尽可能用大货车。
59÷7=8(辆)……3(吨)选8辆大货车和一辆小货车。
14×8+9=121(升)答:运完这批货物至少耗油121升. 。
例2 街道旁有ABCDE 五栋居民楼(见下图B 点为中点),现在要建立一个邮筒,为使五栋楼的居民到邮筒的距离之和最短,邮筒应建立在何处?解:(原则是少向多靠、两边向中间靠。
)所以可参考BC 两点。
B 点:AB +BC +(BC +CD)+(BC +CD +DE)C 点:(AB +BC)+BC +CD +(CD +DE)B 点-C 点=BC答:选C 点。
例3 服装厂的工人每天可以生产4件上衣或7条裤子。
一件上衣和一条裤子为一套。
现有66名工人生产,每天最多能生产多少套服装?66÷(1+74)=42(人) 4×42=168(套) 答:每天最多能生产168套服装.例4 桌子放了60根火柴,甲乙二人轮流取。
每人每次取1—3根,取到最后一根者获胜。
甲有必胜的策略吗?解:60÷(1+3)=15让乙先取。
乙取1个,甲取3个;乙取2个,甲取2两个;乙取3个,甲取1个。
这样可以确保甲胜。
例5在黑板上写下数2、3、4……2010,甲先擦去其中一个数,如此轮流下去,若最后剩下两个数互质时,甲胜;若剩下两个数不互质,乙胜;那么甲有必胜的策略吗?解:把相邻两数分成一组,如:2,(3、4),(5、6),(7、8),(9、10)……2008),(2009、2010)甲先取走2,以后和乙拿同一括号的数即可确保胜利。

突发公共事件下应急物流中的优化运输问题的研究一、本文概述随着社会的快速发展和全球化的深入推进,突发公共事件,如自然灾害、疫情爆发、事故灾难等,对人类社会的影响日益显著。
这些事件往往导致物资短缺、交通受阻、信息传递不畅等问题,对应急物流系统提出了巨大的挑战。
因此,如何在突发公共事件下优化运输问题,提高应急物流的效率,成为了当前研究的热点和难点。
本文旨在探讨突发公共事件下应急物流中的优化运输问题。
我们将对突发公共事件和应急物流的概念进行界定,明确研究范围和对象。
我们将分析突发公共事件对运输系统的影响,包括物资需求的变化、运输网络的破坏、运输能力的下降等。
在此基础上,我们将探讨应急物流中优化运输问题的关键要素,如运输路径的选择、运输资源的调配、运输成本的控制等。
接下来,我们将通过文献综述和案例分析的方法,深入探究突发公共事件下应急物流优化运输问题的研究现状和发展趋势。
我们将总结前人的研究成果和经验教训,分析现有研究的不足和局限性,为后续的研究提供借鉴和参考。
我们将提出一种基于多目标优化的应急物流运输模型,并通过仿真实验验证其有效性和可行性。
该模型将综合考虑运输时间、运输成本、运输风险等多个因素,以实现应急物流运输的最优化。
我们期望通过本研究,能够为突发公共事件下的应急物流运输问题提供新的解决思路和方法,为未来的应急物流管理和实践提供有益的参考和指导。
二、文献综述在应对突发公共事件的过程中,应急物流的优化运输问题一直备受关注。
众多学者针对这一领域进行了深入的研究和探讨。
本节将对前人的研究成果进行系统的文献综述,旨在明确研究现状、挖掘研究不足,为本研究的深入展开提供理论基础和研究方向。
在应急物流的研究方面,学者们主要关注了应急物流体系的构建、应急预案的制定与实施、应急资源的调度与分配等方面。
其中,优化运输问题是应急物流研究中的核心内容之一。
运输路径的选择、运输资源的调配、运输过程的优化等问题都受到了广泛关注。

货物配送的最优化设计的数学模型一、问题的提出。
一公司有二厂,分处a,b两市,另外还有4间具有存贮机构的库房,分别在p,q,r 和s市,公司出售产品给6家客户c1,c2,c3,…,c6,由各库房或直接由工厂向客户供货,配送货物的费用由公司负担单价见下表:受货者供货者a市厂b市厂p库房q r sp库房0.5-q库房0.50.3r库房1.00.5s库房0.20.2客户c11.02.0-1.0--c2--1.50.51.5-c31.5-0.50.52.00.2c42.0-1.51.0-1.5c5---0.50.50.5c61.0-1.0-1.51.5注单位:元/吨:划“-”表示无供货关系.某些客户表示喜欢由某厂或某库房供货,计有:c1—a市厂c2—p库房c5—q库房c6—r库房或s库房a市厂月供货量不能超过150千吨,b市厂月供货量不能超过200千吨.各库房的月最大流通量千吨数为:库房p q r s流通量705010040各客户每月所必须满足的供货量为(单位:千吨)客户c1c2c3c4c5c6要求货量501040356020公司希望确定以下事项:1)如何配货,总费用最低?2)增加工厂和库房的生产能力对配送费用的影响是什么?3)费用单价,工厂和库房生产能力以及客户对供货量的最低要求等,各微小变化对配货方案的影响是什么?4)能不能满足各客户对供货者的喜好选择?如果满足,会引起配送费用提高多少?二、摘要。
在公司给客户配送货物的过程中,有两种情况,一种是由工厂直接向客户提供货物,另一种是由库房向客户提供货物,再结合运输的费用问题我们建立了这个货物配送的最优化设计的数学模型.在这个模型中,我们考虑到了以下几点:1.为了保证模型的一般性,我们不考虑不能配送的问题,对所有可能的运输都设了未知量来建立模型,然后根据模型的条件在处理单价时将不可能运货路线的运输价格设为”无穷大”,在实际处理中给予比一般数据高数量级的数据来进行运算.2.我们将模型中的对象分为三层,第一层为供货者,第三层为受货者,第二层既可以为供货者也可以为受货者,为了使模型更直观,我们在第二层里引入a,b两个工厂加入库房的行列,然后将a,b向a,b运货设为不可能运货路线.3.在模型解答中,因为计算量庞大,为了节约时间,我们调用了matlab里的最优化方法的函数来进行运算.4.另外,在模型的解答过程中,由于运输的单价的相同,我们还发现在满足配送费用最低的情况下配送方案并不唯一,其主要不确定因素我们在模型中给予了讨论。

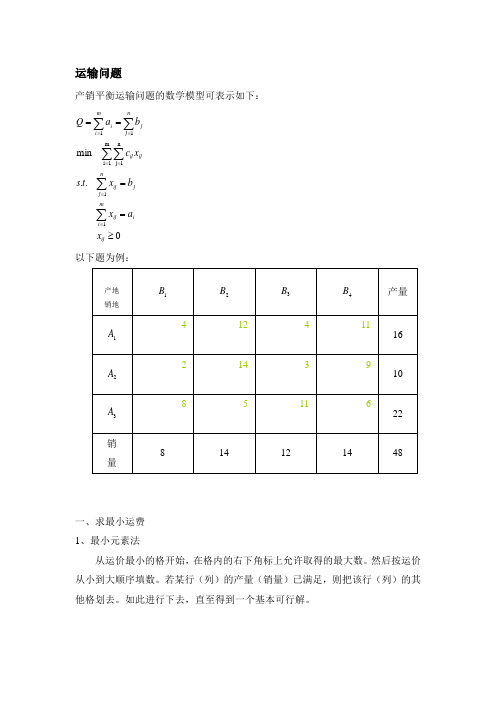
运输问题产销平衡运输问题的数学模型可表示如下:.. min 11m 1i n1j 11≥====∑∑∑∑∑∑======ij i mi ij j nj ij ijij nj jm i i x a x b x t s x c b a Q以下题为例:产地 销地1B 2B 3B 4B产量1A4124 11162A21439103A 8511 622销 量814121448一、求最小运费 1、最小元素法从运价最小的格开始,在格内的右下角标上允许取得的最大数。
然后按运价从小到大顺序填数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
产地 销地1B 2B 3B 4B产量1A4 124 10 116162A2 8143 29103A 85 1411 6822销 量814121448最小运费为:246116685144102382=⨯+⨯+⨯+⨯+⨯+⨯ 2、西北角法从西北角(左上角)格开始,在格内的右下角标上允许取得的最大数。
然后按行(列)标下一格的数。
若某行(列)的产量(销量)已满足,则把该行(列)的其他格划去。
如此进行下去,直至得到一个基本可行解。
产地 销地1B 2B 3B 4B 产量1A4 8 12 84 11162A214 6 3 49103A 8511 861122 销814121448量最小运费为:372=6×14+11×8+3×4+10×6+12×8+4×8 3、V ogel (沃格尔)法① 计算出各行各列中最小元素和次小元素差额(罚数),并标出。
② 在罚数最大的行和列中填上尽可能大的数(若有两个罚数最大,则选择最大罚数所在行或所在列运费最小的)。
若有行或列饱和,划去。
③ 重复以上步骤。
产地 销地1B2B3B 4B产量行罚数1 2 3 41A412412 11416 0 0 0 72A28143910 1 1 1 63A 8514116822 1 2销 量 8 14 12 14 48列 罚 数 1 2 5 1 3 2 2 1 3 3 2 1 2 412二、检验是否是最优解 1、闭回路法闭回路:从空格出发,遇到数字格可以旋转90度,最后回到空格所构成的回路;原理:利用检验数的经济含义;检验数:非基变量增加一个单位引起的成本变化量。
运用线性规划对运输问题进行研究运输问题在企业管理方面的应用一、本文概述随着全球化的推进和市场竞争的日益激烈,运输问题在企业管理中扮演着越来越重要的角色。
如何有效地进行物资运输、降低成本、提高效率,成为了企业运营中必须面对和解决的问题。
线性规划作为一种数学优化技术,为运输问题的研究和解决提供了有力的工具。
本文旨在探讨线性规划在运输问题中的应用,以及它在企业管理中的实际作用。
本文将首先介绍线性规划的基本概念、原理及其在运输问题中的应用原理。
接着,通过具体案例,分析线性规划在运输问题中的实际应用,包括如何建立运输问题的数学模型、如何运用线性规划求解最优运输方案等。
本文还将探讨线性规划在企业管理中的其他应用,如资源分配、生产计划等。
本文将总结线性规划在运输问题和企业管理中的应用效果,并展望未来的发展趋势。
通过本文的研究,我们期望能够帮助企业更好地理解和应用线性规划,优化运输方案,提高运营效率,从而在激烈的市场竞争中获得优势。
也希望本文能为相关领域的研究人员提供参考,推动线性规划在运输问题和企业管理领域的研究和发展。
二、线性规划理论基础线性规划是一种数学方法,用于解决具有线性约束和线性目标函数的优化问题。
它广泛应用于各种领域,包括运输问题。
在企业管理中,线性规划尤其适用于资源分配、生产调度和物流优化等问题。
线性规划问题的基本形式可以描述为:在给定的线性约束条件下,最大化或最小化一个线性目标函数。
这些约束条件和目标函数都是由决策变量的线性组合构成的。
决策变量是在问题中需要优化的变量,例如运输量、生产量等。
在运输问题中,线性规划可以用于优化运输成本、运输时间和运输路线等。
例如,假设一个企业需要将其产品从多个工厂运输到多个销售点,每个工厂和销售点之间的运输成本可能不同。
通过线性规划,企业可以找出一种运输方案,使得总运输成本最低,同时满足各种约束条件,如每个工厂的生产能力、每个销售点的需求量等。
线性规划的理论基础包括线性代数、凸分析和优化理论等。
垃圾运输问题路线最优城市垃圾收运是由产生垃圾的源头运送至处理处置场的全过程操作,包括3 个阶段:①收集———垃圾从产生源到公共贮存容器的过程;②清运———指清运车沿一定路线清除贮存容器内垃圾并将其转运到垃圾转运站的过程(在一定情况下,清运车可直接将垃圾运送至处理处置场);③中转———指在转运站将垃圾装载至大容量转运车,远途运输至处理处置场。
前1 个阶段需要对垃圾产生源分布情况、垃圾产生量及成分等进行调查和预测;后2 个阶段需要运用最优化技术对清运线路和转运站垃圾分配运输进行优化。
1 城市生活垃圾产生量预测方法城市生活垃圾收运模式的设计是在对生活垃圾产生量作正确预测的条件下进行的,因为设计的收运模式,不仅应满足当前垃圾产生量的需求,而且应该能够应对未来几年的变化。
目前,国内外较为普遍使用的数理统计方法为单指数平滑法、线性回归分析法、灰色系统模型分析法。
1. 1 单指数平滑法Yt+1=aXt+(1-a)Yt。
(1)式中:t 为时间;a 为指数平滑系数,介于0~1;Xt 为t 时垃圾产生量的实际观测值;Yt 为t 时垃圾产生量的预测值;Yt+1 为t+1 时垃圾产生量的预测值。
1. 2 线形回归分析法Y=a0+a1x1+a2x2+…+amxm。
(2)式中:Y 为垃圾预测产生量;xi 为影响垃圾产生的多个因素(i=1,2,…,m);ai 为回归系数(i=1,2,…,m)。
影响垃圾产生的因素有很多,如人口数量、工资收入、消费水平、生活习惯、燃料结构等。
对于众多因素,可以采用变量聚类法,对数据进行预处理。
据介绍,经过数据处理后多元回归分析法中很多变量都属“同解”,经过变量与处理后,实际运算时,相当于一元回归的“人口模式”预测法〔1〕。
1. 3 灰色系统模型分析法灰色系统模型(GM)包含模型的变量维数m和阶数n,记作GM (n,m)。
在生活垃圾产生量预测中普遍使用GM(1,1)模型。
通过对原始的时间序列数据进行累加处理后,数据便会出现明显的指数规律,通过进一步分析,可以进行垃圾产生量预测。
货物配送中的路线规划和优化时间就像一把无形的雕刻刀,在任何时刻都在雕刻着人们的生命。
而今天,我们所处的这个时代无疑是一个高速发展的时代,信息技术正在深刻地改变着企业的经营模式。
特别是在电子商务和物流领域,信息技术的应用带来了质的飞跃,使货物配送的效率和成本得到了极大地优化。
本文将探讨货物配送中的路线规划和优化的相关问题。
一、货物配送中路线规划的重要性货物配送中的路线规划和优化是现代物流管理的重要组成部分。
在日常的配送工作中,我们往往要面对复杂的地理环境和各种交通状况,如巨大的交通流量、道路状况的不同、峰值期的拥堵等等,这使得货物配送的路线规划变得复杂而困难。
然而,货物配送中的路线规划和优化对于提高配送效率是极为重要的。
首先,科学的路线规划可以缩短配送路径,从而减少运输时间和物流成本,提高运输速度和货物的安全性。
同时,路线规划也可以避免配送误差,提升配送服务质量,提高客户满意度。
因此说,货物配送中的路线规划是极其重要的。
二、货物配送中路线规划的方法货物配送中路线规划的方法主要有两种:手工规划和智能规划。
手工规划是传统的规划方法,在手工规划中,配送员会根据业务量和经验,结合己有的配送能力进行路线规划。
虽然这种方法较为简单,但需要配送员花费大量的时间和精力去制定每个细节,难以完全控制配送风险,并且难以满足高效、快捷升级的配送需求。
智能规划是一种新型的路线规划方法,其核心是将计算机技术和物流业务相结合,围绕客户需求设置参数,并依据客户的特殊配送要求进行计算。
该方法不依赖对配送员的影响,不受路线障碍和路口严重影响,而是通过智能算法实现自动规划和调度,提升货物配送的速度和准确度。
三、货物配送中路线优化的方法货物配送中路线规划完成后,如何进行路线优化呢?这就要提出路线优化的方法。
路线优化是指在货物配送中对路线进行最优化调整,以达到最低配送成本、最快速配送、最大的交通效益和最大的物流效益。
常见的路线优化方法包括:1.动态路线规划。
摘要:根据运输问题的基本特征,运用最优化的线性规划解决问题,通过实例对运输问题进行优化分析,建立运输问题的线性规划数学模型。
将模型应用于一些特殊的运输问题,从而得到最优化的方案,提高实际运输工作中的经济效益。
关键词:最优化;运输问题;线性规划
1 运输问题的特征
运输问题关心的是以最低的总配送成本把供应中心的任何产品运送到每一个接收中心。
每一个出发地都有一定供应量配送到目的地,每一个目的地都需要一定的需求量。
需求假设:从任何一个出发地到任何一个目的地的货物配送成本和所配送的数量成线性比例关系。
运输问题所需要的数据仅仅是供应量、需求量和单位成本。
这些就是模型参数。
如果一个问题可以完全描述成表1所示的参数表形式,并且符合需求假设和成本假设,那么这个问题(不管其中是否涉及到运输)都适用于运输问题模型,最终目的都是要使配送的总成本最小。
这个模型的参数都包含在参数表中。
下面就通过例题来说明。
A公司是一家汽车生产商,A1、A2是它的工厂,生产的轿车用卡车把它们运送到三个分销仓库:A3、A4、A5。
在下表中列有下列数据:每辆轿车从每个工厂到每个分销仓库所需的运输成本(C ij),每个工厂的供应量,以及每个经销商对轿车的需求量。
求能使运输成本最低的从每个工厂到每个分销仓库运输轿车的数量以及最低的运输成本。
表 1 A公司的运输数据表
解:设X ij(i=1,2;j=1,2,3);为从每个工厂到每个经销商运输轿车的数量,目
标是为了找出能使总运输成本最低的从每个工厂到每个经销商运输轿车的数量。
所以,
目标函数为C=200X11+100X12+300X13+400X21+300X22+200X23
约束条件是:
X11+X12+X13=3000
X21+X22+X23=5000
X11+X21=3000
X12+X22=4000
X31+X32=1000
X ij(i=1,2,j=1,2,3)≥0
用微机很快就可以得出决策变量的下列最优值以及最低的运输成本200万元。
表2 A公司决策变量的最优值表
由上面的例题可以看出,对于一般的运输问题,首先是建立线性规划的模型,模型中包含的内容主要是目标函数和约束条件;然后再应用微机求解。
2 选址
许多公司的管理人员都面临着一个非常重要的决策:在什么地方设置一个新的重要设施。
设施有可能是一个新的工厂、一个新的配送中心、一个新的管理中心或者其他的建筑物。
一般来说,一个建筑物都有几个可供选择的地点。
而且,在经济全球化的今天,这些可供选择的潜在地点很有可能已经超越了国界而在另一个国家中。
在形成决策的过程之中包含了许多很重要的因素,其中一个就是运输成本。
A公司是一家大型石油公司。
公司拥有大型配送网络。
把石油运送到公司的
炼油厂,然后再把石油产品从炼油厂运送到公司的配送中心。
A公司正在持续增加其几种主要产品的市场占有率,因此管理层决定建立一个新的炼油厂来增加公司的产量,接下来要作的决策就是确定在什么地方建设新的炼油厂。
他们确定了三个非常有潜力和吸引力的备选地点。
表中是A公司的一些相关数据,其中A1、A2是已有的炼油厂,B1、B2、B3是被选地点,C1、C2、C3是油田,D1、D2、D3、D4是配送中心。
表3 A公司的相关数据
表4 原油和石油制品的运输成本数据
现在要确定的是每一个新炼油厂建造地点选择带来的总原油运输成本以及每一个新炼油厂建造地点选择带来的总石油制品运输成本。
对于这两种成本来说,一旦确立了建造地点,最优的运输计划也就确定了。
因此,为了找出潜在选择地点的每一种成本,有必要为每一种情况都作出一个最优运输计划,然后再计算出相
应的成本。
以选择在B1建造新的炼油厂为例。
(1)确定最低的总原油运输成本。
设X ij(i=1,2,3, j=1,2,3)为从油田向炼油厂运输原油的数量。
目标函数为:
C1=2X11+4X12+3X13+4X21+5X22+1X23+5X31+7X32+4X33
约束条件:
X11+X12+X13=80
X21+X22+X23=60
X31+X32+X33=100
X11+X21+X31=90
X12+X22+X32=70
X13+X23+X33=80
X ij(i=1,2, j=1,2,3) ≥0
通过微机可以得出决策变量的最优值为:
X11=10 X12=70 X13=0 X21=0 X22=0 X23=60 X31=80 X32=0 X33=20
最低的总原油运输成本为840万元。
(2)确定最低的总石油制品运输成本
设Y ij(i=1,2,3, j=1,2,3,4) 为从炼油厂运输到配送中心的石油制品数量。
目标函数为:
C=5Y11+2Y12+6Y13+8Y14+6Y21+4Y22+3Y23+5Y24+8Y31+6Y32+3Y33+2Y34
Y11+Y12+Y13+Y14=90
Y21+Y22+Y23+Y24=70
Y31+Y32+Y33+Y34=80
Y11+Y21+Y31=60
Y12+Y22+Y32=50
Y13+Y23+Y33=70
Y14+Y24+Y34=6
X ij(i=1,2, j=1,2,3)≥0
通过微机可以得出决策变量的最优值为:
Y11=40 Y12=50 Y13=0 Y14=0 Y21=20 Y22=0 Y23=50 Y24=0 Y31=0 Y32=0 Y33=20 Y34=60
最低的总石油制品的运输成本为750万元。
同理如果选择在B2建造新的炼油厂可以得出最低的总原油运输成本为900万元,最低的总石油运输成本为910万元,如果选择在B3建造新的炼油厂可以得出最低的总原油运输成本为1060万元,最低的总石油运输成本为770万元。
表5 A公司每一个被选厂址所带来的年变动成本
单位:百万
元
经过比较总变动成本,最终可以选择在B1建造新的炼油厂。
3 结束语
所有经理都会遇到有约束条件下的最优化问题,因此线性规划在许多管理问题中都能应用,只要是对生产、制造、投资、财务、工程等求最大利润、最小成本等问题,就基本上可以用线性规划来求解。
作为一个管理人员,应当能够把面临的问题描述为一个线性规划问题并进行分析。
【参考文献】
[1] 胡运权,郭耀煌运筹学教程[M].北京;清华大学出版社,1998
[2] H?克雷格?彼得森,W?克里斯?刘易斯,管理经济学[M].北京;中国人民大学
出版社,2005
[3] 张建中,许绍吉.线性规划[M].北京:科学技术出版社,1997。