菱形练习题(含答案)

初三数学菱形的练习题及答案菱形是初中数学中常见的图形之一，通过练习菱形的题目，学生可以巩固对菱形及其性质的认识，培养解决几何问题的能力。

本文将提供一些初三数学菱形的练习题及答案，帮助学生更好地理解和应用相关知识。

练习题一：根据给定条件，求菱形的周长和面积。

1.已知菱形的对角线长度分别为8cm和12cm，求菱形的周长和面积。

解答：求菱形的周长，需要知道菱形的所有边长。

根据菱形的性质，对角线相交于其垂直平分点，且对角线相等。

设菱形的一个对角线长度为d1=8cm，另一个对角线长度为d2=12cm。

根据性质可知，菱形的边长等于对角线长度的一半。

菱形的周长=4×菱形的边长=4×(d1/2)=4×(8/2)=4×4=16cm菱形的面积= (d1×d2)/2=(8×12)/2=96/2=48cm²所以，该菱形的周长为16cm，面积为48cm²。

练习题二：根据给定条件，判断是否为菱形。

2.在平面直角坐标系中，已知四个点的坐标依次为A(3, 0)、B(0, 2)、C(-3, 0)和D(0, -2)，判断四边形ABCD是否为菱形。

解答：要判断四边形ABCD是否为菱形，需要验证以下两个条件：- 对角线互相垂直；- 对角线相等。

首先计算对角线的长度：AC = √((x2 - x1)² + (y2 - y1)²)= √((-3 - 3)² + (0 - 0)²)= √((-6)²)= √36= 6BD = √((x2 - x1)² + (y2 - y1)²)= √((0 - 0)² + (-2 - 2)²)= √((0)² + (-4)²)= √(0 + 16)= √16= 4由上述计算可知，AC=6，BD=4。

接下来验证两个条件：- 对角线互相垂直：计算斜率k1、k2，若k1*k2=-1则两对角线互相垂直。

菱形练习题大全菱形练习题是一种常见的数学题型，通过练习菱形练习题，可以提高学生的观察能力、逻辑思维能力以及对几何形状的理解能力。

本文将为你介绍一些常见的菱形练习题，并提供详细解答，帮助你更好地掌握这一题型。

一、填空题1. 已知菱形的周长为20厘米，其中一条边长为4厘米，求其另一条边长。

解答：由于菱形的周长等于4倍的边长，所以另一条边长为(20-4)/4=4.5厘米。

2. 若一条菱形的对角线长为10厘米，求其面积。

解答：菱形的面积可以通过对角线求解，即面积=（对角线1×对角线2）/2。

设菱形的对角线分别为a和b，则(a×b)/2=（10×10）/2=50平方厘米。

3. 若一个菱形的一条边长为6厘米，另一条边长为8厘米，求其面积。

解答：菱形的面积可以通过两条边长的乘积来求解，即面积=边长1×边长2/2。

将给定的边长代入公式，得到面积=6×8/2=24平方厘米。

二、选择题1. 在一个菱形ABCD中，∠BAC的度数为多少？B. 90度C. 120度D. 180度解答：由于菱形的对角线相互平分，所以∠BAC=∠DAC=1/2×180度=90度。

选项B为正确答案。

2. 已知一个菱形的周长为24厘米，其一条边长为6厘米，那么该菱形的面积是多少？A. 12平方厘米B. 18平方厘米C. 24平方厘米D. 36平方厘米解答：已知周长为24厘米，而菱形的周长等于4倍的边长，所以该菱形的边长为6个厘米。

将边长代入菱形面积公式，得到面积=6×6/2=18平方厘米。

选项B为正确答案。

3. 在一个菱形ABCD中，角A的度数为60度，那么角B的度数是多少？A. 60度B. 90度D. 180度解答：由于菱形的对角线相互平分，所以∠BAC=∠DAC=1/2×180度=90度。

又∠BAC+∠ABC=180度，所以∠ABC=180度-90度=90度。

选项B为正确答案。

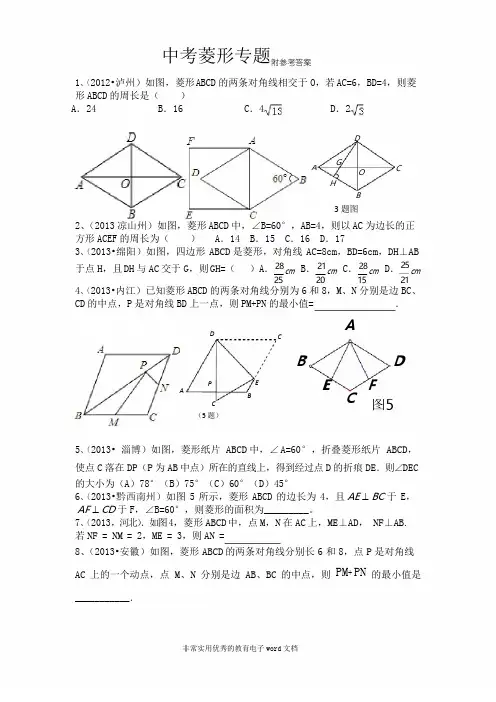
AC图5中考菱形专题 附参考答案1、（2012•泸州）如图，菱形 ABCD 的两条对角线相交于 O ，若 AC=6，BD=4，则菱 形 ABCD 的周长是（ ） A ．24 B ．16 C ．4 D ．2DGO HB3 题图2、（2013 凉山州）如图，菱形 ABCD 中，∠B=60°，AB=4，则以 AC 为边长的正 方形 ACEF 的周长为（ ） A ．14 B ．15 C ．16 D ．173、（2013•绵阳）如图，四边形 ABCD 是菱形，对角线 AC =8cm ，BD =6cm ，DH ⊥AB 于点 H ，且 DH 与 AC 交于 G ，则 GH =（）A ． 28 cm B ． 21 cm C ． 28 cm D ． 25 cm252015214、（2013•内江）已知菱形 ABCD 的两条对角线分别为 6 和 8，M 、N 分别是边 BC 、 CD 的中点，P 是对角线 BD 上一点，则 PM+PN 的最小值= ．DCAB DAPC （5 题）BE E FC5、（2013• 淄博）如图，菱形纸片 ABCD 中，∠ A =60 °，折叠菱形纸片 ABCD ，使点 C 落在 DP （P 为 AB 中点）所在的直线上，得到经过点 D 的折痕 DE ．则∠DEC的大小为（A ）78°（B ）75°（C ）60°（D ）45° 6、（2013•黔西南州）如图 5 所示，菱形 ABCD 的边长为 4，且 AE ⊥ BC 于 E ， AF ⊥ CD 于 F ，∠B=60°，则菱形的面积为_________。

7、（2013，河北）．如图 4，菱形 ABCD 中，点 M ，N 在 AC 上，ME ⊥AD ， NF ⊥AB . 若 NF = NM = 2，ME = 3，则 AN =8、（2013•安徽）如图，菱形 ABCD 的两条对角线分别长 6 和 8，点 P 是对角线AC 上的一个动点，点 M 、N 分别是边 AB 、BC 的中点，则 PM + PN 的最小值是___________．9、（2013•临沂）如图，菱形ABCD中，AB=4，∠B=60°，AE⊥BC，AF⊥CD，垂足分别为E，F，连接△E F，则AEF的面积是．DAPCMBN第8题图10、（2013•黄冈）如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO=∠DCO.10题图11、（2013•遂宁）如图，已知四边形A BCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是E、F，并且DE=DF．求证：（△1）ADE≌△CDF；（2）四边形ABCD是菱形．12、（2013•恩施州）如图所示，在梯形ABCD中，AD∥BC，AB=CD，E、F、G、H 分别为边AB、BC、CD、DA的中点，求证：四边形EFGH为菱形．13、（2013•常州）如图，在△ABC中，AB=AC，∠B=60°，∠FAC、∠ECA是△ABC 的两个外角，AD平分∠FAC，CD平分∠ECA．求证：四边形ABCD是菱形．14、（2013•南宁）如图，在菱形ABCD中，AC为对角线，点E、F分别是边BC、AD的中点．（△1）求证：ABE≌△CDF；（2）若∠B=60°，AB=4，求线段AE的长．15、（2013泰安）如图，在四边形ABCD中，AB=AD，CB=CD，E是CD上一点，BE交AC于F，连接DF．（1）证明：∠BAC=∠DAC，∠AFD=∠CFE．（2）若AB∥CD，试证明四边形ABCD是菱形；（3）在（2）的条件下，试确定E点的位置，∠EFD=∠BCD，并说明理由．16、（2013•乌鲁木齐）如图．在△ABC中，∠ACB=90°，CD⊥AB于D，AE平分∠BAC，分别于BC、CD交于E、F，EH⊥AB于H．连接FH，求证：四边形CFHE是菱形．17、（2013•临沂）如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．（1）求证：AF=DC；（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．18、（2013•龙岩）如图，四边形ABCD是菱形，对角线AC与BD交于点O，且AC=80，BD=60．动点M、N分别以每秒１个单位的速度从点A、D同时出发，分别沿A O D和D A运动，当点N到达点A时，M、N同时停止运动．设运动时间为t秒．（1）求菱形ABCD的周长；（2）记D D MN的面积为S,求S关于t的解析式，并求S的最大值；（3）当t=30秒时，在线段OD的垂直平分线上是否存在点P，使得∠DPO＝∠DON？若存在，这样的点P有几个？并求出点P到线段OD的距离；若不存在，请说明理由．（第18题图）cm B ． cm C ． cmD ． cmAC答案考点：菱形的性质；等边三角形的判定与性质；正方形的性质．分析：根据菱形得出 AB=BC ，得出等边三角形 ABC ，求出 AC ，长，根据正方形的性质得出 AF=EF=EC=AC=4，求出即可． 解答：解：∵四边形 ABCD 是菱形， ∴AB=BC ， ∵∠B=60°，∴△ABC 是等边三角形， ∴AC=AB=4，∴正方形 ACEF 的周长是 AC+CE+EF+AF=4×4=16， 故选 C ．（2013•绵阳）如图，四边形 ABCD 是菱形，对角线 AC =8cm ，BD =6cm ，DH ⊥AB 于点 H ，且DH 与 AC 交于 G ，则 GH =（）A ． 28 21 28 2525 20 15 21DGOH（2013•内江）已知菱形 ABCD 的两条对角线分别为 6 和 8，M 、N 分别是边 BC 、CD 的中点，BP 是对角线 BD 上一点，则 PM+PN 的最小值= 5 ．10 题图考点：轴对称-最短路线问题；菱形的性质．分析：作 M 关于 BD 的对称点 Q ，连接 NQ ，交 BD 于 P ，连接 MP ，此时 MP+NP 的值最小，连接 AC ，求出 OC 、OB ，根据勾股定理求出 BC 长，证出 MP+NP=QN=BC ，即可得出答案．解答：解：作 M 关于 BD 的对称点 Q ，连接 NQ ，交 BD 于 P ，连接 MP ，此时 MP+NP 的值最小，连 接 AC ，∵四边形 ABCD 是菱形， ∴AC ⊥BD ，∠QBP=∠MBP ， 即 Q 在 AB 上，∵MQ⊥BD，∴AC∥MQ，∵M为BC中点，∴Q为AB中点，∵N为CD中点，四边形ABCD是菱形，∴BQ∥CD，BQ=CN，∴四边形BQNC是平行四边形，∴NQ=BC，∵四边形ABCD是菱形，∴CO=AC=3，BO=BD=4，在△Rt BOC中，由勾股定理得：BC=5，即NQ=5，∴MP+NP=QP+NP=QN=5，故答案为：5．点评：本题考查了轴对称﹣最短路线问题，平行四边形的性质和判定，菱形的性质，勾股定理的应用，解此题的关键是能根据轴对称找出P的位置．（2013•遂宁）如图，已知四边形ABCD是平行四边形，DE⊥AB，DF⊥BC，垂足分别是E、F，并且DE=DF．求证：（1△）ADE≌△CDF；（2）四边形ABCD是菱形．（2013•恩施州）如图所示，在梯形ABCD中，AD∥BC，AB=CD，E、F、G、H分别为边AB、BC、CD、DA的中点，求证：四边形EFGH为菱形．（2013•黄冈）如图，四边形ABCD是菱形，对角线AC、BD相交于点O，DH⊥AB于H，连接OH，求证：∠DHO=∠DCO.N A Dt∴MP=t=3∵Sin∠ADO==∴MP=(70-t)17题图（2013龙岩）如图，四边形ABCD是菱形，对角线AC与BD交于点O，且AC=80，BD=60．动点M、分别以每秒１个单位的速度从点、同时出发，分别沿A O D 和D A运动，当点N到达点A时，M、N同时停止运动．设运动时间为秒．（1）求菱形ABCD的周长；（2）记D D MN的面积为S,求S关于t的解析式，并求S的最大值；（3）当t=30秒时，在线段OD的垂直平分线上是否存在点P，使得∠DPO＝∠DON？若存在，这样的点P有几个？并求出点P到线段OD的距离；若不存在，请说明理由．（第25题图）.(1)在菱形ABCD中，∵AC⊥BD∴AD=302+402=50.∴菱形ABCD的周长为200.·····························4分(2)过点M作MP⊥AD，垂足为点P.①当0＜t≤40∵Sin∠OAD=MP OD3==AM AD5351∴S=⨯DN•MP210t2························································································································6分②当40<t≤50时，∴MD=80-tMP AOMD AD452= - t 2 + 28t = - (t - 35)2 + 490 ··························································································8 分⎪⎪10 t ,0 < t ≤ 40则NF = ND • Sin ∠ODA = 30 ⨯ = = 24DF = ND • Cos ∠ODA = 30 ⨯ 30 = = 2 ····································································11 分 ∴FG = OF+ ON 12 + 12 5 1 + 5 tan ∠GOF == 1 +5 =∴ ∠DPK = ∠DPO = ∠DON = ∠FOG ··································································12 分∴PK = ···········································································································13 分∴存在两个点 P 到 OD 的距离都是 15( 5 + 1)∴ S ∆DMN = 1DN • MP2 25 5⎧ 3 2 ∴ S =⎨⎪- 2(t - 35)2 + 490,40 < t ≤ 50 ⎪⎩ 5当 0＜t ≤40 时，S 随 t 的增大而增大，当 t ＝40 时，最大值为 480.当 40＜t ≤50 时，S 随 t 的增大而减小，当 t ＝40 时，最大值为 480.综上所述，S 的最大值为 480. ····························································································· 9 分 （3）存在 2 个点 P ，使得∠DPO =∠DON .········································································ 10 分 方法一：过点 N 作 NF ⊥OD 于点 F ，40 12050 5，90= = 18.50 5∴OF =12，∴ tan ∠NOD =NF 24 OF 12作 ∠NOD 的平分线交 NF 于点 G ，过点 G 作 GH ⊥ON 于点 H . ∴ S ∆ONF 1= OF • NF = S2∆OGN + S ∆OFG 1 1 1 = OF • FG + ON • GH = (OF + ON ) • FG 2 2 2OF • NF 12 + 24 24= =24∴ GF 2 OF 12 1 + 5设 OD 中垂线与 OD 的交点为 K ，由对称性可知：1 12 2 ∴ DK 15 2tan ∠DPK == = PK PK 1 + 515( 5 + 1)2根据菱形的对称性可知，在线段 OD 的下方存在与点 P 关于 OD 轴对称的点 P ' .2.··························································14 分方法二：如图，作 ON 的垂直平分线，交 EF 于点 I ，连结 OI ，IN.过点 N 作 NG ⊥OD ，NH ⊥EF ,垂足分别为 G ，H. 当 t =30 时，DN =OD =30，易知△DNG ∽△DAO ，∴即DN NG DG= = ． DA AO OD 30 NG DG= = ． 50 40 30⎪⎪∴PE=PI+IE=15+155．····························································································13分∴存在两个点P，到OD的距离都是.∴NG=24,DG=18．·······································································································10分∵EF垂直平分OD，∴OE=ED＝15，EG=NH=3．······················································································11分设OI=R，EI=x,则在△Rt OEI中，有R2=152+x2①在△Rt NIH中，有R2=32+(24-x)2②⎧15x=2由①、②可得：⎨⎪R=155⎪⎩22根据对称性可得，在BD下方还存在一个点P'也满足条件．15(5+1)2（2013△?常州）如图，在ABC中，AB=AC，∠B=60°，∠FAC、∠ECA是△ABC的两个外角，AD平分∠FAC，CD平分∠ECA．求证：四边形ABCD是菱形．（2013•南京）如图，将菱形纸片ABCD折迭，使点A恰好落在菱形的对称中心O处，折痕为EF。

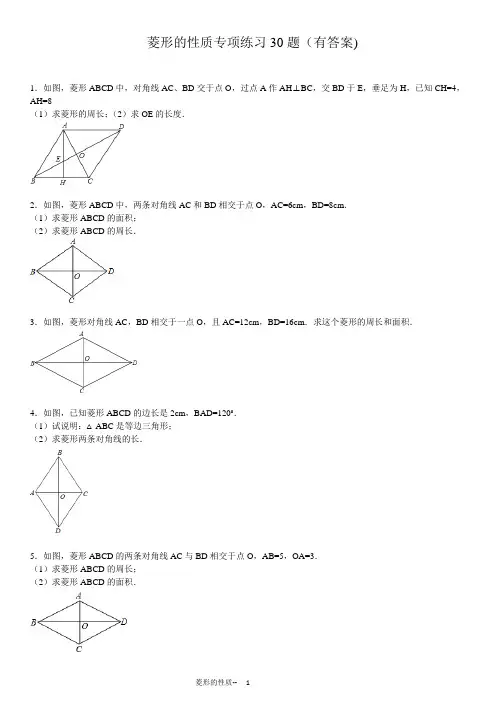
菱形的性质专项练习30题（有答案)1．如图，菱形ABCD中，对角线AC、BD交于点O，过点A作AH⊥BC，交BD于E，垂足为H，已知CH=4，AH=8（1）求菱形的周长；（2）求OE的长度．2．如图，菱形ABCD中，两条对角线AC和BD相交于点O，AC=6cm，BD=8cm．（1）求菱形ABCD的面积；（2）求菱形ABCD的周长．3．如图，菱形对角线AC，BD相交于一点O，且AC=12cm，BD=16cm．求这个菱形的周长和面积．4．如图，已知菱形ABCD的边长是2cm，BAD=120°．（1）试说明：△ABC是等边三角形；（2）求菱形两条对角线的长．5．如图，菱形ABCD的两条对角线AC与BD相交于点O，AB=5，OA=3．（1）求菱形ABCD的周长；（2）求菱形ABCD的面积．6．如图，菱形ABCD的周长为200cm，对角AC与BD交于点O，且AC=60cm，试求菱形ABCD的面积．7．已知：菱形ABCD的两条对角线AC与BD相交于点O，且AC=6，BD=8，求菱形的周长和面积．8．如图，菱形ABCD的对角线AC、BD相交于点O，DE∥AC，AE∥BD．试判断四边形AODE的形状，并说明理由．9．如图，O为菱形ABCD对角线的交点，DE∥AC，CE∥BD．（1）试判断四边形OCED的形状，并说明理由；（2）若AC=6，BD=8，求线段OE的长．10．如图，四边形ABCD是菱形，过AB的中点E作AC的垂线EF，交AD于点M，交CD的延长线于点F．（1）证明：AM=DM；（2）若DF=2，求菱形ABCD的周长；（3）在没有辅助线的前提下，图中共有_________对相似三角形．11．菱形ABCD中，∠B=60°，一块三角板的60°角的顶点绕点A转动，两边分别交BC、CD于点E、F．（1）说明△ABC、△ACD都是等边三角形．（2）判断△AEF的形状，说明理由？（3）如果AB=2，写出△CEF的周长的最小值．12．如图，O是菱形ABCD的对角线的交点，作DE∥AC，CE∥BD，DE，CE交于点E．（1）求证：四边形OCED是矩形；（2）若菱形ABCD的周长为20，矩形OCED的周长为14，求菱形ABCD的面积．13．如图，点E、F分别在菱形ABCD的边BC、AD上，且AF=CE，∠BAE=25°，∠BCD=130°，求∠AFC的度数．14．如图，平行四边形ABCD中，AE是BC边上的高，AE是BC沿BC方向平移，使点E与点C重合，得△GFC．（1）求证：BE=DG：（2）若四边形ABFG是菱形，且AB：BC=2：3，求∠B的度数．15．如图，菱形ABCD中，AE⊥BC，垂足为点E，BE=CE，求∠BAD的度数．16．如图，已知一四边形菜地ABCD为菱形，点E，F分别位于边AB，BC上，AD=6，AE=5BE，BF=5CF，若△DEF 为等边三角形．（1）求∠A的度数；（2）求菱形ABCD的面积．17．如图，已知菱形ABCD，∠B=60°，△ADC内一点M满足∠AMC=120°，若直线BA与CM交于点P，直线BC 与AM交于点Q，求证：P，D，Q三点共线．18．已知：如图，菱形ABCD的对角线交于点O，且AO、BO的长分别是方程x2﹣（2m﹣1）x+4（m﹣1）=0的两根，菱形ABCD的周长为20，求m的值．19．如图所示，在菱形ABCD中，点E，F分别在CD，BC上，且CE=CF，求证：AE=AF．20．已知：菱形ABCD中，对角线AC=16cm，BD=12cm，BE⊥DC于点E，求菱形ABCD的面积和BE的长．21．如图，菱形ABCD中，E是AD中点，EF⊥AC交CB的延长线于点F．（1）DE和BF相等吗？请说明理由．（2）连接AF、BE，四边形AFBE是平行四边形吗？说明理由．22．已知：如图，菱形ABCD中，E、F分别是CB、CD上的点，BE=DF．若AE垂直平分BC，AF垂直平分CD．求证：（1）AE=AF；（2）△AEF为等边三角形．23．如图，在菱形ABCD中，过点A作AE⊥BC，垂足E为BC的中点，连接DE，F为DE上一点，且∠AFE=∠B．（1）求证：△ADF∽△DEC；（2）若AB=4，求DE和AF的长．24．如图，边长为a的菱形ABCD中，∠A=60°，过C任作直线分别交AB、AD的延长线于E、F，连接DE、BF 交于M，若△BEM和△DFM外接圆的半径分别是R1、R2，求证：R1•R2为定值，并求这个定值．25．如图，四边形ABCD为菱形，已知A（0，6），D（﹣8，0）．（1）求点C的坐标；（2）设菱形ABCD对角线AC、BD相交于点E，求经过点E的反比例函数解析式．26．如图，菱形ABCD中，点P是AB的中点，延长DP交CB的延长线于E点．求证：BE=CD．27．已知：如图，菱形ABCD中，E、F分别是CB、CD上的点，BE=DF．（1）求证：AE=AF；（2）若AE垂直平分BC，AF垂直平分CD，求证：△AEF为等边三角形．28．如图，在菱形ABCD中，P是AB上的一个动点（不与A，B重合），连接DP交对角线AC于E，连接EB．求证：∠APD=∠EBC．29．如图，在菱形ABCD中，E是BC延长线上一点，连接AE，使得∠E=∠B，过D作DH⊥AE于H．（1）若AB=10，DH=6，求HE的长；（2）求证：AH=CE+EH．30．如图，已知点O在菱形ABCD内，过点O分别作OE⊥AB于E，OF⊥AD于F，且OE=OF．（1）求证：OB=OD；（2）把菱形换成矩形、平行四边形、等腰三角形，上述结论仍成立吗？（写出结论，不证明）参考答案:1．（1）设AB=x，则BC=x，BH=BC﹣CH=x﹣4，在Rt△ABH中，AH2+BH2=AB2，∴82+（x﹣4）2=x2，解得x=10，∴菱形周长为40．（2）∵AH=8，CH=4，∴AC==4，∴CO=AO=AC=2，∵BC=10，CO=2，∴BO==4∵∠BHE=∠BOC=90°，∠EBH=∠CBO，∴△BHE∽△BOC，∴，∴，∴EH=3，∴AE=AH﹣EH=8﹣3=5，∴OE==2．（1）菱形的对角线为AC=6cm，BD=8cm，则菱形的面积为AC•BD=×6×8=24cm2；（2）菱形对角线互相垂直平分，∴BO=OD=4cm，AO=OC=3cm，∴AB==5cm，故菱形的周长为20cm，答：菱形的周长为20cm，面积为24cm2．3．∵在菱形ABCD中，AC=12cm，BD=16cm，∴S菱形ABCD =×AC×BD=×12×16=96（cm2）．∵四边形ABCD是菱形，∴AC⊥BD，OA=AC=6cm，OB=BD=8cm，∴AB==10cm，∴菱形ABCD的周长为：4×10=40（cm）．故这个菱形的周长为40cm，面积为96cm24．（1）∵四边形ABCD是菱形，∠BAD=120°，∴AB=BC，∠BAC=∠BAD=60°，∴△ABC是等边三角形；（2）∵四边形ABCD是菱形，∴AC⊥BD，∵∠BAC=60°，AB=2cm，∴∠ABO=30°，∴OA AB=1（cm），∴OD==（cm），∴AC=2OA=2cm，BD=2OD=2cm．5．（1）∵四边形ABCD是菱形，AB=5，∴菱形ABCD的周长等于5×4=20；（2）∵四边形ABCD是菱形，∴OA=OC，OB=OD，AC⊥BD，在Rt△AOB中，∠AOB=90°，根据勾股定理，得：OB=，==4，∴AC=2OA=6，BD=2OB=8，∴S菱形ABCD=×AC×BD=×6×8=246．菱形周长为200cm，则AB=50cm，∵AC=60cm，∴AO=30cm，菱形对角线互相垂直，∴△AOB为直角三角形，在Rt△AOB中，BO==40cm，∴BD=2BO=80cm，∴菱形ABCD的面积为S=×60cm×80cm=2400cm2，答：菱形ABCD的面积为2400cm2．7．由菱形对角线性质知，AO=AC=3，BO=BD=4，且AO⊥BO，∴AB=5，∴周长L=4AB=20；∵菱形对角线相互垂直，∴菱形面积是S=AC×BD=24．综上可得菱形的周长为20、面积为24．8．四边形AODE是矩形．∵DE∥AC，AE∥BD，∴四边形AODE是平行四边形，∵四边形ABCD是菱形，∴AC⊥BD∴∠AOD=90°，∴四边形AODE是矩形9．（1）四边形OCED是矩形．理由如下：∵DE∥AC，CE∥BD，∴四边形OCED是平行四边形，∵四边形ABCD是菱形，∴∠COD=90°，∴四边形OCED是矩形；（2）在菱形ABCD中，∵AC=6，BD=8，∴OC=AC=×6=3，OD=BD=×8=4，∴CD===5，在矩形OCED中，OE=CD=510．1）证明：连接BD，∵四边形ABCD是菱形，∴AC⊥BD，∵EM⊥AC，∴EM∥BD，∵E为AB的中点，∴M为AD的中点，∴AM=DM；（2）解：∵EB∥FD，EM∥BD，∴四边形FDBE是平行四边形，∴FD=BD，∵DF=2，∴BE=2，∴AB=2BE=2×2=4，∴菱形ABCD的周长=4AB=4×4=16；（3）设ME与AC的交点为G，相似三角形有：△AGE∽△AGM，△AGE∽△CGF，△AGM∽△CGF，△AEM∽△DFM，△ABC∽△ADC共5对．11．（1）∵菱形ABCD中，AB=BC，AD=CD，∠B=∠D=60°，∴△ABC和△ACD都是等边三角形．（2）∵∠B=∠ACD=60°，AB=AC，∴△ABC是等边三角形，∴∠BAC=∠EAF=60°，∴∠BAE=∠CAF，∴△ABE≌△ACF，∴AE=AF，又∠EAF=60°，∴△AEF是等边三角形；（3）∵EC+CF=BE+EC=BC=2，△AEF是等边三角形，∴EF=AE，∴△CEF的周长=2+AE，由“垂线段最短”，当AE⊥BC时，AE最短，AE=，∴△CEF的周长=2+12．（1）∵DE∥AC，CE∥BD∴四边形OCED为平行四边形，∵AC，BD为菱形的对角线，∴AC⊥BD，即∠COD=90°，∴平行四边形OCED为矩形．（2）菱形ABCD的周长为20，则菱形的边长为5，即=5，矩形OCED的周长为14，则OC+OD=7，解题OC=3，OD=4，∴AC=6，BD=8，∴菱形的面积为×6×8=24．答：菱形ABCD的面积为2413．由菱形ABCD，得∠BAD=∠BCD=130°，∠BAE=25°，∴∠EAF=105°，又∵AF=CE，AD∥BC，∴四边形AECF是平行四边形，则∠AFC=180°﹣∠EAF=180°﹣105°=75°．14．（1）∵∠ABE=∠CDG，∠AEB=∠CGD，AE=CG，∴△ABE≌△CDG，∴BE=DG，（2）四边形ABFG是菱形，则BF=AB，∵AB：BC=2：3∴FC=AB，∵AE是BC沿BC方向平移，使点E与点C重合，得△GFC．∴BE=FC，∴AB=2BE，∴直角△ABE中，∠BAE=30°，∴∠ABE=60°15．∵四边形ABCD是菱形，∴AB=BC，AD∥BC，∵AE⊥BC，BE=CE，∴AB=AC，∴AB=AC=BC，即△ABC是等边三角形，∴∠B=60°，又∵AD∥BC，∴∠BAD=180°﹣∠B=120°16．（1）如图，过E作AD，BC的垂线交AD和CB的延长线于H，G．∵AD∥CB，∴△BGE∽△AHE，∵AB=AD=6，∴AE=BF=5，CF﹣BE=1，令BG=x，GE=y，则EH=5y，AH=5x，在△FGE 中，，在△DEH 中，，根据EF=ED，BE=1，易得EF2=ED2，即有，解得，，∴tan∠A=，∴∠A=60°；（2）由以上求得知，EH=AEsin60°=，，故．17．连接PD，DQ，由已知∠PAC=120°，∠QCA=120°，∴△PAC∽△AMC，△AMC∽△ACQ．∴，．∴AC2=PA•QC，又AC=AD=DC．∴，又∠PAD=∠DCQ=60°，∴△PAD∽△DCQ，∴∠APD=∠CDQ．∴∠PDA+∠ADC+∠CDQ=180°，∴P，D，Q三点共线．18．∵菱形ABCD的周长为20，∴菱形的边长AB=5，由直角三角形的三边关系可得：AO2+BO2=25，又有根与系数的关系可得：AO+BO=2m﹣1，AO•BO=4（m﹣1），∴AO2+BO2=（AO+BO）2﹣2AO•BO=（2m﹣1）2﹣2×4（m﹣1）=25，整理得：4m2﹣12m+9=25，解得：m=4或﹣1（舍去）．故m=419．∵四边形ABCD为菱形，∴AD=AB=CD=CB，∠B=∠D．又∵CE=CF，∴CD﹣CE=CB﹣CF，即DE=BF．∴△ADE≌△ABF．∴AE=AF20．菱形ABCD的面积S=×16×12=96，∵AC⊥BD，∴AB=10，∴CD=AB=10，∴×CD×BE=48，∴BE=cm，所以菱形ABCD的面积为96cm2，BE 的长为cm21．（1）DE=BF．理由如下：如图，设AB、EF相交于G，连接BD，在菱形ABCD中，BD⊥AC，∵EF⊥AC，∴EG∥BD，∵E是AD中点，∴EG是△ABD的中位线，∴AG=BG，又∵AD∥BC，∴∠AEG=∠BFG，在△AEG和△BFG 中，，∴△AEG≌△BFG（AAS），∴AE=BF，∵E是AD中点，∴AE=DE，∴DE=BF；（2）四边形AFBE是平行四边形．理由如下：∵四边形ABCD是菱形，∴AD∥BC，∴AE∥BF，又∵AE=BF，∴四边形AFBE是平行四边形22．（1）∵四边形ABCD是菱形，∴AB=CB=CD=AD，∠B=∠D，∵BE=DF∴△ABE≌△ADF（SAS），∴AE=AF；（2）连接AC，∵AE垂直平分BC，AF垂直平分CD．∴AB=AC=AD，∴AB=AD=BC=CD=AC，∴∠B=60°，∴∠BCD=120°，∴∠EAF=60°，∴△AEF为等边三角形．23．（1）证明：∵∠B+∠C=180°，∠AFE+∠AFD=180°，∠AFE=∠B，∴∠C=∠AFD．∵AD∥BC，∴∠ADF=∠DEC．∵AD=DC，∴△ADF∽△DEC．（2）解：∵AB=4，E为BC的中点，∴BE=2，AE=，DE=．∵△ADF∽△DEC，∴．∴AF=．24．△BEC∽△DCF，∴．∴△BED∽△DBF．∴∠BED=∠DBM．∴∠BME=∠BDM+∠DBM=∠BDM+∠BED=∠ABD= 60°．∴由正弦定理得：2R1=，2R2=．∴R1•R2=•==．25．（1）∵A（0，6），D（﹣8，0），∴OA=6，OD=8，∴由勾股定理可得AD=10，∵四边形ABCD为菱形∴CD=AD=10，∴OC=2，∴C（2，0），（2）∵A（0，6）C（2，0），∴E（1，3），设经过点E 的反比例函数解析式为，将E（1，3）代入求得k=3∴反比例函数解析式为：26．∵点P是AB的中点，∴AP=BP，∵四边形ABCD是菱形，∴AD=DC，AD∥BC，∴∠A=∠PBE，∵在△ADP和△BEP中，，∴△ADP≌△BEP（ASA），∴BE=AD，∵AD=CD，∴BE=CD27．（1）∵四边形ABCD是菱形，∴AB=AD，∠B=∠D，又∵BE=DF，∴△ABE≌△ADF，∴AE=AF；（2）连接AC，∵AE垂直平分BC，AF垂直平分CD，∴AB=AC=AD．∵AB=BC=CD=DA，∴△ABC和△ACD都是等边三角形．∴∠CAE=∠BAE=30°，∠CAF=∠DAF=30°．∴∠EAF=∠CAE+∠CAF=60°又∵AE=AF，∴△AEF是等边三角形．28．∵四边形ABCD是菱形，∴BC=CD，AC平分∠BCD，在△BCE和△DCE 中，，∴△BCE≌△DCE（SAS），∴∠EBC=∠EDC，又AB∥DC，∴∠APD=∠EDC，∴∠EBC=∠APD29．（1）∵四边形ABCD是菱形，∴AD=AB=10，∵DH⊥AE，∴∠AHD=90°，在Rt△ADH中，AH===8，∵∠E=∠B，∴AE=AB=10，∴HE=AE﹣AH=10﹣8=2；证明：（2）过点D作DF⊥BC的延长线于点F，连接DE，∵四边形ABCD是菱形，∴AB∥CD，AD∥BC，AD=CD，∴∠1=∠B，∠2=∠3，∵∠B=∠2，∴∠1=∠3，∵DH⊥AE，DF⊥CF，∴∠4=∠F，在△ADH和△CDF中，，∴△ADH≌△CDF（AAS），∴AH=CF，DH=DF，∴在Rt△DEH和Rt△DEF中，，∴Rt△DEH≌Rt△DEF（HL），∴EH=EF，∵CF=CE+EF，∴AH=CE+EH30．（1）证明：连接OA、AC、BD，∵OE⊥AB，OF⊥AD，且OE=OF，∴∠BAO=∠DAO，∵菱形ABCD，∴AC⊥BD，MB=MD，∠BAC=∠DAC，∴O在AC上，∴OB=OD．（2）解：矩形和平行四边形时，结论不成立，等腰三角形时，结论成立，因为：矩形和平行四边形的对角线不一定平分对角，而等腰三角形的三线合一性质，能得出结论成立菱形的性质--11。

八年级数学《菱形》练习题随堂演练一、填空题1．菱形的对角线长为24和10，则菱形的边长为 ，周长为 .2．菱形的一边与两条对角线构成的二角之比为5：4，则菱形的各内角为 ， ， ， .3．菱形的两条对角线分别为3和7，则菱形的面积为 .4．已知在菱形ABCD 中，E ，F 是BC ，CD 上的点，且AE ＝EF ＝AF ＝AB ，则∠B= .5．已知菱形两邻角的比是1：2，周长为40cm ，则较短对角线的长是 .6．已知菱形的面积等于80cm 2，高等于8cm ，则菱形的周长为 .7．已知菱形ABCD 中AE ⊥BC ，垂足E ，F 分别为BC ，CD 的中点，那么∠EAF 的度数为 .8．顺次连结菱形各边的中点，所得的四边形为 形．二、选择题1．能够判定一个四边形是菱形的条件是（ ）A ．对角线相等且互相平分B ．对角线相等且对角相等C ．对角线互相垂直D ．两组对角分别相等且一条对角线平分一组对角2．菱形ABCD ，若∠A:∠B ＝2：1，∠CAD 的平分线AE 和边CD 之间的关系是（ ）A ．相等B ．互相垂直且不平分C ．互相平分且不垂直D ．垂直且平分3．已知菱形ABCD 的周长为40cm ，BD=34AC ，则菱形的面积为（ ） A ．96cm 2 B ．94cm 2 C ．92cm 2 D ．90cm 24．菱形的周长等于高的8倍，则这个菱形较大内角是（ ）A ．60°B ．90°C ．120°D ．150°5．菱形具有而矩形不具有的性质是（ ）A ．对角线互相平分B ．对角线互相垂直C ．对角线相等D ．对边平行且相等6．下列说法正确的是（ ）A ．对角线相等且互相垂直的四边形是菱形B ．对角线相等的四边形是矩形C ．对角线互相垂直平分的四边形是菱形D ．邻边相等的四边形为菱形7．矩形具有而菱形不具有的性质是（ ）A ．对角相等且互补B ．对角线互相平分C ．一组对边平行，另一组对边相等D ．对角线互相垂直8．菱形的对角线把它分成全等的直角三角形的个数是（ ）A ．4个B ．3个C ．2个D ．1个三、解答题1．如图，在菱形ABCD中，延长AD到E，连结BE交CD于H，交AC于F，且BF＝DE，求证：DH＝HF.2．如图，在菱形ABCD中,E是AD的中点，EF⊥AC交CB的延长于F，交AC于M，求证：AB与EF互相平分．3．已知菱形的面积为24cm2，边长为5cm，求该菱形中一组对边之间的距离．4．已知：如图，在菱形ABCD中，BD是对角线，过D作DE⊥BA交BA延长线于点E，若BD＝2DE，AB＝4，求菱形的面积。

菱形性质习题精选（含答案）菱形性质习题精选一．填空题（共26小题）1．（2015?模拟）如图，在菱形ABCD中，点E是AB上的一点，连接DE交AC于点O，连接BO，且∠AED=50°，则∠CBO=度．2．（2015?模拟）如图，在四边形ABCD中，AB=6，∠ABC=90°，E在CD上，连接AE，BE，∠DAE=75°，若四边形ABED 是菱形，则EC的长度为．3．（2015?模拟）如图，菱形ABCD的对角线AC、BD交于点O，其中AC=8，BD=6，以OC、OB为边作矩形OBEC，矩形OBEC 的对角线OE、BC交于点F，再以CF、FE为边作第一个菱形CFEG，菱形CFEG的对角线FG、CE交于点H，如此继续，得到第n个菱形的周长等于．4．（2015?州市校级模拟）己知菱形相邻两角的度数比为1：5，且它的面积为8，则这个菱形的周长为．5．（2015?模拟）如图，在菱形ABCD中，∠A=45°，DE⊥AB，垂足为E，若CD=4cm，则菱形ABCD的面积是．6．（2015?模拟）如图，菱形ABCD中，对角线AC、BD相交于点O，H为AD边中点，菱形ABCD的周长为40，则OH的长等于．7．（2014?）菱形ABCD中，若对角线长AC=8cm，BD=6cm，则边长AB=cm．8．（2014?）菱形的周长为20cm，两个相邻的角的度数之比为1：2，则较长的对角线长度是cm．9．（2014?）如图，菱形ABCD中，AC、BD相交于点O，若∠BCO=55°，则∠ADO=．10．（2014?宿迁）如图，在平面直角坐标系xOy中，若菱形ABCD的顶点A，B的坐标分别为（﹣3，0），（2，0），点D在y 轴上，则点C的坐标是．11．（2014?眉山）如图，菱形ABCD中，E、F分别是BC、CD 的中点，过点E作EG⊥AD 于G，连接GF．若∠A=80°，则∠DGF的度数为．12．（2014春?期末）如图在菱形ABCD中，∠B=∠EAF=60°，∠BAE=20°，则∠CEF的大小为．13．（2014?模拟）如图，在菱形ABCD中，∠B=60°，AB=2，E、F分别是BC、CD的中点，连接AE、EF、AF，则△AEF的周长为．14．（2014?江都市二模）已知菱形ABCD的对角线相交于点O，AC=6cm，BD=8cm，则菱形的高AE为cm．15．（2014?简阳市模拟）如图，边长为a的正方形发生形变后成为边长为a的菱形，如果这个菱形的一组对边之间的距离为h，记=k，我们把k叫做这个菱形的“形变度”．若变形后的菱形有一个角是60°，则形变度k=．16．（2014?淮区一模）如图，在菱形ABCD中，∠ABC=60°，BC=1cm，以DC为边在菱形的外部作正三角形CDE，连接AE，则AE=cm．17．（2014?惠安县二模）如图，菱形ABCD的边长是2cm，∠A=60°，点E、F分别是边AB、CD上的动点，则线段EF的最小值为cm．18．（2013秋?海陵区期末）如图，将菱形纸片ABCD折叠，使点A恰好落在菱形的对称中心O处，折痕为EF．若菱形ABCD的边长为4cm，∠A=120°，则EF=cm．19．（2014春?仙游县校级期末）如图，以菱形AOBC的顶点O 为原点，对角线OC所在直线为x轴建立平面直角坐标系，若OB=，点C的坐标为（4，0），则点A的坐标为．20．（2014春?期末）如图，在菱形ABCD中，AB=13cm，BC 边上的高AH=5cm，那么对角线AC的长为cm．21．（2014春?泰兴市校级期末）如图，菱形ABCD的周长为16cm，BC的垂直平分线EF 经过点A，则对角线BD长为cm．22．（2014春?建湖县期末）如图，在菱形ABCD中，对角线AC、BD相交于点O，点E在BD的延长线上，且△EAC是等边三角形，若AC=8，AB=5，则ED的长等于．23．（2014春?玄武区期末）如图，在菱形ABCD中，BE⊥AD，垂足为E，且E为AD为中点．则∠ADC=°．24．（2014春?定县期末）如图，菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P 是对角线AC上的一个动点，当P移动到AC的中点时，则PE+PB的值是．25．（2014春?顺义区期末）如图，菱形ABCD中，∠BAD=120°，CF⊥AD于点E，且BC=CF，连接BF交对角线AC于点M，则∠FMC=度．26．（2014秋?武进区期中）如图，依次连结第一个矩形各边的中点得到第一个菱形，再依次连结所得菱形各边的中点得到第二个矩形，按照此方法继续下去．已知第一个矩形的面积为2，则第2013个菱形的面积为．二．解答题27．（2014?县模拟）如图，四边形ABCD是菱形，CE⊥AB交AB延长线于E，CF⊥AD交AD延长线于F，求证：CE=CF．28．（2014?江都市模拟）如图，在菱形ABCD中，点M是对角线AC上一点，且MC=MD．连接DM并延长，交边BC于点F．（1）求证：∠1=∠2；（2）若DF⊥BC，求证：点F是边BC的中点．29．（2014春?期末）如图，在Rt△ABC中，∠B=90°，BC=5，∠C=30°．点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（t＞0）．过点D作DF⊥BC于点F，连接DE、EF．（1）求证：AE=DF；（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果不能，说明理由．30．（2014春?高淳县校级期末）如图，已知菱形ABCD的边长为2，∠B=60°，点P、Q分别是边BC、CD上的动点（不与端点重合），且BP=CQ．（1）图中除了△ABC与△ADC外，还有哪些三角形全等，请写出来；（2）点P、Q在运动过程中，四边形APCQ的面积是否变化，如果变化，请说明理由；如果不变，请求出面积；（3）当点P在什么位置时，△PCQ的面积最大，并请说明理由．31．（2013秋?东海县月考）如图，在菱形ABCD中，点E是AD 边的中点，点M是AB边上的一个动点（不与点A重合），延长ME 交CD的延长线于点N，连接MD，AN．（1）求证：四边形AMDN是平行四边形．（2）若∠DAB=60°，当点M位于何处时，四边形AMDN是矩形？并说明理由．（请在备用图中画出符合题意的图形）32．（2012秋?鼓楼区校级期末）如图所示，在矩形ABCD中，AB=4cm，BC=8cm、点P从点D出发向点A运动，同时点Q从点B 出发向点C运动，点P、Q的速度都是1cm/s．（1）在运动过程中，四边形AQCP可能是菱形吗？如果可能，那么经过多少秒后，四边形AQCP是菱形？（2）分别求出菱形AQCP的周长、面积．参考答案1．50 2．3 3． 4．16 5．8cm 2 6．5 7．5 8．5 9．35° 10．（5，4） 11．50° 12．20°13．3 14．4.8 15． 16．17． 18．2 19．（2，1）20． 21．4 22．4-3 23．120 24．2 25．105 26．27、证明：四边形ABCD 是菱形CE ⊥AE,CF ⊥AF∠DAB=∠CBB,∠DAB=∠FDC,∴∠CBE=∠FDC又 BC=DC,∴Rt △BEC ≌Rt △DFC,∴CE=CF.28、证明：（1）∵四边形ABCD 是菱形，∴AB ∥CD ，∴∠1=∠ACD ，∵MC=MD ，∴∠ACD=∠2，∴∠1=∠2；（2）连接BD ，∵四边形ABCD 是菱形，∴∠ACB=∠ACD ，BC=CD ，∵∠ACD=∠2，∴∠ACB=∠ACD=∠2，∵DF ⊥BC ，∴3∠2=90°，∴∠2=30°，∴∠BCD=∠ACB+∠ACD=60°，∴△BCD 是等边三角形，∴BF=CF ，即点F 是边BC 的中点．29、（1）在△DFC 中，∠DFC =90°，∠C =30°，DC =2t ，∴DF =t .又∵AE=t ，∴AE=DF（2）能.理由如下：∵AB ⊥BC ，DF ⊥BC ，∴AE ∥DF .又AE =DF ，∴四边形AEFD 为平行四边形.∵AB =21AC BC=35 222AC BC AB =+∴()2223521AC AC =+??? ?? ∴AC=1010 2.AD AC DC t ∴=-=-若使AEFD 为菱形，则需10.102,.3AE AD t t t ==-=即即当103t =时，四边形AEFD 为菱形30、（1）△ABP ≌△ACQ ，△APC ≌△AQD ；（2）∵△ACP ≌△ADQ ，∴S △ACP =S △ADQ ，即S 四边形APCQ =S △ACD =3221??；(3为菱形的高) （3）∵△PAQ 是等边三角形，点P 是BC 的中点时，AP 垂直于BC ，AP 最小，∴当AP ⊥BC 时，三角形APQ 的面积最小，故在四边形APCQ 的面积一定，△APQ 面积最小时，△PCQ 的面积最大. 此时BP=1，31、证明：∵四边形ABCD 是菱形∴∠DNM=∠AMN又∵DE=AE ，∠NDE=∠MAE∴△NDE=△MAE∴ND=AM∴ND ∥AM∴四边形ANDM 是平行四边形（2）当点M 是AB 的中点时，四边形AMDN 是矩形证明：如图所示∵四边形AMDN 是矩形，∠DAB=60o∴∠ADM=30o∴AM=AD 21 ∵AD=AB ∴AM=AB 21 即M 是AB 的中点32、解：（1）经过x 秒后，四边形AQCP 是菱形∴DP=X cm AP=CP=AD-DP=(8-X)cm∵DP 2+CD 2=PC 2∴16+X 2=(8-X) 2 解得x=3即经过3秒后四边形是菱形（2）由（1）得菱形的边长为5∴菱形AQCP的周长=5×4=20（㎝）菱形AQCP的面积=5×4=20（㎝2）。

2019年 八年级数学下册 菱形 精选练习一、选择题1.如图，菱形ABCD 中，AB=5，BD=6，则菱形的高为（ ）A.2.4B.4.8C.12D.242.如图，在菱形ABCD 中，AB 的垂直平分线EF 交对角线AC 于点F ，垂足为点E ，连接DF ，若∠CDF=24°，则∠DAB 等于（ ）A ．100°B ．104°C ．105°D ．110°3.如图,在周长为12的菱形ABCD 中,AE=1,AF=2,若P 为对角线BD 上一动点,则EP+FP 的最小值为（ ）A.1B.2C.3D.44.如图,在边长为2的菱形ABCD 中,∠B=45°,AE 为BC 边上的高,将△ABE 沿AE 所在直线翻折得△AB ′E ，AB ′与CD 边交于点F,则B ′F 的长度为（ ）A.1B.C.2-D.2﹣25.如图，在菱形ABCD 中，∠ABC=60°，AB=1，E 为BC 的中点，则对角线BD 上的动点P 到E 、C两点的距离之和的最小值为（ ）A.43B.33C.23 D.216.如图，在菱形ABCD 中，AB=4cm ，∠ADC=120°，点E ，F 同时由A ，C 两点出发，分别沿AB ，CB 方向向点B 匀速移动(到点B 为止)，点E 的速度为1cm/s ，点F 的速度为2cm/s ，经过t 秒△DEF 为等边三角形，则t 的值为( )A.1B.C.D.7.如图，两个完全相同的三角尺ABC和DEF在直线l上滑动，可以添加一个条件，使四边形CBFE为菱形，下列选项中错误的是（）A.BD=AEB.CB=BFC.BE⊥CFD.BA平分∠CBF8.如图，菱形花坛ABCD的边长为6m，∠A=120°，其中由两个正六边形组成的图形部分种花，则种花部分图形的周长为（）A.12mB.20mC.22mD.24m9.如图，菱形ABCD中，E是AD的中点，将△CDE沿CE折叠后，点A和点D恰好重合，若菱形ABCD的面积为4，则菱形ABCD的周长是( )A.8B.16C.8D.1610.如图，在菱形ABCD中，AB=13，对角线AC=10，若过点A作AE⊥BC，垂足为E，则AE的长为( )A.8B.C.D.二、填空题11.如图，正方形ABCD的面积为18，菱形AECF的面积为6，则菱形的边长为．12.把两张宽为2 cm的矩形纸片重叠在一起，然后将其中的一张任意旋转一个角度，则重叠部分(图中的阴影部分)的四边形ABCD的形状为________，其面积的最小值为________cm2.13.如图，在矩形ABCD中，AB=2，BC=4，对角线AC的垂直平分线分别交AD、AC于点E、O，连接CE，则CE的长为．14.如图，四边形ABCD和CEFG都是菱形，连接AG，GE,AE，若∠F=60°，EF=4，则△AEG面积为________.15.如图，四边形ABCD是菱形，O是两条对角线的交点，过O点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为10和6时，则阴影部分的面积为．16.如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为三、解答题17.准备一张矩形纸片，按如图操作：将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．（1）求证：四边形BFDE是平行四边形；（2）若四边形BFDE是菱形，AB=2，求菱形BFDE的面积．18.如图,已知在菱形ABCD中,F为边BC的中点,DF与对角线AC交于M,过M作ME⊥CD于E,∠1=∠2．（1）若CE=1，求BC的长；（2）求证：AM=DF+ME．19.如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且AC=2DE,连接AE交OD于点F,连接CE、OE．（1）求证：OE=CD；（2）若菱形ABCD的边长为2，∠ABC=60°，求AE的长．20.如图所示,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形;(2)①当AM为何值时,四边形AMDN是矩形?②当AM为何值时,四边形AMDN是菱形?21.如图，在矩形ABCD中，AB=4cm，BC=8cm，点P从点D出发向点A运动，运动到点A即停止；同时点Q从点B出发向点C运动，运动到点C即停止．点P、Q的速度的速度都是1cm/s，连结PQ，AQ，CP，设点P、Q运动的时间为t（s）．（1）当t为何值时，四边形ABQP是矩形？（2）当t为何值时，四边形AQCP是菱形？（3）分别求出（2）中菱形AQCP的周长和面积．22. (1)如图,纸片▱ABCD中,AD=5,S=15.过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平▱ABCD移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为( )A.平行四边形B.菱形C.矩形D.正方形(2)如图,在(1)中的四边形纸片AEE/D中,在EE/上取一点F,使EF=4,剪下△AEF,将它平移至△DE/F/的位置,拼成四边形AFF/D.①求证:四边形AFF'D是菱形;②求四边形AFF'D的两条对角线的长.图1 图2答案1.B2.B.3.C4.C5.C.6.D7.A8.C9.A.10.C.11.答案为：；12.答案为：菱形，413.答案为：2.5；14.答案为：15.答案为：15．17.18.（1）解：∵四边形ABCD是菱形，∴AB∥CD，∴∠1=∠ACD，∵∠1=∠2，∴∠ACD=∠2，∴MC=MD，∵ME⊥CD，∴CD=2CE，∵CE=1，∴CD=2，∴BC=CD=2；（2）证明：如图，∵F为边BC的中点，∴BF=CF=BC，∴CF=CE，在菱形ABCD中，AC平分∠BCD，∴∠ACB=∠ACD，在△CEM和△CFM中，∵，∴△CEM≌△CFM（SAS），∴ME=MF，延长AB交DF的延长线于点G，∵AB∥CD，∴∠G=∠2，∵∠1=∠2，∴∠1=∠G，∴AM=MG，在△CDF和△BGF中，∵，∴△CDF≌△BGF（AAS），∴GF=DF，由图形可知，GM=GF+MF，∴AM=DF+ME．19.【解答】（1）证明：四边形ABCD是菱形，∴OA=OC=0.5AC，AD=CD，∵DE∥AC且DE=0.5AC，∴DE=OA=OC，∴四边形OADE、四边形OCED都是平行四边形，∴OE=AD，∴OE=CD；（2）解：∵AC⊥BD，∴四边形OCED是矩形，∵在菱形ABCD中，∠ABC=60°，∴AC=AB=2，∴在矩形OCED中，CE=OD=．∴在Rt△ACE中，AE==．解:（1）略；（2）PC2=PE PF20. (1)证明:∵四边形ABCD是菱形,∴ND∥AM,21.解：（1）当四边形ABQP是矩形时，BQ=AP，即：t=8﹣t，解得t=4．答：当t=4时，四边形ABQP是矩形；（2）设t秒后，四边形AQCP是菱形当AQ=CQ，即=8﹣t时，四边形AQCP为菱形．解得：t=3．答：当t=3时，四边形AQCP是菱形；（3）当t=3时，CQ=5，则周长为：4CQ=20cm，面积为：4×8﹣2××3×4=20（cm2）．。

19.2.1 菱形的性质运用菱形的有关知识进行计算和说理专题练习题1．已知菱形的周长为16 cm，一条对角线长为4 cm，则菱形的4个角分别为()A．30°，150°，30°，150°B．45°，135°，45°，135°C．60°，120°，60°，120°D．以上都不对2．如图，在菱形ABCD中，M，N分别在AB，CD上，且AM＝CN，MN与AC相交于点O，连结BO.若∠DAC＝28°，则∠OBC的度数为()A．28°B．52°C．62°D．72°3．如图，在菱形ABCD中，点E是AB上的一点，连结DE交AC于点O，连结BO，且∠AED＝50°，则∠CBO＝____度．4．如图，在菱形ABCD中，∠ABC＝120°，对角线AC，BD相交于点O，AE平分∠CAD，分别交OD，CD于F，E 两点，求∠AFO的度数．5．如图，在菱形ABCD中，AB＝13 cm，BC边上的高AH＝5 cm，那么对角线AC的长为____cm.6．如图，四边形ABCD是菱形，AC＝8，DB＝6，DH⊥AB于点H，则DH的长为()A.245B.125C ．5D ．4 7．如图，在菱形ABCD 中，对角线AC ＝6，BD ＝10，则菱形ABCD 的面积为____．8．如图，四边形ABCD 是菱形，O 是两条对角线的交点，过O 点的三条直线将菱形分成阴影和空白部分．当菱形的两条对角线的长分别为10和4时，则阴影部分的面积为____．9．如图，O 是菱形ABCD 对角线AC 与BD 的交点，CD ＝5 cm ，OD ＝3 cm, 过点C 作CE ∥DB ，过点B 作BE ∥AC ，CE 与BE 相交于点E .(1)求OC 的长；(2)求四边形OBEC 的面积．10．如图，在菱形ABCD 中，∠BAD ＝44°，AB 的垂直平分线交对角线AC 于点F ，垂足为E ，连结DF ，则∠CDF 等于( )A ．112°B ．114°C ．116°D ．118°11．在菱形ABCD 中，∠A ＝30°，在同一平面内，以对角线BD 为底边作顶角为120°的等腰三角形BDE ，则∠EBC 的度数为 ．12．如图，四边形ABCD 是菱形，CE ⊥AB 交AB 的延长线于点E ，CF ⊥AD 交AD 的延长线于点F ，求证：DF ＝BE .13．如图，在菱形ABCD中，AB＝4，E为BC中点，AE⊥BC，AF⊥CD于点F，CG∥AE，CG交AF于点H，交AD 于点G.(1)求菱形ABCD的面积；(2)求∠CHA的度数．14．如图，在菱形ABCD中，F是BC上任意一点，连结AF交对角线BD于点E，连结EC.(1)求证：AE＝EC；(2)当∠ABC＝60°，∠CEF＝60°时，点F在线段BC上的什么位置？请说明理由．15．如图，将两张长为4，宽为1的矩形纸条交叉并旋转，使重叠部分成为一个菱形．旋转过程中，当两张纸条垂直时，菱形周长的最小值是4，那么菱形周长的最大值是____．16．如图1，在菱形ABCD中，点E，F分别为AB，AD的中点，连结CE，CF.(1)求证：CE＝CF；(2)如图2，若H为AB上一点，连结CH，使∠CHB＝2∠ECB，求证：CH＝AH＋AB.答案：1. C2. C3. 504. ∵在菱形ABCD中，∠ABC＝120°，∴∠BAD＝60°，∵对角线AC，BD相交于点O，∴∠BAC＝∠CAD＝30°，∠DOA ＝90°，∵AE平分∠CAD，∴∠OAF＝15°，∴∠AFO的度数为90°－15°＝75°5. 266. A7. 308. 109. (1)∵四边形ABCD是菱形，∴AC⊥BD，∴在Rt△OCD中，OC＝CD2－OD2＝52－32＝4 (cm)(2)∵CE∥DB，BE∥AC，∴四边形OBEC为平行四边形，又∵AC⊥BD，即∠COB＝90°，∴平行四边形OBEC为矩形，∵OB＝OD，∴S四边形OBEC＝OB·OC＝4×3＝12(cm2)10. B11. 45°或105°12. 连结AC ，∵四边形ABCD 是菱形，∴AC 平分∠DAB ，CD ＝BC ，∵CE ⊥AB ，CF ⊥AD ，∴CE ＝CF ，∠CFD ＝∠CEB ＝90°，∴Rt △CDF ≌Rt △CBE (HL )，∴DF ＝BE13. (1)连结AC ，BD ，并且AC 和BD 相交于点O ，∵AE ⊥BC ，且AE 平分BC ，∴AB ＝AC ＝BC ，∴BE ＝12BC ＝2，∴AE ＝42－22＝23，S ＝BC ·AE ＝4×23＝83， ∴菱形ABCD 的面积是83(2)∵AC ＝AB ＝AD ＝CD ，△ADC 是等边三角形，∵AF ⊥CD ， ∴∠DAF ＝30°，又∵CG ∥AE ，AE ⊥BC ， ∴四边形AECG 是矩形，∴∠AGH ＝90°， ∴∠AHC ＝∠DAF ＋∠AGH ＝120°14. (1)连结AC ，∵BD 也是菱形ABCD 的对角线，∴BD 垂直平分AC ，∴AE ＝EC(2)点F 是线段BC 的中点．理由：在菱形ABCD 中，AB ＝BC ， 又∵∠ABC ＝60°，∴△ABC 是等边三角形，∴∠BAC ＝60°， ∵AE ＝EC ，∴∠EAC ＝∠ACE ，∵∠CEF ＝60°， ∴∠EAC ＝12∠CEF ＝30°，∴∠EAC ＝12∠BAC ，∴AF 是△ABC 的角平分线，∵AF 交BC 于点F ，∴AF 是△ABC 的BC 边上的中线，∴点F 是线段BC 的中点 15.17216.(1)易证△BCE ≌△DCF (SAS )，∴CE ＝CF(2)延长BA 与CF ，交于点G ，∵四边形ABCD 是菱形，∴∠B ＝∠D ，AB ＝BC ＝CD ＝AD ，AF ∥BC ，AB ∥CD ，∴∠G ＝∠FCD ，∵点F 为AD 的中点，且AG ∥CD ，易证△AGF ≌△DCF (AAS )，∴AG ＝CD ，∵AB ＝CD ，∴AG ＝AB ，∵△BCE ≌△DCF ，∴∠ECB ＝∠DCF ＝∠G ，∵∠CHB ＝2∠ECB ，∴∠CHB ＝2∠G ，∵∠CHB ＝∠G ＋∠HCG ，∴∠G ＝∠HCG ，∴GH ＝CH ，∴CH ＝AH ＋AG ＝AH ＋AB。

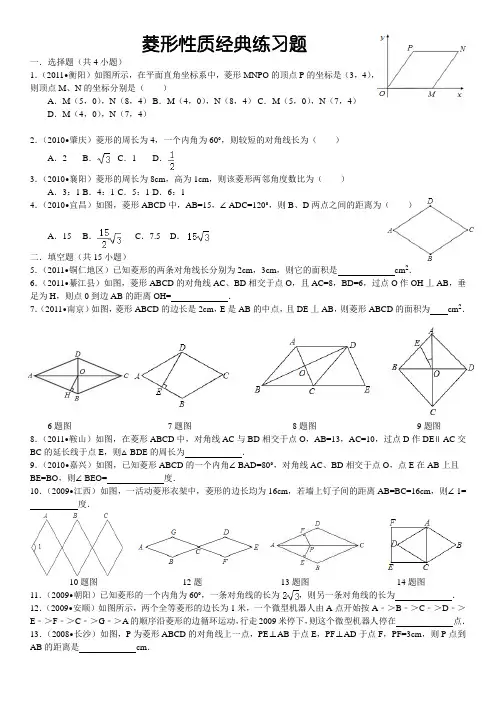
菱形性质经典练习题一．选择题（共4小题）1．（2011•衡阳）如图所示，在平面直角坐标系中，菱形MNPO的顶点P的坐标是（3，4），则顶点M、N的坐标分别是（）A．M（5，0），N（8，4） B．M（4，0），N（8，4） C．M（5，0），N（7，4）D．M（4，0），N（7，4）2．（2010•肇庆）菱形的周长为4，一个内角为60°，则较短的对角线长为（）A．2 B．C．1 D．3．（2010•襄阳）菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（）A．3：1 B．4：1 C．5：1 D．6：14．（2010•宜昌）如图，菱形ABCD中，AB=15，∠ADC=120°，则B、D两点之间的距离为（）A．15 B．C．7.5 D．二．填空题（共15小题）5．（2011•铜仁地区）已知菱形的两条对角线长分别为2cm，3cm，则它的面积是_________cm2．6．（2011•綦江县）如图，菱形ABCD的对角线AC、BD相交于点O，且AC=8，BD=6，过点O作OH丄AB，垂足为H，则点0到边AB的距离OH=_________．7．（2011•南京）如图，菱形ABCD的边长是2cm，E是AB的中点，且DE丄AB，则菱形ABCD的面积为cm2．6题图7题图8题图9题图8．（2011•鞍山）如图，在菱形ABCD中，对角线AC与BD相交于点O，AB=13，AC=10，过点D作DE∥AC交BC的延长线于点E，则△BDE的周长为_________．9．（2010•嘉兴）如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC、BD相交于点O，点E在AB上且BE=BO，则∠BEO=_________度．10．（2009•江西）如图，一活动菱形衣架中，菱形的边长均为16cm，若墙上钉子间的距离AB=BC=16cm，则∠1= _________度．10题图12题13题图14题图11．（2009•朝阳）已知菱形的一个内角为60°，一条对角线的长为，则另一条对角线的长为_________．12．（2009•安顺）如图所示，两个全等菱形的边长为1米，一个微型机器人由A点开始按A﹣＞B﹣＞C﹣＞D﹣＞E﹣＞F﹣＞C﹣＞G﹣＞A的顺序沿菱形的边循环运动，行走2009米停下，则这个微型机器人停在_________点．13．（2008•长沙）如图，P为菱形ABCD的对角线上一点，PE⊥AB于点E，PF⊥AD于点F，PF=3cm，则P点到AB的距离是_________cm．14．（2006•云南）已知：如图，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的正方形ACEF的周长为_________．15．（2005•黄石）已知菱形的周长为40cm，两条对角线之比为3：4，则菱形的面积为_________cm2．16．（2005•新疆）已知菱形的周长是52cm，一条对角线长是24cm，则它的面积是_________cm2．17．（2004•贵阳）如图，菱形ABCD的对角线的长分别为2和5，P是对角线AC上任一点（点P不与点A、C重合），且PE∥BC交AB于E，PF∥CD交AD于F，则阴影部分的面积是_________．17题图18题图19题图18．（2003•温州）如图：菱形ABCD中，AB=2，∠B=120°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值是_________．19．如图：点E、F分别是菱形ABCD的边BC、CD上的点，且∠EAF=∠D=60°，∠FAD=45°，则∠CFE=_________度．三．解答题（共7小题）20．（2011•南昌）如图，四边形ABCD为菱形，已知A（0，4），B（﹣3，0）．（1）求点D的坐标；（2）求经过点C的反比例函数解析式．21．（2011•广安）如图所示，在菱形ABCD中，∠ABC=60°，DE∥AC交BC的延长线于点E．求证：DE=BE．22．（2010•益阳）如图，在菱形ABCD中，∠A=60°，AB=4，O为对角线BD的中点，过O点作OE⊥AB，垂足为E．（1）求∠ABD的度数；（2）求线段BE的长．23．（2010•宁洱县）如图，四边形ABCD是菱形，BE⊥AD、BF⊥CD，垂足分别为E、F．（1）求证：BE=BF；（2）当菱形ABCD的对角线AC=8，BD=6时，求BE的长．24．（2009•贵阳）如图，在菱形ABCD中，P是AB上的一个动点（不与A、B重合），连接DP交对角线AC于E 连接BE．（1）证明：∠APD=∠CBE；（2）若∠DAB=60°，试问P点运动到什么位置时，△ADP的面积等于菱形ABCD面积的，为什么？25．（2006•大连）已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF．请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）．（1）连接_________；（2）猜想：_________=_________；（3）证明：（说明：写出证明过程的重要依据）26．如图所示，在矩形ABCD中，AB=4cm，BC=8cm、点P从点D出发向点A运动，同时点Q从点B出发向点C 运动，点P、Q的速度都是1cm/s．（1）在运动过程中，四边形AQCP可能是菱形吗？如果可能，那么经过多少秒后，四边形AQCP是菱形？（2）分别求出菱形AQCP的周长、面积．答案与评分标准一．选择题（共4小题）1．（2011•衡阳）如图所示，在平面直角坐标系中，菱形MNPO的顶点P的坐标是（3，4），则顶点M、N的坐标分别是（）A．M（5，0），N（8，4） B．M（4，0），N（8，4） C．M（5，0），N（7，4） D．M（4，0），N（7，4）考点：菱形的性质；坐标与图形性质。

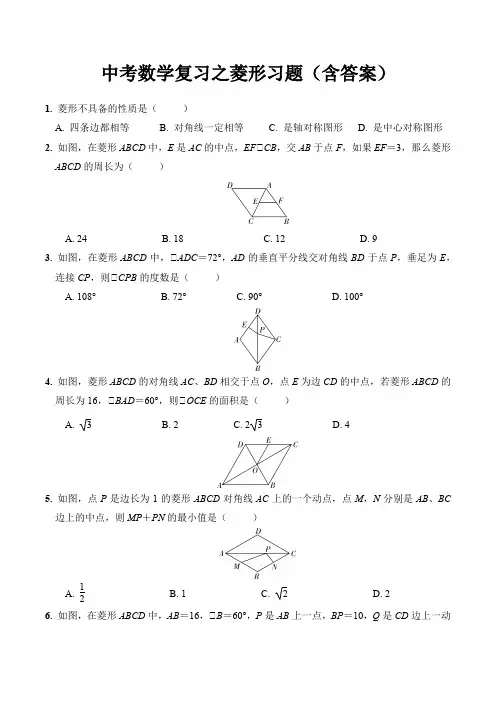
中考数学复习之菱形习题（含答案）1.菱形不具备的性质是（）A. 四条边都相等B. 对角线一定相等C. 是轴对称图形D. 是中心对称图形2.如图，在菱形ABCD中，E是AC的中点，EF∥CB，交AB于点F，如果EF＝3，那么菱形ABCD的周长为（）A. 24B. 18C. 12D. 93.如图，在菱形ABCD中，∠ADC＝72°，AD的垂直平分线交对角线BD于点P，垂足为E，连接CP，则∠CPB的度数是（）A. 108°B. 72°C. 90°D. 100°4.如图，菱形ABCD的对角线AC、BD相交于点O，点E为边CD的中点，若菱形ABCD的周长为16，∠BAD＝60°，则△OCE的面积是（）A. 3B. 2C. 2 3D. 45.如图，点P是边长为1的菱形ABCD对角线AC上的一个动点，点M，N分别是AB、BC边上的中点，则MP＋PN的最小值是（）A. 12 B. 1 C. 2 D. 26.如图，在菱形ABCD中，AB＝16，∠B＝60°，P是AB上一点，BP＝10，Q是CD边上一动点，将四边形APQD沿直线PQ折叠，点A的对应点为A′.当CA′的长度最小时，CQ的长为（）A. 10B. 12C. 13D. 147.如图，在矩形ABCD中，AB＝3，AD＝1，点P在线段AB上运动，设AP＝x，现将纸片折叠，使点D与点P重合，得折痕EF(点E、F为折痕与矩形边的交点)，再将纸片还原，那么使得四边形EPFD为菱形的x的取值范围是______________．8.已知一个菱形的边长为2，较长的对角线长为23，则这个菱形的面积是_________________．9.如图，若菱形ABCD的顶点A，B的坐标分别为(3，0)，(－2，0)，点D在y轴上，则点C 的坐标是_________________．10.如图所示，菱形ABCD的对角线AC、BD相交于点O.若AC＝6，BD＝8，AE⊥BC，垂足为点E，则AE的长为_________________．11.如图，在平行四边形ABCD中，AB＝6，BC＝10，对角线AC⊥AB，点E、F分别是BC、AD上的点，且BE＝DF.(1)求证：四边形AECF是平行四边形；(2)当BE长度为___________时，四边形AECF是菱形．12.如图，在三角形ABC中，∠ACB＝90°，点E是AB边的中点，点F是点E关于AC所在直线的对称点．(1)证明：四边形CF AE为菱形；(2)连接EF交AC于点O，若BC＝26，求线段OF的长．13.如图，在 ABCD中，对角线AC、BD相交于点O，过点O的直线EF分别交BA、DC的延长线于点E、F，且AE＝CF，连接DE、BF.(1)求证：△AOE≌△COF；(2)若∠ABD＝30°，AB⊥AC，①当AE与AB的数量关系为___________时，四边形BEDF是矩形；②当AE与AB的数量关系为___________时，四边形BEDF是菱形．14.如图，在矩形ABCD中，点E在边CD上，将该矩形沿AE折叠，使点D落在边BC上的一点F处，过点F作FG∥CD，交AE于点G，连接DG.(1)求证：四边形DEFG为菱形；(2)若CD＝8，CF＝4，求CEDE的值．参考答案：1-6 BABABD7.1≤x≤38. 239. (－5，4)10.24 511. (1)证明：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，∵BE＝DF，∴AF＝EC，∴四边形AECF是平行四边形；(2)解：∵四边形AECF是菱形，∴AE＝CE，∴∠EAC＝∠ECA，∵AC⊥AB，∴∠BAC＝90°，∴∠B＋∠ECA＝90°，∠BAE＋∠EAC＝90°，∴∠B＝∠BAE，∴AE＝BE，∴BE＝CE＝12BC＝5.12. (1)证明：∵∠ACB＝90°，点E是AB边的中点，∴CE＝12AB＝EA，∵点F是点E关于AC所在直线的对称点，∴AE＝AF，CE＝CF，∴CE＝EA＝AF＝CF，∴四边形CF AE是菱形；(2)解：四边形CF AE是菱形，∴OA＝OC，OE＝OF，∴OE＝12BC＝262＝6，∴OF＝ 6.13. (1)证明：∵四边形ABCD是平行四边形，∴AB ∥CD ，OA ＝OC ， ∴∠EAO ＝∠FCO ， 在△AOE 和△COF 中，⎩⎨⎧OA ＝OC∠EAO ＝∠FCO AE ＝CF， ∴△AOE ≌△COF (SAS )； (2)解：①AE ＝AB ；②AE ＝13AB .14. (1)证明：由折叠的性质可知DG ＝FG ，ED ＝EF ，如图，∠1＝∠2，∵FG ∥CD ， ∴∠1＝∠3， ∴∠2＝∠3， ∴FG ＝FE ，∴DG ＝GF ＝EF ＝DE ， ∴四边形DEFG 为菱形；(2)解：设DE ＝x ，根据折叠的性质得，EF ＝DE ＝x ，EC ＝8－x ， 在Rt △EFC 中，FC 2＋EC 2＝EF 2， 即42＋(8－x )2＝x 2，解得x ＝5，∴CE ＝8－x ＝8－5＝3， ∴CE DE ＝35.。