高二数学专题辅导9

高二下学期数学第九章复习（3）高二下学期数学第九章复习〔3〕空间向量的〔坐标 〕运算〔1〕一、知识要点：1．向量定义： ；相等向量： ； 共线〔平行〕向量： ；共面向量： ； 2．向量加法与数乘向量的差不多性质：〔1〕a b b a +=+ 〔2〕()()a b c a b c ++=++ 〔3〕()a b a b λλλ+=+． 3．空间向量数量积：〔1〕要紧性质：①||||cos ,a b a b a b ⋅=⋅⋅<>〔能够用来求角〕； ②0a b a b ⊥⇔⋅=〔能够用来证明线线垂直〕； ③2||a a a =⋅〔能够用来求线段长〕． 〔2〕运算律：①()()a b a b λλ⋅=⋅； ②a b b a ⋅=⋅； ③()a b c a b a c ⋅+=⋅+⋅．4．共线向量定理： ；空间直线的向量参数方程：OP OA ta =+或(1)OP OA t AB t OA tOB =+⋅=-+〔其中l 过点A ，P 在直线l 上，O 为空间任意一点，a 是l 的方向向量AB a =〕由此判定,,P A B 三点共线⇔ ．5．共面向量定理： ； 据此判定,,,P A B C 四点共面⇔ ． 6．空间向量差不多定理： ； 专门地，假设基底为单位正交基底〔常用,,i j k 表示〕，那么能够建立空间直角坐标系。

7．空间直角坐标系〔右手直角坐标系〕：假设123a a i a j a k =++，那么123(,,)a a a a = 8．空间向量的坐标运算：123(,,)a a a a =，123(,,)b b b b =，那么a b += ；a b -= ；a λ= ；a b ⋅= ；//a b ⇔ ；a b ⊥⇔ ；假设111(,,)A x y z ，222(,,)B x y z ，那么212121(,,)AB x x y y z z =---． 9．夹角和距离公式：〔1〕夹角公式：123(,,)a a a a =，123(,,)b b b b =，那么||a = ；HG ODCBA||b = ；a b ⋅= ；cos ,a b <>= ；〔2〕两点间距离公式：111(,,)A x y z ，222(,,)B x y z ，那么AB d = ；〔3〕向量与平面垂直的意义：假设表示a 的有向线段AB 所在直线垂直于平面α，那么称那个向量垂直于平面α，记为：a α⊥，现在a 叫做平面α的法向量．二、例题分析：例1．12,e e 不平行，122AB e e =+，12332BC e e =+，1224BD e e =+，试判定：,,,A B C D 四点共面吗？并证明你的结论． 提示：⑴能够求得23AB BC =，⑵,,,A B C D 四点共线，从而共面．例2．空间四边形OABC 中，,G H 分不是ABC ∆，OBC ∆的重心，设OA a =，OB b =，OC c =，⑴试用向量,,a b c 表示向量OG 和GH ；⑵证明：//GH 平面OAB ．答案：⑴()13OG a b c =++，13GH a =-；例3．如图在正方体1AC 中，,,M N F 分不是棱11,,AA BB BC 的中点，⑴求证：11D N B F ⊥；⑵求直线CM 与1D N 所成角的余弦值； ⑶求直线1B M 与1D N 所成角的正弦值．答案：⑵1cos 9θ=；⑶sin 5θ=．AB C DA1B1C1D1MNFABC三、课后练习： 班级 学号 姓名1．在平行六面体1111ABCD A B C D -中，M 为AC 与BD 的交点，假设11A B a =，11A D b =，1A A c =，那么1B M =()12c b a +-． 2．设(3,3,1),(1,0,5),(0,1,0)A B C ，那么AB 的中点M 到C 点的距离||CM = 〔 C 〕()A ()B 532()C ()D 3．假设(4,1,5),(4,1,5)M AB -=-，那么 〔 D 〕()A M 与A 重合 ()B M 与B 重合 ()C M 在AB 上 ()D OM AB =4．假设0a b c ++=且||3,||1,||4a b c ===，那么a b b c c a ⋅+⋅+⋅=13-． 5．(1,2,1),(4,2,3),(6,1,4)A B C --，那么ABC ∆的形状是锐角三角形，ABC S ∆=6．||22p =||3q =，,4p q π<>=，求52a p q =+，3b p q =-为边的平行四边形的对角线的长．答案：15,7．：(,4,1)a x =，(2,,1)b y =--，(3,2,)c z =-，//a b ，b c ⊥，求：⑴,,a b c ；⑵()a c +与()b c +所成角的余弦值． 答案：⑴()()()2,4,1,2,4,1,3,2,2a b c ==---=-，⑵ 219-8．在Rt ABC ∆中90,30,1ACB BAC BC ∠=∠==，现将ABC ∆沿着平面ABC 的法向量1AA 平移到111A B C ∆的位置，1AA =M 是1CC 的中点，⑴求异面直线1AB 与1A M 所成角；⑵假设P 是1A M 中点，Q 是1AB 中点，求线段PQ 的长．答案：⑴90；⑵4。

高二数学专题辅导---圆〔一〕根底知识〔1〕圆的定义,〔2〕圆的标准方程,(3)圆的一般方程,〔4〕点和圆的位置关系,〔5〕直线和圆的位置关系解题练习1、设曲线C 的方程为(x －3)2＋(y －2)2＝2,直线l 的方程为x ＋y －3＝0,点P 的坐标为(2,1),那么 ( ) 〔A 〕点P 在直线l 上,但不在曲线C 上 〔B 〕点P 在曲线C 上,但不在直线l 上〔C 〕点P 即在直线l 上又在曲线C 上 〔D 〕点P 即不在直线l 上又不在曲2、 A ＝C ≠0,B ＝0是方程Ax 2＋Bxy ＋Cy 2＋Dx ＋Ey ＋F ＝0表示圆的( )条件〔A 〕充分不必要条件 〔B 〕必要不充分条件 〔C 〕充要条件 〔D 〕不充分不必要条件3、方程x 2+y 2+4mx-2y+5m=0表示圆的充要条件是〔 〕〔A 〕 1m 41<<〔B 〕m 1 〔C 〕41m <〔D 〕41m <或m 1 4、圆x 2＋y 2＋Dx ＋Ey ＋F ＝0的圆心坐标和直径分别是〔 〕〔A 〕(－2D ,－2E ) ；F E D 422－＋ 〔B 〕(2D ,2E ) ；F E D 422－＋ 〔C 〕(－2D ,－2E ) ；21(D 2＋E 2－4F) 〔D 〕(2D ,2E ) ；21(D 2＋E 2－4F) 5、圆的一条直径的两个端点是(2, 0), (2, －2),那么此圆的方程是〔 〕〔A 〕(x －2)2＋(y －1)2=1 〔B 〕(x －2)2＋(y ＋1)2=1〔C 〕(x －2)2＋(y ＋1)2=9 〔D 〕(x ＋2)2+(y ＋1)2=16、一个圆经过三点(－8, －1), (5, 12), (17, 4),那么此圆的圆心坐标是〔 〕〔A 〕(14/3, 5) 〔B 〕(5, 1) 〔C 〕(0, 0) 〔D 〕(5, －1)7、圆的方程是：x 2＋y 2－4x ＋6y ＋9=0,以下直线中通过圆心的是〔 〕〔A 〕3x ＋2y －1=0 〔B 〕3x ＋2y=0 〔C 〕3x －2y=0 〔D 〕3x －2y ＋1=08、曲线是与两定点O (0, 0),A(3,0)的距离的比为21的点的轨迹.这条曲线的方程是〔 〕 (A) (x ＋1)2＋y 2＝4 (B) (x ＋3)2＋y 2＝18 (C) (x －1)2＋y 2＝4 (D) (x －3)2＋y ＝189、假设点〔5a+1,12a 〕在圆〔x-1〕2+y 2=1的内部,那么a 的取值范围是〔 〕〔A 〕∣a ∣<1 〔B 〕∣a ∣<51〔C 〕∣a ∣<131 〔D 〕∣a ∣<21 10、直线3x ＋4y ＋12=0与圆(x －1)2＋(y ＋1)2=9的位置关系是〔 〕〔A 〕过圆心 〔B 〕相切 〔C 〕相离 〔D 〕相交但不过圆心11、直线4x －3y=2与以下哪一个圆相切〔 〕〔A 〕x 2＋y 2＝2 〔B 〕x 2＋y 2＋4x ＋6y ＋4=0〔C 〕x 2＋y 2－2x ＋3y=9 〔D 〕x 2＋y 2－4x ＋6y ＋4=012、圆(x －a)2＋(y －b)2=r 2 过原点,且与y 轴相切,那么a 、b 、r 满足的条件是〔 〕〔A 〕｜a ｜≠｜r ｜,b=0 〔B 〕｜b ｜＝｜r ｜≠0,a=0〔C 〕｜a ｜＝｜b ｜,r ≠0 〔D 〕｜a ｜＝｜r ｜≠0,b=013、圆x 2＋y 2=25截直线4x －3y=20所得的弦的中垂线的方程是〔 〕〔A 〕y=43x 〔B 〕y=－43x 〔C 〕y=－34x 〔D 〕y=34x 14、直线l 过点P(0, 2), 且被圆x 2＋y 2=4所截得的线段长为2,那么l 的斜率为〔 〕 〔A 〕2或－2〔B 〕22或－22〔C 〕3或－3〔D 〕33或－33 15、圆C ：x 2＋y 2＋2x ＋4y －3=0上到直线x ＋y ＋1=0的距离为2的点有〔 〕〔A 〕1个 〔B 〕2个 〔C 〕3个 〔D 〕4个16、圆心是(4, 7), 与直线3x －4y+1=0相切的圆的方程是17、与直线x ＋y －1=0相切于点(2, －1),圆心在直线2x ＋y=0上的圆的方程是18、以原点为圆心,在直线3x ＋4y ＋15=0上截得的弦长为8的圆的方程是 .19、与两条平行直线x ＋3y －5=0, x ＋3y －3=0相切,圆心在直线2x ＋y ＋3=0上的圆的方程是20、A(－1, 0)、B(5, 0), P 是圆x 2＋y 2－4x －5=0上的点,且和A 、B 不重合,那么k AP ·k BP =21、两条直线y=x ＋2, y=2x ＋a ＋1的交点在圆x 2＋y 2=4的内部,那么a 的取值范围是22、与两直线x-y+3=0及x-y-1=0都相切的圆的半径为23、求经过点P 〔6,－4〕且被圆x 2+y 2=20截得的弦长为 62的直线方程24、P (3, 0)是圆x 2＋y 2－8x －2y ＋12=0内的一点(1) 在圆上分别求出到点P 有最远距离和最近距离的点的坐标(2) 分别求出圆中过P 点的最短弦和最长弦所在直线的方程。

《 直 线 方 程 》 专 题 辅 导内容提要：本文是从知识要点、典型题型和解题技巧、一题多解、错解分析等方面，对《有向线段、定比分点》、《直线方程》进行专题复习，期望对高三的同学有所帮助。

知识要点：有向线段的数量和长度、两点间的距离、线段的定比分点、线段的中点坐标公式、三角形的重心坐标公式、直线的斜率、直线方程的几种形式。

典型题型和解题技巧一、 有向线段、定比分点 １．两点间距离公式的应用例１ 已知：1)(2+=x x f ，求证：|||)()(|b a b f a f -≤- 证明：如图１，设Ａ，Ｂ坐标分别为（１，a ）和 (1,b) 则||1)(|,|1)(22BO b b f AO a a f =+==+= |a –b|=|AB|.当b a ≠时，则三角形ＡＯＢ中，由||AO|-|BO||<|AB| 得｜f(a)-f(b)|<|a-b| 当a = b 时，|OA|=|OB| ,|a-b|=0, 故有 ｜f(a)-f(b)|=|a-b| 综上所述，得|||)()(|b a b f a f -≤-２．定比分点公式的应用 （１）公式的“逆用”例２ 如图２，已知两点Ａ（４，１）和Ｂ（－１，３），求线段ＡＢ和y 轴交 点Ｍ的坐标。

解：设点Ｍ的坐标为（０,y 0）,且λ=MBAM ，则，由定比分点公式得 4,1)1(40=∴+-+=λλλ,于是513413410=+⨯+=y ，即点M 的坐标是)513,0(M 。

（２）注意利用平面几何知识例3 如图3，已知A （5，-1）， B （-1，7），C （1，2），求的中A ABC ∠∆ 平分线AD 的长。

解：10)17()51(||22==++=AB5)12()15(||22=++-=AC 则由,2||||||||===AC AB CD BD λ 设点D （x 0,y 0）,则31211210=+⨯+-=x ，311212270=+⨯+=y即)311,31(D ，于是3214)3111()315(||22=--+-=AD说明：本例运用了三角形角平分线的性质：若AD 是ABC ∆的内角平分线，则|AB|：|AC|=|BD|：|CD|，在学习解析几何时，要尽可能地挖掘出所给图形的几何性质，以简化解题。

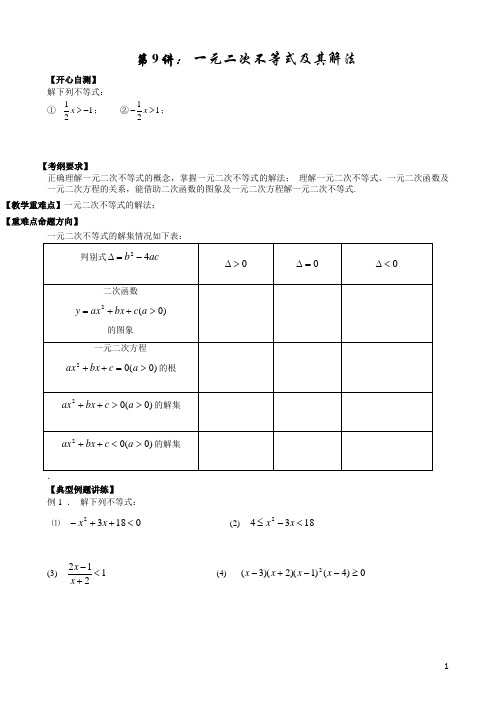
第9讲： 一元二次不等式及其解法【开心自测】解下列不等式：① 112x >-； ②112x ->；【考纲要求】正确理解一元二次不等式的概念，掌握一元二次不等式的解法； 理解一元二次不等式、一元二次函数及一元二次方程的关系，能借助二次函数的图象及一元二次方程解一元二次不等式.【教学重难点】一元二次不等式的解法；【重难点命题方向】一元二次不等式的解集情况如下表： 判别式ac b 42-=∆ 0>∆0=∆ 0<∆ 二次函数)0(2>++=a c bx ax y的图象一元二次方程)0(02>=++a c bx ax 的根)0(02>>++a c bx ax 的解集)0(02><++a c bx ax 的解集．【典型例题讲练】例1 ． 解下列不等式：⑴ 01832<++-x x (2) 18342<-≤x x(3)1212<+-x x (4) 0)4()1)(2)(3(2≥--+-x x x x例2设关于x 的不等式210ax bx ++>的解集为1{|1}3x x -<<，求a ，b.小结：二次不等式给出解集，既可以确定对应的二次函数图象开口方向（即a 的符号），又可以确定对应的二次方程的两个根，由此可根据根与系数关系建立系数字母关系式，或通过代入法求解不等式.变式：已知二次不等式20ax bx c ++<的解集为1{|3x x <或1}2x >，求关于x 的不等式20cx bx a -+>的解集.例3 2{|430}A x x x =-+<，2{|280}B x x x a =-+-≤，且A B ⊆，求a 的取值范围.小结：（1）解一元二次不等式含有字母系数时，要讨论根的大小从而确定解集.（2）集合间的关系可以借助数轴来分析，从而确定端点处值的大小关系.例4 若关于m 的不等式2(21)10mx m x m -++-≥的解集为空集，求m 的取值范围.变式1：解集为非空.变式2：解集为一切实数.小结：m 的不同实数取值对不等式的次数有影响，当不等式为一元二次不等式时，m 的取值还会影响二次函数图象的开口方向，以及和x 轴的位置关系. 因此求解中，必须对实数m 的取值分类讨论.例5．已知不等式02>++c bx ax 的解集为()βα,，且βα<<0，求不等式02<++a bx cx 的解集．练习：已知不等式02>++q px x 的解集为{}2131|<<-x x ，求不等式012>++px qx 的解集．例6．当a 为何值时，不等式01)1()1(22<----x a x a 的解是全体实数．、练习：已知常数R a ∈，解关于x 的不等式022<+-a x ax ．例7已知函数))(2lg(2)(),1lg()(R t t x x g x x f ∈+=+=⑴．当1-=t 时，解不等式)()(x g x f ≤；⑵．如果当]1,0[∈x 时，)()(x g x f ≤恒成立，求实数t 的取值范围．【基础限时训练】1．解不等式: (1) 03222>-+-x x (2) 01692≤+-x x⑶ 0)273)(132(22>+-+-x x x x ⑷23253≤--x x2．若关于x 的不等式01>+-x a x 的解集为),4()1,(+∞--∞ ，则实数a = ．3．已知不等式022>++c x ax 的解集为2131<<-x ，则=+c a ．4．若关于x 的方程09222=--k x kx 两实根有一个大于2，而另一个根小于2，则实数k 的取值范围是5．已知二次函数)(x f 的二次项系数为a ，且不等式x x f 2)(->的解集为)3,1(，⑴若方程06)(=+a x f 有两个相等的实数根，求)(x f 的解析式；⑵若)(x f 的最大值为正数，求实数a 的取值范围.【拔高限时训练】1. 函数2112y x x =+-的定义域是（ ）.A ．{|4x x <-或3}x >B ．{|43}x x -<<C ．{|4x x ≤-或3}x ≥D ．{|43}x x -≤≤2. 不等式2223931711()()33x x x x --+-≤的解集是（ ）.A ．[2，4]B ．(,2][4,)-∞+∞C ．RD ．(,2][4,)-∞-+∞3. 集合A={2|540}x x x -+≤，B=2{|560}x x x -+≥，则A B =（ ）.A ．{|12x x ≤≤或34}x ≤≤B ．{|12x x ≤≤且34}x ≤≤C ．{1，2，3，4}D ．{|41x x -≤≤-或23}x ≤≤4. 不等式(5)(2)0x x --<的解集为 .5. 已知两个圆的半径分别为1和5，圆心距满足210240d d -+<，则两圆的位置关系为 .6．已知不等式组⎪⎩⎪⎨⎧<+-<+-08603422x x x x 的解集是不等式0922<+-a x x 的解集的子集，则实数a 的取值范围是 ．7．已知不等式03)1(4)54(22>+---+x m x m m 对一切实数x 恒成立，求实数m 的取值范围【李老师5分钟答疑】。

高二数学第九章练习题在高二数学第九章练习题中，我们将练习和巩固在这一章节所学的知识和技能。

本文将按照题目的要求，呈现一些典型的练习题解答，帮助读者更好地理解和掌握这一章节内容。

一、函数与导数1. 计算下列函数的导数：（1）f(x) = 3x^2 - 2x + 1（2）g(x) = sin(x) + cos(x)解析：（1）对多项式函数来说，求导就是将每一项的指数乘以系数，并将指数减一。

因此，对于f(x) = 3x^2 - 2x + 1，它的导数为f'(x) = 6x - 2。

（2）对于三角函数的求导，我们需要使用三角函数的导数公式。

根据导数公式，对于g(x) = sin(x) + cos(x)，它的导数为g'(x) = cos(x) - sin(x)。

二、数列与数学归纳法1. 求下列数列的通项公式：（1）2, 5, 8, 11, ...（2）1, 3, 6, 10, ...解析：（1）对于等差数列来说，通项公式可以表示为an = a1 + (n-1)d，其中a1为首项，d为公差。

因此，对于这个数列，首项a1为2，公差d 为3，所以它的通项公式为an = 2 + 3(n-1)。

（2）对于这个数列来说，相邻两项之差逐次递增，可以发现，第n 项与前n-1项的差正好为n。

因此，这个数列的通项公式为an = 1 + 2 +3 + ... + n，即an = n(n+1)/2。

三、平面向量1. 求下列向量的数量积：（1）a = (1, 2), b = (-3, 4)（2）c = (2i + 3j), d = (4i - 2j)解析：（1）对于向量的数量积，可以直接将两个向量对应位置的分量相乘，然后求和。

因此，对于a = (1, 2)和b = (-3, 4)，它们的数量积为a·b = 1*(-3) + 2*4 = 5。

（2）对于向量c = (2i + 3j)和d = (4i - 2j)，它们的数量积为c·d =2*4 + 3*(-2) = 2。

高二数学下第九章复习讲义第1讲平面的基本性质一、典型例题例1、用符号语言写出下列图形应满足的条件图（1）图（2）分析；根据图形；准确地想象点、线、面这些基本元素的关系；然后用集合的符号语言表示出来。

书写的规律一般是：先平面再直线；最后为点。

在（1）中：平面α∩平面β= ；a∩α=A；b∩α=B在（2）中：α∩β= ；a⊂α；b⊂β；a∩ =P； b∩ =P；c∥ 。

例2、作出满足下列条件的图形：图（1）图（2）（1）α∩β=AB；a⊂α；b⊂β；a∥AB；b∩AB=M；（2）正方体ABCD—A1B1C1D1中；O为正方形ABCD中心；A1C∩平面C1BD=M；求作点M。

分析：（1）作图的顺序与读图的顺序相同；先平面再直线再到点。

如图（1）（2）设法把点M放到某两个平面的交线上；∵M∈A1C；A1C⊂平面AA1C1C（由AA1∥C1C；A1A；CC1是可以确定一个平面的）；∴M∈平面AA1C1C。

又M∈平面C1BD；∴M为平面AA1C1C与平面C1BD的公共点。

观察图象可知；C1、O也为上述两个平面的公共点；即平面AA1C1C∩平面C1BD=C1O。

∵M∈C1O；又M∈A1C；∴C1O∩A1C=M；即平面AA1C1C1内；两直线C1O与A1C的公共点就是所求作的点M。

评注：题（2）首先体现了转化的思想；将在空间难以把握的线面交点转化为同一平面内的线线交点；确定了交点的位置。

其次；将直线A1C放在平面AA1C1C内思考；这是处理直线典型的一种思考方法。

借助于平面AA1C1C；点M的位置就越来越具体了。

这种类似于平面几何辅助直线的平面；称之为辅助平面。

在研究空间图形时；经常要作这样的辅助平面。

进一步研究M点性质；还可发现M为A1C的三等分点；M是△C1BD的重心（中心）。

例3、求证：两两相交且不过同一点的四条直线共面。

分析：以文字语言出现的几何证明题；首先要“翻译”为符号语言写成已知、求证的形式；并辅之以正确的图形；然后再进行证明。

高二下学期数学第九章复习（4）空间向量的（坐标 ）运算（2）一、基础训练：1．已知空间三点的坐标为)2,5,1(-A 、)1,4,2(B 、)2,3,(+q p C ，若A 、B 、C 三点共线，则=p 3 ，=q 2 ． 2．在平行六面体1111D C B A ABCD -中， 4=AB ，3=AD ，51=AA ，o BAD 90=∠，o DAA BAA 6011=∠=∠，则1AC．3．O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足()||||AB AC OP OA AB AC λ=++u u u r u u u ru u u r u u u r u u u r u u u r ，[0,)λ∈+∞，则P 的轨迹一定通过ABC ∆的（ B ）()A 外心 ()B 内心 ()C 重心 ()D 垂心4．若(1,1,3)A m n +-，(2,,2)B m n m n -，(3,3,9)C m n +-三点共线，则m n +=0．5．已知(0,2,3)A ，(2,1,6)B -，(1,1,5)C -，若||a =r 且,a AB a AC ⊥⊥r u u u r r u u u r，则a r 的坐标为()()1,1,1,1,1,1---．6．已知,是空间二向量，若||3,||2,||a b a b ==-=r r r ra r 与b r 的夹角为60o ．7．已知向量)3,2,1(-=a ，)1,1,1(=b ，则向量a 在向量b方向上的射影向量的模为3． 二、例题分析：例1．在平行四边形ABCD 中，1==AC AB ，090=∠ACD ，将它沿对角线AC 折起，使AB与CD 成060角，求B 、D间的距离．（答案：2,）例2．在矩形ABCD 中，已知1=AB ，a BC =，⊥PA 平面ABCD ，2=PA ，若BC 边上存在唯一一点Q ，使得DQ PQ ⊥，M 是AD 上一点，M 在平面PQD 上的射影恰好是PQD ∆的重心，求线段AM 的长度及M 到平面PQD 的距离．（答案：23） PABCDM例3．在ABC ∆中2AB BC AC ===，现将ABC ∆沿着平面ABC 的法向量1AA uuu r平移到111A B C ∆的位置，31=BB ，D 是AB 的中点，F 是11C A 的中点，E 在1BB 上，⑴当131BB BE =时，求直线EC 与DF 所成角的大小； ⑵当E 点在1BB 上变化时，BE 为多长时DF CE ⊥．答案：⑴2arccos 10；⑵23．三、课后练习： 班级 学号 姓名1．四面体SABC 中，SC ＝AB ＝１，SA 与BC 中点分别为,P Q ，且22PQ =，则异面直线AB 与SC 所成的角为90o ．2．已知CD AB 2=，且点A 、B 、C 、D 不共线，则下列结论正确的是 （ D ）()A 四边形ABCD 是平行四边形 ()B 四边形ABDC 是平行四边形()C 四边形ABCD 是梯形()D 四边形ABDC 是梯形3．已知32134e e e a -+=，321245e e e b +-=，其中},,{321e e e 是一组正交基底，b r及a 之间的夹角的余弦值为13065． 4．从O 点出发的三条射线两两垂直，空间一点P 到这三条射线的距离分别为,,a b c ，则P 到O 的距离为2222a b c ++． 5．已知平面α内的60BOC ∠=o ，OA a =，OA 是平面α的斜线段，且45AOB AOC ∠=∠=o ，则点A 到平面α的距离为3a．6．如图，,,,,,M N E F G H 分别是四面体ABCD 中各棱的中点，若此四面体的对棱相等，则EF u u u r 与GH u u u u r 所成的角等于90o； ()EF NH MG ⋅+=u u u r u u u u r u u u u r_0．EDA B C AB C11F7．已知空间三个点(2,0,2)P -,(1,1,2)Q -和(3,0,4)R -，设a PQ =r u u u r ,b PR =r u u ur ，⑴求a r 与b r的夹角θ（用反三角函数表示）；⑵试确定实数k ，使ka b +r r 与2ka b -r r互相垂直；⑶试确定实数k ，使ka b +r r 与a kb +r r互相平行．答案：⑴10arccos 10⎛⎫- ⎪ ⎪⎝⎭；⑵52,2-；⑶1k =±． 8．如图，点P 是矩形ABCD 外一点，⊥PA 平面ABCD ，M 、N 分别是AB 、PC 的中点，⑴求证：AB MN ⊥；⑵若PDA θ∠=，能否确定θ使得MN 是异面直线AB 与PC 的公垂线？若可以确定θ，试求θ的值？若不能，说明理由． 答案：⑵ 45o．9．已知ABC ∆，将ABC ∆沿着平面ABC 的法向量1AA uuu r平移到111A B C ∆的位置，11BC AB ⊥，11BC AC ⊥，求证：11AB AC =．PA B C D M N。

高二数学暑期专题辅导材料一.温习内容温习〔第五章 平面向量〕二. 知识要点：1. 向量的概念：向量是既有大小，又有方向的量。

向量的大小〔长度〕叫做向量的模，模是非正数，可以比拟大小，但由于方向不能比拟大小，所以，向量不可以比拟大小，这是数量与向量的最大差异。

2. 向量的表示方法：〔1〕几何表示法。

向量可以用有向线段表示，如：A →B（）字母表示法：如、或、等。

2a b AB BC →→3. 零向量与单位向量：零向量：长度为零的向量叫做零向量，记作0。

单位向量：长度等于1个单位长度的向量叫做单位向量。

4. 平行向量、相等向量、共线向量。

平行向量〔共线向量〕：方向相反或相反的非零向量叫做平行向量。

规则0与任一向量平行，平行向量也叫做共线向量。

相等向量：长度相等且方向相反的向量叫做相等向量。

恣意两个相等的非零向量都可以用同一条有向线段表示。

5. 向量的加法：已知向量、，在平面内任取一点，作，，则向量叫a b A AB a BC b AC →=→=→做与的和，记作，即。

求两个向量和的运算，叫做向量的加a b a b AC a b +→=+法。

留意：〔1〕两个向量的和仍为向量。

〔2〕关于零向量与任一向量a 有a+0=0+a=a 。

6. 向量的加法法那么 〔1〕三角形法那么：〔首尾衔接〕 〔2〕平行四边形法那么：〔共终点〕 7. 向量的加法运算律。

〔1〕交流律：a+b=b+a〔2〕结合律：a+(b+c)=(a+b)+c8. 相反向量：与a 长度相等，方向相反的向量叫做a 的相反向量，记作-a 。

零向量的相反向量为零向量。

相反向量性质： （）1--=()a a（）20a a a a +-=-+=()()（）如、为相反向量，那么，，30a b a b b a a b =-=-+=9. 向量的减法：向量a 加上向量b 的相反向量叫做a 与b 的差。

记 a b a b -=+-()求两个向量差的运算叫做向量的减法。

高二数学课外辅导第一讲 解 析 法解析法又叫坐标法。

它是通过建立坐标系，把图形的几何条件用坐标或代数式表示出来。

然或进行代数运算，推出某些图形的性质及边角关系。

用坐标法证明几个重要定理或结论：1．平行四边形对角线的平方和等于四边形的平方和。

2．三角形的三条高（中线、角的平分线）相交于一点。

3．已知∠A ，b ，c ，求角的平分线AD 的长。

4．等边三角形内任意一点到三边的距离之和等于一个常数。

5．求证：)d c )(b a ()bd ac (22222++≤+。

练 习 题1． 菱形ABCD 的面积为9，顶点A 、C 分别在x 轴、y 轴上，顶点B 、D 在直线y =x （x >0）上，且BD=3，求菱形四个顶点的坐标。

2． 圆G 内接四边形ABCD ，AC ⊥BD ，E 、F 分别为AD 、BC 的中点，O 为对角线的交点，求证：OFGE 是平行四边形。

3． 在R t △ABC 中，∠A=900，D 、E 是斜边BC 的三等分点，若AD=sinx ，AE=cosx ，求BC 的长。

4．（1）求函数74x 10x 25x y 22+-++=的最小值； （2）求函数134851422++-++=x x x x y 的最大值。

5． 平面上三点A （－1，0），B （2，4），C （4，5）处分别放置质量为3克，4克，5克的重物，求这三质点的重心。

6． △ABC 中，若A （－2，1），B （5，0），C （3，6），D 点是BC 的中点，E 点是AC 的一个三等分点，求线段AD 与BE 的交点M 的坐标。

7． 已知点P （4，3），试在坐标轴上求与点P 距离等于a （a .>4）的点，并计算由这些点所围成的凸多边形的面积。

8． 函数232+-+=x x x y .的值域是___________________________.（2001.11）9．在平面直角坐标系中，方程b a b yx a yx ,(122=-++为不相等的两个实数）所代表的曲线是_______________________________.（1994. 选6）10．已知点集 {+-=⎭⎬⎫⎩⎨⎧≤-+-=2222)4(),(,)25()4()3(),(x y x B y x y x A ⎭⎬⎫>-22)25()5(y ，则点集B A 中的整点个数是________________.（1994. 填3） 11．已知方程)(2*∈=-N n x k n x 在区间]12,12(+-n n 上有两个不等的实根，则k的取值的范围是_________________________________.（1995.选4）12．直角坐标平面上，满足不等式组⎪⎩⎪⎨⎧≤+≥≤100313y x x y x y 的整点个数是___________.（1995.填4） 13．把圆1)1(22=-+y x 与椭圆9)1(922=++y x 的公共点用线段连接起来，所得的图形是_____________________________.（1996.选1）14．直角坐标平面中，若方程222)32()12(+-=+++y x y y x m 表示的曲线椭圆，则m的取值的范围是_________________________________.（1997.选4）15．过双曲线1222=-y x 的右焦点作直线l 交双曲线A 、B 两点，若实数λ使得│AB │=λ的直线恰有3条，则λ=___________（1997.填1）16．若椭圆4)(422=-+a y x 与抛物线y x 22=有公共点，则a 的取值的范围是_______________________.（1998.填5）17． 在平面直角坐标系中，满足2)1()1(22<-+-y x 的整点个数是_____.（1999.选2）18．已知点A 为双曲线122=-y x 的左顶点，点B 和点C 在双曲线的右支上，ABC ∆是等边三角形，则ABC ∆的面积是___________.(2000. .选3)。

2017—2018高二数学必修五导学案编号：09 编制人：孙衍常惠守华李国明审核人: 包科领导：包级领导：班级：姓名：小组：评价：高二数学高效课堂资料课题：等比数列预习案使用时间：2017.09.10【使用说明及学法指导】利用15分钟先精读一遍教材P44—P47，对概念、定理、公式进行勾画理解，并能用自己的语言阐述其内涵，在针对预习案进行二次研究。

【预习目标】通过对细胞分裂的观察抽象出等比数列的概念，归纳出等比数列通项公式，并能简单应用。

【课标要求】通过实例，理解等比数列的概念。

探索并掌握等比数列的通项公式。

能在具体的问题情境中，发现数列的等比关系，并能用有关知识解决相应的问题。

体会等比数列与指数函数的关系。

【核心素养】逻辑推理、抽象概括、数学运算. 【重点】等比数列的定义、通项、性质. 【难点】等比数列通项公式、前n 项和公式的推导、性质.【预习导学】【情境引入】（1）某种细胞开始时有1个,1h 后分裂成2个,2h 后分裂成4个,3h 后分裂成8个,如此进行下去,nh 后细胞的数目n a 等于多少呢？（2）一台计算机有病毒可以感染3台计算机，经过n 次感染后中毒的计算机数n b 又为多少？问题1：情境引入当中的几个数列有什么共同特点？试用一个式子描述等比数列的定义.问题2：如果等比数列{n a }的首项是1a ，公比为q ，那么根据等比数列的定义得到：qa a q a a q a a nn 12312,,如何得到1a 与n a 的关系式？其关系式怎样？【思考1】请用图象法表示出数列2nna ：问题3：等比数列是怎样定义的？其通项公式如何？【思考2】等比数列nna 32的首项和公比是什么？问题4：等比中项是怎样定义的？【思考3】任意两数都有等比中项吗？4与9的等比中项是多少？【我的疑惑】- 2 -课题：等比数列探究案使用时间：2017.09.10【学习目标】通过实例，能够掌握等比数列的通项公式及性质，体会等比数列在实际生活中的应用价值.探究一：等比数列通项公式的应用【例1】已知数列{}n a 的通项公式为32nn a ，证明这个数列是等比数列.【拓展】已知数列{}n a 是等比数列，*,,,m n p q N ,且m np q .证明：q p nm a a a a .【总结与反思】探究二：等比数列的综合应用【例2】某市近10年内的GDP 增长速度相同，第2年GDP 是19亿元，第6年GDP 是9亿元，问第10年该市的GDP 为多少？【总结与反思】【选做】在等比数列{}n a 中，若q>1，且756482,5,6a a a a a a 则.。