第五章 三角形单元测试卷(含答案)

2018-2019学年江镜中学三角形单元测试卷学校:___________姓名：___________班级：___________考号：___________一．选择题（共10小题）1．用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（ ）A．B．C．D．2．在生产和生活中，一些图形的性质得到广泛使用，请找出下列四个图形中使用性质与其它三个不同的是（ ）A．起重机B．活动挂架C．伸缩门D．升降平台3．下列长度的三条线段（单位：cm）能组成三角形的是（ ）A．1，2，1B．4，5，9C．6，8，13D．2，2，44．如图，在△ABC中，CD是∠ACB的外角平分线，且CD∥AB，若∠ACB＝100°，则∠B的度数为（ ）A．35°B．40o C．45o D．50o5．将两个直角三角板如图所示放置，DF恰好经过点C，AB与EF在同一条直线上，则∠BCF＝（ ）第4题第5题A．30°B．45°C．60°D．75°6．下列图形中，能确定∠1＞∠2的是（ ）A．B．C．D．7．已知非直角三角形ABC中，∠A＝45°，高BD与CE所在直线交于点H，则∠BHC的度数是（ ）A．45°B．45°或135°C．45°或125°D．135°8．下面的多边形中，内角和与外角和相等的是（ ）A．B．C．D．9．下列说法中正确的是（ ）A．三角形的角平分线是一条射线B．三角形的一个外角大于任何一个内角C．任意三角形的外角和都是180°D．内角和是1080°的多边形是八边形10．将若干个大小相等的正五边形排成环状，如图所示是前3个五边形，要完成这一圆环还需_______个正五边形（ ）A．6B．7C．8D．9二．填空题（共6小题）11．若n边形的每个内角都为135°，则n＝ ．12．如图，某人从点A出发，前进5m后向右转60°，再前进5m后又向右转60°，这样一直走下去，当他第一次回到出发点A时，共走了 m．13．如图△ABC中，将边BC沿虚线翻折，若∠1+∠2＝102°，则∠A的度数是 ．第12题第13题14．若△ABC中，∠ACB是钝角，AD是BC边上的高，若AD＝2，BD＝3．CD＝1，则△ABC的面积等于 ．15．一个凸多边形的内角中，最多有 个锐角．16．用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ABCDE，其中∠BAC＝ 度．三．解答题（共19小题）17．在△ABC中，AB＝9，BC＝2，并且AC为奇数，那么△ABC的周长为多少？18．在△ABC中，CD⊥AB于D，CE是∠ACB的平分线，∠A＝20°，∠B＝60°．求∠BCD和∠ECD的度数．19．在△ABC中，∠ACB＝90°，CD为AB边上的高，BE平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE＝∠CEF．20．如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．（1）CD与EF平行吗？为什么？（2）如果∠1＝∠2，且∠3＝115°，∠A＝30°，求∠B的度数．21．如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题．（1）将下面的表格补充完整：正多边形的边数3456 (18)∠α的度数 …… （2）根据规律，是否存在一个正n边形，使其中的∠α＝20°？若存在，直接写出n的值；若不存在，请说明理由．（3）根据规律，是否存在一个正n边形，使其中的∠α＝21°？若存在，直接写出n的值；若不存在，请说明理由．22．四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交直线AE于点O．（1）若点O在四边形ABCD的内部，①如图1，若AD∥BC，∠B＝40°，∠C＝70°，则∠DOE＝ °；②如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来．（2）如图3，若点O在四边形ABCD的外部，请你直接写出∠B、∠C、∠DOE之间的数量关系．2019年06月03日735608的初中数学组卷参考答案与试题解析一．选择题（共10小题）1．用三角板作△ABC的边BC上的高，下列三角板的摆放位置正确的是（ ）A．B．C．D．【分析】根据高线的定义即可得出结论．【解答】解：B，C，D都不是△ABC的边BC上的高，故选：A．【点评】本题考查的是作图﹣基本作图，熟知三角形高线的定义是解答此题的关键．2．在生产和生活中，一些图形的性质得到广泛使用，请找出下列四个图形中使用性质与其它三个不同的是（ ）A．起重机B．活动挂架C．伸缩门D．升降平台【分析】根据三角形的稳定性解答即可．【解答】解：因为三角形具有稳定性，所以只有A应用三角形的稳定性，而其他三个选项是利用四边形的不稳定性，所以A使用性质与其它三个不同，故选：A．【点评】此题考查三角形的稳定性，关键是根据三角形的稳定性和四边形的不稳定性解答．3．下列长度的三条线段（单位：cm）能组成三角形的是（ ）A．1，2，1B．4，5，9C．6，8，13D．2，2，4【分析】三角形的任意两边的和大于第三边，根据三角形的三边关系就可以求解．【解答】解：根据三角形的三边关系，知A、1+1＝2，不能够组成三角形，故本选项错误；B、4+5＝9，不能够组成三角形，故本选项错误；C、6+8＞13，能够组成三角形，故本选项正确；D、2+2＝4，不能够组成三角形，故本选项错误．故选：C．【点评】本题考查了三角形的三边关系，在运用三角形三边关系判定三条线段能否构成三角形时，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形．4．如图，在△ABC中，CD是∠ACB的外角平分线，且CD∥AB，若∠ACB＝100°，则∠B的度数为（ ）A．35°B．40o C．45o D．50o【分析】根据平行线的性质和三角形的外角性质解答即可．【解答】解：∵∠ACB＝100°，∴∠ECB＝80°，∵CD是∠ACB的外角平分线，∴∠DCB＝40°，∵CD∥AB，∴∠B＝∠DCB＝40°，故选：B．【点评】此题考查三角形外角的性质，关键是根据平行线的性质和三角形的外角性质解答．5．将两个直角三角板如图所示放置，DF恰好经过点C，AB与EF在同一条直线上，则∠BCF＝（ ）A．30°B．45°C．60°D．75°【分析】根据三角形内角和定理计算即可．【解答】解：在△BCF中，∵∠BFC＝45°，∠B＝60°，∴∠BCF＝180°﹣45°﹣60°＝75°，故选：D．【点评】本题考查三角形的内角和定理，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．6．下列图形中，能确定∠1＞∠2的是（ ）A．B．C．D．【分析】分别根据对顶角相等、平行线的性质、三角形外角的性质对四个选项进行逐一判断即可．【解答】解：A、∵∠1与∠2是对顶角，∴∠1＝∠2，故本选项错误；B、若两条直线平行，则∠1＝∠2，若所截两条直线不平行，则∠1与∠2无法进行判断，故本选项正确；C、∵∠1是∠2所在三角形的一个外角，∴∠1＞∠2，故本选项正确；D、∵已知三角形是直角三角形，∴由直角三角形两锐角互余可判断出∠1＝∠2．故选：C．【点评】本题考查的是对顶角相等、平行线的性质、三角形外角的性质及直角三角形的性质，熟知以上知识是解答此题的关键．7．已知非直角三角形ABC中，∠A＝45°，高BD与CE所在直线交于点H，则∠BHC的度数是（ ）A．45°B．45°或135°C．45°或125°D．135°【分析】①△ABC是锐角三角形时，先根据高线的定义求出∠ADB＝90°，∠BEC＝90°，然后根据直角三角形两锐角互余求出∠ABD，再根据三角形的一个外角等于与它不相邻的两个内角的和列式进行计算即可得解；②△ABC是钝角三角形时，根据直角三角形两锐角互余求出∠BHC＝∠A，从而得解．【解答】解：①如图1，△ABC是锐角三角形时，∵BD、CE是△ABC的高线，∴∠ADB＝90°，∠BEC＝90°，在△ABD中，∵∠A＝45°，∴∠ABD＝90°﹣45°＝45°，∴∠BHC＝∠ABD+∠BEC＝45°+90°＝135°；②如图2，△ABC是钝角三角形时，∵BD、CE是△ABC的高线，∴∠A+∠ACE＝90°，∠BHC+∠HCD＝90°，∵∠ACE＝∠HCD（对顶角相等），∴∠BHC＝∠A＝45°．综上所述，∠BHC的度数是135°或45°．故选：B．【点评】本题主要考查了直角三角形的性质，三角形的内角和定理，三角形的高线，难点在于要分△ABC是锐角三角形与钝角三角形两种情况讨论，作出图形更形象直观．8．下面的多边形中，内角和与外角和相等的是（ ）A．B．C．D．【分析】根据多边形的内角和公式（n﹣2）•180°与多边形的外角和定理列式进行计算即可得解．【解答】解：设多边形的边数为n，根据题意得（n﹣2）•180°＝360°，解得n＝4．故选：B．【点评】本题考查了多边形的内角和公式与外角和定理，熟记公式与定理是解题的关键．9．下列说法中正确的是（ ）A．三角形的角平分线是一条射线B．三角形的一个外角大于任何一个内角C．任意三角形的外角和都是180°D．内角和是1080°的多边形是八边形【分析】分别根据三角形的角平分线、三角形外角的性质、多边形内角和定理对各选项进行逐一分析即可．【解答】解：A、三角形的角平分线是一条线段，故本选项错误；B、三角形的一个外角大于任何一个和它不相邻的内角，故本选项错误；C、任意多边形的外角和都是360°，故本选项错误；D、1080°÷180°+2＝8，即内角和是1080°的多边形是八边形，故本选项正确．故选：D．【点评】本题考查的是多角形内角和定理，三角形的有关概念，熟知三角形的内角与外角的关系是解答此题的关键．10．将若干个大小相等的正五边形排成环状，如图所示是前3个五边形，要完成这一圆环还需_______个正五边形（ ）A．6B．7C．8D．9【分析】先根据多边形的内角和公式（n﹣2）•180°求出正五边形的每一个内角的度数，再延长五边形的两边相交于一点，并根据四边形的内角和求出这个角的度数，然后根据周角等于360°求出完成这一圆环需要的正五边形的个数，然后减去3即可得解．【解答】解：五边形的内角和为（5﹣2）•180°＝540°，所以正五边形的每一个内角为540°÷5＝108°，如图，延长正五边形的两边相交于点O，则∠1＝360°﹣108°×3＝360°﹣324°＝36°，360°÷36°＝10，∵已经有3个五边形，∴10﹣3＝7，即完成这一圆环还需7个五边形．故选：B．【点评】本题考查了多边形的内角和公式，延长正五边形的两边相交于一点，并求出这个角的度数是解题的关键，注意需要减去已有的3个正五边形．二．填空题（共6小题）11．若n边形的每个内角都为135°，则n＝　8　．【分析】首先求得外角的度数，然后利用多边形的外角和是360度，列式计算即可求解．【解答】解：外角的度数是：180﹣135＝45°，则n＝360°÷45°＝8．故答案为：8．【点评】本题考查了正多边形的性质，正确理解多边形的外角和定理是关键．12．如图，某人从点A出发，前进5m后向右转60°，再前进5m后又向右转60°，这样一直走下去，当他第一次回到出发点A时，共走了　30　m．【分析】从A点出发，前进5m后向右转60°，再前进5m后又向右转60°，…，这样一直走下去，他第一次回到出发点A时，所走路径为正多边形，根据正多边形的外角和为360°，判断多边形的边数，再求路程．【解答】解：依题意可知，某人所走路径为正多边形，设这个正多边形的边数为n，则60n＝360，解得n＝6，∴他第一次回到出发点A时一共走了：5×6＝30（m），故答案为：30．【点评】本题考查了多边形的外角和，正多边形的判定与性质．关键是根据每一个外角判断多边形的边数．13．如图△ABC中，将边BC沿虚线翻折，若∠1+∠2＝102°，则∠A的度数是　51°　．【分析】延长B'E，C'F，交于点D，依据∠A＝∠D，∠AED+∠AFD＝258°，即可得到∠A的度数．【解答】解：如图，延长B'E，C'F，交于点D，由折叠可得，∠B＝∠B'，∠C＝∠C'，∴∠A＝∠D，又∵∠1+∠2＝100°，∴∠AED+∠AFD＝360°﹣102°＝258°，∴四边形AEDF中，∠A＝（360°﹣258°）＝51°，故答案为：51°．【点评】本题主要考查了三角形内角和定理，解决问题的关键是构造四边形，利用四边形内角和进行计算．14．若△ABC中，∠ACB是钝角，AD是BC边上的高，若AD＝2，BD＝3．CD＝1，则△ABC的面积等于　2　．【分析】首先根据题意画出图形，求出BC，再根据三角形的面积公式列式计算即可．【解答】解：如图．∵BD＝3，CD＝1，∴BC＝BD﹣CD＝2，又∵AD是BC边上的高，AD＝2，∴△ABC的面积＝BC•AD＝×2×2＝2．故答案为2．【点评】本题考查了三角形的面积，三角形的高的定义，掌握钝角三角形的高的画法进而画出图形是解题的关键．15．一个凸多边形的内角中，最多有　3　个锐角．【分析】根据任意凸多边形的外角和是360°．可知它的外角中，最多有3个钝角，则内角中，最多有3个锐角．【解答】解：一个凸多边形的内角中，最多有3个锐角．【点评】注意每个内角与其相邻的外角是邻补角，由于多边形的外角和是不变的，所以要分析内角的情况可以借助外角来分析．16．用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ABCDE，其中∠BAC＝　36　度．【分析】利用多边形的内角和定理和等腰三角形的性质即可解决问题．【解答】解：∵∠ABC＝＝108°，△ABC是等腰三角形，∴∠BAC＝∠BCA＝36度．【点评】本题主要考查了多边形的内角和定理和等腰三角形的性质．n边形的内角和为：180°（n﹣2）．三．解答题（共19小题）17．在△ABC中，AB＝9，BC＝2，并且AC为奇数，那么△ABC的周长为多少？【分析】根据三角形的三边关系，就可以求出AC的范围，再结合AC为奇数确定AC的值，从而得到△ABC的周长．【解答】解：根据三角形三边关系有AB﹣BC＜AC＜AB+BC，所以9﹣2＜AC＜9+2，即7＜AC＜11．又因为AC为奇数，所以AC＝9．所以△ABC的周长＝9+9+2＝20．【点评】考查了三角形的三边关系，同时注意奇数这一条件．18．在△ABC中，CD⊥AB于D，CE是∠ACB的平分线，∠A＝20°，∠B＝60°．求∠BCD和∠ECD 的度数．【分析】由CD⊥AB与∠B＝60°，根据两锐角互余，即可求得∠BCD的度数，又由∠A＝20°，∠B＝60°，求得∠ACB的度数，由CE是∠ACB的平分线，可求得∠ACE的度数，然后根据三角形外角的性质，求得∠CEB的度数．【解答】解：∵CD⊥AB，∴∠CDB＝90°，∵∠B＝60°，∴∠BCD＝90°﹣∠B＝90°﹣60°＝30°；∵∠A＝20°，∠B＝60°，∠A+∠B+∠ACB＝180°，∴∠ACB＝100°，∵CE是∠ACB的平分线，∴∠ACE＝∠ACB＝50°，∴∠CEB＝∠A+∠ACE＝20°+50°＝70°，∠ECD＝90°﹣70°＝20°【点评】此题考查了三角形的内角和定理，三角形外角的性质以及三角形高线，角平分线的定义等知识．此题难度不大，解题的关键是数形结合思想的应用．19．已知△ABC中，∠ACB＝90°，CD为AB边上的高，BE平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE＝∠CEF．【分析】题目中有两对直角，可得两对角互余，由角平分线及对顶角可得两对角相等，然后利用等量代换可得答案．【解答】证明：∵∠ACB＝90°，∴∠1+∠3＝90°，∵CD⊥AB，∴∠2+∠4＝90°，又∵BE平分∠ABC，∴∠1＝∠2，∴∠3＝∠4，∵∠4＝∠5，∴∠3＝∠5，即∠CFE＝∠CEF．【点评】本题考查了三角形角平分线、中线和高的有关知识；正确利用角的等量代换是解答本题的关键．20．如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．（1）CD与EF平行吗？为什么？（2）如果∠1＝∠2，且∠3＝115°，∠A＝30°，求∠B的度数．【分析】（1）先根据垂直的定义得到∠CDB＝∠EFB＝90°，然后根据同位角相等，两直线平行可判断EF∥CD；（2）由EF∥CD，根据平行线的性质得∠2＝∠BCD，而∠1＝∠2，所以∠1＝∠BCD，根据内错角相等，两直线平行得到DG∥BC，所以∠ACB＝∠3＝105°，根据三角形的内角和即可得到结论．【解答】解：（1）CD与EF平行．理由如下：∵CD⊥AB，EF⊥AB，∴∠CDB＝∠EFB＝90°，∴EF∥CD；（2）∵EF∥CD，∴∠2＝∠BCD，∵∠1＝∠2，∴∠1＝∠BCD，∴DG∥BC，∴∠ACB＝∠3＝115°，∵∠A＝30°，∴∠B＝35°．【点评】本题考查了平行线的判定与性质：同位角相等，两直线平行；内错角相等，两直线平行；两直线平行，同位角相等．21．如果一个多边形的各边都相等，且各内角也都相等，那么这个多边形就叫做正多边形，如图，就是一组正多边形，观察每个正多边形中∠α的变化情况，解答下列问题．（1）将下面的表格补充完整：正多边形的边数3456 (18)∠α的度数　60° 45° 36° 30°　……　10°　（2）根据规律，是否存在一个正n边形，使其中的∠α＝20°？若存在，直接写出n的值；若不存在，请说明理由．（3）根据规律，是否存在一个正n边形，使其中的∠α＝21°？若存在，直接写出n的值；若不存在，请说明理由．【分析】（1）根据多边形内角和公式求出多边形的内角和，再根据三角形内角和定理求出即可；（2）根据表中的结果得出规律，根据规律得出方程，求出方程的解即可；（3）根据表中的结果得出规律，根据规律得出方程，求出方程的解即可．【解答】解：（1）填表如下：正多边形的边数3456 (18)∠α的度数60°45°36°30°……10°故答案为：60°，45°，36°，30°，10°；（2）存在一个正n边形，使其中的∠α＝20°，理由是：根据题意得：°＝20°，解得：n＝9，即当多边形是正九边形，能使其中的∠α＝20°；（3）不存在，理由如下：假设存在正n边形使得∠α＝21°，得，解得：，又n是正整数，所以不存在正n边形使得∠α＝21°．【点评】本题考查了多边形的内角与外角和等腰三角形的性质，能求出多边形的一个内角的度数是解此题的关键，注意：多边形的内角和＝（n﹣2）×180°．22．四边形ABCD中，∠BAD的角平分线与边BC交于点E，∠ADC的角平分线交直线AE于点O．（1）若点O在四边形ABCD的内部，①如图1，若AD∥BC，∠B＝40°，∠C＝70°，则∠DOE＝　125　°；②如图2，试探索∠B、∠C、∠DOE之间的数量关系，并将你的探索过程写下来．（2）如图3，若点O在四边形ABCD的外部，请你直接写出∠B、∠C、∠DOE之间的数量关系．【分析】（1）①根据平行线的性质和角平分线的定义可求∠BAE，∠CDO，再根据三角形外角的性质可求∠AEC，再根据四边形内角和等于360°可求∠DOE的度数；②根据三角形外角的性质和角平分线的定义可得∠DOE和∠BAD、∠ADC的关系，再根据四边形内角和等于360°可求∠B、∠C、∠DOE之间的数量关系；（2）g根据四边形和三角形的内角和得到∠BAD+∠ADC＝360°﹣∠B﹣∠C，∠EAD+∠ADO＝180°﹣∠DOE，根据角平分线的定义得到∠BAD＝2∠EAD，∠ADC＝2∠ADO，于是得到结论．【解答】解：（1）①∵AD∥BC，∠B＝40°，∠C＝70°，∴∠BAD＝140°，∠ADC＝110°，∵AE、DO分别平分∠BAD、∠CDA，∴∠BAE＝70°，∠ODC＝55°，∴∠AEC＝110°，∴∠DOE＝360°﹣110°﹣70°﹣55°＝125°；故答案为：125；②∠B+∠C+2∠DOE＝360°，理由：∵∠DOE＝∠OAD+∠ADO，∵AE、DO分别平分∠BAD、∠CDA，∴2∠DOE＝∠BAD+∠ADC，∵∠B+∠C+∠BAD+∠ADC＝360°，∴∠B+∠C+2∠DOE＝360°；（2）∠B+∠C＝2∠DOE，理由：∵∠BAD+∠ADC＝360°﹣∠B﹣∠C，∠EAD+∠ADO＝180°﹣∠DOE，∵AE、DO分别平分∠BAD、∠CDA，∴∠BAD＝2∠EAD，∠ADC＝2∠ADO，∴∠BAD+∠ADC＝2（∠EAD+∠ADO），∴360°﹣∠B﹣∠C＝2（180°﹣∠DOE），∴∠B+∠C＝2∠DOE．【点评】此题考查了多边形内角与外角，平行线的性质，角平分线的定义，关键是熟练掌握四边形内角和等于360°的知识点．。

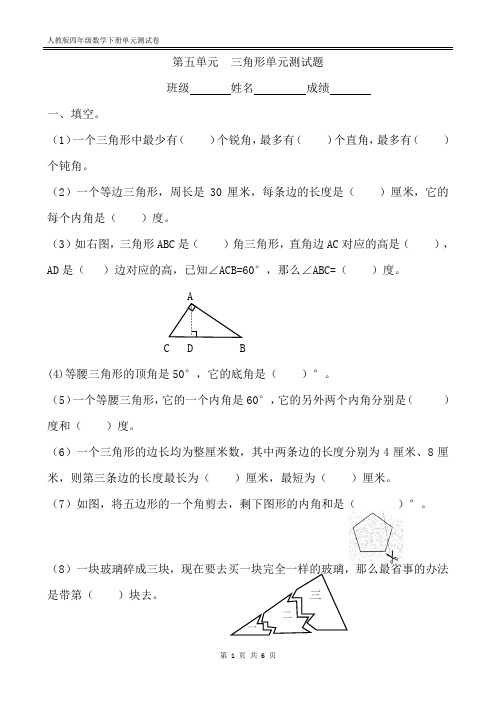
第五单元三角形单元测试题班级姓名成绩一、填空。

（1）一个三角形中最少有（）个锐角，最多有（）个直角，最多有（）个钝角。

（2）一个等边三角形，周长是30厘米，每条边的长度是（）厘米，它的每个内角是（）度。

（3）如右图，三角形ABC是（）角三角形，直角边AC对应的高是（），AD是（）边对应的高，已知∠ACB=60°，那么∠ABC=（）度。

C D B(4)等腰三角形的顶角是50°，它的底角是（）°。

（5）一个等腰三角形，它的一个内角是60°，它的另外两个内角分别是（）度和（）度。

（6）一个三角形的边长均为整厘米数，其中两条边的长度分别为4厘米、8厘米，则第三条边的长度最长为（）厘米，最短为（）厘米。

（7）如图，将五边形的一个角剪去，剩下图形的内角和是（）°。

（8）一块玻璃碎成三块，现在要去买一块完全一样的玻璃，那么最省事的办法是带第（）块去。

三二一二、选择题。

（1）衣架设计成下图这样的形状是应用了（）。

A.三角形稳定性B.四边形稳定性C.三角形不稳定性D.四边形不稳定性（2）下面每组的三根小棒，能拼成三角形的是（）。

A.2cm、3cm、6cmB.3cm、4cm、6cmC.4cm、5cm、9cmD.4cm、6cm、10cm（3）在三角形ABC中，∠A的度数正好等于∠B与∠C的度数之和，三角形ABC 一定是（）。

A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形（4）从5根长分别是3厘米、4厘米、5厘米、6厘米、7厘米的小棒中选择3根摆三角形，一共有（）种不同的选择方法。

A.3B.5C.7D.9（5）下面（）的说法不正确的。

A.等腰三角形的底角可能是钝角。

B.有一个角是60°的等腰三角形是等边三角形。

C.直角三角形中的两个锐角的和等于90°。

D.锐角三角形任意两个内角的和大于90°。

（6）已知三角形ABC为直角三角形，∠B=90°。

新人教版四年级下册《第5章三角形》小学数学-有答案-单元测试卷（24）一、填一填．（18分）．1. 一个三角形有________条边，________个内角和________个顶点。

2. 三角形按角分类分为________三角形、________三角形和________三角形。

3. 一个三角形，最多有________个直角，最多有________个钝角，最少有________个锐角。

4. 两个完全相同的直角三角形可以拼成一个________，也可以拼成一个________．5. 在等腰三角形里，两腰________，两个底角也________．6. 如果把直角三角形的一条直角边看作高，那么另一条直角边就是________．7. 一个直角三角形的一个锐角等于45度，另一个锐角等于________，这个三角形又叫________．8. 个三角形，如果三个内角都相等，那么它一定是________三角形；如果有两个内角相等，那么它一定是________三角形。

二、判断，正确的画“√”，错误的画“×”．（8分）直角三角形的两个锐角的和一定等于90∘．________．（判断对错）三角形中任意两个角的和大于第三个角。

________．（判断对错）三角形的任意两边的和大于第三边。

________．（判断对错）钝角三角形只有一条高。

________．（判断对错）．三角形中最大的角不小于60度。

________．（判断对错）等边三角形是特殊的等腰三角形。

________．（判断对错）．三角形的内角和是180∘，平行四边形的内角和是360∘．________．（判断对错）用三根不一样长的小棒一定能围成一个三角形。

________．（判断对错）三、选一选．（8分）等边三角形是（）三角形。

A.直角B.钝角C.锐角一个三角形有两个角都是45∘，这个三角形一定不是（）三角形。

A.锐角B.直角C.等腰把一个等边三角形平均分成两个小三角形，其中一个小三角形的内角和是（）度。

（必考题）小学数学四年级下册第五单元三角形测试卷（含答案解析）一、选择题1．下面各组线段能围成三角形的是（）。

A. 3厘米、4厘米、7厘米B. 4厘米、3厘米、6厘米C. 6厘米、6厘米、12厘米2．三角形中，已知两条边长分别为1.8厘米和1.3厘米，第三条边可能长（）。

A. 3厘米B. 3.2厘米C. 3.1厘米D. 0.5厘米3．在一个三角形中，其中两角之和是130°，另一个角是（）。

A. 30°B. 40°C. 50°4．在直角三角形中，一个锐角是36°，另一个锐角是（）。

A. 144°B. 54°C. 44°5．一个三角形的两条边分别是5厘米，10厘米，第三条边的长度可能是（）厘米。

A. 5 B. 12 C. 186．一个等腰三角形的顶角是80°，那么另外两个内角分别是（）。

A. 40°和60°B. 80°和20°C. 50°和50°7．下面三组木棒中（）不能拼成三角形。

（单位：厘米）A.B.C.8．根据下列描述，一定是锐角三角形的是（）。

A. 有一个内角是85°的三角形B. 有两个内角都是锐角的三角形C. 其中最大的内角小于90°D. 等腰三角形9．下面三组小棒不能围成三角形的是（）A. 6cm、6cm、12cmB. 4cm、6cm、7cmC. 3cm、3cm、3cm10．下列各线段，不能围成三角形的是（）A. 6cm 6cm 6cmB. 7cm 4cm 4cmC. 2cm 4cm 6cm11．莉莉用三根小棒摆成一个三角形，两根小棒的长度分别是4厘米和7厘米，第三根小棒的长度不可能是（）。

A. 3厘米B. 4厘米C. 5厘米12．一个三角形两个内角的和小于第三个角，这个三角形一定是（）三角形。

A. 直角B. 钝角C. 锐角D. 等边二、填空题13．一个三角形的两条边分别是6厘米和5厘米，第三条边比________厘米长，比________厘米短。

四年级下册数学单元测试卷-第五单元三角形-人教版(含答案)一、选择题(共5题，共计20分)1、一个等腰三角形，它的顶角是一个底角的3倍，它的顶角是（）。

A.108°B.72°C.36°2、下面每组中的三条线段，不能围成三角形的是（）。

A.5cm、8cm、3cmB.17cm、16cm、2cmC.1dm、6cm、0.06m3、下图中，三角形的三条边相等，则每个角是( )。

A.30°B.40°C.60°4、一个等腰三角形，它的顶角是一个底角的3倍，它的顶角是（）。

A.108°B.72°C.36°5、下面三组小棒中，能围城三角形的一组是（）。

A. B. C.二、填空题(共8题，共计24分)6、如下图，一块三角形玻璃损坏了一个角，这个角的度数是________，原来这块玻璃的形状是________三角形。

7、一个等腰三角形的一个底角是55°，它的顶角是________度；如果它的顶角是30度，它的底角是________度．8、如图，△ABC为一个等腰直角三角形，则∠A=________°，∠B=________°，∠C=________°．9、________都相等的三角形叫等边三角形，它的每个角都是________角。

10、有3cm、8cm的小棒各两根，选其中三根围成一个等腰三角形，它的周长是________cm。

11、一条红领巾的顶角是130°，它的一个底角是________度。

12、想一想：下面图中有几个正方形？有几个长方形？有几个三角形？有________个正方形，有________个长方形，有________个三角形。

13、两条边相等的三角形是________。

三、判断题(共4题，共计8分)14、所有三角形的内角和都是180°。

（）15、芳芳画出了三条边的长分别是4cm、10cm和5cm的三角形。

【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

】第五单元检测一、填空题。

1.三角形有()条边,()个角。

2.直角三角形的内角和是(),如果将两个完全相同的直角三角形拼成一个大的直角三角形,这个大的直角三角形的内角和是()。

3.用一根长48厘米的铁丝围成一个等边三角形,这个等边三角形的边长是()厘米。

4.一个三角形中至少有()个锐角,最多有()个钝角。

5.一个直角三角形,有一个锐角是35°,另一个锐角是()。

6.在许多建筑中,经常可以见到三角形,是因为三角形具有()。

7.至少用()个完全相同的直角三角形可以拼成一个长方形;至少用()个同样的等边三角形可以拼成一个梯形。

8.已知∠1、∠2、∠3是三角形中的三个内角,其中∠1=70°,∠2=35°,那么∠3=()。

二、判断题。

(正确的画“ ”,错误的画“✕”)1.有两个角是锐角的三角形一定是锐角三角形。

()2.两个直角三角形一定可以拼成一个长方形。

()3.等腰三角形一定是锐角三角形。

()4.一个三角形中不可能有两个钝角,但可能有两个直角。

()5.等腰三角形可能是直角三角形也可能是钝角三角形。

()6.直角三角形只有一条高。

()三、选择题。

(把正确答案的序号填在括号里)1.红领巾是一个()三角形,还是一个()三角形。

A.锐角B.直角C.钝角D.等腰2.两个完全一样的()三角形,一定能拼成一个正方形。

A.锐角B.直角C.钝角D.等腰直角3.一个三角形的两条边分别是7厘米、15厘米,第三条边的长度可能是()厘米。

A.8B.20C.25D.504.下面能围成三角形的一组线段是()(单位:厘米)。

A.6、7、8B.3、5、8C.4、6、11D.2、4、6四、仔细想,认真画。

1.画出下面每个三角形的底边上的高。

2.在下面的方格图中画一个三角形,使它既是钝角三角形又是等腰三角形。

五、分一分。

六、解决问题。

1.一个等腰三角形的底边长9厘米,腰比底边少2厘米,这个三角形的周长是多少厘米?2.在一个直角三角形中,其中一个锐角的度数是另一个锐角的2倍。

全等三角形单元测试题一、填空题（每小题4分,共32分）.1．已知：///≌，/ABC A B C∆∆∠=∠，70B B∠=∠，/A A=，则AB cmC∠=︒，15 /∠=_________，//CA B=__________．∆中，AB=AC，AD⊥BC于D点，E、F分别为DB、DC的中点，则图中共有全等三角2．如图1，在ABC形_______对．图1 图2 图33．已知△AB C≌△A′B′C′，若△ABC的面积为10 cm2，则△A′B′C′的面积为______ cm2，若△A′B′C′的周长为16 cm，则△AB C的周长为________cm．4．如图2所示，∠1=∠2，要使△ABD≌△ACD，需添加的一个条件是________________(只添一个条件即可)．5．如图3所示，点F、C在线段BE上，且∠1=∠2，BC=EF，若要使△ABC≌△DEF，则还需补充一个条件________，依据是________________．6．三角形两外角平分线和第三个角的内角平分线_____一点，且该点在三角形______部．7．如图4，两平面镜α、β的夹角θ，入射光线AO平行于β，入射到α上，经两次反射后的出射光线CB平行于α，则角θ等于________．图4 图5 图68．如图5，直线AE ∥BD ，点C 在BD 上，若AE ＝4，BD ＝8，△ABD 的面积为16，则ACE △ 的面积为______．二、选择题（每小题4分,共24分）9．如图6，AE ＝AF ，AB ＝AC ，EC 与B F 交于点O ，∠A ＝600，∠B ＝250，则∠EOB 的度数为（ ）A 、600B 、700C 、750D 、85010．△ABC ≌△DEF ，且△ABC 的周长为100 cm ，A 、B 分别与D 、E 对应，且AB ＝35 cm ，DF =30 cm ，则EF 的长为( )A ．35 cmB ．30 cmC ．45 cmD ．55 cm11．图7是一个由四根木条钉成的框架，拉动其中两根木条后，它的形状将会改变，若固定其形状，下列有四种加固木条的方法，不能固定形状的是钉在________两点上的木条．( )A ．A 、FB ．C 、E C ．C 、AD ．E 、F12．要测量河两岸相对的两点A 、B 的距离，先在AB 的垂线BF 上取两点C 、D ，使CD =•BC ，再定出BF的垂线DE ，使A 、C 、E 在一条直线上，可以证明△EDC ≌△ABC ，•得到ED =AB ，因此测得ED 的长就是AB 的长（如图8），判定△EDC ≌△ABC 的理由是（ ）A ．边角边公理B ．角边角公理；C ．边边边公理D ．斜边直角边公理13．如图9，在△ABC 中，∠A :∠B :∠C =3:5:10，又△MNC ≌△ABC ，则∠BCM ：∠BCN 等于（ ）A ．1:2B ．1:3C ．2:3D ．1:414．如图10，P 是∠AOB 平分线上一点，CD ⊥OP 于F ，并分别交OA 、OB 于CD ，则CD _____P 点到∠AOB N A M C B 图7 图8 图9 图10两边距离之和．( )A．小于B．大于C．等于D．不能确定三、解答题（共46分）中，∠ACB=90°，延长BC至B'，使15．已知如图11，ABCC B'=BC，连结A B'．求证：△AB B'是等腰三角形．参考答案。

第五章单元测试一、选择题（本大题共10个小题，每小题3分，共30分．每小题均有四个选项，其中只有一项符合题目要求）1.下列四幅图中，灯光与影子的位置合理的是（）A.B.C.D.2.下列立体图形中，俯视图不是圆的是（）A.B.C.D.3.如图所示物体的左视图是（）A.B.C.D.4.如图是由10个同样大小的小正方体摆成的几何体，将小正方体①移走后，则关于新几何体的三视图描述正确的是（）A.俯视图不变，左视图不变B.主视图改变，左视图改变C.俯视图不变，主视图不变D.主视图改变，俯视图改变5.如图，正三棱柱的左视图是（）A.B.C.D.6.如图是由几个相同大小的小正方体搭建而成的几何体的主视图和俯视图，则搭建这个几何体所需要的小正方体的个数至少为（）A.5B.6C.7D.87.一个圆柱体的三视图如图所示，若其俯视图为圆，则这个圆柱体的体积为（）A.24B.24pC.96D.96p8.如图，这是一个机械零部件，该零部件的左视图是（）A.B.C.D.9.右图是由一个长方体和一个球组成的几何体，它的主视图是（）A.B.C.D.10.图2是图1中长方体的三视图．若用S 表示面积，且22S x x =主＋，2S x x =左＋，则S =俯（）图1图2A .232x x ＋＋B .22x ＋C .221x x ＋＋D .223x x＋二、填空题（本大题共6个小题，每小题4分，共24分）11.已知某几何体的三视图如图所示，其中俯视图为等边三角形，则该几何体的左视图的面积为________．12.如图是由若干个大小相同的小正方体堆砌而成的几何体，那么，其三种视图中面积最小的是________．13.如图是某天内电线杆在不同时刻的影长，按先后顺序应当排列为________．A B C D14.如图是一个几何体的三视图，那么这个几何体是________．15.如图，上、下底面为全等的正六边形礼盒，其主视图与左视图均由矩形构成，主视图中大矩形边长如图，左视图中包含两个全等的矩形．如果用彩色胶带按如图包扎礼盒，所需胶带长度至少为________cm ．（精确到0.001 cm ）16.用小立方体搭成的几何体，它的主视图和左视图如图，则这个几何体最少需________个小立方体，最多需________个小立方体．三、解答题（本大题共9个小题，共96分）17.（10分）请你在下面画一个正四棱锥的三视图．18.（10分）一位美术老师在课堂上进行立体模型素描教学时，把由圆锥与圆柱组成的几何体（如图，圆锥在圆柱上底面正中间放置）摆在讲桌上，请你分别画出这个几何体的三视图．19.（10分）如图，画出每个木杆在灯光下的影子．20.（10分）如图，小明与同学合作，利用太阳光线测量旗杆的高度，身高1.6 m的小明落在地面上的影长BC=．为 2.4 m（1）请你在图中画出旗杆在同一时刻阳光照射下落在地面上的影子EG；EG=，请求出旗杆DE的高度．（2）若小明测得此刻旗杆落在地面的影长16 m21.（10分）如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长为1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上的影长为21米，留在墙上的影高为2米，求旗杆的高度．22.（10分）如图，教学楼旁边有一棵大树，课外兴趣小组的同学在阳光下测得一根长为1 m的竹竿的影长为0.9 m，同一时刻这棵树落在地上的影长为2.7 m，落在墙上的影长为1.2 m，请你计算树高为多少．23.（12分）某工厂要加工一批茶叶罐，设计者给出了茶叶罐的三视图（如图），请你按照三视图确定制作每个密封罐所需钢板的面积．（单位：mm）24.（12分）如图是某个几何体的三视图．（1）请描述这个几何体的形状；（2）按三视图的图上的实际尺寸，画出它的表面展开图（按6:1比例缩小）；（3）若三视图的实际尺寸如图所示，求这个几何体的侧面积和表面积．25.（12分）如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高为2 m的标杆CD和EF，两标杆相隔52 m，并且建筑物AB、标杆CD和EF在同一竖直平面内．从标杆CD后退2 m到点G 处，在G处测得建筑物顶端A与标杆顶端C在同一条直线上；从标杆EF后退4 m到点H处，在点H处测得建筑物顶端A与标杆顶端E在同一条直线上，求建筑物的高．第五章单元测试答案解析一、1.【答案】B 2.【答案】C 3.【答案】B 4.【答案】A 5.【答案】A 6.【答案】B【解析】综合主视图和俯视图，底层有4个小正方体，第二层最少有2个小正方体，因此搭建这个几何体所需的小正方体个数至少是6个，故选B ．7.【答案】B【解析】由三视图知圆柱体的底面圆的直径为4，所以底面圆的面积为4p ，高为6，根据体积=底面积×高知体积为24p ，故选B ．【考点】三视图的数据计算体积8.【答案】C 9.【答案】C 10.【答案】A【解析】∵()222S x x x x ==主++，()21S x x x x =+=+左，∴长方体的长为2x +，宽为1x +，∴()()22132S x x x x =++=++俯．故选A ．11.【答案】2【解析】该几何体是一个三棱柱，底面等边三角形边长为2 cm ，三棱柱的高为3，所以，其3=（2cm ）．12.【答案】左视图【解析】设小正方体的棱长为1，则主视图的面积为5，左视图的面积为3，俯视图的面积为5，所以左视图的面积最小．13.【答案】DABC【解析】 根据在北半球，太阳光下的影子变化的规律，从早晨到傍晚物体的指向是：西－西北－北－东北－东，影长由长变短，再变长．可得顺序为DABC ．14.【答案】圆柱体（空心）15.【答案】431.769【解析】由主视图知正六边形最长的对角线为60 cm ，而礼盒上面每一根胶带长为正六边形的相对两边距离，所以需胶带至少为26206120431.769´+´=»（cm ）．16.【答案】513【解析】通过观察想象出原几何体可能的形状，这个几何体至少需5个小立方体，最多需13个小立方体，如答图分别代表最少和最多的情况．图中的数字代表正方体的个数．17.【答案】解：如答图．18.【答案】解：如答图．19.【答案】解：如答图．20.【答案】解：（1）影子EG 如图所示；（2）∵DG AC ∥，∴G C Ð=Ð，∴Rt Rt ABC DEG △∽△，∴AB BC DE EG =，即1.6 2.416DE =，解得323DE =，∴旗杆的高度为32m 3．21.【答案】解：如图，过点C 作CE AB ^于点E ∵CD BD ^，AB BD ^，∴90EBD CDB CEB Ð=Ð=Ð=°，∴四边形CDBE 为矩形，∴21 m BD CE ==， 2 m CD BE ==，设 m AE x =，则1:1.5:21x =，解得14x =，故旗杆高14216AB AE BE =+=+=（米）22.【答案】解：如图，设墙上的影高CD 落在地面上时的长度为 m x ，树高为 m h ，∵某一时刻测得长为1 m 的竹竿影长为0.9 m ，墙上的影高CD 为1.2 m ，∴1 1.20.9x=，解得 1.08x =（m ），∴树的影长为1.08 2.7 3.78+=（m ），∴10.9 3.78h=，解得 4.2h =（m ）答：树高为4.2米．23.【答案】解：由三视图可知茶叶罐的形状为圆柱体，并且茶叶罐的底面直径2R 为100 mm ，高H 为150 mm ．∵每个密封罐所需钢板的面积即为该圆柱的表面积，∴222S R RHp p =+表面积2250250150p p =´+´´20000p =（2mm ）则制作每个密封罐所需钢板的面积为220000 mm p ．24.【答案】解：（1）底面是上底为80 mm ，下底为140 mm ，高为的等腰梯形，棱长为120 mm 的直四棱柱．（2）如图所示．（3）2601208012014012040800S =´´+´+´=侧（2mm ）801402408002408002S S S +=+=+´´=+表侧底（2mm ）25.【答案】解：∵AB BH ^，CD BH ^，EF BH ^，∴AB CD EF ∥∥，∴CDG ABG △∽△，∴EFH ABH △∽△，∴CD DGAB DG BD =+，∴EF FHAB FH DF BD=++．∵ 2 m CD DG EF ===，52 m DF =， 4 m FH =，∴222AB BD =+，24452AB BD =++，∴242452BD BD=+++，解得52BD =．∴22252AB =+，解得54AB =．则建筑物的高为54 m ．。

人教版数学四下三角形单元测试卷精选（含答案)5学校:___________姓名：___________班级：___________考号：___________一、选择题1．如图线段AB、AC、AD、AE中最短的一条是（）A．AB B．AC C．AD D．AE2．下面三组棒中不能搭成三角形的是( )A．B．C．3．下列长度的各组线段中，能围成三角形的是（）A．3 3 6 B．3 7 11 C．2.5 4.5 2D．8 9 104．如果三角形的两条边的长分别是5厘米和8厘米，第三条边的长度范围应是（）A．大于3厘B．大于13厘米C．大于3厘米并且小于13厘米D．小于3厘米或大于13厘米5．一个钝角三角形的其中一个锐角是40°，另一个锐角一定小于（）A．90°B．50°C．49°D．40°6．如图，小华的家在A处，书店在B处，星期日小明到书店去买书，他想尽快的赶到书店，请你帮助他选择一条最近的路线（）A．A→C→D→B B．A→C→F→B C．A→C→E→F→B D．A→C→M→B 7．当三角形中两个内角之和等于第三个角时，这是一个（）三角形。

A．锐角B．直角C．钝角8．能拼成一个长方形的是两个完全一样的()三角形．A．锐角B．直角C．钝角9．工人师傅加固一个平行四边形框架，最牢固的是（）A．B．C．10．如果一个三角形的两个内角度数的和等于第三个内角的度数，那么这个三角形是（）．A．钝角三角形B．锐角三角形C．直角三角形D．无法判断二、填空题11．把一个平行四边形分成两个梯形，这两个梯形的内角和都是（______），如果把这个平行四边形分成两个三角形，这两个三角形的内角和都是（______）。

12．求下面各图中∠1的度数．（1）（2）13．如图，已知∠1＝49°，求∠2=_____、∠3=_____、∠4=_______14．一共有________个三角形．15．数一数.（______）个三角形（______）条线段16．一个三角形三条边的长度分别为3厘米、3厘米、4厘米，按照边来分，这是一个（_________）三角形；围成这个三角形至少要（__________）厘米长的绳子。