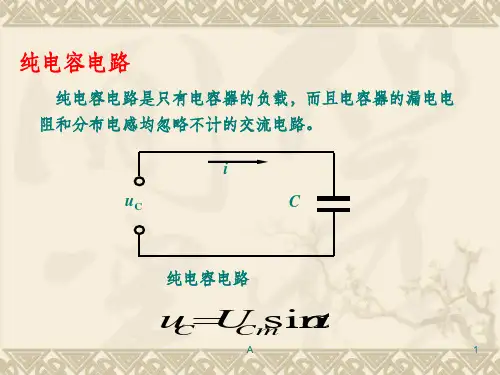
纯电容电路
- 格式:ppt
- 大小:1.24 MB
- 文档页数:21

交流电纯电容电路中的电功率三种状态
功率主要有三种状态,分别是瞬时功率、有功功率、无功功率。
纯电容电路中的功率
瞬时功率
瞬时功率等于电压uc与电路ic的乘积(也就是任何时候的电容两端的电压乘以流通的电流,电功率计算公式:U·I=P),其变化规律如下图所示:
有功功率
从右图中可知,瞬时功率在一个周期内交替变化两次,两次为正,两次为负。
则表明瞬时功率在一个周期内的平均功率值为零。
它表明:在纯电容电路中,只有电容与电源进行能量交换,而无能量消耗,所以有功功率为零。
它和电感元件相似是个储能元件。
无功功率
纯电容电路中瞬时功率的最大值叫做无功功率,它表示电容器与电源之间能量交换的规模,以Qc表示。
上述公式中:Qc:表示电容器的无功功率Var或Kvar(无功功率的单位千伏安)Uc:表示电容器两极间电压的有效值(V)Ic:表示纯电容电路中电流有效值(A)Xc:表示电容器的容抗(Ω)
电容功率计算题
题目:在纯电容电路中,已知电容器的电容C=500/πuF(微法),交流电频率f=50Hz,交流电压Uc=220V,求:Xc、Ic、Qc。
思路解析:这个题目给出的电容是微法,而容抗公式里面用的是法(F),所有先统一电容单位,C=0.000159法,然后通过容抗公式可以计算出此电容容抗为20Ω ,题中Ic 是大写,也就是有效值,根据公式Ic=Uc/Xc可计算出Ic=11A,然后通过功率计算工时Qc=UcIc即可计算出无功功率2420(Var)。


单相交流电路概述在直流电路中,电路的参数只有电阻R 。
而在交流电路中,电路的参数除了电阻R 以外,还有电感L 和电容C 。
它们不仅对电流有影响,而且还影响了电压与电流的相位关系。
因此,研究交流电路时,在确定电路中数量关系的同时,必须考虑电流与电压的相位关系,这是交流电路与直流电路的主要区别。
本节只简单介绍纯电阻、纯电感、纯电容电路。
一、纯电阻电路纯电阻电路是只有电阻而没有电感、电容的交流电路。
如白炽灯、电烙铁、电阻炉组成的交流电路都可以近似看成是纯电阻电路,如图3—7所示。
在这种电路中对电流起阻碍作用的主要是负载电阻。
加在电阻两端的正弦交流电压为u ,在电路中产生了交流电流i ,在纯电阻电路中,龟压和电流瞬时值之间的关系,符合欧姆定律,即:/i u R =由于电阻值不随时间变化,则电流与电压的变化是一致的。
就是说,电压为最大值时,电流也同时达到最大值;电压变化到零时,电流也变化到零。
如图3—8所示。
纯电阻电路中,电流与电压的这种关系称为“同相”。
通过电阻的电流有效值为:/I U R =公式3—14是纯电阻电路的有效值。
在纯电阻电路中,电流通过电阻所做的功与直流电路的计算方法相同,即:22P UI I R U R ===二、纯电感电路纯电感电路是只有电感而没有电阻和电容的电路。
如由电匪很小的电感线圈组成的交流电路,都可近似看成是纯电感电路,如图3—9所示。
在如图3—9所示的纯电感电路中;如果线圈两端加上正弦交流电压,则通过线圈的电流i 也要按正弦规律变化。
由于线圈中电流发生变化,在线圈中就产生自感电动势,它必然阻碍线圈电流变化。
经过理论分析证明,由于线圈中自感电动势的存在,使电流达到最大值的时间,要比电压滞后90︒,即四分之一周期。
也就是说,在纯电感电路中,虽然电压和电流都按正弦规律变化,但两者不是同相的,如图3—10所示,正弦电流比线圈两端正弦电压滞后90︒,或者说,电压超前电流90︒。
理论证明,纯电感电路中线圈端电压的有效值U ,与线圈通过电流的有效值之间的关系是:L //I U L U X ω==L ω是电感线圈对角频率为叫的交流电所呈现的阻力,称为感抗,用L X 表示,即: L 2X L fL ωπ==式中 L X ——感抗(Ω);f ——频率(Hz);L ——电感(H)。

纯电容电路纯电容电路由绝缘电阻很大、介质损耗很小的电容器组成的交流电路.可以近似认为纯电容电路。
1) 电压与电流的相位关系当电容器接到交流电流上时,由于外加交变电压在不断变化,电容器就不断进行充、放电,电路中就产生交变电流,其数值等于电容极板上电荷量的变化率,即式中——电容两端电压变化率。
纯电容电路中正弦电压和电流的波形如图2 -26所示。
把一个周期内的电压变化也分为四个阶段来分析:(1)在电压的第一个1/4周期内,电容两端电压由零增加到正向的最大值,电压变化率为正,所以电流为正,这就是充电电流。
电压为零时,电压变化率最大,充电电流最大;电压为最大值时,电压变化率为零,充电电流为零。
(2)在电压的第二个1/4周期内,电容两端电压由正的最大减小到零,电压变化率为负,电流为负,这就是放电电流。
在电压最大时,放电电流为零;在电压为零时,放电电流与充电电流相反。
(3)在电压的第三个1/4周期内,电压由零变化到负的最大,电容器反向充电,电流为负值。
(4)在电压的第四个1/4周期内,电压由负的最大变化到零,电容器反向放电,电流变为正值图2-26中画出了电容上电流的波形图。
由图可见,电容电流的变化规律为正弦波形图,其频率与电压相同;电容上的电流超前电压90°,它们的相量图如图2-27所示。
2)电流与电压的关系我们也可以像纯电感电路那样做一个交流电压加在纯电容上的实验,通过分析数据,也能得到与纯电感类似的结论。
在纯电容电路中,电压与电流有效值之比为一常数.用Xc来表示.称为容抗,或与感抗类似,容抗Xc在电容电路中起着阻碍电流通过的作用,它的单位也是欧姆(Ω).经分析证明,容抗Xc与电容C、频率f的乘积成反比,即式中C—电容器的电容量(F);f—电源电压的频率(Hz)Ω—电源电压的角频率(rad/s),ω=2Πf3)纯电容电路的功率纯电容电路中的瞬时功率与纯电感电路中的功率很相似,其瞬时电压值与瞬时电流值逐点相乘,就可以画出如图2-28所示的瞬时功率波形图。


纯电容交流电路欧姆定律符号法表示形式为
在纯电容交流电路中,电容器是电路中的主要元件。
电容器的电容量
可以通过欧姆定律来计算。
欧姆定律是电学中最基本的定律之一,它
描述了电流、电压和电阻之间的关系。
在交流电路中,欧姆定律的符
号法表示形式为:
I = V/Z
其中,I表示电流,V表示电压,Z表示阻抗。
在纯电容交流电路中,
阻抗的计算公式为:
Z = 1/(jωC)
其中,j表示虚数单位,ω表示角频率,C表示电容量。
根据这个公式,我们可以得出纯电容交流电路中电容器的阻抗是一个纯虚数,其大小
与角频率成反比例关系。
在纯电容交流电路中,电流的相位落后于电压的相位90度。
这是因为电容器的电流与电压之间存在90度的相位差。
这个相位差是由于电容器的电压和电流之间的相位差引起的。
当电压达到峰值时,电流为零;当电流达到峰值时,电压为零。
在纯电容交流电路中,电容器的功率因数为零。
这是因为电容器只能存储电能,而不能消耗电能。
因此,电容器不会产生有用的功率,其功率因数为零。
总之,在纯电容交流电路中,电容器是电路中的主要元件,其阻抗是一个纯虚数,电流相位落后于电压相位90度,功率因数为零。
欧姆定律的符号法表示形式为I=V/Z,其中Z的计算公式为Z=1/(jωC)。
这些基本概念对于理解和分析纯电容交流电路非常重要。




教学设计方案学科名称:电工电子技术与技能授课班级:设计者:年月日第周教学过程结构教学环节教师活动学生活动教学媒体设计意图【一、复习】1.正弦交流电旋转矢量表示法。
2.电功率的计算方法。
【二、引入新课】纯电阻是理想元件,但有些实际负载(如电炉)可以看成是纯电阻负载。
由于交流电路的特性,本节将研究电流、电压及功率的瞬时值等。
【三、讲授新课】4.2.1 纯电阻电路1、电压与电流的关系(1)纯电阻电路如图4.9(a)所示。
设图示方向为参考方向,电压的初相为零。
即tUuωsinm=根据欧姆定律tRURuiωsinm==得i = I m sinω t(2)纯电阻电路电流和电压关系(波形如图4.9(b)所示)为1)电压u和电流i的频率相同;2)电压u和电流i的相位相同;3)最大值和有效值仍然满足欧姆定律:RUI mm=RUI=(3)矢量关系如图4.9(c)所示。
学生自己动手画出矢量图,并分析其中的关系多媒体让学生认识纯电阻电路及其电压与电流关系掌握矢量图的画法(a)电路图(b)电压和电流的波形(c)矢量图图4.9纯电阻电路2.功率(1)瞬时功率:每个瞬间电压与电流的乘积。
p = u⋅ i = U m sinω t ⋅ I m sinω t=U m I m sin2ω t= 2 U I sin2ω t纯电阻电路瞬时功率的变化曲线如图4.10所示。
图4.10纯电阻电路有功功率纯电阻瞬时功率始终在横轴上方,说明它总为正值,它总是在从电源吸收能量,是个耗能元件。
(2)有功功率(平均功率)有功功率(平均功率):取瞬时功率在一个周期内的平均值其数学表达式为2mmIUP=或PRUIRUI22===有功功率如图4.10所示,是一定值。
是电流和电压有效值的乘积,也是电流和电压最大值乘积的一半。
例[4.5]电炉的额定电压U N = 220 V,额定功率P N=1 000 W,把它接到220 V 的工频交流电源上工作。
求电炉的电流和电阻值。
实验四纯电感/纯电容电路电流与电压间相位关系
一、实验目的
1.学习使用双踪示波器。
2.掌握纯电感和纯电容电路电流、电压间的相位关系。
二、实验设备
三、实验原理
1、在R、L串联电路中,R很小,和感抗比起来可以忽略,将电路近似视为
纯电感电路。
R两端的电压波形与电流波形同相,R、L两端电压波形可以看成线圈两端的电压波形。
通过双踪示波器观察比较两个波形的相位差。
2、R、C串联电路的实验原理与R、L串联电路相同。
用同样的方法观察、
比较R、C串联电路电压与电流的相位差。
四、实验步骤
1、把电阻R和电感线圈L按下列电路图(a)连接好。
y1代表电流i,y2代表
电压u,将它们输入双踪示波器,观察电流、电压波形间的关系。
并确定其相位差。
记录于下表一。
2、把电阻R和电容C按图(b)所示电路连接好。
将电流信号y1,电压信号
y2,输入双踪示波器,观察波形,确定相位差。
记录于下表二。
实验电路图:
表一 纯电感电路相位差
表二 纯电容电路相位差
五、回答问题
1、在上述实验中,为什么电流、电压的相位差只是接近90o ,而不等于90o 。
2、为什么电容电路比电感电路产实验效果要好一些?
六、注意事项
注意将两个输入量y1和y2公共端A 按在一起。
七、实验小结
分析纯电感电路与纯电容电路的相位关系。
(
a
)
(
b
)。