电介质物理新版第二章 静电场中的电介质
- 格式:doc
- 大小:3.85 MB
- 文档页数:71






§2 静电场中的导体和电介质§2-1 静电场中的导体1. 导体的静电平衡条件当电荷静止不动时,电场散布不随转变,该体系就达到了静电平衡。
在导体中存在自由电荷,它们在电场的作用下可以移动,从而改变电荷的散布……导体内自由电荷无宏观运动的状态。
导体的静电平衡的必要条件是其体内图2-1导体的静电平衡场强处处为零。
从静电平衡的条件动身可以取得以下几点推论:推论1)导体是等位体,导体表面是等位面:2)导体表面周围的场强处处与它的表面垂直:因为电力线处处与等位面正交,所以导体外的场强必与它的表面垂直。
(注意:本章所用的方式与第一章不同,而是假定这种平衡以达图2-2导体对等位面的控制作用到,以平衡条件动身结合静电场的普遍规律分析问题。
)2.电荷散布1) 体内无电荷,电荷只散布在导体的表面上:当带电导体处于静电平衡时,导体内部不存在净电荷(即电荷的体密度)电荷仅散布在导体的表面。
可以用高斯定理来证明:设导体内有净电荷,则可在导体内部作一闭合的曲面,将包围起来,依静电条件知S面上处处, 即由高斯定理必有q=02) 面电荷密度与场强的关系:当导体静电平衡时,导体表面周围空间的 与该处导体表面的面电荷密度 有如下关系:论证: 在电荷面密度为 的点取面元设 点为导体表面之外周围空间的点,面元。
充分小,可以为 上的面电荷密度 是均匀的,以为横截面作扁圆柱形高斯面(S ),上底面过P 点,把电荷q= 包围起来. 通太高斯面的电通量是:3) 表面曲率的影响、尖端放电导体电荷如何散布,定量分析研究较复杂,这不仅与这个导体的形状有关,还和它周围有何种带电体有关。
对孤立导体,电荷的散布有以下定性的规律:图2-3导体表面场强与电荷面密度曲率较大的地方(凸出而尖锐处),电荷密度e 较大;曲率较小的地方(较平坦处)电荷密度e 较小;曲率为负的地方(凹进去向)电荷密度e 更小。
1) 端放电的利和弊3 导体壳(腔内无带电体情况)大体性质:当导体壳内无带电体时,在静电平衡当导体壳内无 带电体时,在静电平衡下:导体壳内表面上处处无电荷,电荷仅散布在外 表面;空腔内无带电场,空腔内电位处处相等。
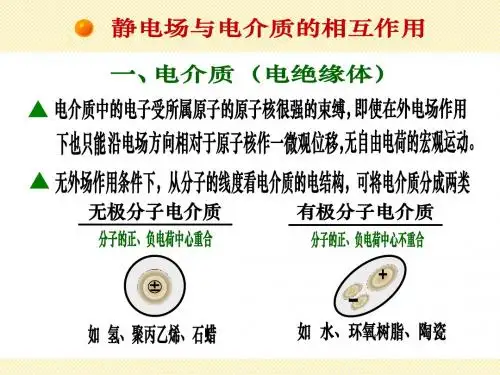

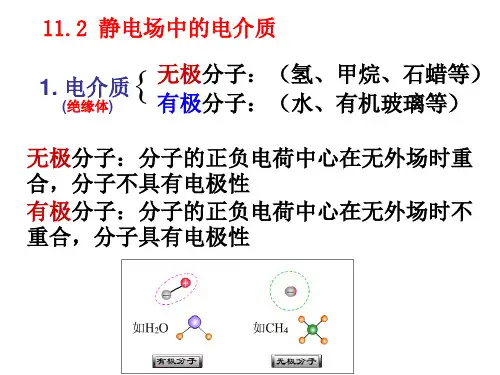
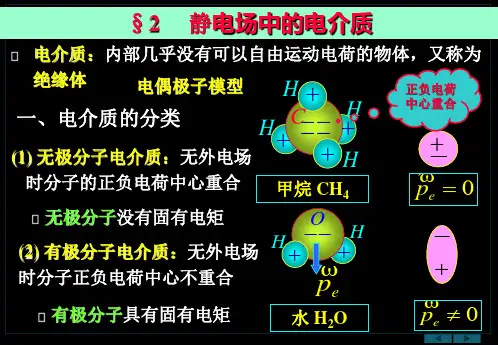
校内讲义电介质物理二〇〇六年十二月前言电介质是在电场作用下具有极化能力并能在其中长期存在电场的一种物质。
其特征是以正、负电荷重心不重合的电极化方式传递、存储或记录电的作用和影响,但其中其主要作用的是束缚电荷。
极化是电介质的基本属性,也是电介质多种实际应用(如储存静电能)的基础。
电介质物理学主要是研究界之内不束缚电荷在电场(包括光频电场)、应力、温度等作用下的电极化及运动过程,阐明电极化规律与介质结构的关系,揭示介质宏观介电性质的微观机制,同时也研究介电性质的测量方法,以及各种电介质的性能,进而发展电介质的效用。
电介质的物理形态可以是气体、液体或固体,自然界中分布极广,本讲义主要介绍固体电介质。
电介质与金属对电场的响应特性是不同的,金属中的电子是共有化的,金属内有自由载流子,使金属具有良好的导电性,它们以传导的方式来传递电的作用和影响。
在电介质体内,一般情况下只具有被束缚的电荷,在电场的作用下只能以感应的方式,即电极化(在电场作用下正、负电荷中心不重合)的方式来传递和记录电的影响。
尽管对不同种类的电介质,电极化的机制各不相同,但是以电极化方式响应电场的作用却是共同的。
因此,研究电介质在电场作用下发生极化的物理过程并推导出相应的规律,是电介质物理的重要课题之一。
由于实际电介质与理想电介质不同,在电场作用下,实际电介质存在泄漏电流和电能的耗散以及在强电场下可能导致的电介质破坏,因此,电介质物理除了研究极化外,还要研究有关电介质的电导、损耗、以及击穿特性。
这些就是经典的电介质物理研究的主要内容。
20世纪20年代,关于原子结构和分子结构的研究开始发展的时候,电极化基本过程的研究也发展起来,它从物理学分离出来并成为一个独立分支。
目前备受关注的课题包括:(1)材料性质的第一性原理计算;(2)驰豫铁电体;(3)非均匀介质;(4)有限尺寸材料;(5)电解质的驰豫特性研究;(6)微波介质和低介电常数材料电介质物理学始于物质结构研究密不可分的基础学科,研究的中心问题试电极化与驰豫,故涉及物质结构中束缚电荷的分布、带电粒子间的相互作用,以及这些粒子在外电场作用下的运动和驰豫等。
这些是物质结构中带有根本性的问题。
所以电介质物理学研究中产生的新概念、新理论促进了其他学科的发展。
历史上,电介质物理学的发展对于促进分子物理学、固体物理的发展曾带来深刻的作用。
现在,对于促进非线性光学、促进固体光谱学的发展也有着不可磨灭的贡献;在一定意义上形成了这些分支学科的奠基石,同时也是这些学科登堂入室的必由之路。
近年来,由于激光技术和非晶态理论的发展,电介质物理又将成为凝聚态物理最基础的组成部分。
高新技术的发展为电介质物理提供了广阔的用武之地,也为学科的发展创造了机遇。
例如,场致发光可以用于显示,显示技术不属于电介质物理范畴,但近年来用高介材料余场致发光材料复合时,内场的观点可为降低发光场强提供理论依据。
在纳米技术上、机器人等可能影响人类生活方式的领域中电介质的机、电、广、热、声之间的耦合效应将会得到充分的利用,电介质物理将成为这些领域发展的理论基础之一。
光信息处理领域中介电非线性、机电耦合等原理可望得到广泛应用,与此同时,如何更深入地理解高新技术领域中所应用的电解质的性能和参数,从而对其改进和提高提供指导,这为电介质物理的研究提供了有价值的空间。
可见在交叉学科研究中电介质物理将不断丰富自己的研究内容。
本讲义主要取材于下面参考书:[1] 张良莹、姚熹:《电介质物理》,西安交通大学出版社,西安,1991。
[2] 李翰如:《电介质物理导论》,成都科技大学出版社,成都,1990。
[3] 殷志文:《电介质物理》(第二版),科学出版社,北京,2006第二章 静电场中的电介质1.1 电介质的极化本节主要讨论各向同性线性电介质在电场中的行为,并以均匀电介质在均匀电场中的行为作为特例进行具体分析。
这里所说的均匀是指电介质的性质不随空间坐标发生变化,所说的各向同性是指电介质的参数不随场量的方向发生变化;所说的线性是指电介质的参数不随场量的数值发生变化。
1.电极化电极化即电介质极化,简称极化,它是电介质基本电学行为之一。
在外电场作用下,在电介质内部感生偶极矩的现象,称为电介质的极化。
电介质在电场作用下的极化程度用极化强度矢量P 来表示,极化强度P是电介质单位体积内的感生偶极矩。
它可表示如下: VP v ∆=∑→∆μ 0lim (2-1) 式中μ为极化粒子的感应偶极矩,V ∆为体积元。
由式可见,P 是空间坐标的函数,可用()'''z y x P 或()'r P 表示。
在国际制中,极化强度的单位是库仑/米2(C/m 2).2.极化电荷及其建立的电场(1)极化电荷及退极化电场电介质极化所产生的感应偶极矩,作为场源,在电介质外部空间(真空中)和电介质内部都建立了电场。
如果电介质的体积为V ',在V '内,位于()r '处的体积元dV 中的感应偶极矩为()''dV r P ,它在电介质以外的场点()r 形成的电位P d ϕ,根据偶极子电场公式可得 ()()''41''''4120020dV RR r P dV r r r r r r r P d p =⋅='--⋅-= πεπεϕ (2-2) 整个体积V'内的感应偶极矩在场点()r 形成的电位应用叠加原理,对上式积分可得()()⎰⋅='200''41v P dV RR r P r πεϕ (2-3)根据标量函数的梯度,有201'11RR R R R grad -=-∇=∇= (2-4) 式中▽是作用于不加撇的坐标的,∇'则是作用于加撇的坐标的,将式(2-4)代入式(2-3)可得()()⎰∇⋅='0'1''41v P dV R r P r πεϕ (2-5) 根据散度的基本性质()()()()Rr P r P R r P R r P R div 11]'1[]'1[∇⋅+⋅∇=⋅∇= (2-6) 将式(2-6)代入式(2-5)有()()()[]⎰⎰⋅∇-+⎥⎦⎤⎢⎣⎡⋅∇=''00''41''41v v p dV R r P dV R r P r πεπεϕ (2-7) 对上式右端第一项应用散度定理可得 ()()⎰⎰⋅=⎥⎦⎤⎢⎣⎡⋅∇''00''41''41v A A d R r P dV R r P πε (2-8) 式中'A 为体积V'的界面,00,''n dA n A d =为'A d 外法线方向的单位面元矢量。
将上式与电荷连续分布在表面A '上,其面电荷密度为()'r σ,在场点)(r 处的电位公式相比较,可以看出:()0'n r P ⋅ 是电介质表面某处'A d 上或()'r 处的面电荷密度,这个电荷是由电介质极化产生的。
因此是面极化电荷密度,以()'r p σ表示,于是可写为 ()()()()'cos '''00r P r P n r P r n ==⋅=θσ (2-9)式中θ为P 与n 间的夹角。
以上关系表明,电介质表面某处()'r 面极化电荷密度()'r P σ在数值上等于该处极化强度P ()'r 在外表面法线方向(n 方向)上分量()r P n '。
将式(2-7)右端第二项与体分布电荷场源,体电荷密度为()'r ρ,在场点®的电位公式比较,可以看出:()'r P ⋅∇-是电介质内部()r '处的体电荷密度,同样,这个电荷是由电介质极化而产生的,因此是体极化电荷密度,以()'r P σ表示:()()''r P r P ⋅-∇=ρ (2-10)上式表明:当极化强度P 随空间位置发生变化时,在电介质内部有极化电荷存在。
在均匀极化的电介质中P ()'r 是恒量,因此()'r ρ=0,这时电介质体内不存在极化电荷。
以上分析表明,电介质极化既感生表面电荷,又感生内部电荷,显然这两种极化电荷都是束缚电荷。
极化在电介质中感生极化电荷和在电介质中感生偶极矩是同一物理事实的两种表现。
面极化电荷密度与休极化电荷密度与极化强度一样也是表征电介质极化的物理量。
式(2-9)和式(2-10)分别表示了它们之间的相互关系。
将式(2-9)和式(2-10)代入式(2-7)有()()()[]()()⎥⎦⎤⎢⎣⎡+=⋅∇-+⋅=⎰⎰⎰⎰''0''0''''41''''41V P A P A V P dV R r dV R r dV R r P dA R n r P r ρσπεπεϕ (2-11) 这是极化电荷在电介质外部建立的电位,其电场强度可写为()()()⎥⎦⎤⎢⎣⎡+=⎰⎰''0220''''41A V P P P dV R R r dA R R r r E ρσπε (2-12) 电介质极化也可以用极化电荷来表征,这样就可以把体积为V'的极化电介质看成是具有极化电荷的V '空间。
因此V '空间内的电场与V '空间外的电场一样,可以用式(2-11)和式(2-12)进行计算。
以上分析表明,电介质极化对电场的影响可以等效地用极化电荷在真空中建立的电场来描述。
习惯上把极化电荷形成的电场称为退极化电场。
退极化电场的大小与电介质试样的几何形状有关,或者说与电极的几何形状有关。
对于平行板电极,若极板的面积为A ,极间距离为d ,且A 的线度远大于d ,极板上充电后,若忽略边缘效应,则可认为电极上电荷均匀分布,两极间的电场为均匀电场,电场强度处处相等。
如极间充以各向同性的线性均匀电介质,则电介质均匀极化,计划强度处处相等,由式(2-10)可得体极化电荷密度P ρ为零0=⋅-∇=P P ρ (2-13)面极化电荷密度P σ根据式(2-9)可得P P n P P -==⋅=πρcos即在紧靠极板的介质表面,面极化电荷密度在数值上等于极化强度P 的负值。
这表明,电介质表面的极化电荷与相邻极板上自由电荷符号相反,这是电介质中感应生成的束缚电荷,如图(2-1)所示。
由于极化电荷总是与自由电荷异号,因此,极化电荷削弱自由电荷建立的电场,故称为退极化电场P E 。