绳上的“死结”和“活结”模型分解

物理建模系列(三)绳上的“死结”和“活结”模型[模型概述]1的物体，∠ACB＝30°；图乙中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG拉住，EG与水平方向也成30°，在轻杆的G点用细绳GF拉住一个质量为M2的物体，求：(1)细绳AC段的张力F T AC与细绳EG的张力F T EG之比；(2)轻杆BC对C端的支持力；(3)轻杆HG对G端的支持力．【思路点拨】图甲中细绳跨过定滑轮与物体M1相连，属于“活结”模型，细绳AC 和CD张力大小相等，细绳对定滑轮的合力方向沿∠ACD的角平分线方向；图乙中细绳EG 和细绳GF为连接于G点的两段独立的绳，属于“死结”模型，细绳EG和细绳GF的张力不相等，轻杆对G点的弹力沿轻杆方向．【解析】题图甲和乙中的两个物体M1、M2都处于平衡状态，根据平衡的条件，首先判断与物体相连的细绳，其拉力大小等于物体的重力；分别取C点和G点为研究对象，进行受力分析如图甲和乙所示，根据平衡规律可求解．(1)图甲中细绳AD跨过定滑轮拉住质量为M1的物体，物体处于平衡状态，细绳AC段的拉力F TAC＝F T CD＝M1g图乙中由F T EG sin 30°＝M2g，得F T EG＝2M2g.所以F T ACF T EG＝M1 2M2.(2)图甲中，三个力之间的夹角都为120°，根据平衡规律有F N C＝F T AC＝M1g，方向与水平方向成30°，指向右上方．(3)图乙中，根据平衡规律有F T EG sin 30°＝M2g，F T EG cos 30°＝F N G，所以F N G＝M2g cot 30°＝3M2g，方向水平向右．【答案】(1)M12M2(2)M1g，方向与水平方向成30°指向右上方(3)3M2g，方向水平向右[高考真题]1．(2013·重庆卷，1)如图所示，某人静躺在椅子上，椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G，则椅子各部分对他的作用力的合力大小为()A．G B．G sin θC．G cos θD．G tan θ【解析】运用力的平衡条件，可求得椅子对人的作用力．选人为研究对象，人受到重力和椅子各部分对他的作用力的合力，根据力的平衡条件可知，椅子对他的作用力的合力与重力等大、反向，故选项A正确．【答案】 A2．(2013·课标卷Ⅱ，15)如图，在固定斜面上的一物块受到一外力F的作用，F平行于斜面向上．若要物块在斜面上保持静止，F的取值应有一定范围，已知其最大值和最小值分别为F1和F2(F2>0)．由此可求出()A．物块的质量B．斜面的倾角C．物块与斜面间的最大静摩擦力D．物块对斜面的正压力【解析】物块受与斜面平行的外力F作用，而在斜面上静止，此时摩擦力的大小和方向将随F的变化而变化．设斜面倾角为θ，由平衡条件F1－mg sin θ－F fmax＝0，F2－mg sinθ＋F fmax ＝0，解得F fmax ＝F 1－F 22，故选项C 正确． 【答案】 C3.(2016·课标卷Ⅲ，17)如图，两个轻环a 和b 套在位于竖直面内的一段固定圆弧上；一细线穿过两轻环，其两端各系一质量为m 的小球．在a 和b 之间的细线上悬挂一小物块．平衡时，a 、b 间的距离恰好等于圆弧的半径．不计所有摩擦．小物块的质量为( )A.m 2 B ．32m C.mD ．2m【解析】 根据题意设悬挂小物块的点为O ′，圆弧的圆心为O ，由于ab ＝R ，所以三角形Oab 为等边三角形，根据几何知识可得∠aO ′b ＝120°，而一条绳子上的张力大小相等，故T ＝mg ，小物块受到两条绳子的拉力作用大小相等，夹角为120°，故受到的拉力的合力等于mg ，因为小物块受到绳子的拉力和自身重力作用，处于平衡状态，故拉力的合力等于小物块的重力为mg ，所以小物块的质量为m ，C 正确．【答案】 C[名校模拟]4．(2018·安徽合肥段考)将两个质量均为m 的小球a 、b 用细线相连后，再用细线悬挂于O 点，如图所示，用力F 拉小球b ，使两个小球都处于静止状态，且细线Oa 与竖直方向的夹角保持θ＝30°，则F 达到最小时Oa 绳上的拉力为( )A.3mg B ．mg C.32mg D ．12mg【解析】 以两个小球组成的整体为研究对象，分析受力，作出F 在不同方向时整体的受力图，根据平衡条件可知，F 与T 的合力与重力2mg 总是大小相等、方向相反，由力的合成图可知，当F 与绳子Oa 垂直时，F 有最小值，即图中2位置，F 的最小值为F min ＝2mg sin 30°＝mg ，T ＝2mg cos 30°＝3mg ，A 正确．【答案】 A5.(2018·广东仲元中学月考)如图所示，跳伞运动员打开伞后经过一段时间，将在空中保持匀速降落．已知运动员和他身上装备的总重力为G 1(不包括伞面)，圆顶形降落伞伞面的重力为G 2，有8条相同的拉线，一端与飞行员相连(拉线重力不计)，另一端均匀分布在伞面边缘上(图中没有把拉线都画出来)，每根拉线和竖直方向都成30°角．那么每根拉线上的张力大小为( )A.G 14 B ．3G 112 C.G 1＋G 28D ．3G 1＋G 212【解析】 对运动员进行受力分析可知，8条拉线拉力的合力与运动员的重力等大反向，即8条拉线在水平方向的分力的合力为零，竖直方向分力的合力与运动员的重力等大反向，根据对称性可知，8条拉线的张力大小都相等，每条拉线的张力在竖直方向的分力F y ＝F cos 30°，且8F y ＝G 1，可得F ＝G 18cos 30°＝G 143＝3G 112，故B 正确，A 、C 、D 错误．【答案】 B 6.(2018·山东泰安高三上学期期中)在日常生活中，力的分解有着广泛的应用．如图为用斧子把树桩劈开的图示，斧子对木桩施加一个向下的力F 时，产生了大小相等的两个侧向分力F 1、F 2，下列关系正确的是( )A ．F ＝2F 1sin(θ2)B ．F ＝2F 1sin θC ．F ＝2F 1cos(θ2)D ．F ＝2F 1cos θ【解析】 F 1、F 2与水平方向的夹角为θ2，则F ＝2F 1sin θ2，A 对．【答案】 A课时作业(五) [基础小题练]1．(2018·广州调研)如图，三个大小相等的力F ，作用于同一点O ，则合力最小的是( )【解析】 根据矢量合成的平行四边形定则可知，C 选项的合力为零，即合力最小，C 正确．【答案】 C2.(2018·淮安模拟)我国海军在南海某空域举行实兵对抗演练，某一直升机在匀速水平飞行过程中遇到突发情况，立即改为沿虚线方向斜向下减速飞行，则空气对其作用力可能是( )A ．F 1B ．F 2C ．F 3D ．F 4【解析】 因为直升机沿虚线方向斜向下减速飞行，故合力沿虚线向上，直升机受到竖直向下的重力以及空气作用力两个力，要想合力沿虚线向上，则根据矢量三角形可得空气对其作用力可能为F 1，如图所示．【答案】 A3.(2018·石家庄模拟)如图所示，一个“Y”形弹弓顶部跨度为L ，两根相同的橡皮条自由长度均为L ，在两橡皮条的末端用一块软羊皮(长度不计)做成裹片．若橡皮条的弹力与形变量的关系满足胡克定律，且劲度系数为k ，发射弹丸时每根橡皮条的最大长度为2L (弹性限度内)，则发射过程中裹片对弹丸的最大作用力为( )A ．kLB ．2kL C.32kL D ．152kL 【解析】 设发射弹丸瞬间两橡皮条间的夹角为2θ，则sin θ＝L 22L ＝14，cos θ＝1－sin 2θ＝154.发射过程中裹片对弹丸的最大作用力为F 合＝2F cos θ，F ＝kx ＝kL ，故F 合＝2kL ·154＝152kL ，D 正确． 【答案】 D4．手握轻杆，杆的另一端安装有一个小滑轮C ，支持着悬挂重物的绳子，如图所示，现保持滑轮C 的位置不变，使杆柄向上转动一个角度，则杆对滑轮C 的作用力将()A ．变大B ．不变C ．变小D ．无法确定【解析】 杆对滑轮C 的作用力大小等于两绳上拉力的合力，由于两绳上拉力的合力不变，故杆对滑轮C 的作用力不变．【答案】 B5．如图所示，作用于O 点的三个力F 1、F 2、F 3合力为零，F 1沿－y 方向，大小已知．F 2与＋x 方向夹角为θ(θ<90°)，大小未知．下列说法正确的是()A．F3可能指向第二象限B．F3一定指向第三象限C．F3与F2的夹角越小，则F3与F2的合力越小D．F3的最小可能值为F1cos θ【解析】因F1、F2、F3的合力为零，故F3应与F2、F1的合力等大反向，故F3可能指向第二象限，也可能指向第三象限，选项A正确，B错误；F3、F2的合力与F1等大反向，而F1大小、方向均已知，故F3与F2的合力与其夹角大小无关，选项C错误；当F3与F2垂直时，F3最小，其最小值为F1cos θ，选项D正确．【答案】AD6.(2018·六安一中二模)如图所示，两个质量为m1的小球套在竖直放置的光滑支架上，支架的夹角为120°，用轻绳将两球与质量为m2的小球连接，绳与杆构成一个菱形，则m1∶m2为()A．1∶1 B．1∶2C．1∶ 3 D．3∶2【解析】将小球m2的重力按效果根据平行四边形定则进行分解如图，由几何知识得T＝m2g，对m1受力分析，由平衡条件，在沿杆的方向有：m1g sin 30°＝T sin 30°，得：T＝m1g，可见m1∶m2＝1∶1，故选A.【答案】 A[创新导向练]7．生活实际——千斤顶中的力学原理(2018·贵阳监测)如图所示是轿车常用的千斤顶，当摇动把手时，螺纹轴就能迫使千斤顶的两臂靠拢，从而将汽车顶起．当车轮刚被顶起时汽车对千斤顶的压力为1.0×105 N，此时千斤顶两臂间的夹角为120°.下列判断正确的是()A．此时千斤顶每臂受到的压力大小均为5.0×104 NB ．此时千斤顶对汽车的支持力为1.0×104 NC ．若继续摇动把手，将汽车顶起，千斤顶每臂受到的压力将增大D ．若继续摇动把手，将汽车顶起，千斤顶每臂受到的压力将减小【解析】 车轮刚被顶起时，千斤顶两臂支持力的合力为千斤顶对汽车的支持力，等于汽车对千斤顶的压力，大小为1.0×105 N ，B 项错误；两臂夹角为120°，由力的合成可知千斤顶每臂受到的压力为1.0×105 N ，A 项错误；继续摇动把手，将汽车顶起，千斤顶两臂夹角减小，每臂受到的压力减小，D 项正确，C 项错误．【答案】 D8．生活实际——以“减速带”为背景考查力的合成问题减速带是交叉路口常见的一种交通设施，车辆驶过减速带时要减速，以保障行人的安全．当汽车前轮刚爬上减速带时，减速带对车轮的弹力为F ，下图中弹力F 画法正确且分解合理的是( )【解析】 减速带对车轮的弹力方向垂直车轮和减速带的接触面，指向受力物体，故A 、C 错误；按照力的作用效果分解，将F 可以分解为水平方向和竖直方向，水平方向的分力产生的效果减慢汽车的速度，竖直方向上分力产生向上运动的作用效果，故B 正确，D 错误．【答案】 B9．人体生理——关节运动中所包含的力学问题如右图所示，人屈膝下蹲时，膝关节弯曲的角度为θ.设此时大小腿部的肌肉群对膝关节的作用力F 的方向水平向后，且大腿骨和小腿骨对膝关节的作用力大致相等，那么脚掌所受小腿骨沿竖直方向的力约为( )A.F2sin (θ2)B ．F 2cos (θ2)C.F 2tan (θ2)D ．F 2tan(θ2)【解析】 根据题意先将肌肉群对膝关节的作用力F 沿大腿骨和小腿骨方向分解，然后再分解小腿骨方向的分力，即可知D 正确．【答案】 D10．科技生活——缓冲门中的力学问题分析如图所示为缓慢关门时(图中箭头方向)门锁的示意图，锁舌尖角为37°，此时弹簧弹力为24 N ，锁舌表面较光滑，摩擦不计(sin 37°＝0.6，cos 37°＝0.8)，下列说法正确的是( )A ．此时锁壳碰锁舌的弹力为40 NB ．此时锁壳碰锁舌的弹力为30 NC ．关门时锁壳碰锁舌的弹力逐渐增大D ．关门时锁壳碰锁舌的弹力保持不变【解析】 锁壳碰锁舌的弹力分解如图所示，其中F 1＝F N sin 37°，且此时F 1大小等于弹簧的弹力为24 N ，解得锁壳碰锁舌的弹力为40 N ，选项A 正确，B 错误；关门时，弹簧的压缩量增大，弹簧的弹力增大，故锁壳碰锁舌的弹力逐渐增大，选项C 正确，D 错误．【答案】 AC[综合提升练]11．(2018·山东泰安高三上学期期中)质量为m 的物体置于倾角为θ＝37°的固定斜面上，物体与斜面之间的动摩擦因数为μ＝0.2.如图甲所示，先用平行于斜面的推力F 1作用于物体上，使其能沿斜面匀速上滑；若改用水平推力F 2作用于物体上，也能使物体沿斜面匀速上滑，如图乙所示．求两次推力大小之比F 1F 2.(sin 37°＝0.6，cos 37°＝0.8)【解析】 根据共点力平衡条件可得F 1＝mg sin θ＋μF N F N ＝mg cos θF 2cos θ＝mg sin θ＋μF ′N F ′N ＝mg cos θ＋F 2sin θ 整理得F 1F 2＝cos θ－μsin θ代入数值得F 1F 2＝0.68. 【答案】 0.6812．电梯修理员或牵引专家常常需要监测金属绳中的张力，但不能到绳的自由端去直接测量．某公司制造出一种能测量绳中张力的仪器，工作原理如图所示，将相距为L 的两根固定支柱A 、B (图中的小圆圈表示支柱的横截面)垂直于金属绳水平放置，在A 、B 的中点用一可动支柱C 向上推动金属绳，使绳在垂直于A 、B 的方向竖直向上发生一个偏移量d (d ≪L )，这时仪器测得金属绳对支柱C 竖直向下的作用力为F .(1)试用L 、d 、F 表示这时金属绳中的张力F T ；(2)如果偏移量d ＝10 mm ，作用力F ＝400 N ，L ＝250 mm ，计算金属绳中张力的大小．【解析】 (1)设C ′点受两边金属绳的张力分别为F T1和F T2，BC 与BC ′的夹角为θ，如图所示．依对称性有：F T1＝F T2＝F T由力的合成有：F ＝2F T sin θ 根据几何关系有sin θ＝d d 2＋L 24联立上述二式解得F T ＝F2dd 2＋L 24则d ≪L ，故F T ＝FL 4d. (2)将d ＝10 mm ，F ＝400 N ，L ＝250 mm 代入F T ＝FL 4d解得F T ＝2.5×103 N ，即金属绳中的张力为2.5×103 N. 【答案】 (1)FL4d (2)2.5×103 N。

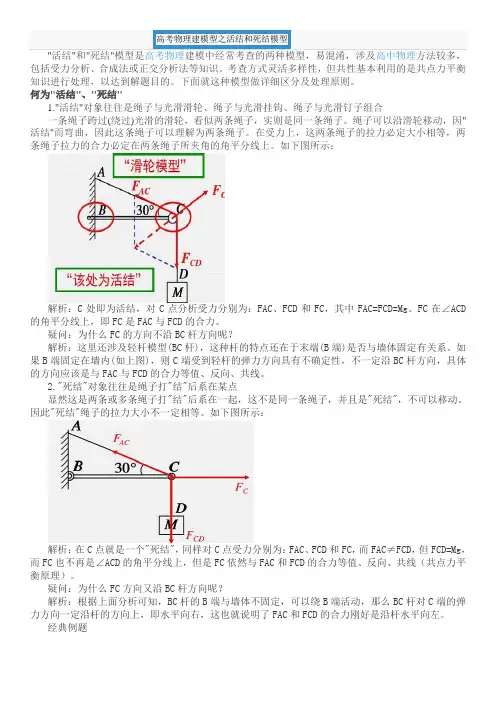
高考物理建模型之活结和死结模型"活结"和"死结"模型是高考物理建模中经常考查的两种模型，易混淆，涉及高中物理方法较多，包括受力分析、合成法或正交分析法等知识。

考查方式灵活多样性，但共性基本利用的是共点力平衡知识进行处理，以达到解题目的。

下面就这种模型做详细区分及处理原则。

何为"活结"、"死结"1."活结"对象往往是绳子与光滑滑轮、绳子与光滑挂钩、绳子与光滑钉子组合一条绳子跨过(绕过)光滑的滑轮，看似两条绳子，实则是同一条绳子。

绳子可以沿滑轮移动，因"活结"而弯曲，因此这条绳子可以理解为两条绳子。

在受力上，这两条绳子的拉力必定大小相等，两条绳子拉力的合力必定在两条绳子所夹角的角平分线上。

如下图所示：解析：C处即为活结，对C点分析受力分别为：FAC、FCD和FC，其中FAC=FCD=Mg。

FC在∠ACD 的角平分线上，即FC是FAC与FCD的合力。

疑问：为什么FC的方向不沿BC杆方向呢？解析：这里还涉及轻杆模型(BC杆)，这种杆的特点还在于末端(B端)是否与墙体固定有关系。

如果B端固定在墙内(如上图)，则C端受到轻杆的弹力方向具有不确定性，不一定沿BC杆方向，具体的方向应该是与FAC与FCD的合力等值、反向、共线。

2."死结"对象往往是绳子打"结"后系在某点显然这是两条或多条绳子打"结"后系在一起，这不是同一条绳子，并且是"死结"，不可以移动。

因此"死结"绳子的拉力大小不一定相等。

如下图所示：解析：在C点就是一个"死结"，同样对C点受力分别为：FAC、FCD和FC，而FAC≠FCD，但FCD=Mg，而FC也不再是∠ACD的角平分线上，但是FC依然与FAC和FCD的合力等值、反向、共线（共点力平衡原理）。

物理建模系列(三)绳上的“死结”和“活结”模型［模型I ^述］“死结”模型“死结”可理解为把绳子分成两段，且不可以沿绳子移动的结点.“死 结”两侧的绳因结而变成了两根独立的绳，因此由“死结”分开的两段绳子 上的弹力不一定相等.“活结”模型“活结”可理解为把绳子分成两段， 且可以沿绳子移动的结点.“活结”一般是由绳跨过滑轮或者绳上『光滑挂钩而形成的.绳子虽然因“活结” 而弯曲，但实际上是同一根绳，所以由“活结”分开的两段绳子上弹力的大 小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线^例 如图甲所示，细绳 AD 跨过固定的水平轻杆 BC 右端的定滑轮挂彳一个质量为 M i 的物体，/ACB = 30°;图乙中轻杆 HG 一端用钱链固定在竖直墙上， 另一端G 通过细绳EG 拉住，EG 与水平方向也成30°,在轻杆的G 点用细绳G F 拉住一个质量为 M2的物体，求：(1)细绳AC 段的弓^力F TAC 与细绳EG 的张力 (2)轻杆BC 对C 端的支持力； (3)轻杆HG 对G 端的支持力.【思路点拨】 图甲中细绳跨过定滑轮与物体 和CD 张力大小相等，细绳对定滑轮的合力方向沿/ 和细绳GF 为连接于G 点的两段独立的绳，属于 不相等，轻杆对 G 点的弹力沿轻杆方向.【解析】 题图甲和乙中白两个物体 M i 、 判断与物体相连的细绳，其拉力大小等于物体的重力; 行受力分析如图甲和乙所示，根据平衡规律可求解.(1)图甲中细绳AD 跨过定滑轮拉住质量为M i 的物体，物体处于平衡状态，细绳 AC 段的拉力 F TAC = F TCD = M i g图乙中由 F TEG Sin 30 = M 2g,得 F TEG = 2M 2g. 所以上皿=出F TEG 之比;M i 相连，属于“活结”模型，细绳 AC ACD 的角平分线方向；图乙中细绳EG“死结”模型，细绳EG 和细绳GF 的张力M 2都处于平衡状态，根据平衡的条件，首先 分别取 C 点和G 点为研究对象，进甲乙FTEG 2M2.（2）图甲中，三个力之间的夹角都为120 °,根据平衡规律有F Nc=F TAc=M i g,方向与水平方向成30°,指向右上方.（3）图乙中，根据平衡规律有F TEG Sin 30 = M2g,F TEG cos 30 = F NG,所以F NG=M2gcot 30 = y{3M2g,方向水平向右.【答案】（1）2Ml；（2）M i g，方向与水平方向成30。

模型02 活结与死结(解析版)死结:可理解为把绳子分成两段,且不可以沿绳子移动的结点。

“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。

活结:可理解为把绳子分成两段,且可以沿绳子移动的结点。

“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的。

绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。

【典例1】 [2017·全国卷Ⅲ]一根轻质弹性绳的两端分别固定在水平天花板上相距80cm 的两点上，弹性绳的原长也为80cm.将一钩码挂在弹性绳的中点，平衡时弹性绳的总长度为100cm ；再将弹性绳的两端缓慢移至天花板上的同一点，则弹性绳的总长度变为(弹性绳的伸长始终处于弹性限度内)( )A ．86cmB ．92cmC ．98cmD ．104cm 【答案】B【解析】由题可知，挂上钩码后，如图甲所示．此时弹性绳长度为100cm ，则θ＝37°，sinθ＝0.6.对结点O 进行受力分析如图乙所示，则由图乙得2Tsinθ＝mg ，当将两端缓慢移动至同一点时，由受力分析可得：2T′＝mg ，由弹性绳上弹力为F ＝kx 得出T x ＝T′x′，由题可知x ＝100cm －80cm ＝20cm ，则移动后弹性绳伸长长度为x′＝12cm ，那么弹性绳总长度变为L ＝L0＋x′＝92cm ，B 正确．【变式训练1】（2019·天津卷）2018年10月23日，港珠澳跨海大桥正式通车。

为保持以往船行习惯，在航道处建造了单面索（所有钢索均处在同一竖直面内）斜拉桥，其索塔与钢索如图所示。

下列说法正确的是A ．增加钢索的数量可减小索塔受到的向下的压力B ．为了减小钢索承受的拉力，可以适当降低索塔的高度C ．索塔两侧钢索对称且拉力大小相同时，钢索对索塔的合力竖直向下D．为了使索塔受到钢索的合力竖直向下，索塔两侧的钢索必须对称分布【答案】C【解析】A、以桥身为研究对象，钢索对桥身的拉力的合力与桥身的重力等大反向，则钢索对索塔的向下的压力数值上等于桥身的重力，增加钢索的数量钢索对索塔的向下的压力数值不变，故A错误；B、由图甲可知，当索塔高度降低后，α变大，cosα变小，故T变大，故B错误C、由B的分析可知，当钢索对称分布时，，钢索对索塔的合力竖直向下，故C正确D、受力分析如图乙，由正弦定理可知，只要，钢索AC、AB的拉力F AC、F AB进行合成，合力竖直向下，钢索不一定要对称分布，故D错误；综上分析：答案为C。

物理建模系列(三)绳上的“死结”和“活结”模型[模型概述]1的物体，∠ACB＝30°；图乙中轻杆HG一端用铰链固定在竖直墙上，另一端G通过细绳EG 拉住，EG与水平方向也成30°，在轻杆的G点用细绳GF拉住一个质量为M2的物体，求：(1)细绳AC段的张力F T AC与细绳EG的张力F T EG之比；(2)轻杆BC对C端的支持力；(3)轻杆HG对G端的支持力．【思路点拨】图甲中细绳跨过定滑轮与物体M1相连，属于“活结”模型，细绳AC 和CD张力大小相等，细绳对定滑轮的合力方向沿∠ACD的角平分线方向；图乙中细绳EG 和细绳GF为连接于G点的两段独立的绳，属于“死结”模型，细绳EG和细绳GF的张力不相等，轻杆对G点的弹力沿轻杆方向．【解析】题图甲和乙中的两个物体M1、M2都处于平衡状态，根据平衡的条件，首先判断与物体相连的细绳，其拉力大小等于物体的重力；分别取C点和G点为研究对象，进行受力分析如图甲和乙所示，根据平衡规律可求解．(1)图甲中细绳AD跨过定滑轮拉住质量为M1的物体，物体处于平衡状态，细绳AC段的拉力F TAC＝F T CD＝M1g图乙中由F T EG sin 30°＝M2g，得F T EG＝2M2g.所以F T ACF T EG＝M12M2.(2)图甲中，三个力之间的夹角都为120°，根据平衡规律有F N C＝F T AC＝M1g，方向与水平方向成30°，指向右上方．(3)图乙中，根据平衡规律有F T EG sin 30°＝M2g，F T EG cos 30°＝F N G，所以F N G＝M2g cot 30°＝3M2g，方向水平向右．【答案】(1)M12M2(2)M1g，方向与水平方向成30°指向右上方(3)3M2g，方向水平向右[高考真题]1．(2013·重庆卷，1)如图所示，某人静躺在椅子上，椅子的靠背与水平面之间有固定倾斜角θ.若此人所受重力为G，则椅子各部分对他的作用力的合力大小为()A．G B．G sin θC．G cos θD．G tan θ【解析】运用力的平衡条件，可求得椅子对人的作用力．选人为研究对象，人受到重力和椅子各部分对他的作用力的合力，根据力的平衡条件可知，椅子对他的作用力的合力与重力等大、反向，故选项A正确．【答案】 A2．(2013·课标卷Ⅱ，15)如图，在固定斜面上的一物块受到一外力F的作用，F平行于斜面向上．若要物块在斜面上保持静止，F的取值应有一定范围，已知其最大值和最小值分别为F1和F2(F2>0)．由此可求出()A．物块的质量B．斜面的倾角C．物块与斜面间的最大静摩擦力D．物块对斜面的正压力【解析】物块受与斜面平行的外力F作用，而在斜面上静止，此时摩擦力的大小和方向将随F的变化而变化．设斜面倾角为θ，由平衡条件F1－mg sin θ－F fmax＝0，F2－mg sinθ＋F fmax＝0，解得F fmax＝F1－F22，故选项C正确．【答案】 C3.(2016·课标卷Ⅲ，17)如图，两个轻环a 和b 套在位于竖直面内的一段固定圆弧上；一细线穿过两轻环，其两端各系一质量为m 的小球．在a 和b 之间的细线上悬挂一小物块．平衡时，a 、b 间的距离恰好等于圆弧的半径．不计所有摩擦．小物块的质量为( )A.m 2 B ．32m C.mD ．2m【解析】 根据题意设悬挂小物块的点为O ′，圆弧的圆心为O ，由于ab ＝R ，所以三角形Oab 为等边三角形，根据几何知识可得∠aO ′b ＝120°，而一条绳子上的张力大小相等，故T ＝mg ，小物块受到两条绳子的拉力作用大小相等，夹角为120°，故受到的拉力的合力等于mg ，因为小物块受到绳子的拉力和自身重力作用，处于平衡状态，故拉力的合力等于小物块的重力为mg ，所以小物块的质量为m ，C 正确．【答案】 C[名校模拟]4．(2018·安徽合肥段考)将两个质量均为m 的小球a 、b 用细线相连后，再用细线悬挂于O 点，如图所示，用力F 拉小球b ，使两个小球都处于静止状态，且细线Oa 与竖直方向的夹角保持θ＝30°，则F 达到最小时Oa 绳上的拉力为( )A.3mg B ．mg C.32mg D ．12mg【解析】 以两个小球组成的整体为研究对象，分析受力，作出F 在不同方向时整体的受力图，根据平衡条件可知，F 与T 的合力与重力2mg 总是大小相等、方向相反，由力的合成图可知，当F 与绳子Oa 垂直时，F 有最小值，即图中2位置，F 的最小值为F min ＝2mg sin 30°＝mg ，T ＝2mg cos 30°＝3mg ，A 正确．【答案】 A5.(2018·广东仲元中学月考)如图所示，跳伞运动员打开伞后经过一段时间，将在空中保持匀速降落．已知运动员和他身上装备的总重力为G 1(不包括伞面)，圆顶形降落伞伞面的重力为G 2，有8条相同的拉线，一端与飞行员相连(拉线重力不计)，另一端均匀分布在伞面边缘上(图中没有把拉线都画出来)，每根拉线和竖直方向都成30°角．那么每根拉线上的张力大小为( )A.G 14 B ．3G 112 C.G 1＋G 28D ．3G 1＋G 212【解析】 对运动员进行受力分析可知，8条拉线拉力的合力与运动员的重力等大反向，即8条拉线在水平方向的分力的合力为零，竖直方向分力的合力与运动员的重力等大反向，根据对称性可知，8条拉线的张力大小都相等，每条拉线的张力在竖直方向的分力F y ＝F cos 30°，且8F y ＝G 1，可得F ＝G 18cos 30°＝G 143＝3G 112，故B 正确，A 、C 、D 错误．【答案】 B 6.(2018·山东泰安高三上学期期中)在日常生活中，力的分解有着广泛的应用．如图为用斧子把树桩劈开的图示，斧子对木桩施加一个向下的力F 时，产生了大小相等的两个侧向分力F 1、F 2，下列关系正确的是( )A ．F ＝2F 1sin(θ2)B ．F ＝2F 1sin θC ．F ＝2F 1cos(θ2)D ．F ＝2F 1cos θ【解析】 F 1、F 2与水平方向的夹角为θ2，则F ＝2F 1sin θ2，A 对．【答案】 A课时作业(五)[基础小题练]1．(2018·广州调研)如图，三个大小相等的力F，作用于同一点O，则合力最小的是()【解析】根据矢量合成的平行四边形定则可知，C选项的合力为零，即合力最小，C 正确．【答案】 C2.(2018·淮安模拟)我国海军在南海某空域举行实兵对抗演练，某一直升机在匀速水平飞行过程中遇到突发情况，立即改为沿虚线方向斜向下减速飞行，则空气对其作用力可能是()A．F1B．F2C．F3D．F4【解析】因为直升机沿虚线方向斜向下减速飞行，故合力沿虚线向上，直升机受到竖直向下的重力以及空气作用力两个力，要想合力沿虚线向上，则根据矢量三角形可得空气对其作用力可能为F1，如图所示．【答案】 A3.(2018·石家庄模拟)如图所示，一个“Y”形弹弓顶部跨度为L，两根相同的橡皮条自由长度均为L，在两橡皮条的末端用一块软羊皮(长度不计)做成裹片．若橡皮条的弹力与形变量的关系满足胡克定律，且劲度系数为k，发射弹丸时每根橡皮条的最大长度为2L(弹性限度内)，则发射过程中裹片对弹丸的最大作用力为()A ．kLB ．2kL C.32kL D ．152kL 【解析】 设发射弹丸瞬间两橡皮条间的夹角为2θ，则sin θ＝L 22L ＝14，cos θ＝1－sin 2θ＝154.发射过程中裹片对弹丸的最大作用力为F 合＝2F cos θ，F ＝kx ＝kL ，故F 合＝2kL ·154＝152kL ，D 正确． 【答案】 D4．手握轻杆，杆的另一端安装有一个小滑轮C ，支持着悬挂重物的绳子，如图所示，现保持滑轮C 的位置不变，使杆柄向上转动一个角度，则杆对滑轮C 的作用力将()A ．变大B ．不变C ．变小D ．无法确定【解析】 杆对滑轮C 的作用力大小等于两绳上拉力的合力，由于两绳上拉力的合力不变，故杆对滑轮C 的作用力不变．【答案】 B5．如图所示，作用于O 点的三个力F 1、F 2、F 3合力为零，F 1沿－y 方向，大小已知．F 2与＋x 方向夹角为θ(θ<90°)，大小未知．下列说法正确的是()A ．F 3可能指向第二象限B ．F 3一定指向第三象限C ．F 3与F 2的夹角越小，则F 3与F 2的合力越小D ．F 3的最小可能值为F 1cos θ【解析】 因F 1、F 2、F 3的合力为零，故F 3应与F 2、F 1的合力等大反向，故F 3可能指向第二象限，也可能指向第三象限，选项A 正确，B 错误；F 3、F 2的合力与F 1等大反向，而F 1大小、方向均已知，故F 3与F 2的合力与其夹角大小无关，选项C 错误；当F 3与F 2垂直时，F3最小，其最小值为F1cos θ，选项D正确．【答案】AD6.(2018·六安一中二模)如图所示，两个质量为m1的小球套在竖直放置的光滑支架上，支架的夹角为120°，用轻绳将两球与质量为m2的小球连接，绳与杆构成一个菱形，则m1∶m2为()A．1∶1 B．1∶2C．1∶ 3 D．3∶2【解析】将小球m2的重力按效果根据平行四边形定则进行分解如图，由几何知识得T＝m2g，对m1受力分析，由平衡条件，在沿杆的方向有：m1g sin 30°＝T sin 30°，得：T＝m1g，可见m1∶m2＝1∶1，故选A.【答案】 A[创新导向练]7．生活实际——千斤顶中的力学原理(2018·贵阳监测)如图所示是轿车常用的千斤顶，当摇动把手时，螺纹轴就能迫使千斤顶的两臂靠拢，从而将汽车顶起．当车轮刚被顶起时汽车对千斤顶的压力为1.0×105 N，此时千斤顶两臂间的夹角为120°.下列判断正确的是()A．此时千斤顶每臂受到的压力大小均为5.0×104 NB．此时千斤顶对汽车的支持力为1.0×104 NC．若继续摇动把手，将汽车顶起，千斤顶每臂受到的压力将增大D．若继续摇动把手，将汽车顶起，千斤顶每臂受到的压力将减小【解析】车轮刚被顶起时，千斤顶两臂支持力的合力为千斤顶对汽车的支持力，等于汽车对千斤顶的压力，大小为1.0×105 N，B项错误；两臂夹角为120°，由力的合成可知千斤顶每臂受到的压力为1.0×105 N，A项错误；继续摇动把手，将汽车顶起，千斤顶两臂夹角减小，每臂受到的压力减小，D项正确，C项错误．【答案】 D8．生活实际——以“减速带”为背景考查力的合成问题减速带是交叉路口常见的一种交通设施，车辆驶过减速带时要减速，以保障行人的安全．当汽车前轮刚爬上减速带时，减速带对车轮的弹力为F ，下图中弹力F 画法正确且分解合理的是( )【解析】 减速带对车轮的弹力方向垂直车轮和减速带的接触面，指向受力物体，故A 、C 错误；按照力的作用效果分解，将F 可以分解为水平方向和竖直方向，水平方向的分力产生的效果减慢汽车的速度，竖直方向上分力产生向上运动的作用效果，故B 正确，D 错误．【答案】 B9．人体生理——关节运动中所包含的力学问题如右图所示，人屈膝下蹲时，膝关节弯曲的角度为θ.设此时大小腿部的肌肉群对膝关节的作用力F 的方向水平向后，且大腿骨和小腿骨对膝关节的作用力大致相等，那么脚掌所受小腿骨沿竖直方向的力约为( )A.F 2sin (θ2)B ．F 2cos (θ2)C.F 2tan (θ2)D ．F 2tan(θ2)【解析】 根据题意先将肌肉群对膝关节的作用力F 沿大腿骨和小腿骨方向分解，然后再分解小腿骨方向的分力，即可知D 正确．【答案】 D10．科技生活——缓冲门中的力学问题分析如图所示为缓慢关门时(图中箭头方向)门锁的示意图，锁舌尖角为37°，此时弹簧弹力为24 N ，锁舌表面较光滑，摩擦不计(sin 37°＝0.6，cos 37°＝0.8)，下列说法正确的是( )A ．此时锁壳碰锁舌的弹力为40 NB ．此时锁壳碰锁舌的弹力为30 NC ．关门时锁壳碰锁舌的弹力逐渐增大D ．关门时锁壳碰锁舌的弹力保持不变【解析】 锁壳碰锁舌的弹力分解如图所示，其中F 1＝F N sin 37°，且此时F 1大小等于弹簧的弹力为24 N ，解得锁壳碰锁舌的弹力为40 N ，选项A 正确，B 错误；关门时，弹簧的压缩量增大，弹簧的弹力增大，故锁壳碰锁舌的弹力逐渐增大，选项C 正确，D 错误．【答案】 AC[综合提升练]11．(2018·山东泰安高三上学期期中)质量为m 的物体置于倾角为θ＝37°的固定斜面上，物体与斜面之间的动摩擦因数为μ＝0.2.如图甲所示，先用平行于斜面的推力F 1作用于物体上，使其能沿斜面匀速上滑；若改用水平推力F 2作用于物体上，也能使物体沿斜面匀速上滑，如图乙所示．求两次推力大小之比F 1F 2.(sin 37°＝0.6，cos 37°＝0.8)【解析】 根据共点力平衡条件可得F 1＝mg sin θ＋μF N F N ＝mg cos θ F 2cos θ＝mg sin θ＋μF ′N F ′N ＝mg cos θ＋F 2sin θ 整理得F 1F 2＝cos θ－μsin θ代入数值得F 1F 2＝0.68.【答案】 0.6812．电梯修理员或牵引专家常常需要监测金属绳中的张力，但不能到绳的自由端去直接测量．某公司制造出一种能测量绳中张力的仪器，工作原理如图所示，将相距为L 的两根固定支柱A 、B (图中的小圆圈表示支柱的横截面)垂直于金属绳水平放置，在A 、B 的中点用一可动支柱C 向上推动金属绳，使绳在垂直于A 、B 的方向竖直向上发生一个偏移量d (d ≪L )，这时仪器测得金属绳对支柱C 竖直向下的作用力为F .(1)试用L 、d 、F 表示这时金属绳中的张力F T ；(2)如果偏移量d ＝10 mm ，作用力F ＝400 N ，L ＝250 mm ，计算金属绳中张力的大小．【解析】 (1)设C ′点受两边金属绳的张力分别为F T1和F T2，BC 与BC ′的夹角为θ，如图所示．依对称性有：F T1＝F T2＝F T由力的合成有：F ＝2F T sin θ 根据几何关系有sin θ＝d d 2＋L 24联立上述二式解得F T ＝F2dd 2＋L 24则d ≪L ，故F T ＝FL4d.(2)将d ＝10 mm ，F ＝400 N ，L ＝250 mm 代入F T ＝FL4d解得F T ＝2.5×103 N ，即金属绳中的张力为2.5×103 N. 【答案】 (1)FL4d (2)2.5×103 N。

2024年高考物理一轮复习导学练活结与死结绳模型、动杆和定杆模型和受力分析导练目标导练内容目标1活结与死结绳模型目标2动杆和定杆模型目标3受力分析【知识导学与典例导练】一、活结与死结绳模型1．“活结”模型模型结构模型解读模型特点“活结”把绳子分为两段，且可沿绳移动，“活结”一般由绳跨过滑轮或绳上挂一光滑挂钩而形成，绳子因“活结”而弯曲，但实际为同一根绳“活结”绳子上的张力大小处处相等常见模型力学关系和几何关系端点A上下移动挡板MN左右移动①T1=T2=G2sinθ②l1cosθ+l2cosθ=d(l1+l2)cosθ=dcosθ=dl因为d和l都不变，所以根据cosθ=dl可知θ也不变，则T1和T2也不变。

因为MN左右移动时，d变化，而l不变，根据cosθ=dl可知θ将变化，则T1和T2也变。

常见模型力学关系和几何关系端点A左右移动两物体质量比变①角度：θ4=2θ3=2θ2=4θ1②拉力：T=M Q g③2M Q cosθ2=M P 两物体质量比不变，左右移动轻绳端点，角度都不变。

角度变，但让保持原有倍数关系。

1如图所示，一根不可伸长的光滑轻质细绳通过轻滑轮挂一重物，细绳一端系在竖直墙壁的A点，另一端系在倾斜墙壁的B点，现将细绳右端从B点沿倾斜墙壁缓慢向下移动到与A点等高的B′点。

在移动过程中，关于细绳拉力大小变化情况正确的是()A.先变小后变大B.变大C.变小D.不变2在如图所示装置中，两物体质量分别为m1和m2，滑轮直径大小可忽略。

设动滑轮P两侧的绳与竖直方向夹角分别为α和β。

整个装置能保持静止。

不计动滑轮P的质量和一切摩擦。

则下列法正确的有()A.α一定等于βB.m 1一定大于m2C.m1一定小于m2D.m1可能大于2m23“死结”模型模型结构模型解读模型特点“死结”把绳子分为两段，且不可死结两侧的绳子张力不一定相等沿绳子移动，“死结”两侧的绳因结而变成两根独立的绳4如图所示，将三段轻绳相结于O点，其中OA绳的一端拴在墙上，OB绳的下方悬挂甲物体，OC绳跨过光滑定滑轮悬挂乙物体。

绳的活结与死结模型、动杆和定杆模型特训目标特训内容目标1绳子类的“死结”问题(1T -4T )目标2绳子类的“活结”问题(5T -8T )目标3有关滑轮组的“活结”问题(9T -12T )目标4定杆和动杆问题(13T -16T )【特训典例】一、绳子类的“死结”问题1如图所示，质量为m =2.4kg 的物体用细线悬挂处于静止状态。

细线AO 与天花板之间的夹角为53°，细线BO 水平，若三根细线能承受最大拉力均为100N ，重力加速度g 取10m/s 2，不计所有细线的重力，sin37°=0.6，cos37°=0.8。

下列说法正确的是()A.细线BO 上的拉力大小30NB.细线AO 上的拉力大小18NC.要使三根细线均不断裂，则细线下端所能悬挂重物的最大质量为8kgD.若保持O 点位置不动，沿顺时针方向缓慢转动B 端，则OB 绳上拉力的最小值为19.2N 【答案】C【详解】AB ．以结点O 为研究对象，受到重力、OB 细线的拉力和OA 细线的拉力，如图所示根据平衡条件结合图中几何关系可得细线BO 上的拉力大小为F BO =mg tan37°=18N 同理，可解得细线AO 上的拉力大小F AO =mgcos37°=30N 故AB 错误；C ．若三根细线能承受的最大拉力均为100N ，根据图中力的大小关系可得，只要OA 不拉断，其它两根细线都不会拉断，故有m max g =F max cos37°解得m max =F max cos37°g =100×0.810kg =8kg ，故C 正确；D ．当OB 与OA 垂直时，OB 细线的拉力最小，根据几何关系结合平衡条件可得F min =mg sin37°=2.4×10×0.6N =14.4N 故D 错误。

故选C 。

2如图所示，两个质量均为m 的小球a 和b 套在竖直固定的光滑圆环上，圆环半径为R ，一不可伸长的细线两端各系在一个小球上，细线长为23R 。

难点7绳上死结和活结问题的分析
“死结”可理解为把绳子分成两段，且不可以沿绳子移动的结点．“死结”一般是由结住而形成的，“死结”两侧的绳因结住而变成了两根独立的绳，因此由“死结”分开的两段绳子上的弹力不一定捆等，
“活结”可理解为把绳子分成两段，且可以沿绳子移动的结点．“活结”-般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的，绳子虽然因“活结”而弯曲，但实际上是同一根绳，所以由“活结”分开的两段绳孚上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线．
典列8
图甲图乙
如图甲所示，质量为m的物体用细绳OC悬挂在支架上的0点，沿水平方向的轻杆OB的B端由铰链固定，可绕B点自由转动，细绳OA与轻杆OB所成的角为θ，求细绳OA中张力T的大小和轻杆OB对细绳的弹力
F的大小．
N
点拨
涉及绳子的死结和活结问题时要能区别两类模型：
(1)绳与杆的一端连接为结点，如典例8，此时绳子OA 的拉力不等于物体的重力;
(2)绳跨过光滑滑轮，如图所示，此时绳子BC 的拉力等于物体的重力．滑轮受到绳的作用力是两部分绳子拉力的合力，两部分绳子拉力大小均为mg ，合力方向沿两绳的角平分线．
深化
摩擦力和弹力都属于接触力．两物体间存在摩擦力必存在弹力，存在弹力不一定存在摩擦力．
解析
由题意知，绳的结点O 相当于死结，分析结点O 的受力情况如图乙所示，它受到细绳OA 的拉力T,轻杆OB 的弹力N F 和细绳OC 的拉力
（大小等于重力mg ）,其中T ，N F 的合力一定与mg 平衡，即等大反向，解力的三角形可得：θθcot ,mg F mg T N ==。

绳的活结与死结模型、动杆和定杆模型特训目标特训内容目标1绳子类的“死结”问题(1T -4T )目标2绳子类的“活结”问题(5T -8T )目标3有关滑轮组的“活结”问题(9T -12T )目标4定杆和动杆问题(13T -16T )【特训典例】一、绳子类的“死结”问题1如图所示，质量为m =2.4kg 的物体用细线悬挂处于静止状态。

细线AO 与天花板之间的夹角为53°，细线BO 水平，若三根细线能承受最大拉力均为100N ，重力加速度g 取10m/s 2，不计所有细线的重力，sin37°=0.6，cos37°=0.8。

下列说法正确的是()A.细线BO 上的拉力大小30NB.细线AO 上的拉力大小18NC.要使三根细线均不断裂，则细线下端所能悬挂重物的最大质量为8kgD.若保持O 点位置不动，沿顺时针方向缓慢转动B 端，则OB 绳上拉力的最小值为19.2N 【答案】C【详解】AB ．以结点O 为研究对象，受到重力、OB 细线的拉力和OA 细线的拉力，如图所示根据平衡条件结合图中几何关系可得细线BO 上的拉力大小为F BO =mg tan37°=18N 同理，可解得细线AO 上的拉力大小F AO =mgcos37°=30N 故AB 错误；C ．若三根细线能承受的最大拉力均为100N ，根据图中力的大小关系可得，只要OA 不拉断，其它两根细线都不会拉断，故有m max g =F max cos37°解得m max =F max cos37°g =100×0.810kg =8kg ，故C 正确；D ．当OB 与OA 垂直时，OB 细线的拉力最小，根据几何关系结合平衡条件可得F min =mg sin37°=2.4×10×0.6N =14.4N 故D 错误。

故选C 。

2如图所示，两个质量均为m 的小球a 和b 套在竖直固定的光滑圆环上，圆环半径为R ，一不可伸长的细线两端各系在一个小球上，细线长为23R 。

模型02 活结与死结(解析版)死结:可理解为把绳子分成两段,且不可以沿绳子移动的结点。

“死结”两侧的绳因结而变成了两根独立的绳,因此由“死结”分开的两段绳子上的弹力不一定相等。

活结:可理解为把绳子分成两段,且可以沿绳子移动的结点。

“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的。

绳子虽然因“活结”而弯曲,但实际上是同一根绳,所以由“活结”分开的两段绳子上弹力的大小一定相等,两段绳子合力的方向一定沿这两段绳子夹角的角平分线。

【典例1】[2017·全国卷Ⅲ]一根轻质弹性绳的两端分别固定在水平天花板上相距80cm的两点上，弹性绳的原长也为80cm.将一钩码挂在弹性绳的中点，平衡时弹性绳的总长度为100cm；再将弹性绳的两端缓慢移至天花板上的同一点，则弹性绳的总长度变为(弹性绳的伸长始终处于弹性限度内)() A．86cm B．92cm C．98cm D．104cm【答案】B【解析】由题可知，挂上钩码后，如图甲所示．此时弹性绳长度为100cm，则θ＝37°，sinθ＝0.6.对结点O 进行受力分析如图乙所示，则由图乙得2Tsinθ＝mg，当将两端缓慢移动至同一点时，由受力分析可得：2T′＝mg，由弹性绳上弹力为F＝kx得出Tx＝T′x′，由题可知x＝100cm－80cm＝20cm，则移动后弹性绳伸长长度为x′＝12cm，那么弹性绳总长度变为L＝L0＋x′＝92cm，B正确．【变式训练1】（2019·天津卷）2018年10月23日，港珠澳跨海大桥正式通车。

为保持以往船行习惯，在航道处建造了单面索（所有钢索均处在同一竖直面内）斜拉桥，其索塔与钢索如图所示。

下列说法正确的是A．增加钢索的数量可减小索塔受到的向下的压力B．为了减小钢索承受的拉力，可以适当降低索塔的高度C．索塔两侧钢索对称且拉力大小相同时，钢索对索塔的合力竖直向下D．为了使索塔受到钢索的合力竖直向下，索塔两侧的钢索必须对称分布【答案】C【解析】A、以桥身为研究对象，钢索对桥身的拉力的合力与桥身的重力等大反向，则钢索对索塔的向下的压力数值上等于桥身的重力，增加钢索的数量钢索对索塔的向下的压力数值不变，故A错误；B、由图甲可知，当索塔高度降低后，α变大，cosα变小，故T变大，故B错误C、由B的分析可知，当钢索对称分布时，，钢索对索塔的合力竖直向下，故C正确D、受力分析如图乙，由正弦定理可知，只要，钢索AC、AB的拉力F AC、F AB进行合成，合力竖直向下，钢索不一定要对称分布，故D错误；综上分析：答案为C。

第五讲：绳上的‘死结’和‘活结’杆中的“活杆”与“死杆”模型一、“活结”与“死结”绳是物体间连接的一种方式，当多个物体用绳连接的时候，其间必然有“结”的出现，根据“结”的形式不同，可以分为“活结”和“死结”两种.1. “活结”“活结”可理解为把绳子分成两段，且可以沿绳子移动的结点．“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的．绳子虽然因“活结”而弯曲，但实际上是同根绳，所以由“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线．2. “死结”“死结”可理解为把绳子分成两段，且不可沿绳子移动的结点。

“死结”一般是由绳子打结而形成的，“死结”两侧的绳子因打结而变成两根独立的绳子。

死结的特点：1.绳子的结点不可随绳移动2.“死结”两侧的绳子因打结而变成两根独立的绳子，因此由“死结”分开的两端绳子上的弹力不一定相等【典例1】如图所示，将一细绳的两端固定于两竖直墙的Ａ、Ｂ两点，通过一个光滑的挂钩将某重物挂在绳上，下面给出的四幅图中有可能使物体处于平衡状态的是（）【典例2】如图所示，一轻绳的两端分别固定在不等高的A、B两点，现用另一轻绳将一物体系于O点，设轻绳AO、BO相互垂直，α>β，且两绳中的拉力分别为F A、F B，物体受到的重力为G，下列表述正确的是( )A．F A一定大于G B．F A一定大于F BC．F A一定小于F B D．F A与F B大小之和一定等于G第2题图第3题图【典例3】如图所示，在水平天花板的A点处固定一根轻杆a，杆与天花板保持垂直．杆的下端有一个轻滑轮O.另一根细线上端固定在该天花板的B点处，细线跨过滑轮O，下端系一个重为G的物体，BO段细线与天花板的夹角为θ＝30°.系统保持静止，不计一切摩擦．下列说法中正确的是( )A．细线BO对天花板的拉力大小是2G B．a杆对滑轮的作用力大小是2G C．a杆和细线对滑轮的合力大小是G D．a杆对滑轮的作用力大小是G 【典例4】如图所示，长为5 m的细绳的两端分别系于竖立在地面上的相距为4 m的两杆的顶端A、B，绳上挂一个光滑的轻质挂钩，其下连着一个重为12 N的物体，平衡时绳中的张力F T为多大？当A点向上移动少许，重新平衡后，绳与水平面夹角、绳中张力如何变化？.【典例5】如图所示，AO、BO和CO三根绳子能承受的最大拉力相等，O为结点，OB与竖直方向夹角为θ，悬挂物质量为m。

2024年高考物理一轮大单元综合复习导学练专题10活结与死结绳模型、动杆和定杆模型和受力分析导练目标导练内容目标1活结与死结绳模型目标2动杆和定杆模型目标3受力分析【知识导学与典例导练】一、活结与死结绳模型1．“活结”模型【例1】如图所示，一根不可伸长的光滑轻质细绳通过轻滑轮挂一重物，细绳一端系在竖直墙壁的A点，另一端系在倾斜墙壁的B点，现将细绳右端从B点沿倾斜墙壁缓慢向下移动到与A点等高的B′点。

在移动过程中，关于细绳拉力大小变化情况正确的是（）A．先变小后变大B．变大C．变小D．不变【答案】B【详解】如下图，设绳子总长度为L，BD垂直于AB′，最开始时AO与竖直方向的夹角为θ，根据对称性有AO sinθ＋BO sinθ=L sinθ=AD绳子右端从B点移动到B′O点移动到O′点，B′O′与竖直方向夹角为α，根据对称性有AO′sinα＋BO′sinα=L sinα=AB′因为AB′>AD所以α>θ则绳子移动后，绳子之间的夹角变大，而两段绳子的拉力大小相同，合力大小始终等于重物的重力大小，根据力的平行四边形定则，两段绳子的拉力大小变大。

故选B。

【例2】在如图所示装置中，两物体质量分别为1m和2m，滑轮直径大小可忽略。

设动滑轮P两侧的绳与竖直方向夹角分别为α和β。

整个装置能保持静止。

不计动滑轮P的质量和一切摩擦。

则下列法正确的有（）2m A．α一定等于βB．1m一定大于2m C．1m一定小于2m D．1m可能大于2【答案】A【详解】绳子连续通过定滑轮和动滑轮，绳子上的拉力相同，整个装置能保持静止，则绳子上的拉力大小与2m 的重力大小相同，即2T m g =对滑轮P 进行受力分析可得1sin cos cos cos T T T T m gαβαβ=+=解得122cos m m αβα==故1m 一定小于22m ，当60αβ==︒时，有12T m g m g ==故选A 。

2．“死结”模型模型结构模型解读模型特点“死结”把绳子分为两段，且不可沿绳子移动，“死结”两侧的绳因结而变成两根独立的绳死结两侧的绳子张力不一定相等【例3】如图所示，将三段轻绳相结于O 点，其中OA 绳的一端拴在墙上，OB 绳的下方悬挂甲物体，OC 绳跨过光滑定滑轮悬挂乙物体。

物理建模1-绳上的“死结”和“活结”模型绳上的“死结”和“活结”模型济源高级中学物理组李卫华·物理模型概述物理模型是一种理想化的物理形态，所谓“建模”就是将较复杂的研究对象或物理过程，通过用理想化、简单化、抽象化、类比化等手段，突出事物的本质特征和规律形成样板式的概念、实物体系或情境过程，即物理建模.实际问题模型化是高中阶段处理物理问题的基本思路和方法，当我们遇到实际的运动问题时，要建立我们高中阶段学习过的熟知的物理模型，下面介绍的是绳上的“死结”和“活结”模型．1．“死结”模型(1)“死结”可理解为把绳子分成两段．(2)“死结”是不可以沿绳子移动的结．(3)“死结”两侧的绳因结住而变成了两根独立的绳．(4)“死结”分开的两段绳子上的弹力不一定相等．(如典例1)2．“活结”模型(1)“活结”可理解为把绳子分成两段．(2)“活结”是可以沿绳子移动的结点．(3)“活结”一般是由绳跨过滑轮或者绳上挂一光滑挂钩而形成的．绳子虽然因“活结”而弯曲，但实际上是同一根绳．(4)“活结”分开的两段绳子上弹力的大小一定相等，两段绳子合力的方向一定沿这两段绳子夹角的平分线．(如典例2)典例1 如图2-2-9所示，一根细线两端分别固定在A、B点，质量为m的物体上面带一个小夹子，开始时用夹子将物体固定在图示位置，OA段细线水平，OB段细线与水平方向的夹角为θ＝45°，现将夹子向左移动一小段距离，移动后物体仍处于静止状态，关于OA、OB 两段细线中的拉力大小，下列说法正确的是()．图2-2-9A．移动前，OA段细线中的拉力等于物体所受的重力大小B．移动前，OA段细线中的拉力小于物体所受的重力大小C．移动后，OB段细线中拉力的竖直分量不变D．移动后，OB段细线中拉力的竖直分量变小解析取O点为研究对象，受力如图所示，由图知：T OA＝T OB cos θ，T OB sin θ＝mg，当θ＝45°时，T OA＝mg，A对；向左移动一小段距离后，O点位置下移，OB段细线中拉力的竖直分量与OA 段细线中拉力的竖直分量之和等于重力大小，即OB段细线中拉力的竖直分量变小，D对．答案AD典例2 如图2-2-10所示，杆BC的B端用铰链接在竖直墙上，另一端C为一滑轮．重物G 上系一绳经过滑轮固定于墙上A点处，杆恰好平衡．若将绳的A端沿墙缓慢向下移(BC杆、滑轮、绳的质量及摩擦均不计)，则()．图2-2-10A．绳的拉力增大，BC杆受绳的压力增大B．绳的拉力不变，BC杆受绳的压力增大C．绳的拉力不变，BC杆受绳的压力减小D．绳的拉力不变，BC杆受绳的压力不变解析选取绳子与滑轮的接触点为研究对象，对其受力分析，如图所示，绳中的弹力大小相等，即T1＝T2＝G，C点处于三力平衡状态，将三个力的示意图平移可以组成闭合三角形，如图虚线所示，设AC段绳子与竖直墙壁间的夹角为θ，则根据几何知识可知F＝2G sin θ，当绳的2A端沿墙缓慢向下移时，θ增大，F也增大，根据牛顿第三定律知，BC杆受绳的压力增大，B正确．答案 B练习1．如图2-2-11所示，两个质量均为m的物体分别挂在支架上的B点(如图甲所示)和跨过滑轮的轻绳BC上(如图乙所示)，图甲中轻杆AB可绕A点转动，图乙中水平轻杆一端A 插在墙壁内，已知θ＝30°，则图甲中轻杆AB受到绳子的作用力F1和图乙中滑轮受到绳子的作用力F2分别为()．图2-2-11A．F1＝mg、F2＝3mg B．F1＝3mg、F2＝3mgC．F1＝33mg、F2＝mg D．F1＝3mg、F2＝mg答案 D2．如图2-2-19所示，一轻绳的两端分别固定在不等高的A、B两点，现用另一轻绳将一物体系于O点，设轻绳AO、BO相互垂直，α>β，且两绳中的拉力分别为F A、F B，物体受到的重力为G，下列表述正确的是()．图2-2-19A．F A一定大于GB．F A一定大于F BC．F A一定小于F BD．F A与F B大小之和一定等于G解析物体受力分析如图所示，由三力平衡的知识可知，F A、F B的合力大小等于G，方向竖直向上，F A＝G sin α，F B＝G sin β.故F A一定小于G，A选项错误；因为α>β，故F A一定大于F B，B选项正确、C选项错误；F A与F B大小之和大于G，D选项错误．答案 B3．如图2-2-20所示，A、B两物体的质量分别为m A、m B，且m A>m B，整个系统处于静止状态．滑轮的质量和一切摩擦均不计，如果绳一端由Q点缓慢地向左移到P点，整个系统重新平衡后，物体A的高度和两滑轮间绳与水平方向的夹角θ变化情况是()．图2-2-20A．物体A的高度升高，θ角变大B．物体A的高度降低，θ角变小C．物体A的高度升高，θ角不变D．物体A的高度不变，θ角变小解析最终平衡时，绳的拉力F大小仍为m A g，由二力平衡可得2F sin θ＝m B g，故θ角不变，但因悬点由Q到P，左侧部分绳子变长，故A应升高，所以C正确．答案 C练习4：（2013年福建理综）。

2023届高三物理一轮复习重点热点难点专题特训专题09 绳的活结与死结模型、动杆和定杆模型特训目标特训内容目标1 绳子类的“死结”问题（1T—4T）目标2 绳子类的“活结”问题（5T—8T）目标3 有关滑轮组的“活结”问题（9T—12T）目标4定杆和动杆问题（13T—16T）一、绳子类的“死结”问题1．如图所示，将三段轻绳相结于O点，其中OA绳的一端拴在墙上，OB绳的下方悬挂甲物体，OC绳跨过光滑定滑轮悬挂乙物体。

OC绳与竖方向的夹角为α=70°。

OA绳与竖直方向的夹角为β（未知）。

若甲、乙两物体的质量均为m=2kg，重力加速度g取10m/s2，sin55°≈0.82。

根据所学的知识，不需计算，推理出OA绳的拉力约为（）A．16N B．23N C．31N D．41N【答案】B【详解】甲、乙两物体的质量均为m=2kg，则OC绳的拉力与OB绳的拉力均为20N，这两个力的合力与OA绳的拉力大小相等，方向相反。

由几何关系可知OC绳的拉力与OB绳的拉力夹角为110°，而夹角为120°均为20N的两个力的合力大小为20N。

所以OC绳的拉力与OB绳的拉力的合力接近20N。

所以根据所学的知识，不需计算，推理出OA绳的拉力约为B选项的23N。

故选B。

2．如图所示，两个轻环P和Q套在位于竖直面你的一固定“∧”形光滑框架上，框架两边与竖直方向的夹角均为30°，两段伸长可忽略的细绳，一端分别系在P、Q环上，另一端与绳套系在一起，结点为O。

现在绳套上挂一小物块，平衡时细绳OP所受拉力大小为F，拉直时两段细绳长度相等，不计细绳与绳套的重力。

小物块的重力大小为（）A ．2FB ．FC 3D 23【答案】B 【详解】如图所示对P 、Q 小环分析，小环受光滑杆的支持力和绳子的拉力，根据平衡条件，这两个力是一对平衡力，支持力是垂直于杆子向上的，故绳子的拉力也是垂直于杆子的，故两细绳之间的夹角为120︒，由几何关系可知，两根绳子与竖直方向之间的夹角都是903060︒-︒=︒所以绳子OQ 的拉力也是F ，两根绳子的长度相等，对结点O 受力分析如图所示，根据平衡条件可知，由几何关系可知，三个力之间的夹角都是120︒，所以G F =故B 正确，ACD 错误。