角平分线的专题复习ppt课件

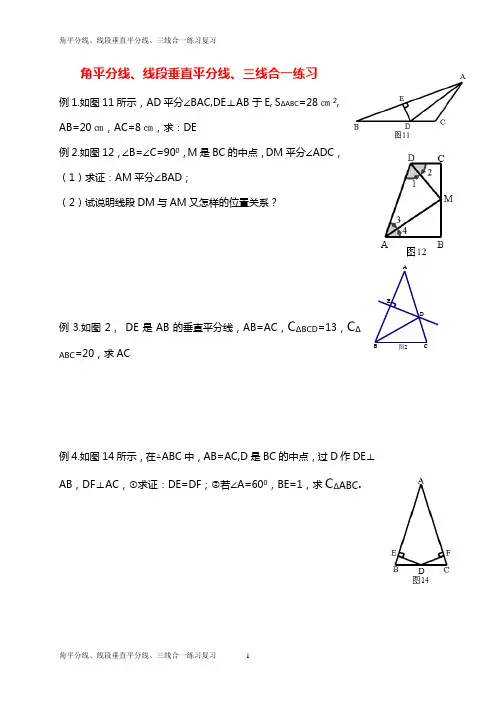
角平分线、线段垂直平分线、三线合一练习例1.如图11所示，AD平分∠BAC,DE⊥AB于E, S∆ABC=28㎝2, AB=20㎝，AC=8㎝，求：DE例2.如图12，∠B=∠C=900，M是BC的中点，DM平分∠ADC，（1）求证：AM平分∠BAD；（2）试说明线段DM与AM又怎样的位置关系？例3.如图2，DE是AB的垂直平分线，AB=AC，C∆BCD=13，C∆ABC=20，求AC例4.如图14所示，在△ABC中，AB=AC,D是BC的中点，过D作DE⊥AB，DF⊥AC，①求证：DE=DF；②若∠A=600，BE=1，求C∆ABC.图2EDCBA例5.如图15，等边三角形ABC中，D是AC的中点，延长BC到E使CE=CD，过D作DF⊥BC，求证：F是BE的中点。

练习：1. 如图3，∠C=900，AC=BC,AD是∠BAC的平分线，DE⊥AB，若AB=8㎝,求C∆DEB2.如图5，OB 、OC 分别平分∠ABC 、∠ACB ，OD ⊥BC ，OD=3，C ∆CAB =12, 求S ∆ABC3. 如图9，△ABC 中∠C=900，AD 平分∠BAC ，AB=10，AC=8，求S ∆ABD ：S ∆ADC 的值4.如图2， DE 是AB 的垂直平分线， AE=3，C ∆BCD =13，求C ∆ABC5.如图2， DE 是AB 的垂直平分线，BC=3，C ∆BCD =13，求ACOD 图5CBA图2EDCBA6.如图2，DE是AB的垂直平分线，AB=AC，C∆BCD=13，C∆ABC=20，求AB7.如图12，AB=AC，点D是BC的中点，AB平分∠DAE，AE⊥BE，求证：AD=AE。

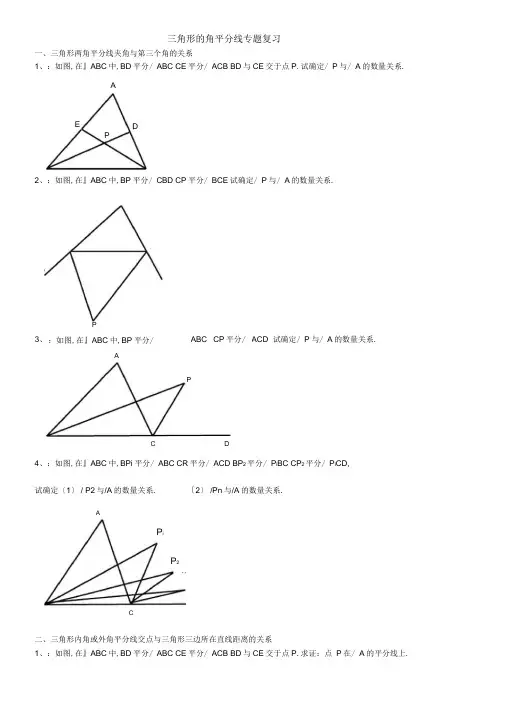
三角形的角平分线专题复习一、三角形两角平分线夹角与第三个角的关系1、：如图,在』ABC 中,BD 平分/ ABC CE 平分/ ACB BD 与CE 交于点P .试确定/ P 与/ A 的数量关系.A2、：如图,在』ABC 中,BP 平分/ CBD CP 平分/ BCE 试确定/ P 与/ A 的数量关系.4、：如图,在』ABC 中,BPi 平分/ ABC CR 平分/ ACD BP 2平分/ P i BC CP 2平分/ P i CD,试确定〔1〕 / P2与/A 的数量关系.〔2〕 /Pn 与/A 的数量关系.二、三角形内角或外角平分线交点与三角形三边所在直线距离的关系1、：如图,在』ABC 中,BD 平分/ ABC CE 平分/ ACB BD 与CE 交于点P .求证：点 P 在/ A 的平分线上.3、 P：如图,在』ABC 中,BP 平分/ABC CP 平分/ ACD 试确定/ P 与/ A 的数量关系.P EDA PCD A P iP 2CA练习1、找出到』ABC三边距离相等的点点P到AB边的距离为1, △ ABC的周长为10,那么△ ABC的面积为ABC的外角,BP平分/ CBD CP平分/ BCE判断点P是否在/ A的平分线上?3、：如图,/ AC皿/ABC的外角,BP平分/ ABC CP平分/ ACQ判断点P是否在/ A的平分线上练习3、找出到a, b, c 三条直线距离相等的点练习4、〔思考题〕如图,在^ ABC 中,/ ABC=105 , / ACB=40 , CE 是角平分线,F 是CB 延长线上的一点, D 是AC 上一点, / CBD=30 ,求/ ABF 和/ ADE 的度数.三、角平分线与平行线1、如图,在』AB8, / ABG 口/ ACB 勺平分线交于点 Q 过O 点作EF// BC 交AB 于E,交AC 于F, BE=5, CF =3, 求EF 的长.2、,在』ABC 中,/ ABC 的平分线与/ ACB 的外角平分线交于点 D,过D 作DE//BC 交AC 与F,交AB 于E, 求证：EF=BE- CF例1.如图,：AD 是 ABC 的角平分线,DE 、DF 分别是 ABD 和 ACD 的高. 求证：AE AF.a例2.：如图,BD 是 ABC 的平分线, AB BC , P 在BD 上,PM AD , PN CD .求证：PM PN .例4,：如图,在 ABC 中, 求证：ACCD AB .例5、如图, AB//DC , A D 90 ,点E 在AD 上,BE 平分 ABC, CE 平分 BCD .例6.：如图,在 ABC 中,BE 、CF 分别平分 求证：点O 在A 的平分线上.例3.如图,：在求证：AD EF ABC 中AD 是 BAC 的平分线, DE AB 于 E, DF AC 于 F.求证：BC AB DC .1、以下说法正确的有几个〔同步测试(1)角的平分线上的点到角的两边的距离相等； (2)三角形两个内角的平分线交点到三边距离相等； (3)三角形两个内角的平分线的交点到三个顶点的距离相等； (4)点E 、F 分别在/ AOB 的两边上,P 点到E 、F 两点距离相等,所以 P 点在/ AOB 的平分线上； (5) 假设OC 是/ AOB 的平分线,过 OC 上的点P 作OC 的垂线,交 OB 于D,交OA 于E,那么线段 PD 、PE 的长分别是P 点到角两边的距离A. 2 B 3 C 4D 5 2、在^ ABC 中,/ C= 900 , BC= 16cm, / A 的平分线 AD 交 BC 于 D ,且CD: DB=3: 5,那么D 到AB 的距离等于23、：如图 1, BD 是/ ABC 的平分线,DELAB 于 E, S ABC 36cm AB = 18cm,BC = 12cm,求 DE 的长4.如图,： BD CD, BF AC 于 F, CE AB 于 E.求证：D 在 BAC 的平分线上.5、：如图 2, /B = /C=90°, M 是BC 中点,DM 平分/ ADC求证：AM 平分/ DAB6 .如图,ABC 是等腰直角三角形,的周长. A 90 ,BD 是 ABC 的平分线,DE BC 于 E, BC 10cm,求 DEC7.如图,：在 ABC 中,外角 CBD 和求证：点F 在 DAE 的平分线上. 8、如图,AD 〃BC>^E 在线段AB 上,ADE CDE, DCE ECB,图2BCE 的平分线求证：CD AD BC.9、：如图3,在△ ABC中,/ B=60°, △ ABC的角平分线AD、CE线相交于点O 求证：AE+CD = AC A,/ACB=20° ,CE 是/ACB 的平分线,D 是BC上一点,假设/ DAC= 20° ,10.如图在^ABC 中,/BAC=100 求/CED的度数.C11.在四边形ABCD 中,BC> BA,AD= CD,BD平分/ ABC,/C= 72°,求/ BAD的度数ADBC。

专题11 角平分线的一个结论及其推广【专题综述】角平分线的意义及性质是三角形中的重要解题应用性质之一，也是中考题型常出现的重要性质之一，本文将三角形角平分线定理作一推广,并探讨其解平面几何题上的一些应用。

【方法解读】一、双内角平分线例1 如图，△ABC 中，∠ABC 、∠AC B 的平分线相交于点I.你能归纳出∠BIC 和∠A 的关系吗？ICBA【举一反三】（2016春•东台市月考）如图，△ABC 中，∠ABC 和∠ACB 的角平分线相交于点I ，爱动脑筋的小明同学在写作业时，发现了如下规律：（1）若∠A=50°，则∠BIC=115°=90°+250︒； （2）若∠A=90°，则∠BIC=135°=90°+290︒；（3）若∠A=130°，则∠BIC=155°=90°+2130︒；（4）根据上述规律，或∠A=150°，则∠BIC= ． （5）请你用数学表达式归纳出∠BIC 与∠A 的关系： ． （6）请证明你的结论．二、双外角平分线例2 如图，点 O 是△ABC 的外角∠DBC 和∠BCE 的平分线的交点，试判断∠BOC 和∠A 有何关系？O EDIC BA【举一反三】（2015秋•津南区校级期中）（1）如图a，在△ABC中，∠ABC，∠ACB的平分线相交于点O，①若∠ABC=40°，∠ACB=50°，则∠BOC的度数为；②若∠A=76°，则∠BOC的度数为；③你能找出∠A与∠BOC之间的数量关系吗？注明理由．（2）如图b，点O是△ABC的两外角平分线BO，CO的交点，那么∠BOC与∠A有怎样的数量关系？注明理由．三、内外角平分线例3 如图，点D是△ABC的内角∠ABC和外角∠ACE的平分线的交点，试探究∠D与∠A有何关系？【举一反三】已知如图1，∠ABC，∠ACB的平分线交于I，根据下列条件分别求出∠BIC的度数；你能发现∠BIC与∠A的关系吗？并说明理由．（1）变式一：如图2，点P是△ABC的中外两角∠DBC与∠ECB平分线的交点，试探索∠BPC与∠A的数量关系，并说明理由．（2）变式二：如图3，已知在△ABC中，BD平分∠ABC，CD平分△ABC的外角∠ACE，BD、CD相交于D，试探索∠A与∠D的数量关系，并说明理由．【强化训练】1.（探索题）如图△ABC中，∠ABC，∠ACB的平分线相交于点O．（1）若∠ABC=40°，∠ACB=80°，求∠BOC；（2）你能找出∠A与∠BOC之间的数量关系吗？2.（2017秋•抚顺县期中）如图，在△ABC中，∠ABC与∠ACB的平分线交于点O．（1）如图1，∠A=90°，则∠BOC=；（2）如图2，∠A=80°，求∠BOC的度数；（3）从上述计算中，你能发现∠BOC与∠A的关系吗？请直接写出∠B0C与∠A的关系．3.如图1，在△ABC中，∠A=72°，∠ABC与∠ACB的平分线交于I．（1）求∠BIC的度数；（2）如图2，如果∠ABC和∠ACB的三等分线分别交于点D，E，求∠BDC和∠BEC的度数；（3）设想一下，如果∠ABC和∠ACB的n等分线相交，你能求出它们所成钝角的度数吗？4.（2016•内江）问题引入：（1）如图①，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC=（用α表示）；如图②，∠CBO=∠ABC，∠BCO=∠ACB，∠A=α，则∠BOC=（用α表示）拓展研究：（2）如图③，∠CBO=∠DBC ，∠BCO=∠ECB ，∠A=α，请猜想∠BOC= （用α表示），并说明理由． 类比研究：（3）BO 、CO 分别是△ABC 的外角∠DBC 、∠ECB 的n 等分线，它们交于点O ，∠CBO=n1∠DBC ，∠BCO=n1∠ECB ，∠A=α，请猜想∠BOC= ．5.（2017春•雨城区校级期中）如图，BI ，CI 分别平分△ABC 的外角∠DBC 和∠ECB ， （1）若∠ABC=40°，∠ACB=36°，求∠BIC 的大小； （2）若∠A=96°，试求∠BIC ；（3）根据前面问题的求解，请归纳∠BIC 和∠A 的数量关系并进行证明．6.已知：如图，O 是△ABC 的内角∠ABC 和外角∠ACE 的平分线的交点． （1）若∠A=46°，求∠BOC ；（2）若∠A=n°，用n 的代数式表示∠BOC 的度数．7.（2015秋•德州校级月考）如图1，在△ABC 中，∠A=40°，BP 平分∠ABC ，CP 平分∠ACB ， （1）∠BPC= 度；（2）猜想∠A 与∠P 之间有什么关系？并证明你的猜想；（3）如图2，若点P为∠ABC与外角∠ACE的角平分线的交点，试猜想并证明∠A与∠P的关系．8.（2015秋•舟山校级月考）如图，已知∠A=n°，若P1点是∠ABC和外角∠ACE的角平分线的交点，P2点是∠P1BC和外角∠P1CE的角平分线的交点，P3点是∠P2BC和外角∠P2CE的交点…依此类推，则∠P n=（）A． B． C．D．9.（2012春•相城区期中）（1）如图1，BO、CO分别是△ABC中∠ABC和∠ACB的平分线，则∠BOC与∠A的关系是（直接写出结论）；（2）如图2，BO、CO分别是△ABC两个外角∠CBD和∠BCE的平分线，则∠BOC与∠A的关系是，请证明你的结论．（3）如图3，BO、CO分别是△ABC一个内角和一个外角的平分线，则∠BOC与∠A的关系是，请证明你的结论．（4）利用以上结论完成以下问题：如图4，已知：∠DOF=90°，点A、B分别是射线OF、OD上的动点，△ABO的外角∠OBE的平分线与内角∠OAB的平分线相交于点P，猜想∠P的大小是否变化？请证明你的猜想．10.（2016春•雅安校级期中）认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题．（1）探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．（2）探究2：如图2中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？请说明理由．（3）探究3：如图3中，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？（直接写出结论）（4）拓展：如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？（直接写出结论）．（5）运用：如图5，五边形ABCDE中，∠BCD、∠EDC的外角分别是∠FCD、∠GDC，CP、DP分别平分∠FCD和∠GDC且相交于点P，若∠A=140°，∠B=120°，∠E=90°，则∠CPD=度．。

角平分线专题类型一】角平分线倒角模型例1、把一副学生用三角板(30 、60 、90 )和(45 、45 、90 )如图(1)放置在平面直角坐标系中,点 A在y轴正半轴上,直角边AC与y轴重合,斜边AD与y轴重合,直角边AE交x轴于F,斜边AB交x 轴于G,O是AC中点, AC 8.(1)把图 1 中的Rt AED 绕 A 点顺时针旋转度(0 90 )得图2, 此时AGH 的面积是10, AHF的面积是8,分别求F、H、B三点的坐标;(2)如图3, 设AHF 的平分线和AGH 的平分线交于点M, EFH 的平分线和FOC 的平分线交于点N,当改变的大小时, N M 的值是否会改变?若改变,请说明理由;若不改变,请求出其值.检测1、如图，已知点A是y轴上一动点，B是x轴上一动点，点C在线段OB 上，连接AC，AC 正好是OAB的角平分线，ABD DBx ，问动点A，B在运动的过程中，AC与BD所在直线的夹角是否发生变化，请说明理由；若不变，请直接写出具体值。

检测2、如图探究与发现：探究一：我们知道，三角形的一个外角等于与它不相邻的两个内角的和．那么，三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢？已知：如图1，∠ FDC与∠ ECD分别为△ ADC的两个外角，试探究∠ A与∠FDC+∠ECD的数量关系．探究二：三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系？已知：如图2，在△ ADC中，DP、CP分别平分∠ ADC和∠ ACD，试探究∠ P与∠ A的数量关系．探究三：若将△ ADC改为任意四边形ABCD呢？已知：如图3，在四边形ABCD中，DP、CP分别平分∠ ADC和∠ BCD，试利用上述结论探究∠ P 与∠ A+∠B的数量关系．探究四：若将上题中的四边形ABCD改为六边形ABCDE（F 图4）呢？请直接写出∠ P与∠A+∠B+∠E+∠F 的数量关系：．【类型二】点在线，垂两边例2、如图（1），Rt ABC中，ACB 90 ，CD AB ，垂足为 D 。

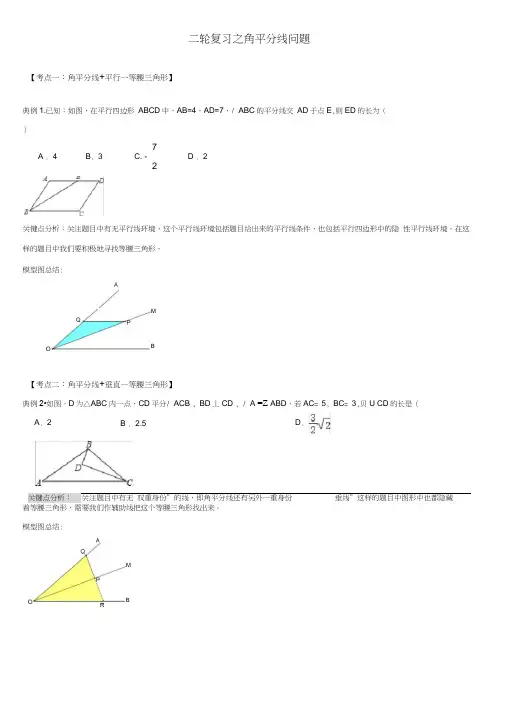
二轮复习之角平分线问题【考点一：角平分线+平行一等腰三角形】典例1.已知：如图，在平行四边形 ABCD 中，AB=4，AD=7，/ ABC 的平分线交 AD 于点E ,则ED 的长为（）7A . 4B . 3 C. - D . 22关键点分析：关注题目中有无平行线环境，这个平行线环境包括题目给出来的平行线条件，也包括平行四边形中的隐 性平行线环境，在这样的题目中我们要积极地寻找等腰三角形。

模型图总结:【考点二：角平分线+垂直—等腰三角形】典例2•如图，D 为△ABC 内一点，CD 平分/ ACB , BD 丄CD , / A =Z ABD ，若AC = 5, BC = 3,贝U CD 的长是（ 关键点分析： 关注题目中有无 双重身份”的线，即角平分线还有另外一重身份 垂线”这样的题目中图形中也都隐藏着等腰三角形，需要我们作辅助线把这个等腰三角形找出来。

模型图总结: B . 2.5 MBD .A . 2 R MB【考点三：见角平分线一作双垂】典例3.如图，△ABC 中，BC 的垂直平分线 DP 与/ BAC 的角平分线相交于点 D ，垂足为点P ,/ BAC=84，则/关键点分析：遇到角的平分线作双垂，应用角平分线的性质定理解题是基本的辅助线。

模型图总结：【考点四：见角平分线一作对称】典例 4.如图，在 A ABC 中，AD 平分/ BAC , / C=2/ B ，若 AC=3 , CD=2，贝U AB=轴对称性是角平分线的本质属性，所以遇到含有角平分线的题目经常需要将角平分线一侧的三角形作对称处理，利用角的轴对称性来解决问题。

模型图总结:【模型应用】1. 已知0C 平分/ AOB ，点P 为0C 上一点，PD 丄OA 于D ,且 PD=3cm ,过点 P 作 PE // 0A 交 0B 于 E , /AOB=30° ,2.如图，在矩形 ABCD 中，AB=5 , AD=3，点M 在边 3. M 是A ABC 的边BC 的中点，AN 平分/ BAC , BN 丄AN 于点N ，且AB=10 , BC=15, MN=3，则A ABC 的周长等4. 如图，在Rt A ABC 中，/ ACB=90 0, CD 丄AB ,垂足为D , AF 平分/ CAB ,交CD 于点E ,交CB 于点F ,若AC=3 ,AB=5，贝U CE 的长为（ ）。

高三第二轮专题复习专题（6）——三角形的“角平分线”、“中线”和“高线”类型1、三角形的内角平分线问题例1、如图，在ABC ∆中，D 是BC 上的点，AD 平分BAC ∠，ABD ∆面积是ADC ∆面积的2倍.（1）求sin sin B C；（2）若1,2AD DC ==，求BD 和AC 的长.答案：（1）12；（2）1. 变式1、已知AD 为ABC ∆内角A 的角平分线，03,5,120AB AC BAC ==∠=，求AD 的长度.答案：158.变式2、在ABC ∆中，2,1AB AC ==,角A 的平分线1AD =，求ABC ∆的面积S .类型2、三角形的中线问题例2、在ABC ∆中，2,3,AB AC BC ==边上的中线2AD =，求ABC ∆的面积S .答案：4. 变式：在ABC ∆中，内角,,A B C 的对边长分别为,,a b c ，已知函数()sin(2)6f x x π=-满足： 对于任意,()()x R f x f A ∈≤恒成立．（1）求角A 的大小；（2）若a =BC 边上的中线AM 长的取值范围．解（1）由题意，∵对于任意,()()x R f x f A ∈≤恒成立， ∴()sin(2)6f x x π=-的最大值为()f A ， 当()f x 取得最大值时，22,62x k k Z πππ-=+∈，即,3x k k ππ=+∈Z ， ∴,3A k k ππ=+∈Z ，又∵A 是三角形的内角，即0A π<<，∴3A π=．（2）∵AM 是BC 边上的中线，∴在ABM ∆中，2232cos 4AM AM AMB c +-∠=， ①在ACM ∆中，2232cos 4AM AM AMC b +-∠=， ② 又∵AMB AMC π∠=-∠，∴cos cos AMB AMC ∠=-∠，①＋②得 222324b c AM +=-．由余弦定理222222cos 33a b c bc b c bc π=+-=+-=， ∵2222032b c b c bc +<+-=≤，∴2236b c <+≤，∴23944AM <≤32AM <≤ 类型3、三角形的高线例3、在ABC ∆中，角,,A B C 的对边分别为,,a b c ，且满足sin a A =. （1）求角B 的大小；（2）若点M 为BC 的中点，且AM AC =，求sin BAC ∠的值.答案：（1）3π；（2. 变式：已知ABC ∆的一个内角为0120，并且三边长构成公差为4的等差数列，求ABC ∆的面积.答案：类型4、四边形问题例4、在平面四边形ABCD 中，075,2A B C BC ====，求AB 的取值范围.答案：.变式：在平面四边形ABCD 中，内角A C 与互补，1,3,2AB BC CD DA ====.（1）求角C 和边BD ；（2）求四边形ABCD 的面积.答案：（1）,3C BD π∠==（2）。