图形和变换测试题(一).

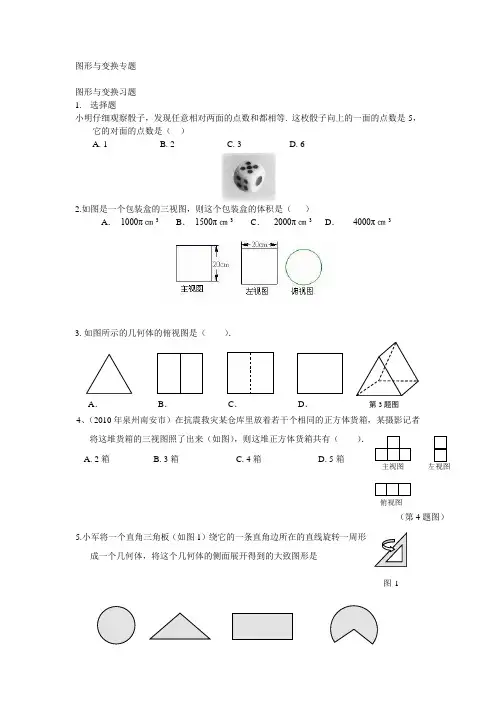
图形与变换专题图形与变换习题 1. 选择题小明仔细观察骰子，发现任意相对两面的点数和都相等. 这枚骰子向上的一面的点数是5，它的对面的点数是（ ）A. 1B. 2C. 3D. 62.如图是一个包装盒的三视图，则这个包装盒的体积是（ ）A ． 1000π㎝3B ． 1500π㎝3C ． 2000π㎝3D ． 4000π㎝33.如图所示的几何体的俯视图是（ ）．A ．B ．C ．D ．4、（2010年泉州南安市）在抗震救灾某仓库里放着若干个相同的正方体货箱，某摄影记者 将这堆货箱的三视图照了出来（如图），则这堆正方体货箱共有（ ）． A. 2箱 B. 3箱 C. 4箱 D. 5箱5.小军将一个直角三角板（如图1）绕它的一条直角边所在的直线旋转一周形成一个几何体，将这个几何体的侧面展开得到的大致图形是主视图左视图俯视图（第4题图）1图第3题图第6题 Ａ． B ． C ． D ．6.（2010宁波市）骰子是一种特别的数字立方体（见右图），它符合规则：相对两面的点数之和总是7．下面四幅图中可以折成符合规则骰子的是（ ）填空题1．小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数如图2所示，则电子表的实际时刻是＿＿2． 9点30分时，钟表的时针和分针之间的夹角是___3．在等边三角形、正方形、直角三角形、等腰梯形中，既是轴对称图形，又是中心对称图形的是＿＿＿.4．下列图形均可以由“基本图案”通过变换得到。

(填序号) (1)通过平移变换但不能通过旋转变换得到的图案是 (2)可以通过旋转变换但不能通过平移变换得到的图案是 (3)既可以由平移变换, 也可以由旋转变换得到的图案是① ② ③ ④ ⑤5. 如图，如果正方形CDEF 旋转后能与正方形ABCD 重合，那么图形所在的平面上可以做旋转中心的点共有6.如图，已知边长为6的等边三角形ABC 纸片，点E 在AC 边上， 点F 在AB 边上，沿EF 折叠，使点A 落在BC 边上的点D 的位置，且 ED ⊥BC,则CE 的长是(31224 )．2. 解答题1画出右图1所示的两个几何体的三种视图．2. 如图1，电线杆上有一盏路灯O ，电线杆与三个等高的标杆整齐划一地排列在马路的一侧，AB 、CD 、EF 是三个标杆，相邻的两个标杆之间的距离都是2 m ，已知AB 、CD 在灯光下的影长分别为BM = 1.6 m ，DN = 0.6 m.（1）请画出路灯O 的位置和标杆EF 在路灯灯光下的影子； （2）求标杆EF 的影长．图13.如图是一个几何体的三视图 . （1）写出这个几何体的名称；（2）根据所示数据计算这个几何体的表面积；（3）如果一只蚂蚁要从这个几何体中的点B出发，沿表面爬到AC 的中点D ，请你求出这个线路的最短路程 .4. 已知：等腰三角形OAB 在直角坐标系中的位置如图，点A 的坐图6-12（1）标为（-），点B 的坐标为（－6，0）.(1)若三角形OAB 关于y 轴的轴对称图形是三角形O A B ''， 请直接写出A 、B 的对称点A'B '、的坐标； (2)若将三角形OAB 沿x 轴向右平移a 个单位， 此时点A 恰好落在反比例函数y =图像上，求a 的值； (3)若三角形OAB 绕点O 按逆时针方向旋转α度（090α<<）. ① 当α=30时点B 恰好落在反比例函数ky x=的图像上，求k 的值． ②问点A 、B 能否同时落在①中的反比例函数的图像上，若能，求出α 的值；若不能，请说明理由. 图形与变换测试题选择题（每题4分共16分）1. 下图所示几何体的主视图是（ ）1.A .2. B .3. C .4.D .2.下列立体图形中，侧面展开图是扇形的是( )3. 一个正方体的表面展开图如图所示，则原正方体中的“★”所在面的对面所标的字是（ ） A ．上 B ．海 C ．世 D ．博4.有一正方体，六个面上分别写有数字1、2、3、4、5、6，有三个人从不同的角度观察的 结果如图所示。

2019年七年级下册数学单元测试题第二章图形的变换一、选择题1．把一个图形先沿着一条直线进行轴对称变换，再沿着与这条直线平行的方向平移，我们把这样的图形变换叫做滑动对称变换. 在自然界和日常生活中，大量地存在这种图形变换（如图（1））. 结合轴对称变换和平移变换的有关性质，你认为在滑动对称变换过程中，两个对应三角形（如图（2））的对应点所具有的性质是（）A．对应点连线与对称轴垂直B．对应点连线被对称轴平分C．对应点连线被对称轴垂直平分D．对应点连线互相平行答案：B2．如图，将四边形AEFG变换到四边形ABCD，其中E，G分别是AB，AD的中点，下列叙述不正确的是（）A．这种变换是相似变换B．对应边扩大到原来的2倍C．各对应角度数不变D．面积扩大到原来的2倍答案：D3．如图△ABC与△A′B′C′关于直线MN对称，P为MN上任意一点，下列说法不正确的是（）A．AP=A′PB．MN垂直平分AA′,CC′C．这两个三角形面积相等D．直线AB，A′B′的交点不一定在MN上解析：D4．下列图案是几种名车的标志，在这几个图案中，是轴对称图形的有（）A．1个B．2个C．3个D．4个答案：C5．下列图形不一定是轴对称图形的是（）A．等边三角形B．长方形C．等腰三角形D答案：D6．下面给出的是一些产品的商标图案，从几何图形的角度看（不考虑文字和字母），既是轴对称图形又能旋转l80°后与原图重合的是（）答案：C7．下列图形中，旋转60°后可以和原图形重合的是（）A．正六边形B．正五边形C．正方形D．正三角形答案：A8．下列对于旋转的判断中，正确的是（）A．图形旋转时，图形的形状发生了改变B．图形旋转时，图形的大小发生了改变C．图形旋转时，图形的位置发生了改变D．图形旋转时，图形的形状、大小和位置都发生了改变答案：C9．把△ABC先向左平移1 cm，再向右平移2 cm，再向左平移3 cm。

再向右平移4 cm，……，经这样移动l00次后，最后△ABC所停留的位置是（）A．△ABC左边50 cm B．△ABC右边50 cm C．△ABC左边l m D．△ABC右边l m 答案：B10．如图所示，矩形ABCD沿着AE折叠，使D点落在BC边上的F点处，若∠BAF=50°，则∠EAF的度数为（）A．50°B．45°C．40°D．20°答案：D11．小宇同学在一次手工制作活动中，先把一张矩形纸片按图①的方式进行折叠，使折痕的左侧部分比右侧部分短l cm；展开后按图②的方式再折叠一次，使第二次折痕的左侧部分比右侧部分长lcm，再展开后，在纸上形成的两条折痕之问的距离是（）A．0．5 cm B．1 cm C．1．5 cm D．2 cm答案：B二、填空题12．用有45°直角三角板画∠AOB=45°，并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°，则三角板的斜边与射线OA的夹角 为．解析：22°13．如图，已知△ABC中的∠C=50°，则放大镜下△ABC中∠C=_______．解析：50°14．如图，∠AOB=90°，它绕点O旋转30°后得到∠COD，•则∠AOC=•_____，•∠BOC=_____，∠COD=______．解析：30°，60°，90°15．下图是一些国家的国旗，其中是轴对称图形的有__________个．解析：316．观察图形：其中是轴对称图形的是 (填序号) .解析：①②③④⑥17．已知△CDE是△CAB经相似变换后得到的像，且∠A=30°，∠CDE=30°，AB=4，DE=2，AC=3，则CD= ．解析：3218．下列各图中，从左到右的变换分别是什么变换?解析：轴对称变换，相似变换，旋转变换，平移变换19．判断下列各组图形分别是哪种变换?解析：轴对称，平移，旋转，相似20．直角三角形作相似变换，各条边放大到原来的3倍，则放大后所得图形面积是原图形面积的倍．解析：921．等边三角形ABC绕着它的中心，至少旋转度才能与其本身重合．解析：12022．点A和点A′关于直线l成轴对称，则直线l和线段AA′的位置关系是：．解析：垂直且平分三、解答题23．如图所示，将△ABC经相似变换、边长扩大一倍得到像△A′B′C′．(1)请你画出像△A′B′C′．(2)猜测△A′B′C′的面积是△ABC的面积的多少倍．解析：(1)图略；(2)S 4A B C ABC S S '''∆∆=24．如图，在小正方形组成的“L”形图中，请你用三种方法分别在图中添画一个小正方形使它成为轴对称图形．解析：图略25．如图所示的轴对称图形的对称轴都不止一条，请把它们都画出来．解析：略26．已知，如图□ABCD ．(1)画出□A 1B 1C 1D 1，使□A 1B 1C 1D 1与□ABCD 关于直线MN 对称；(2)画出□A 2B 2C 2D 2，使□A 2B 2C 2D 2与□A 1B 1C 1D 1关于直线EF 对称．解析：略27．画出图中图形的对称轴，并给予必要的作图说明．解析：略28．如图所示，在一块长为20 m，宽为14 m的草地上有一条宽为2 m的曲折的小路，你能运用所学的知识求出这块草地的绿地面积吗?解析：216 m229．你看到过如图所示的图案吗? 这个图案可以由什么基本图形经怎样的平移得到?解析：可以由“V”平移得到30．电子跳蚤在数轴上的一点A，第一次从点A0向左平移1个单位到达点A l，第二次由点A l向右平移2个单位到达点A2，第三次由点A2向左平移3个单位到达点A3，第四次由点A3向右平移4个单位到达点A4，…．按以上规律平移了l00次，电子跳蚤处于数轴上的点A100所表示的数恰是2058，则电子跳蚤的初始位置点A0所表示的数是多少?解析：200831．如图所示，准备一张正方形的纸．沿如图①所示的虚线对折两次，得到一个小正方形；再沿图②的虚线对折；在得到的直角三角形上画出如图③所示的图形，再将阴影部分剪下来；打开你的作品．是一个旋转图形吗?旋转多少度后能与自身重合?你还能画出更有创意的作品吗?解析：它是一个旋转图形，旋转90°后与自身重合32．如图，方格中有一条美丽可爱的小金鱼．(1)若方格的边长为1，则小鱼的面积为；(2)画出小鱼向左平移3格后的图形．解析：(1)16；(2)图略33．数学兴趣小组的同学想利用树影测树高，在阳光下他们测得一根长为1 m的竹竿的影长为0．9 m．此刻测量树影，发现树的影子不全落在地上，有一部分影子落在墙壁上，如图所示，同学们测得地面上的影子长为3．6 m，墙壁上的影子长为0．9 m．又知以树和地面上的树影为边的三角形与同一时刻以竹竿和地面上的影子为边的三角形是一个相似变换，求这棵树的实际高度．解析：4．9m34．如图所示，在方格纸中，有两个形状、大小完全相同的图形，请指出如何运用轴对称、平移、旋转这三种运动，将一个图形重合到另一个图形上．解析：把△ABC先绕点A逆时针旋转90°，再向上平移2个单位，然后以D点所在的竖格子线为对称轴进行轴对称变换35．如图所示是视力表中的一部分．以第一个图形为基本图形．请分析后三个图形可以根据基本图形作怎样的变换得到．解析：略36．如图所示，有三个正方形的花坛，准备把每个花坛都分成形状、大小相同的四块，种不同的花草．现向大家征集设计图案，图①是某同学设计的图案，请你在图②、③中再设计两种不同的图案．解析：略37．请你用正方形、三角形、•圆设计一个有具体形象的轴对称图形（例如下图的脸谱），并给你的作品取一个适当的名字．解析：略38．如图，请用三种方法，在已知图案上再添上一个小正方形后，使其成为轴对称图形，并画出对称轴．解析：略39．如图，直线a是一个轴对称图形的对称轴，画出这个轴对称图形的另一半，并说明这个轴对称图形是一个什么图形，它一共有几条对称轴.(不写作法，保留作.图痕迹.)解析：是一个正五角星，它共有五条对称轴. 如图所示：40．如图所示，△ABC是等腰直角三角形，点D在BC上，将△ABD按逆时针旋转至△AFE的位置，问：(1)此旋转的旋转中心是哪一个点?(2)此旋转的角度为多少度?(3)若点M为AB的中点，则旋转后点M转到了什么位置?解析：(1)点A；(2)45°；(3)AF的中点。

故选B．
【点睛】
本题主要考查图形的轴对称以及勾股定理的实际应用，把立体图形化为平面图形，掌握“马饮水”模型，是解题的关键．
11．下列字母中：H、F、A、O、M、W、Y、E，轴对称图形的个数是（）
A．5 B．4 C．6 D．7
【答案】D
【解析】从第一个字母研究，只要能够找到一条对称轴，令这个字母沿这条对称轴折叠后，两边的部分能够互相重合，就是轴对称图形，可以得出：字母H、A、O、M、W、Y、E这七个字母，属于轴对称图形.
本题考查了平行四边形的性质、折叠的性质、三角形的内角和定理等知识，属于常考题型，熟练掌握上述基本知识是解题关键．
15．下列几何图形中，既是轴对称图形又是中心对称图形的是（ ）
A． B． C． D．
【答案】C
【解析】
【分析】
根据轴对称图形与中心对称图形的概念求解．
【详解】
A、是轴对称图形，不是中心对称图形，故本选项错误；
B、可以通过平移得到，不符合题意；
C、不可以通过平移得到，符合题意；
D、可以通过平移得到，不符合题意．
故选C．
【点睛】
本题考查平移的性质，属于基础题，要掌握图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转．
2．在平行四边形、菱形、矩形、正方形这四种图形中，是轴对称图形的有( )
故选：D.
12．把一副三角板如图（1）放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝4，CD＝5．把三角板DCE绕着点C顺时针旋转15°得到△D1CE1（如图2），此时AB与CD1交于点O，则线段AD1的长度为（）
A． B． C． D．4
【答案】A
【解析】

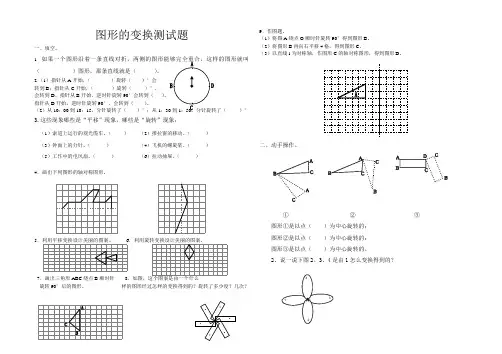
图形的变换测试题一、填空。

1.（）图形，那条直线就是（）。

2.（1）指针从A开始，（）旋转（）°会转到B；指针从C开始，（）旋转（）°，会转到D。

指针从B开始，逆时针旋转90°会转到（）。

指针从D开始，逆时针旋转90°，会转到（）。

（2）从10：00到10：15，分针旋转了（）°；从1：30到1：）°3.这些现象哪些是“平移”现象，哪些是“旋转”现象：（1）索道上运行的观光缆车。

（）（2）推拉窗的移动。

（）（3）钟面上的分针。

（）（4）飞机的螺旋桨。

（）（5）工作中的电风扇。

（）（6）拉动抽屉。

（）4．画出下列图形的轴对称图形。

5．利用平移变换设计美丽的图案。

6．利用旋转变换设计美丽的图案。

7．画出三角形ABC绕点B顺时针8．如图，这个图案是由一个什么旋转90°后的图形。

样的图形经过怎样的变换得到的？旋转了多少度？几次？9．作图题。

（1）将图A绕点O顺时针旋转90°得到图形B。

（2）将图形B再向右平移4格，得到图形C。

（3）以直线l为对称轴，作图形C的轴对称图形，得到图形D。

二、动手操作。

①②③图形①是以点（）为中心旋转的；图形②是以点（）为中心旋转的；图形③是以点（）为中心旋转的。

2、说一说下图2、3、4是由1怎么变换得到的？三、画出下列图形的对称轴。

四、 请按照给出的对称轴画出第一个图形的对称图形，第二个图形请向上移动3格。

五、通过平移或旋转设计一个新的图案。

六、分别画出将向上平移3格、向右平移8格后得到的图形。

（6%）七、画出绕点“O”顺时针旋转90度后的图形。

画出绕点“A” 逆时针旋转90度后的图形。

（6%）八、画出下面图形的轴对称图形。

（5%）。

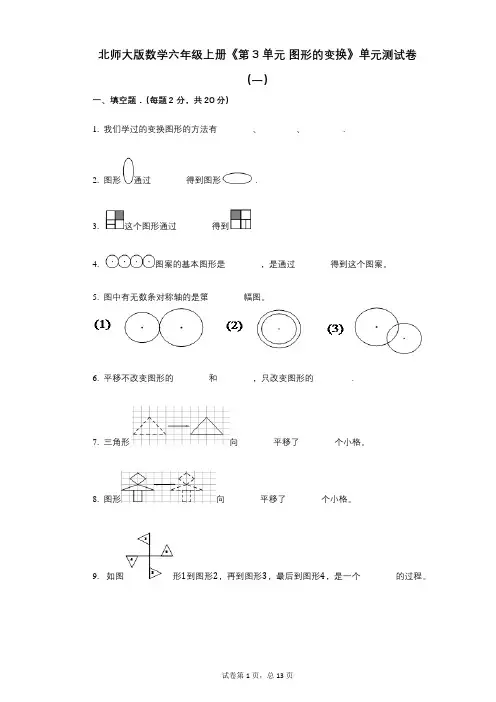
北师大版数学六年级上册《第3单元图形的变换》单元测试卷（一）一、填空题．（每题2分，共20分）1. 我们学过的变换图形的方法有________、________、________．2. 图形通过________得到图形．3. 这个图形通过________得到4. 图案的基本图形是________，是通过________得到这个图案。

5. 图中有无数条对称轴的是第________幅图。

6. 平移不改变图形的________和________，只改变图形的________．7. 三角形向________平移了________个小格。

8. 图形向________平移了________个小格。

9. 如图形1到图形2，再到图形3，最后到图形4，是一个________的过程。

10. 如图的基本图形是________，它是由基本图形经过________或________设计而成的。

二、画一画（8分）画出对称图形的另一半三、解决问题．（72分）观察方格纸中图形的变换，完成下面的问题。

（1）A经过怎样的变换得到图形B？（2）图形B又经过怎样的变换得到图形C？（3）你还有什么办法，能将右图中图形A变换得到图形C？以虚线为对称轴作图形A的对称图形B，再将图形B向左平移7格得到图形C．淘气和笑笑玩游戏，分别从A、B处出发，沿半圆行驶到C、D．（1）笑笑所跑中路线半径为20米，他跑过的路是________米。

（2）淘气所跑的路程的半径是________米，他跑过的路程是________米。

（3）他俩跑过的路程相差________米。

一次体育比赛结束时，7名获奖运动员想到握手，如果每2人握一次手，共握几次手？实际操作。

(1)以直线l为对称轴作图形A的轴对称图形，得到图形B．(2)将图形B绕点O逆时针旋转90∘，得到图形C．(3)将图形C向左平移5格，得到图形D．一种麦田的自动旋转喷灌装置的射程15米。

它能喷灌的面积有多少平方米？（1）以直线MN为对称轴作图A的轴对称图形得到图形B．（2）将图形B绕点O顺时针旋转90∘，得到图形C．（3）将图形C向右平移5格，得到图形D．请你按照前面三个图形的规律，画出后面三个图形。

解析：略 28．在如图所示的6个箭头中，哪几个箭头是可以通过平移得到的，请你们指出它们的序号 ．
解析：①与⑤可以通过平移得到
29．如图所示，由六个边长为a的小正方形构成的一个图形，请你移动其中一个小正方形的 位置使整个图形成为轴对称图形．请你试一试，并画出两种移法．
解析：略 30．如图所示，下面两个图形是旋转变换所得的图形，它们分剐可绕自身图形中的哪一点 至少旋转多少度后与它本身重合?
解析：①绕正方形对角线交点，逆时针旋转90°；②绕整个图形对角线的交点，旋转l80° 31．小林用七巧板拼一只飞翔的鸽子，现在还剩一块有一个锐角是45°的直角三角形ABC （左下角）应该放在黑色的三角形这个位置上．你能帮助小林通过变换直角三角形ABC放 到黑色的三角形这个位置上吗？请说明你是通过怎样的变换实现你的目标的．
C．180°
D．不确定
答案：C
3．下列生活现象中，属于相似变换的是（ ）
A．抽屉的拉开
B．荡秋千
C．汽车刮雨器的运动 D．投影片的文字经投影变换到屏幕
答案：D
4．如图，身高为1．6
m的某学生想测量一棵大树的高度，她沿着树影BA由B向A走去，当走到C点时，她的影子
顶端正好与树的影子顶端重合，测得BC=3．2 m，CA=0．8 m，那么树的高度为（ ）
2019年七年级下册数学单元测试题
第二章 图形的变换
一、选择题
1．钟表的分针匀速转一周需要1小时，经过35分钟，分针旋转的角度是（ ）
A．180°
B．200°
C．210°
D．220°
答案：C
2．如图，AC与BD互相平分于点O，则△AOB至少绕点O旋转多少度才可与△COD重合
（）
A．60°

北师大版六年级上册《第3章图形的变换》单元测试卷一．填空．1. 如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形就是________，折痕所在的直线叫做________．2. 圆的对称轴有________条，半圆形的对称轴有________条。

3. ________三角形有三条对称轴，________三角形有一条对称轴。

4. 正方形有________条对称轴，长方形有________条对称轴，等腰梯形有________条对称轴。

5. 在钟面上（如图），分针绕点O旋转300表示时间经过________分；时间经过15分钟，分针绕O点旋转________度。

6. 观察物体，从________面看到的是；从________面看到的是；从________面看到的是．7. 学校有8个队参加跳绳比赛，每两队赛一场比赛采用淘汰制决出冠军、亚军共需比赛________场。

二．判断．通过一个圆的圆心的直线是这个圆的对称轴。

________．圆是轴对称图形，每一条直径都是它的对称轴。

________．等腰梯形是对称图形。

________（判断对错）正方形只有一条对称轴。

________．三、判断题．（判断下列句子的对错．对的打“√”，错的打“×”；电梯的升降运动属于平移现象。

________．（判断对错）四名运动员，如果每两人握一次手，共握了6次手。

________．（判断对错）午餐时，肉吃得越多，对身体越好。

________．（判断对错）运动员跑步时要经过弯道，所以起跑线的位置不一样。

________．（判断对错）正方形、长方形、半圆、等腰三角形都是轴对称图形。

________．（判断对错）四、选择题．运动员在100米直跑道上，进行100米跑决赛，他们的起跑线（）A.位置一样B.位置不一样C.位置不确定下列图形中对称轴最多的是（）A.长方形B.正方形C.平行四边形八点五折就是原价的（）A.85%B.8.5%C.80.5%甲数的20%等于乙数的16．（甲乙不为0），（）A.甲数大于乙数B.甲数小于乙数C.甲数等于乙数某厂去年产值16万元，今年比去年多4万元，今年比去年增加（）A.2.5%B.25%C.250%五、计算：计算下面各题。

专题17图形变换（平移、旋转、对称）一．选择题（2022·湖南娄底）1. 下列与2022年冬奥会相关的图案中，是中心对称图形的是（）A. B. C. D.【答案】D【解析】【分析】中心对称图形定义：如果一个图形绕某一点旋转180度，旋转后的图形能和原图形回完全重合，那么这个答图形叫做中心对称图形，根据中心对称图形定义逐项判定即可．【详解】解：根据中心对称图形定义，可知D符合题意，故选：D．【点睛】本题考查中心对称图形的识别，掌握中心对称图形的定义是解决问题的关键．（2022·四川自贡）2. 剪纸与扎染、龚扇被称为自贡小三绝，以下学生剪纸作品中，轴对称图形是（）A. B.C. D.【答案】D【解析】【分析】根据轴对称图形的定义判断即可．【详解】∵不是轴对称图形,∴A不符合题意；∵不是轴对称图形,∴B不符合题意；∵不是轴对称图形,∴C不符合题意；∵是轴对称图形,∴D符合题意；故选D．【点睛】本题考查了轴对称图形即沿着某条直线折叠，直线两旁的部分完全重合，熟练掌握定义是解题的关键．（2022·山东泰安）3. 下列图形：其中轴对称图形的个数是（）A. 4B. 3C. 2D. 1【答案】B【解析】【分析】对每个图形逐一分析，能够找到对称轴的图形就是轴对称图形．【详解】从左到右依次对图形进行分析：第1个图在竖直方向有一条对称轴，是轴对称图形，符合题意；第2个图在水平方向有一条对称轴，是轴对称图形，符合题意；第3个图找不到对称轴，不是轴对称图形，不符合题意；第4个图在竖直方向有一条对称轴，是轴对称图形，符合题意；因此，第1、2、4都是轴对称图形，共3个．故选：B．【点睛】本题考查轴对称图形的概念，解题的关键是寻找对称轴．（2022·江苏苏州）0,2，点B是x轴正半轴上的一点，将线段AB绕点A按4. 如图，点A的坐标为()m，则m的值为（）逆时针方向旋转60°得到线段AC．若点C的坐标为(),3A.【答案】C【解析】【分析】过C作CD⊥x轴于D，CE⊥y轴于E，根据将线段AB绕点A按逆时针方向旋转60°得到线段AC，可得△ABC是等边三角形，又A（0，2），C（m，3），即得AC BC AB==，可得BD=m=．OB=m=，即可解得3【详解】解：过C 作CD ⊥x 轴于D ，CE ⊥y 轴于E ，如图所示：∵CD ⊥x 轴，CE ⊥y 轴，∴∠CDO =∠CEO =∠DOE ＝90°，∴四边形EODC 是矩形，∵将线段AB 绕点A 按逆时针方向旋转60°得到线段AC ，∴AB ＝AC ，∠BAC ＝60°，∴△ABC 是等边三角形，∴AB ＝AC ＝BC ，∵A （0，2），C （m ，3），∴CE ＝m ＝OD ，CD ＝3，OA ＝2，∴AE ＝OE −OA ＝CD −OA ＝1，∴AC BC AB ===，在Rt △BCD 中，BD =在Rt △AOB 中，OB ==∵OB ＋BD ＝OD ＝m ，m =，化简变形得：3m 4−22m 2−25＝0，解得：3m =或3m =-（舍去），∴m=，故C正确．故选：C．【点睛】本题考查直角坐标系中的旋转变换，解题的关键是熟练应用勾股定理，用含m的代数式表示相关线段的长度．（2022·浙江湖州）5. 如图，将△ABC沿BC方向平移1cm得到对应的△A′B′C′．若B′C=2cm，则BC′的长是（）A. 2cmB. 3cmC. 4cmD. 5cm【答案】C【解析】【分析】据平移的性质可得BB′=CC′=1，列式计算即可得解．【详解】解：∵△ABC沿BC方向平移1cm得到△A′B′C′，∴BB′=CC′=1cm，∵B′C=2cm，∴BC′= BB′+ B′C+CC′=1+2+1=4（cm）．故选：C．【点睛】本题考查了平移的性质，熟记性质得到相等的线段是解题的关键．（2022·浙江嘉兴）6. “方胜”是中国古代妇女的一种发饰，其图案由两个全等正方形相叠组成，寓意是同心吉祥．如图，将边长为2cm的正方形ABCD沿对角线BD方向平移1cm得''''，形成一个“方胜”图案，则点D，B′之间的距离为（）到正方形A B C DA. 1cmB. 2cmC. 1)cmD. －1)cm 【答案】D【解析】【分析】先求出BD，再根据平移性质求得BB'=1cm，然后由BD BB-′求解即可．【详解】解：由题意，BD=，由平移性质得BB'=1cm，∴点D，B′之间的距离为DB'=BD BB-′=（1）cm，故选：D．【点睛】本题考查平移性质、正方形的性质，熟练掌握平移性质是解答的关键．（2022·湖南怀化）7. 如图，△ABC沿BC方向平移后的像为△DEF，已知BC=5，EC=2，则平移的距离是（）A. 1B. 2C. 3D. 4【答案】C【解析】【分析】根据题意判断BE的长就是平移的距离，利用已知条件求出BE即可．【详解】因为ABC沿BC方向平移，点E是点B移动后的对应点，所以BE的长等于平移的距离，由图可知，点B、E、C在同一直线上，BC=5，EC=2，所以BE=BC-ED=5-2=3,故选C．【点睛】本题考查了平移，正确找出平移对应点是求平移距离的关键．（2022·湖南邵阳）8. 下列四种图形中，对称轴条数最多的是（）A. 等边三角形B. 圆C. 长方形D. 正方形【答案】B【解析】【分析】分别求出各个图形的对称轴的条数，再进行比较即可．【详解】解：因为等边三角形有3条对称轴；圆有无数条对称轴；长方形有2条对称轴；正方形有4条对称轴；经比较知，圆的对称轴最多．故选：B．【点睛】此题考查了轴对称图形对称轴条数的问题，解题的关键是掌握轴对称图形对称轴的定义以及性质．（2022·江苏连云港）9. 下列图案中，是轴对称图形的是（）A. B. C. D.【答案】A【解析】【分析】根据轴对称图形的概念逐项分析判断即可，轴对称图形的概念：平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形．【详解】A.是轴对称图形，故该选项正确，符合题意；B.不是轴对称图形，故该选项不正确，不符合题意；C.不是轴对称图形，故该选项不正确，不符合题意；D.不是轴对称图形，故该选项不正确，不符合题意；故选A【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．（2022·四川遂宁）10. 下面图形中既是轴对称图形又是中心对称图形的是（）科克曲线笛卡尔心形线阿基米德螺旋线赵爽弦图A. 科克曲线B. 笛卡尔心形线C. 阿基米德螺旋线D. 赵爽弦图【答案】A【解析】【分析】根据轴对称图形和中心对称图形的概念，对各选项分析判断即可得解．把一个图形绕某一点旋转180°，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形；如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．【详解】解：A、科克曲线既是轴对称图形又是中心对称图形，故本选项符合题意；B、笛卡尔心形线是轴对称图形，不是中心对称图形，故本选项不符合题意；C、阿基米德螺旋线不是轴对称图形，也不是中心对称图形，故本选项不符合题意；D、赵爽弦图不是轴对称图形，是中心对称图形，故本选项不符合题意．故选：A．【点睛】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．（2022·新疆）11. 平面直角坐标系中，点P (2，1)关于x 轴对称的点的坐标是（ ）A. ()2,1B. ()2,1-C. ()2,1-D. ()2,1--【答案】B【解析】【分析】直接利用关于x 轴的对称点的坐标特点：横坐标不变，纵坐标互为相反数，得出答案．【详解】解：点P （2，1）关于x 轴对称的点的坐标是（2，-1）．故选：B ．【点睛】本题主要考查了关于x 轴对称点的性质，正确掌握横纵坐标的关系是解题关键．（2022·天津） 12. 在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（ ）A. B. C. D.【答案】D【解析】【分析】根据轴对称图形的概念对各项分析判断即可得解．【详解】A ．不是轴对称图形，故本选项错误；B ．不是轴对称图形，故本选项错误；C ．不是轴对称图形，故本选项错误；D ．是轴对称图形，故本选项正确．故选：D ．【点睛】本题考查轴对称图形，理解轴对称图形的概念是解答的关键．（2022·天津）13. 如图，在△ABC 中，AB =AC ，若M 是BC 边上任意一点，将△ABM 绕点A 逆时针旋转得到△ACN ，点M 的对应点为点N ，连接MN ，则下列结论一定正确的是（ ）A. AB AN =B. AB NC ∥C. AMN ACN ∠=∠D. MN AC ⊥【答案】C【解析】 【分析】根据旋转的性质，对每个选项逐一判断即可．【详解】解：∵将△ABM 绕点A 逆时针旋转得到△ACN ，∴△ABM ≌△ACN ， ∴AB =AC ，AM =AN ，∴AB 不一定等于AN ，故选项A 不符合题意； ∵△ABM ≌△ACN ，∴∠ACN =∠B ，而∠CAB 不一定等于∠B ，∴∠ACN 不一定等于∠CAB ，∴AB 与CN 不一定平行，故选项B 不符合题意； ∵△ABM ≌△ACN ，∴∠BAM =∠CAN ，∠ACN =∠B ，∴∠BAC =∠MAN ，∵AM =AN ，AB =AC ，∴△ABC 和△AMN 都是等腰三角形，且顶角相等， ∴∠B =∠AMN ，∴∠AMN =∠ACN ，故选项C 符合题意；∵AM =AN ，而AC 不一定平分∠MAN ，∴AC 与MN 不一定垂直，故选项D 不符合题意； 故选：C ． 【点睛】本题考查了旋转的性质，等腰三角形的判定与性质．旋转变换是全等变换，利用旋转不变性是解题的关键．（2022·江苏扬州）14. 如图，在ABC ∆中，AB AC <，将ABC 以点A 为中心逆时针旋转得到ADE ，点D 在BC 边上，DE 交AC 于点F ．下列结论：①AFE DFC △△；②DA 平分BDE ∠；③CDF BAD ∠=∠，其中所有正确结论的序号是（ ）A. ①②B. ②③C. ①③D. ①②③【答案】D【解析】【分析】根据旋转的性质可得对应角相等，对应边相等，进而逐项分析判断即可求解．【详解】解：∵将ABC 以点A 为中心逆时针旋转得到ADE ，∴ADE ABC ≌， E C ∴∠=∠，AFE DFC ∠=∠，∴AFE DFC △△，故①正确；ADE ABC ≌，AB AD ∴=，ABD ADB ∴∠=∠，ADE ABC ∠=∠，ADB ADE ∴∠=∠，∴DA 平分BDE ∠，故②正确；ADE ABC ≌，BAC DAE ∴∠=∠，BAD CAE ∴∠=∠，AFE DFC △△，CAE CDF ∴∠=∠，CDF BAD ∠=∠∴，故③正确故选D【点睛】本题考查了性质的性质，等边对等角，相似三角形的性质判定与性质，全等三角形的性质，掌握以上知识是解题的关键．（2022·四川南充）15. 如图，将直角三角板ABC 绕顶点A 顺时针旋转到AB C ''△，点B '恰好落在CA 的延长线上，3090∠=︒∠=︒，B C ，则BAC '∠为（ ）A. 90︒B. 60︒C. 45︒D. 30【答案】B【解析】 【分析】根据直角三角形两锐角互余，求出BAC ∠的度数，由旋转可知BAC B AC ''∠=∠，在根据平角的定义求出BAC '∠的度数即可．【详解】∵3090∠=︒∠=︒，B C ，∴90903060BAC B ∠=︒-∠=︒-︒=︒，∵由旋转可知60B A BAC C ''∠=︒∠=，∴618060860100C B A BA BA C C '''=︒-∠=︒-︒-︒=︒∠∠-，故答案选：B ．【点睛】本题考查直角三角形的性质以及图形的旋转的性质，找出旋转前后的对应角是解答本题的关键．（2022·山东泰安）16. 如图，将正方形网格放置在平面直角坐标系中，其中每个小正方形的边长均为1，ABC ∆经过平移后得到111A B C ∆，若AC 上一点(1.2,1.4)P 平移后对应点为1P ，点1P 绕原点顺时针旋转180，对应点为2P ，则点2P 的坐标为（ ，A. (2.8,3.6)B. 2.8,6()3.--C. (3.8,2.6)D. ( 3.8, 2.6)--【答案】A【解析】 【详解】分析：由题意将点P 向下平移5个单位，再向左平移4个单位得到P 1，再根据P 1与P 2关于原点对称，即可解决问题，详解，由题意将点P 向下平移5个单位，再向左平移4个单位得到P 1，∵P ，1.2，1.4，，∴P 1，，2.8，，3.6，，∵P 1与P 2关于原点对称，∴P 2，2.8，3.6，，故选A，点睛：本题考查了坐标与图形变化，平移变换，旋转变换等知识，解题的关键是理解题意，灵活运用所学知识解决问题，属于中考常考题型．（2022·湖北宜昌）17. 将四个数字看作一个图形，则下列四个图形中，是中心对称图形的是（ ）A.B. C. D.【答案】D【解析】【分析】中心对称图形的定义：把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，根据中心对称图形的定义逐项判定即可．【详解】解：根据中心对称图形定义，可知符合题意， 故选：D ．【点睛】本题考查中心对称图形，掌握中心对称图形定义，能根据定义判定图形是否是中心对称图形是解决问题的关键．（2022·湖南常德）18. 如图，在Rt ABC △中，90ABC ∠=︒，30ACB ∠=︒，将ABC 绕点C 顺时针旋转60︒得到DEC ，点A 、B 的对应点分别是D ，E ，点F 是边AC 的中点，连接BF ，BE ，FD ．则下列结论错误的是（ ）A. BE BC =B. BF DE ∥，BF DE =C. 90DFC ∠=︒D. 3DG GF =【答案】D【解析】 【分析】根据旋转的性质可判断A ；根据直角三角形的性质、三角形外角的性质、平行线的判定方法可判断B ；根据平行四边形的判定与性质以及全等三角形的判定与性质可判断C ；利用等腰三角形的性质和含30°角的直角三角形的性质可判断D ．【详解】A ．∵将，ABC 绕点C 顺时针旋转60°得到，DEC ，∴∠BCE =∠ACD =60°，CB =CE ，∴△BCE 是等边三角形，∴BE =BC ，故A 正确；B ．，点F 是边AC 中点，，CF =BF =AF =12AC ，，，BCA =30°，，BA =12AC ，，BF =AB =AF =CF ，，，FCB =，FBC =30°，延长BF 交CE 于点H ，则∠BHE =∠HBC +∠BCH =90°，∴∠BHE =∠DEC =90°，∴BF //ED ，∵AB =DE ，∴BF =DE ，故B 正确．C ．∵BF ∥ED ，BF =DE ，∴四边形BEDF 是平行四边形，∴BC =BE =DF ，∵AB =CF ， BC =DF ，AC =CD ，∴△ABC ≌△CFD ，∴=90DFC ABC ∠=∠︒，故C 正确；D ．∵∠ACB =30°， ∠BCE =60°，∴∠FCG =30°，∴FG =12CG ，∴CG =2FG ．∵∠DCE =∠CDG =30°，∴DG =CG ，∴DG =2FG ．故D 错误．故选D ．【点睛】本题考查了旋转的性质，全等三角形的判定与性质，等边三角形的判定与性质，含30°角的直角边等于斜边的一半，以及平行四边形的判定与性质等知识，综合性较强，正确理解旋转性质是解题的关键．（2022·湖南常德） 19. 国际数学家大会每四，举行一届，下面四届国际数学家大会会标中是中心对称图形的是（）A. B.C. D.【答案】B【解析】【分析】根据中心对称的概念对各图形分析判断即可得解．【详解】解：A不是中心对称图形，故A错误；B是中心对称图形，故B正确；C不是中心对称图形，故C错误；D不是中心对称图形，故D错误；故选B．【点睛】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180︒后两部分重合，理解并掌握如何判断中心对称图形的条件是解题的关键．（2022·河北）20. 题目：“如图，∠B＝45°，BC＝2，在射线BM上取一点A，设AC＝d，若对于d的一个数值，只能作出唯一一个△ABC，求d的取值范围．”对于其答案，甲答：d≥，乙答：d＝1.6，丙答：d=）2A. 只有甲答的对B. 甲、丙答案合在一起才完整C. 甲、乙答案合在一起才完整D. 三人答案合在一起才完整【答案】B【解析】 【分析】过点C 作CA BM '⊥于A '，在A M '上取A A BA ''''=，发现若有两个三角形，两三角形的AC 边关于A C '对称，分情况分析即可【详解】过点C 作CA BM '⊥于A '，在A M '上取A A BA ''''=∵∠B ＝45°，BC ＝2，CA BM '⊥∴BA C '是等腰直角三角形∴A C BA ''===∵A A BA ''''=∴2A C ''==若对于d 的一个数值，只能作出唯一一个△ABC通过观察得知：点A 在A '点时，只能作出唯一一个△ABC （点A 在对称轴上），此时d =的答案；点A 在A M ''射线上时，只能作出唯一一个△ABC （关于A C '对称的AC 不存在），此时2d ≥，即甲的答案，点A 在BA ''线段（不包括A '点和A ''点）上时，有两个△ABC （二者的AC 边关于A C '对称）；故选：B【点睛】本题考查三角形的存在性质，勾股定理，解题关键是发现若有两个三角形，两三角形的AC边关于A C'对称（2022·山西）21. 2022年4月16日，神舟十三号载人飞船圆满完成全部既定任务，顺利返回地球家园．六个月的飞天之旅展现了中国航天科技的新高度下列航天图标，其文字上方的图案是中心对称图形的是（）A. B. C. D.【答案】B【解析】【分析】利用中心对称图形的定义直接判断．【详解】解：根据中心对称图形的定义，四个选项中，只有B选项的图形绕着某点旋转180°后能与原来的图形重合，故选B．【点睛】本题考查中心对称图形的判定，掌握中心对称图形的定义是解题的关键．中心对称图形：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，这个点叫做它的对称中心．（2022·河南）22. 如图，在平面直角坐标系中，边长为2的正六边形ABCDEF的中心与原点O∥轴，交y轴于点P．将，OAP绕点O顺时针旋转，每次旋转90°，则重合，AB x第2022次旋转结束时，点A的坐标为（）A. )1-B. (1,-C. ()1-D. (【答案】B【解析】【分析】首先确定点A 的坐标，再根据4次一个循环，推出经过第2022次旋转后，点A 的坐标即可．【详解】解：正六边形ABCDEF 边长为2，中心与原点O 重合，AB x ∥轴， ∴AP ＝1， AO ＝2，∠OP A ＝90°，∴OP∴A （1，第1次旋转结束时，点A -1）；第2次旋转结束时，点A 的坐标为（-1，；第3次旋转结束时，点A 的坐标为（1）；第4次旋转结束时，点A 的坐标为（1；∵将，OAP 绕点O 顺时针旋转，每次旋转90°，∴4次一个循环，∵2022÷4＝505……2，∴经过第2022次旋转后，点A 的坐标为（-1，，故选：B【点睛】本题考查正多边形与圆，规律型问题，坐标与图形变化﹣旋转等知识，解题的关键是学会探究规律的方法，属于中考常考题型．（2022·四川宜宾）23. 如图，ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒，点D 是BC 边上的动点（不与点B 、C 重合），DE 与AC 交于点F ，连结CE ．下列结论：①BD CE =；②DAC CED ∠=∠；③若2BD CD =，则45CF AF =；④在ABC 内存在唯一一点P ，使得PA PB PC ++的值最小，若点D 在AP 的延长线上，且AP 的长为2，则2CE =+ ）A. ①②④B. ①②③C. ①③④D. ①②③④ 【答案】B【解析】【分析】证明BAD CAE ≌，即可判断①，根据①可得ADB AEC ∠=∠，由180ADC AEC ∠+∠=︒可得,,,A D C E 四点共圆，进而可得DAC DEC ∠=∠，即可判断②，过点A 作AG BC ⊥于G ,交ED 的延长线于点H ，证明FAH FCE ∽，根据相似三角形的性质可得45CF AF =，即可判断③，将APC △绕A 点逆时针旋转60度，得到AB P ''△，则APP '是等边三角形，根据当,,,B P P C ''共线时，PA PB PC ++取得最小值，可得四边形ADCE 是正方形，勾股定理求得DP ， 根据CE AD AP PD ==+即可判断④． 【详解】解：ABC 和ADE 都是等腰直角三角形，90BAC DAE ∠=∠=︒， ,,AB AC AD AE BAD CAE ∴==∠=∠BAD CAE ∴△≌△BD CE ∴=故①正确；BAD CAE ≌ADB AEC ∴∠=∠180ADC AEC ∴∠+∠=︒,,,A D C E ∴四点共圆，CD CD =DAC DEC ∴∠=∠故②正确；如图，过点A 作AG BC ⊥于G ,交ED 的延长线于点H ，BAD CAE ≌,45,45ACE ABD ACB ∴∠=∠=︒∠=︒90DCE ∴∠=︒FC AH ∴∥2BD CD =，BD CE =1tan 2DC DEC CE ∴∠==,13CD BC = 设6BC a =，则2DC a =，132AG BC a ==，24EC DC a == 则32GD GC DC a a a =-=-=FC AH ∥1tan 2GD H GH ∴== 22GH GD a ∴==325AH AG GH a a a ∴=+=+=AH ，CE ，FAH FCE ∴∽CF CE AF AH∴= 4455CF a AF a ∴== 则45CF AF =； 故③正确如图，将ABP 绕A 点逆时针旋转60度，得到AB P ''△，则APP '是等边三角形，PA PB PC PP P B PC B C '''+++∴'+=≥，当,,,B P P C ''共线时，PA PB PC ++取得最小值，此时180********CPA APP '∠=-∠=︒-=︒︒︒，180********APB AP B AP P ∠=∠=︒-∠=︒-︒='''︒，360360*********BPC BPA APC ∠=︒-∠-∠=︒-︒-︒=︒，此时120APB BPC APC ∠=∠=∠=︒，AC AB AB '==，AP AP '=，APC AP B ''∠=∠，AP B APC ''∴≌，PC P B PB ''∴==，60APP DPC '∠=∠=︒，DP ∴平分BPC ∠，PD BC ∴⊥，,,,A D C E 四点共圆，90AEC ADC ∴∠=∠=︒，又AD DC BD ==,BAD CAE ≌，AE EC AD DC ∴===，则四边形ADCE 是菱形，又90ADC ∠=︒，∴四边形ADCE 是正方形，9060150B AC B AP PAC P AP ''''∠=∠+∠+∠=︒+︒=︒，则'B A BA AC ==，()1180152B ACB B AC '''∠=∠=︒-∠=︒， 30PCD ∠=︒，DC ∴=，DC AD =，2AP =，则)12AP AD DP DP =-==，1DP ∴==， 2AP =，3CE AD AP PD ∴==+=，故④不正确，故选B ．【点睛】本题考查了旋转的性质，费马点，圆内接四边形的性质，相似三角形的性质与判定，全等三角形的性质与判定，勾股定理，解直角三角形，正方形的性质与判定，掌握以上知识是解题的关键．二．填空题（2022·云南）24. 点A （1，-5）关于原点的对称点为点B ，则点B 的坐标为______．【答案】（-1，5）【解析】【分析】根据若两点关于坐标原点对称，横纵坐标均互为相反数，即可求解．【详解】解：∵点A （1，-5）关于原点的对称点为点B ，∴点B 的坐标为（-1，5）．故答案为：（-1，5）【点睛】本题主要考查了平面直角坐标系内点关于原点对称的特征，熟练掌握若两点关于坐标原点对称，横纵坐标均互为相反数是解题的关键．（2022·湖南湘潭）25. 如图，一束光沿CD 方向，先后经过平面镜OB 、OA 反射后，沿EF 方向射出，已知120AOB ∠=︒，20CDB ∠=︒，则∠=AEF _________．【答案】40°##40度【解析】【分析】根据入射角等于反射角，可得,CDB EDO DEO AEF ∠=∠∠=∠，根据三角形内角和定理求得40OED ∠=︒，进而即可求解．【详解】解：依题意，,CDB EDO DEO AEF ∠=∠∠=∠，∵120AOB ∠=︒，20CDB ∠=︒，20CDB EDO ∴∠=∠=︒，∴18040OED ODE AOB ∠=-∠-∠=︒，∴40AEF DEO ∠=∠=︒．故答案为：40．【点睛】本题考查了轴对称的性质，三角形内角和定理的应用，掌握轴对称的性质是解题的关键．（2022·浙江丽水）26. 一副三角板按图1放置，O 是边()BC DF 的中点，12cm BC =．如图2，将ABC 绕点O 顺时针旋转60︒，AC 与EF 相交于点G ，则FG 的长是___________cm ．【答案】3【解析】【分析】BC 交EF 于点N ，由题意得，=90EDF BAC ∠=∠︒，60DEF ∠=︒，30DFE ∠=︒，=45ABC ACB ∠=∠︒，BC =DF =12，根据锐角三角函数即可得DE ，FE ，根据旋转的性质得ONF △是直角三角形，根据直角三角形的性质得3ON =，即3NC =，根据角之间的关系得CNG △是等腰直角三角形，即3NG NC ==cm ，根据90FNO FED ∠=∠=︒，30NFO DFE ∠=∠=︒得FON FED △∽△，即ON FNDE DF=，解得FN = 【详解】解：如图所示，BC 交EF 于点N ，由题意得，=90EDF BAC ∠=∠︒，60DEF ∠=︒，30DFE ∠=︒，=45ABC ACB ∠=∠︒，BC =DF =12，在Rt EDF 中，12tan tan 60DF DE EDF ===∠︒12sin sin 60DF EF EDF ===∠︒∵△ABC 绕点O 顺时针旋转60°，∴60BOD NOF ∠=∠=︒，∴90NOF F ∠+∠=︒，∴18090FNO NOF F ∠=︒-∠-∠=︒，∴ONF △是直角三角形， ∴132ON OF ==（cm ）， ∴3NC OC ON =-=（cm ），∵90FNO ∠=︒，∴18090GNC FNO ∠=︒-∠=︒，∴NGC 是直角三角形，∴18045NGC GNC ACB ∠=-∠-∠=︒，∴CNG △是等腰直角三角形，∴3NG NC ==cm ，∵90FNO FED ∠=∠=︒，30NFO DFE ∠=∠=︒，∴FON FED △∽△， 即ON FN DE DF=，12FN =，FN =∴3FG FN NG =-=（cm ），故答案为：3．【点睛】本题考查了直角三角形的性质，相似三角形的判定与性质，旋转的性质，解题的关键是掌握这些知识点．（2022·河南）27. 如图，将扇形AOB 沿OB 方向平移，使点O 移到OB 的中点O '处，得到扇形A O B '''．若∠O ＝90°，OA ＝2，则阴影部分的面积为______．【答案】3π+【解析】【分析】设A O '与扇形AOB 交于点C ，连接OC ，解Rt OCO '，求得60O C COB '=∠=︒，根据阴影部分的面积为()OCO A O B OCB S S S''''--扇形扇形，即可求解．【详解】如图，设A O '与扇形AOB 交于点C ，连接OC ，如图O '是OB 的中点11122OO OB OA '∴===, OA ＝2， AOB ∠＝90°，将扇形AOB 沿OB 方向平移，90A O O ''∴∠=︒1cos 2OO COB OC '∴∠== 60COB ∴∠=︒sin 60O C OC '∴=︒=∴阴影部分的面积为()OCO A O B OCB S S S ''''--扇形扇形OCO AOB OCB S S S ''=-+扇形扇形22906012213603602ππ=⨯-⨯+⨯32π=+故答案为：32π+ 【点睛】本题考查了解直角三角形，求扇形面积，平移的性质，求得60COB ∠=︒是解题的关键．（2022·河南）28. 如图，在Rt △ABC 中，∠ACB ＝90°，AC BC ==，点D 为AB 的中点，点P 在AC 上，且CP ＝1，将CP 绕点C 在平面内旋转，点P 的对应点为点Q ，连接AQ ，DQ ．当∠ADQ ＝90°时，AQ 的长为______．【解析】【分析】连接CD ，根据题意可得，当∠ADQ ＝90°时，分Q 点在线段CD 上和DC 的延长线上，且1CQ CP ==，勾股定理求得AQ 即可．【详解】如图，连接CD ，在Rt △ABC 中，∠ACB ＝90°，AC BC ==4AB ∴=，CD AD ⊥，122CD AB ∴==， 根据题意可得，当∠ADQ ＝90°时，Q 点在CD 上，且1CQ CP ==，211DQ CD CQ ∴=-=-=，如图，在Rt ADQ △中，AQ ===在Rt ADQ △中，2,3AD CD QD CD CQ ===+=AQ ∴===【点睛】本题考查了旋转的性质，勾股定理，直角三角形斜边上中线的性质，确定点Q 的位置是解题的关键．（2022·浙江金华）29. 如图，在Rt ABC 中，90,30,2cm ACB A BC ∠=︒∠=︒=．把ABC 沿AB 方向平移1cm ，得到A B C '''，连结CC '，则四边形AB C C ''的周长为_____cm ．【答案】8+【解析】【分析】通过勾股定理，平移的特性，特殊角的三角函数，分别计算出四边形的四条边长，再计算出周长即可．【详解】解：∵90,30,2cm ACB A BC ∠=︒∠=︒=，∴AB =2BC =4，∴∵把ABC 沿AB 方向平移1cm ，得到A B C '''，∴1CC '=，=4+1=5AB '， =2B C BC ''=，∴四边形的周长为：1528++=+故答案为：8+【点睛】本题考查勾股定理，平移的特性，特殊角的三角函数，能够熟练掌握勾股定理是解决本题的关键．（2022·四川德阳）30. 如图，直角三角形ABC 纸片中，90ACB ∠=︒，点D 是AB 边上的中点，连接CD ，将ACD △沿CD 折叠，点A 落在点E 处，此时恰好有CE AB ⊥．若1CB =，那么CE =______．【解析】【分析】根据D 为AB 中点，得到AD =CD =BD ，即有，A =，DCA ，根据翻折的性质有，DCA =，DCE ，CE =AC ，再根据CE ，AB ，求得，A =，BCE ，即有，BCE =，ECD =，DCA =30°，则有，A =30°，在Rt △ACB 中，即可求出AC ，则问题得解．【详解】，，ACB =90°，，，A +，B =90°，，D 为AB 中点，，在直角三角形中有AD =CD =BD ，，，A =，DCA ，根据翻折的性质有，DCA =，DCE ，CE =AC ，，CE ，AB ，，，B +，BCE =90°，，，A +，B =90°，，，A =，BCE ，，，BCE =，ECD =，DCA ，，，BCE +，ECD +，DCA=，ACB =90°，，，BCE =，ECD =，DCA =30°，，A =30°，，在Rt △ACB 中，BC =1， 则有13tan tan 30BC AC A ===∠，CE AC ==【点睛】本题考查了翻折的性质、直角三角形斜边中线的性质、等边对等角以及解直角三角形的知识，求出，BCE =，ECD =，DCA =30°是解答本题的关键． （2022·山东泰安）31. 如图，将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，点O ，B 的对应点分别为O ′，B ′，连接BB ′，则图中阴影部分的面积是__________________．【答案】23π 【解析】 【分析】连接OO ′，BO ′，根据旋转的性质得到AO AO '=，OA OB =，O B OB ''=，60OAO '∠=︒，120AOB AO B ''∠=∠=︒，推出△OAO ′是等边三角形，得到60AOO '∠=︒，因为∠AOB ＝120°，所以60O OB '∠=︒，则OO B '是等边三角形，得到120AO B '∠=︒，得到30O B B O BB ''''∠=∠=︒，90B BO '∠=︒，根据直角三角形的性质得24B O OB '==，根据勾股定理得B B '=，用B OB '△的面积减去扇形O OB '的面积即可得．【详解】解：如图所示，连接OO ′，BO ′，∵将半径为2，圆心角为120°的扇形OAB 绕点A 逆时针旋转60°，∴AO AO '=，OA OB =，O B OB ''=，60OAO '∠=︒，120AOB AO B ''∠=∠=︒ ∴△OAO ′是等边三角形，∴60AOO '∠=︒，OO OA '=，∴点O '在，O 上，∵∠AOB ＝120°，∴60O OB '∠=︒，∴OO B '是等边三角形，∴120AO B '∠=︒，∵120AO B ''∠=︒，∴120B O B ''∠=︒， ∴11(180)(180120)3022O B B O BB B O B ''''''∠=∠=︒-∠=⨯︒-︒=︒， ∴180180306090B BO OB B B OB '''∠=︒-∠-∠=︒-︒-︒=︒，∴24B O OB '==，在Rt B OB '中，根据勾股定理得，B B '==∴图中阴影部分的面积=2160222=223603B OB O OB S S ''⨯-=⨯⨯扇形ππ，故答案为：23π． 【点睛】本题考查了圆与三角形，旋转的性质，勾股定理，解题的关键是掌握这些知识点．（2022·湖南怀化）32. 已知点A （﹣2，b ）与点B （a ，3）关于原点对称，则a ﹣b =______．【答案】5【解析】【分析】根据平面直角坐标系中，关于原点对称的点横、纵坐标都互为相反数，求出a ，b 的值即可．【详解】∵点A （﹣2，b ）与点B （a ，3）关于原点对称，∴2a =，3b =-，∴()235a b -=--=故答案为：5．【点睛】本题考查平面直角坐标系中，关于原点对称的点的坐标的特点，掌握特殊位置关系的点的坐标变化是解答本题的关键．（2022·浙江台州）33. 如图，△ABC 的边BC 长为4cm ．将△ABC 平移2cm 得到△A ′B ′C ′，且BB ′⊥BC ，则阴影部分的面积为______2cm ．【答案】8【解析】【分析】根据平移的性质即可求解．【详解】解：由平移的性质S △A ′B ′C ′=S △ABC ，BC =B ′C ′，BC ∥B ′C ′，∴四边形B ′C ′CB 为平行四边形，∵BB ′⊥BC ，∴四边形B ′C ′CB 为矩形，∵阴影部分的面积=S △A ′B ′C ′+S 矩形B ′C ′CB -S △ABC=S 矩形B ′C ′CB=4×2=8(cm 2)．故答案为：8．【点睛】本题考查了矩形的判定和平移的性质：①平移不改变图形的形状和大小；②经过平移，对应点所连的线段平行且相等，对应线段平行且相等，对应角相等．三．解答题（2022·湖南湘潭）34. 如图，在平面直角坐标系中，已知ABC 的三个顶点的坐标分别为()1,1A -，()4,0B -，()2,2C -．将ABC 绕原点O 顺时针旋转90︒后得到111A B C △．（1）请写出1A 、1B 、1C 三点的坐标：1A _________，1B _________，1C _________（2）求点B 旋转到点1B 的弧长．【答案】（1）（1，1）；（0，4）；（2，2）（2）2π【解析】【分析】（1）将，ABC绕着点O按顺时针方向旋转90°得到，A1B1C1，点A1，B1，C1的坐标即为点A，B，C绕着点O按顺时针方向旋转90°得到的点，由此可得出结果．（2）由图知点B旋转到点1B的弧长所对的圆心角是90º，OB=4，根据弧长公式即可计算求出．【小问1详解】解：将，ABC绕着点O按顺时针方向旋转90°得到，A1B1C1，点A1，B1，C1的坐标即为点A，B，C绕着点O按顺时针方向旋转90°得到的点，所以A1（1，1）；B1（0，4）；C1（2，2）【小问2详解】解：由图知点B旋转到点1B的弧长所对的圆心角是90度，OB=4，∴点B旋转到点1B的弧长=904 180π⨯⨯=2π【点睛】本题主要考查点的旋转变换和弧长公式，解题的关键是熟练掌握旋转变换的定义和弧长公式．（2022·湖北武汉）35. 如图是由小正方形组成的96⨯网格，每个小正方形的顶点叫做格点．ABC的三个顶点都是格点．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．（1）在图（1）中，D，E分别是边AB，AC与网格线的交点．先将点B绕点E 旋转180︒得到点F，画出点F，再在AC上画点G，使DG BC∥；（2）在图（2）中，P是边AB上一点，BACα∠=．先将AB绕点A逆时针旋转。

2021-2021学年北京版小学四年级数学下册《第4单元图形变换》单元测试题一．选择题（共8小题）1．将图形按顺时针方向旋转90°后的图形是（）A．B．C．D．2．把正方形的右边剪去一块补到上面（如图），得到的图形是（）A．B．C．D．3．如图中，小鱼向右平移了（）格。

A．1B．2C．3D．44．图中，图①向左平移了（）格．A．6B．4C．35．从7时到9时，时针按（）A．顺时针旋转60°B．顺时针旋转90°C．顺时针旋转180°6．下列图案中，（）是由图案的一部分经过旋转得到的．A．B．C．7．如图△ABC经过怎样的平移得到△DEF（）A．把△ABC向左平移4个单位，再向下平移2个单位B．把△ABC向右平移4个单位，再向下平移2个单位C．把△ABC向右平移4个单位，再向上平移2个单位D．把△ABC向左平移4个单位，再向上平移两个单位8．如图是由经过（）变换得到了．A．旋转B．平移C．对称二．填空题（共10小题）9．图形的变换方式有平移、、．10．我们可以利用、和，设计出美丽的图案．11．（1）图形2可以看作是图形1绕点顺时针旋转，又向平移格得到的．（2）图形4可以看作是图形1绕点时针旋转，又向平移格得到的．12．看图填一填．指针从“12”绕点到0顺时针旋转30°到“”；指针从“1”绕点0顺时针旋转90°到“”；指针从“6”绕点0逆时针旋转°到“3”；指针从“8”绕点0逆时针旋转°到“10”．13．在图中，既能通过旋转又能通过轴对称变换得到的图形是A．B．C．D．14．如图指针从A点开始，绕O点顺时针旋转90°，指针到点．15．图A先向平移格，再向平移格，得到图B。

16．如图，把三角形A平移到三角形B，可以先向平移格，再向平移格．17．如图中，要把图形①移到图形②的位置，应该先向平移6格，再向上平移格．18．图形①是以点为中心时针旋转的，在图①标出各点的对应点．图形②是以点为中心时针旋转的，在图②标出各点的对应点．图形③是以点为中心时针旋转的，在图③标出各点的对应点．三．判断题（共5小题）19．在图中，以直线为轴旋转，可以得出圆锥只有1个．．（判断对错）2021角三角形沿着一条直角边旋转之后形成一个圆锥体。

2019年七年级下册数学单元测试题第二章图形的变换一、选择题1．如图所示的几张图中，相似图形是（）A．①和②B．①和③C．①和④D．②和③答案：C2．当身边没有量角器时，怎样得到一些特定度数的角呢？动手操作有时可以解“燃眉之急”．如图，已知长方形ABCD，我们按如下步骤操作可以得到一个特定的角：（1）以点A所在直线为折痕，折叠纸片，使点B落在AD上，折痕与BC交于E；（2）将纸片展平后，再一次折叠纸片，以E所在直线为折痕，使点A落在BC上，折痕EF交AD于F．则∠AFE的度数为（）A．60︒B．67.5︒C．72︒D．75︒解析：B3．如图是跳棋盘，其中格点上的黑色点为棋子，剩余的格点上没有棋子，我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿直线隔着棋子对称跳行，跳行一次称为一步.已知点A 为己方一枚棋子，欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最小步数为（）A．2步B．3步C．4步D．5步答案：B4．如图所示，将一张矩形的纸对折，然后用针尖在上面扎出“S”，再把它铺平，铺开后图形是（）答案：A5．如图所示，△ABC平移后得到△DEF，若∠BNF=100°，则∠DEF的度数是（） A．120°B．100°C．80°D．50°答案：C6．平移前有两条直线互相垂直，那么这两条直线平移后（）A．互相平行B．互相垂直C．相交但不垂直D．无法确定答案：B7．如图所示，不能通过基本图形平移得到的是（）答案：D8．下列生活现象中，属于相似变换的是（）A．抽屉的拉开B．汽车刮雨器的运动C．荡秋千D．投影片的文字经投影变换到屏幕答案：D9．按照图①的排列规律，在d内应选②中的（）答案：B10．下列各选项中，右边图形与左边图形成轴对称的图形是（）A． B．C．D．答案：C11．如图，每个正方形均由边长为l的小正方形组成，则下列图形中的三角形（阴影部分）是△ABC经相似变换后得到的像是（）答案：A12．下列基本图形中，经过平移、旋转或轴对称变换后，不能得到最右边图的是（）答案：C13．如图，把边长为2的正方形的局部进行图①～图④的变换，拼成图⑤，那么图⑤的面积是（）A．18 B．16 C．12 D．8答案：B14．下列现象中，不属于旋转变换的是（）A．钟摆的运动 B．行驶中汽车车轮 C．方向盘的转动 D．电梯的升降运动答案：D15．如图，将四边形AEFG变换到四边形ABCD，其中E，G分别是AB，AD的中点，下列叙述不正确的是（）A．这种变换是相似变换B．对应边扩大到原来的2倍C．各对应角度数不变D．面积扩大到原来的2倍答案：D16．从图形的几何性质考虑，下列图形中，有一个与其他三个不同，它是（）A．B． C．D．答案：C17．如图所示的一些交通标志中，是轴对称图形的有（）.A． 1个B． 2个C．3个D．4个答案：B18．如图所示，绕旋转中心旋转60°后能与自身重合的是（）答案：A二、填空题19．如图，把五边形ABCDO变换到五边形CDEFO，应用了哪种图形变换？请完整地叙述这个变换：解析：应用了旋转变换，五边形 CDBFO是由五边形ABCDO绕点 0接顺时针方向旋转90°得到的.20．如图，△ABO按逆时针旋转变换到△CDO，在这个变换中，旋转中心是_____，•BO 变换到了_______，∠C是由______旋转变换得到的．解析：点O ，DO, ∠A21．试找出如图所示的每个正多边形的对称轴的条数，并填下表格中．根据上表，请就一个正n 边形对称轴的条数作一猜想_________(用n 表示)． 解析：3，4，5，6，7，8，n 条22．解析：王（轴对称图形都可以）23．如图，△A ′B ′C ′是△ABC 经旋转变换后的像， (1)旋转中心是 ,旋转角度是 ； (2)图中相等的线段：OA= ，OB= ，OC= ，AB= ，BC= ，CA= ． (3)图中相等的角：∠CAB= ，∠BCA= ，∠AOA ′= = ．解析： (3)∠C ′A ′B ′，∠B ′C ′A ′，∠BOB ′，∠COC ′ (1)0，60°；(2)OA ′，OB ′，OC ′，A ′B ′，B ′C ′，C ′A ′；24．如图所示，△DEF 是△ABC 绕点O 旋转后得到的，则点C 的对应点是点 ，线段AB 的对应线段是线段 ，∠B 的对应角是 ．解析：F ，DE ，∠E25．如图所示的四个两两相联的等圆．右边的三个圆可以看做是左边的圆经过 得到的．解析：平移26．从汽车的后视镜中看见某车车牌的后5位号码是，该车牌的后5位号码实际是．解析：BA62927．点A和点A′关于直线l成轴对称，则直线l和线段AA′的位置关系是：．解析：垂直且平分28．请写出是轴对称图形的英文字母(至少写出五个) ．解析：A，C，E，H，K等三、解答题29．请你用正方形、三角形、•圆设计一个有具体形象的轴对称图形（例如下图的脸谱），并给你的作品取一个适当的名字．解析：略30．画出如图所示的轴对称图形的对称轴，并回答下列问题：(1）连结BD，则对称轴和线段BD有怎样的位置关系？(2）原图形中有哪些相等的角？哪些全等的三角形？(3）分别作出图形中点F、G的对称点．解析：如图所示，连结BD，作线段BD的垂直平分线m，直线m•就是所求的对称轴．(1）对称轴垂直平分线段BD；(2）原图形中相等的角有：∠B=∠D，∠BAC=∠DEC，∠BCA=∠DCE，∠CAE=∠CEA ，∠BCE=∠DCA ，∠BAE=∠DEA ．全等的三角形有：△ABC 和△EDC ； (3）点F 、G 的对称点分别是F ′、G ′，如图所示．31． 将下列各图形的变换与变换的名称用线连起来：解析：略．32．如图所示，在方格纸中如何通过平移或旋转这两种变换，由图形A 得到图形B ，再由图形B 得到图形C?(对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回答出旋转中心、旋转方向和旋转角度)解析：将图形A 向上平移4个单位长度，得到图形B ；将图形B 以点P 1为旋转中心顺时针旋转90°，再向右平移4个单位长度得到图形C 或将图形B 向右平移4个单位长度，再以P 2为旋转中心顺时针旋转90°得到图形C 33．如图，在网格中有一个四边形图案ABCO ．平移变换相似变换旋转变换轴对称变换(1)请你画出此图案绕点O顺时方向旋转90°，l80°，270°的图案，你会得到一个美丽的图案，千万不要将阴影位置涂错；(2)若网格中每个小正方形的边长为l，旋转后点A的对应点依次为A1，A2，A3，求四边形AA1A2A3的面积；解析：(1)图略；(2)3434．如图所示，图①和图②都是轴对称图形，依照①和②，把③，④也画成轴对称图形．解析：略35．如图所示，在方格纸上作下列相似变换：(1)把图①中三角形的每条边放大到原来的3倍；(2)把图②中H的每条边缩小到原来的12．解析：略36．图②、③、④、⑤分别由图①变换而成的，请你分析它们的形成过程．解析：由图①经过连续四次绕圆心顺时针旋转90°得到37．如图，将△ABC先向上平移5格得到△A′B′C′，再以直线MN为对称轴，将△A′B′C′作轴对称变换，得到△A″B″C″，作出△A′B′C′和△A″B″C″．解析：略38．如图所示是在镜子中看到的某时刻时钟的情况，请问此时实际是几点钟?解析：3：2539．如图所示，△ABC与△DEF是关于直线l的轴对称图形，请说出它们的对应线段和对应角．解析：AC和DE，AB和DF，BC和FE；∠A和∠D，∠C和∠E，∠B和∠F40．如图所示，图①，图②分别是6×6正方形网格上两个轴对称图形(阴影部分)，其面积分别为S A,S B(网格中最小的正方形面积为l平方单位)．请观察图形并解答下列问题：(1)填空：S A:S B的值是．(2)请你在图③的网格上画出一个面积为8个平方单位的轴对称图形．解析：(1)9：11；(2)略。

解析：将图形A向上平移4个单位长度，得到图形B；将图形B以点P1为旋转中心顺时针旋转 90°，再向右平移4个单位长度得到图形C或将图形B向右平移4个单位长度，再以P2为旋转 中心顺时针旋转90°得到图形C 29．如图所示，图①和图②都是轴对称图形，依照①和②，把③，④也画成轴对称图形 ．
解析：略 30．△ABC，△A1B1C1和△A2B2C2在方格纸中的位置如图所示．方格纸每格的边长为1． (1)将△ABC向下平移 格得到△A1B1C1； (2)将△A1B1C1的各边长放大 倍，得到△A2B2C2； (3)分别计算△A2B2C2和△ABC的面积，并说明△A2B2C2的面积是△ABC的面积的多少倍．
D． 15:10
答案：B
20．如图，正方形ABCD的边长是3
cm，一个边长为1cm的小正方形沿着正方形ABCD的边AB BC CD DA
AB连续地翻转，那么这个小正方形第一次回到起始位置时，小正方形中箭头的方向（ ）
A．朝左
B．朝上
C．朝右
D．朝下
答案：B
21．在下面四个图形中，既包含图形的旋转，又有图形的轴对称设计的是（ ）
⑵如图，由16个相同的小正方形拼成的正方形网格，现将其中的两个小正方形涂黑（如图 ）．请你用两种不同的方法分别在下图中再将两个空白的小正方形涂黑，使它成为轴对称 图形．
解析：略． 28．如图所示，在方格纸中如何通过平移或旋转这两种变换，由图形A得到图形B，再由图 形B得到图形C?(对于平移变换要求回答出平移的方向和平移的距离；对于旋转变换要求回 答出旋转中心、旋转方向和旋转角度)
解析：(1)特征一：都是轴对称图形；特征二：这些图形的面积都等于4个单位面积等； (2)图略 37．如图所示，草原上两个居民点A，B在河流 l 的同旁，一汽车从A出发到B，途中需到河边加水，汽车在哪一点加水可使行驶的路程最短 ?在图中画出该点．

浙教版初中数学试卷2019-2020年七年级数学下册《图形和变换》精选试卷学校：__________题号一二三总分得分评卷人得分一、选择题1．(2分)如图所示是一个风筝的图案，它是轴对称图形，量得∠B=30°，则∠E的大小为（）A． 30°B． 35°C．40°D． 45°'2．(2分)现实生活中存在大量的平移现象，下列现象属于平移变换的是（）A．行进中自行车车轮的运动B．急刹车后汽车在路面上的滑动C．人与镜子中的像D．台球在桌面上从一点到另一点的运动3．(2分)如图1所示是一张画有小白兔的卡片，卡片正对一面镜子，这张卡片在镜子里的影像是下列各图中的（）图1 A． B． C． D．4．(2分)下列“QQ表情”中属于轴对称图形的是（）A． B． C．D．5．(2分)下列各组图形，可以经过平移变换由一个图形得到另一个图形的是（）A． B． C． D．6．(2分)下列扑克牌中,以牌的对角线交点为旋转中心,旋转180O后能与原图形重合的有（）A．4张B．3张C．2张7．(2分)在下图中，与图形变换相同的是（）8．(2分) 下列图形不一定是轴对称图形的是（）A．等边三角形B．长方形C．等腰三角形D．直角三角形9．(2分)赵师傅透过平举的放大镜从正上方看到水平桌面上的菱形图案的一角（如图所示），那么∠A与放大镜中的∠C的大小关系是（）A．∠A=∠C B．∠A＞∠CC．∠A＜∠C D．∠A与∠C的大小无法比较10．(2分)一个四边形通过旋转形成另一个四边形，下列说法中，正确的是（）A．这两个四边形一定是轴对称图形B．这两个四边形一定可以通过互相平移得到C．旋转中，任意一对对应点的连线必过旋转中心D．旋转中，一个四边形上的每一点绕旋转中心沿相同的方向转动的角度相等11．(2分)把△ABC先向左平移1 cm，再向右平移2 cm，再向左平移3 cm。

再向右平移4 cm，……，经这样移动l00次后，最后△ABC所停留的位置是（）A．△ABC左边50 cm B．△ABC右边50 cm C．△ABC左边l m D．△ABC右边l m 12．(2分)如图所示，将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆孔，最后将正方形纸片展开，得到的图案是（）评卷人得分二、填空题13．(2分)如图，△ABC可看作是△DEC通过变换得到的.14．(2分)中央电视台大风车栏目的图标如图（1）所示，其中心为点0，半圆ACB 固定，其半径为2r，车轮绕中心旋转 180°能与原来的图形重合，轮片是半圆形，小红通过观察发现车轮旋转过程中留在半圆ACB内的轮片面积是不变的(如图(2))，这个不变的面积值是 .15．(2分)从8:55到9:15,钟表的分针转动的角度是_____，时针转动的角度是．16．(2分)试找出如图所示的每个正多边形的对称轴的条数，并填下表格中．正多边形的边数345678对称轴的条数根据上表，请就一个正n边形对称轴的条数作一猜想_________(用n表示)．17．(2分)已知∠AOB是由∠DEF经过平移变换得到的,且∠AOB+∠DEF=1200.则∠AOB= 度.18．(2分)如图，校园里有一块边长为20 m的正方形空地，准备在空地上种草坪，草坪上有横竖各3条小路，每条小路的宽度都为2 m，则草坪的面积为．19．(2分)某市城区地图(比例尺为l：8000)上，安居街和新兴街的长度分别是15cm和10cm，那么安居街的实际长度是，安居街与薪兴街的实际长度的比是．20．(2分)如图①所示，魔术师把4张扑克牌放在桌子上，然后蒙住眼睛，请一位观众上台，把某一张牌旋转180°，魔术师解除蒙具后，看到如图②所示的4张扑克牌，他很快确定哪一张牌被旋转过，到底哪一张?答：．21．(2分)如图所示的五角星绕中心点旋转一定的角度后能与自身完全重合，则其旋转的角度至少为．22．(2分)汉字中有许多字是由一个字经过平移而得来的，如“木”平移可得到“林”、“森”．请你至少写出三个字是由另一个汉字平移而得来的字．23．(2分)观察你生活中的各处，举出三个平移的现象：．24．(2分)如图所示的五家银行行标中，是轴对称图形的有 (填序号)．评卷人得分三、解答题25．(7分)尺规作图：把图(实线部分)补成以虚线l为对称轴的轴对称图形，你会得到一只美丽蝴蝶的图案(不用写作法，保留作图痕迹).26．(7分)如图，在△ABC中，∠A=110°，∠B=35°，请你应用变换的方法得到一个三角形使它与△ABC全等，且要求得到的三角形与原△ABC组成一个四边形．请角两种变换方法解决上述问题．27．(7分)如果想剪出如图所示的图案，你怎样剪?设法使剪的次数尽可能少．28．(7分)用四块如图①所示的瓷砖拼成一个正方形图案，使拼成的图案成一个轴对称图形(如图②)．请你分别在图③、图④中各画一种与图②不同的拼法，要求两种拼法各不相同，且是轴对称图形．29．(7分)请通过平移如图所示的图形，设计两种图案．30．(7分)认真观察图①的4个图中阴影部分构成的图案，回答下列问题：(1)请写出这四个图案都具有的两个共同特征．特征一：；特征二：．(2)请在图②中设计出你心中最美丽的图案，使它也具备你所写出的上述特征．【参考答案】***试卷处理标记，请不要删除评卷人得分一、选择题1．A2．B3．C4．C5．A6．C7．B8．D9．A10．D11．B12．C评卷人得分二、填空题13．轴对称14．2r15．120°，10°16．3，4，5，6，7，8，n条17．60度18．196 m219．1．2 km，3：220．第一张方块421．72°22．如“品”，“焱”．“淼”，“晶”等23．答案不唯一，例如：电梯移动；火车移动；汉字中“晶”可以由“日”平移得到24．①②③评卷人得分三、解答题25．如图：26．略．27．由于该图是轴对称图形，所以先把纸对折，然后沿折痕把对称轴的一侧图画上，再进行剪28．略29．略30．(1)特征一：都是轴对称图形；特征二：这些图形的面积都等于4个单位面积等；(2)图略。

A．电梯从一楼升到了八楼
B．电风扇叶片的转动
C．火车在笔直的铁路上行驶
D．一块石子扔进河里，水波在不断扩大
4．(2 分)下面每组图形中的两个图形不是通过相似变换得到的是（ ）
5．(2 分)将下列图形绕着一个点旋转 1200 后，不能与原来的图形重合的是（ ）
6．(2 分)把一个正方形三次对折后沿虚线剪下, 如图所示，
以下四个图形中，不能通过上述方式得到的是（ ）
12．(2 分)已知∠A=56°，把么 A 先向左平移 2cm，再向上平移 3 cm，则∠A 的大小
（）
A．变大
B．不变
C．变小
D．无法确定
13．(2 分)当身边没有量角器时，怎样得到一些特定度数的角呢？动手操作有时可以解“燃
眉之急”．如图，已知长方形 ABCD，我们按如下步骤操作可以得到一个特定的角：（1）
则所得的图形是（ ）
7．(2 分) 如图，每个小正方形网格的边长都为 1，右上角的圆柱体是由左下角的圆柱体经
过平移得到的.下列说法错误的是（ ）
A．先沿水平方向向右平移 4 个单位长度，再向上沿垂直的方向平移 4 个单位长度，
然后再沿水平方向向右平移 3 个单位长度
B．先沿水平方向向右平移 7 个单位长度，再向上沿垂直的方向平移 4 个单位长度
21．(7 分)如图是某设计师在方格纸中设计图案的一部分，请你帮他完成余下的工作： (1）作出关于直线 AB 的轴对称图形；
(2）将你画出的部分连同原图形绕点 O 逆时针旋转 90°；
(3）发挥你的想象，给得到的图案适当涂上阴影，让它变得更加美丽． A
O
B
22．(7 分)如图，△BDE,△CEF 都是由△ABC 经平移变换得到的像，已知∠ABC=700, ∠ ACB=450.

人教版二年级下册数学第三单元试卷教材基础知识针对性训练与基本能力巩固提高一、选择。

1．—个正方体所有的面上共有( )个角。

A．无数B．6 C．242．下列各角中，( )是直角，( )是锐角，( )是钝角。

A B C D E F3．下列图形中，( )通过旋转后与下图是相同的。

4．把一个角放在放大镜下看，这个角和原来相比( )。

A．变大了B．变小了C．没有变化5．下图中右上角的空白小长方形框中缺少的是( )图形。

二、填空。

1．下面滑梯中有很多角，请你写出图中的角各是什么角?∠1是( )角∠2是( )角∠3是( )角∠4是( )角2．在我们学过的角中，( )角比直角小，( )角比直角大。

3．图中共有( )个角。

4．一个五边形有( )个角。

5．把24÷4，6×7，20÷5，7×8，25＋4，8×8这些算式按结果从大到小的顺序排列起来依次是( )。

三、应用。

1．王老师买来45本故事书，每5本包成一包，共包多少包?分给一年级3包后，还剩多少包? 2．除夕夜玲玲和3个姐姐一起包了36个饺子，求平均每人包几个。

3．妈妈买来30米布，做床单用了12米，还剩下多少米?如果做一套衣服要用3米布，剩下的布还能做几套衣服?探究拓展能力强化训练与应用综合能力的养成1．(探究题)一张长方形的纸片有4个角，用剪刀沿直线剪掉1个角后，还剩下几个角?2．(作图题)按下面的要求在图中画一条线段。

(1)增加两个直角(2)增加3个直角(3)增加4个直角3．(计数题)图中有几个直角、锐角、钝角?4．(推理题)已知1个西瓜8千克，求一个菠萝和1个南瓜各有多重。

5．(竞赛题)将31，44，52，67，39，26，18，3这八个数分别填到下面的○里，使每条线上三个数之和都等于100。

答案：第三单元单元测试教材基础知识针对性训练与基本能力巩固提高一、1．C 2．B，D， F A， E C 3．B 4．C 5．A二、1．钝，锐，直，钝2．锐，钝3． 34． 55．８×8，7×8，6×7，25＋4，24÷4，20÷5三、1．45÷5＝9(包)，9－3＝6(包)2．1＋3＝4(人)，36÷4＝9(个)3．30－12＝18(米)，18÷3＝6(套)探究拓展能力强化训练与应用综合能力的养成1．3个，4个或5个提示：图中黑色表示剪掉的部分，所以还剩下3，4，5个角(如图所示)3．4个直角，10个锐角，10个钝角4．菠萝4千克南瓜8千克提示：由图可以看出：1个西瓜重量＝2个菠萝重量＝1个南瓜重量＝8千克。

2019年七年级下册数学单元测试题第二章图形的变换一、选择题1．下列图案，能通过某基本图形旋转得到，但不能通过平移得到的是（）答案：A2．下列英文字母中是轴对称图形的是（）A．S B．H C．P D．Q答案：B3．如图所示，是轴对称图形的个数有（）A．4个B．3个C．2个D．1个答案：B4．把一张长方形的纸片按如图所示的方式折叠，EM，FM为折痕，折叠后的C点落在B′M或B′M的延长线上，那么∠EMF的度数是（）A．85°B．90°C．95°D．100°答案：B5．如图所示，矩形ABCD沿着AE折叠，使D点落在BC边上的F点处，若∠BAF=50°，则∠EAF的度数为（）A．50°B．45°C．40°D．20°答案：D6．平移前有两条直线互相垂直，那么这两条直线平移后（）A．互相平行B．互相垂直C．相交但不垂直D．无法确定答案：B7．如图是条跳棋棋盘．其中格点上的黑色为棋子．剩余的格点上没有棋子．我们约定跳棋游戏的规则是：把跳棋棋子在棋盘内沿直线隔着棋子对称跳行．跳行一次称为一步．已知点A为乙方一枚棋子．欲将棋子A跳进对方区域（阴影部分的格点），则跳行的最少步数为（）A．2步B．3步C．4步D．5步答案：B8．下列对于旋转的判断中，正确的是（）A．图形旋转时，图形的形状发生了改变B．图形旋转时，图形的大小发生了改变C．图形旋转时，图形的位置发生了改变D．图形旋转时，图形的形状、大小和位置都发生了改变答案：C9．如图，0是正六边形ABCDE的中心，下列图形可由△OBC平移得到的是（）A．△OAF B．△OAB C．△OCD D．△OEF答案：A10．赵师傅透过平举的放大镜从正上方看到水平桌面上的菱形图案的一角（如图所示），那么∠A与放大镜中的∠C的大小关系是（）A．∠A=∠C B．∠A＞∠CC．∠A＜∠C D．∠A与∠C的大小无法比较答案：A11．某园林占地面积约为800000 m2，若按比例尺1：2000缩小后，其面积大约相当于（）A．一个篮球的面积B．一张乒乓球台面的面积C．《钱江晚报》一个版面的面积D．《数学》课本封面的面积答案：C12．如图，AC与BD互相平分于点O，则△AOB至少绕点O旋转多少度才可与△COD•重合（）A．60°B．30°C．180°D．不确定答案：C13．如图，每个小正方形网格的边长都为1，右上角的圆柱体是由左下角的圆柱体经过平移得到的．下列说法错误．．的是（）A．先沿水平方向向右平移4个单位长度，再向上沿垂直的方向平移4个单位长度，然后再沿水平方向向右平移3个单位长度B．先沿水平方向向右平移7个单位长度，再向上沿垂直的方向平移4个单位长度C．先向上沿垂直的方向平移4个单位长度，再沿水平方向向右平移7个单位长度D．直接沿正方形网格的对角线方向移动7个单位长度答案：D14．下列各图中，是轴对称图案的是（）A．B．C．D．答案：B15．下列说法中，正确的是（）A．图形平移的方向只有水平方向和竖直方向B．图形平移后，它的位置、大小、形状都不变C．图形平移的方向不是唯一的，可向任何方向平行移动D．图形平移后对应线段不可能在一条直线上答案：C16．如图所示，不能通过基本图形平移得到的是（）答案：D二、填空题17．如图(1)硬纸片ABCD 的边长是4cm，点E、F分别是AB、BC边的中点，若沿左图中的虚线剪开，拼成如图 (2}所示的一栋“小别墅”，则图中阴影部分的面积和是 cm2.解答题解析：418．请举出生活中两个常见的反映旋转变换的例子：______________．解析：略19．计算机软件中，大部分都有“复制”、“粘贴”功能，如在“Word”中，可以把一个图形复制后粘贴在同一个文件上，通过“复制”、“粘贴”得到的图形可以看作原图经过变换得到的．解析：平移变换20．如图，点P关于OA、OB对称点分别是P1、P2，P1P2分别交OA、OB于点C、D，P1P2=6cm，则△PCD的周长为．解析：6cm21．下列各图中，从左到右的变换分别是什么变换?解析：轴对称变换，相似变换，旋转变换，平移变换22．如图是一个个五叶风车示意图，它可以看做是由“基本图案”绕着点O通过次旋转得到的．解析：△0AB，423．如图，△A′B′C′是△ABC经旋转变换后的像，(1)旋转中心是 ,旋转角度是；(2)图中相等的线段：OA= ，OB= ，OC= ，AB= ，BC= ，CA= ．(3)图中相等的角：∠CAB= ，∠BCA= ，∠AOA′= = ．解析： (3)∠C′A′B′，∠B′C′A′，∠BOB′，∠COC′(1)0，60°；(2)OA′，OB′，OC′，A′B′，B′C′，C′A′；24．如图所示的方格纸中，把正方形先向右平移2格，再向下平移2格，则平移后得到的正方形与原正方形重叠部分的面积为 (每个小方格的边长为1)．解析：125．如图所示，图①经过变为图②，再经过变为图③．解答题解析：平移变换，轴对称变换26．如图所示是按照一定规律画出的一列“树形”图．经观察可以发现：图②比图①多出3个“树枝”，图③比图②多出6个“树枝”，图④比图③多出l2个“树枝”．照此规律，图⑦将比图⑥多出个“树枝”．解析：9627．轴对称图形和轴对称的区别在于前者是对个图形而言的，而后者是对个图形而言的．解析：1，2三、解答题28．如图，请你用三种方法把左边的小正方形分别平移到右边的三个图形中，使它成为轴对称图形.解析：如图：29．如图，请用三种方法，在已知图案上再添上一个小正方形后，使其成为轴对称图形，并画出对称轴．解析：略30．在下图中，将图中的小船沿箭头方向平移6格，作出平移后的图形．解析：略31．请你用正方形、三角形、•圆设计一个有具体形象的轴对称图形（例如下图的脸谱），并给你的作品取一个适当的名字．解析：略32．分析图中△ABC 经过怎样的变换得到△BCG , △CDE 和△CEF.解析：△ABC 以BC 为对称轴作轴对称变换得到△BCG ， △ABC 向右平移BC 的长度得到△CDE ，再以CE 的中点为旋转中心旋转180度得到△CEF ．33． 已知△ABC 和直线m ，以直线m 为对称轴，画△ABC 轴对称变换后所得的图形.解析：略．34．如图所示，有一条小船，(1)若把小船平移，使点A 平移到点B ，请你在图中画出平移后的小船；(2)若该小船先从点A 航行到达岸边l 的点P 处补给后再航行到点B，但要求航程最短，试A B mC在图中画出点P的位置．解析：略35．如图所示，有三个正方形的花坛，准备把每个花坛都分成形状、大小相同的四块，种不同的花草．现向大家征集设计图案，图①是某同学设计的图案，请你在图②、③中再设计两种不同的图案．解析：略36．如图所示，在方格纸中，有两个形状、大小完全相同的图形，请指出如何运用轴对称、平移、旋转这三种运动，将一个图形重合到另一个图形上．解析：把△ABC先绕点A逆时针旋转90°，再向上平移2个单位，然后以D点所在的竖格子线为对称轴进行轴对称变换37．如图所示的图案，此图案可由怎么样的基本图形通过平移得到?请你分析．解析：略38．如图所示，正六边形的边长为a，作相似变换，使所得的像扩大到原来的2倍，并写出所画正六边形的边长．解析：图略，2a39．如图，是设计师设计的方桌图案的一部分，请你运用旋转的方法，画出该图形在左上方的正方形网格上绕0点顺时针依次旋转90°，l80°，270°后的图形，你会得到一个美丽的立体图案，你来试一试吧!解析：略40．请通过平移如图所示的图形，设计两种图案．解析：略。

函函函函函函函函函函一、单选题（本大题共11小题，共55分）1. 为了得到函数y =sin(2x −π3)+1的图象，可将函数y =sin2x 的图象( ) A. 向右平移π6个单位长度，再向上平移1个单位长度 B. 向右平移π3个单位长度，再向下平移1个单位长度 C. 向左平移π6个单位长度，再向下平移1个单位长度 D. 向左平移π3个单位长度，再向上平移1个单位长度2. 若函数y =sin(ωx +π3)的图象向右平移π6个单位长度后与函数y =cosωx 的图象重合，则ω的值可能为( )A. −1B. −2C. 1D. 23. 为了得到函数y =sin(3x −π6)的图象，需将函数y =sin(x −π6)的图象上所有点的( ) A. 纵坐标变为原来的3倍，横坐标不变 B. 横坐标变为原来的3倍，纵坐标不变 C. 横坐标变为原来的13，纵坐标不变D. 纵坐标变为原来的13，横坐标不变4. 函数y =sin2x 的图象可由函数y =cos(2x +π6)的图象( ) A. 向左平移π12个单位长度得到 B. 向右平移π6个单位长度得到 C. 向左平移π4个单位长度得到D. 向右平移π3个单位长度得到5. 将函数y =sin(4x −π3)图象上的横坐标进行怎样的变换，得到y =sin(2x −π3)的图象( ) A. 伸长了2倍B. 伸长了12倍C. 缩短了12倍D. 缩短了2倍6. 把函数y =sin(2x −π4)的图象向左平移π8个单位长度，所得到的图象对应的函数是( ) A. 奇函数B. 偶函数C. 既是奇函数也是偶函数D. 非奇非偶函数7. 已知函数f(x)=sin(x +π3).给出下列结论：①f(x)的最小正周期为2π； ②f(π2)是f(x)的最大值；③把函数y =sinx 的图象上的所有点向左平移π3个单位长度，可得到函数y =f(x)的图象． 其中所有正确结论的序号是( )A. ①B. ①③C. ②③D. ①②③8. 把函数y =f(x)图像上所有点的横坐标缩短到原来的12倍，纵坐标不变，再把所得曲线向右平移π3个单位长度，得到函数y =sin(x −π4)的图像，则f(x)=( )A. sin(x 2−7π12)B. sin(x 2+π12)C. sin(2x −7π12)D. sin(2x +π12)9. 为了得到函数y =sin (2x −π3)的图象，只需把函数y =sin (2x +π6)的图象( ) A. 向左平移π4个单位长度 B. 向右平移π4个单位长度 C. 向左平移π2个单位长度D. 向右平移π2个单位长度10. 先把函数f(x)=sin (x −π6)的图象上各点的横坐标变为原来的12(纵坐标不变)，再把新得到的图象向右平移π3个单位，得到y =g(x)的图象，当x ∈(π4,3π4)时，函数g(x)的值域为( )A. (−√32,1]B. (−12,1]C. (−√32,√32)D. [−1,0)11. 要得到函数y =2cos(x2+π6)sin(π3−x2)−1的图象，需将y =12sinx +√32cosx 的图象( ) A. 向左平移π4个单位长度 B. 向右平移π4个单位长度 C. 向左平移π2个单位长度D. 向右平移π2个单位长度二、多选题（本大题共2小题，共10分）12. (多选)下列四种变换方式，其中能将y =sinx 的图象变为y =sin(2x +π4)的图象的是( ) A. 向左平移π4个单位长度，再将横坐标缩短为原来的12 B. 横坐标缩短为原来的12，再向左平移π8个单位长度 C. 横坐标缩短为原来的12，再向左平移π4个单位长度 D. 向左平移π8个单位长度，再将横坐标缩短为原来的1213. 将函数y =cos (2x +π3)的图象向左平移π4个单位长度得到函数f(x)图象，则( )A. y =sin (2x +π3)是函数f(x)的一个解析式 B. 直线x =7π12是函数f(x)图象的一条对称轴 C. 函数f(x)是周期为π的奇函数D. 函数f(x)的递减区间为[kπ−5π12,kπ+π12](k ∈Z)三、填空题（本大题共4小题，共20分）14. 函数y =sin(2x −π4)图象上所有点的横坐标保持不变，将纵坐标 (填“伸长”或“缩短”)为原来的 倍，将会得到函数y =3sin(2x −π4)的图象．15. 函数y =sin(2x +π3)的图象可由y =cos(2x +π4)的图象 得到．16. 函数y =cos(2x +φ)(−π≤φ<π)的图象向右平移π2个单位后，与函数y =sin(2x +π3)的图象重合，则φ= ．17. 若函数f(x)=32sin2x −3√32cos2x 的图象为C ，则下列结论中正确的序号是 ．①图象C 关于直线x =11π12对称； ②图象C 关于点(2π3,0)对称；③函数f(x)在区间(−π12,5π12)内不是单调的函数；④由y =3sin2x 的图象向右平移π3个单位长度可以得到图象C ． 四、解答题（本大题共1小题，共12分）18. (本小题12分)把函数y =f(x)的图象上的各点向右平移π6个单位长度，然后把横坐标伸长到原来的2倍，再把纵坐标缩短到原来的23，所得图象的解析式是y = 2sin(12x +π3)，求f(x)的解析式．答案和解析1.解：∵y =sin⁡(2x −π3)+1=sin2(x −π6)+1，∴把y =sin2x 的图象上所有的点向右平移π6个单位长度，再向上平移1个单位长度 即可得到函数y =sin(2x −π3)+1的图象．故选A ．2.解：函数y =sin(ωx +π3)的图象向右平移π6个单位后，可得函数y =sin [ω(x −π6)+π3]的图象，再根据所得函数的图象与函数y =cosωx 的图象重合，∴π3−ω⋅π6=2kπ+π2，k ∈Z ， ∴当k =0时，ω=−1．故选A ．3.解：将函数y =sin(x −π6)的图象横坐标变为原来的13，纵坐标不变即可得到函数y =sin(3x −π6)的图象．故选C ．4.解：由sin2x =cos⁡(2x −π2)=cos⁡[2(x −π3)+π6]，所以函数y =sin2x 的图象可由函数y =cos(2x +π6)的图象向右平移π3个长度单位，故选D ． 5.解：将函数y =sin(4x −π3)图象上的横坐标伸长为原来的2倍即可得到y =sin(2x −π3)的图象．故选A ．6.解：把函数y =sin(2x −π4)的图象向左平移π8个单位长度，得到y =sin[2(x +π8)−π4]=sin2x 为奇函数，故选A ．7.解：因为f(x)=sin(x +π3)，①由周期公式可得，f(x)的最小正周期T =2π，故①正确； ②f(π2)=sin(π2+π3)=sin 5π6=12，不是f(x)的最大值，故②错误；③根据函数图象的平移法则可得，函数y =sinx 的图象上的所有点向左平移π3个单位长度，可得到函数y =f(x)的图象，故③正确．故选：B ．8.解：∵把函数y =f(x)图像上所有点的横坐标缩短到原来的12倍，纵坐标不变，再把所得曲线向右平移π3个单位长度，得到函数y =sin(x −π4)的图像，∴把函数y =sin(x −π4)的图像，向左平移π3个单位长度，得到y =sin(x +π3−π4)=sin(x +π12)的图像；再把图像上所有点的横坐标变为原来的2倍，纵坐标不变，可得f(x)=sin(12x +π12)的图像．故选：B ．9.解：y =sin (2x +π6)=sin 2(x +π12)，y =sin (2x −π3)=sin 2(x −π6)，所以将y =sin (2x +π6)的图象向右平移π4个单位长度得到y =sin (2x −π3)的图象．故选B ． 10.解：把函数f(x)=sin(x −π6)的图象上各点的横坐标变为原来的12倍(纵坐标不变)，可得函数y =sin(2x −π6)的图象；再把新得到的图象向右平移π3个单位，得到y =g(x)=sin[2(x −π3)−π6]=sin(2x −5π6)的图象．当x ∈(π4,3π4)时，2x −5π6∈(−π3,2π3)， 故当2x −5π6趋于−π3时，g(x)的最小值趋于−√32，当2x −5π6=π2时，g(x)取得最大值为1，故选：A ．11.解：y =2cos(x 2+π6)sin(π3−x 2)−1=2cos(x 2+π6)sin[π2−(π6+x 2)]−1=2cos(x 2+π6)cos(π6+x2)−1=cos(x +π3)，又y =12sinx +√32cosx = sin(x +π3)向左平移π2个单位长度y =sin(x +π3+π2)=cos(x +π3)，故选C ．12.解：将y =sinx 的图象先向左平移π4个单位长度，再将横坐标缩短为原来的12或先横坐标缩短为原来的12，再向左平移π8个单位长度都可以得到y =sin(2x +π4)的图象．故选AB13.解：由题意，函数y =cos (2x +π3)的图象向左平移π4个单位长度得到函数f(x)=cos⁡[2(x +π4)+π3]=cos⁡(2x +5π6)，于是下面对各选项进行分析： 对A ，因为y =cos⁡(2x +5π6)=−sin⁡(2x +π3)，x ∈R ，故A 不正确；对B ，因为f(x)=cos⁡(2x +5π6)，根据余弦函数图像性质可知，其对称轴为2x +5π6=kπ,k ∈Z ，即x =kπ2−5π12,k ∈Z ，取k =2，可知x =7π12是函数f (x )图象的一条对称轴，故B 正确；对C ，因为f(x)=cos⁡(2x +5π6)，其最小正周期为T =2π2=π，又f(0)=cos⁡(5π6)=−√32≠0，可知C 不正确；对D ，因为f(x)=cos⁡(2x +5π6)，根据余弦函数图像性质可知，令2kπ⩽2x +5π6⩽2kπ+π， k ∈Z ，即得单调递减区间为x ∈[kπ−5π12,kπ+π12](k ∈Z)，故D 正确．故选BD ．14. 解：A =3>1，故函数y = sin(2x −π4)图象上所有点的横坐标保持不变，将纵坐标伸长为原来的3倍即可得到函数y =3sin(2x −π4)的图象．15.解：y =cos(2x +π4)=sin(2x +π4+π2)=sin(2x +3π4)， 将函数y =sin(2x +3π4)的图象向右平移5π24个单位长度可得函数y =sin(2x +π3)的图象．16.解：将y =cos (2x +φ)的图象向右平移π2个单位长度后，得到y =cos [2(x −π2)+φ]的图象，化简得y =−cos (2x +φ)，又可变形为y =sin (2x +φ−π2)．由题意可知φ−π2=π3+2kπ(k ∈Z )，所以φ=5π6+2kπ(k ∈Z )，结合−π≤φ<π，知φ=5π6．故答案为5π6．17.解：f(x)=32sin2x −3√32cos2x =3sin(2x −π3)，因为当x =11π12时，f(x)=3sin(2×11π12−π3)=3sin3π2=−3，所以直线x =11π12是图象C 的对称轴，故①正确；因为当x =2π3时，f(x)=3sin(2×2π3−π3)=0，所以函数图象C 关于点(2π3,0)对称，故②正确；令−π2≤2x −π3≤π2，解得x ∈[−π12,5π12]，所以函数的一个增区间是[−π12,5π12]，因此f(x)在区间(−π12,5π12)上是增函数，故③不正确； 由y =3sin2x 的图象向右平移π3个单位，得到的图象对应的函数表达式为 y =3sin2(x −π3)=3sin(2x −2π3)，故④不正确．故答案为：①②． 18.解：y =2sin(12x +π3)的图象的纵坐标伸长为原来的32，得到y = 3sin(12x +π3);再将其横坐标缩短到原来的12，得到y =3sin(x +π3);再将其图象上的各点向左平移π6个单位长度，得到y =3sin(x +π2)=3cosx ，故f(x)=3cosx.。

2019年七年级下册数学单元测试题第二章图形的变换一、选择题1．三个等圆圆心分别在正三角形ABC的三个顶点上，此图案可看作其中的一个圆绕正三角形ABC的中心旋转得到的，其旋转角为（）A．60°B．80°C．45°D．120°解析：D2．下列时刻在电子表显示中成轴对称的为（）A．06：01：O6 B．15：11：21 C．08：10：13 D．04：08：O4答案：B3．一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时，它所看到的全身像是（）答案：A4．平移前有两条直线互相垂直，那么这两条直线平移后（）A．互相平行B．互相垂直C．相交但不垂直D．无法确定答案：B5．如图所示，绕旋转中心旋转60°后能与自身重合的是（）答案：A6．将如图①所示的火柴棒房子变成如图②所示的火柴棒房子，需要旋转两根火柴，请你指出按逆时针旋转的火柴棒是（）A．a，b B．b，c C． b，d D．C，d答案：B7．如图所示，将一张正方形纸片沿图①中虚线剪开后，能拼成图②中的四个图形，则其中轴对称图形的个数是（）A．1个B．2个C．3个D．4个答案：C8．将一圆形纸片对折后再对折，得到右图，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是（）答案：C9．如图，0是正六边形ABCDE的中心，下列图形可由△OBC平移得到的是（）A．△OAF B．△OAB C．△OCD D．△OEF答案：A10．下列各组图形，可以经过平移变换由一个图形得到另一个图形的是（）A． B． C． D．答案：A11．小明的运动衣号在镜子中的像是，则小明的运动衣号码是（）A． B． C． D．答案：A12．下列图形中：角、线段、直角三角形、等边三角形、长方形，其中一定是轴对称图形的有（）A．2个B．3个C．4个D．5个答案：C13．下列说法中正确的是（）A．两个全等三角形一定成轴对称B．两个成轴对称的三角形一定是全等的C．三角形的一条中线把三角形分成以中线为对称轴的两个图形D．三角形的一条高把三角形分成以高线为对称轴的两个图形答案：B14．一个三角形的三边长分别是5，6，7，另一个三角形和它是相似图形，其最长边长为10．5，则另一个三角形的周长是（）A．23 B．27 C．29 D．33答案：B15．用一个 5倍的放大镜去观察一个三角形，对此，四位同学有如下说法. 甲说：三角形的每个内角都扩大到原来的5倍；乙说：三角形每条边都扩大到原来的5倍；丙说：三角形的面积扩大到原来的5倍；丁说：三角形的周长扩大到原来的5倍.上述说法中，正确的个数是（）A．1 B．2 C．3 D． 3答案：B16．如图，把边长为2的正方形的局部进行图①～图④的变换，拼成图⑤，那么图⑤的面积是（）A．18 B．16 C．12 D．8答案：B二、填空题17．如图，线段A′B°是线段AB经一次旋转变换得到的，旋转的角度是 .解析：130°18．以△ABD 的边AB、AD为边分别向外作正方形ACEB和ADGF，连接DC、BF.利用旋转的观点，在此题中，△ADC绕着点逆时针旋转度可以得到△ .解析：A ,90, ABF19．如图,把五边形ABCD Ｏ变换到五边形CDEFO,应用了哪种图形变换?请完整地叙述这个变换: ．解析：五边形ABCD Ｏ绕着点O 顺时针方向旋转90°得到五边形CDEFO20．观察图形：其中是轴对称图形的是 (填序号) .解析：①②③④⑥21．直角三角形作相似变换，各条边放大到原来的3倍，则放大后所得图形面积是原图形面积的 倍．解析：922．如图，由三角形ABC 平移得到的三角形有 个．解析：523．用笔尖扎重叠的纸得到如图成轴对称的两个图案，在图中找出：(1)两对对应点 ， ；(2)两组对应线段 ， ；(3)两组对应角 ， ．解析：略24．轴对称图形和轴对称的区别在于前者是对 个图形而言的，而后者是对 个图形而言的．解析：1，2三、解答题25．如图所示，在方格纸上作下列相似变换：(1)把图①中三角形的每条边放大到原来的3倍；(2)把图②中H 的每条边缩小到原来的12．解析：略26．如图所示的轴对称图形的对称轴都不止一条，请把它们都画出来．解析：略27．如图所示，其中的图案是小树的一半，以树干为对称轴画出小树的另一半．解析：略28．如图所示，历史上最有名的军师诸葛孔明，率精兵与司马仲对阵，孑L明一挥羽扇．军阵瞬时由图①变为图②．其实只移动了其中3“骑”而已，请问如何移动?解析：略29．如图，大正方形的边长为9 cm，阴影部分的宽为1 cm，试用平移的方法求出空白部分的面积．解析：49 cm230．图②、③、④、⑤分别由图①变换而成的，请你分析它们的形成过程．解析：由图①经过连续四次绕圆心顺时针旋转90°得到31．电子跳蚤在数轴上的一点A，第一次从点A0向左平移1个单位到达点A l，第二次由点A l向右平移2个单位到达点A2，第三次由点A2向左平移3个单位到达点A3，第四次由点A3向右平移4个单位到达点A4，…．按以上规律平移了l00次，电子跳蚤处于数轴上的点A100所表示的数恰是2058，则电子跳蚤的初始位置点A0所表示的数是多少?解析：200832．如图所示，已知直线l和m，l⊥m．(1)将折线ABC先以直线l为对称轴作镜面对称变换，然后以直线m为轴，将所得的像作镜面对称，作出经两次变换所得的像；(2)如果要使(1)题图形变换最终的像回到原来的折线ABC，那么应作怎样的图形变换?解析：(1)图略；(2)以直线l与m交点为旋转中心顺时针旋转l80．33．如图，古代有一位将军，他每天都要从驻地M处出发，到河边饮水，再到河岸同侧的军营A处巡视．他该怎样走才能使路程最短?你能帮助这位将军解决这个问题吗？解析：略34．(1)观察如图中①～④中阴影部分构成的图案，请写出这四个图案都具有的两个共同特征:(2)借助图⑤的网格，请设计一个新的图案，使该图案同时具有你在解答(1)中所定的两个共同特征．解析：(1)答案不唯一，可以是：①都是轴对称图形；②面积都等于四个小正方形的面积之和等等；(2)答案不唯一，略35．先阅读下面材料：如图①所示，把△ABC 沿直线BC 平移BC 的长度，可以变到△ECD 的位置； 如图②所示，以BC 为对称轴把△ABC 翻转180°，可以变到△DBC 的位置； 如图③所示，以A 点为旋转中心，把△ABC 旋转l80°，可以变到△AED 的位置．像这样，其中一个三角形是由另一个三角形按平移、轴对称、旋转等方法变成的，这种只改变位置，不改变形状和大小的图形变换，叫做三角形的全等变换．再回答问题：(1)如图④所示，在正方形ABCD 中，E 是AD 的中点，F 是BC 延长线上的一点，且AF=12AB ．则△ABE 变到△ADF 的位置，可通过平移、轴对称、旋转中的哪一种方法?答： ．(2)指出图中的线段BE 与DF 之间的位置关系和大小关系 ．解析：(1)旋转；(2)EB ⊥DF 且EB=DF36．用四块如图①所示的瓷砖拼成一个正方形图案，使拼成的图案成一个轴对称图形(如图②)．请你分别在图③、图④中各画一种与图②不同的拼法，要求两种拼法各不相同，且是轴对称图形．解析：略37．如图所示，有一条小船，(1)若把小船平移，使点A 平移到点B ，请你在图中画出平移后的小船；(2)若该小船先从点A 航行到达岸边l 的点P 处补给后再航行到点B ，但要求航程最短，试在图中画出点P 的位置．解析：略38．如图请用三种方法，在已知图案上再添上一个小正方形后，使其成为轴对称图形，并画出对称轴.解析：略．39．如图，（1）在方格纸上作下列相似变换：把△ABC 的每条边扩大到原来的2倍；(2）放大后的图形的周长是原图形周长的多少倍？(3）放大后的图形的面积是原图形面积的多少倍？方方方解析：（1）略，（2）2，（3）440．在日常生活中有许多物体旋转现象，如钟表上的秒针在不停地转动、电风扇的叶片转动等，请你再举出一些其他有关旋转的例子．解析：略。