ch4-信息论与编码技术(MATLAB实现)-朱春华-清华大学出版社

《信息论》实验指导书—-应用M A T L A B软件实现-CAL-FENGHAI.-(YICAI)-Company One1《信息与编码理论》上机实验指导书———————应用MATLAB软件实现UPC通信工程系前言本实验系列是采用MATLAB软件，主要针对《信息论基础》课程中的相关内容进行的实验。

MATLAB是一完整的并可扩展的计算机环境，是一种进行科学和工程计算的交互式程序语言。

它的基本数据单元是不需要制定维数的矩阵，它可直接用于表达数学的算式和技术概念，解决同样的数值计算问题，使用MATLAB要比使用Basic、Fortran和C语言等提高效率许多倍。

MATLAB还是一种有利的教学工具，在大学的线性代数课程以及其它领域的高一级课程的教学中，已称为标准的教学工具。

该指导书共安排了4个实验，现就一些情况作简要说明：各实验要求学生在MATLAB系统上尽量独立完成，弄懂。

实验内容紧扣课程教学内容的各主要基本概念，希望同学们在完成每个实验后，对所学的内容起到巩固和加深理解的作用。

每个实验做完后必须交一份实验报告。

恳请各位实验老师和同学在实验中提出宝贵意见，以利于以后改进提高。

目录实验一离散信源及其信息测度 (3)实验二离散信道及其容量 (6)实验三无失真信源编码 (8)实验四有噪信道编码 (10)附录部分常用MATLAB命令 (12)实验一 离散信源及其信息测度一、[实验目的]离散无记忆信源是一种最简单且最重要的信源，可以用完备的离散型概率空间来描述。

本实验通过计算给定的信源的熵，加深对信源及其扩展信源的熵的概念的理解。

二、[实验环境]windows XP,MATLAB三、[实验原理]信源输出的各消息的自信息量的数学期望为信源的信息熵，表达式如下 1()[()]()log ()qi i i H X E I xi p x p x ===-∑信源熵是信源的统计平均不确定性的描述，是概率函数()p x 的函数。

信息论实验报告姓名胡小辉班级电子信息工程0902 学号 **********1.实验目的1、掌握哈夫曼编码、费诺编码、汉明码原理；2、熟练掌握哈夫曼树的生成方法；3、学会利用matlab、C语言等实现Huffman编码、费诺编码以及hamming编码。

2.实验原理Huffman编码：哈夫曼树的定义：假设有n个权值，试构造一颗有n个叶子节点的二叉树，每个叶子带权值为wi，其中树带权路径最小的二叉树成为哈夫曼树或者最优二叉树；实现Huffman编码原理的步骤如下：1. 首先将信源符号集中的符号按概率大小从大到小排列。

2. 用0和1表示概率最小的两个符号。

可用0表示概率小的符号，也可用1表示概率小的符号，但整个编码需保持一致。

3. 将这两个概率最小的符号合并成一个符号，合并符号概率为最小概率之和，将合并后的符号与其余符号组成一个N-1的新信源符号集，称之为缩减符号集。

4. 对缩减符号集用步骤1,2操作5. 以此类推，直到只剩两个符号，将0和1分别赋予它们。

6. 根据以上步骤，得到0,1赋值，画出Huffman码树，并从最后一个合并符号回朔得到Huffmaan编码。

费诺编码：费诺编码的实现步骤：1、将信源消息符号按其出现的概率大小依次排列：。

2、将依次排列的信源符号按概率值分为两大组，使两个组的概率之和近似相同，并对各组赋予一个二进制码元“0”和“1”。

3、将每一大组的信源符号再分为两组，使划分后的两个组的概率之和近似相同，并对各组赋予一个二进制符号“0”和“1”。

4、如此重复，直至每个组只剩下一个信源符号为止。

5、信源符号所对应的码字即为费诺码。

hamming编码：若一致监督矩阵H 的列是由不全为0且互不相同的所有二进制m(m≥2的正整数)重组成，则由此H矩阵得到的线性分组码称为[2m-1,2m-1-m，3]汉明码。

我们通过（7，4）汉明码的例子来说明如何具体构造这种码。

设分组码（n，k）中，k = 4，为能纠正一位误码，要求r≥3。

信息论与编码课程作业_huffman编码的matlab_实现信息论与编码课程作业——霍夫曼编码求信源熵和存储前后的信息量的变化一：设计目的：1、学习离散信源平均信息量的计算方法。

2、理解和掌握huffman 编码的基本原理，实现对信源符号的huffman 编码3、熟悉 Matlab 编程；二：设计原理和思路1.信源熵的计算：公式： 21()log a I a p = Matlab 实现：I=log2(1/p) 或I=-log2(p) 熵（平均自信息）的计算公式22111()log log qq i i i i i i H x p p p p ====-∑∑Matlab 实现：HX=sum(-x.*log2(x))；或者h=h-x(i)*log2(x(i));2.霍夫曼编码原理;分为两步，首先是码树形成过程：对信源概率进行合并形成编码码树。

然后是码树回溯过程：在码树上分配编码码字并最终得到Huffman 编码。

1、码树形成过程：将信源概率按照从小到大顺序排序并建立相应的位置索引。

然后按上述规则进行信源合并，再对信源进行排序并建立新的位置索引，直到合并结束。

在这一过程中每一次都把排序后的信源概率存入矩阵p 中，位置索引存入矩阵m 中。

这样，由排序之后的概率矩阵 p 以及索引矩阵m 就可以恢复原概率矩阵P 了，从而保证了回溯过程能够进行下去。

2、码树回溯过程：在码树上分配编码码字并最终得到Huffman 编码。

从索引矩阵M 的末行开始回溯。

(1) 在p 的末行2元素位置填入0和1。

(2) 根据该行索引1位置指示，将索引1位置的编码（‘1’）填入上一行的第一、第二元素位置，并在它们之后分别添加‘0’和‘1’。

(3) 将索引不为‘1’的位置的编码值（‘0’）填入上一行的相应位置（第3 列）。

(4) 以m的倒数第二行开始向上，重复步骤(1) ～(3)，直到计算至m的首行为止。

三：设计代码：>> clear all;format longdisp(strcat('信息论与编码课程作业——霍夫曼编码求信源熵和存储前后的信息量的变化',13));histgram=zeros(1,255);[c,map]=imread('C:\Documents and Settings\Administrator\桌面\infomation\lenna.bmp');x=rgb2gray(c);[a,b]=size(x);for i=1:afor j=1:bk=x(i,j);histgram(k)=histgram(k)+1;endendf=histgram/a/b;symbols=find(f~=0); %灰度值p=f(symbols); %概率L=length(p);pp=p;%霍夫曼编码m=zeros(L-1,L);for i=1:L-1[p,mark]=sort(p);m(L-i,1:L-i+1)=mark(1:L-i+1);p=[p(1)+p(2),p(3:L),1];endc=cell(L-1,L);c(1,1)={'0'};c(1,2)={'1'};for i=2:L-1;ind=find(m(i-1,:)==1);temp=char(c(i-1,ind));c(i,1)={[temp,'0']};c(i,2)={[temp,'1']};snc=find(m(i-1,:)~=1);for j=3:i+1;con=snc(j-2);c(i,j)=c(i-1,con);endendcodeL=[];averge_long=0;H1=0;disp(strcat('灰度值',32,32,32,'概率',32,32,32,32,32,32,32,32,32,'霍夫曼编码:'));for i=1:L;ind=find(m(L-1,:)==i);code=char(c(L-1,ind));codeLength(i)=length(code);averge_long=averge_long+pp(i)*codeLength(i);H1=H1+pp(i)*log2(1/pp(i));disp(strcat(32,num2str(symbols(i)),32,32,32,num2str(pp(i)),3 2,32, code));enddisp(strcat('信源熵=',num2str(H1),32,32,32,32,'平均码字长度=',num2str(averge_long),32,32,32,32,32,'压缩比=',num2str(8/averge_long)));四：设计运行结果：信息论与编码课程作业——霍夫曼编码求信源熵和存储前后的信息量的变化灰度值概率霍夫曼编码:30 1.5259e-005 101000111100001031 1.5259e-005 101000111100001136 1.5259e-005 101000111100000037 1.5259e-005 101000111100000139 6.1035e-005 1010001111000140 7.6294e-005 1110010101001041 6.1035e-005 0111010111011042 6.1035e-005 0111010111011143 9.1553e-005 1110010101001144 0.00018311 111011101010145 0.00021362 00111101101146 0.00022888 01110101111047 0.00024414 01110101111148 0.00039673 0011110110049 0.00048828 1010001110050 0.00065613 1110010101151 0.00090027 011101011052 0.00086975 001111011153 0.0013123 111001011054 0.0013733 111011101156 0.0018005 01110101057 0.0025177 11010001158 0.0036621 0111111059 0.0033722 0101111060 0.0046539 1100110161 0.0055847 1111010162 0.0061188 001001063 0.0080261 100111064 0.0075226 100001165 0.0083466 101010166 0.0088806 101111167 0.0092773 110011168 0.0095367 110101069 0.0086517 101101070 0.0084229 101011071 0.0075378 100010172 0.0071564 011011173 0.0061493 001001174 0.0056 1111011075 0.0053864 1110110076 0.0045319 1100011177 0.0043488 1011000178 0.0042114 1010111079 0.0039063 1000111180 0.0041199 1010100181 0.0035706 0110101182 0.0039368 1001011083 0.0037537 1000010084 0.003479 0110101086 0.0033417 0101101087 0.0032501 0100110088 0.0034027 0110000189 0.0031128 0011010090 0.0031433 0011110091 0.0036774 0111111192 0.0041046 1010011094 0.0038452 1000111095 0.004364 1011100096 0.0037842 1000110097 0.0037079 1000001198 0.0033722 0101111199 0.0040741 10100001 100 0.0040741 10100010 101 0.0038147 10001101 102 0.0040588 10011111 103 0.0041046 10100111 104 0.004364 10111001 105 0.0048218 11010111 106 0.0052185 11100100 107 0.0049591 11011010 108 0.005188 11100001 109 0.0047455 11010110 110 0.0052032 11100011 111 0.0054474 11110100 112 0.0057526 11111011 113 0.0065308 0100111 114 0.0079346 1001100 115 0.010223 1101111116 0.0095825 1101100 117 0.0089417 1100000 118 0.0086975 1011011 119 0.0081787 1010010 120 0.007782 1001001121 0.0066376 0101011 122 0.0059357 11111111 123 0.0056458 11110111 124 0.0051575 11100000 125 0.0052948 11101001 126 0.005188 11100010 127 0.0059814 0000001 128 0.0058594 11111101 129 0.0065613 0101010 130 0.0062561 0011011 131 0.006897 0110100132 0.0072479 0111011 133 0.0073242 0111110 134135 0.0075226 1000100 136 0.0077515 1001000138 0.008606 1011001139 0.0091095 1100100 140 0.012115 000010141 0.012115 000011142 0.012741 001110143 0.012329 001100144 0.010941 1111001145 0.010147 1101110146 0.0089417 1100001 147 0.0088043 1011101 148 0.0091095 1100101 149 0.010712 1110101150 0.011337 1111100151 0.010513 1110011152 0.012878 010000153 0.012268 001010154 0.013138 010100155 0.012238 001000156 0.012939 010001157 0.012115 000100158 0.012955 010010159 0.012207 000111160 0.011993 000001161 0.013916 011001162 0.012177 000110163 0.012299 001011164 0.0094604 1101001 165 0.0089874 1100010 166 0.0088501 1011110 167 0.0056915 11111010 168 0.0059357 0000000 169 0.0071716 0111001 170 0.0057678 11111100 171 0.0054016 11101111 172 0.0054169 11110001 173 0.0058746 11111110 174 0.0072937 0111100 175 0.0070953 0110110 176177 0.0061035 0001011 178 0.0054016 11110000 179 0.0053864 11101101 180 0.0046692 11010000182 0.0036774 10000000183 0.0033875 01100000184 0.0033264 01011000185 0.0031281 00110101186 0.0035706 01110000187 0.0033264 01011001188 0.0033569 01011011189 0.0036011 01110100190 0.0040436 10011110191 0.0034485 01100010192 0.0036774 10000001193 0.0032654 01001101194 0.0034485 01100011195 0.003006 00010100196 0.0033722 01011100197 0.0036774 10000010198 0.0042419 10110000199 0.0045166 11000110200 0.0041046 10101000201 0.0052643 11101000202 0.0050354 11011011203 0.0045319 11001100204 0.0039825 10011010205 0.0040588 10100000206 0.0039673 10010111207 0.0037537 10000101208 0.0033722 01011101209 0.0026703 111011100210 0.0022125 110100010211 0.0018768 101000110212 0.0015259 000101010213 0.0013428 1110010111214 0.0012665 1110010100215 0.0007782 0011110100216 0.00079346 0011110101217 0.00061035 10100011111218 0.00054932 10100011101219 0.00065613 11101110100220 0.00035095 111011101011 221 0.00033569 111001010101 222 0.00030518 101000111101 223 0.00021362 011101011100 224 0.00016785 1110111010100225 0.00019836 001111011010226 0.00015259 1110010101000227 0.00010681 0111010111010228 6.1035e-005 10100011110010230 3.0518e-005 101000111100110231 1.5259e-005 10100011110011110232 1.5259e-005 10100011110011111233 1.5259e-005 1010001111001110信源熵=7.2193 平均码字长度=7.2492 压缩比=1.1036五：设计新得体会：通过这学期对信息论和编码的学习，以及这次的设计，使我了解了很多东西，也使以前所学的知识得以巩固！，通过这次的设计，进一步学习了离散信源平均信息量、平均码长和压缩比的计算方法。

吉林建筑大学电气与电子信息工程学院信息理论与编码课程设计报告设计题目：哈夫曼编码的分析与实现专业班级：电子信息工程101学生姓名：学号：指导教师：吕卅王超设计时间：2013.11.18－2013.11.29一、设计的作用、目的《信息论与编码》是一门理论与实践密切结合的课程,课程设计是其实践性教学环节之一，同时也是对课堂所学理论知识的巩固和补充。

其主要目的是加深对理论知识的理解，掌握查阅有关资料的技能，提高实践技能，培养独立分析问题、解决问题及实际应用的能力。

通过完成具体编码算法的程序设计和调试工作，提高编程能力，深刻理解信源编码、信道编译码的基本思想和目的，掌握编码的基本原理与编码过程，增强逻辑思维能力，培养和提高自学能力以及综合运用所学理论知识去分析解决实际问题的能力，逐步熟悉开展科学实践的程序和方法二、设计任务及要求通过课程设计各环节的实践，应使学生达到如下要求：1. 理解无失真信源编码的理论基础，掌握无失真信源编码的基本方法；2. 掌握哈夫曼编码/费诺编码方法的基本步骤及优缺点；3. 深刻理解信道编码的基本思想与目的，理解线性分组码的基本原理与编码过程；4. 能够使用MATLAB 或其他语言进行编程，编写的函数要有通用性。

三、设计内容一个有8个符号的信源X ，各个符号出现的概率为：编码方法：先将信源符号按其出现的概率大小依次排列，并取概率最小的字母分别配以0和1两个码元（先0后1或者先1后0，以后赋值固定），再将这两个概率相加作为一个新字母的概率，与未分配的二进制符号的字母重新排队。

并不断重复这一过程，直到最后两个符号配以0和1为止。

最后从最后一级开始，向前返回得到各个信源符号所对应的码元序列，即为对应的码字。

哈夫曼编码方式得到的码并非唯一的。

在对信源缩减时，两个概率最小的符号合并后的概率与其他信源符号的概率相同时，这两者在缩减中的排序将会导致不同码字，但不同的排序将会影响码字的长度，一般讲合并的概率放在上面，12345678,,,,,()0.40.180.10.10.070.060.050.04X x x x x x x x x P X ⎡⎤⎧⎫=⎨⎬⎢⎥⎣⎦⎩⎭这样可获得较小的码方差。

《信息论与编码技术》实验教案一、实验目的1. 理解信息论基本概念，如信息量、信道容量等。

2. 掌握编码技术的基本原理，如Hamming 编码、卷积编码等。

3. 学会使用仿真工具进行信息论与编码技术的实验。

二、实验原理1. 信息论基本概念：信息量、信道容量、误码率等。

2. 编码技术原理：Hamming 编码、卷积编码、解码算法等。

3. 仿真工具的使用：调用相关函数，设置参数，观察实验结果。

三、实验内容1. 实验一：信息量计算与信道容量分析利用仿真工具随机比特序列，计算信息量。

改变信道参数，分析信道容量变化。

2. 实验二：Hamming 编码与解码编写Hamming 编码器和解码器，进行编码和解码操作。

分析误码率与编码位数的关系。

3. 实验三：卷积编码与解码编写卷积编码器和解码器，进行编码和解码操作。

分析误码率与卷积编码器参数的关系。

4. 实验四：不同编码方案性能比较分别使用Hamming 编码和卷积编码对相同长度比特序列进行编码。

比较两种编码方案的误码率和信息传输效率。

5. 实验五：信息论与编码技术在实际应用中的案例分析分析数字通信系统中信息论与编码技术的应用。

了解信息论与编码技术在无线通信、图像传输等领域的应用。

四、实验步骤1. 实验一：信息量计算与信道容量分析随机比特序列，计算信息量。

设置信道参数，观察信道容量变化。

2. 实验二：Hamming 编码与解码编写Hamming 编码器和解码器，进行编码和解码操作。

改变编码位数，分析误码率变化。

3. 实验三：卷积编码与解码编写卷积编码器和解码器，进行编码和解码操作。

改变卷积编码器参数，分析误码率变化。

4. 实验四：不同编码方案性能比较使用Hamming 编码和卷积编码对相同长度比特序列进行编码。

比较两种编码方案的误码率和信息传输效率。

5. 实验五：信息论与编码技术在实际应用中的案例分析分析数字通信系统中信息论与编码技术的应用案例。

了解信息论与编码技术在无线通信、图像传输等领域的应用。

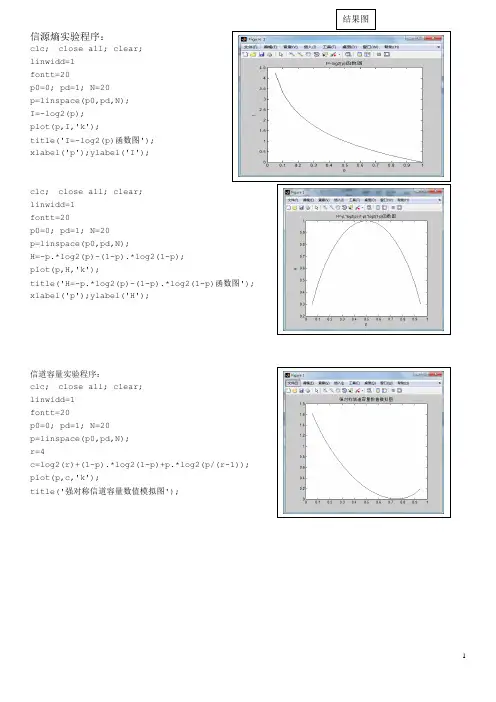
结果图信源熵实验程序：clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);I=-log2(p);plot(p,I,'k');title('I=-log2(p)函数图');xlabel('p');ylabel('I');clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);H=-p.*log2(p)-(1-p).*log2(1-p);plot(p,H,'k');title('H=-p.*log2(p)-(1-p).*log2(1-p)函数图');xlabel('p');ylabel('H');信道容量实验程序：clc; close all; clear;linwidd=1fontt=20p0=0; pd=1; N=20p=linspace(p0,pd,N);r=4c=log2(r)+(1-p).*log2(1-p)+p.*log2(p/(r-1));plot(p,c,'k');title('强对称信道容量数值模拟图');有噪信道编码--费诺不等式程序：结果图clc;close all;clear;r=3;p0=0.00001;pd=0.99999;N=2000;p=linspace(p0,pd,N);q=1-p;H=-p.*log2(p)-q.*log2(q);hold onHH=H+p.*log2(r-1)title('费诺不等式示意图');box onxlabel('PE');ylabel('H(X/Y)');plot(p,HH,'k:')hold onhold onfill([p,1],[HH,0],[0.6,0.6,0.6])stem((r-1)/r,1.59,'--.r')text(0.66,1.6,'最大值')香农编码程序：clc;clear all;close all;p=[0.2 0.19 0.18 0.17 0.15 0.1 0.01]; if sum(p)<1||sum(p)>1error('输入概率不符合概率分布')end[p index]=sort(p,'descend');n=length(p);pa=zeros(n,1);for ii=2:npa(ii)=pa(ii-1)+p(ii-1);endk=ceil(-log2(p));%码字长度计算c=cell(1,n);%生成元胞数组，用来存不同长度的码字for ii=1:nc{ii}='';tmp=pa(ii);for jj=1:k(ii)tmp=tmp*2;if tmp>=1tmp=tmp-1;%c{ii}{jj}='1';c{ii}=[char(c{ii}),'1']; else%c{ii}{jj}='0';c{ii}=[char(c{ii}),'0']; endendend c(index)=c;%换回原来的顺序codelength=zeros(1,n);%码长初始化for ii=1:nfprintf(['第',num2str(ii),'个消息对应为']);disp(c{ii});%显示码字codelength(ii)=length(c{ii});%endn_average=sum(codelength.*p) %平均码长fprintf('平均码长为');disp(n_average);H=-sum(p.*log2(p));fprintf('信源熵');disp(H);x=H/(n_average.*log2(2))fprintf('编码效率');disp(x);figureh=stem(1:n,codelength);%axis([0 n+1 0 n+1]);set(h,'MarkerFaceColor','blue','linewidth',2)实验结果结果图第1个消息对应为000第2个消息对应为001第3个消息对应为011第4个消息对应为100第5个消息对应为101第6个消息对应为1110第7个消息对应为1111110n_average = 3.1400平均码长为 3.1400信源熵 2.6087x =0.8308编码效率 0.8308费诺编码程序：endfor rr=2:2:needgroupnum*2index2=index_aftergroup(rr,:);for ii=index2(1):index2(2)c{ii}=[char(c{ii}),'1']; endendflag=0;index_p=[];for rr=1:needgroupnum*2indextmp=index_aftergroup(rr,:); if(indextmp(2)-indextmp(1)+1>1) flag=1;index_p=[index_p;indextmp]; endendjj=jj+1;endc(index)=c;codelength=zeros(1,N);for ii=1:Nfprintf(['第',num2str(ii),'个消息对应为']);disp(c{ii});codelength(ii)=length(c{ii}); endn_average=sum(codelength.*p)fprintf('平均码长为');disp(n_average);H=-sum(p.*log2(p));fprintf('信源熵');disp(H);x=H/(n_average.*log2(2))fprintf('编码效率');disp(x); figureh=stem(1:N,codelength);axis([0 N+1 0 N+1]);set(h,'MarkerFaceColor','blue','linewidth',2)endfunction index_aftergroup=func_group(p,index_p)index=index_p(1):index_p(2);n=length(index);p0=p(index);sump0=sum(p0);half_sump0=sump0/2;for ii=1:n-1tmpsum=sum(p0(1:ii));if abs(tmpsum-half_sump0)<=abs(tmpsum-half_sump0+p0(ii+1))index_aftergroup=[index(1) index(ii);index(ii+1) index(n)]; break;endendend实验结果结果图第1个消息对应为00第2个消息对应为010第3个消息对应为011第4个消息对应为10第5个消息对应为110第6个消息对应为1110第7个消息对应为1111n_average = 2.7400平均码长为 2.7400信源熵 2.6087x =0.9521编码效率 0.9521霍夫曼编码程序：clc;clear all;close all; A=[0.4 0.2 0.2 0.1 0.1]; A=sort(A,'descend');T=A;[m,n]=size(A);B=zeros(n,n-1);B(:,1)=T;r=B(n,1)+B(n-1,1);T(n-1)=r; T(n)=0;T=sort(T,'descend');t=n-1;for j=2:n-1B(1:t,j)=T(1:t);K=find(T==r);%B(n,j)=K(end);B(n,j)=K(1);r=(B(t-1,j)+B(t,j));T(t-1)=r;T(t)=0;T=sort(T,'descend');t=t-1;endB;ENDc1=sym('[1,0]');ENDc=ENDc1;t=3;d=1;for j=n-2:-1:1for i=1:t-2if i>1&&B(i,j)==B(i-1,j)d=d+1;elsed=1;endB(B(n,j+1),j+1)=-1;temp=B(:,j+1);x=find(temp==B(i,j));ENDc(i)=ENDc1(x(d));endy=B(n,j+1);ENDc(t-1)=[char(ENDc1(y)),'1']; ENDc(t)=[char(ENDc1(y)),'0'];t=t+1;ENDc1=ENDc;endA%排序后的原概率序列ENDc%编码结果for i=1:n[a,b]=size(char(ENDc(i)));L(i)=b;endavlen=sum(L.*A)%平均码长selen=(L-avlen).^2%?mselen=sum((selen).*A)%码长均方差H=-A*(log2(A'))%?P=H/avlen%?figure;subplot(2,1,1)h=stem(1:n,selen);%axis([0 n+1 0 max(selen)+0.1]);set(h,'MarkerFaceColor','blue','lin ewidth',2)xlabel('信源向上排');ylabel('方差值selen');hold onplot(0:n+1,mselen*ones(1,n+2),'r',' linewidth',2);hold offlegend('每个信源码长与平均码长的方差','码长均方差');A=[0.4 0.2 0.2 0.1 0.1];A=sort(A,'descend');T=A;[m,n]=size(A);B=zeros(n,n-1); B(:,1)=T;r=B(n,1)+B(n-1,1);T(n-1)=r;T(n)=0;T=sort(T,'descend');t=n-1;for j=2:n-1B(1:t,j)=T(1:t);K=find(T==r);B(n,j)=K(end);%B(n,j)=K(1);r=(B(t-1,j)+B(t,j));T(t-1)=r;T(t)=0;T=sort(T,'descend');t=t-1;endB;ENDc1=sym('[1,0]');ENDc=ENDc1;t=3;d=1;for j=n-2:-1:1for i=1:t-2if i>1&&B(i,j)==B(i-1,j)d=d+1;elsed=1;endB(B(n,j+1),j+1)=-1;temp=B(:,j+1);x=find(temp==B(i,j));ENDc(i)=ENDc1(x(d));endy=B(n,j+1);ENDc(t-1)=[char(ENDc1(y)),'1'];ENDc(t)=[char(ENDc1(y)),'0'];t=t+1;ENDc1=ENDc;endA%排序后的原概率序列ENDc%编码结果for i=1:n[a,b]=size(char(ENDc(i)));L(i)=b;endavlen=sum(L.*A)%平均码长selen=(L-avlen).^2%?mselen=sum((selen).*A)%码长均方差H=-A*(log2(A'))%?P=H/avlen%?subplot(2,1,2)h=stem(1:n,selen);%axis([0 n+1 0 max(selen)+0.1]);set(h,'MarkerFaceColor','blue','linewidth',2)xlabel('信源向下排');ylabel('方差值selen');hold onplot(0:n+1,mselen*ones(1,n+2),'r','linewidth',2);hold offlegend('每个码长与平均码长的方差','码长均方差');实验结果A = 0.4000 0.2000 0.20000.1000 0.1000ENDc =[ 11, 1, 0, 101, 100]avlen = 1.8000selen = 0.0400 0.6400 0.64001.4400 1.4400mselen =0.5600H =2.1219P =1.1788A =0.4000 0.2000 0.20000.1000 0.1000ENDc =[ 0, 10, 111, 1101, 1100]avlen =2.2000selen = 1.4400 0.0400 0.64003.2400 3.2400mselen =1.3600H =2.1219P =0.9645结果图。

第一章绪论（第一讲）（2课时）主要内容：（1）教学目标（2）教学计划（3）参考书（4）考试问题（5）信息论的基本概念（6）信息论发展简史和现状（7）通信系统的基本模型重点：通信系统的基本模型难点：通信系统的基本模型特别提示：运用说明：本堂课作为整本书的开篇，要交待清楚课程开设的目的，研究的内容，对学习的要求；在讲解过程中要注意结合一些具体的应用实例，避免空洞地叙述，以此激发同学的学习兴趣，适当地加入课堂提问，加强同学的学习主动性。

信息论与编码(Informatic s & Coding)开场白教学目标：本课程主要讲解香农信息论的基本理论、基本概念和基本方法，以及编码的理论和实现原理。

介绍信息的统计度量，离散信源，离散信道和信道容量；然后介绍无失真信源编码、有噪信道编码，以及限失真信源编码等，然后介绍信道编码理论，最后也简单介绍了密码学的一些知识。

教学重点：信息度量、无失真信源编码、限失真信源编码、信道编码的基本理论及实现原理。

教学计划：信息论：约20学时信道编码：约19学时*密码学：约8学时参考书：1．信息论与编码，曹雪虹张宗橙编，北京邮电大学出版社，20012．信息论—基础理论与应用，傅祖芸编著，电子工业出版社，20013．信息理论与编码，姜丹钱玉美编著4．信息论与编码，吴伯修归绍升祝宗泰俞槐铨编著，1987考试问题：第一章绪论信息论的基本概念信息论发展简史和现状通信系统的基本模型§1.1 信息论的基本概念信息论是一门应用近代数理统计方法来研究信息的传输和处理的科学。

在涉及这门课程的具体内容之前，很有必要在引言中，首先放宽视野，从一般意义上描述、阐明信息的基本含意。

然后，再把眼光收缩到信息论的特定的研究范围中，指明信息论的假设前提，和解决问题的基本思路。

这样，就有可能帮助读者，在学习、研究这门课程之前，建立起一个正确的思维方式，有一个正确的思路，以便深刻理解、准确把握以下各章节的具体内容。

信息论与编码技术简介信息论与编码技术是计算机科学与通信工程领域中非常重要的研究方向，对于数字通信、数据压缩、错误检测与纠正等问题具有重要意义。

信息论是研究信息传输、存储和处理的数学理论，而编码技术则是利用信息论的基本原理设计和实现高效的编码方案。

本文将对信息论和编码技术进行介绍，并介绍其中的一位杰出研究者朱春华的贡献。

信息论信息论是由克劳德·香农于1948年提出的，他在论文《通信的数学原理》中系统地提出了信息论的基本概念和理论框架。

信息论主要研究信息传输的性质和限制，以及如何通过编码和解码来实现有效地信息传输。

在信息论中，最基本的概念是信息量。

信息量的单位是比特（bit），表示一条信息所携带的信息量。

信息量与信息的概率分布有关，对于概率为p的事件，其信息量为-log(p)。

这意味着，概率越小的事件所携带的信息量越大。

除了信息量，信息论还研究了其他重要概念，如熵、条件熵、互信息等。

熵是用来描述信息源的不确定性的度量，而条件熵是在已知一些先验信息的情况下，对信息源的不确定性进行度量的。

信息论的理论框架不仅可以用于描述信息的传输和存储，还可以用于优化通信系统的设计。

通过研究信道容量和编码理论，我们可以设计出高效的数字通信系统，以尽可能地提高通信速率和可靠性。

编码技术编码技术是利用信息论的基本原理设计和实现高效的编码方案。

编码技术在数字通信、数据压缩、错误检测与纠正等领域具有重要应用。

在数字通信中，编码技术用于将消息转化为数字信号，并通过信道进行传输。

常用的编码技术有霍夫曼编码、香农-法诺编码等。

这些编码技术通过将常用的消息用较短的码字表示，来提高信息传输的效率。

在数据压缩中，编码技术可以将冗余的信息进行压缩，以减少数据的存储和传输量。

编码技术可以通过去除冗余信息和利用统计特性来实现数据的高效压缩。

错误检测与纠正是编码技术的另一个重要应用领域。

在数据传输过程中，由于信道噪声或其他原因，可能会导致传输数据中出现错误。