锐角三角形函数及应用

锐角三角函数及应用
锐角三角函数是指在直角三角形中，角度小于90度的三角函数，包括正弦函数、余弦函数和正切函数。

这些函数在数学、物理、工程等领域中都有广泛的应用。

正弦函数是指一个角的对边与斜边的比值，即sinθ=对边/斜边。

在三角函数中，正弦函数是最基本的函数之一，它在三角形的计算中有着重要的作用。

例如，在测量高度时，可以利用正弦函数计算出物体的高度。

余弦函数是指一个角的邻边与斜边的比值，即cosθ=邻边/斜边。

余弦函数也是三角函数中的基本函数之一，它在计算角度时有着重要的作用。

例如，在计算机图形学中，可以利用余弦函数计算出两个向量之间的夹角。

正切函数是指一个角的对边与邻边的比值，即tanθ=对边/邻边。

正切函数在三角形的计算中也有着重要的作用。

例如，在测量斜率时，可以利用正切函数计算出斜率的大小。

除了在三角形的计算中，锐角三角函数还有着广泛的应用。

在物理学中，正弦函数和余弦函数可以用来描述波的运动，例如声波和光波。

在工程学中，正弦函数和余弦函数可以用来描述交流电的变化，例如电压和电流的变化。

在计算机科学中，正切函数可以用来计算图像的旋转和缩放。

锐角三角函数是数学中的重要概念，它们在各个领域中都有着广泛的应用。

掌握锐角三角函数的概念和应用，对于学习数学、物理、工程和计算机科学等领域都有着重要的意义。

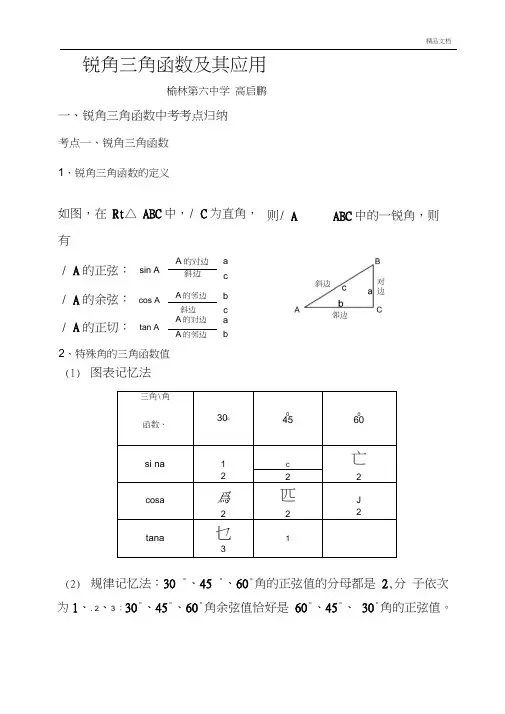
锐角三角函数及其应用榆林第六中学 高启鹏一、锐角三角函数中考考点归纳考点一、锐角三角函数 1、锐角三角函数的定义如图，在 Rt △ ABC 中，/ C 为直角， 有(1) 图表记忆法三角\角 函数、304560si na1 c亡222 cosa爲匹J222tana乜31(2) 规律记忆法：30 °、45 °、60°角的正弦值的分母都是 2,分 子依次为1、. 2、3 ；30°、45°、60°角余弦值恰好是 60°、45°、 30°角的正弦值。

/ A 的正弦： sin A A 的对边a 斜边 c / A 的余弦： cos A A 的邻边b 斜边c / A 的正切： tan AA 的对边a A 的邻边b2、特殊角的三角函数值则/ A ABC 中的一锐角，则（3）口诀记忆法口诀是：“一、二、三，三、二、一，三、九、二十七，弦比二，切比三，分子根号不能删.”前三句中的1，2，3；3，2，1；3，9，27,分别是30°，45 °，60°角的正弦、余弦、正切值中分子根号内的值.弦比二、切比三是指正弦、余弦的分母为2，正切的分母为3.最后一句，讲的是各函数值中分子都加上根号，不能丢掉.如tan60 °二旦 ,3，tan45 =— 1 .这种方法有趣、简单、3 3易记.考点二、解直角三角形1、由直角三角形中的已知元素求出其他未知元素的过程，叫做解直角三角形。

2、解直角三角形的类型和解法如下表：考点二、锐角二角函数的实际应用（咼频考点）仰角、俯角、坡度（坡比）、坡角、方向角仰角、俯角在视线与水平线所成的锐角中，视线在水平线上方的角叫仰角，视线在水平线下方的角叫俯角。

坡度（坡比）、坡角坡面的铅直高度h和水平宽度1的比叫坡度（坡比），用字母i表示；坡面与水平线的夹角叫坡角,i tan Pl指北或指南的方向线与目标方向线所成的小于90°的锐角叫做方向角.注意：东北方向指北偏东45方向，东南方向指南偏方向角东45 方向，西北方向指北偏西45方向，西南方向指南偏西45°方向.我们一般画图的方位为上北下南，左西右东.二、锐角三角函数常见考法（一）、锐角三角函数以选择题的形式出现.例1、（2016?陕西）已知抛物线y二-x2-2x+3与x轴交于A B两点，将这条抛物线的顶点记为C,连接AG BC则tan / CAB的值为（）A.丄B . ■- C •」D ■ 2【考点】抛物线与x轴的交点；锐角三角函数的定义.CD：【解析】先求出A B、C坐标，作CDL AB于D,根据tan / ACD=-即可计算.o【解答】解：令y=0,则-x —2x+3=0,解得x=—3或1,不妨设A （—3,0）,B (1, 0),2 2• y二—x - 2x+3=—( x+1) +4,「•顶点C (- 1, 4),如图所示，作CDL AB于D.故答案为D.（二）、锐角三角函数以填空题的形式出现例2、（2016?陕西）请从以下两个小题中任选一个作答，若多选，则按第一题计分.A. —个多边形的一个外角为45°,则这个正多边形的边数是8 .B. 运用科学计算器计算：3.「sin73 ° 52’〜11.9 .（结果精确到0.1 ）【考点】计算器一三角函数；近似数和有效数字；计算器一数的开方；多边形内角与外角.【解析】（1）根据多边形内角和为360°进行计算即可；（2）先分别求得3. 7和sin73 ° 52 '的近似值，再相乘求得计算结果.【解答】解：（1）v正多边形的外角和为360° 二这个正多边形的边数为：360°宁45° =8(2) 3 i sin73 °52’ 〜12.369 x0.961 〜11.9故答案为：8, 11.9例3、（2015?陕西）如图，有一滑梯 AB,其水平宽度AC 为5.3米，铅直高 度BC 为2.8米，则/ A 的度数约为 27.8（用科学计算器计算，结果精【考点】解直角三角形的应用-坡度坡角问题. 【解析】直接利用坡度的定义求得坡角的度数即可. 【解答】 解：T tan / A 」"1〜0.5283 ,AC 5. 3•••/ A=27.8°, 故答案为：27.8 ° .【点评】本题考查了坡度坡角的知识，解题时注意坡角的正切值 等于铅直高度与水平宽度的比值，难度不大.例4、（2014?陕西）用科学计算器计算：一 一；+3tan56 °〜10.02 （结果精确到0.01 ） 计算器一三角函数；计算器一数的开方.先用计算器求出tan56°的值，再计算加减运解：「丨〜5.5678 , tan56 °〜1.4826 , 则-1 +3tan56 °〜5.5678+3 X 1.4826 〜10.02故答案是：10.02 .【点评】 本题考查了计算器的使用，要注意此题是精确到【考点】 【分析】0.01.例5、（2014?陕西）如图，在正方形 ABC ［中, AD=1将厶ABD绕点B 顺时针旋转45 °得到△ A BD ，此时A D 与CD 交于【考点】 旋转的性质【分析】 利用正方形和旋转的性质得出 A D=A E ,进而利用 勾股定理得出BD 的长，进而利用锐角三角函数关系得出 DE 的长 即可.【解答】 解：由题意可得出：/ BDC=45，/ DA E=90° , •••/ DEA =45°,••• A D=A E ,•••在正方形ABCD 中AD=1 • AB=A B=1, • BD=:':, • A D 二；:-1,•••在 Rt △ DA E 中,DE备=2-五故答案为：2-血.【点评】此题主要考查了正方形和旋转的性质以及勾股定理、2~41锐角三角函数关系等知识，得出 A D 的长是解题关键.(三) 、锐角三角函数定义以解答题的形式出现例6、( 12分)(2015?陕西)如图，在每一个四边形 ABC 冲，均有AD// BC ；CDL BC / ABC=60 , AD=8 BC=12(1) 如图①，点M 是四边形ABCDi AD 上的一点，则厶BMC 勺面积为 24「；; (2) 如图②，点N 是四边形ABCD* AD 上的任意一点，请你求出△ BNC 周长 的最小值；(3) 如图③，在四边形ABCD 勺边AD 上，是否存在一点P,使得cos / BPC 的 值最小？若存在，求出此时cos / BPC 勺值；若不存在，请说明理由.【考点】四边形综合题.. 【专题】综合题.【解析】(1)如图①，过A 作AE ! BC 可得出四边形AECF 为矩形，得到EC=ADBE 二B G EC 在直角三角形 ABE 中，求出AE 的长，即为三角形 BMC 勺高，求 出三角形BMC 面积即可；(2) 如图②，作点C 关于直线AD 的对称点C ,连接C N, C D, C B 交AD 于点 N ,连接 CN ，贝卩 BN+NC 二BN+NO BC =BN +CN ，可得出厶 BNC 周长的最小值BN C 的周长=BN +CN +BC 二BC+BC 求出即可；(3) 如图③所示，存在点P,使得cos /BPC 的值最小，作BC 的中垂线PQ 交BC 于点Q 交AD 于点P,连接BP CP 作厶BPC 的外接圆Q 圆O 与直线PQ 交于点N,则PB=PC 圆心0在PN 上，根据AD 与BC 平行，得到圆0与AD 相AD圈②图①ACc图③切，根据PQ=DC判断得到PQ大于BQ可得出圆心0在BC上方，在AD上任取一点P',连接P‘ B, P C, P‘ B交圆0于点M连接MC可得/ BPC= / BM OZ BP C,即/ BPC最小，cos/ BPC的值最小，连接0B求出即可.【解答】解：(1)如图①，过A作AE±BC二四边形AEC助矩形，••• EC=AD=8 BE二B G EC=12- 8=4,在Rt△ ABE中, / ABE=60 , BE=4•AB=2BE=8 AE=：・，二=4 二则S A BM千BC? AE=24 -;;故答案为：24. -；；(2)如图②，作点C关于直线AD的对称点C,连接C N, C D, C B交AD于点N,连接CN，贝卩BN+NC二BN+NO BC =BN +CN ,•△ BNC周长的最小值为△ BN C的周长=BN +CN +BC=BC +BCv AD// BC AE! BC / ABC=60 ,•过点A 作AE! BC 则CE=AD=8•BE=4 AE=B? tan60 ° 二酣1,•CC =2CD=2AE=8,v BC=12•BC=血/+防2=4阿,•△ BNC周长的最小值为4 1+12;(3)如图③所示，存在点P,使得cos/ BPC的值最小，作BC的中垂线PQ交BC于点Q交AD于点P,连接BP, CR作厶BPC的外接精品文档圆Q 圆0与直线PQ交于点N,贝S PB=PC圆心0在PN上，v AD// BC•••圆0与AD相切于点P,v PQ=DC=4>6,•PQ> BQ•/BPG 90°，圆心O在弦BC的上方，在AD上任取一点P',连接P‘ B, P‘ C, P‘ B交圆0于点M连接MC•••/ BPC y BM OZ BP C,•/ BPC最大，cos / BPC的值最小，连接0B 贝卩/ BON=/BPN/ BPCv 0B=0P=4 - 0Q在Rt△ B0C中，根据勾股定理得：0Q+62二（砸-0Q 2,解得：0Q二:；，2•0B二：,2•cos / BPC二co/ B0Q==l,P厂则此时cos/ BPC的值为一.【点评】此题属于四边形综合题，涉及的知识有：勾股定理，矩形的判定与性质，对称的性质，圆的切线的判定与性质，以及锐角三角函数定义，熟练掌握定理及性质是解本题的关键.例7、(10分)(2014年陕西省)已知抛物线C: y二-x2+bx+c经过A (- 3, 0)和B (0, 3)两点，将这条抛物线的顶点记为M它的对称轴与x轴的交点记为N.(1)求抛物线C的表达式；(2)求点M的坐标；(3)将抛物线C平移到C,抛物线C的顶点记为M',它的对称轴与x轴的交点记为N'.如果以点M N M、N为顶点的四边形是面积为16的平行四边形，那么应将抛物线C怎样平移？为什么？新课标xk b1. c om【考点】二次函数图象与几何变换；二次函数的性质；待定系数法求二次函数解析式；平行四边形的性质.菁优网版权所有【分析】(1)直接把A(- 3, 0)和B(0, 3)两点代入抛物线y二-x2+bx+c, 求出b, c 的值即可；(2)根据(1)中抛物线的解析式可得出其顶点坐标；(3)根据平行四边形的定义，可知有四种情形符合条件，如解答图所示.需要分类讨论.【解答】解: (1)V抛物线y二-x2+bx+c经过A (- 3, 0)和B (0, 3)两占J \\、’解得仁2,故此抛物线的解析式为：y二-x2- 2x+3；(2)v由(1)知抛物线的解析式为：y二-x2- 2x+3,•••当x=- 一= - = - 1 时，y=4, xKb 1.C omSa 2X ( -1) ，‘，• M(- 1, 4).（3J由题意，以点MN、M、N为顶点的平行四边形的边MN勺对边只能是M‘ N, •MN/ M N 且MN二M N.•MN NN =16,•NN =4.i ）当M、N M、N为顶点的平行四边形是？ MNN M时，将抛物线C向左或向右平移4个单位可得符合条件的抛物线C ;ii ）当M N M、N为顶点的平行四边形是？ MNMN时，将抛物线C先向左或向右平移4个单位，再向下平移8个单位，可得符合条件的抛物线C . •上述的四种平移，均可得到符合条件的抛物线C .【点评】本题考查了抛物线的平移变换、平行四边形的性质、待定系数法及二次函数的图象与性质等知识点.第（3）问需要分类讨论，避免漏解.例8、(12分)(2014?陕西)问题探究(1)如图①，在矩形ABCD K AB=3 BC=4如果BC边上存在点巳使厶APD 为等腰三角形，那么请画出满足条件的一个等腰三角形△ APD并求出此时BP 的长；(2)如图②，在△ ABC中，/ ABC=60 , BC=12 AD是BC边上的高，E、F分别为边AB AC的中点，当AD=6时，BC边上存在一点Q 使/ EQF=90，求此时BQ 的长；问题解决(3)有一山庄，它的平面图为如图③的五边形ABCDE山庄保卫人员想在线段CD 上选一点M安装监控装置，用来监视边AB现只要使/ AMB大约为60°, 就可以让监控装置的效果达到最佳，已知/ A二/ E=Z D=90°, AB=270m AE=400mED=285m CD=340m问在线段CD上是否存在点M 使/ AMB=60 ? 若存在，请求出符合条件的DM的长，若不存在，请说明理由.A D團①图②團③【考点】圆的综合题；全等三角形的判定与性质；等边三角形的性质；勾股定理；三角形中位线定理；矩形的性质；正方形的判定与性质；直线与圆的位置关系；特殊角的三角函数值.菁优网版权所有【专题】压轴题；存在型.【分析】（1）由于△ PAD是等腰三角形，底边不定，需三种情况讨论，运用三角形全等、矩形的性质、勾股定理等知识即可解决问题.（2）以EF为直径作。

三角形锐角函数三角形是几何学中的重要概念之一，它具有许多重要的性质和特点。

在三角形中，角是一个重要的要素，而锐角是其中一种特殊的角。

本文将探讨三角形锐角函数的概念、性质和应用。

一、锐角的定义在三角形中，锐角是指其角度小于90度的角。

也就是说，锐角的度数在0度到90度之间。

锐角具有许多特点和性质，而三角形锐角函数就是基于这些特点和性质而定义的。

二、三角形锐角函数的定义三角形锐角函数是一类函数，用于描述锐角的各种关系。

常见的三角形锐角函数有正弦函数、余弦函数和正切函数，分别用sin、cos 和tan表示。

这些函数可以帮助我们计算三角形中的各种参数。

三、正弦函数正弦函数是三角形锐角函数中最常用的函数之一。

它表示三角形中某一锐角的对边与斜边之比。

正弦函数的定义如下：sin(θ) = 对边 / 斜边四、余弦函数余弦函数也是三角形锐角函数中常用的函数之一。

它表示三角形中某一锐角的邻边与斜边之比。

余弦函数的定义如下：cos(θ) = 邻边 / 斜边五、正切函数正切函数是三角形锐角函数中另一个常用的函数。

它表示三角形中某一锐角的对边与邻边之比。

正切函数的定义如下：tan(θ) = 对边 / 邻边六、三角形锐角函数的性质三角形锐角函数具有许多重要的性质和关系。

其中一些性质如下：1. 正弦函数的值在-1到1之间，即 -1 ≤ sin(θ) ≤ 1。

2. 余弦函数的值也在-1到1之间，即 -1 ≤ cos(θ) ≤ 1。

3. 正切函数的值可以是任意实数。

七、三角形锐角函数的应用三角形锐角函数在实际应用中具有广泛的应用价值。

它们可以用于解决各种与三角形相关的问题，例如测量高度、距离、角度等。

以下是一些常见的应用场景：1. 在建筑工程中，可以利用三角形锐角函数计算建筑物的高度。

2. 在导航和地理测量中，可以利用三角形锐角函数计算两个位置之间的距离。

3. 在物理学和工程学中，可以利用三角形锐角函数计算物体的运动轨迹和速度。

初中锐角三角函数及应用锐角三角函数是指角度小于90度的三角函数，包括正弦、余弦和正切。

这些函数在数学和物理学中有着广泛的应用。

首先，我们来介绍一下锐角三角函数的定义和性质。

在一个直角坐标系中，对于一个锐角ABC（角A小于90度）, 我们可以定义正弦函数sinA 为点B的纵坐标除以斜边AC的长度，余弦函数cosA 为点B的横坐标除以斜边AC的长度，正切函数tanA 为点B的纵坐标除以横坐标。

其中，sinA、cosA和tanA都是角A的函数。

这些函数有许多重要的性质。

首先，它们的定义域都是锐角的正数集合，即(0,90)。

其次，它们的值域都是(-1,1)，即在定义域内，这些函数的值都在-1到1之间变化。

此外，正弦函数和余弦函数还具有周期性，周期为360度或2π弧度。

也就是说，对于一个锐角A，sin(A+360k) = sinA，cos(A+360k) = cosA，其中k 为整数。

在应用方面，锐角三角函数有着广泛的作用。

首先，它们被广泛应用于三角计算。

例如，我们可以利用正弦定理或余弦定理，通过已知边和角来求解三角形的其他未知边和角。

这在测量、建筑、工程等领域都有着重要的应用。

其次，锐角三角函数在物理学中也有着重要的应用。

例如，对于一个斜抛运动的物体，我们可以利用正弦函数和余弦函数来分析其垂直和水平方向上的运动。

它们可以帮助我们计算物体的落点、飞行时间、最大高度等。

另外，锐角三角函数还与周期函数和图像有着密切的关系。

它们的图像可以通过函数的周期性来得到。

例如，正弦函数的图像是一个周期为2π的曲线，具有对称性和单调性，而余弦函数的图像是一个周期为2π的曲线，也具有对称性和反单调性。

此外，锐角三角函数还与三角恒等式有着重要的联系。

三角恒等式是指对于锐角A和B，成立的恒等关系。

利用三角恒等式，我们可以化简复杂的三角函数表达式，简化计算过程。

总的来说，锐角三角函数是数学中一类重要的函数，具有广泛的应用。

它们不仅在三角计算和几何题目中有着重要作用，还与物理学、周期函数和三角恒等式等有着紧密的联系。

锐角三角函数及应用经典例题锐角三角函数是指在单位圆上，从原点出发，与 x 轴正半轴之间的夹角小于90° 的角的三角函数。

其中包括正弦函数sinα、余弦函数cosα、正切函数tanα，以及它们的倒数函数cscα、secα、cotα。

锐角三角函数在数学中有广泛的应用，尤其在几何、物理以及工程学中涉及到角度测量、距离计算等方面经常用到。

下面我们来看一些经典的例题，以加深对锐角三角函数的理解：例题1：已知在锐角 ABC 中，边长 BC = 5, AC = 13、求角 A 的正弦值 sinA、余弦值 cosA 和正切值 tanA。

解答：由于边长BC=5,AC=13，我们可以根据勾股定理求得边长AB=√(AC^2-BC^2)=12角 A 的正弦值 sinA = BC / AC = 5 / 13，余弦值 cosA = AB / AC = 12 / 13，正切值 tanA = BC / AB = 5 / 12例题2：已知在锐角 ABC 中，角B = 35°，边长 BC = 8、求角 A 的正弦值 sinA、余弦值 cosA 和正切值 tanA。

解答：由于已知角B = 35°，边长 BC = 8，我们可以根据正弦函数的定义求得角 A 的正弦值为 sinA = BC / AC。

由于 sinA = BC / AC，我们可以得到 AC = BC / sinA = 8 /sin(180° - A - B)。

根据余弦定理，可以计算出边长AC = √(AB^2 + BC^2 - 2 * AB * BC * cosB)。

代入已知的B = 55° 和 BC = 8，我们可以求得AC = √(AB^2 +8^2 - 2 * AB * 8 * cos35°)。

我们可以进一步根据余弦函数的定义计算 AB 的值，即 cosA = AB / AC，所以 AB = AC * cosA。

锐角三角函数1. 锐角三角函数的定义：如图所示：在Rt △ABC 中，∠C ＝90°，a ，b ，c 分别是∠A ，∠B ，∠C 的对边。

（1）∠A 的正弦：sinA ＝a cA ∠的对边＝斜边； （2）∠A 的余弦：b cA ∠的邻边＝斜边； （3）∠A 的正切：a bA A ∠∠的对边＝的邻边； （4）∠A 的余切：A b A a ∠∠的邻边＝的对边 （是正切的倒数）。

2.30°，45°，60°角的三角函数值：1sin 302︒=，2sin 452︒=，3sin 602︒=； 3cos302︒=，2cos 452︒=，1cos 602︒=； 3tan 303︒=，tan 451︒=，tan 603︒=。

例题1：求下列各式的值：（1）22cos 60sin 60︒+︒ （2）cos 45tan 45sin 45︒-︒︒3.锐角三角函数之间的关系：（1）平方的关系：22sin cos 1A A +=；（2）商的关系： sin tan cos A A A=; （3）互余两角的三角函数关系：sin(90)cos A A ︒-=，cos(90)sin A A ︒-=。

注意：锐角的正弦和正切值随着角度的增大而增大；锐角的余弦值随着角度的增大而减小；对于锐角A 有0sin 1,0cos 1,tan 0,A A A <<<<>且他们都没有单位。

4.直角三角形的有关性质及判定：（1）直角三角形的性质：①直角三角形两个锐角互余；②直角三角形斜边上的中线等于斜边的一半；③在直角三角形中，如果有一个锐角等于30︒，那么它所对的直角边等于斜边的一半；④在直角三角形中，如果有一条直角边等于斜边的一半，那么它所对的锐角等于30︒；⑤在直角三角形中，两条直角边a ，b 的平方和等于斜边c 的平方，即222a b c +=；⑥1122Rt S ch ab ==（h 为斜边上的高），外接圆半径R ＝2c ＝斜边上的中线，内切圆半径r ＝2a b c +-。

完整版)锐角三角函数超经典讲义锐角三角函数锐角三角函数是三角函数的一种，包括正弦、余弦和正切。

在一个锐角三角形中，锐角的对边、邻边和斜边之间的比例就是锐角三角函数。

具体来说，对于锐角A，其正弦、余弦和正切分别表示为sinA、cosA和XXX。

其中，XXX表示A的对边与斜边的比，cosA表示A的邻边与斜边的比，XXX表示A的对边与邻边的比。

这些符号都是完整的，单独的“sin”没有意义。

在用大写字母表示角度时，一般省略“∠”符号。

在求解锐角三角函数时，关键在于构造以此锐角所在的直角三角形。

例如，在一个直角三角形ABC中，如果已知∠C=90°，cosB=4/5，则AC：BC：AB=3：4：5.另外，需要注意的是，正弦、余弦和正切是实数，没有单位，它们的大小只与角的大小有关，而与所在直角三角形无关。

例1：在矩形ABCD中，E是BC边上的点，AE=BC，DF⊥AE，垂足为F，连接DE。

证明△ABE≌△DFA，并求sin∠EDF的值。

解：首先，连接AC，易得△ABC为等腰直角三角形，∠BAC=45°。

又因为AE=BC，所以△ABE和△ACD相似，即∠ABE=∠ACD，∠XXX∠ADC。

又因为∠ADC=90°，所以∠AEB=90°。

因此，△ABE和△DFA是全等三角形。

接下来，求sin∠EDF的值。

由于∠BAC=45°，所以∠AED=45°。

由于△ABE和△DFA全等，所以∠XXX∠BAE=45°。

因此，sin∠EDF=sin45°=1/√2.例2：在△ABC中，∠A=60°，∠B=45°，AB=8，求△ABC面积（结果可保留根号）。

解：由于∠A=60°，∠B=45°，所以∠C=75°。

根据三角函数的定义，可以得到：sin75°=cos15°=(sin60°cos45°+cos60°sin45°)/2=√6+√2/4cos75°=sin15°=(sin60°cos45°-cos60°sin45°)/2=√6-√2/4因此，△ABC面积为S=(1/2)AB·BC·sin75°=4(√6+√2)。

锐角三角函数 一、锐角三角函数 1、正弦：在△ABC 中，∠C=90°，我们把锐角A 的对边与斜边的叫做∠A 的正弦，记做sinA 。

2、余弦：在△ABC 中，∠C=90°，我们把锐角A 的邻边与斜边的叫做∠A 的余弦，记做cosA 。

3、正切：在△ABC 中，∠C=90°，我们把锐角A 的对边与邻边的叫做∠A 的正切，记做tanA 。

4、余切：在△ABC 中，∠C=90°，我们把锐角A 的邻边与对边的叫做∠A 的余切，记做cotA 。

[注]：0°、30°、45°、60°、90°特殊角的三角函数值二、解直角三角形1、定义：已知边和角（两个，其中必有一边）→所有未知的边和角。

2、依据：①边的关系：222c b a =+；②角的关系：A+B=90°；③边角关系：三角函数的定义。

(注意：尽量避免使用中间数据和除法) [注]：（1）三角形面积公式：111sin sin sin 222S ab C bc A ca B ===. （2）正弦定理 ：2sin sin sin a b cR A B C ===. （3）余弦定理：2222cos a b c bc A =+-;2222cos b c a ca B =+-;2222cos c a b ab C =+-三、实际应用1、仰角：视线在水平线上方的角；俯角：视线在水平线下方的角。

(2)坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。

用字母i 表示，即hi l=。

把坡面与水平面的夹角记作α(叫做坡角)，那么tan hi lα==。

概率一、随机事件和概率 1、 事件的分类：（1）不可能事件：事件一定不会发生 （2）必然事件：事件一定会发生（2）随机事件：事件有可能发生，也有可能不发生2、概率：对于一个事件A ，我们把刻画其发生可能性的大小的数值叫做事件A 的概率，记做：P(A)特点：每次试验结果只有有限个；各种结果出现的可能性相等。

初中数学锐角三角函数知识点锐角三角函数是初中数学中的一个重要知识点。

本文将系统地介绍锐角三角函数的概念、性质和应用。

一、概念1.边长比在直角三角形中，我们可以定义三角函数。

对于锐角三角形，也可以把边长比看作三角函数的定义。

定义如下：- 正弦函数（sin）：指的是对边比斜边的比值，即sinA = 对边AB / 斜边AC。

- 余弦函数（cos）：指的是邻边比斜边的比值，即cosA = 邻边BC / 斜边AC。

- 正切函数（tan）：指的是对边比邻边的比值，即tanA = 对边AB / 邻边BC。

2.三角函数值的取值范围在锐角三角形中，三角函数的取值范围是(0,1)。

具体来说-正弦函数的值在0到1之间变化。

-余弦函数的值在0到1之间变化。

-正切函数的值在0到正无穷之间变化。

二、性质1.互余关系在锐角三角形中，对于同一个角的正弦和余弦函数，它们的数值互为倒数。

即sinA = 1 / cosA，cosA = 1 / sinA。

证明：由定义可知sinA = 对边AB / 斜边AC，cosA = 邻边BC / 斜边AC。

所以sinA / cosA = (对边AB / 斜边AC) / (邻边BC / 斜边AC) = 对边AB / 邻边BC = tanA。

又由于tanA = sinA / cosA，所以sinA = 1 / cosA。

同理可证cosA = 1 / sinA。

2.正切函数的性质在锐角三角形中，正切函数具有以下性质：-任何一个角的正切函数的值是唯一的。

- 对于锐角A和其补角（即90°-A），它们的正切值互为相反数。

（tanA = -tan(90°-A)）。

三、应用锐角三角函数在实际生活和学习中有着广泛的应用，以下是一些常见的应用：1.三角函数在测量中的应用例如，在建筑和工程中，我们经常需要测量高度、角度等，锐角三角函数可以帮助我们计算和测量。

2.角度的计算通过使用正弦函数、余弦函数和正切函数，我们可以根据已知的边长比计算出对应的角度。

锐角三角形的三角函数三角函数是数学中的重要概念，它们在几何、物理学等领域中具有广泛的应用。

其中，锐角三角函数是指以锐角为自变量的三角函数。

本文将介绍锐角三角形的三角函数，并探讨其性质和应用。

一、正弦函数正弦函数是将一个锐角的相对边长度与斜边长度的比值定义为该锐角的正弦。

用符号表示为 sin，其计算公式如下：sin A = 相对边长度 / 斜边长度正弦函数的定义域为(0°, 90°)，值域为[0, 1]。

正弦函数具有周期性，即 sin(A + 180°) = -sinA。

二、余弦函数余弦函数是将一个锐角的邻边长度与斜边长度的比值定义为该锐角的余弦。

用符号表示为 cos，其计算公式如下：cos A = 邻边长度 / 斜边长度余弦函数的定义域为(0°, 90°)，值域为(0, 1]。

余弦函数也具有周期性，即 cos(A + 180°) = -cosA。

三、正切函数正切函数是将一个锐角的相对边长度与邻边长度的比值定义为该锐角的正切。

用符号表示为 tan，其计算公式如下：tan A = 相对边长度 / 邻边长度正切函数的定义域为(0°, 90°)，值域为(0, +∞)。

正切函数也具有周期性，即 tan(A + 180°) = tanA。

四、余切函数余切函数是将一个锐角的邻边长度与相对边长度的比值定义为该锐角的余切。

用符号表示为 cot，其计算公式如下：cot A = 邻边长度 / 相对边长度余切函数的定义域为(0°, 90°)，值域为(0, +∞)。

余切函数也具有周期性，即 cot(A + 180°) = cotA。

五、正割函数和余割函数正割函数是将一个锐角的斜边长度与邻边长度的比值定义为该锐角的正割。

用符号表示为 sec，其计算公式如下：sec A = 斜边长度 / 邻边长度正割函数的定义域为(0°, 90°)，值域为(1, +∞)。

专题12 锐角三角函数及其应用锐角三角函数的定义与运算1．（2022•湖州）如图，已知在Rt△ABC中，∠C＝90°，AB＝5，BC＝3．求AC的长和sin A 的值．2．（2023•金华）计算：（﹣2023）0+﹣2sin30°+|﹣5|．3．（2021•衢州）计算：+（）0﹣|﹣3|+2cos60°．4．（2021•金华）计算：（﹣1）2021+﹣4sin45°+|﹣2|．5．（2021•杭州）计算：sin30°＝．6．（2022•绍兴）（1）计算：6tan30°+（π+1）0﹣．（2）解方程组：．7．（2022•金华）计算：（﹣2022）0﹣2tan45°+|﹣2|+．解直角三角形的应用8．（2021•金华）如图是一架人字梯，已知AB＝AC＝2米，AC与地面BC的夹角为α，则两梯脚之间的距离BC为（）A．4cosα米B．4sinα米C．4tanα米D．米9．（2022•台州）如图1，梯子斜靠在竖直的墙上，其示意图如图2．梯子与地面所成的角α为75°，梯子AB长3m，求梯子顶部离地竖直高度BC．（结果精确到0.1m；参考数据：sin75°≈0.97，cos75°≈0.26，tan75°≈3.73）10．（2022•金华）图1是光伏发电场景，其示意图如图2，EF为吸热塔，在地平线EG上的点B，B′处各安装定日镜（介绍见图3）．绕各中心点（A，A'）旋转镜面，使过中心点的太阳光线经镜面反射后到达吸热器点F处．已知AB＝A'B'＝1m，EB＝8m，EB'＝8 m，在点A观测点F的仰角为45°．（1）点F的高度EF为m．（2）设∠DAB＝α，∠D'A'B'＝β，则α与β的数量关系是．11．（2023•温州）根据背景素材，探索解决问题．测算发射塔的高度背景素材 某兴趣小组在一幢楼房窗口测算远处小山坡上发射塔的高度MN （如图1），他们通过自制的测倾仪（如图2）在A ，B ，C 三个位置观测，测倾仪上的示数如图3所示．经讨论，只需选择其中两个合适的位置，通过测量、换算就能计算发射塔的高度问题解决任务1分析规划选择两个观测位置：点 A 和点 B （答案不唯一） ．获取数据 写出所选位置观测角的正切值，并量出观测点之间的图上距离．任务2 推理计算计算发射塔的图上高度MN ．任务3换算高度楼房实际宽度DE 为12米，请通过测量换算发射塔的实际高度．注：测量时，以答题纸上的图上距离为准，并精确到1mm ．12．（2023•宁波）某综合实践研究小组为了测量观察目标时的仰角和俯角，利用量角器和铅锤自制了一个简易测角仪，如图1所示．（1）如图2，在P点观察所测物体最高点C，当量角器零刻度线上A，B两点均在视线PC上时，测得视线与铅垂线所夹的锐角为α，设仰角为β，请直接用含α的代数式示β．（2）如图3，为了测量广场上空气球A离地面的高度，该小组利用自制简易测角仪在点B，C分别测得气球A的仰角∠ABD为37°，∠ACD为45°，地面上点B，C，D在同一水平直线上，BC＝20m，求气球A离地面的高度AD．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）13．（2023•浙江）图1是某住宅单元楼的人脸识别系统（整个头部需在摄像头视角范围内才能被识别），其示意图如图2，摄像头A的仰角、俯角均为15°，摄像头高度OA＝160cm，识别的最远水平距离OB＝150cm．（1）身高208cm的小杜，头部高度为26cm，他站在离摄像头水平距离130cm的点C处，请问小杜最少需要下蹲多少厘米才能被识别？（2）身高120cm的小若，头部高度为15cm，踮起脚尖可以增高3cm，但仍无法被识别，社区及时将摄像头的仰角、俯角都调整为20°（如图3），此时小若能被识别吗？请计算说明．（精确到0.1cm，参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27，sin20°≈0.34，cos20°≈0.94，tan20°≈0.36）三角函数综合运用14．（2022•温州）如图，在△ABC中，AD⊥BC于点D，E，F分别是AC，AB的中点，O 是DF的中点，EO的延长线交线段BD于点G，连结DE，EF，FG．（1）求证：四边形DEFG是平行四边形．（2）当AD＝5，tan∠EDC＝时，求FG的长．15．（2021•温州）如图，在▱ABCD中，E，F是对角线BD上的两点（点E在点F左侧），且∠AEB＝∠CFD＝90°．（1）求证：四边形AECF是平行四边形；（2）当AB＝5，tan∠ABE＝，∠CBE＝∠EAF时，求BD的长．16．（2022•丽水）如图，已知菱形ABCD的边长为4，E是BC的中点，AF平分∠EAD交CD于点F，FG∥AD交AE于点G．若cos B＝，则FG的长是（）A．3B．C．D．17．（2021•宁波）如图，在矩形ABCD中，点E在边AB上，△BEC与△FEC关于直线EC 对称，点B的对称点F在边AD上，G为CD中点，连结BG分别与CE，CF交于M，N 两点．若BM＝BE，MG＝1，则BN的长为，sin∠AFE的值为．18．（2021•金华）已知：如图，矩形ABCD的对角线AC，BD相交于点O，∠BOC＝120°，AB＝2．（1）求矩形对角线的长；（2）过O作OE⊥AD于点E，连结BE．记∠ABE＝α，求tanα的值．19．（2022•绍兴）如图，AB＝10，点C是射线BQ上的动点，连结AC，作CD⊥AC，CD ＝AC，动点E在AB延长线上，tan∠QBE＝3，连结CE，DE，当CE＝DE，CE⊥DE时，BE的长是．20．（2023•杭州）第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”．如图，在由四个全等的直角三角形（△DAE，△ABF，△BCG，△CDH）和中间一个小正方形EFGH拼成的大正方形ABCD中，∠ABF＞∠BAF，连接BE．设∠BAF＝α，∠BEF＝β，若正方形EFGH与正方形ABCD的面积之比为1：n，tanα＝tan2β，则n＝（）A．5B．4C．3D．221．（2022•金华）一配电房示意图如图所示，它是一个轴对称图形．已知BC＝6m，∠ABC ＝α，则房顶A离地面EF的高度为（）A．（4+3sinα）m B．（4+3tanα）m C．（4+）m D．（4+）m 22．（2021•温州）图1是第七届国际数学教育大会（ICME）会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形OABC．若AB＝BC＝1，∠AOB＝α，则OC2的值为（）A．+1B．sin2α+1C．+1D．cos2α+123．（2021•衢州）图1是某折叠式靠背椅实物图，图2是椅子打开时的侧面示意图，椅面CE与地面平行，支撑杆AD，BC可绕连接点O转动，且OA＝OB，椅面底部有一根可以绕点H转动的连杆HD，点H是CD的中点，F A，EB均与地面垂直，测得F A＝54cm，EB＝45cm，AB＝48cm．（1）椅面CE的长度为cm．（2）如图3，椅子折叠时，连杆HD绕着支点H带动支撑杆AD，BC转动合拢，椅面和连杆夹角∠CHD的度数达到最小值30°时，A，B两点间的距离为cm（结果精确到0.1cm）．（参考数据：sin15°≈0.26，cos15°≈0.97，tan15°≈0.27）24．（2021•金华）如图1是一种利用镜面反射，放大微小变化的装置．木条BC上的点P处安装一平面镜，BC与刻度尺边MN的交点为D，从A点发出的光束经平面镜P反射后，在MN上形成一个光点E．已知AB⊥BC，MN⊥BC，AB＝6.5，BP＝4，PD＝8．（1）ED的长为．（2）将木条BC绕点B按顺时针方向旋转一定角度得到BC′（如图2），点P的对应点为P′，BC′与MN的交点为D′，从A点发出的光束经平面镜P′反射后，在MN上的光点为E′．若DD′＝5，则EE′的长为．25．（2023•绍兴）图1是某款篮球架，图2是其示意图，立柱OA垂直地面OB，支架CD 与OA交于点A，支架CG⊥CD交OA于点G，支架DE平行地面OB，篮筐EF与支架DE在同一直线上，OA＝2.5米，AD＝0.8米．∠AGC＝32°．（1）求∠GAC的度数；（2）某运动员准备给篮筐挂上篮网，如果他站在凳子上，最高可以把篮网挂到离地面3米处，那么他能挂上篮网吗？请通过计算说明理由．（参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62）26．（2023•台州）教室里的投影仪投影时，可以把投影光线CA，CB及在黑板上的投影图象高度AB抽象成如图所示的△ABC，∠BAC＝90°，黑板上投影图象的高度AB＝120cm，CB与AB的夹角∠B＝33.7°，求AC的长．（结果精确到1cm．参考数据：sin33.7°≈0.55，cos33.7°≈0.83，tan33.7°≈0.67）27．（2023•丽水）如图，某工厂为了提升生产过程中所产生废气的净化效率，需在气体净化设备上增加一条管道A﹣D﹣C，已知DC⊥BC，AB⊥BC，∠A＝60°，AB＝11m，CD＝4m，求管道A﹣D﹣C的总长．28．（2022•嘉兴）小华将一张纸对折后做成的纸飞机如图1，纸飞机机尾的横截面是一个轴对称图形，其示意图如图2，已知AD＝BE＝10cm，CD＝CE＝5cm，AD⊥CD，BE⊥CE，∠DCE＝40°．（1）连结DE，求线段DE的长．（2）求点A，B之间的距离．（结果精确到0.1cm．参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）29．（2022•宁波）每年的11月9日是我国的“全国消防安全教育宣传日”，为了提升全民防灾减灾意识，某消防大队进行了消防演习．如图1，架在消防车上的云梯AB可伸缩（最长可伸至20m），且可绕点B转动，其底部B离地面的距离BC为2m，当云梯顶端A在建筑物EF所在直线上时，底部B到EF的距离BD为9m．（1）若∠ABD＝53°，求此时云梯AB的长．（2）如图2，若在建筑物底部E的正上方19m处突发险情，请问在该消防车不移动位置的前提下，云梯能否伸到险情处？请说明理由．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.3）30．（2022•绍兴）圭表（如图1）是我国古代一种通过测量正午日影长度来推定节气的天文仪器，它包括一根直立的标杆（称为“表”）和一把呈南北方向水平固定摆放的与标杆垂直的长尺（称为“圭”），当正午太阳照射在表上时，日影便会投影在圭面上，圭面上日影长度最长的那一天定为冬至，日影长度最短的那一天定为夏至．图2是一个根据某市地理位置设计的圭表平面示意图，表AC垂直圭BC，已知该市冬至正午太阳高度角（即∠ABC）为37°，夏至正午太阳高度角（即∠ADC）为84°，圭面上冬至线与夏至线之间的距离（即DB的长）为4米．（1）求∠BAD的度数．（2）求表AC的长（最后结果精确到0.1米）．（参考数据：sin37°≈，cos37°≈，tan37°≈，tan84°≈）31．（2021•台州）图1是放置在水平地面上的落地式话筒架实物图，图2是其示意图．支撑杆AB垂直于地面l，活动杆CD固定在支撑杆上的点E处．若∠AED＝48°，BE＝110cm，DE＝80cm，求活动杆端点D离地面的高度DF．（结果精确到1cm，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11）32．（2021•宁波）我国纸伞的制作工艺十分巧妙．如图1，伞不管是张开还是收拢，伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC，且AB＝AC，从而保证伞圈D能沿着伞柄滑动．如图2是伞完全收拢时伞骨的示意图，此时伞圈D已滑动到点D'的位置，且A，B，D′三点共线，AD′＝40cm，B为AD′中点．当∠BAC＝140°时，伞完全张开．（1）求AB的长．（2）当伞从完全张开到完全收拢，求伞圈D沿着伞柄向下滑动的距离．（参考数据：sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）。

锐角三角函数与正弦定理余弦定理应用三角函数是数学中一类重要的函数，而锐角三角函数是指与直角三角函数相对应的三角函数，它在解决各种实际问题时发挥着重要的作用。

本文将探讨锐角三角函数及其应用中的正弦定理和余弦定理。

一、锐角三角函数1. 正弦函数在锐角三角函数中，正弦函数（sin）是我们最为熟悉的函数之一。

正弦函数是通过一个锐角对应的直角三角形中的对边与斜边的比值来定义的。

我们用sin表示正弦函数，其中角度表示为θ，那么正弦函数的定义可以表示为：sin(θ) = 对边/斜边正弦函数在几何学和物理学中有广泛的应用，例如在力学领域中，它可以用于描述物体在斜面上的运动。

2. 余弦函数与正弦函数相似，余弦函数（cos）也是锐角三角函数中的一种。

余弦函数是通过一个锐角对应的直角三角形中的邻边与斜边的比值来定义的。

我们用cos表示余弦函数，其中角度表示为θ，那么余弦函数的定义可以表示为：cos(θ) = 邻边/斜边余弦函数也在各个领域中有广泛的应用，比如电路中的交流电信号可以用余弦函数来描述。

二、正弦定理与余弦定理除了锐角三角函数之外，正弦定理和余弦定理也是解决三角形相关问题时常用的定理。

1. 正弦定理正弦定理是用来描述三角形中边与角之间的关系的。

对于一个任意的三角形ABC，其边长分别为a、b、c，对应的角度分别为A、B、C。

那么正弦定理可以表示为：a/sin(A) = b/sin(B) = c/sin(C)正弦定理的应用范围较广，在测量角度时，我们可以利用正弦定理来计算无法直接测量的角度。

2. 余弦定理余弦定理是用来描述三角形中边与角之间的关系的。

对于一个任意的三角形ABC，其边长分别为a、b、c，对应的角度分别为A、B、C。

那么余弦定理可以表示为：c^2 = a^2 + b^2 - 2ab*cos(C)余弦定理的应用非常广泛，特别是在解决三角形的边长和角度之间的关系问题时。

三、锐角三角函数与正弦定理余弦定理的应用在实际问题中，锐角三角函数及其应用通常用于解决各种三角形相关的计算及测量问题。

应用锐角三角函数解实际问题锐角三角函数是数学中一个重要的概念，它能够帮助我们解决日常生活中的实际问题。

本文将从四个方面来讨论锐角三角函数在实际问题中的应用。

首先，锐角三角函数可以解决根据两条边求三角形面积的问题。

设有一个三角形ABC，其中AB=2，BC=3，则可以使用锐角三角函数求解这个三角形的面积。

首先，我们需要根据已知条件计算出三角形ABC的内角度数，即α=60°，可以由两条边求出其它边的长度AC=2.5。

然后，我们可以使用锐角三角函数中的S=1/2absinα公式，来求出三角形ABC的面积，即S=1/2*2*3*sin60°=3.464。

其次，锐角三角函数可以解决根据两个内角和外角求三角形面积的问题。

设有一个三角形ABC，其中A=60°，B=30°，C=90°，则可以使用锐角三角函数求解这个三角形的面积。

首先，我们需要根据已知条件计算出三角形ABC的边长，即AB=2，BC=2，可以由两个内角求出外角的长度AC=3。

然后，我们可以使用锐角三角函数中的S=1/2a bsinα公式，来求出三角形ABC的面积，即S=1/2*2*2*sin90°=2.000。

此外，锐角三角函数还可以用来解决求抛物线焦点距离中心点的问题。

假设有一个抛物线y=-1/4x^2，其中x为横坐标，y为纵坐标，则可以使用锐角三角函数求出抛物线的焦点距离中心点的距离为2。

首先，我们需要根据抛物线的模型求出抛物线的焦点坐标(0,1/2)，然后通过三角函数来求出焦点距离中心点的距离，即a=√(0-1/2)^2+(1/2)^2=√2。

最后，锐角三角函数还可以应用于光学中，用来求解折射率等问题。

假设有一个简单的透镜系统，镜片一边入射面和出射面之间有n条光线，可以使用锐角三角函数求出透镜系统的折射率。

这里，我们可以先分别求出入射面和出射面的角度α1、α2，再用反射率的定义，即n1sinα1=n2sinα2，求出折射率n2。