狂刷37 空间角与距离 (原卷版)

1 专题八 立体几何
狂刷36 空间角与距离
1．如图，在正方体1AC 中，异面直线AC 与1A B 所成的夹角为
A ．30
B ．45
C ．60
D ．90
【答案】C
【解析】在正方体1111ABCD A B C D -中，连接11,CD AD ，则11CD A B ∥，
则异面直线AC 与1A B 所成的角等于直线AC 与1CD 所成的角，即为1ACD ∠，
又由1ACD △为等边三角形，所以160ACD ∠=，即异面直线AC 与1A B 所成的角等于60. 故选C.
【名师点睛】本题主要考查了异面直线所成角的求解，其中解答中根据几何体的结构特征，把异面直线所成的角转化为相交直线所成的角是解答异面直线所成角的关键，着重考查了推理与论证能力，以及转化思想的应用.由题意，在正方体中把异面直线AC 与1A B 所成的角转化成直线AC 与1CD 所成的角，即可求解.
2．在正三棱锥P ABC -中，三条侧棱两两垂直且侧棱长为1，则点P 到平面ABC 的距离为
A ．3
B ．2
C ．33
D ．23。

1 专题八 立体几何
狂刷37 立体几何的综合
1．设m ，n 是两条不同的直线，α，β是两个不同的平面，则下列命题中正确的是
A ．若α⊥β，m ⊥α，则m ∥β
B ．若m ∥α，n ⊂α，则m ∥n
C ．若α∩β=m ，n ∥α，n ∥β，则m ∥n
D ．若α⊥β，且α∩β=m ，点A ∈α，直线AB ⊥m ，则AB ⊥β
【答案】
C
故选C ．
【名师点睛】本题考查的知识点是平面与平面之间的位置关系，直线与平面之间的位置关系，熟练掌握空间线与线，线与面，面与面之间的关系的判定方法及性质定理，是解答本题的关键．对每一个选项逐一判断得解.
2．某几何体的三视图如图所示，则该几何体的各条棱中，最长的棱与最短的棱所在直线所成角的正切值为。

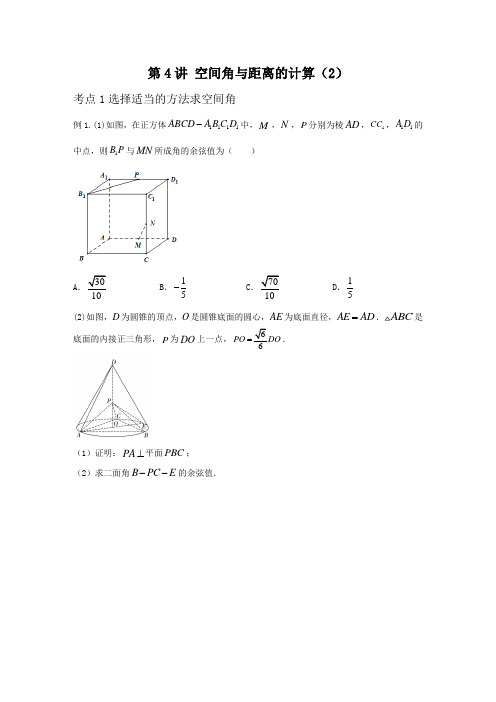
第4讲 空间角与距离的计算（2）考点1选择适当的方法求空间角例1.(1)如图，在正方体1111ABCD A B C D -中，M ，N ，P 分别为棱AD ，1CC ，11A D 的中点，则1B P 与MN 所成角的余弦值为（ ）A ．3010B ．15- C ．7010 D ．15(2)如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE AD =．ABC 是底面的内接正三角形，P 为DO 上一点，6PO DO =．（1）证明：PA ⊥平面PBC ；（2）求二面角B PC E --的余弦值．【跟踪演练】1.(1)当动点P 在正方体1111ABCD A B C D -的棱DC 上运动时，异面直线1D P 与1BC 所成角的取值范围（ ）A ．,64ππ⎡⎤⎢⎥⎣⎦B ．,63ππ⎡⎤⎢⎥⎣⎦C ．,43ππ⎡⎤⎢⎥⎣⎦D ．,32ππ⎡⎫⎪⎢⎣⎭(2) 如图，三棱柱ABC DEF -的侧面BEFC 是边长为1的正方形，面BEFC ⊥面ADEB ，4AB =，60DEB ∠=︒，G 是DE 的中点,在线段BC 上存在一点P ，使二面角P GE B --为45︒，求BP 的长考点2 用向量法解决开放性、探索性问题例 2.(1)如图，在五面体ABCDEF 中，面ABCD 是正方形，AD DE ⊥，4=AD ，2DE EF ==，且π3EDC ∠=．（1）求证：AD ⊥平面CDEF ；（2）求直线BD 与平面ADE 所成角的正弦值；（3）设M 是CF 的中点，棱AB 上是否存在点G ，使得//MG 平面ADE ？若存在，求线段AG 的长；若不存在，说明理由．(2)在四棱锥P ABCD -中，PA ⊥平面ABCD ，23PA =，//DC AB ，90DAB ∠=︒，3AB =，2AD CD ==，M 是棱PD 的中点.（1）求异面直线DP 与BC 所成的角的余弦值；（2）求AM 与平面PBC 所成的角的大小；（3）在棱PB 上是否存在点Q ，使得平面QAD 与平面ABCD 所成的锐二面角的大小为60°？若存在，求出AQ 的长；若不存在，说明理由.【跟踪演练】2.-中，PD⊥底面ABCD，底面ABCD是边长为2的正方形，(1)如图，在四棱锥P ABCD=，F，G分别是PB，AD的中点．PD DC（Ⅰ）求证：GF⊥平面PCB；（Ⅱ）求平面PAB与平面PCB的夹角的大小；（III）在线段AP上是否存在一点M，使得DM与平面ADF所成角为30︒？若存在，求出M点坐标，若不存在，请说明理由．-中，PD⊥底面ABCD，底面ABCD是边长为2的正方形，(2)如图，在四棱锥P ABCD=，F，G分别是PB，AD的中点．PD DC（1）求证：GF⊥平面PCB；（2）求平面PAB与平面PCB夹角的余弦值；（3）在AP上是否存在一点M，使得DM与PC所成角为60︒？若存在，求出M点坐标，若不存在，请说明理由．考点2 立体几何综合问题例3.(1)已知正方体1111ABCD A B C D -的棱长为1，给出下列四个命题：①对角线1AC 被平面1A BD 和平面11B CD 、三等分；②正方体的内切球、与各条棱相切的球、正方体的外接球的表面积之比为1:2:3；③以正方体的顶点为顶点的四面体的体积都是16；④正方体与以A 为球心，1为半径的球的公共部分的体积是6π．其中正确的序号是（ ） A ．①② B ．②④ C ．①②③ D ．①②④(2)如图，直二面角D AB E --中，四边形ABCD 是边长为2的正方形，AE EB =，F 为CE 上的点，且BF ⊥平面ACE .（1）求证：AE ⊥平面BCE ；（2）求二面角B AC E --的大小的正弦值；（3）求点D 到平面ACE 的距离.(1)(多选)在正方体1111ABCD A B C D -中，2AB =，E 、F 分别为1BB 、CD 中点，P 是1BC 上的动点，则下列说法正确的有（ ）A ．1A F AE ⊥B ．三棱锥1P AED -的体积与点P 位置有关系C ．平面1AED 截正方体1111ABCD A B C D -的截面面积为92 D ．点1A 到平面1AED 的距离为2(2)如图，多面体ABCDEF 中，四边形ABCD 是菱形，060ABC ∠=，FA ⊥平面ABCD ，//,2 2.FA ED AB FA ED ===（1）求二面角F BC A --的大小的正切值；（2）求点E 到平面AFC 的距离；（3）求直线FC 与平面ABF 所成的角的正弦值.一、单项选择题：本题共6小题，每小题5分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在长方体1111ABCD A B C D -中，1AB AD ==，12AA =，设AC 交BD 于点O ，则异面直线1A O 与1BD 所成角的余弦值为（ ）A ．41515-B ．41515C ．439-D ．4392.如图在棱长为2的正方体1111ABCD A B C D -中，点E 是AD 的中点，那么异面直线1D E 和1A B 所成的角的余弦值等于（ ）A ．10B ．15C ．45D ．233.已知四面体ABCD 中，AB ，BC ，BD 两两垂直，2BC BD ==，AB 与平面ACD 所成角的正切值为12，则点B 到平面ACD 的距离为（ ） A ．3 B ．23 C ．5 D ．25 4.如图，矩形ADFE ，矩形CDFG ，正方形ABCD 两两垂直，且2AB =，若线段DE 上存在点P 使得GP BP ⊥，则边CG 长度的最小值为 ( )A ．4B ．43C ．2D ．35.已知ABC ∆是由具有公共直角边的两块直角三角板（Rt ACD ∆与Rt BCD ∆）组成的三角形，如左下图所示.其中，45,60CAD BCD ∠=∠=.现将Rt ACD ∆沿斜边AC 进行翻折成1D AC ∆（1D 不在平面ABC 上）.若,M N 分别为BC 和1BD 的中点，则在ACD ∆翻折过程中，下列命题不正确的是（ ）A ．在线段BD 上存在一定点E ，使得EN 的长度是定值B ．点N 在某个球面上运动C ．存在某个位置，使得直线1AD 与DM 所成角为60D ．对于任意位置，二面角1D AC B --始终大于二面角1D BC A --二、多项选择题：本题共3小题，每小题5分，共15分．在每小题给出的选项中，有多项符合题目要求,全部选对的得5分，有选错的得0分，部分选对的得3分．6.在棱长为1的正方体1111ABCD A B C D -中，下列结论正确的是（ ）A ．异面直线AC 与1BC 所成的角为3π B ．1DA 是平面11ABC D 的一个法向量 C ．二面角1A B C B --的正切值为22 D ．正方体1111ABCD A B C D -的外接球的体积为327. 如图，已知棱长为2的正方体1111ABCD A B C D -中，点P 在线段1B C 上运动，下列结论正确的是（ ）A.异面直线AP 与1DD 所成的角范围为ππ,32⎡⎤⎢⎥⎣⎦； B.平面1PBD ⊥平面11AC D ；C.点P 到平面11AC D 的距离为定值233； D.存在一点P ，使得直线AP 与平面11BCC B 所成的角为π3. 其中正确的结论是___________. 三、填空题：本题共3小题，每小题5分，多空题，第一空2分，第二空3分，共15分．8.如图，正三棱柱ABC ­A 1B 1C 1的所有棱长都相等，E ，F ，G 分别为AB ，AA 1，A 1C 1的中点，则B 1F 与平面GEF 所成角的正弦值为________．9. 如图，在正四棱柱1111ABCD A B C D -中，122AA AB ==，则点C 到平面1BDC 的距离为_____________10.如图，在等腰梯形ABCD 中，//AB DC ，6AB =，过点D 作DM AB ⊥交AB 于点M ，2DM AM CD ===，现将AMD 沿MD 折起，使平面AMD ⊥平面MBCD ，连接AB ､AC ,则直线AB 与平面AMC 所成角的正弦值为____________;当13AP AB =时，则二面角P MC B --的余弦值为__________.四、解答题：本题共4小题，共40分。

第3讲 空间角与距离的计算（1）考点1用综合法求线线角与线面角例1.(1)如图，正三棱柱的九条棱都相等，三个侧面都是正方形，M 、N 分别是BC 和11A C 的中点，则MN 与1AB 所成角的余弦值为（ ）A ．105B ．1010-C ．105-D ．1010(2)如图，在三棱锥D ABC -中，AB BC CD DA ===，90,,,ABC E F O ︒∠=分别为棱,,BC DA AC 的中点，记直线EF 与平面BOD 所成角为θ，则θ的取值范围是（ ）A ．0,4π⎛⎫ ⎪⎝⎭B ．,43ππ⎛⎫ ⎪⎝⎭C ．,42ππ⎛⎫ ⎪⎝⎭D ．,62ππ⎛⎫ ⎪⎝⎭【跟踪演练】1.(1)如图在四面体PABC 中，PC ⊥平面ABC ，AB BC CA PC ===，那么直线AP 和CB 所成角的余弦值（ ）A 2B ．22C ．12D ．24-(2)在正三棱锥S ABC -中，底面是边长等于23的等边三角形，侧棱4SA =，则侧棱与底面所成的角为（ ）A ．60B ．45C ．30D ．75考点2 用综合法求二面角例2.(1)如图，在四棱锥A BCDE -中，已知四边形BCDE 为平行四边形，平面ABE ⊥平面BCDE ，2AB AE BC CE ====，90BAE ∠=︒，点O 为BE 的中点.则二面角A-BC-O 的正切值为____________.(2)如图，四棱锥P ABCD -中，ABCD 为矩形，平面PAD ⊥平面 ABCD ，PA PD =，Q 是线段PC 上的点(不含端点).设AQ 与BC 所成的角为α，AQ 与平面 ABCD 所成的角为β，二面角Q AB C --的平面角为γ，则（ ）A ．αβγ<<B ．βαγ<<C ．γβα<<D ．βγα<<【跟踪演练】2.(1)在棱长为2的正四面体ABCD 中，点E ，F ，G 分别为棱BC ，CD ，DA 的中点，则二面角G BC D --余弦值的大小为____________(2) 如图，在正四棱锥P ABCD -中，设直线PB 与直线DC 、平面ABCD 所成的角分别为α、β，二面角P CD B --的大小为γ，则（ ）A ．,αβγβ>>B ．,αβγβ><C ．,αβγβ<>D ．,αβγβ<<考点3 体积法求点面距离例3.(1)如图，在正方体1111ABCD A B C D -中，棱长为1，E F 、分别为11C D 与AB 的中点，1B 到平面1A FCE 的距离为（ ）A ．32B ．63C ．105D ．305(2)正三棱柱111ABC A B C -的所有定点均在表面积为8π的球O 的球面上，3AB =则1B 到平面1A BC 的距离为（ ）A ．1B ．65C ．435D 3【跟踪演练】3.(1)如图，正四棱锥P ABCD -的高为2，且底面边长也为2，则点A 到平面PBC 的距离为（ ）A ．455B 25C ．54D 5 (2)已知在正四棱柱1111ABCD A B C D -中，2AB =，122CC =，E 为1CC 的中点，则点1C 与平面BDE 的距离为（ ）A ．2B 3C 2D ．1【仿真练习】一、单项选择题：本题共6小题，每小题5分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．在正方体1111ABCD A B C D -中，E ，F ，P ，Q 分别为1A B ，11B D ，1A D ，1CD 的中点，则异面直线EF 与PQ 所成角的大小是（ ） A ．4π B ．6π C ．3π D ．2π 2.已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC 的中心,则1AB 与底面ABC 所成角的正弦值为（ ）A ．13B 23．23 3.直三棱柱111ABC A B C -的侧棱13CC =，底面ABC 中，90ACB ∠=，2AC BC ==则点1B 到平面1A BC 的距离为（ ）A ．311B ．22C ．32D ．3224.已知长方体1111ABCD A B C D -的高12,26,AA AC ==11,AB x AD y ==，则当x y +最大时，二面角111A B D C --的余弦值为（ ）A ．15B ．15- C ．5D ．5-5.日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球（球心记为O ），地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面．在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40︒，则晷针与点A 处的水平面所成角为（ ）A ．20︒B ．40︒C ．50︒D ．90︒二、多项选择题：本题共3小题，每小题5分，共15分．在每小题给出的选项中，有多项符合题目要求,全部选对的得5分，有选错的得0分，部分选对的得3分．6.在正方体ABCD-A 1B 1C 1D 1中，E ，F ，G 分别为BC ，CC 1，BB 1的中点，则（ ）A ．D 1D ⊥AFB ．A 1G ∥平面AEFC ．异面直线A 1G 与EF 所成角的余弦值为1010D ．点G 到平面AEF 的距离是点C 到平面AEF 的距离的2倍7.如图，已知正方体1ABCD ABC D -的棱长为a ，E 是棱CD 上的动点.则下列结论中正确的有（ ）A ．11EB AD ⊥B ．二面角11E A B A --的大小为4π C ．三棱锥11A B D E -体积的最小值为313aD ．1//DE 平面11A B BA三、填空题：本题共3小题，每小题5分，多空题，第一空2分，第二空3分，共15分．8.如图，在四棱锥P ABCD -中，PD ⊥平面ABCD ，1PD DC BC ===，2AB =，//AB DC ，90BCD ∠=，则点A 到平面PBC 的距离为______________.9.如图，多面体ABCED 中，面ABD ⊥面ABC ，面BCE ⊥面ABC ，//DE 面ABC ，23AB =，BE CE =，2AD BD BC ===.则BEC ∠的大小为_________；若2DE =，则二面角B DE C --的余弦值为_____________.10.如图，已知多面体ABCDEF 中，四边形ABCD 为梯形，//AD BC ，AB AD ⊥，AF ⊥平面ABCD ，//DE AF ，22AB BC AF AD DE ====，P 为线段FC (包括端点)上的一个动点，则直线BP 与直线AE 所成角的正弦值的最小值为_________.四、解答题：本题共4小题，共40分。

1 第八章 立体几何 第08节 立体几何中的向量方法(Ⅱ)—求空间角与距离 【考纲解读】 考 点 考纲内容 5年统计 分析预测

立体几何中的向量方法(Ⅱ)—求空间角与距离

能用向量方法解决直线与直线、直线与平面、平面与平面的夹角的计算问题,了解向 量方法在研究立体几何问题中的应用.

2013•新课标I. 18;II.18； 2014•新课标I. 12,19;II.11,18; 2015•新课标I. 18;II.19； 2016•新课标I.11,18；II.14,19;III.19; 2017•新课标I.18;II.10,19;III.16,19. 1.以几何体为载体，综合考查平行或垂直关系证明，以及角与距离的计算. 2.利用几何法证明平行、垂直关系，利用空间向量方法求角或距离. 3.备考重点： (1) 掌握空间向量的坐标运算； (2)掌握角与距离的计算方法方法.

【知识清单】 1. 异面直线所成的角 1.两条异面直线所成的角 ①定义：设a，b是两条异面直线，过空间任一点O作直线a′∥a，b′∥b，则a′与b′所夹的锐角或直角叫做a与b所成的角．

②范围：两异面直线所成角θ的取值范围是(0,]2．

③向量求法：设直线a，b的方向向量为a，b，其夹角为φ，则有cos|cos|||||||abab. 对点练习： 【2017课标II，理10】已知直三棱柱111CC中，C120，2，1CCC1，则异面直线1与1C所成角的余弦值为（ ）

A．32 B．155 C．105 D．33 2. 直线与平面所成角 2

1．直线和平面所成角的求法：如图所示，设直线l的方向向量为e，平面α的法向量为n，直线l与平面α所成的角为φ，两向量e与n的夹角为θ，则有sin φ＝|cos θ|＝|e·n||e||n|.

对点练习： 【2017浙江，19】（本题满分15分）如图，已知四棱锥P–ABCD，△PAD是以AD为斜边的等腰直角三角形，ADBC//，CD⊥AD，PC=AD=2DC=2CB，E为PD的中点．学=

外心；b.如果顶点到底面各边距离相等或侧面与底面所成的角相等，那么顶点落在底面上的射影是底面三角形的内心(或旁心)；c.如果侧棱两两垂直或各组对棱互相垂直，那么顶点落在底面上的射影是底面三角形的垂心；〔4〕二面角的X围在课本中没有给出，一般是指(0,]，解题时要注意图形的位置和题目的要求。

作二面角的平面角常有三种方法①棱上一点双垂线法：在棱上任取一点，过这点在两个平面内分别引棱的垂线，这两条射线所成的角，就是二面角的平面角；②面上一点三垂线法：自二面角的一个面上一点向另一面引垂线，再由垂足向棱作垂线得到棱上的点〔即垂足〕，斜足与面上一点连线和斜足与垂足连线所夹的角，即为二面角的平面角；③空间一点垂面法：自空间一点作与棱垂直的平面，截二面角得两条射线，这两条射线所成的角就是二面角的平面角斜面面积和射影面积的关系公式：SScos(S为原斜面面积,S为射影面积,为斜面与射影所成二面角的平面角)这个公式对于斜面为三角形,任意多边形都成立.是求二面角的好方法.当作二面角的平面角有困难时,如果能找得斜面面积的射影面积,可直接应用公式,求出二面角的大小2．空间的距离〔1〕点到直线的距离：点Ｐ到直线a的距离为点Ｐ到直线a的垂线段的长，常先找或作a所在平面的垂线，得垂足为Ａ，过Ａ作a的垂线，垂足为Ｂ连ＰＢ，那么由三垂线定理可直线得线段ＰＢ即为点Ｐ到直线a的距离。

在直角三角形ＰＡＢ中求出ＰＢ的长即可。

点到平面的距离：点Ｐ到平面的距离为点Ｐ到平面的垂线段的长．常用求法①作出点Ｐ到平面的垂线后求出垂线段的长；②转移法，如果平面的斜线上两点Ａ，Ｂ到斜足Ｃ的距离ＡＢ，ＡＣ的比为m:n，那么点Ａ，Ｂ到平面的距离之比也为m:n．特别地，ＡＢ＝ＡＣ时，点Ａ，Ｂ到平面的距离相等；③体积法〔2〕异面直线间的距离：异面直线a,b间的距离为a,b间的公垂线段的长．常有求法①先证线段ＡＢ为异面直线a,b的公垂线段，然后求出ＡＢ的长即可．②找或作出过b且与a平行的平面，那么直线a到平面的距离就是异面直线a,b间的距离．③找或作出分别过a,b且与b，a分别平行的平面，那么这两平面间的距离就是异面直线a,b间的距离．④根据异面直线间的距离公式求距离。

第七节 空间角与距离考纲解读1. 掌握各种角的定义，弄清异面直线所成的角与两直线所成的角，二面角与二面角的平面角，直线与平面所成的角和斜线与平面所成的角，二面角与两平面所成的角的联系与区别 ，弄清他们各自的取值范围 。

2. 细心体会求空间角的转化和数形结合思想，熟练掌握平移，射影等方法。

命题趋势探究异面直线所成角，线面角，二面角时高考中考查的热点，解答与空间角有关的问题时既可用传统法，又可用向量法。

在新课程标准下，对立体几何的基本理论知识要求有所降低，因此应用向量这一工具解题更为重要，特别是要熟练掌握利用空间图形的特殊性，构造适当的空间直角坐标系解决问题的方法，并能灵活应用。

空间角是立体几何中的一个重要概念，它是空间图形的一个突出量化指标，是空间图形位置关系的具体体现，故以高频的考点出现在历届高考试题中，在选择题，填空题及解答题中均有出现。

知识点精讲 一、 空间角的定义和范围 （1） 两条异面直线所成角θ的范围是0]2π（，，当θ=2π时，这两条异面直线互相垂直。

（2） 斜线AO 与它在平面α内的射影AB 所成角θ叫做直线与平面所成的角。

平面的斜线和平面所成的角，是这条斜线和这个平面内的任一直线所成角中最小的角，如果直线和平面垂直，那么直线与平面所成的角为2π；如果直线和平面平行或直线在平面内，那么就是直线和平面所成的角为0.直线和平面所成的角的范围为[0]2π，；斜线和平面所成的角的范围为(0,).2π（3） 从一条直线出发的两个半平面所组成的角叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面，棱为l ，两个平面分别为α，β的二面角记做α-l -β，二面角的范围是[0,]π （4） 一个平面垂直于二面角的公共棱l ，且与两个半平面的交线分别是射线OA ，OB ，则∠AOB 叫做二面角的平面角，平面角是直角的二面角叫做直二面角，相交成直二面角的两个平面垂直。

二、 点到平面距离的定义点到平面的距离即点到它在平面内的正射影的距离。