2018年高考数学总复习 9.7 抛物线

简解抛物线问题的三种途径一、回归定义例 1 点(32)P ，在抛物线24y x =的内部，F 是抛物线的焦点，在抛物线上求一点M ，使MP MF +最小，并求此最小值． 解：过M 作准线l 的垂线MA ，垂足为A ，那么由抛物线的定义有MF MA =．MP MF MP MA +=+∴，显然当P M A ，，三点共线时，MP MF +最小． 此时，M 点的坐标为(12)，，最小值为4．二、设而不求例2 抛物线28y x =-的弦PQ 被点(11)A -，平分，求弦PQ 所在的直线方程．解：设PQ 的端点1122()()P x y Q x y ，，，，那么有21122288y x y x ⎧=-⎪⎨=-⎪⎩，， 两式相减得121212()()8()y y y y x x +-=--， ∴21214y y x x -=--，即4PQ k =-． 故弦PQ 所在的直线方程为14(1)y x -=-+，即4x y ++=．三、运用向量例3 过抛物线22(0)y px p =>的焦点F 的直线与抛物线相交于A B ，两点，自A B ，向准线作垂线，垂足分别为A B ''，，求证：90A FB ''∠=°．证明：抛物线的焦点02p F ⎛⎫ ⎪⎝⎭，， 设A B ，两点的纵坐标分别为12y y ，，易得212y y p =-．又1222p p A y B y ⎛⎫⎛⎫''-- ⎪ ⎪⎝⎭⎝⎭，，，， 那么12()()FA p y FB p y ''=-=-，，，， 故222120FA FB p y y p p ''=+=-=·， 那么FA FB ''⊥，即90A FB ''∠=°．。

第九节抛物线(一)1.掌握抛物线的定义、几何图形、标准方程及简单性质.2.理解数形结合的思想.知识梳理一、抛物线的定义平面内到定点F的距离等于到定直线l(定点不在定直线上)的距离的点的轨迹是抛物线．其中定点叫做焦点，定直线叫做准线．注意：当定点在定直线上时，点的轨迹是过该定点且与定直线垂直的一条直线．二、抛物线的类型、标准方程及其几何性质(注意：表中各式的p>0)标准方程y2＝2px y2＝－2px x2＝2py x2＝－2py图形焦点F ⎝⎛⎭⎫p2，0 F ⎝⎛⎭⎫－p2，0 F ⎝⎛⎭⎫0，p 2 F ⎝⎛⎭⎫0，－p 2 准线 x ＝－p 2x ＝p 2y ＝－p 2y ＝p 2 范围 x ≥0，y ∈Rx ≤0，y ∈R x ∈R ，y ≥0x ∈R ，y ≤0 对称轴 x 轴y 轴顶点 (0,0) 离心率e ＝1焦半径||PF ＝ p2 ＋x 1||PF ＝ p2 ＋||x 1||PF ＝ p2 ＋y 1||PF ＝ p2 ＋||y 1基础自测1．(2013·四川卷)抛物线y 2＝8x 的焦点到直线x －3y ＝0的距离是( ) A ．2 3B ．2C. 3D ．1解析：抛物线y 2＝8x 的焦点为F (2,0)，由点到直线的距离公式得F (2,0)到直线x －3y ＝0的距离d ＝|2－3×0|12＋(－3)2＝22＝1.故选D.答案：D2．一动圆的圆心在抛物线x 2＝－8y 上，且动圆恒与直线y －2＝0相切，则动圆必过定点( )A ．(4,0)B ．(0，－4)C ．(2,0)D ．(0，－2)解析：由抛物线的定义知到焦点距离与到准线的距离相等，动圆必过焦点(0，－2)．答案：D3．若动点P 到点F (2,0)的距离与它到直线x ＋2＝0的距离相等，则点P 的轨迹方程为____________．解析：由抛物线定义知点P 的轨迹是以F (2,0)为焦点，直线x ＝－2为准线的抛物线，所以p ＝4，所以其方程为y 2＝8x .答案：y 2＝8x4．若抛物线y 2＝2px 的焦点与椭圆x 26＋y 22＝1的右焦点重合，则p 的值为________． 解析：椭圆x 26＋y 22＝1的右焦点为(2,0)，所以抛物线y 2＝2px 的焦点为(2,0)，则p ＝4.答案：41．(2013·新课标全国Ⅰ卷)O 为坐标原点，F 为抛物线C ：y 2＝42x 的焦点，P 为C 上一点，若|PF |＝42，则△POF 的面积为( )A ．2B ．2 2C ．2 3D ．4解析：由y 2＝42x 知：焦点F (2，0)，准线x ＝－ 2.设P 点坐标为(x 0，y 0)，则x 0＋2＝42，所以x 0＝32，所以y 20＝42×32＝24， 所以|y 0|＝26，所以S △POF ＝12×2×26＝2 3.故选C.答案：C2．已知平面内一动点P 到点F (1,0)的距离与点P 到y 轴的距离的差等于1. (1)求动点P 的轨迹C 的方程；(2)过点F 作两条斜率存在且互相垂直的直线l 1，l 2，设l 1与轨迹C 相交于点A ，B ，l 2与轨迹C 相交于点D ，E ，求A D →·E B →的最小值．解析：(1)设动点P 的坐标为(x ，y )，由题意有(x －1)2＋y 2－|x |＝1.化简得y 2＝2x ＋2|x |.当x ≥0时，y 2＝4x ；当x <0时，y ＝0. 所以，动点P 的轨迹C 的方程为y 2＝4x (x ≥0)和y ＝0(x <0)．(2)由题意知，直线l 1的斜率存在且不为0，设为k ，则l 1的方程为y ＝k (x －1)．由⎩⎪⎨⎪⎧y ＝k (x －1)，y 2＝4x得k 2x 2－(2k 2＋4)x ＋k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1，x 2是上述方程的两个实根，于是x 1＋x 2＝2＋4k 2，x 1x 2＝1.因为l 1⊥l 2，所以l 2的斜率为－1k.设D (x 3，y 3)，E (x 4，y 4)，则同理可得x 3＋x 4＝2＋4k 2，x 3x 4＝1.故A D →·E B →＝(A F →＋F D →)·(E F →＋F B →)＝A F →·E F →＋A F →·F B →＋F D →·E F →＋F D →·F B →＝|A F →|·|F B →|＋|F D →|·|E F →|＝(x 1＋1)(x 2＋1)＋(x 3＋1)(x 4＋1)＝x 1x 2＋(x 1＋x 2)＋1＋x 3x 4＋(x 3＋x 4)＋1 ＝1＋⎝⎛⎭⎫2＋4k 2＋1＋1＋(2＋4k 2)＋1＝8＋4⎝⎛⎭⎫k 2＋1k 2≥8＋4×2k 2·1k2＝16. 当且仅当k 2＝1k2，即k ＝±1时，AD →·E B →取得最小值16.1．(2013·汕头一模)已知点P 在抛物线y 2＝4x 上，那么点P 到点Q (2，－1)的距离与点P 到抛物线焦点距离之和取得最小值时，点P 的坐标为________．解析：因为y 2＝4x ，所以p ＝2，焦点坐标为(1,0)，依题意可知当P ，Q 和焦点三点共线且点P 在中间的时候，距离之和最小如图，故P 的纵坐标为－1，然后代入抛物线方程求得x ＝14.答案：⎝⎛⎭⎫14，－12．在平面直角坐标系xOy 中，动点P 到定点F ()1，0的距离与到定直线l ：x ＝－1的距离相等．(1)求动点P 的轨迹E 的方程；(2)过点F 作倾斜角为45°的直线m 交轨迹E 于点A ，B ，求△AOB 的面积． 解析：(1)设P ()x ，y ，由抛物线定义知，点P 的轨迹E 为抛物线，方程为y 2＝4x .(2)m ：y ＝x －1，代入y 2＝4x ，消去x 得y 2－4y －4＝0.设A ()x 1，y 1，B ()x 2，y 2，则||y 2－y 1＝42，所以S △AOB ＝12×||OF ×||y 2－y 1＝12×1×42＝2 2.。

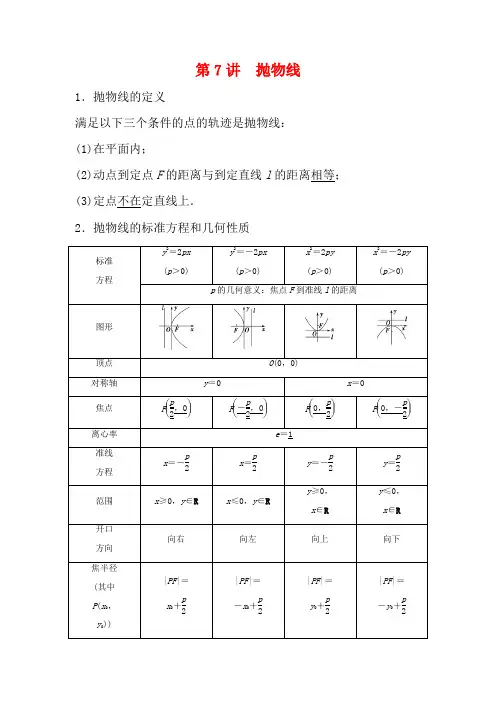
第7讲 抛物线1．抛物线的定义满足以下三个条件的点的轨迹是抛物线： (1)在平面内；(2)动点到定点F 的距离与到定直线l 的距离相等； (3)定点不在定直线上．2．抛物线的标准方程和几何性质标准 方程y 2＝2px(p ＞0)y 2＝－2px(p ＞0)x 2＝2py(p ＞0)x 2＝－2py(p ＞0)p 的几何意义：焦点F 到准线l 的距离图形顶点 O (0，0)对称轴 y ＝0x ＝0焦点 F ⎝ ⎛⎭⎪⎫p 2，0 F ⎝ ⎛⎭⎪⎫－p 2，0 F ⎝⎛⎭⎪⎫0，p 2 F ⎝ ⎛⎭⎪⎫0，－p 2离心率 e ＝1准线 方程 x ＝－p 2x ＝p 2y ＝－p 2y ＝p 2范围 x ≥0，y ∈Rx ≤0，y ∈Ry ≥0，x ∈Ry ≤0， x ∈R开口方向 向右向左向上向下焦半径 (其中P (x 0， y 0))|PF |＝x 0＋p 2|PF |＝ －x 0＋p2|PF |＝ y 0＋p 2|PF |＝ －y 0＋p23.与焦点弦有关的常用结论 (以右图为依据)设A (x 1，y 1)，B (x 2，y 2)． (1)y 1y 2＝－p 2，x 1x 2＝p 24.(2)|AB |＝x 1＋x 2＋p ＝2psin 2θ(θ为AB 的倾斜角)．(3)1|AF |＋1|BF |为定值2p.(4)以AB 为直径的圆与准线相切． (5)以AF 或BF 为直径的圆与y 轴相切．判断正误(正确的打“√”，错误的打“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线．( )(2)若直线与抛物线只有一个交点，则直线与抛物线一定相切．( )(3)若一抛物线过点P (－2，3)，则其标准方程可写为y 2＝2px (p >0)．( )(4)抛物线既是中心对称图形，又是轴对称图形．( ) 答案：(1)× (2)× (3)× (4)×(教材习题改编)抛物线y ＝－14x 2的焦点坐标是( )A ．(0，－1)B ．(0，1)C ．(1，0)D ．(－1，0)解析：选A.抛物线y ＝－14x 2的标准方程为x 2＝－4y ，开口向下，p＝2，p2＝1，故焦点为(0，－1)．顶点在原点，对称轴为坐标轴，且过点P (－4，－2)的抛物线的标准方程是( ) A ．y 2＝－xB ．x 2＝－8yC ．y 2＝－8x 或x 2＝－yD ．y 2＝－x 或x 2＝－8y解析：选D.设抛物线为y 2＝mx ，代入点P (－4，－2)，解得m ＝－1，则抛物线方程为y 2＝－x ；设抛物线为x 2＝ny ，代入点P (－4，－2)，解得n ＝－8，则抛物线方程为x 2＝－8y .(教材习题改编)焦点在直线2x ＋y ＋2＝0上的抛物线的标准方程为________．解析：抛物线的标准方程的焦点都在坐标轴上，直线2x ＋y ＋2＝0与坐标轴的交点分别为(－1，0)与(0，－2)，故所求的抛物线的焦点为(－1，0)或(0，－2)，当焦点为(－1，0)时，易得抛物线标准方程为y 2＝－4x .当焦点为(0，－2)时，易得抛物线标准方程为x 2＝－8y . 答案：y 2＝－4x 或x 2＝－8y设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是________．解析：如图所示，抛物线的准线l 的方程为x ＝－2，F 是抛物线的焦点，过点P 作PA ⊥y 轴，垂足是A ，延长PA 交直线l 于点B ，则|AB |＝2，由于点P 到y 轴的距离为4，则点P 到准线l 的距离|PB |＝4＋2＝6，所以点P 到焦点的距离|PF |＝|PB |＝6. 答案：6抛物线的定义(高频考点)抛物线的定义是高考的热点，考查时多以选择题、填空题形式出现，个别高考题有一定难度．高考对该内容的考查主要有以下三个命题角度：(1)求抛物线的标准方程；(2)求抛物线上的点与焦点的距离； (3)求距离和的最值．[典例引领]角度一 求抛物线的标准方程(2018·天津模拟)已知动圆过定点F ⎝ ⎛⎭⎪⎫p 2，0，且与直线x ＝－p2相切，其中p >0，则动圆圆心的轨迹E 的方程为________________．【解析】 依题意得，圆心到定点F ⎝ ⎛⎭⎪⎫p 2，0的距离与到直线x ＝－p2的距离相等，再依抛物线的定义可知，动圆圆心的轨迹E 为抛物线，其方程为y 2＝2px . 【答案】 y 2＝2px角度二求抛物线上的点与焦点的距离(2017·高考全国卷Ⅱ)已知F是抛物线C：y2＝8x的焦点，M 是C上一点，FM的延长线交y轴于点N.若M为FN的中点，则|FN|＝____________．【解析】法一：依题意，抛物线C：y2＝8x的焦点F(2，0)，准线x＝－2，因为M是C上一点，FM的延长线交y轴于点N，M为FN的中点，设M(a，b)(b>0)，所以a＝1，b＝22，所以N(0，42)，|FN|＝4＋32＝6.法二：依题意，抛物线C：y2＝8x的焦点F(2，0)，准线x＝－2，因为M是C上一点，FM的延长线交y轴于点N，M为FN的中点，则点M的横坐标为1，所以|MF|＝1－(－2)＝3，|FN|＝2|MF|＝6.【答案】6角度三求距离和的最值已知抛物线y2＝4x的焦点是F，点P是抛物线上的动点，又有点B(3，2)，则|PB|＋|PF|的最小值为________．【解析】如图，过点B作BQ垂直准线于Q，交抛物线于点P1，则|P1Q|＝|P1F|，则有|PB|＋|PF|≥|P1B|＋|P1Q|＝|BQ|＝4.即|PB|＋|PF|的最小值为4.【答案】4若本例中的B点坐标改为(3，4)，试求|PB|＋|PF|的最小值．解：由题意可知点(3，4)在抛物线的外部．因为|PB|＋|PF|的最小值即为B，F两点间的距离，所以|PB |＋|PF |≥|BF |＝42＋22＝16＋4＝2 5.即|PB |＋|PF |的最小值为2 5.抛物线定义的应用(1)利用抛物线的定义解决此类问题，应灵活地进行抛物线上的点到焦点的距离与到准线距离的等价转化．即“看到准线想到焦点，看到焦点想到准线”．(2)注意灵活运用抛物线上一点P (x ，y )到焦点F 的距离|PF |＝|x |＋p 2或|PF |＝|y |＋p2. [通关练习]1．已知抛物线C ：y 2＝x 的焦点为F ，A (x 0，y 0)是C 上一点，|AF |＝54x 0，则x 0＝( ) A ．1 B ．2 C ．4D ．8解析：选A.由题意知抛物线的准线为x ＝－14.因为|AF |＝54x 0，根据抛物线的定义可得x 0＋14＝|AF |＝54x 0，解得x 0＝1.2．已知动点P 的坐标(x ，y )满足方程5（x －1）2＋（y －2）2＝|3x ＋4y ＋12|，则点P 的轨迹是( ) A ．圆 B ．椭圆 C ．双曲线D ．抛物线解析：选 D.由5（x －1）2＋（y －2）2＝|3x ＋4y ＋12|⇒（x －1）2＋（y －2）2＝|3x ＋4y ＋12|5，所以动点P 到定点(1，2)的距离等于其到直线l ：3x ＋4y ＋12＝0的距离，所以点P 的轨迹是抛物线．3．已知F 是抛物线y 2＝x 的焦点，A ，B 是该抛物线上的两点，且|AF |＋|BF |＝3，则线段AB 的中点到y 轴的距离为( ) A.34 B ．1 C.54D.74解析：选C.如图所示，设抛物线的准线为l ，AB 的中点为M ，作AA 1⊥l 于A 1，BB 1⊥l 于B 1，MM 1⊥l 于M 1，由抛物线的定义知p ＝12，|AA 1|＋|BB 1|＝|AF |＋|BF |＝3，则点M 到y 轴的距离为|MM 1|－p 2＝12(|AA 1|＋|BB 1|)－14＝54.故选C.抛物线的性质[典例引领](1)(2016·高考全国卷Ⅰ)以抛物线C 的顶点为圆心的圆交C 于A 、B 两点，交C 的准线于D 、E 两点．已知|AB |＝42，|DE |＝25，则C 的焦点到准线的距离为( )A ．2B ．4C ．6D ．8(2)(2018·东北四市模拟)若点P 为抛物线y ＝2x 2上的动点，F 为抛物线的焦点，则|PF |的最小值为( ) A ．2 B.12 C.14D.18【解析】 (1)由题意，不妨设抛物线方程为y 2＝2px (p ＞0)，由|AB |＝42，|DE |＝25，可取A ⎝ ⎛⎭⎪⎫4p，22，D ⎝ ⎛⎭⎪⎫－p 2，5，设O 为坐标原点，由|OA |＝|OD |，得16p 2＋8＝p24＋5，得p ＝4，所以选B.(2)由题意知x 2＝12y ，则F ⎝⎛⎭⎪⎫0，18，设P (x 0，2x 20)，则|PF |＝x 2＋⎝⎛⎭⎪⎫2x 20－182＝4x 40＋12x 20＋164＝2x 20＋18，所以当x 20＝0时，|PF |min ＝18.【答案】 (1)B (2)D抛物线性质的应用技巧(1)利用抛物线方程确定及应用其焦点、准线时，关键是将抛物线方程化成标准方程．(2)要结合图形分析，灵活运用平面图形的性质以形助数．[通关练习]1．(2018·河南中原名校联考)抛物线y 2＝2px (p >0)的焦点为F ，O 为坐标原点，M 为抛物线上一点，且|MF |＝4|OF |，△MFO 的面积为43，则抛物线的方程为( ) A ．y 2＝6x B ．y 2＝8x C ．y 2＝16xD ．y 2＝15x 2解析：选 B.设M (x ，y )，因为|OF |＝p2，|MF |＝4|OF |，所以|MF |＝2p ，由抛物线定义知x ＋p2＝2p ，所以x ＝32p ，所以y ＝±3p ，又△MFO 的面积为43，所以12×p2×3p ＝43，解得p ＝4(p ＝－4舍去)．所以抛物线的方程为y 2＝8x .2.如图是抛物线形拱桥，当水面在l 时，拱顶离水面2 m ，水面宽4 m ．当水面宽为2 6 m 时，水位下降了________ m.解析：以抛物线的顶点为坐标原点，水平方向为x 轴建立平面直角坐标系，设抛物线的标准方程为x 2＝－2py (p >0)，把(2，－2)代入方程得p ＝1，即抛物线的标准方程为x 2＝－2y .将x ＝6代入x 2＝－2y 得：y ＝－3，又－3－(－2)＝－1，所以水面下降了1 m.答案：1直线与抛物线的位置关系[典例引领](2016·高考全国卷Ⅰ)在直角坐标系xOy 中，直线l ：y ＝t (t ≠0)交y 轴于点M ，交抛物线C ：y 2＝2px (p ＞0)于点P ，M 关于点P 的对称点为N ，连接ON 并延长交C 于点H . (1)求|OH ||ON |；(2)除H 以外，直线MH 与C 是否有其他公共点？说明理由． 【解】 (1)由已知得M (0，t )，P ⎝ ⎛⎭⎪⎫t 22p ，t .又N 为M 关于点P 的对称点，故N ⎝ ⎛⎭⎪⎫t 2p ，t ，ON 的方程为y ＝ptx ，代入y 2＝2px ，整理得px 2－2t 2x ＝0，解得x 1＝0，x 2＝2t2p.因此H ⎝ ⎛⎭⎪⎫2t 2p ，2t .所以N 为OH 的中点，即|OH ||ON |＝2.(2)直线MH 与C 除H 以外没有其他公共点．理由如下： 直线MH 的方程为y －t ＝p2t x ，即x ＝2tp(y －t )．代入y 2＝2px 得y 2－4ty ＋4t 2＝0， 解得y 1＝y 2＝2t ，即直线MH 与C 只有一个公共点，所以除H 以外直线MH 与C 没有其他公共点．直线与抛物线位置关系的判断直线y ＝kx ＋m (m ≠0)与抛物线y 2＝2px (p >0)联立方程组，消去y ，得到k 2x 2＋2(mk －p )x ＋m 2＝0的形式．当k ＝0时，直线和抛物线相交，且与抛物线的对称轴平行，此时与抛物线只有一个交点；当k ≠0时，设其判别式为Δ，(1)相交：Δ>0⇔直线与抛物线有两个交点； (2)相切；Δ＝0⇔直线与抛物线有一个交点； (3)相离：Δ<0⇔直线与抛物线没有交点．[提醒] 过抛物线外一点总有三条直线和抛物线有且只有一个公共点：两条切线和一条平行于对称轴的直线．[通关练习]1．过点(－2，1)斜率为k 的直线l 与抛物线y 2＝4x 只有一个公共点，则由k 的值组成的集合为________． 解析：设l 的方程为y －1＝k (x ＋2)，由方程组⎩⎪⎨⎪⎧y ＝kx ＋（2k ＋1）y 2＝4x，得ky 2－4y ＋4(2k ＋1)＝0，①当k ＝0时，y ＝1，此时x ＝14，l 与抛物线仅有一个公共点⎝ ⎛⎭⎪⎫14，1. ②当k ≠0时，由Δ＝－16(2k 2＋k －1)＝0，得k ＝－1或k ＝12，所以k的值组成的集合为⎩⎨⎧⎭⎬⎫0，－1，12.答案：⎩⎨⎧⎭⎬⎫0，－1，122.(2018·湖南长沙四县联考)如图，已知点F 为抛物线E ：y 2＝2px (p >0)的焦点，点A (2，m )在抛物线E 上，且|AF |＝3. (1)求抛物线E 的方程；(2)已知点G (－1，0)，延长AF 交抛物线E 于点B ，证明：GF 为∠AGB 的平分线．解：(1)由抛物线定义可得|AF |＝2＋p2＝3，解得p ＝2.所以抛物线E 的方程为y 2＝4x .(2)证明：因为点A (2，m )在抛物线E 上， 所以m 2＝4×2，解得m ＝22，即A (2，22)， 又F (1，0)，所以直线AF 的方程为y ＝22(x －1)，由⎩⎪⎨⎪⎧y ＝22（x －1），y 2＝4x ，得2x 2－5x ＋2＝0，解得x ＝2或12，所以B ⎝ ⎛⎭⎪⎫12，－2. 又G (－1，0)，所以k GA ＝223，k GB ＝－223，所以k GA ＋k GB ＝0，所以∠AGF ＝∠BGF ， 所以GF 为∠AGB 的平分线．抛物线定义的实质可归结为“一动三定”；一个动点M ，一个定点F (抛物线的焦点)，一条定直线l (抛物线的准线)，一个定值1(抛物线的离心率)． 抛物线最值问题的求法(1)求抛物线上一点到定直线的最小距离，可以利用点到直线的距离公式表示出所求的距离，再利用函数求最值的方法求解，亦可转化为抛物线过某点的切线与定直线平行时，两直线间的距离问题．(2)求抛物线上一点到定点的最值问题，可以利用两点间的距离公式表示出所求距离，在利用函数求最值的方法求解时，要注意抛物线上点的设法及变量的取值范围． 易错防范(1)区分y ＝ax 2(a ≠0)与y 2＝2px (p >0)，前者不是抛物线的标准方程．(2)求标准方程要先确定形式，必要时要进行分类讨论，标准方程有时可设为y 2＝mx 或x 2＝my (m ≠0)．1．已知点A (－2，3)在抛物线C ：y 2＝2px (p >0)的准线上，记C 的焦点为F ，则直线AF 的斜率为( ) A ．－43B ．－1C ．－34D ．－12解析：选C.由已知，得准线方程为x ＝－2，所以F 的坐标为(2，0)．又A (－2，3)，所以直线AF 的斜率为k ＝3－0－2－2＝－34.2．若点A ，B 在抛物线y 2＝2px (p >0)上，O 是坐标原点，若正三角形OAB 的面积为43，则该抛物线方程是( ) A ．y 2＝233xB ．y 2＝3x C ．y 2＝23xD ．y 2＝33x解析：选 A.根据对称性，AB ⊥x 轴，由于正三角形的面积是43，故34AB 2＝43，故AB ＝4，正三角形的高为23，故可以设点A 的坐标为(23，2)，代入抛物线方程得4＝43p ，解得p ＝33，故所求的抛物线方程为y 2＝233x .故选A. 3．(2018·皖北协作区联考)已知抛物线C ：x 2＝2py (p >0)，若直线y ＝2x 被抛物线所截弦长为45，则抛物线C 的方程为( ) A ．x 2＝8yB ．x 2＝4yC ．x 2＝2y D ．x 2＝y解析：选C.由⎩⎪⎨⎪⎧x 2＝2py ，y ＝2x 得⎩⎪⎨⎪⎧x ＝0，y ＝0或⎩⎪⎨⎪⎧x ＝4p ，y ＝8p ，即两交点坐标为(0，0)和(4p ，8p )，则（4p ）2＋（8p ）2＝45，得p ＝1(舍去负值)，故抛物线C 的方程为x 2＝2y .4．(2018·湖南省五市十校联考)已知抛物线y 2＝2x 上一点A 到焦点F 的距离与其到对称轴的距离之比为5∶4，且|AF |>2，则点A 到原点的距离为( ) A.41 B ．22 C ．4D ．8解析：选B.令点A 到点F 的距离为5a ，点A 到x 轴的距离为4a ，则点A的坐标为⎝ ⎛⎭⎪⎫5a －12，4a ，代入y 2＝2x 中，解得a ＝12或a ＝18(舍)，此时A (2，2)，故点A 到原点的距离为2 2.5．(2018·太原模拟)已知抛物线C ：y 2＝8x 的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点．若FP →＝4FQ →，则|QF |等于( ) A.72 B.52 C ．3D ．2解析：选C.因为FP →＝4FQ →，所以|FP →|＝4|FQ →|，所以|PQ ||PF |＝34.如图，过Q 作QQ ′⊥l ，垂足为Q ′，设l 与x 轴的交点为A ，则|AF |＝4，所以|PQ ||PF |＝|QQ ′||AF |＝34，所以|QQ ′|＝3，根据抛物线定义可知|QQ ′|＝|QF |＝3.6．(2018·云南大理州模拟)在直角坐标系xOy 中，有一定点M (－1，2)，若线段OM 的垂直平分线过抛物线x 2＝2py (p >0)的焦点，则该抛物线的准线方程是________．解析：依题意可得线段OM 的垂直平分线的方程为2x －4y ＋5＝0，把焦点坐标⎝⎛⎭⎪⎫0，p 2代入可求得p ＝52，所以准线方程为y ＝－54.答案：y ＝－547．(2018·河北六校模拟)抛物线C ：y 2＝2px (p >0)的焦点为F ，点O 是坐标原点，过点O ，F 的圆与抛物线C 的准线相切，且该圆的面积为36π，则抛物线的方程为________． 解析：设满足题意的圆的圆心为M . 根据题意可知圆心M 在抛物线上， 又因为圆的面积为36π，所以圆的半径为6，则|MF |＝x M ＋p 2＝6，即x M ＝6－p2，又由题意可知x M ＝p 4，所以p 4＝6－p2，解得p ＝8.所以抛物线方程为y 2＝16x .答案：y 2＝16x8．已知抛物线C 1：y ＝12p x 2(p >0)的焦点与双曲线C 2：x 23－y 2＝1的右焦点的连线交C 1于第一象限的点M .若C 1在点M 处的切线平行于C 2的一条渐近线，则p ＝________．解析：抛物线的焦点坐标为⎝⎛⎭⎪⎫0，p 2，双曲线的右焦点坐标为(2，0)，所以上述两点连线的方程为x 2＋2yp＝1.双曲线的渐近线方程为y ＝±33x .对函数y ＝12p x 2，y ′＝1p x .设M (x 0，y 0)，则1p x 0＝33，即x 0＝33p ，代入抛物线方程得y 0＝16p ，由于点M 在直线x 2＋2y p ＝1上，所以36p ＋2p ×p 6＝1，解得p ＝43＝433.答案：4339．顶点在原点，焦点在x 轴上的抛物线截直线y ＝2x －4所得的弦长|AB |＝35，求此抛物线方程．解：设所求的抛物线方程为y 2＝ax (a ≠0)，A (x 1，y 1)，B (x 2，y 2)，把直线y ＝2x －4代入y 2＝ax ，得4x 2－(a ＋16)x ＋16＝0，由Δ＝(a ＋16)2－256>0，得a >0或a <－32. 又x 1＋x 2＝a ＋164，x 1x 2＝4，所以|AB |＝（1＋22）[（x 1＋x 2）2－4x 1x 2] ＝5⎣⎢⎢⎡⎦⎥⎥⎤⎝⎛⎭⎪⎫a ＋1642－16＝35，所以5⎣⎢⎢⎡⎦⎥⎥⎤⎝⎛⎭⎪⎫a ＋1642－16＝45， 所以a ＝4或a ＝－36.故所求的抛物线方程为y 2＝4x 或y 2＝－36x .10．已知抛物线y 2＝2px (p >0)的焦点为F ，A 是抛物线上横坐标为4，且位于x 轴上方的点，A 到抛物线准线的距离等于5，过A 作AB 垂直于y 轴，垂足为B ，OB 的中点为M .(1)求抛物线的方程；(2)若过M 作MN ⊥FA ，垂足为N ，求点N 的坐标． 解：(1)抛物线y 2＝2px 的准线为x ＝－p2，于是4＋p2＝5，所以p ＝2.所以抛物线方程为y 2＝4x . (2)因为点A 的坐标是(4，4)， 由题意得B (0，4)，M (0，2)． 又因为F (1，0)，所以k FA ＝43，因为MN ⊥FA ，所以k MN ＝－34.又FA 的方程为y ＝43(x －1)，①MN 的方程为y －2＝－34x ，②联立①②，解得x ＝85，y ＝45，所以点N的坐标为⎝ ⎛⎭⎪⎫85，45.1．(2018·甘肃兰州模拟)设O 为坐标原点，P 是以F 为焦点的抛物线y 2＝2px (p >0)上任意一点，M 是线段PF 上的点，且|PM |＝2|MF |，则直线OM 的斜率的最大值为( ) A.33 B.23 C.22D ．1解析：选C.由题意得F ⎝ ⎛⎭⎪⎫p 2，0，设P ⎝ ⎛⎭⎪⎫y 202p ，y 0， 显然当y 0<0时，k OM <0；当y 0>0时，k OM >0.要求k OM 的最大值，则y 0>0，则OM →＝OF →＋FM →＝OF →＋13FP →＝OF →＋13(OP →－OF →)＝13OP →＋23OF →＝⎝ ⎛⎭⎪⎫y 206p ＋p 3，y 03，所以k OM ＝y 03y 206p ＋p 3＝2y 0p ＋2p y 0≤22y 0p ·2p y 0＝22， 当且仅当y 20＝2p 2时，取得等号．2．(2018·福建省普通高中质量检查)过抛物线y 2＝4x 的焦点F 的直线l 交抛物线于A ，B 两点，交其准线于点C ，且A ，C 位于x 轴同侧，若|AC |＝2|AF |，则|BF |等于( ) A ．2 B ．3 C ．4D ．5解析：选C.设抛物线的准线与x 轴交于点D ，则由题意，知F (1，0)，D (－1，0)，分别作AA 1，BB 1垂直于抛物线的准线，垂足分别为A 1，B 1，则有|AC ||FC |＝|AA 1||FD |，所以|AA 1|＝43，故|AF |＝43.又|AC ||BC |＝|AA 1||BB 1|，即|AC ||AC |＋|AF |＋|BF |＝|AF ||BF |，亦即2|AF |3|AF |＋|BF |＝|AF ||BF |，解得|BF |＝4，故选C.3．(2017·高考北京卷)已知抛物线C ：y 2＝2px 过点P (1，1)．过点(0，12)作直线l 与抛物线C 交于不同的两点M ，N ，过点M 作x轴的垂线分别与直线OP 、ON 交于点A ，B ，其中O 为原点． (1)求抛物线C 的方程，并求其焦点坐标和准线方程； (2)求证：A 为线段BM 的中点．解：(1)由抛物线C ：y 2＝2px 过点P (1，1)，得p ＝12.所以抛物线C的方程为y 2＝x . 抛物线C的焦点坐标为⎝ ⎛⎭⎪⎫14，0，准线方程为x ＝－14.(2)证明：由题意，设直线l 的方程为y ＝kx ＋12(k ≠0)，l 与抛物线C 的交点为M (x 1，y 1)，N (x 2，y 2)． 由⎩⎪⎨⎪⎧y ＝kx ＋12，y 2＝x得4k 2x 2＋(4k －4)x ＋1＝0. 则x 1＋x 2＝1－k k 2，x 1x 2＝14k2.因为点P 的坐标为(1，1)，所以直线OP 的方程为y ＝x ，点A 的坐标为(x 1，x 1)．直线ON 的方程为y ＝y 2x 2x ，点B 的坐标为⎝⎛⎭⎪⎫x 1，y 2x 1x 2.因为y 1＋y 2x 1x 2－2x 1＝y 1x 2＋y 2x 1－2x 1x 2x 2＝⎝ ⎛⎭⎪⎫kx 1＋12x 2＋⎝⎛⎭⎪⎫kx 2＋12x 1－2x 1x 2x 2＝（2k －2）x 1x 2＋12（x 2＋x 1）x 2＝（2k －2）×14k 2＋1－k 2k2x 2＝0， 所以y 1＋y 2x 1x 2＝2x 1. 故A 为线段BM 的中点．4．(2018·湖南六校联考)已知抛物线的方程为x 2＝2py (p >0)，其焦点为F ，点O 为坐标原点，过焦点F 作斜率为k (k ≠0)的直线与抛物线交于A ，B 两点，过A ，B 两点分别作抛物线的两条切线，设两条切线交于点M . (1)求OA →·OB →；(2)设直线MF 与抛物线交于C ，D 两点，且四边形ACBD 的面积为323p 2，求直线AB 的斜率k .解：(1)设直线AB 的方程为y ＝kx ＋p2，A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧x 2＝2py ，y ＝kx ＋p 2，得x 2－2pkx －p 2＝0， 则⎩⎪⎨⎪⎧x 1＋x 2＝2pk ，x 1·x 2＝－p 2， 所以OA →·OB →＝x 1·x 2＋y 1·y 2＝－34p 2.(2)由x 2＝2py ，知y ′＝xp，所以抛物线在A ，B 两点处的切线的斜率分别为x 1p ，x 2p，所以直线AM 的方程为y －y 1＝x 1p(x －x 1)，直线BM 的方程为y －y 2＝x 2p (x －x 2)，则可得M ⎝⎛⎭⎪⎫pk ，－p 2.所以k MF ＝－1k，所以直线MF 与AB 相互垂直．由弦长公式知，|AB |＝k 2＋1|x 1－x 2|＝k 2＋1·4p 2k 2＋4p 2＝2p (k 2＋1)，用－1k代替k 得，|CD |＝2p ⎝ ⎛⎭⎪⎫1k2＋1，四边形ACBD 的面积S ＝12·|AB |·|CD |＝2p 2⎝⎛⎭⎪⎫2＋k 2＋1k 2＝323p 2，解得k 2＝3或k 2＝13，即k ＝±3或k ＝±33.。

A 组基础对点练1．(2018·沈阳质量监测)抛物线y ＝4ax 2(a ≠0)的焦点坐标是()A ．(0，a)B ．(a,0) C.0，116aD.116，0解析：将y ＝4ax 2(a ≠0)化为标准方程得x 2＝14a y(a ≠0)，所以焦点坐标为0，116a，所以选C. 答案：C2．(2018·辽宁五校联考)已知AB 是抛物线y 2＝2x 的一条焦点弦，|AB |＝4，则AB 中点C 的横坐标是()A ．2 B.12C.32D.52解析：设A(x 1，y 1)，B(x 2，y 2)，则|AB|＝x 1＋x 2＋p ＝4，又p ＝1，所以x 1＋x 2＝3，所以点C 的横坐标是x 1＋x 22＝32.答案：C3．(2018·邯郸质检)设F 为抛物线y 2＝2x 的焦点，A 、B 、C 为抛物线上三点，若F 为△ABC的重心，则|FA →|＋|FB →|＋|FC →|的值为()A ．1B ．2C ．3D ．4解析：依题意，设点A(x 1，y 1)、B(x 2，y 2)、C(x 3，y 3)，又焦点F 12，0，x 1＋x 2＋x 3＝3×12＝32，则|FA →|＋|FB →|＋|FC →|＝(x 1＋12)＋(x 2＋12)＋x 3＋12＝(x 1＋x 2＋x 3)＋32＝32＋32＝3.选C.答案：C4．(2018·沈阳质量监测)已知抛物线x 2＝4y 的焦点为F ，准线为l ，P 为抛物线上一点，过P作P A ⊥l 于点A ，当∠AFO ＝30°(O 为坐标原点)时，|PF|＝________.解析：设l 与y 轴的交点为B ，在Rt △ABF 中，∠AFB ＝30°，|BF |＝2，所以|AB|＝233，设P(x 0，y 0)，则x 0＝±233，代入x 2＝4y 中，得y 0＝13，从而|PF|＝|P A|＝y 0＋1＝43. 答案：435．已知抛物线C的方程为y2＝2px(p＞0)，⊙M的方程为x2＋y2＋8x＋12＝0，如果抛物线C 的准线与⊙M相切，那么p的值为__________．解析：将⊙M的方程化为标准方程：(x＋4)2＋y2＝4，圆心坐标为(－4,0)，半径r＝2，又抛物线的准线方程为x＝－p2，∴|4－p2|＝2，解得p＝12或4.答案：12或46.如图，过抛物线y2＝2px(p＞0)的焦点F的直线l依次交抛物线及其准线于点A，B，C，若|BC|＝2|BF|，且|AF|＝3，则抛物线的方程是__________．解析：分别过点A、B作准线的垂线AE、BD，分别交准线于点E、D(图略)，则|BF|＝|BD|，∵|BC|＝2|BF|，∴|BC|＝2|BD|，∴∠BCD＝30°，又|AE|＝|AF|＝3，∴|AC|＝6，即点F是AC的中点，根据题意得p＝32，∴抛物线的方程是y2＝3x.答案：y2＝3x7．已知抛物线y2＝4px(p＞0)的焦点为F，圆W：(x＋p)2＋y2＝p2的圆心到过点F的直线l 的距离为p.(1)求直线l的斜率；(2)若直线l与抛物线交于A、B两点，△WAB的面积为8，求抛物线的方程．解析：(1)易知抛物线y2＝4px(p＞0)的焦点为F(p,0)，依题意直线l的斜率存在且不为0，设直线l的方程为x＝my＋p，因为W(－p,0)，所以点W到直线l的距离为|－p－p|1＋－m2＝p，解得m＝±3，所以直线l的斜率为±33.(2)由(1)知直线l的方程为x＝±3y＋p，由于两条直线关于x轴对称，不妨取x＝3y＋p，联立x＝3y＋p，y2＝4px，消去x得y2－43py－4p2＝0，设A(x1，y1)，B(x2，y2)，则y1＋y2＝43p，y1y2＝－4p2，所以|AB|＝1＋32·43p2＋4×4p2＝16p，因为△WAB的面积为8，所以12p×16p＝8，得p＝1，所以抛物线的方程为y2＝4x.8．已知抛物线C1：x2＝2py(p＞0)，O是坐标原点，点A，B为抛物线C1上异于O点的两点，以OA为直径的圆C2过点 B.(1)若A(－2,1)，求p的值以及圆C2的方程；(2)求圆C2的面积S的最小值(用p表示)．解析：(1)∵A(－2,1)在抛物线C 1上，∴4＝2p ，p ＝2.又圆C 2的圆心为－1，12，半径为|OA|2＝52，∴圆C 2的方程为(x ＋1)2＋y －122＝54.(2)记A(x 1，x 212p )，B(x 2，x 222p )．则OB →＝(x 2，x 222p)，AB →＝(x 2－x 1，x 22－x 212p)．由OB →·AB →＝0知，x 2(x 2－x 1)＋x 22x 22－x 214p 2＝0.∵x 2≠0，且x 1≠x 2，∴x 22＋x 1·x 2＝－4p 2，∴x 1＝－x 2＋4p2x 2.∴x 21＝x 22＋16p 4x 22＋8p 2≥216p 4＋8p 2＝16p 2，当且仅当x 22＝16p 4x 22，即x 22＝4p 2时取等号．又|OA|2＝x 21＋x 414p2＝14p2(x 41＋4p 2·x 21)，注意到x 21≥16p 2，∴|OA|2≥14p 2(162·p 4＋4p 2·16p 2)＝80p 2.而S ＝π·|OA |24，∴S ≥20πp 2，即S 的最小值为20πp 2，当且仅当x 22＝4p 2时取得．B 组能力提升练1．(2018·唐山统考)已知抛物线y 2＝2px(p ＞0)，过点C(－2,0)的直线l 交抛物线于A 、B 两点，坐标原点为O ，OA →·OB →＝12. (1)求抛物线的方程；(2)当以AB 为直径的圆与y 轴相切时，求直线l 的方程．解析：(1)设l ：x ＝my －2，代入y 2＝2px ，得y 2－2pmy ＋4p ＝0.(*) 设A(x 1，y 1)，B(x 2，y 2)，则y 1＋y 2＝2pm ，y 1y 2＝4p ，则x 1x 2＝y 21y 224p2＝4.因为OA →·OB →＝12，所以x 1x 2＋y 1y 2＝12，即4＋4p ＝12，得p ＝2，抛物线的方程为y 2＝4x.(2)(1)中(*)式可化为y 2－4my ＋8＝0，y 1＋y 2＝4m ，y 1y 2＝8. 设AB 的中点为M ，则|AB|＝2x M ＝x 1＋x 2＝m(y 1＋y 2)－4＝4m 2－4，①又|AB|＝1＋m 2|y 1－y 2|＝1＋m216m 2－32，②由①②得(1＋m 2)(16m 2－32)＝(4m 2－4)2，解得m 2＝3，m ＝±3.所以，直线l 的方程为x ＋3y ＋2＝0或x －3y ＋2＝0. 2.如图，由部分抛物线：y 2＝mx ＋1(m ＞0，x ≥0)和半圆x 2＋y 2＝r 2(x ≤0)所组成的曲线称为“黄金抛物线C ”，若“黄金抛物线C ”经过点(3,2)和－12，32.(1)求“黄金抛物线C ”的方程；(2)设P(0,1)和Q(0，－1)，过点P 作直线l 与“黄金抛物线C ”相交于A ，P ，B 三点，问是否存在这样的直线l ，使得QP 平分∠AQB ？若存在，求出直线l 的方程；若不存在，说明理由．解析：(1)∵“黄金抛物线C ”过点(3,2)和－12，32，∴r 2＝－122＋322＝1,4＝3m ＋1，∴m ＝1. ∴“黄金抛物线C ”的方程为y 2＝x ＋1(x ≥0)和x 2＋y 2＝1(x ≤0)．(2)假设存在这样的直线l ，使得QP 平分∠AQB ，显然直线l 的斜率存在且不为0，设直线l ：y ＝kx ＋1，联立y ＝kx ＋1y 2＝x ＋1，消去y ，得k 2x 2＋(2k －1)x ＝0，∴x B ＝1－2kk 2，y B ＝1－k k ，即B 1－2k k 2，1－kk，∴k BQ ＝k 1－2k ，联立y ＝kx ＋1x 2＋y 2＝1，消去y ，得(k 2＋1)x 2＋2kx ＝0，∴x A ＝－2k k 2＋1，y B＝1－k2k 2＋1，即A －2kk 2＋1，1－k 2k 2＋1，∴k AQ ＝－1k，∵QP 平分∠AQB ，∴k AQ ＋k BQ ＝0，∴k 1－2k －1k＝0，解得k ＝－1±2，由图形可得k ＝－1－2应舍去，∴k ＝2－1，∴存在直线l ：y ＝(2－1)x ＋1，使得QP 平分∠AQB.。

第九章 解析几何 9.7 抛物线 理1．抛物线的概念平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线． 2．抛物线的标准方程与几何性质【知识拓展】1．抛物线y 2＝2px (p >0)上一点P (x 0，y 0)到焦点F ⎝ ⎛⎭⎪⎫p 2，0的距离|PF |＝x 0＋p2，也称为抛物线的焦半径．2．y 2＝ax 的焦点坐标为⎝ ⎛⎭⎪⎫a 4，0，准线方程为x ＝－a4.3．设AB 是过抛物线y 2＝2px (p >0)焦点F 的弦， 若A (x 1，y 1)，B (x 2，y 2)，则(1)x 1x 2＝p 24，y 1y 2＝－p 2.(2)弦长|AB |＝x 1＋x 2＋p ＝2psin 2α(α为弦AB 的倾斜角)．(3)以弦AB 为直径的圆与准线相切．(4)通径：过焦点垂直于对称轴的弦，长等于2p ，通径是过焦点最短的弦． 【思考辨析】判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内与一个定点F 和一条定直线l 的距离相等的点的轨迹一定是抛物线．( × ) (2)方程y ＝ax 2(a ≠0)表示的曲线是焦点在x 轴上的抛物线，且其焦点坐标是(a4，0)，准线方程是x ＝－a4.( × )(3)抛物线既是中心对称图形，又是轴对称图形．( × )(4)AB 为抛物线y 2＝2px (p >0)的过焦点F (p 2，0)的弦，若A (x 1，y 1)，B (x 2，y 2)，则x 1x 2＝p 24，y 1y 2＝－p 2，弦长|AB |＝x 1＋x 2＋p .( √ )1．(2016·四川)抛物线y 2＝4x 的焦点坐标是( ) A ．(0,2) B ．(0,1) C ．(2,0) D ．(1,0)答案 D解析 ∵对于抛物线y 2＝ax ，其焦点坐标为⎝ ⎛⎭⎪⎫a4，0，∴对于y 2＝4x ，焦点坐标为(1,0)．2．(2016·甘肃张掖一诊)过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1，y 1)，Q (x 2，y 2)两点，如果x 1＋x 2＝6，则|PQ |等于( ) A ．9 B ．8 C ．7 D ．6 答案 B解析 抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1. 根据题意可得，|PQ |＝|PF |＋|QF |＝x 1＋1＋x 2＋1＝x 1＋x 2＋2＝8.3．设抛物线y 2＝8x 的准线与x 轴交于点Q ，若过点Q 的直线l 与抛物线有公共点，则直线l 的斜率的取值范围是( )A.⎣⎢⎡⎦⎥⎤－12，12 B ．[－2,2]C ．[－1,1]D ．[－4,4]答案 C解析 Q (－2,0)，设直线l 的方程为y ＝k (x ＋2)，代入抛物线方程，消去y 整理得k 2x 2＋(4k 2－8)x ＋4k 2＝0，由Δ＝(4k 2－8)2－4k 2·4k 2＝64(1－k 2)≥0， 解得－1≤k ≤1.4．(教材改编)已知抛物线的顶点是原点，对称轴为坐标轴，并且经过点P (－2，－4)，则该抛物线的标准方程为________________． 答案 y 2＝－8x 或x 2＝－y解析 设抛物线方程为y 2＝2px (p ≠0)或x 2＝2py (p ≠0)．将P (－2，－4)代入，分别得方程为y 2＝－8x 或x 2＝－y .5．(2017·合肥调研)已知抛物线y 2＝2px (p >0)的准线与圆x 2＋y 2－6x －7＝0相切，则p 的值为________． 答案 2解析 抛物线y 2＝2px (p >0)的准线为x ＝－p2，圆x 2＋y 2－6x －7＝0，即(x －3)2＋y 2＝16， 则圆心为(3,0)，半径为4.又因为抛物线y 2＝2px (p >0)的准线与圆x 2＋y 2－6x －7＝0相切，所以3＋p2＝4，解得p ＝2.题型一 抛物线的定义及应用例1 设P 是抛物线y 2＝4x 上的一个动点，若B (3,2)，则|PB |＋|PF |的最小值为________． 答案 4 解析 如图，过点B 作BQ 垂直准线于点Q ， 交抛物线于点P 1，则|P 1Q |＝|P 1F |.则有|PB |＋|PF |≥|P 1B |＋|P 1Q |＝|BQ |＝4.即|PB|＋|PF|的最小值为4.引申探究1．若将本例中的B点坐标改为(3,4)，试求|PB|＋|PF|的最小值．解由题意可知点(3,4)在抛物线的外部．∵|PB|＋|PF|的最小值即为B，F两点间的距离，∴|PB|＋|PF|≥|BF|＝42＋22＝16＋4＝25，即|PB|＋|PF|的最小值为2 5.2．若将本例中的条件改为：已知抛物线方程为y2＝4x，直线l的方程为x－y＋5＝0，在抛物线上有一动点P到y轴的距离为d1，到直线l的距离为d2，求d1＋d2的最小值．解由题意知，抛物线的焦点为F(1,0)．点P到y轴的距离d1＝|PF|－1，所以d1＋d2＝d2＋|PF|－1.易知d2＋|PF|的最小值为点F到直线l的距离，故d2＋|PF|的最小值为|1＋5|12＋－2＝32，所以d1＋d2的最小值为32－1.思维升华与抛物线有关的最值问题，一般情况下都与抛物线的定义有关．由于抛物线的定义在运用上有较大的灵活性，因此此类问题也有一定的难度．“看到准线想焦点，看到焦点想准线”，这是解决抛物线焦点弦有关问题的重要途径．设P是抛物线y2＝4x上的一个动点，则点P到点A(－1,1)的距离与点P到直线x＝－1的距离之和的最小值为________．答案 5解析如图，易知抛物线的焦点为F(1,0)，准线是x＝－1，由抛物线的定义知：点P到直线x＝－1的距离等于点P到F的距离．于是，问题转化为在抛物线上求一点P，使点P到点A(－1,1)的距离与点P到F(1,0)的距离之和最小，显然，连接AF与抛物线相交的点即为满足题意的点，此时最小值为[1－－2＋－2＝ 5.题型二 抛物线的标准方程和几何性质 命题点1 求抛物线的标准方程例2 已知双曲线C 1：x 2a 2－y 2b2＝1(a >0，b >0)的离心率为2.若抛物线C 2：x 2＝2py (p >0)的焦点到双曲线C 1的渐近线的距离为2，则抛物线C 2的方程为( ) A ．x 2＝833yB ．x 2＝1633yC ．x 2＝8y D ．x 2＝16y答案 D解析 ∵x 2a 2－y 2b2＝1的离心率为2，∴c a ＝2，即c 2a 2＝a 2＋b 2a 2＝4，∴b 2a 2＝3，ba＝ 3. x 2＝2py (p >0)的焦点坐标为⎝ ⎛⎭⎪⎫0，p 2，x 2a 2－y2b2＝1的渐近线方程为y ＝±b a x ，即y ＝±3x .由题意得p21＋32＝2，∴p ＝8.故C 2的方程为x 2＝16y .命题点2 抛物线的几何性质例3 已知抛物线y 2＝2px (p >0)的焦点为F ，A (x 1，y 1)，B (x 2，y 2)是过F 的直线与抛物线的两个交点，求证： (1)y 1y 2＝－p 2，x 1x 2＝p 24；(2)1|AF |＋1|BF |为定值； (3)以AB 为直径的圆与抛物线的准线相切． 证明 (1)由已知得抛物线焦点坐标为(p2，0)．由题意可设直线方程为x ＝my ＋p2，代入y 2＝2px ，得y 2＝2p ⎝ ⎛⎭⎪⎫my ＋p 2，即y 2－2pmy －p 2＝0.(*)则y 1，y 2是方程(*)的两个实数根，所以y 1y 2＝－p 2. 因为y 21＝2px 1，y 22＝2px 2，所以y 21y 22＝4p 2x 1x 2，所以x 1x 2＝y 21y 224p 2＝p 44p 2＝p 24.(2)1|AF |＋1|BF |＝1x 1＋p 2＋1x 2＋p2 ＝x 1＋x 2＋px 1x 2＋p 2x 1＋x 2＋p 24.因为x 1x 2＝p 24，x 1＋x 2＝|AB |－p ，代入上式，得1|AF |＋1|BF |＝|AB |p 24＋p2AB |－p ＋p24＝2p(定值)．(3) 设AB 的中点为M (x 0，y 0)，分别过A ，B 作准线的垂线，垂足为C ，D ，过M 作准线的垂线，垂足为N ，则|MN |＝12(|AC |＋|BD |)＝12(|AF |＋|BF |)＝12|AB |.所以以AB 为直径的圆与抛物线的准线相切．思维升华 (1)求抛物线标准方程的常用方法是待定系数法，其关键是判断焦点位置、开口方向，在方程的类型已经确定的前提下，由于标准方程只有一个参数p ，只需一个条件就可以确定抛物线的标准方程．(2)在解决与抛物线的性质有关的问题时，要注意利用几何图形的形象、直观的特点来解题，特别是涉及焦点、顶点、准线的问题更是如此．(1)(2016·全国乙卷)以抛物线C 的顶点为圆心的圆交C 于A ，B 两点，交C 的准线于D ，E 两点．已知|AB |＝42，|DE |＝25，则C 的焦点到准线的距离为( ) A ．2 B ．4 C ．6 D ．8(2)(2016·昆明三中、玉溪一中统考)抛物线y 2＝2px (p >0)的焦点为F ，已知点A 、B 为抛物线上的两个动点，且满足∠AFB ＝120°.过弦AB 的中点M 作抛物线准线的垂线MN ，垂足为N ，则|MN ||AB |的最大值为( ) A.33 B ．1 C.233D ．2 答案 (1)B (2)A解析 (1)不妨设抛物线C ：y 2＝2px (p >0)，则圆的方程可设为x 2＋y 2＝r 2(r >0)，如图，又可设A (x 0,22)，D ⎝ ⎛⎭⎪⎫－p 2，5， 点A (x 0,22)在抛物线y 2＝2px 上，∴8＝2px 0，① 点A (x 0,22)在圆x 2＋y 2＝r 2上，∴x 20＋8＝r 2，②点D ⎝ ⎛⎭⎪⎫－p2，5在圆x 2＋y 2＝r 2上，∴5＋⎝ ⎛⎭⎪⎫p 22＝r 2，③ 联立①②③，解得p ＝4，即C 的焦点到准线的距离为p ＝4，故选B. (2)设|AF |＝a ，|BF |＝b ，分别过A 、B 作准线的垂线，垂足分别为Q 、P ， 由抛物线的定义知，|AF |＝|AQ |，|BF |＝|BP |， 在梯形ABPQ 中，2|MN |＝|AQ |＋|BP |＝a ＋b .|AB |2＝a 2＋b 2－2ab cos 120°＝a 2＋b 2＋ab ＝(a ＋b )2－ab . 又ab ≤(a ＋b2)2，所以(a ＋b )2－ab ≥(a ＋b )2－14(a ＋b )2＝34(a ＋b )2，得到|AB |≥32(a ＋b )， 所以|MN ||AB |≤12a ＋b32a ＋b＝33， 即|MN ||AB |的最大值为33. 题型三 直线与抛物线的综合问题 命题点1 直线与抛物线的交点问题例4 已知抛物线C ：y 2＝8x 与点M (－2,2)，过C 的焦点且斜率为k 的直线与C 交于A 、B 两点．若MA →·MB →＝0，则k ＝________. 答案 2解析 抛物线C 的焦点为F (2,0)，则直线方程为y ＝k (x －2)，与抛物线方程联立，消去y 化简得k 2x 2－(4k 2＋8)x ＋4k 2＝0.设点A (x 1，y 1)，B (x 2，y 2)． 则x 1＋x 2＝4＋8k2，x 1x 2＝4.所以y 1＋y 2＝k (x 1＋x 2)－4k ＝8k，y 1y 2＝k 2[x 1x 2－2(x 1＋x 2)＋4]＝－16.因为MA →·MB →＝(x 1＋2，y 1－2)·(x 2＋2，y 2－2)＝(x 1＋2)(x 2＋2)＋(y 1－2)(y 2－2)＝x 1x 2＋2(x 1＋x 2)＋y 1y 2－2(y 1＋y 2)＋8＝0，将上面各个量代入，化简得k 2－4k ＋4＝0，所以k ＝2. 命题点2 与抛物线弦的中点有关的问题例5 (2016·全国丙卷)已知抛物线C ：y 2＝2x 的焦点为F ，平行于x 轴的两条直线l 1，l 2分别交C 于A ，B 两点，交C 的准线于P ，Q 两点． (1)若F 在线段AB 上，R 是PQ 的中点，证明：AR ∥FQ ；(2)若△PQF 的面积是△ABF 的面积的两倍，求AB 中点的轨迹方程．(1)证明 由题意知，F ⎝ ⎛⎭⎪⎫12，0，设l 1：y ＝a ，l 2：y ＝b ，则ab ≠0，且A ⎝ ⎛⎭⎪⎫a 22，a ，B ⎝ ⎛⎭⎪⎫b 22，b ，P ⎝ ⎛⎭⎪⎫－12，a ，Q ⎝ ⎛⎭⎪⎫－12，b ， R ⎝ ⎛⎭⎪⎫－12，a ＋b 2. 记过A ，B 两点的直线为l ，则l 的方程为2x －(a ＋b )y ＋ab ＝0. 由于F 在线段AB 上，故1＋ab ＝0.记AR 的斜率为k 1，FQ 的斜率为k 2，则k 1＝a －b 1＋a 2＝a －b a 2－ab ＝1a ＝－ab a ＝－b ＝b －0－12－12＝k 2. 所以AR ∥FQ .(2)解 设过AB 的直线为l ，设l 与x 轴的交点为D (x 1,0)， 则S △ABF ＝12|b －a ||FD |＝12|b －a |⎪⎪⎪⎪⎪⎪x 1－12， S △PQF ＝|a －b |2. 由题意可得|b －a |⎪⎪⎪⎪⎪⎪x 1－12＝|a －b |2，所以x 1＝1，x 1＝0(舍去)． 设满足条件的AB 的中点为E (x ，y )． 当AB 与x 轴不垂直时，由k AB ＝k DE 可得2a ＋b ＝y x －1(x ≠1)．而a ＋b 2＝y ，所以y 2＝x －1(x ≠1)．当AB 与x 轴垂直时，E 与D 重合，此时E 点坐标为(1,0)， 所以，所求轨迹方程为y 2＝x －1(x ≠1)．思维升华 (1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系．(2)有关直线与抛物线的弦长问题，要注意直线是否过抛物线的焦点．若过抛物线的焦点，可直接使用公式|AB |＝x 1＋x 2＋p ，若不过焦点，则必须用一般弦长公式．(3)涉及抛物线的弦长、中点、距离等相关问题时，一般利用根与系数的关系采用“设而不求”、“整体代入”等解法．提醒：涉及弦的中点、斜率时一般用“点差法”求解．(2017·北京东城区质检)已知抛物线C ：y 2＝2px (p >0)的焦点为F ，直线y ＝4与y 轴的交点为P ，与C 的交点为Q ，且|QF |＝54|PQ |.(1)求C 的方程；(2)过F 的直线l 与C 相交于A 、B 两点，若AB 的垂直平分线l ′与C 相交于M 、N 两点，且A 、M 、B 、N 四点在同一圆上，求l 的方程．解 (1)设Q (x 0,4)，代入y 2＝2px ，得x 0＝8p.所以|PQ |＝8p ，|QF |＝p 2＋x 0＝p 2＋8p.由题设得p 2＋8p ＝54×8p，解得p ＝－2(舍去)或p ＝2. 所以C 的方程为y 2＝4x . (2)依题意知l 与坐标轴不垂直， 故可设l 的方程为x ＝my ＋1(m ≠0)． 代入y 2＝4x ，得y 2－4my －4＝0.设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝4m ，y 1y 2＝－4. 故AB 的中点为D (2m 2＋1,2m )， |AB |＝m 2＋1|y 1－y 2|＝4(m 2＋1)．又l ′的斜率为－m ，所以l ′的方程为x ＝－1my ＋2m 2＋3.将上式代入y 2＝4x ，并整理得y 2＋4my －4(2m 2＋3)＝0.设M (x 3，y 3)，N (x 4，y 4)，则y 3＋y 4＝－4m，y 3y 4＝－4(2m 2＋3)．故MN 的中点为E (2m 2＋2m 2＋3，－2m)，|MN |＝ 1＋1m2|y 3－y 4|＝m 2＋2m 2＋1m 2，由于MN 垂直平分AB ，故A ，M ，B ，N 四点在同一圆上等价于|AE |＝|BE |＝12|MN |，从而14|AB |2＋|DE |2＝14|MN |2，即4(m 2＋1)2＋(2m ＋2m )2＋(2m2＋2)2＝m 2＋2m 2＋m 4，化简得m 2－1＝0，解得m ＝1或m ＝－1. 所求直线l 的方程为x －y －1＝0或x ＋y －1＝0.7．直线与圆锥曲线问题的求解策略典例 (12分)已知抛物线C ：y ＝mx 2(m >0)，焦点为F ，直线2x －y ＋2＝0交抛物线C 于A ，B 两点，P 是线段AB 的中点，过P 作x 轴的垂线交抛物线C 于点Q . (1)求抛物线C 的焦点坐标；(2)若抛物线C 上有一点R (x R,2)到焦点F 的距离为3，求此时m 的值；(3)是否存在实数m ，使△ABQ 是以Q 为直角顶点的直角三角形？若存在，求出m 的值；若不存在，请说明理由．思维点拨 (3)中证明QA →·QB →＝0.解 (1)∵抛物线C ：x 2＝1m y ，∴它的焦点F (0，14m )．[2分](2)∵|RF |＝y R ＋14m ，∴2＋14m ＝3，得m ＝14.[4分](3)存在，联立方程⎩⎪⎨⎪⎧y ＝mx 2，2x －y ＋2＝0，消去y 得mx 2－2x －2＝0，依题意，有Δ＝(－2)2－4×m ×(－2)>0⇒m >－12.[6分]设A (x 1，mx 21)，B (x 2，mx 22)，则⎩⎪⎨⎪⎧x 1＋x 2＝2m，x 1·x 2＝－2m.(*)∵P 是线段AB 的中点，∴P (x 1＋x 22，mx 21＋mx 222)，即P (1m ，y P )，∴Q (1m ，1m )．[8分]得QA →＝(x 1－1m ，mx 21－1m)，QB →＝(x 2－1m ，mx 22－1m)，若存在实数m ，使△ABQ 是以Q 为直角顶点的直角三角形，则QA →·QB →＝0， 即(x 1－1m )·(x 2－1m )＋(mx 21－1m )(mx 22－1m)＝0，[10分]结合(*)化简得－4m 2－6m＋4＝0，即2m 2－3m －2＝0，∴m ＝2或m ＝－12，而2∈(－12，＋∞)，－12∉(－12，＋∞)．∴存在实数m ＝2，使△ABQ 是以Q 为直角顶点的直角三角形．[12分]解决直线与圆锥曲线的位置关系的一般步骤： 第一步：联立方程，得关于x 或y 的一元二次方程；第二步：写出根与系数的关系，并求出Δ>0时参数范围(或指出直线过曲线内一点)； 第三步：根据题目要求列出关于x 1x 2，x 1＋x 2(或 y 1y 2，y 1＋y 2)的关系式，求得结果； 第四步：反思回顾，查看有无忽略特殊情况．1．(2017·昆明调研)已知抛物线C 的顶点是原点O ，焦点F 在x 轴的正半轴上，经过F 的直线与抛物线C 交于A 、B 两点，如果OA →·OB →＝－12，那么抛物线C 的方程为( ) A ．x 2＝8y B ．x 2＝4y C ．y 2＝8x D ．y 2＝4x答案 C解析 由题意，设抛物线方程为y 2＝2px (p >0)，直线方程为x ＝my ＋p2，联立⎩⎪⎨⎪⎧y 2＝2px ，x ＝my ＋p2，消去x 得y 2－2pmy －p 2＝0，设A (x 1，y 1)，B (x 2，y 2)，则y 1＋y 2＝2pm ，y 1y 2＝－p 2，得OA →·OB →＝x 1x 2＋y 1y 2＝(my 1＋p 2)(my 2＋p 2)＋y 1y 2＝m 2y 1y 2＋pm 2(y 1＋y 2)＋p 24＋y 1y 2＝－34p 2＝－12⇒p ＝4，即抛物线C 的方程为y 2＝8x .2．已知抛物线y 2＝2px (p >0)，过其焦点且斜率为1的直线交抛物线于A 、B 两点，若线段AB 的中点的纵坐标为2，则该抛物线的准线方程为( ) A ．x ＝1 B ．x ＝－1 C ．x ＝2 D ．x ＝－2 答案 B解析 ∵y 2＝2px (p >0)的焦点坐标为(p2，0)，∴过焦点且斜率为1的直线方程为y ＝x －p2，即x ＝y ＋p2，将其代入y 2＝2px ，得y 2＝2py ＋p 2，即y 2－2py －p 2＝0.设A (x 1，y 1)，B (x 2，y 2)， 则y 1＋y 2＝2p ，∴y 1＋y 22＝p ＝2，∴抛物线的方程为y 2＝4x ，其准线方程为x ＝－1.3．(2016·上饶四校联考)设抛物线C ：y 2＝3px (p >0)的焦点为F ，点M 在C 上，|MF |＝5，若以MF 为直径的圆过点(0,2)，则抛物线C 的方程为( ) A ．y 2＝4x 或y 2＝8x B ．y 2＝2x 或y 2＝8x C ．y 2＝4x 或y 2＝16x D ．y 2＝2x 或y 2＝16x答案 C解析 ∵抛物线C ：y 2＝3px (p >0)的焦点为F (3p 4，0)，∴|OF |＝3p4，∵以MF 为直径的圆过点(0,2)，设A (0,2)，连接AF ，AM ，可得AF ⊥AM ，在Rt△AOF 中，|AF |＝4＋9p 216，∴sin∠OAF ＝|OF ||AF |＝3p 44＋9p 216，根据抛物线的定义，得直线AO 切以MF 为直径的圆于点A ， ∴∠OAF ＝∠AMF ，可得在Rt△AMF 中，sin∠AMF ＝|AF ||MF |＝3p 44＋9p 216，∵|MF |＝5，|AF |＝4＋9p 216，∴4＋9p 2165＝3p 44＋9p 216，整理得4＋9p 216＝15p 4，解得p ＝43或p ＝163，∴C 的方程为y 2＝4x 或y 2＝16x .4．已知抛物线y 2＝2px (p >0)的焦点弦AB 的两端点坐标分别为A (x 1，y 1)，B (x 2，y 2)，则y 1y 2x 1x 2的值一定等于( )A ．－4B ．4C ．p 2D ．－p 2答案 A解析 ①若焦点弦AB ⊥x 轴， 则x 1＝x 2＝p 2，∴x 1x 2＝p 24； ∴y 1＝p ，y 2＝－p ，∴y 1y 2＝－p 2， ∴y 1y 2x 1x 2＝－4. ②若焦点弦AB 不垂直于x 轴， 可设AB 的直线方程为y ＝k (x －p2)，联立y 2＝2px ，得k 2x 2－(k 2p ＋2p )x ＋p 2k 24＝0，则x 1x 2＝p 24.∴y 1y 2＝－p 2.故y 1y 2x 1x 2＝－4. 5.如图，过抛物线y 2＝2px (p >0)的焦点F 的直线交抛物线于点A 、B ，交其准线l 于点C ，若|BC |＝2|BF |，且|AF |＝3，则此抛物线的方程为( )A ．y 2＝9x B ．y 2＝6x C ．y 2＝3x D ．y 2＝3x 答案 C 解析 如图，分别过A 、B 作AA 1⊥l 于A 1，BB 1⊥l 于B 1，由抛物线的定义知：|AF |＝|AA 1|，|BF |＝|BB 1|，∵|BC |＝2|BF |，∴|BC |＝2|BB 1|，∴∠BCB 1＝30°，∴∠AFx ＝60°，连接A 1F ，则△AA 1F 为等边三角形，过F 作FF 1⊥AA 1于F 1，则F 1为AA 1的中点，设l 交x 轴于K ，则|KF |＝|A 1F 1|＝12|AA 1|＝12|AF |，即p ＝32，∴抛物线方程为y 2＝3x .故选C.6．抛物线y 2＝4x 的焦点为F ，点P (x ，y )为该抛物线上的动点，若点A (－1,0)，则|PF ||PA |的最小值是( )A.12B.22C.32D.223 答案 B解析 抛物线y 2＝4x 的准线方程为x ＝－1， 如图，过P 作PN 垂直直线x ＝－1于N ，由抛物线的定义可知|PF |＝|PN |，连接PA ， 在Rt△PAN 中，sin∠PAN ＝|PN ||PA |， 当|PN ||PA |＝|PF ||PA |最小时，sin∠PAN 最小， 即∠PAN 最小，即∠PAF 最大，此时，PA 为抛物线的切线，设PA 的方程为y ＝k (x ＋1)，联立⎩⎪⎨⎪⎧y ＝k x ＋，y 2＝4x ，得k 2x 2＋(2k 2－4)x ＋k 2＝0，所以Δ＝(2k 2－4)2－4k 4＝0，解得k ＝±1，所以∠PAF ＝∠NPA ＝45°， |PF ||PA |＝|PN ||PA |＝cos∠NPA ＝22，故选B. 7．设F 为抛物线C ：y 2＝3x 的焦点，过F 且倾斜角为30°的直线交C 于A ，B 两点，则|AB |＝________. 答案 12解析 焦点F 的坐标为⎝ ⎛⎭⎪⎫34，0，方法一 直线AB 的斜率为33， 所以直线AB 的方程为y ＝33⎝ ⎛⎭⎪⎫x －34， 即y ＝33x －34，代入y 2＝3x ，得13x 2－72x ＋316＝0. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝212，所以|AB |＝x 1＋x 2＋p ＝212＋32＝12.方法二 由抛物线焦点弦的性质可得 |AB |＝2p sin 2θ＝3sin 230°＝12. 8．已知抛物线C ：y 2＝2px (p >0)的准线为l ，过M (1,0)且斜率为3的直线与l 相交于点A ，与C 的一个交点为B ，若AM →＝MB →，则p ＝________. 答案 2 解析 如图，由AB 的斜率为3， 知∠α＝60°，又AM →＝MB →， ∴M 为AB 的中点．过点B 作BP 垂直准线l 于点P ， 则∠ABP ＝60°，∴∠BAP ＝30°， ∴|BP |＝12|AB |＝|BM |.∴M 为焦点，即p2＝1，∴p ＝2.9．已知椭圆E 的中心在坐标原点，离心率为12，E 的右焦点与抛物线C ：y 2＝8x 的焦点重合，A ，B 是C 的准线与E 的两个交点，则|AB |＝________.答案 6解析 抛物线y 2＝8x 的焦点为(2,0)， 准线方程为x ＝－2.设椭圆方程为x 2a 2＋y 2b 2＝1(a >b >0)，由题意，c ＝2，c a ＝12，可得a ＝4，b 2＝16－4＝12. 故椭圆方程为x 216＋y 212＝1.把x ＝－2代入椭圆方程，解得y ＝±3. 从而|AB |＝6.*10.设直线l 与抛物线y 2＝4x 相交于A ，B 两点，与圆(x －5)2＋y 2＝r 2(r >0)相切于点M ，且M 为线段AB 的中点．若这样的直线l 恰有4条，则r 的取值范围是________________．答案 (2,4) 解析 如图，设A (x 1，y 1)，B (x 2，y 2)，M (x 0，y 0)，则⎩⎪⎨⎪⎧y 21＝4x 1，y 22＝4x 2，两式相减得，(y 1＋y 2)(y 1－y 2)＝4(x 1－x 2)．当l 的斜率k 不存在时，符合条件的直线l 必有两条． 当k 存在时，x 1≠x 2， 则有y 1＋y 22·y 1－y 2x 1－x 2＝2， 又y 1＋y 2＝2y 0，所以y 0k ＝2. 由CM ⊥AB ，得k ·y 0－0x 0－5＝－1， 即y 0k ＝5－x 0，因此2＝5－x 0，x 0＝3， 即M 必在直线x ＝3上．将x ＝3代入y 2＝4x ， 得y 2＝12，则有－23<y 0<2 3.因为点M 在圆上，所以(x 0－5)2＋y 20＝r 2， 故r 2＝y 20＋4<12＋4＝16.又y 20＋4>4(为保证有4条，在k 存在时，y 0≠0)， 所以4<r 2<16，即2<r <4.11．(2016·沈阳模拟)已知过抛物线y 2＝2px (p >0)的焦点，斜率为22的直线交抛物线于A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)两点，且|AB |＝9.(1)求该抛物线的方程；(2)O 为坐标原点，C 为抛物线上一点，若OC →＝OA →＋λOB →，求λ的值． 解 (1)直线AB 的方程是y ＝22(x －p2)，与y 2＝2px 联立，从而有4x 2－5px ＋p 2＝0. 所以x 1＋x 2＝5p4，由抛物线定义得|AB |＝x 1＋x 2＋p ＝5p4＋p ＝9，所以p ＝4，从而抛物线方程为y 2＝8x .(2)由于p ＝4，则4x 2－5px ＋p 2＝0， 即x 2－5x ＋4＝0，从而x 1＝1，x 2＝4， 于是y 1＝－22，y 2＝42， 从而B (4,42)．设C (x 3，y 3)，则OC →＝(x 3，y 3)＝(1，－22)＋λ(4,42) ＝(4λ＋1,42λ－22)．又y 23＝8x 3，即[22(2λ－1)]2＝8(4λ＋1)， 整理得(2λ－1)2＝4λ＋1， 解得λ＝0或λ＝2.12．设P ，Q 是抛物线y 2＝2px (p >0)上相异两点，P ，Q 到y 轴的距离的积为4，且OP →·OQ →＝0.(1)求该抛物线的标准方程；(2)过点Q 的直线与抛物线的另一交点为R ，与x 轴的交点为T ，且Q 为线段RT 的中点，试求弦PR 长度的最小值．解 (1)设P (x 1，y 1)，Q (x 2，y 2)，∵OP →·OQ →＝0，则x 1x 2＋y 1y 2＝0.又点P ，Q 在抛物线上，∴y 21＝2px 1，y 22＝2px 2，代入得y 212p ·y 222p ＋y 1y 2＝0，y 1y 2＝－4p 2，∴|x 1x 2|＝y 1y 224p2＝4p 2.又|x 1x 2|＝4， ∴4p 2＝4，p ＝1，∴抛物线的标准方程为y 2＝2x .(2)设直线PQ 过点E (a,0)且方程为x ＝my ＋a ，联立方程组⎩⎪⎨⎪⎧x ＝my ＋a ，y 2＝2x ，消去x 得y 2－2my －2a ＝0， ∴⎩⎪⎨⎪⎧y 1＋y 2＝2m ，y 1y 2＝－2a ，①设直线PR 与x 轴交于点M (b,0)， 则可设直线PR 的方程为x ＝ny ＋b ， 并设R (x 3，y 3)，同理可知，⎩⎪⎨⎪⎧y 1＋y 3＝2n ，y 1y 3＝－2b ，②由①②可得y 3y 2＝ba.由题意得，Q 为线段RT 的中点， ∴y 3＝2y 2，∴b ＝2a .又由(1)知，y 1y 2＝－4，代入①， 可得－2a ＝－4，∴a ＝2， ∴b ＝4，y 1y 3＝－8， ∴|PR |＝1＋n 2|y 1－y 3| ＝1＋n 2·y 1＋y 32－4y 1y 3＝21＋n 2·n 2＋8≥4 2. 当n ＝0，即直线PR 垂直于x 轴时， |PR |取最小值4 2.*13.如图，由部分抛物线：y 2＝mx ＋1(m >0，x ≥0)和半圆x 2＋y 2＝r 2(x ≤0)所组成的曲线称为“黄金抛物线C ”，若“黄金抛物线C ”经过点(3,2)和(－12，32)．(1)求“黄金抛物线C ”的方程；(2)设P (0,1)和Q (0，－1)，过点P 作直线l 与“黄金抛物线C ”相交于A ，P ，B 三点，问是否存在这样的直线l ，使得QP 平分∠AQB ？若存在，求出直线l 的方程；若不存在，说明理由．解 (1)∵“黄金抛物线C ”过点(3,2)和(－12，32)，∴r 2＝(－12)2＋(32)2＝1,4＝3m ＋1，∴m ＝1.∴“黄金抛物线C ”的方程为y 2＝x ＋1(x ≥0)和x 2＋y 2＝1(x ≤0)．(2)假设存在这样的直线l ，使得QP 平分∠AQB ，显然直线l 的斜率存在且不为0，设直线l ：y ＝kx ＋1，联立⎩⎪⎨⎪⎧y ＝kx ＋1，y 2＝x ＋1，消去y ，得k 2x 2＋(2k －1)x ＝0，∴x B ＝1－2k k ，y B ＝1－k k，即B (1－2k k 2，1－k k)，∴k BQ ＝k1－2k，联立⎩⎪⎨⎪⎧y ＝kx ＋1，x 2＋y 2＝1，消去y ，得(k 2＋1)x 2＋2kx ＝0，∴x A ＝－2k k 2＋1，y A ＝1－k 2k 2＋1，即A (－2k k 2＋1，1－k2k 2＋1)，∴k AQ ＝－1k，∵QP 平分∠AQB ，∴k AQ ＋k BQ ＝0， ∴k1－2k －1k＝0，解得k ＝－1±2，由图形可得k ＝－1－2应舍去，∴k ＝2－1， ∴存在直线l ：y ＝(2－1)x ＋1，使得QP 平分∠AQB .。

9.7 抛物线一、选择题1．抛物线x 2＝(2a －1)y 的准线方程是y ＝1，则实数a ＝( ) A.52 B.32 C ．－12 D ．－32解析 根据分析把抛物线方程化为x 2＝－2⎝ ⎛⎭⎪⎫12－a y ，则焦参数p ＝12－a ，故抛物线的准线方程是y ＝p 2＝12－a 2，则12－a2＝1，解得a ＝－32.答案 D2．若抛物线y 2＝2px (p >0)的焦点在圆x 2＋y 2＋2x －3＝0上，则p ＝( )A.12 B ．1 学.科. C ．2D ．3解析 ∵抛物线y 2＝2px (p >0)的焦点为(p2，0)在圆x 2＋y 2＋2x －3＝0上，∴p 24＋p－3＝0，解得p ＝2或p ＝－6(舍去)． 答案 C3．已知抛物线y 2＝2px (p ＞0)的准线与圆x 2＋y 2－6x －7＝0相切，则p 的值为( )．A.12B ．1C ．2D ．4 解析 抛物线y 2＝2px (p ＞0)的准线为x ＝－p2，圆x 2＋y 2－6x －7＝0，即(x －3)2＋y 2＝16，则圆心为(3,0)，半径为4；又因抛物线y 2＝2px (p ＞0)的准线与圆x 2＋y 2－6x －7＝0相切，所以3＋p2＝4，解得p ＝2.答案 C4．已知直线l 过抛物线C 的焦点，且与C 的对称轴垂直，l 与C 交于A ，B 两点，|AB |＝12，P 为C 的准线上一点，则△ABP 的面积为( )． A ．18 B ．24 C ．36 D ．48 解析 如图，设抛物线方程为y 2＝2px (p ＞0)． ∵当x ＝p2时，|y |＝p ，∴p ＝|AB |2＝122＝6. 又P 到AB 的距离始终为p ，∴S △ABP ＝12×12×6＝36. 学。

科。

答案 C5. 过抛物线的焦点的直线交抛物线于两点，点是原点，若,则的面积为（ ） A ． B ． C ． D ．答案 C6．将两个顶点在抛物线y 2＝2px (p ＞0)上，另一个顶点是此抛物线焦点的正三角形个数记为n ，则( )．A ．n ＝0B ．n ＝1C ．n ＝2D ．n ≥3 学,科,网Z,X,X,K]解析 结合图象可知，过焦点斜率为33和－33的直线与抛物线各有两个交点，所以能够构成两组正三角形．本题也可以利用代数的方法求解，但显得有些麻烦． 答案 C7．已知点P 是抛物线y 2＝2x 上的一个动点，则点P 到点(0,2)的距离与P 到该抛物线准线的距离之和的最小值为( )A.172 B ．3 C. 5 D.92解析 依题设P 在抛物线准线的投影为P ′，抛物线的焦点为F ，则F ⎝ ⎛⎭⎪⎫12，0.依抛物线的定义知P 到该抛物线准线的距离为|PP ′|＝|PF |，则点P 到点A (0,2)的距离与P 到该抛物线准线的距离之和d ＝|PF |＋|PA |≥|AF |＝⎝ ⎛⎭⎪⎫122＋22＝172. 答案 A 二、填空题8．设抛物线y 2＝2px (p >0)的焦点为F ，点A (0,2)．若线段FA 的中点B 在抛物线上，则B 到该抛物线准线的距离为________．解析 设抛物线的焦点F ⎝ ⎛⎭⎪⎫p 2，0，由B 为线段FA 的中点，所以B ⎝ ⎛⎭⎪⎫p 4，1，代入抛物线方程得p ＝2，则B 到该抛物线准线的距离为p 4＋p 2＝3p 4＝324.答案 3249．已知动圆过点(1,0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为________．解析 设动圆的圆心坐标为(x ，y )，则圆心到点(1,0)的距离与其到直线x ＝－1的距离相等，根据抛物线的定义易知动圆的圆心的轨迹方程为y 2＝4x . 答案 y 2＝4x10．已知抛物线y 2＝4x 的焦点为F ，准线与x 轴的交点为M ，N 为抛物线上的一点，且满足|NF |＝32|MN |，则∠NMF ＝________. Z*xx*k解析 过N 作准线的垂线，垂足是P ，则有PN ＝NF ，∴PN ＝32MN ，∠NMF ＝∠MNP .又cos ∠MNP ＝32， ∴∠MNP ＝π6，即∠NMF ＝π6. 答案π611．设圆C 位于抛物线y 2＝2x 与直线x ＝3所围成的封闭区域(包含边界)内，则圆C 的半径能取到的最大值为________．解析 依题意，结合图形的对称性可知，要使满足题目约束条件的圆的半径最大，圆心位于x 轴上时才有可能，可设圆心坐标是(a,0)(0＜a ＜3)，则由条件知圆的方程是(x －a )2＋y 2＝(3－a )2.由⎩⎨⎧x －a 2＋y 2＝3－a2y 2＝2x消去y 得x 2＋2(1－a )x ＋6a －9＝0，结合图形分析可知，当Δ＝[2(1－a )]2－4(6a －9)＝0且0＜a ＜3，即a ＝4－6时，相应的圆满足题目约束条件，因此所求圆的最大半径是3－a ＝6－1. 答案6－112. 过抛物线的焦点作直线交抛物线于两点，若则= 。