120个常用函数集标注

高等数学公式大全及常见函数图像文件编码（008-TTIG-UTITD-GKBTT-PUUTI-WYTUI-8256）高等数学公式导数公式： 基本积分表：ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ三角函数的有理式积分：一些初等函数：两个重要极限：三角函数公式：·诱导公式：·和差角公式： ·和差化积公式：2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(·倍角公式： ·半角公式： ·正弦定理：R CcB b A a 2sin sin sin === ·余弦定理：C ab b a c cos 2222-+= ·反三角函数性质：arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹（Leibniz ）公式： 中值定理与导数应用： 曲率：定积分的近似计算： 定积分应用相关公式： 空间解析几何和向量代数： 多元函数微分法及应用 微分法在几何上的应用：),,(),,(),,(30))(,,())(,,())(,,(2)},,(),,,(),,,({1),,(0),,(},,{,0),,(0),,(0))(())(())(()()()(),,()()()(000000000000000000000000000000000000000000000000000z y x F z z z y x F y y z y x F x x z z z y x F y y z y x F x x z y x F z y x F z y x F z y x F n z y x M z y x F G G F F G G F F G G F F T z y x G z y x F z z t y y t x x t M t z z t y y t x x z y x M t z t y t x z y x z y x z y x yx y x x z x z z y z y -=-=-=-+-+-==⎪⎩⎪⎨⎧====-'+-'+-''-='-='-⎪⎩⎪⎨⎧===、过此点的法线方程：：、过此点的切平面方程、过此点的法向量：，则：上一点曲面则切向量若空间曲线方程为：处的法平面方程：在点处的切线方程：在点空间曲线ωψϕωψϕωψϕ方向导数与梯度：上的投影。

高等数学公式大全及常见函数图像修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】高等数学公式导数公式：ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x Cx dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ基本积分表：三角函数的有理式积分：一些初等函数：两个重要极限：三角函数公式：·诱导公式：·和差角公式： ·和差化积公式：2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(·倍角公式：·半角公式：·正弦定理：R CcB b A a 2sin sin sin === ·余弦定理：C ab b a c cos 2222-+= ·反三角函数性质：arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹（Leibniz ）公式：中值定理与导数应用：曲率：定积分的近似计算：定积分应用相关公式：空间解析几何和向量代数：多元函数微分法及应用微分法在几何上的应用：),,(),,(),,(30))(,,())(,,())(,,(2)},,(),,,(),,,({1),,(0),,(},,{,0),,(0),,(0))(())(())(()()()(),,()()()(000000000000000000000000000000000000000000000000000z y x F z z z y x F y y z y x F x x z z z y x F y y z y x F x x z y x F z y x F z y x F z y x F n z y x M z y x F G G F F G G F F G G F F T z y x G z y x F z z t y y t x x t M t z z t y y t x x z y x M t z t y t x z y x z y x z y x yx y x x z x z z y z y -=-=-=-+-+-==⎪⎩⎪⎨⎧====-'+-'+-''-='-='-⎪⎩⎪⎨⎧===、过此点的法线方程：：、过此点的切平面方程、过此点的法向量：，则：上一点曲面则切向量若空间曲线方程为：处的法平面方程：在点处的切线方程：在点空间曲线ωψϕωψϕωψϕ方向导数与梯度：上的投影。

高等数学公式导数公式： 基本积分表：三角函数的有理式积分：ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数：两个重要极限：三角函数公式：·诱导公式：·和差角公式： ·和差化积公式：2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin(μμμ·倍角公式： ·半角公式： ·正弦定理：R CcB b A a 2sin sin sin === ·余弦定理：C ab b a c cos 2222-+= ·反三角函数性质：arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹（Leibniz ）公式： 中值定理与导数应用： 曲率：定积分的近似计算： 定积分应用相关公式： 空间解析几何和向量代数： 多元函数微分法及应用 微分法在几何上的应用：),,(),,(),,(30))(,,())(,,())(,,(2)},,(),,,(),,,({1),,(0),,(},,{,0),,(0),,(0))(())(())(()()()(),,()()()(000000000000000000000000000000000000000000000000000z y x F z z z y x F y y z y x F x x z z z y x F y y z y x F x x z y x F z y x F z y x F z y x F n z y x M z y x F G G F F G G F F G G F F T z y x G z y x F z z t y y t x x t M t z z t y y t x x z y x M t z t y t x z y x z y x z y x yx y x x z x z z y z y -=-=-=-+-+-==⎪⎩⎪⎨⎧====-'+-'+-''-='-='-⎪⎩⎪⎨⎧===、过此点的法线方程：：、过此点的切平面方程、过此点的法向量：，则：上一点曲面则切向量若空间曲线方程为：处的法平面方程：在点处的切线方程：在点空间曲线ϖϖωψϕωψϕωψϕ方向导数与梯度：上的投影。

数学函数公式大全，初中数学函数公式大全及图解数学函数公式大全？一般的，在一个变化过程中，假设有两个变量x、y，如果对于任意一个x都有唯一确定的一个y和它对应，那么就称y是x的函数，其中x是自变量，y是因变量，x的取值范围叫做这个函数的定义域，相应y的取值范围叫做函数的值域。

下面所整理的高中数学函数知识点归纳总结，供参考。

一、一次函数定义与定义式:自变量x和因变量y有如下关系:y=kx+b则此时称y是x的一次函数。

特别地，当b=0时，y是x的正比例函数。

即:y=kx(k为常数，k≠0)二、一次函数的性质:1.y的变化值与对应的x的变化值成正比例，比值为k即:y=kx+b(k为任意不为零的实数b取任何实数)2.当x=0时，b为函数在y轴上的截距。

三、一次函数的图像及性质:1.作法与图形:通过如下3个步骤(1)列表;(2)描点;(3)连线，可以作出一次函数的图像--一条直线。

因此，作一次函数的图像只需知道2点，并连成直线即可。

(通常找函数图像与x轴和y轴的交点)2.性质:(1)在一次函数上的任意一点p(x，y)，都满足等式:y=kx+b。

(2)一次函数与y轴交点的坐标总是(0，b)，与x 轴总是交于(-b/k，0)正比例函数的图像总是过原点。

3.k，b与函数图像所在象限:当k0时，直线必通过一、三象限，y随x的增大而增大;当k当b0时，直线必通过一、二象限;当b=0时，直线通过原点当b0时，直线必通过三、四象限。

特别地，当b=o时，直线通过原点o(0，0)表示的是正比例函数的图像。

初中数学函数公式大全？1.三角函数公式：两角和公式sin(a+b) =sinacosb+cosasinb sin(a-b) = sinacosb-cosasinb ? cos(a+b) = cosacosb-sinasinb cos(a-b) =cosacosb+sinasinb tan(a+b) = (tana+tanb)/(1-tanatanb) tan(a-b) = (tana-tanb)/(1+tanatanb) cot(a+b) = (cotacotb-1)/(cotb+cota) ? cot(a-b) = (cotacotb+1)/(cotb-cota)倍角公式sin2a=2sina?cosacos2a=cosa^2-sina^2=1-2sina^2=2cosa^2-1tan2a=2tana/（1-tana^2）（注：sina^2 是sina的平方sin2（a）诱导公式：sin(-α) = -sinαcos(-α) =cosαsin(π/2-α) = cosα cos(π/2-α) = sinαsin(π/2+α) = cosα cos(π/2+α) = -sinαsin(π-α) = sinαcos(π-α) = -cosαsin(π+α) = -sinα cos(π+α) = -cosα tana= sina/cosa tan（π/2＋α）＝－cotα tan（π/2－α）＝cotαtan（π－α）＝－tanα tan（π＋α）＝tanα2.乘法原理：n=n1・n2・......・nn3.加法原理：m=m1+m2+......+mm4.排列组合公式(可以去查）注意：全排列公式：当m＝n时，为全排列pnn=n(n－1)(n－2)…3・2・1＝n！检举回答人的补充 2009-07-16 18:10 .椭圆的标准方程有两种，取决于焦点所在的坐标轴：1）焦点在x轴时，标准方程为：x^2/a^2+y^2/b^2=1 (ab0) 2）焦点在y轴时，标准方程为：x^2/b^2+y^2/a^2=1 (ab0) 2.数列极限：设是一数列，如果存在常数a，当n无限增大时，an无限接近（或趋近）于a，则称数列收敛，a称为数列的极限，或称数列收敛于a，记为liman=a。

高等数学公式大全及常见函数图像
高等数学公式
导数公式：
基本积分表：
三角函数的有理式积分：
一些初等函数： 两个重要极限：
三角函数公式：
·诱导公式：
函数
角A
sin
cos
tg
ctg
-α
-sinα
cosα
-tgα
-ctgα
90°-α
cosα
sinα
ctgα
tgα
90°+α
cosα
-sinα
-ctgα
-tgα
180°-α
·半角公式：
·正弦定理： ·余弦定理：
·反三角函数性质：
高阶导数公式——莱布尼兹（Leibniz）公式：
中值定理与导数应用：
曲率：
定积分的近似计算：
定积分应用相关公式：
空间解析几何和向量代数：
多元函数微分法及应用
微分法在几何上的应用：
方向导数与梯度：
多元函数的极值及其求法：
重积分及其应用：
柱面坐标和球面坐标：
(*)式的通解
两个不相等实根
两个相等实根
一对共轭复根
二阶常系数非齐次线性微分方程
sinα
-cosα
-tgα
-ctgα
180°+α
-sinα
-cosα
tgα
ctgα
270°-α
-cosα
-sinα
ctgα
tgα
270°+α-cLeabharlann sαsinα-ctgα
-tgα
360°-α
-sinα
cosα
-tgα
-ctgα
360°+α
sinα

高等数学公式导数公式：基本积分表：三角函数的有理式积分：222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=，　，　，　ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数： 两个重要极限：三角函数公式： ·诱导公式：·和差角公式： ·和差化积公式：2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβα-+-+=--+=+βαβαβαβαβαβαβαβαβαtg tg tg tg tg ⋅±=±=±±=±1)(sin sin cos cos )cos(sin cos cos sin )sin(μμxxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22）双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·倍角公式：·半角公式：ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理：R CcB b A a 2sin sin sin === ·余弦定理：C ab b a c cos 2222-+=·反三角函数性质：arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹（Leibniz ）公式：)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑ΛΛΛ中值定理与导数应用：拉格朗日中值定理。

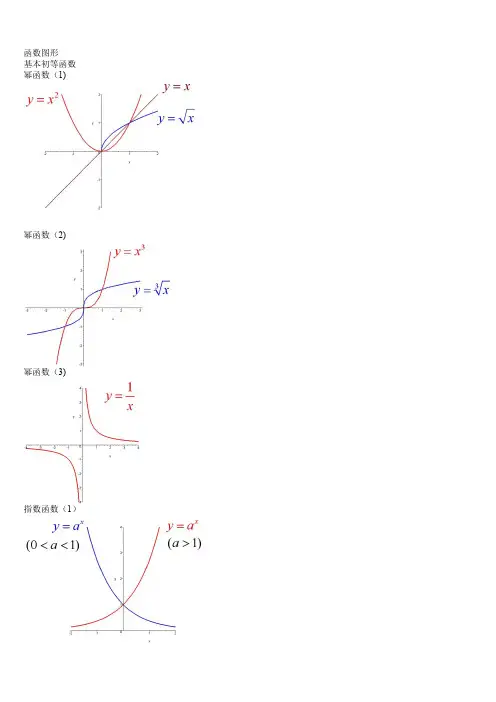
函数图形 基本初等函数 幂函数（1)幂函数（2)幂函数（3)指数函数（1）指数函数（2）指数函数（3）对数函数（1）对数函数（2）三角函数（1）三角函数（2）三角函数（3）三角函数（4）反三角函数（1）反三角函数（2）反三角函数（3）反三角函数（5）反三角函数（6）反三角函数（7）双曲函数（1）双曲函数（2）双曲函数（3）双曲函数（5）双曲函数（6）双曲函数（7）反双曲函数（2）反双曲函数（3）反双曲函数（4）反双曲函数（6）y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质 (1) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x 的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e 的值(1)e的值(2)等价无穷小(x->0)sinx等价于x arcsinx等价于xtanx 等价于xarctanx 等价于x 1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性 (1)数列的夹逼性 (2)赠送以下资料考试知识点技巧大全一、考试中途应饮葡萄糖水大脑是记忆的场所，脑中有数亿个神经细胞在不停地进行着繁重的活动,大脑细胞活动需要大量能量。

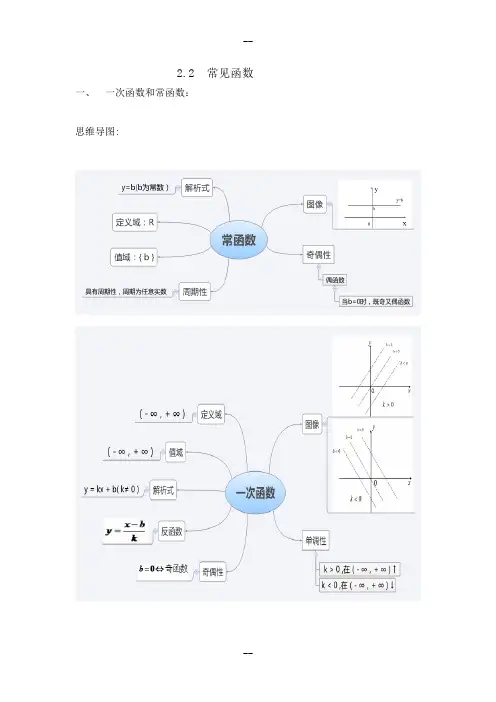
2.2常见函数一、一次函数和常函数：思维导图:（一） 、一次函数 (二）、常函数 定义域：（- ∞,+ ∞） 定义域: （- ∞,+ ∞） 值 域:（- ∞,+ ∞) 正 k=０ 反 值 域:{ b }解析式：y = ｋｘ ＋ b ( ｋ≠ 0 ) 解析式:y ＝ ｂ （ b 为常数)图 像:一条与x 轴、y 轴相交的直线 图 像：一条与x 轴平行或重合的直线b x x ｏ x ｂ=0b<0b=0 b>0b<０Ｋ ＞ 0 k < 0单调性: ｋ > 0 ,在（- ∞,+ ∞）↑ 单调性:在(－ ∞,＋ ∞)上不单调k ＜ 0 ,在(- ∞,＋ ∞)↓奇偶性：奇函数⇔=0b 奇偶性: 偶函数 非奇非偶⇔≠0b周期性: 非周期函数 周期性:周期函数,周期为任意非零实数反函数:在（- ∞，＋ ∞)上有反函数 反函数:在(－ ∞，＋ ∞)上没有反函数反函数仍是一次函数例题：-- 二、二次函数1、定义域:(- ∞,＋ ∞）2、值 域： ),44[,02+∞-∈>ab ac y a]44,(,02ab ac y a --∞∈<3、解析式：)0(2≠++=a c bx ax y ４、图 像:一条开口向上或向下的抛物线开口向下，开口向上；正负：增大，开口缩小绝对值：随着,00<>a a a a正半轴相交与负半轴相交与y c y c c,0,0><对称轴：ab x 2-=对称轴： ；)44,2(2ab ac ab --顶点： 轴交点个数图像与x ac b →-=∆42:与x 轴交点的个数。

两个交点,0>∆一个交点,0=∆无交点,0<∆5、单调性:↑+∞-↓--∞>),2[]2,(,0ab ab a↓+∞-↑--∞<),2[]2,(,0ab ab a６、奇偶性:偶函数⇔=0b 7、周期性：非周期函数８、反函数：在(- ∞，＋ ∞)上无反函数,上及其子集上有反函数或在),2[]2,(+∞---∞ab ab例题:三、反比例函数和重要的分式函数(一）、反比例函数 (二)、分式函数bax dcx y ++= 定义域：（- ∞，0)∪(０，+ ∞） 定义域：),(),(+∞---∞aba b 值 域:（－ ∞，0)∪（０,+ ∞) 值 域: ),(),(+∞-∞a c a c解析式：)0()(≠=k xk x f 解析式:)(a bx b ax d cx y -≠++=图 像:以x 轴、y 轴为渐进线的双曲线 图 像：以abx -=和a c y =为渐近线的双曲线y y0 x 0 xk > 0 k ＜ 0单调性： k>0,(- ∞,0)↓,(０,＋ ∞)↓ 单调性:在),(a b --∞和),(+∞-ab上 k<0,(- ∞，０）↑,(0,＋ ∞）↑ 单调性相同 奇偶性:奇函数 奇偶性：非奇非偶 对称性:关于原点对称 对称性:关于点),(aca b -成中心对称周期性:非周期函数 周期性:非周期函数 反函数:在定义域上有反函数， 反函数：在定义域有反函数,反函数是其本身。

各种函数归纳总结函数是计算机编程中最基本的组织单元之一，能够接受输入参数并产生输出结果。

在编程中，我们经常会使用各种函数来进行不同的计算和操作。

本文将对一些常见的函数进行归纳总结，介绍它们的功能和使用方法。

一、数学函数1. abs() 函数：返回指定数字的绝对值。

例如，abs(-5) 的结果为 5。

2. pow() 函数：返回指定数字的指定次方。

例如，pow(2, 3) 的结果为 8，表示 2 的 3 次方。

3. sqrt() 函数：返回指定数字的平方根。

例如，sqrt(16) 的结果为4。

4. round() 函数：返回指定数字的四舍五入值。

例如，round(3.6) 的结果为 4。

二、字符串函数1. len() 函数：返回指定字符串的长度。

例如，len("Hello") 的结果为5，表示字符串包含5个字符。

2. upper() 函数：将指定字符串中的所有字母转换为大写字母。

例如，upper("hello") 的结果为 "HELLO"。

3. lower() 函数：将指定字符串中的所有字母转换为小写字母。

例如，lower("HELLO") 的结果为 "hello"。

4. strip() 函数：去除指定字符串首尾的空格。

例如，strip(" hello ")的结果为 "hello"。

三、列表函数1. len() 函数：返回指定列表的长度。

例如，len([1, 2, 3]) 的结果为 3，表示列表包含3个元素。

2. append() 函数：向列表末尾添加指定元素。

例如，my_list = [1, 2,3]，执行 my_list.append(4) 后，my_list 的值为 [1, 2, 3, 4]。

3. pop() 函数：移除列表中指定位置的元素并返回该元素的值。

⾼数中常⽤到的三⾓函数公式总表三⾓公式总表⒈L 弧长=αR=nπR 180 S 扇=21L R=21R 2α=3602R n ?π⒉正弦定理：A asin =B b sin =Cc sin = 2R （R 为三⾓形外接圆半径）⒊余弦定理：a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cosc 2=a 2+b2-2ab C cos bca cb A 2cos 222-+=⒋S ⊿=21a a h ?=21ab C sin =21bc A sin =21ac B sin =Rabc 4=2R 2A sin B sin C sin=A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=CB A c sin 2sin sin 2=pr =))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三⾓形内切圆半径)⒌同⾓关系：⑴商的关系：①θtg =x y =θθcos sin =θθsec sin ? ②θθθθθcsc cos sin cos ?===y x ctg ③θθθtg ry==cos sin ④θθθθcsc cos 1sec ?===tg x r ⑤θθθctg rx==sin cos ⑥θθθθsec sin 1csc ?===ctg y r ⑵倒数关系：1sec cos csc sin =?=?=?θθθθθθctg tg ⑶平⽅关系：1csc sec cos sin 222222=-=-=+θθθθθθctg tg ⑷)sin(cos sin 22?θθθ++=+b a b a（其中辅助⾓?与点（a,b ）在同⼀象限，且ab tg =?）⒍函数y=++?)sin(?ωx A k 的图象及性质：（0,0>>A ω）振幅A ，周期T =ωπ2, 频率f =T1, 相位?ω+?x ，初相?⒎五点作图法：令?ω+x 依次为ππππ2,23,,20 求出x 与y ，依点()y x ,作图⒏诱导公试三⾓函数值等于α的同名三⾓函数值，前⾯加上⼀个把α看作锐⾓时，原三⾓函数值的符号；即：函数名不变，符号看象限三⾓函数值等于α的异名三⾓函数值，前⾯加上⼀个把α看作锐⾓时，原三⾓函数值的符号;即：函数名改变，符号看象限⒐和差⾓公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos(µ=± ③βαβαβαtg tg tg tg tg ?±=±µ1)( ④)1)((βαβαβαtg tg tg tg tg ?±=±µ⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ?-?-?-??-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ??=++ ii).1222222=++Ctg B tg C tg A tg B tg A tg ⒑⼆倍⾓公式：(含万能公式) ①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-=③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=⒒三倍⾓公式：①)60sin()60sin(sin 4sin 4sin 33sin 3θθθθθθ+?-?=-= ②)60cos()60cos(cos 4cos 4cos 33cos 3θθθθθθ+?-?=+-=③)60()60(313323θθθθθθθ+?-?=--=tg tg tg tg tg tg tg ⒓半⾓公式：（符号的选择由2θ所在的象限确定）①2cos 12sinθθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg⒔积化和差公式：[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++=()[]βαβαβα--+-=cos )cos(21sin sin ⒕和差化积公式：①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos 2cos 2cos cos βαβαβα-+=+ ④2 sin2sin 2cos cos βαβαβα-+-=- ⒖反三⾓函数：⒗最简单的三⾓⽅程。

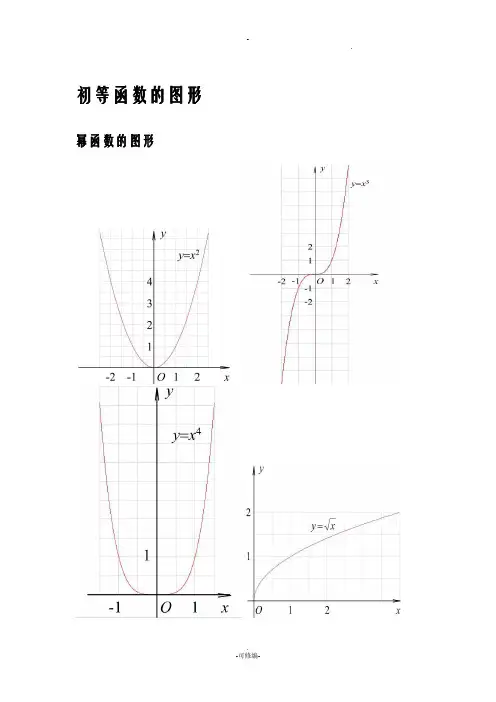
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscαcosα·secαtanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA •CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A)=2cos 1A -cos(2A )=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=AA cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosa cos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan2a a+ cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a -其它公式a •sina+b •cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a •sin(a)-b •cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数 sinh(a)=2e -e -a a cosh(a)=2e e -a a tg h(a)=)cosh()sinh(a a 公式一设α为任意角，终边一样的角的同一三角函数的值相等：sin 〔2k π＋α〕= sin αcos 〔2k π＋α〕= cos αtan 〔2k π＋α〕= tan αcot 〔2k π＋α〕= cot α公式二设α为任意角，π+α的三角函数值与α的三角函数值之间的关系： sin 〔π＋α〕= -sin αtan〔π＋α〕= tanαcot〔π＋α〕= cotα公式三任意角α与-α的三角函数值之间的关系：sin〔-α〕= -sinαcos〔-α〕= cosαtan〔-α〕= -tanαcot〔-α〕= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系：sin〔π-α〕= sinαcos〔π-α〕= -cosαtan〔π-α〕= -tanαcot〔π-α〕= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系：sin〔2π-α〕= -sinαcos〔2π-α〕= cosαtan〔2π-α〕= -tanα公式六2π±α及23π±α与α的三角函数值之间的关系： sin 〔2π+α〕= cos α cos 〔2π+α〕= -sin α tan 〔2π+α〕= -cot α cot 〔2π+α〕= -tan α sin 〔2π-α〕= cos α cos 〔2π-α〕= sin α tan 〔2π-α〕= cot α cot 〔2π-α〕= tan α sin 〔23π+α〕= -cos α cos 〔23π+α〕= sin α tan 〔23π+α〕= -cot α cot 〔23π+α〕= -tan αsin 〔23π-α〕= -cos α cos 〔23π-α〕= -sin α tan 〔23π-α〕= cot α cot 〔23π-α〕= tan α (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用A •sin(ωt+θ)+B •sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明〔全部〕公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b ≤a ≤b|a-b|≥|a|-|b|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注：韦达定理判别式b2-4a=0 注：方程有相等的两实根b2-4ac>0 注：方程有一个实根b2-4ac<0 注：方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注：其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注：角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注：〔a,b〕是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注：D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的外表积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注：其中,S'是直截面面积，L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h--------------------------------------------------------------------------------------------三角函数积化和差和差化积公式记不住就自己推，用两角和差的正余弦：cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减，可以得到2组积化和差:相加：cosAcosB=[cos(A+B)+cos(A-B)]/2相减：sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减，可以得到2组积化和差:相加：sinAcosB=[sin(A+B)+sin(A-B)]/2相减：sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差，然后倒过来就是和差化积了不知道这样你可以记住伐，实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论：(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβsin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。

基本函数公式大全下面是一些基本的函数公式，这些公式适用于数学、物理、化学等领域：1.线性函数线性函数的一般形式为：f(x) = ax + b，其中a和b为常数。

2.二次函数二次函数的一般形式为：f(x) = ax^2 + bx + c，其中a、b和c为常数。

3.平方根函数平方根函数的一般形式为：f(x)=√x，其中x为正实数。

4.立方函数立方函数的一般形式为：f(x)=x^3，其中x为实数。

5.指数函数指数函数的一般形式为：f(x)=a^x，其中a为正实数且不等于16.对数函数对数函数的一般形式为：f(x) = loga(x)，其中a为正实数且不等于17.正弦函数正弦函数的一般形式为：f(x) = sin(x)，其中x为弧度。

8.余弦函数余弦函数的一般形式为：f(x) = cos(x)，其中x为弧度。

9.正切函数正切函数的一般形式为：f(x) = tan(x)，其中x为弧度。

10.反正弦函数反正弦函数的一般形式为：f(x) = arcsin(x)，其中x为-1到1之间的实数。

11.反余弦函数反余弦函数的一般形式为：f(x) = arccos(x)，其中x为-1到1之间的实数。

12.反正切函数反正切函数的一般形式为：f(x) = arctan(x)，其中x为任意实数。

13.绝对值函数绝对值函数的一般形式为：f(x)=，x，其中x为实数。

14.阶乘函数阶乘函数的一般形式为：f(n)=n!，其中n为非负整数。

15.斯特林公式斯特林公式可以用来估计阶乘函数的值：n!≈√(2πn)(n/e)^n，其中n为正整数。

16.泰勒级数泰勒级数是一种将函数表示为无穷级数的方法，可以用来近似计算函数的值。

17.欧拉公式欧拉公式表明对于任意实数x，有e^(ix) = cos(x) + isin(x)，其中e为自然对数的底，i为虚数单位。

18.离散傅里叶变换离散傅里叶变换是一种将离散序列转换为频谱分析的方法，可以用来分析信号和图像。

函函 数 大 全链接函数基本知识函数索引日期与时间函数数学与三角函数逻辑函数查找与引用函数数据库函数文本函数统计函数财务函数工程函数信息函数定义返回从开始日期算起的数月之前或之后的序列号.返回指定月份数之前或之后的某月份的最后的日期序列号.返回自开始日期算起相隔指定天数之前或之后(不包括周末和专门指定的假日)的日期的序列号.计算除了周六、日和休息日之外的工作天数计算期间内的年数、月数、天数按一年360天计算两个日期之间的天数计算指定期间占一年的比率计算从1月1日算起的第几个星期从年、月、日来计算日期从表示日期的文本来计算序列号值从时、分、秒来计算出时间的序列号值从表示时间的文本来计算序列号值计算当前的日期计算当前的日期和时间和星期从日期中提取出"年"从日期中提取出"月"从日期中提取出"日"计算出与日期相对应的星期从时间中提取出"时"从时间中提取出"分"从时间中计算出"分"求和计算对满足条件的单元格的数值求和计算满足条件的单元格人个数计算积先计算多个数组的元素之间的乘积再求和计算平方和计算两个数组中对应元素的平方之和计算两个数组中对应元素的平方差之和计算两个数组中对应元素的差的平方之和计算各种总计值将数值向下舍入为最接近的整数根据指定的位数位置向下舍入计算根据指定的位数位置向下舍入根据指定的位数位置向上舍入根据指定的位数位置四舍五入向下舍入为指定的倍数向上舍入为指定的倍数舍入指定值的倍数向上舍入最接近的偶数向上舍入最接近的奇数计算出商的整数部分计算余数倍数计算最大公约数计算最小公倍数计算绝对值计算正负符号计算阶乘计算双阶倍乘返回从给定元素数目的集合中选取若干元素的排列数计算组合数或二项系数计算多项系数计算幂级数计算平方根计算圆周率的倍数的平方根计算幂乘计算自然对数e的幂乘计算以指定的数值为底的对数计算常用对数计算自然对数计算圆周率的近似值将角度转换为弧度将弧度转换为度计算正弦值计算余弦值计算正切值计算反正弦值计算反余弦值计算反正切值计算x-y坐标的反正切值计算双曲正弦值计算双曲余弦值计算比曲正切值计算双曲反正弦值计算双曲反余弦值计算比曲反正切值值计算矩阵行列式的值计算矩阵的逆矩阵计算两数组矩阵的乘积产生大于或等于0且小于1的随机数产生指定数值之间的随机数根据条件满足与否返回不同的值检测所有的条件是否为真检测任意一项条件是否为真对表示条件的参数的逻辑值求反表示总是为真表示总是为假按照垂直方向搜索区域按照水平方向搜索区域(向量形式)搜索单行或单列(数组形式)搜索区域或查找对应值返回搜索值的相对位置计算指定位置的单元格引用(单元格引用方式)返回行和列交差位置的单元格引用(数组形式)返回行和列交叉位置的值间接引用单元格的内容从参数表中选择特定的值位置返回单元格引用或单元格的位置返回序列号返回行序号计算列数返回引用或数组的行数计算指定区域的区域个数行和列的转置创建超链接从支持COM自动化的程序中获取实时的数据将全角字符(双字节字符)转换成半角字符(单字节字符)将半角字符转换成全角字符将所有英文字母转换成大写字母将所有英文字母转换成寂写字母将英文单词的开头字母转换成大写字母将表示数值的文本转换成数值统计文本字符串中字符数目(计算文本的长度)计算文本的字节数将多个字符文本或单元格中的数据连接在一起，显示在一个单元格中从一个文本字符串的第一个字符开始，截取指定数目的字符从一个文本字符串的最后一个字符开始，截取指定数目的字符从一个文本字符串的指定位置开始，截取指定数目的字符根据指定的位置和字节提取字符检索字符位置(区分大小写)检索字节位置(区分大小写)检索字符位置(不区分大小写)检索字节位置(不区分大小写)替换检索的文本替换指定字符数的文本替换指定字节数的文本删除多余的空格字符删除非打印字符返回字符代码返回与字符代码相对的字符给数值添加_符号和千位分隔符给数值附加上美元符号和千位分隔符将数值转换成泰语的货币格式的文本给数值附加千位分隔符和小数分隔符将数值转换成自由的显示格式文本将数值转换成罗马数字检查两文本是否完全相同根据指定次数重复文本只在参数为文本时返回将数值转换成汉字的文本计算日期和数值的个数计算数据的个数计算空白单元格的个数计算数值数据的平均值计算所有数据的平均值剔除异常数据后计算平均值计算几何平均值计算调和平均值计算数据群的为数计算数据群的众数计算数值的最大值计算所有数据的最大值计算数值的最小值计算所有数据的最小值计算从大到小顺序下某一位置的数值计算从小开始指定位置的数值计算位置(排位)计算区间里所含数值的个数计算百分位数计算四分位数计算使用百分率的位置通过数值计算无偏方差通过所有数据计算无偏方差通过数值计算方差通过所有数据计算方差通过数值推测数据集的标准偏差通过数值推测数据集的标准偏差通过数值计算标准偏差通过数值计算标准偏差计算平均偏差计算变动计算标准化变量计算峰度计算偏斜度使用回归曲线进行预测使用重回归分析进行预测计算回归斜线的斜率计算回归斜线的计算截距通过重回归分析计算系数和常数项计算回归曲线的标准误差计算回归曲线的的适合度使用指数回归曲线进行预测计算指数回归曲线的系数和底数计算相关系数计算相关系数计算协方差计算数据集对应的置信区间计算下限值到上限值概率计算二项分布的概率和累积概率计算累积二项概率在基准值以下时的最大值计算负二项分布的概率计算超几何分布的概率计算POISSON分布的概率计算正态分布的概率和累积概率计算累积正态分布的反函数计算标准正态分布的累积概率计算标准正态分布的累积概率的反函数计算对数正态分布的累积概率计算对数正态分布的累积概率反函数计算卡方分布的上侧概率计算卡方分布的上侧概率的反函数进行卡方检验计算t分布的概率计算t分布的反函数进行t检验检验正态数据集的平均值计算F公布的概率计算F公布的反函数进行t检验进行FISHER变换计算FISHER变换的反函数计算指数分布函数的值计算伽玛公布函数的值计算伽玛公布函数的反函数计算伽玛函数的自然对数计算Beta分布的累积函数的值计算Beta分布的累积函数的反函数计算韦伯分布的值计算贷款的还款额和分期储蓄的存款额计算贷款偿还额的本金相应部分计算贷款偿还额的本金相应部分的累计计算贷款偿还额的利息相应部分计算贷款偿还额的利息相应部分的累计计算本金均分偿还时的利息计算当前价格计算将来的价格计算利率变动存款的将来价格计算贷款的偿还时间和分期储蓄的存款时间计算贷款或分期储蓄的利率计算实际年利率计算名目年利率计算定期现金流量的净现值由不定期的现金流量计算净现值由定期的现金流量计算内部利益率由不定期的现金流量计算内部利益率由定期现金流量计算内部利益率函数计算定期付息证券的利率计算定期付息证券的当前价格计算定期付息证券的利息计算之前的付息日计算最近的付息日到成交日的天数计算成交日到下一付息日的天数计算定期成交日到期日的付息次数。

(1) [数学函数公式大全]高中数学公式大全函数公式高中数学函数知识点总结(1)高中函数公式的变量因变量，自变量。

在用图象表示变量之间的关系时，通常用水平方向的数轴上的点自变量，用竖直方向的数轴上的点表示因变量。

(2)一次函数①若两个变量,间的关系式可以表示成(为常数，不等于0)的形式，则称是的一次函数。

②当=0时，称是的正比例函数。

(3)高中函数的一次函数的图象及性质①把一个函数的自变量与对应的因变量的值分别作为点的横坐标与纵坐标，在直角坐标系内描出它的对应点，所有这些点组成的图形叫做该函数的图象。

②正比例函数=的图象是经过原点的一条直线。

③在一次函数中，当0，O，则经2、3、4象限;当0，0时，则经1、2、4象限;当0，0时，则经1、3、4象限;当0，0时，则经1、2、3象限。

④当0时，的值随值的增大而增大，当0时，的值随值的增大而减少。

(4)高中函数的二次函数①一般式，对称轴是顶点是;②顶点式，对称轴是顶点是;③交点式，其中，是抛物线与x轴的交点(5)高中函数的二次函数的性质①函数的图象关于直线对称。

②时，在对称轴 ()左侧，值随值的增大而减少;在对称轴()右侧;的值随值的增大而增大。

当时，取得最小值③时，在对称轴 ()左侧，值随值的增大而增大;在对称轴()右侧;的值随值的增大而减少。

当时，取得最大值9 高中函数的图形的对称(1)轴对称图形①如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形，这条直线叫做对称轴。

②轴对称图形上关于对称轴对称的两点确定的线段被对称轴垂直平分。

(2)中心对称图形①在平面内，一个图形绕某个点旋转180度，如果旋转前后的图形互相重合，那么这个图形叫做中心对称图形，这个点叫做他的对称中心。

②中心对称图形上的每一对对应点所连成的线段都被对称中心平分。

(2) [数学函数公式大全]高中数学公式大全三角函数公式锐角三角函数公式sin α=∠α的对边 / 斜边cos α=∠α的邻边 / 斜边tan α=∠α的对边 / ∠α的邻边cot α=∠α的邻边 / ∠α的对边倍角公式Sin2A=2SinACosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=(2tanA)/(1-tanA^2)(注SinA^2 是sinA的平方 sin2(A) )三倍角公式sin3α=4sinα·sin(π/3+α)sin(π/3-α)cos3α=4cosα·cos(π/3+α)cos(π/3-α)tan3a=tan a · tan(π/3+a)· tan(π/3-a)三倍角公式推导sin3a=sin(2a+a)=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=(A^2+B^2)^(1/2)sin(α+t)，其中sint=B/(A^2+B^2)^(1/2)cost=A/(A^2+B^2)^(1/2)tant=B/AAsinα+Bcosα=(A^2+B^2)^(1/2)cos(α-t)，tant=A/B 降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=covers(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=(sinα/2+cosα/2)^2=2sina(1-sin2a)+(1-2sin2a)sina=3sina-4sin3acos3a=cos(2a+a)=cos2acosa-sin2asina=(2cos2a-1)cosa-2(1-sin2a)cosa=4cos3a-3cosasin3a=3sina-4sin3a=4sina(3/4-sin2a)=4sina[(√3/2)2-sin2a]=4sina(sin260°-sin2a)=4sina(sin60°+sina)(sin60°-sina)=4sina*2sin[(60+a)/2]cos[(60°-a)/2]*2sin[(60°-a)/2]cos[(60°-a)/2]=4sinasin(60°+a)sin(60°-a)cos3a=4cos3a-3cosa=4cosa(cos2a-3/4)=4cosa[cos2a-(√3/2)2]=4cosa(cos2a-cos230°)=4cosa(cosa+cos30°)(cosa-cos30°)=4cosa*2cos[(a+30°)/2]cos[(a-30°)/2]*{-2sin[(a+30°)/2]sin[(a-30°)/2]} =-4cosasin(a+30°)sin(a-30°)=-4cosasin[90°-(60°-a)]sin[-90°+(60°+a)]=-4cosacos(60°-a)[-cos(60°+a)]=4cosacos(60°-a)cos(60°+a)上述两式相比可得tan3a=tanatan(60°-a)tan(60°+a)半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))学习方法网[三角和sin(α+β+γ)=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sin α·sinβ·sinγcos(α+β+γ)=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sin α·sinβ·cosγtan(α+β+γ)=(tanα+tanβ+tanγ-tanα·tanβ·tanγ)/(1-tanα·tanβ-tanβ·tan γ-tanγ·tanα)两角和差cos(α+β)=cosα·cosβ-sinα·sinβcos(α-β)=cosα·cosβ+sinα·sinβsin(α±β)=sinα·cosβ±cosα·sinβtan(α+β)=(tanα+tanβ)/(1-tanα·tanβ)tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ)和差化积sinθ+sinφ=2 sin[(θ+φ)/2] cos[(θ-φ)/2]sinθ-sinφ=2 cos[(θ+φ)/2] sin[(θ-φ)/2]cosθ+cosφ=2 cos[(θ+φ)/2] cos[(θ-φ)/2]cosθ-cosφ=-2 sin[(θ+φ)/2] sin[(θ-φ)/2] tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB) 积化和差sinαsinβ=[cos(α-β)-cos(α+β)] /2cosαcosβ=[cos(α+β)+cos(α-β)]/2sinαcosβ=[sin(α+β)+sin(α-β)]/2cosαsinβ=[sin(α+β)-sin(α-β)]/2诱导公式sin(-α)=-sinαcos(-α)=cosαtan (—a)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαsin(π/2+α)=cosαcos(π/2+α)=-sinαsin(π-α)=sinαcos(π-α)=-cosαsin(π+α)=-sinαcos(π+α)=-cosαtanA=sinA/cosAtan(π/2+α)=-cotαtan(π/2-α)=cotαtan(π-α)=-tanαtan(π+α)=tanα诱导公式记背诀窍奇变偶不变，符号看象限万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]其它公式(1)(sinα)^2+(cosα)^2=1(2)1+(tanα)^2=(secα)^2(3)1+(cotα)^2=(cscα)^2证明下面两式,只需将一式,左右同除(sinα)^2,第二个除(cosα)^2即可(4)对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-Ctan(A+B)=tan(π-C)(tanA+tanB)/(1-tanAtanB)=(tanπ-tanC)/(1+tanπtanC)整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπ(n∈Z)时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论(5)cotAcotB+cotAcotC+cotBcotC=1(6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)(7)(cosA)^2+(cosB)^2+(cosC)^2=1-2cosAcosBcosC(8)(sinA)^2+(sinB)^2+(sinC)^2=2+2cosAcosBcosC(9)sinα+sin(α+2π/n)+sin(α+2π*2/n)+sin(α+2π*3/n)+……+sin[α+2π*(n-1)/n]=0cosα+cos(α+2π/n)+cos(α+2π*2/n)+cos(α+2π*3/n)+……+cos[α+2π*(n-1)/n]=0 以及sin^2(α)+sin^2(α-2π/3)+sin^2(α+2π/3)=3/2tanAtanBtan(A+B)+tanA+tanB-tan(A+B)=0(3) [数学函数公式大全]数学公式大全高中数学一次/二次函数详解高中数学一次/二次函数详解一一次/二次函数知识详解知识点详解文档包含了一次函数、二次函数的定义、表示、性质、图像、应用等。

（完整）函数大全编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（（完整）函数大全）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为（完整）函数大全的全部内容。

Excel常用函数公式大全1、查找重复内容公式：=IF(COUNTIF(A:A,A2)>1,"重复"，”")。

2、用出生年月来计算年龄公式:=TRUNC((DAYS360（H6，”2009/8/30"，FALSE）)/360，0）。

3、从输入的18位身份证号的出生年月计算公式:=CONCATENATE(MID(E2，7，4)，”/”,MID（E2，11，2），"/”，MID(E2,13,2）)。

4、从输入的身份证号码内让系统自动提取性别，可以输入以下公式：=IF（LEN(C2）=15，IF（MOD（MID（C2，15,1),2)=1,"男"，”女"）,IF（MOD(MID（C2，17，1),2)=1,”男”,”女"））公式内的“C2"代表的是输入身份证号码的单元格。

1、求和: =SUM（K2：K56） -—对K2到K56这一区域进行求和；2、平均数： =AVERAGE（K2:K56) -—对K2 K56这一区域求平均数；3、排名: =RANK(K2,K＄2:K＄56) ——对55名学生的成绩进行排名;4、等级： =IF(K2>=85，"优”，IF（K2〉=74,”良"，IF(K2>=60，”及格”,”不及格"））)5、学期总评: =K2＊0.3+M2*0。

高等数学公式导数公式：基本积分表：三角函数的有理式积分：222212211cos 12sin u dudx x tg u u u x u u x +==+-=+=，　，　，　ax x a a a ctgx x x tgx x x x ctgx x tgx a x x ln 1)(log ln )(csc )(csc sec )(sec csc )(sec )(22='='⋅-='⋅='-='='222211)(11)(11)(arccos 11)(arcsin x arcctgx x arctgx x x x x +-='+='--='-='⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰+±+=±+=+=+=+-=⋅+=⋅+-==+==Ca x x a x dx C shx chxdx C chx shxdx Ca a dx a Cx ctgxdx x C x dx tgx x Cctgx xdx x dx C tgx xdx x dx xx)ln(ln csc csc sec sec csc sin sec cos 22222222C axx a dx C x a xa a x a dx C a x ax a a x dx C a xarctg a x a dx Cctgx x xdx C tgx x xdx Cx ctgxdx C x tgxdx +=-+-+=-++-=-+=++-=++=+=+-=⎰⎰⎰⎰⎰⎰⎰⎰arcsin ln 21ln 211csc ln csc sec ln sec sin ln cos ln 22222222⎰⎰⎰⎰⎰++-=-+-+--=-+++++=+-===-Cax a x a x dx x a Ca x x a a x x dx a x Ca x x a a x x dx a x I nn xdx xdx I n n nn arcsin 22ln 22)ln(221cos sin 2222222222222222222222ππ一些初等函数： 两个重要极限：三角函数公式： ·诱导公式：·和差角公式： ·和差化积公式：2sin2sin 2cos cos 2cos2cos 2cos cos 2sin2cos 2sin sin 2cos2sin2sin sin βαβαβαβαβαβαβαβαβαβαβαβα-+=--+=+-+=--+=+αββαβαβαβαβαβαβαβαβαβαβαctg ctg ctg ctg ctg tg tg tg tg tg ±⋅=±⋅±=±=±±=±1)(1)(sin sin cos cos )cos(sin cos cos sin )sin( xxarthx x x archx x x arshx e e e e chx shx thx e e chx e e shx x x xx xx xx -+=-+±=++=+-==+=-=----11ln21)1ln(1ln(:2:2:22）双曲正切双曲余弦双曲正弦...590457182818284.2)11(lim 1sin lim0==+=∞→→e xxxx x x·倍角公式：·半角公式：ααααααααααααααααααcos 1sin sin cos 1cos 1cos 12cos 1sin sin cos 1cos 1cos 122cos 12cos 2cos 12sin -=+=-+±=+=-=+-±=+±=-±=ctg tg·正弦定理：R CcB b A a 2sin sin sin === ·余弦定理：C ab b a c cos 2222-+=·反三角函数性质：arcctgx arctgx x x -=-=2arccos 2arcsin ππ高阶导数公式——莱布尼兹（Leibniz ）公式：)()()()2()1()(0)()()(!)1()1(!2)1()(n k k n n n n nk k k n k n n uv v u k k n n n v u n n v nu v u v u C uv +++--++''-+'+==---=-∑中值定理与导数应用：拉格朗日中值定理。

常见函数公式及性质概览函数是数学中的基本概念，广泛应用于各个领域。

不同类型的函数有不同的公式和性质。

以下是一些常见函数及其基本公式的大全：1. 一次函数一次函数是最简单的线性函数，形式为y=kx+b，其中k是斜率，b是截距。

2. 二次函数二次函数的形式为y=ax2+bx+c，其中a≠0。

其顶点坐标为(−b2a,c−b2，对称轴为x=−b2a。

4a)3. 幂函数幂函数的一般形式为y=x n，其中n是实数。

特别地，当n=1时，为一次函数；当n=2时，为二次函数；当n=0时（定义域x≠0），为y=1；当n<0时，函数图像经过第二、四象限。

4. 指数函数指数函数的一般形式为y=a x（a>0,a≠1）。

当a>1时，函数图像上升；当0<a<1时，函数图像下降。

5. 对数函数对数函数的一般形式为y=log a x（a>0,a≠1）。

对数函数是指数函数的反函数。

特别地，自然对数底数为e，记为y=lnx。

6. 三角函数●正弦函数：y=sinx●余弦函数：y=cosx●正切函数：y=tanx=sinxcosx（注意cosx≠0）●余切函数：y=cotx=1tanx=cosxsinx（注意sinx≠0）●正割函数：y=secx=1cosx（注意cosx≠0）●余割函数：（注意sinx≠0）7. 反三角函数反三角函数是三角函数的反函数，包括arcsinx，arccosx，arctanx等。

8. 双曲函数双曲函数是类似于三角函数的另一类函数，包括双曲正弦，双曲余弦，双曲正切等。

9. 绝对值函数绝对值函数y=|x|的定义为：|x|={ x if x≥0−x if x<010. 分段函数分段函数是在不同区间上有不同定义的函数，例如：f(x)={ x2if x≥0−x if x<0这些只是函数世界中的冰山一角，不同类型的函数有着各自的特性和应用。

希望这能为你提供一个良好的起点！。