(完整版)圆柱体的体积练习题
- 格式:doc
- 大小:35.51 KB
- 文档页数:4

圆柱体的体积练习题圆柱体是几何中常见的一个形体,它的体积计算是数学中的基础知识之一。
下面通过一些练习题来巩固对圆柱体体积计算方法的理解和运用。
练习题一:某个圆柱体的底面半径为5cm,高度为10cm,求其体积。
解析:圆柱体的体积公式为:V = πr²h,其中V表示体积,r表示底面半径,h表示高度。
根据题目中的数据,代入公式计算:V = π × 5² × 10 = 250π cm³经过计算得知,该圆柱体的体积为250π cm³。
练习题二:一个圆柱体的体积为1000cm³,底面积为50π cm²,求其高度。
解析:根据题目中的数据,我们知道圆柱体的体积为1000cm³,底面积为50π cm²。
圆柱体的体积公式为:V = πr²h,底面积公式为:A = πr²。
将底面积公式代入体积公式,得出高度h的表达式:V = A × h1000 = 50π × h解方程可得:h = 1000 / (50π)h = 20 / πh ≈ 6.37 cm所以,该圆柱体的高度约为6.37 cm。
练习题三:一个圆柱体的体积为150 cm³,高度为8 cm,求其底面半径。
解析:根据题目中的数据,我们知道圆柱体的体积为150 cm³,高度为8 cm。
圆柱体的体积公式为:V = πr²h。
将已知数据代入公式,得出底面半径r的表达式:150 = πr² × 8r² = 150 / (8π)r² = 5.96解方程可得:r ≈ √5.96r ≈ 2.44 cm所以,该圆柱体的底面半径约为2.44 cm。
练习题四:一个圆柱体的底面半径为12 cm,体积为904.32 cm³,求其高度。
解析:根据题目中的数据,我们知道圆柱体的底面半径为12 cm,体积为904.32 cm³。

六年级下册圆柱的体积练习题1.把圆柱的侧面沿高剪开,得到一个,这个的长等于圆柱底面的,宽等于圆柱的,所以圆柱的侧面积等于。
2、单位换算1升=毫升=立方分米=立方厘米 1平方米=平方分米1公顷=平方米15平方厘米=平方分米.5立方米=立方分米 2.4立方分米=升毫升4070立方分米=立方米3立方分米40立方厘米=立方厘米325立方米=立方分米 380毫升=升毫升基础练习 1.将4个棱长为1分米的正方体拼成一个长方体,这个长方体的表面积是平方分米,体积是立方分米。
2.一个圆柱底面半径2分米,侧面积是113.04平方分米,这个圆柱体的高是分米。
3.一根长20厘米的圆钢,分成一样长的两段,表面积增加20平方厘米,原钢材的体积是立方厘米。
4、把一根圆柱形木料截成3段,表面积增加了45.12平方厘米,这根木料的底面积是平方厘米。
5.一个圆柱体的底面半径为r,侧面展开图形是一个正方形。
圆柱的高是。
6、一个圆柱的底面周长是12.56厘米,高是6厘米,那么底面半径是厘米,底面积是平方厘米,侧面积是平方厘米,体积是立方厘米。
7、一个圆柱和一个圆锥的底面积相等,高也相等,那么圆柱的体积是圆锥的倍,圆柱的体积的就等于圆锥的体积。
8一个圆柱体和一个圆锥体的底面积和体积分别相等,已知圆柱体的高6厘米,那么圆锥体的高是厘米。
9、等底等高的圆柱和圆锥的体积相差16立方米,这个圆柱的体积是立方米,圆锥的体积是立方米。
10、一个体积为60立方厘米的圆柱,削成一个最大的圆锥,这个圆锥的体积是立方厘米。
11、圆柱的底面半径是3厘米,体积是6.28立方厘米,这个圆柱的高是厘米。
12、一个圆柱体高4分米,体积是40立方分米,比与它等底的圆锥体的体积多10立方分米。
这个圆锥体的高是分米。
13、把一段圆钢切削成一个最大的圆锥体,切削掉的部分重8千克,这段圆钢重千克.14、一个圆锥的体积是7.2立方米,与它等底等高的圆柱的体积是立方米.15、一个棱长是4分米正方体容器装满水后,倒入一个底面积是12平方分米的圆锥体容器里正好装满,这个圆锥体的高是分米。

小学数学圆柱体的体积练习题一、填空题1. 一个圆柱体的底面半径为5cm,高为8cm,它的体积是_____________ cm³。
2. 一个圆柱体的面积为1570cm²,高为10cm,它的底面半径是_____________ cm。
3. 一个圆柱体的体积为200πcm³,高为20cm,底面半径是_____________ cm。
4. 一个圆柱体的体积为1500cm³,高为15cm,它的底面半径是_____________ cm。
二、计算题1. 计算一个圆柱体的底面积为28cm²,高为10cm的体积。
解答:我们可以使用圆柱体的体积公式V = πr²h。
已知底面积(πr²)= 28cm²,高(h)= 10cm。
代入公式进行计算:V = π × (r=√(28÷π))² × 10≈ 3.14 × (√(28÷3.14))² × 10≈ 3.14 × (5.3)² × 10≈ 3.14 × 28.09 × 10≈ 879.705 cm³所以,这个圆柱体的体积约为879.705 cm³。
2. 已知一个圆柱体的体积为1000cm³,高为5cm,求其底面半径。
解答:我们可以通过圆柱体的体积公式进行计算。
已知体积(V)= 1000cm³,高(h)= 5cm。
代入公式进行计算:1000 = π × r² × 5r² = 1000 ÷ (5 × π)r² ≈ 63.66r ≈ √63.66r ≈ 7.989 cm所以,这个圆柱体的底面半径约为7.989 cm。
三、应用题某饮料公司生产圆柱形包装饮料瓶,底面半径为4cm,高为15cm。

六年级数学圆柱体积练习题(附答案)1、填空。
1)一个圆柱体,底面周长是125.6厘米,高是12厘米,它的侧面积是()平方厘米。
答案:377.6平方厘米。
2)一个圆柱体,底面半径是3厘米,高是5厘米,它的侧面积是()平方厘米,表面积是()平方厘米。
答案:侧面积约为94.2平方厘米,表面积约为150.8平方厘米。
3)把一张长8分米,宽5分米的白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米。
答案:40平方分米。
4)一个圆柱体,底面半径是3厘米,高是15厘米,它的表面积是()平方厘米。
答案:226.08平方厘米。
5)一个长方体和一个圆柱的体积相等,高也相等,那么它们的底面积()。
答案:相等。
6)一根横截面面积是10平方厘米的圆柱形钢材,长是2米,它的体积是()立方厘米。
答案:2000立方厘米。
7)把一个体积是18立方厘米的圆柱削成一个最大的圆锥,削成的圆锥体积是()立方厘米。
答案:6立方厘米。
8)一个圆柱和一个圆锥的体积和底面积相等,圆锥的高是9厘米,圆柱的高是()厘米。
答案:18厘米。
9)圆锥的底面半径是2厘米,体积是6.28厘米,这个圆锥的高是()厘米。
答案:5厘米。
10)一个棱长是4分米的正方体装满水后,倒入一个底面积是12平方分米的圆锥体里正好装满,这个圆锥体的高是()分米。
答案:10分米。
11)把圆柱体的侧面展开,得到一个矩形,它的长等于圆柱底面周长,宽等于圆柱的高.12)一个圆柱体,底面周长是94.2厘米,高是25厘米,它的侧面积是()平方厘米.答案:1884平方厘米。
13)一个圆柱体,底面半径是2厘米,高是6厘米,它的侧面积是()平方厘米.答案:24π平方厘米。
14)一个圆柱体的侧面积是12.56平方厘米,底面半径是2分米,它的高是()厘米.答案:2厘米。
15)把一张长8分米,宽5分米的白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米.答案:40平方分米。
16)把一张边长为5.5厘米的正方形白纸,围成一个圆柱形纸筒,这个纸筒的侧面积是()平方分米.答案:30.8平方分米。
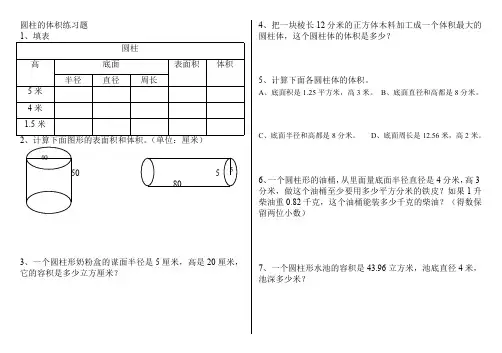
圆柱的体积练习题1、填表圆柱底面高半径直径周长表面积体积5米4米1.5米2(单位:厘米)3、一个圆柱形奶粉盒的谋面半径是5厘米,高是20厘米,它的容积是多少立方厘米?4、把一块棱长12分米的正方体木料加工成一个体积最大的圆柱体,这个圆柱体的体积是多少?5、计算下面各圆柱体的体积。
A、底面积是1.25平方米,高3米。
B、底面直径和高都是8分米。
C、底面半径和高都是8分米。
D、底面周长是12.56米,高2米。
6、一个圆柱形的油桶,从里面量底面半径直径是4分米,高3分米,做这个油桶至少要用多少平方分米的铁皮?如果1升柴油重0.82千克,这个油桶能装多少千克的柴油?(得数保留两位小数)7、一个圆柱形水池的容积是43.96立方米,池底直径4米,池深多少米?8、一口周长是6.28米的圆柱形水井,它的深是10米,平时蓄水深度是井深的0.8倍,这口井平时的水量是多少立方米?9、一个长8分米,宽6分米,高4分米的长方体与一个圆柱体的体积相等,高相等,这个圆柱的底面积是多少?10、一段圆柱形钢材,长50厘米,横截面半径是4厘米,如果每立方厘米钢是7.9克,这段钢材的重量是多少千克?(得数保留一位小数)12、有一段底面是环形的钢管,外圆直径是40厘米,内圆直径是20厘米,这根钢管长250厘米,求这根钢管的体积是多少立方厘米?圆柱的体积练习二1、一个圆柱的底面半径是6厘米,高是2分米,求这个圆柱的体积。
2、小刚有一个圆柱形的水杯,水杯的底面半径是5厘米,高是10厘米,有资料显示:每人每天的正常饮水量大约是1升,小刚一天要喝几杯水?3、一个圆柱形水桶,底面直径和高都是40厘米,用这个水桶容积的85%装水,每升水重1千克,桶中的水大约有多少千克?4、一个底面半径是10米的圆柱形蓄水池,能蓄水2512立方米,若再挖深2米,可蓄水多少立方米?5、一个圆柱形油桶,内底面直径是40厘米,高是50厘米,它的容积是多少升?如果1升柴油重0.85千克,这具油桶可装柴油多少千克?(得数保留整千克)6、一个圆柱形玻璃杯底面半径是10厘米,里面装不水,水的高度是12厘米,把一小块铁块放进杯中,水上升到15厘米,这块铁块重多少克?(每立方厘米铁重7.8克)7、下图是一个长15厘米,宽6厘米、高15厘米的长方体钢制机器零件,中间有一个底面半径为5求这个零件的体积。

圆柱体体积表的练习题一、填空题1. 圆柱体的体积公式是 V = ________。
2. 若圆柱体的底面半径为 r,高为 h,则体积 V = ________。
3. 一个圆柱体的底面直径为 10cm,高为 20cm,其体积为________ cm³。
4. 当圆柱体的底面半径和高都增加一倍时,体积变为原来的________ 倍。
5. 已知圆柱体的体积为500π cm³,底面半径为 5cm,则高为________ cm。
二、选择题A. V = πr²hB. V = πr² + hC. V = 2πrhD. V = 2πr²2. 一个圆柱体的底面半径为 3cm,高为 4cm,其体积为多少?A. 36π cm³B. 12π cm³C. 24π cm³D. 48π cm³3. 若圆柱体的底面半径和高相等,下列哪个选项是正确的?A. 体积为πr²hB. 体积为2πr²C. 体积为4πr²D. 体积为8πr²4. 圆柱体的底面积为25π cm²,高为 10cm,其体积为多少?A. 250π cm³B. 50π cm³C. 125π cm³D. 75π cm³5. 下列哪个条件不能确定圆柱体的体积?A. 底面半径和高B. 底面直径和高C. 底面周长和高D. 底面面积和底面直径三、计算题1. 已知圆柱体的底面半径为 7cm,高为 10cm,求其体积。
2. 一个圆柱体的底面直径为 14cm,高为 30cm,求其体积。
3. 若圆柱体的体积为900π cm³,底面半径为 15cm,求其高。
4. 计算底面半径为 5cm,高为 12cm 的圆柱体体积。
5. 已知圆柱体的底面周长为 31.4cm,高为 20cm,求其体积。
圆柱体体积表的练习题(续)四、应用题1. 一个圆柱形水桶,底面直径为1米,桶内水深0.8米,求桶内水的体积。

小学圆柱体积应用题100例附答案(完整版)题目1一个圆柱的底面半径是2 厘米,高是5 厘米,求这个圆柱的体积。
答案:圆柱体积= 底面积×高= π×2²×5 = 20π≈62.8(立方厘米)题目2圆柱的底面直径是6 厘米,高是8 厘米,体积是多少?答案:底面半径= 6÷2 = 3 厘米,体积= π×3²×8 = 72π≈226.08(立方厘米)题目3一个圆柱,高10 厘米,底面周长是18.84 厘米,求体积。
答案:底面半径= 18.84÷(2×π) = 3 厘米,体积= π×3²×10 = 90π≈282.6(立方厘米)题目4圆柱的底面半径为4 厘米,体积是200.96 立方厘米,求高。
答案:底面积= π×4²= 16π平方厘米,高= 体积÷底面积= 200.96÷(16π) = 4(厘米)题目5已知圆柱的高是12 厘米,体积是301.44 立方厘米,求底面半径。
答案:设底面半径为r 厘米,π×r²×12 = 301.44,r²= 301.44÷(12π) = 8,r = 2√2 厘米题目6一个圆柱形水桶,底面直径40 厘米,高50 厘米,能装多少升水?答案:底面半径= 40÷2 = 20 厘米,体积= π×20²×50 = 20000π≈62800(立方厘米)= 62.8 升题目7圆柱的体积是471 立方厘米,高15 厘米,求底面面积。
答案:底面面积= 体积÷高= 471÷15 = 31.4(平方厘米)题目8一根圆柱形钢材,底面半径 5 厘米,长2 米,这根钢材的体积是多少?答案:2 米= 200 厘米,体积= π×5²×200 = 5000π≈15700(立方厘米)题目9一个圆柱形容器,底面面积是31.4 平方分米,高8 分米,能装多少立方分米的水?答案:体积= 底面积×高= 31.4×8 = 251.2(立方分米)题目10圆柱的底面周长是12.56 分米,高6 分米,体积是多少?答案:底面半径= 12.56÷(2×π) = 2 分米,体积= π×2²×6 = 24π≈75.36(立方分米)题目11一个圆柱形花柱,底面直径 1 米,高3 米,体积是多少立方米?答案:底面半径= 1÷2 = 0.5 米,体积= π×0.5²×3 = 0.75π≈ 2.355(立方米)题目12圆柱的体积是376.8 立方厘米,底面半径3 厘米,求高。

圆柱的体积100道题假如你正在准备中学数学考试,那么,你应该已经知道圆柱的体积怎样计算了。
其实,即使你已经学过了这个概念,仍然需要进行反复的练习,这样你才能真正掌握圆柱体积的计算方法。
本文将介绍100个圆柱体积问题,希望能够帮助你巩固知识。
1. 一个长为10的圆柱,直径为5,求它的体积。
2. 一个半径为3的圆柱,高为10,求它的体积。
3. 一个高为5的圆柱,直径为8,求它的体积。
4. 一个长为15的圆柱,半径为2,求它的体积。
5. 一个半径为5的圆柱,高为6,求它的体积。
6. 一个高为8的圆柱,半径为4,求它的体积。
7. 一个长为14的圆柱,半径为3,求它的体积。
8. 一个高为7的圆柱,半径为5,求它的体积。
9. 一个长度为12,直径为6的圆柱,求它的体积。
10.一个半径为4,高为12的圆柱,求它的体积。
11.一个长为16,半径为3的圆柱,求它的体积。
12.一个高为9,半径为7的圆柱,求它的体积。
13.一个长度为10,直径为3的圆柱,求它的体积。
14.一个半径为6,高为15的圆柱,求它的体积。
15.一个长为18,半径为2的圆柱,求它的体积。
16.一个高为11,半径为4的圆柱,求它的体积。
17.一个长度为20,直径为6的圆柱,求它的体积。
18.一个半径为5,高为8的圆柱,求它的体积。
19.一个长为22,半径为3的圆柱,求它的体积。
20.一个高为13,半径为6的圆柱,求它的体积。
……79.一个长度为56,直径为14的圆柱,求它的体积。
80.一个半径为8,高为18的圆柱,求它的体积。
81.一个长为58,半径为5的圆柱,求它的体积。
82.一个高为19,半径为7的圆柱,求它的体积。
83.一个长度为60,直径为16的圆柱,求它的体积。
84.一个半径为6,高为20的圆柱,求它的体积。
85.一个长为62,半径为7的圆柱,求它的体积。
86.一个高为21,半径为8的圆柱,求它的体积。
87.一个长度为64,直径为18的圆柱,求它的体积。



小学六年级圆柱体体积10题以下是10道适合小学六年级学生练习的圆柱体体积计算题目,旨在帮助学生掌握圆柱体体积的计算方法,并加深对圆柱体空间概念的理解。
1.基础计算:一个圆柱体的底面半径是3厘米,高是5厘米。
它的体积是多少立方厘米?2.改变底面半径计算:一个圆柱体的高是10厘米,如果底面半径增加1厘米,它的体积会增加多少立方厘米?3.改变高度计算:一个圆柱体的底面半径是4厘米,如果高度增加2厘米,它的体积会变成多少立方厘米?4.利用体积相等:一个圆柱体的体积是94.2立方厘米,底面半径是3厘米。
它的高是多少厘米?5.半径与高度的关系:一个圆柱体的底面半径是高的一半。
如果它的体积是314立方厘米,那么它的底面半径和高分别是多少?6.单位换算:一个圆柱体的底面直径是2分米,高是15厘米。
它的体积是多少立方厘米?(1分米= 10厘米)7.实际应用:一个圆柱形水桶的底面半径是20厘米,高是40厘米。
它最多能装多少升水?(1立方分米= 1升)8.组合体积:有两个相同的圆柱体,每个的底面半径是2厘米,高是5厘米。
将它们拼在一起(底面对底面),新的体积是多少?9.分割体积:一个圆柱体的体积是125.6立方厘米,底面半径是4厘米。
如果沿着高平均切成两个相同的小圆柱体,每个小圆柱体的体积是多少?10.综合应用:一个圆柱形粮仓的底面周长是31.4米,高是6米。
如果每立方米粮食重750千克,这个粮仓最多能装多少吨粮食?这些题目涵盖了圆柱体体积计算的不同方面,包括基础计算、单位换算、实际应用以及与其他数学概念的结合。
通过练习这些题目,学生可以巩固对圆柱体体积计算方法的理解,并提升解决实际问题的能力。
小学圆柱体体积试题及答案一、题目描述:下面是关于圆柱体体积的试题,请根据题目要求计算圆柱体的体积,并附上详细答案。
1. 一个圆柱体的底面半径为3cm,高度为8cm,求其体积。
2. 一个圆柱体的底面直径为10m,高度为12m,求其体积。
3. 一个圆柱体的底面半径为5cm,高度为4cm,求其体积。
二、解答及计算过程:1. 圆柱体的体积计算公式为:V = π * r^2 * h,其中 V 表示体积,π取3.14,r表示底面半径,h表示高度。
根据题目中给出的数据,代入公式进行计算:V = 3.14 * 3^2 * 8 = 3.14 * 9 * 8 = 226.08 (立方厘米)答案:该圆柱体的体积为226.08立方厘米。
2. 圆柱体的体积计算公式为:V = π * r^2 * h,其中 V 表示体积,π取3.14,r表示底面半径,h表示高度。
根据题目中给出的数据,代入公式进行计算:V = 3.14 * (10/2)^2 * 12 = 3.14 * 5^2 * 12 = 942 (立方米)答案:该圆柱体的体积为942立方米。
3. 圆柱体的体积计算公式为:V = π * r^2 * h,其中 V 表示体积,π取3.14,r表示底面半径,h表示高度。
根据题目中给出的数据,代入公式进行计算:V = 3.14 * 5^2 * 4 = 3.14 * 25 * 4 = 314 (立方厘米)答案:该圆柱体的体积为314立方厘米。
三、总结:通过以上题目的计算,我们可以得出圆柱体体积的计算公式为:V = π * r^2 * h。
根据题目给出的半径和高度,可以代入公式进行计算得出体积的值。
在计算过程中,要注意保留合适的小数位数,以确保计算结果的准确性。
掌握了圆柱体体积的计算方法,可以帮助我们更好地理解和应用圆柱体的相关概念和性质。
圆柱体的体积练习题〔一〕1 .把一个棱长是6分米的正方体木块,削成一个最大的圆柱体,这个圆柱体的体积是多少立方分米?2.有一个高为6.28分米的圆柱体的机件,它的侧面积展开正好是一个正方形, 求这个机件的体积.3 .要制作容量是62.8升的圆柱形铁桶,如果底面半径是2分米,高应是多少分米?4.一个圆柱形油桶,装满了油,把桶里的油倒出3/4,还剩20升,油桶高8分米,油桶的底面积是多少平方分米?5 .把一种空心混凝土管道,内直径是40厘米,外直径是80厘米,长300厘米, 求浇制100节这种管道需要多少混凝土?6.一个圆柱体的底面半径是4厘米,高8厘米,求它的体积和外表积.7 .做一个无盖的圆柱形铁皮水桶,高30厘米,底面直径20厘米,做这个水桶至少要用多少平方分米的铁皮?这个水桶能装多少千克的水?〔1立方分米水重1千克〕圆柱体的体积练习题〔二〕1、一个圆柱形油桶,从里面量的底面半径是20厘米,高是2分米.这个油桶的容积是多少?2、把一个棱长是6分米的正方形木块,削成一个最大的圆柱,需要削去多少立方分米的木块?3、一个圆柱体的体积是10立方分米,底面积是2.5平方分米,它的高是多少分米?4、一个圆柱的底面周长是12.56分米,高是3米,它的体积是多少立方分米?5、一根长2米的圆木,截成两段后,外表积增加了24平方厘米,这根圆木原来的体积是多少?6、一个底面直径是6厘米的茶杯里,装有7厘米高的水,放入一块小石头,水面上升到10厘米,这个石头的体积是多少立方厘米?7、把一张长62.8厘米,宽31.4厘米的长方形硬纸片,卷成一个圆柱形纸筒, 它的体积是多少?8、一个圆柱体的侧面积是31.4平方厘米,底面周长是6.28厘米,这个圆柱体的体积是多少立方厘米圆柱体的体积练习题〔三〕1、一个圆柱体汽油桶,从里面量底面半径20厘米、高1米.如果每立方米汽油重0.73千克,这个油桶最多能装汽油多少千克?2、把一个棱长6分米的正方体木块切削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?3、将一个棱长为6分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱有多长?4、一个底面半径为3分米,高为8分米圆柱形水槽,把一块石块完全浸入这个水槽,水面上升了2分米,这块石块的体积是多少?5、一个无盖的圆柱形水桶,侧面积是188.4平方分米,底面周长是62.8分米做这个水桶至少要多少平方分米?这个水桶的容积是多少立方分米?6、把一个长、宽、高分别是9cm 7cm 3cm的长方体铁块和一个棱长是5cm的正方体铁块,熔铸成一个圆柱体.这个圆柱体的底面直径是20cm,高是多少厘米?7、将一个圆柱体沿着底面直径切成两个半圆柱,外表积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米?8、用一块长50厘米,宽30厘米的长方形铁皮做圆柱形容器的侧面,再另用一块铁皮做底,怎样做才能使此容器的容积最大?9、用一块长60厘米、宽40厘米的铁皮做圆柱形水桶的侧面,另找一块铁皮做底.这样做成的铁桶的容积最大是多少?圆柱体的体积练习题〔四〕1、一个长方体长7厘米,宽4厘米,高6厘米,把它削成一个体积最大的圆柱体,圆柱体的体积是多少?2、在一只底面半径为20厘米的圆柱形小桶里,有一半径为10厘米的圆柱形钢材浸没在水中.当钢材从桶里取出后,桶里的水下降了3厘米.求这段钢材的长.3、在半径为20厘米的圆柱形储水桶里,有一段截面为正方形的方钢浸没在水中, 正方形的边长是4厘米.当这段方钢从水中取出时,桶里的水面下降了0.5厘米这段方钢长多少厘米?4、一个圆柱形的玻璃杯中盛有水,水面高 2.5cm,玻璃杯内侧的底面积是72平方厘米,在这个杯中放进棱长6cm的正方体铁块后,水面没有淹没铁块,这时水面高多少厘米?5、有一种饮料瓶的瓶身呈圆柱形〔不包括瓶颈〕,容积是30分米3.现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余局部的高度为5厘米. 瓶内现有饮料多少立方分米?6、把一个底面半径是1厘米的圆柱体侧面展开,得到一个正方形,这个圆柱体的体积是多少立方厘米?7、在一底面半径为30厘米的圆柱形容器内,有一半径为20 H米的圆柱形钢材浸没在水中.当取出钢材之后,水面下降了4厘米.求圆钢的长度.。
圆柱的体积练习题圆柱的体积练习题圆柱是我们日常生活中常见的几何体之一,它的形状简单而又美观。
在几何学中,我们经常需要计算圆柱的体积,因此掌握计算圆柱体积的方法是非常重要的。
本文将通过一些练习题来帮助读者巩固对圆柱体积的理解和计算能力。
练习题一:已知圆柱的底面半径为5厘米,高度为10厘米,求其体积。
解析:圆柱的体积公式为V = πr²h,其中V表示体积,π表示圆周率(取近似值3.14),r表示底面半径,h表示高度。
根据题目中给出的数据,代入公式进行计算即可得到答案。
V = 3.14 * 5² * 10 = 3.14 * 25 * 10 = 785立方厘米练习题二:已知圆柱的体积为1000立方米,底面半径为8米,求其高度。
解析:根据圆柱的体积公式V = πr²h,我们可以通过已知的体积和底面半径来求解高度。
将已知的数据代入公式,可以得到关于h的方程式,然后解方程即可求得高度。
1000 = 3.14 * 8² * h解方程可得h = 1000 / (3.14 * 64) ≈ 4.99米练习题三:已知圆柱的体积为200立方厘米,高度为6厘米,求其底面半径。
解析:同样地,我们可以利用圆柱的体积公式来求解底面半径。
将已知的数据代入公式,得到关于r的方程式,然后解方程即可求得底面半径。
200 = 3.14 * r² * 6解方程可得r² = 200 / (3.14 * 6) ≈ 10.17r ≈ √10.17 ≈ 3.19厘米练习题四:已知圆柱的体积为5000立方米,高度为15米,求其底面半径。
解析:同样地,我们可以利用圆柱的体积公式来求解底面半径。
将已知的数据代入公式,得到关于r的方程式,然后解方程即可求得底面半径。
5000 = 3.14 * r² * 15解方程可得r² = 5000 / (3.14 * 15) ≈ 33.56r ≈ √33.56 ≈ 5.8米通过以上练习题,我们可以看到计算圆柱体积的方法是相对简单的,只需要将已知的数据代入体积公式,并进行简单的计算即可得到答案。
圆柱的体积专项练习60题(有答案)ok1.一个长为4米,宽为2米的长方形,以其长边为轴旋转一周后,得到一个圆柱体。
该圆柱体的体积为16π立方米。
2.根据所给的数据,利用圆柱体的表面展开图计算其体积。
答案为75.36立方米。
3.以长方形纸片的虚线为剪切线,将阴影部分剪下,围成一个圆柱体。
圆柱体的体积可以表示为V=πr^2h。
当r=8.91厘米,π取3.14时,圆柱体的体积为1976.28立方毫米。
4.把长为18.84米,宽为12米的长方形铁皮卷成一个圆筒,再加上一个底部,形成一个铁桶。
该铁桶的最大容积为1357.17立方米。
5.将长为3米,宽为2米,高为5米的长方体木料削成一个最大的圆柱体。
该圆柱体的体积为6.283π立方米。
6.将长方体木料,长为8厘米,宽为6厘米,高为10厘米加工成一个最大的圆柱形模型。
该圆柱形模型的体积为150.796π立方厘米。
7.将长为30厘米的圆柱钢筋锯成两段同样的小圆柱,表面积增加了40平方厘米。
原来圆柱形钢筋的体积为141.371π立方厘米。
8.已知圆柱的高为5dm,过底面圆心垂直切开,将圆柱分成相等的两半,表面积增加60dm^2.该圆柱的体积为29.166π立方分米。
9.将圆柱形木料沿底面直径劈成两半,表面积增加120平方厘米。
若拦腰截成两个小圆柱,表面积增加157平方厘米。
原圆柱形木料的体积为1047.198π立方毫米。
10.将圆柱体削成最大的圆锥体,削去的体积为12.56立方米。
已知圆柱的底面周长为6.28米,求圆柱的高。
圆柱的高为2.5米。
11.将长为1.5米的圆柱形钢材截成三段后,表面积比原来增加了9.6平方分米。
该钢材原来的体积为44.178π立方分米。
12.将长为2米的圆柱形木料截成相等的三段,表面积增加24平方厘米。
原来的木料的体积为314.159π立方厘米。
13.将长方体木块,长为10米,宽为8米,高为6米削成一个最大的圆柱体。
该圆柱的体积为100π立方米。
圆柱的体积练习题圆柱是几何学中常见的三维图形,它由一个圆形的底面和与底面平行且与圆周相切的两个平行面组成。
计算圆柱的体积是几何学中的一个重要问题。
在本文中,我们将通过一些练习题来巩固我们对圆柱体积的计算方法的理解。
练习题1:一个圆柱的底面半径为4 cm,高度为10 cm,求其体积。
解题方法:根据圆柱的体积公式 V = πr²h,其中 V 表示体积,r 表示底面半径,h 表示高度。
将给定的数值代入公式,计算得到体积:V = π× 4²× 10 = 160π cm³练习题2:一个圆柱的体积为500 cm³,底面半径为6 cm,求其高度。
解题方法:根据圆柱的体积公式 V = πr²h,将给定的数值代入公式,解方程求得高度 h:h = 500 / (36π) ≈ 4.39 cm练习题3:一个圆柱的体积为1000 cm³,高度为8 cm,求其底面半径。
解题方法:根据圆柱的体积公式 V = πr²h,将给定的数值代入公式,解方程求得底面半径 r:1000 = πr²× 8r² = 1000 / (8π)r ≈√(1000 / (8π)) ≈ 5.03 cm练习题4:一个圆柱的体积为150π cm³,高度为12 cm,求其底面半径。
解题方法:根据圆柱的体积公式 V = πr²h,将给定的数值代入公式,解方程求得底面半径 r:r² = (150π× 12) / πr ≈√(150 × 12) ≈ 18.83 cm通过以上练习题,我们巩固了计算圆柱体积的方法。
计算圆柱体积的关键是熟练掌握圆柱的体积公式 V = πr²h,并且能够根据已知条件进行适当的代入和求解。
在解题过程中,我们还需要注意单位的转换和计算的准确性。
通过这些练习题,我们加深了对圆柱体积计算的理解,并学会了如何根据已知条件求解未知量。
圆柱体积练习题圆柱体是由一个圆形的底面和与底面平行的上下两个平行圆形面围成的立体。
计算圆柱体的体积是数学中一个基本的几何运算。
下面将介绍一些圆柱体积的练习题,帮助你熟练掌握计算圆柱体积的方法。
练习题1:一个圆柱体的底面半径为4 cm,高度为10 cm,求其体积。
解答:首先根据圆柱体的体积公式V=πr²h,其中r为底面半径,h为高度,π取近似值3.14。
将题目中给出的数值代入公式计算:V = 3.14 * 4² * 10V ≈ 3.14 * 16 * 10V ≈ 502.4 cm³练习题2:一个油桶的形状是一个圆柱体,底面半径为2 m,高度为3 m。
如果将油桶倒置,油从底部倒出,剩余的体积能存储多少升的油?解答:将油桶倒置后,剩余的体积即为底面面积乘以高度。
油桶的底面半径为2 m,高度为3 m。
首先计算底面面积,使用圆的面积公式S=πr²:S = 3.14 * 2²S ≈ 3.14 * 4S ≈ 12.56 m²再计算剩余的体积,使用公式V=S*h:V = 12.56 * 3V ≈ 37.68 m³将体积从立方米转换为升,1 m³ = 1000 L,所以37.68 m³ ≈ 37680 L。
因此剩余的体积能存储37680升的油。
练习题3:一个花盆的形状是一个圆柱体,底面直径为10 cm,高度为20 cm。
如果将花盆装满水,需要多少升的水?解答:首先需要求出底面半径,底面直径为10 cm,半径等于直径的一半。
r = 10 / 2r = 5 cm接下来使用圆柱体的体积公式计算体积,注意将半径转换为米。
V = 3.14 * (5/100)² * 20V ≈ 3.14 * 0.05² * 20V ≈ 3.14 * 0.0025 * 20V ≈ 0.157 m³将体积从立方米转换为升,1 m³ = 1000 L,所以0.157 m³ ≈ 157 L。
1.把一个棱长是6分米的正方体木块,削成一个最大的圆柱体,这个圆柱体的体积是多少立方分米?
2.有一个高为6.28分米的圆柱体的机件,它的侧面积展开正好是一个正方形,求这个机件的体积.
3.要制作容量是62.8升的圆柱形铁桶,如果底面半径是2分米,高应是多少分米?
4.一个圆柱形油桶,装满了油,把桶里的油倒出3/4 ,还剩20升,油桶高8分米,油桶的底面积是多少平方分米?
5.把一种空心混凝土管道,内直径是40厘米,外直径是80厘米,长300厘米,求浇制100节这种管道需要多少混凝土?
6.一个圆柱体的底面半径是4厘米,高8厘米,求它的体积和表面积.
7.做一个无盖的圆柱形铁皮水桶,高30厘米,底面直径20厘米,做这个水桶至少要用多少平方分米的铁皮?这个水桶能装多少千克的水?(1立方分米水重1千克)
1、一个圆柱形油桶,从里面量的底面半径是20厘米,高是2分米。
这个油桶的容积是多少?
2、把一个棱长是6分米的正方形木块,削成一个最大的圆柱,需要削去多少立方分米的木块?
3、一个圆柱体的体积是10立方分米,底面积是2.5平方分米,它的高是多少分米?
4、一个圆柱的底面周长是12.56分米,高是3米,它的体积是多少立方分米?
5、一根长2米的圆木,截成两段后,表面积增加了24平方厘米,这根圆木原来的体积是多少?
6、一个底面直径是6厘米的茶杯里,装有7厘米高的水,放入一块小石头,水面上升到10厘米,这个石头的体积是多少立方厘米?
7、把一张长62.8厘米,宽31.4厘米的长方形硬纸片,卷成一个圆柱形纸筒,它的体积是多少?
8、一个圆柱体的侧面积是31.4平方厘米,底面周长是6.28厘米,这个圆柱体的体积是多少立方厘米
1、一个圆柱体汽油桶,从里面量底面半径20厘米、高1米。
如果每立方米汽油重0.73千克,这个油桶最多能装汽油多少千克?
2、把一个棱长6分米的正方体木块切削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?
3、将一个棱长为6分米的正方体钢材熔铸成底面半径为3分米的圆柱体,这个圆柱有多长?
4、一个底面半径为3分米,高为8分米圆柱形水槽,把一块石块完全浸入这个水槽,水面上升了2分米,这块石块的体积是多少?
5、一个无盖的圆柱形水桶,侧面积是188.4平方分米,底面周长是62.8分米。
做这个水桶至少要多少平方分米?这个水桶的容积是多少立方分米?
6、把一个长、宽、高分别是9cm、7cm、3cm的长方体铁块和一个棱长是5cm的正方体铁块,熔铸成一个圆柱体。
这个圆柱体的底面直径是20cm,高是多少厘米?
7、将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米?
8、用一块长50厘米,宽30厘米的长方形铁皮做圆柱形容器的侧面,再另用一块铁皮做底,怎样做才能使此容器的容积最大?
9、用一块长60厘米、宽40厘米的铁皮做圆柱形水桶的侧面,另找一块铁皮做底。
这样做成的铁桶的容积最大是多少?
1、一个长方体长7厘米,宽4厘米,高6厘米,把它削成一个体积最大的圆柱体,圆柱体的体积是多少?
2、在一只底面半径为20厘米的圆柱形小桶里,有一半径为10厘米的圆柱形钢材浸没在水中。
当钢材从桶里取出后,桶里的水下降了3厘米。
求这段钢材的长。
3、在半径为20厘米的圆柱形储水桶里,有一段截面为正方形的方钢浸没在水中,正方形的边长是4厘米。
当这段方钢从水中取出时,桶里的水面下降了0.5厘米。
这段方钢长多少厘米?
4、一个圆柱形的玻璃杯中盛有水,水面高2.5cm,玻璃杯内侧的底面积是72平方厘米,在这个杯中放进棱长6cm的正方体铁块后,水面没有淹没铁块,这时水面高多少厘米?
5、有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是30分米3。
现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余部分的高度为5厘米。
瓶内现有饮料多少立方分米?
6、把一个底面半径是1厘米的圆柱体侧面展开,得到一个正方形,这个圆柱体的体积是多少立方厘米?
7、在一底面半径为30厘米的圆柱形容器内,有一半径为20厘米的圆柱形钢材浸没在水中。
当取出钢材之后,水面下降了4厘米。
求圆钢的长度。