运筹学——.整数规划和分配问题

运筹学的基本名词解释汇总运筹学是一门研究如何在有限资源下做出最优决策的学科。

它涵盖了多个子领域，包括线性规划、整数规划、动态规划、网络优化、排队论、决策分析等等。

在本篇文章中，我将深入解释其中一些基本的运筹学名词。

一、线性规划线性规划是运筹学中最常用的方法之一。

它用于解决在给定的约束条件下，如何最大化或最小化一个线性目标函数的问题。

具体来说，线性规划问题可以用如下形式表示：Maximize（或Minimize）：C₁X₁ + C₂X₂ + ... + CnXnSubject to：A₁₁X₁ + A₁₂X₂ + ... + A₁nXn ≤ b₁A₂₁X₁ + A₂₂X₂ + ... + A₂nXn ≤ b₂...An₁X₁ + An₂X₂ + ... + AnnXn ≤ bnX₁, X₂, ..., Xn ≥ 0其中，C₁，C₂，...，Cn为目标函数的系数，X₁，X₂，...，Xn为决策变量，Aij为约束条件的系数，bi为约束条件的右手边。

线性规划在供应链管理、资源分配、生产计划等各个领域都有广泛的应用。

二、整数规划整数规划是线性规划的一个扩展。

在整数规划中，决策变量被限制为整数值，而不仅仅是非负实数。

这在某些情况下更符合实际问题的特点。

整数规划可以用于解决许多实际问题，例如旅行商问题、资源分配问题等。

整数规划的形式与线性规划相似，只是添加了一个约束条件：X₁, X₂, ..., Xn为整数整数规划是一个NP难问题，在实际应用中通常通过割平面法、分支定界法等方法来求解。

三、动态规划动态规划是一种解决多阶段决策问题的方法。

在动态规划中，问题被分解为一系列阶段，每个阶段都有一组决策变量。

每个阶段的决策都基于之前阶段的决策结果，从而达到最优解。

动态规划可以用于解决诸如背包问题、最短路径问题等在实际问题中普遍存在的多阶段决策问题。

四、网络优化网络优化是研究在网络结构下如何优化资源分配和信息流动的方法。

运筹学中的整数规划问题分析运筹学是运用数学和定量分析方法，通过对系统的建模和优化，来解决实际问题的学科。

其中整数规划是运筹学中的一个重要分支，它在许多实际情况中得到广泛应用。

本文将对整数规划问题进行分析，并探讨其解决方法与应用领域。

一、整数规划问题定义及特点整数规划是一类线性规划问题的扩展，其目标函数和约束条件中的变量取值限定为整数。

通常，整数规划问题可以形式化表示为：Max/Min Z = c₁x₁ + c₂x₂ + ... + cₙxₙs.t.a₁₁x₁ + a₁₂x₂ + ... + a₁ₙxₙ ≤ b₁a₂₁x₁ + a₂₂x₂ + ... + a₂ₙxₙ ≤ b₂...aₙ₁x₁ + a₂₂x₂ + ... + aₙₙxₙ ≤ bₙx₁, x₂, ..., xₙ ∈ Z其中，Z为目标函数值，x₁, x₂, ..., xₙ为待求解的整数变量，c₁, c₂, ..., cₙ为目标函数的系数，aᵢₙ为约束条件的系数，b₁, b₂, ..., bₙ为约束条件的右端常数。

整数规划问题的特点在于整数约束条件的引入，使其解空间变得有限，增加了问题的复杂性。

与线性规划问题相比，整数规划问题更接近实际情况，能够更准确地描述和解决很多实际问题。

二、整数规划问题的解决方法解决整数规划问题的方法主要有以下几种：穷举法、剪枝法、分支定界法、动态规划法等。

具体使用哪种方法需要根据问题的规模和特点来确定。

1. 穷举法是最简单直观的方法，通过枚举搜索整数解空间中的每一个可能解来寻找最优解。

然而，由于整数解空间往往非常大，这种方法在实际问题中往往是不可行的。

2. 剪枝法是一种通过对解空间进行剪枝操作，减少搜索空间的方法。

通过合理选择剪枝条件，可以避免对明显无解的解空间进行搜索，从而提高求解效率。

3. 分支定界法是一种将整数规划问题不断分解为子问题，并对子问题进行界定的方法。

通过不断缩小问题规模，并计算上下界确定最优解的位置，可以有效地求解整数规划问题。

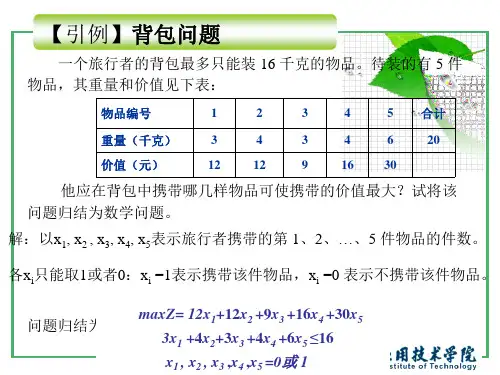
第四章 整数规划与分配问题一、建立下列问题的数学模型1、P143, 4.1 利用0－1变量对下列各题分别表示成一般线性约束条件 (a) 221≤+x x 或53221≥+x x ； (b) x 取值0,3,5,7中的一个； (c) 变量x 或等于0，或50≥； (d) 若21≤x ，则12≥x ，否则42≤x ； (e) 以下四个约束条件中至少满足两个：6225433121≥+≥≤≤+x x x x x x ，，，。

解：(a) 设⎩⎨⎧=否则。

，个条件起作用；第1i ,0y i （i=1,2）,M 为任意大正数。

则有 ⎪⎩⎪⎨⎧=+≥++≤+1y y My -5x 3x 2My 2x x 21221121(b) 设⎩⎨⎧=≠=ix i x y i ,1,0，7,5,3,0=i ，则原条件可表示为⎩⎨⎧=++++++=1753075307530y y y y y y y y x(c) 设⎩⎨⎧≥==50,10,0x x y ，则原条件可表示为⎪⎩⎪⎨⎧≥--≥≤0)1(50x M y x yM x(d)⎩⎨⎧=否则。

，组条件起作用；第1i ,0y i （i=1,2）,M 为任意大正数。

则有⎪⎪⎪⎩⎪⎪⎪⎨⎧=++≤->-≥+≤.1,4,2,1,22122211211y y My x My x My x My x (e)设⎩⎨⎧=个条件不成立第个条件成立第i ,1i ,0y i ，4,3,2,1i =，则原条件可表示为：⎪⎪⎪⎩⎪⎪⎪⎨⎧≤+++-≥+-≥+≤+≤+2y y y y My 6x x My 2x M y 2x M y 5x x 43214433321121 2、P143, 4.2 某钻井队要从以下10个可供选择的井位确定5个钻井探油，目的是使得总的钻探费用最小。

若10个井位代号为101S ,...,S ，相应的钻探费用为101C ,...,C ，并且井位的选择要满足下列条件：（1）或选择1S 和7S ，或选择8S ；（2）选择了3S 或4S 就不能选择5S ，反过来也一样； （3）在10962S ,S ,S ,S 中最多只能选两个。

运筹学中的线性规划和整数规划运筹学是一门涉及决策分析、优化、模型构建和仿真等知识领域的学科，应用广泛，如供应链管理、交通规划、制造业生产、金融投资等方面。

其中，线性规划和整数规划是运筹学中最为基础和重要的优化技术，被广泛应用于各个领域。

一、线性规划线性规划是一种在一组线性约束条件下，求解线性目标函数极值问题的数学方法。

在生产、运输、选址等问题中，线性规划都有着重要的应用。

其数学模型可以表示为：$\max c^Tx$$s.t. Ax \leq b,x\geq 0$其中$c$为目标函数的向量，$x$为决策变量向量，$A$为约束矩阵，$b$为约束向量，$c^Tx$表示目标函数的值，$\leq$表示小于等于。

如果目标函数和约束都是线性的，则可以通过线性规划的求解方法来确定决策变量的最优值。

线性规划的求解方法一般分为单纯形法和内点法两种方法。

单纯性法是线性规划中最为常用的方法，通过对角线交替调整，逐步从可行解中寻找最优解，收敛速度较快，但是存在不稳定的情况。

内点法是近年来发展起来的用于求解大规模线性规划问题的数值方法，其核心思想是迭代求解一系列线性方程组，每次保持解在可行域内部，直到找到最优解为止。

这种方法对大规模问题求解能力强，使用较多。

二、整数规划整数规划是线性规划的升级版，它要求决策变量必须取整数值。

整数规划在很多实际问题中都有着重要的应用，比如很多生产过程中需要将生产数量取整数，物流路径问题需要选取整数条路径等。

与线性规划不同的是，整数规划是NP难问题，没有一种有效的算法能够完全解决所有的整数规划问题。

因此，通常需要采用分支定界、割平面等方法来求解。

分支定界是一种常用的整数规划求解方法。

它通过将整数规划问题分为多个子问题，依次求解这些子问题并优化当前最优解，以逐步逼近最优解。

割平面法则是在分支定界方法的基础上加入约束条件，使得求解过程更加严格化，最终得到更好的结果。

总的来说，运筹学中线性规划和整数规划是不可或缺的优化工具，我们可以通过理论和实践加深对它们的理解。

整数规划与分配问题第四章整数规划与分配问题§4.1整数规划的特点及作⽤⽤单纯形法求解线性规划的结果往往得到分数或⼩数解。

但在很多实际问题中，全部或部分变量的取值必须是整数，如⼈或者机器设备不可分割。

此外还有⼀些问题，如要不要在某地建设⼯⼚，可选⽤⼀个逻辑变量x ，令1x =表⽰在该地建⼚，0x =表⽰不在该地建⼚，逻辑变量也只允许取整数值的⼀类变量。

在⼀个整数规划中要求全部变量取整数值的，称纯整数线性规划或纯整数规划；只要求⼀部分变量取整数值的，称为混合整数（线性）规划；在纯整数规划问题中，若所有变量只允许取0，1两个值，则称其为0-1规划。

有⼈认为，对整数规划问题的求解可以先不考虑对变量的整数约束，作为⼀般线性规划问题来求解，当解为⾮整数时可⽤四舍五⼊或凑整数寻找最优解，其实这种⽅法是不可⾏的，原因有以下两点：⼀、⽤凑整的⽅法计算量很⼤，⽽况还不⼀定能找到最优解。

如某线性规划问题的最优解为()()12 4.6 5.5x x =，⽤凑整数的⽅法时需⽐较与12,x x 的上述数值最接近的四种组合：(4,5),(5,5),(4,6),(5,6)如果问题中有10个变量，就要⽐较1021024=个整数解组合，⽽且最优解还不⼀定在这些组合中。

⼆、放松约束也⽆法求出其最优解例12121212max 322314.0.5 4.5,0,z x x x x s t x x x x =++≤??+≤??≥?整数如果不考虑整数约束，称为上述线性规划问题的松弛问题，松弛问题的最优解为：123.25, 2.5x x ==取整以后123,2x x ==是可⾏解，但1212123,3;4,2;4,3x x x x x x ======都不是可⾏解，⽽123,2x x ==对应的⽬标函数值123213z x x =+=却不是最优解，然⽽最优解是12124,1,max 3214x x z x x ===+=。

直接对松弛问题进⾏求解都⽆法求得整数规划问题的最优解，这就需要对整数线性规划问题有特殊的求解⽅法。