割补法和分割法培训资料
- 格式:doc
- 大小:43.00 KB
- 文档页数:2


割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积. (单位:厘米)8 2练习1如图中的每个数字分别表示所对应的线段的长度(单位:米)•这个图形的面积等于多少平例题2如图,在正方形ABCD内部有一个长方形. EFGH .已知正方形ABCD的边长是6厘米, 图中线段AE、AH都等于2厘米.求长方形EFGH的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF (如图),线段DF=3.6厘米, BE=2.8厘米,那么三角形AEF的面积等于_______________ 平方厘米.B例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.21如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为______________________ cm •A D例题4.如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?例6.选做题例5如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形平方厘米,那么正方形B的面积是多少平方厘米?A的面积是36已知一个四边形 ABCD 的两条边的长度和三个角(如下图所示),求四边形ABCD 的面积是多少? 作业:1•如图所示,平行四边形的面积是 12,把一条对角线四等分, 将四等分点与平行四边形另外 两个顶点相连•图中阴影部分的面积总和是多少?2. . (2013秋?诸暨市校级期中)如图,已知一个四边形的四条边 分别是3, 4, 13和12,其中/ B=90。

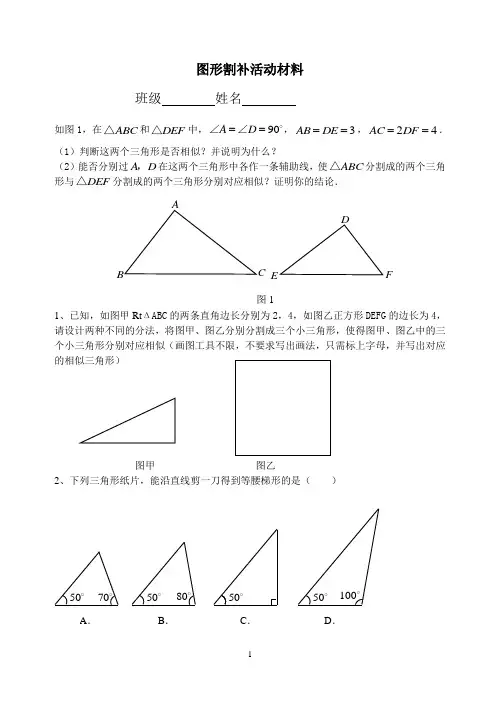
图形割补活动材料班级 姓名如图1,在ABC △和DEF △中,90A D ==∠∠,3AB DE ==,24AC DF ==.(1)判断这两个三角形是否相似?并说明为什么?(2)能否分别过A D ,在这两个三角形中各作一条辅助线,使ABC △分割成的两个三角形与DEF △分割成的两个三角形分别对应相似?证明你的结论.1、已知,如图甲Rt ΔABC 的两条直角边长分别为2,4,如图乙正方形DEFG 的边长为4,请设计两种不同的分法,将图甲、图乙分别分割成三个小三角形,使得图甲、图乙中的三个小三角形分别对应相似(画图工具不限,不要求写出画法,只需标上字母,并写出对应的相似三角形)图甲 图乙2、下列三角形纸片,能沿直线剪一刀得到等腰梯形的是( )50 70A .50 80B .50100C .50 D .图1 E F3、例1、如图,把一个正方形割去四分之一,将如下的部分分成3个相同的部分(图甲);将如下的部分分成4个相同的部分(图乙)。
仿照示例,请你将一个正三角形割去四分之一后余下的部分,(1)分成3个相同的部分(在图1中画出示意图);(2)分成4个相同的部分(在图2中画出示意图)。
你还能利用所得的4个相同的部分拼成一个平行四边形吗?若能,画出大致的示意图。
(图甲)(图乙)图 1图 2练习:1、如图,在△ABC中,∠A=110°,∠B=35°,请你应用变换的方法得到一个三角形使它与△ABC全等,且要求得到的三角形与原△ABC组成一个四边形。
(1)要求用两种变换方法解决上述问题;(写出变换名称,画出图形即可)(2)指出四边形是什么图形?(不要求证明)说明:如用两种平移变换方法解决此题算一种变换;两种变换是指平移,旋转等不同变换。
系中,直线y=233kx+m(-12≤k≤12)12、在平面直角坐标经过点A(23,4),且与y轴相交于点C.点B在y轴上,O为坐标原点,且OB=OA +7-2 7.记△ABC的面积为S.(1)求m的取值范围;(2)求S关于m的函数关系式;(3)设点B在y轴的正半轴上,当S取得最大值时,将△ABC沿AC折叠得到△AB′C,求点B′的坐标.30、(本小题满分8分)已知正方形ABCD的边长AB=k(k是正整数),正△PAE的顶点P在正方形内,顶点E在边AB上,且AE=1. 将△PAE在正方形内按图1中所示的方式,沿着正方形的边AB、BC、CD、DA、AB、……连续地翻转n次,使顶点..P.第一次回到原来的起始位置.(1)如果我们把正方形ABCD的边展开在一直线上,那么这一翻转过程可以看作是△PAE在直线上作连续的翻转运动. 图2是k=1时,△PAE沿正方形的边连续翻转过程的展开示意图. 请你探索:若k=1,则△PAE沿正方形的边连续翻转的次数n= 时,顶点..P.第一次回到原来的起始位置.A BCDPE14.一个大长方体是由四个完全一样的小长方体拼成的,如果每个小长方体的长、宽、高分别是3、1、1,那么这个大长方体的表面积可能有 种不同的值,其中最小值为 .(2)若k =2,则n = 时,顶点..P .第一次回到原来的起始位置;若k =3,则 n = 时,顶点..P .第一次回到原来的起始位置. (3)请你猜测:使顶点..P .第一次回到原来的起始位置的n 值与k 之间的关系(请用含k 的代数式表示n ).23.(10分)直角三角形通过剪切可以拼成一个与该直角三角形面积相等的矩形。

第十一、十二讲格点与割补本讲知识点1.分割法1)正所谓“大事化小”,把不规则的大图形化为规则的小图形,来进行计算.2)在对格点图形的分割计算时,不一定要分到最小的基本单位。
一般来说分为中等大小的,可以计算的规则形状比较方便。
2.割补法1)是“以小见大”,把不规则图形周围添上规则的小图形,使总面积便于计算.2)此外,在图形中进行适当的分割拼补,把不规则的形状拼成规则形状,也是常见的方法.3.格点面积公式1)在最小的正方形面积为1的图形中:正方形格点多边形面积=边界格点数÷2+内部格点数-1.2)在最小正三角形面积为1的图形中:三角形格点多边形面积=边界格点数+内部格点数×2-1.3)在使用公式法计算格点多边形面积时,要注意公式的适用条件.4)在多个格点图形相关的问题中,要注重利用它们之间的共同点来帮助计算.5)对于很多非格点图形的面积计算,分割和添补的方法依然适用.6)特别的,在图形中恰当的添加格线进行分制,能更好的体现围形的结构,以及整体和部分的数量关系,而在添补中,看见某些特殊角度,如45°、60°、120°等时,可以联想到一些特殊的图形,如,等腰直角三角形,正三角形等等.精选例题例题1.如图,分别在如下三种情况中,求出图中格点图形的面积:(1)相邻格点距离为1;(2)相邻格点距离为2;(3)最小正方形面积为2.例题2.如图,下图的正方形格点,单位正方形面积为1,分别求出两个图形的面积.例题3.如图,下图的正方形格点中,单位正方形面积为3,求出图形面积.练习1.如图,分别在如下两种情况中,求出图中格点图形的面积:(1)最小正三角形面积为1;(2)最小正三角形形面积为2.例题4.如图,下图的三角形格点,单位正三角形面积为1,分别求出两个图形的面积.例题5.如图,下图的正三角形格点中,单位正三角形面积为5,求出图形面积.例题6.下图点阵间隔为1,请利用方形格点公式,填出下表:练习2.下图三角形点阵所能连出的最小三角形面积为1,请利用三角形格点公式,填出下表:例题7.如图,单位正方形面积为1,利用格点公式计算下面阴影图形的面积,并再用一种其他方法计算检查.例题8.(1)在图1的正方形格点中,左图面积是45,那么右图的面积是多少?(2)图2的左右两个大三角形相同,左图的单位正三角形面积为100,右图的单位正三角形面积是多少?例题9.把同一个三角形的三条边分别四等分、六等分,适当连接这些分点,便得到了若干个面积相等的小三角形,已知图1中副影部分的面积是63平方厘米,那么图2中的阴影部分的面积是多少平方厘米?例题10.如图,对下列图形进行适当的格线划分,使得能恰当的体现出阴影部分与总面积的关系,并进行相应计算:(1)大正方形面积为90,连结各边中点得到阴影正方形,求阴影面积.(2)大正三角形面积为90.每边取三等分点,连结得到阴影正六边形,求阴影面积.(3)大正六边形面积为90,连结其中3个顶点得到阴影正三角形,求阴影面积.(4)大等腰直角三角形面积为90,如图放入一个阴影正方形,求阴影面积.例题11.在面积为72平方厘米的正六边形中,按图中不同方式切割(切割点均为等分),形成的阴影部分面积分别是多少?例题12.如图,大正方形和小正方形的边长分别为6厘米和2厘米,G、N、M分别为AF、AB、ED边上的中点,求四边形GNME的面积.例题13.如图,在长方形ABCD中,O是长方形的中心,BC长20厘米,AB长12厘米,=,3DE AE4=,那么阴影部分的面积是多少平方厘米?CF DEBE=,三角形AEF的面积是37,那么长例题14.如图,在长方形ABCD中,3DF=,11方形ABCD的面积是多少?例题15.甲乙两个六边形的内角都是120°,其边长如图所示,那么甲,乙面积分别是边长为1的正三角形面积的多少倍?例题16.求阴影部分面积:例题17.两个等腰直角三角形直角边分别长10厘米和6厘米,那么三角形DGE面积是多少平方厘米?思考创新思考1.下图为一个等边三角格点阵,可连出的最小的三角形面积是1,请在图中以给出点为顶点面一个面积为13的三角形.思考2.如图,平面上有16个点,每个点都钉上钉子,形成间隔为1厘米的4行4列的正方形钉阵,现在有许多皮筋,可以套出几种面积的三角形?请各举一例.思考3.正方形格点如图,原有格点的单位正方形面积为68,利用原有格点在图中划分新的格线,分别划出两种新的情况,那么这两种新格线的单位小正方形的面积分别是多少?思考4.如图,把长方形纸片ABCD的一角折起,使点D恰好与AB的中点F重合,若三角形EDC的面积是10.那么长方形ABCD的面积是多少?思考5.如下图,在一平行四边形纸片上割去了①,②两个直角三角形,已知三角形①两条直角边分别为2厘米和5厘米,三角形②两条直角边分别为5厘米和8厘米,求图中阴影部分的面积.第十一讲格点割补(一)思维冲浪1.如图所示,每一个小方格的面积都是1,那么用祖线围成的图形的面积是________.2.已知图中相邻两格点的距离均为2厘米,那么图中连出多边形的面积是______平方厘米.3.如图所示,图中最小的“□”面积是2,那么阴影部分面积分别为________.4.如图,如果每个小三角形的面积都是1cm2,那么连接A,B,C三点的三角形的面积是________cm2.5.如图,如果每一个小三角形的面积是2平方厘米,那么四边形ABCD的面积是________平方厘米.6.如图所示,图中最小的“Δ”面积是2,那么阴影部分面积分别为_______.7.如图所示,每个小方格格的边长为1.那么阴影部分的面积是多少?8.图中相邻三点所形成的等边三角形的面积为1,求五边形的面积.9.如图,大正六边形的面积为108,求阴影部分的面积为多少?10.图中水平,竖直方向相邻两个格点的距离都是1,请你求出图中“8”、“0”,“9”的面积各是多少.第十二讲格点割补(二)思维冲浪1.把同一个三角形的三条边分别五等分、七等分,连接这账分点,便得到了若干个面积相等的小三角形,左图中阴影部分的面积是294平方分米,那么右图中阴影部分的面积是________平方分米.2.下图是一个面积为24的正六边形,阴影部分的面积是__________.3.如图所示,ABCD是长方形,长AD等于7.2厘米,宽AB等于5厘米,CDEF是平行四边形,如果BH的长是3厘米,那么图中阴影部分面积是________平方厘米.4.在下图中,三角形ABC和DEF是两个完全相同的等腰直角三角形,其中DF长9厘米,CF长3厘米,那么阴影部分的面积是________平方厘米.5.如图,大正方形和小正方形的边长分别为6厘米和2厘米,G、N分别为AF、AB边上的中点,那么四边形GNCE的面积是__________平方厘米.6.如图所示,三个长方形APHM、BNHP、CQHN的面积分别是7、4、6、则阴影部分的面积是__________.7.如图所示,为一个等边三角格点阵,可连出的最小的三角形面积是1,请在图中以给出点为顶点画一个面积为7的三角形.8.如图所示,为一个边长为2的正方形,其中阴影部分的面积为多少?9.图中大正方形边长为8,小正方形边长为4,求阴影部分面积.10.如图,一个正方形,与4个等腰直角三角形,恰好拼成了一个长方形,如果正方形的面积是16,那么,长方形的面积是________.。
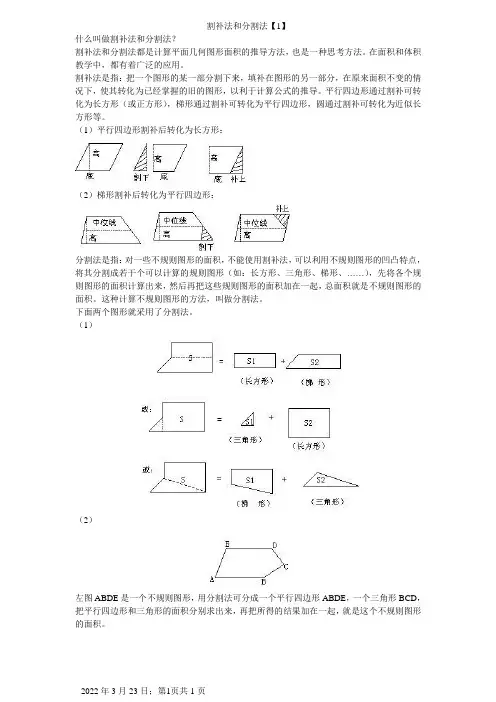
割补法和分割法【1】
什么叫做割补法和分割法?
割补法和分割法都是计算平面几何图形面积的推导方法,也是一种思考方法。
在面积和体积教学中,都有着广泛的应用。
割补法是指:把一个图形的某一部分割下来,填补在图形的另一部分,在原来面积不变的情况下,使其转化为已经掌握的旧的图形,以利于计算公式的推导。
平行四边形通过割补可转化为长方形(或正方形),梯形通过割补可转化为平行四边形,圆通过割补可转化为近似长方形等。
(1)平行四边形割补后转化为长方形:
(2)梯形割补后转化为平行四边形:
分割法是指:对一些不规则图形的面积,不能使用割补法,可以利用不规则图形的凹凸特点,将其分割成若干个可以计算的规则图形(如:长方形、三角形、梯形、……),先将各个规则图形的面积计算出来,然后再把这些规则图形的面积加在一起,总面积就是不规则图形的面积。
这种计算不规则图形的方法,叫做分割法。
下面两个图形就采用了分割法。
(1)
(2)
左图ABDE是一个不规则图形,用分割法可分成一个平行四边形ABDE,一个三角形BCD,把平行四边形和三角形的面积分别求出来,再把所得的结果加在一起,就是这个不规则图形的面积。
2022年3月23日;第1页共1页。

五年级几何奥数专题之第三讲割补法(含答案)一、知识点1、割补法分割法是将几何体分割成若干部分,利用整体与部分的关系来解决所求问题。
2、分割成规则图形在组合图形中,除了多边形外,还有圆、扇形、弓形与三角形、矩形、平行四边形、梯形等图形组合而成的不规则图形,为了计算它们的面积,常常需要变动图形的位置或对图形进行分割、旋转、拼补,使它变成可以计算出面积的规则图形。
二、学习目标1、我能够了解割补法。
2、我能够应用割补法解决图形面积问题。
三、典型例题例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积(单位:厘米)。
练习1图中的数字分别表示对应线段的长度,试求下面多边形的面积(单位:厘米)。
如图所示,在正方形ABDC内部有一个长方形EFGH,已知正方形ABDC的边长是6厘米,图中线段AE、AH都等于2厘米,求长方形EFGH的面积。
练习2(1)如图所示,在正方形ABCD内部有三角形CEF,已知正方形ABCD的边长是6厘米,图中线段AE、AF都等于2厘米,求三角形CEF的面积。
(2)如图所示,在一个等腰直角三角形中,削去一个三角形后,剩下一个上底长5厘米、下底长6厘米的等腰梯形(阴影部分)。
求这个梯形的面积。
如图所示,大正方形的边长为10厘米,连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3如图所示,大正三角形的面积为10平方厘米。
连接大正三角形的各边中点得到四个小正三角形,取各个小正三角形的中心,再将每个小正三角形的中心和顶点相连,得到三个一样的小三角形,那么图中阴影部分的面积总和等于多少平方厘米?例题4如图,把两个相同的正三角形的各边分别三等分和四等分,并连接这些等分点。
已知左图中阴影部分的面积是48平方分米,请问:右图中阴影部分的面积是多少平方分米?如图,把两个同样大小的正方形分别分成5×5和3×3的方格表,左图阴影部分的面积是162,请问右图中阴影部分的面积是多少?选讲题※求下图中四边形ABCD的面积(单位:厘米)。

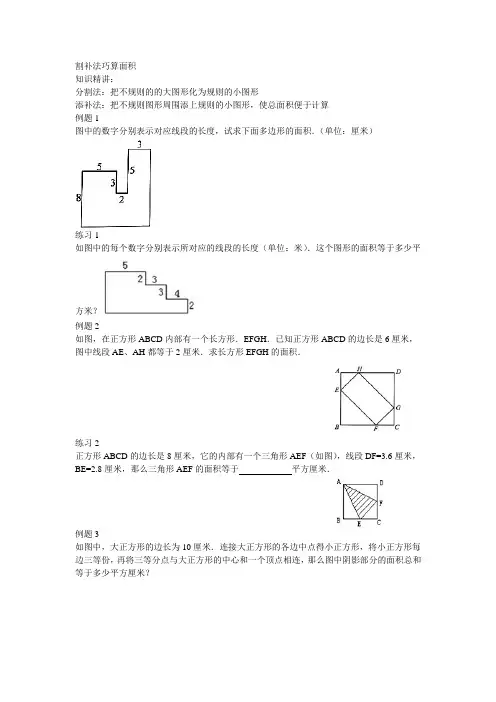
割补法巧算面积知识精讲:分割法:把不规则的的大图形化为规则的小图形添补法:把不规则图形周围添上规则的小图形,使总面积便于计算例题1图中的数字分别表示对应线段的长度,试求下面多边形的面积.(单位:厘米)练习1如图中的每个数字分别表示所对应的线段的长度(单位:米).这个图形的面积等于多少平方米?例题2如图,在正方形ABCD内部有一个长方形.EFGH.已知正方形ABCD的边长是6厘米,图中线段AE、AH都等于2厘米.求长方形EFGH的面积.练习2正方形ABCD的边长是8厘米,它的内部有一个三角形AEF(如图),线段DF=3.6厘米,BE=2.8厘米,那么三角形AEF的面积等于平方厘米.例题3如图中,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等份,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?练习3.1.如图所示,正方形ABCD的边长acm,则图中阴影部分的面积为cm2.例题4. 如图1和图2,把两个相同的正三角形的各边分别五等分和七等分,并连接这些分点.已知图1中阴影部分的面积是294平方分米.请问:图2中的阴影部分的面积是多少平方分米?练习47.如图所示,将三个相同的长方形从上到下排列,依次进行两等分、三等分、四等分,各取出其中的一份画上阴影,则阴影部分的面积占全部面积的几分之几?选做题例5 如图,在两个相同的等腰直角三角形中各作一个正方形,如果正方形A的面积是36平方厘米,那么正方形B的面积是多少平方厘米?例6.已知一个四边形ABCD的两条边的长度和三个角(如下图所示),求四边形ABCD的面积是多少?作业:1.如图所示,平行四边形的面积是12,把一条对角线四等分,将四等分点与平行四边形另外两个顶点相连. 图中阴影部分的面积总和是多少?2. .(2013秋•诸暨市校级期中)如图,已知一个四边形的四条边AB,BC,CD和DA的长分别是3,4,13和12,其中∠B=90°,求这个四边形的面积3. 求阴影部分面积.4.求阴影部分面积.5. 求阴影部分面积:6.求阴影部分面积.7. 求阴影部分面积.8.(2011秋•宁波期中)求阴影部分的面积.9. 求阴影部分的面积.10. 求阴影部分的面积.11.求阴影部分的面积.12.求阴影部分的面积.。

我们知道长方形、正方形的面积计算公式为:长方形的面积=长×宽正方形的面积=边长×边长但是这两组计算公式只适用于求解相应的规则图形的面积,如果遇到更为复杂的、不规则的直线形多边形(指多边形的边是直线段)的面积求解问题时,它们就无法直接用于求解了。
那么,如何来解决这一难题呢?实际上,尽管它们无法直接用于求解,但我们可以在适当地转化图形后再求助于它们,也就是它们能够间接地帮助我们,这里所说的“转化”是指对直多边形进行适当的分割与添补,使之转化为标准的长方形或正方形,这种方法我们称之为割补法。
掌握这方法的关键在于根据待求图形的特征,采用适当的割补使之变为长方形或正方形,为保持面积不变,应将多补上的部分的面积减去,未补上的部分的面积应加上。
[例1】有一形如图la的板(图中的每个数字分别表示所对应的线段的长度,单位:厘米),求它的面积等于多少平方厘米?解答☆解法一将图1a分割成长方形,可以有两种较简单的方法(见图1b、lc),图形都被分割成三个长方形。
以第一种分割法为例(图1b),利用长方形的面积公式可计算出图形的面积(我们可以记之为S)。
S=(1+2+3)×(3+4+5)-1×4-(1+2)×5=72-4-15=53(平方厘米)答:所求的面积为53平方厘米。
[例2】有一个长方形,如果宽减少2米,面积就减少24平方米。
如果长增长3米,面积就增加27平方米。
求这个长方形的面积。
思路剖析根据题意,可以画出如下直观图(图3):观察图3a,从宽减少2米面积就减少24平方米这个条件,我们可以求出这个长方形的长是24÷2=12(米)。
=(1+2+3)×3+(2+3)×4+5×3=18+20+15=53(平方厘米)☆解法二上面的方法是将图形分割成若干个长方形,然后求图形的面积,也就是使用了分割法。
实际上,我们还可以将图形添补成一个大的长方形(见图2),然后利用大长方形面积与两个小长方形面积之差,求出图形的面积,亦即采用添补法。

第34讲 割补法与等积法一、知识与方法1 割补法割补法包括分割法和补体法,求一个几何体的体积可以将这个几何体分割成几个柱体,锥体,分别求出雉体和柱体的体积, 从而得出几何体的体积,这种方法称为分割法. 用于直接解题较困难,分割后化繁为简,使问题较易获得解快,但有时候,所给的几何体并不复杂,却很难直接计算求解,这类几何体实际上是一个常规几何体的一部分. 通过添补适当的几何体,将其扩展为新的、其特征为我们比较熟悉的几何体,以便于从整体上宏观把握,处理局部问题的一种方法称为补体法,体现了拓展空间, 从更广阁的范围内处理局部问题的整体思想.分割法与补体法合在一起称为割袳法. 2 等积法(又称等积变换法)(1)利用三棱锥的“等积性”,即体积计算时可以任一个面作为三棱雉的底面. (1)求体积时,可选择“容易计算”的方式来计算; (2)利用“等积法”可求“点到面的吟离”,关键是在面中选取 3 个点,与已知点构成三棱锥.(2) 等积变换法充分体现了转化的数学思想,在运用过程中要充分注意距离之间的等价转换.二、典型例题【例1 】(1) 如图384-所示,已知多面体ABC DEFG -中, ,AB AC ,AD 两两互相垂直,平面//ABC 平面DEFG , 平面//BEF 平面,2,1ADGC AB AD DG AC EF =====, 则该多面体的体积为 ( ). A. 2 B. 4C. 6D. 8(2) 如图385-所示,在多面体ABCDEF 中, 已知ABCD 是边长为 1 的正方形, 且,ADE BCF 均为正三角形. //,2EF AB EF =, 则该多面体的体 积为( ).A. 3C.43D.32【分析】本例两小题给出的都是不规则几何体,直接求体积比较困难,可以将这个几何体分割成若干规则的几何体,从而得出几何体的体积(求规则几何体的体积再合成),也可认运用补体法补成一个规则几何体再求解,如第(1) 问,可把题中给出的几何体分割成两个三棱柱或补成一个正方体;第(2)问,不同的分割可以引发一题多解与发散思维,这种解法体现了割补思想和等积变换思想.【解析】 (1) 【解法一】(割)如图386-所示,过点C 作CH DG ⊥于H , 联结EH ,把多面体分割成一个直三棱柱DEH ABC -和一个斜三 棱柱BEF CHG -. 于是所求几何体的体积为112122122DEHBEF V SAD SDE ⎛⎫⎛⎫=⋅+⋅=⨯⨯⨯+⨯⨯⨯ ⎪ ⎪⎝⎭⎝⎭2 4.=【解法二】(补)如图387-所示. 将多面体补成棱长为 2 的正方 体. 显然所求的多面体的体积为该正方体体积的一半. 于是所求几何体的体积31242V =⨯=.(2) 【解法一】 (分割法一)如图388-所示,分别过,A B 作EF 的垂 线, 垂足分别为点,G H , 联结,DG CH .则原几何体分割为两个三棱雉和一个直三棱柱,锥高12, 柱高 1. AG ==取AD 中点M , 则2MG =111,12224434AGDSV =⨯⨯=∴=+⨯⨯⨯12=【解法二】 (分割法二)如图389-所示,取EF 中点P , 则原几何体分割为两个三棱雉和一个四棱雉,易知三棱雉P AED -和三棱雉P BCF -都是棱长为 1 的正四面体,四棱雉P ABCD -为棱长为 1 的正四棱雉.2111233V =⨯+⨯=【例 2】已知直三棱柱111ABC A B C -中, 222A B C 是用一平面截得的截面,且21AA h =,2223,BB h CC h ==, 若ABC 的面积为.S 求证:介于截面与下底面之间的几何体的体积为()12313V S h h h =++.【分析】由于几何体222A B C ABC -是一个不规则的几何体,为求得其体积不妨采用分割或补体的方法来求解和证明. 【解析】【证法一】 (分割)为了讨论方便, 不妨设123h h h , 可将几何体222ABC A B C -分割成一个小直三棱柱与两个三棱雉. 如图390-所示,过2A 作23//A B AB 交2B B 于3B , 过3B 作33//B C BC 交2C C 于3.C 联结23A C ,23B C , 则几何体222ABC A B C -被分割成直三棱柱233ABC A B C -、三棱雉2233B A B C -、二棱锥2A 232B C C -设,BC x A =到BC 的距离为d , 则12S xd =. 由于 ()23322331211,3ABC A B C B A B C V Sh V S h h --==-,()()223223231311111.3323A B C c B C C V Sd h h x d S h h -=⋅=⋅-⋅⋅=- 故()2222332233223212313ABC A B C ABC A B C B A B C A B C C V V V V S h h h ----=++=++. 【证法二】(补体)将几何体222ABC A B C -以ABC 为底面进行两次等几何体补形,使侧棱的长均为123h h h ++, 这样就将不规则的几何体补形为新的直三棱柱. 而原几何体的体积等于这个新直三棱柱体积的13, 故()222123 1133ABC A B C V V S h h h -==++新直三榬柱.【例 3】如图391-所示,三棱锥A BCD -中, AB ⊥平面BCD ,CD BD ⊥ (1) 求证: CD ⊥平面ABD ;(2) 若1,AB BD CD M ===为AD 中点,求三棱雉A MBC -的体积.【分析】利用三棱锥的“等积法”,即体积计算时,可以任一个面作为三棱锥的底面,利用“等积法”可求“点到面的距离”,关键是在面中选取三个点,与已知,点构成三棱锥.等积变换法充分体现了转化的数学思想,在运用过程中要充分注意距离之间的等价转换.【解析】(1) 证明: :AB ⊥平面,,BCD CD BD CD ⊥⊂平面,ABD BD ⊂平面ABD ,CD ∴⊥平面.ABD(2)【解法一】由AB ⊥平面BCD ,得AB BD ⊥,11,.2ABDAB BD S==∴= M 为AD 中点, ABM11.24ABDSS ∴==由()1知,CD ⊥平面ABD ,∴三棱锥C ABM -的高1h CD ==.因此三棱雉A MBC -的体积B 13A MBC C ABM A MV V S h --==⋅1.12=【解法二】由AB ⊥平面BCD 知,平面ABD ⊥平面BCD .又平面ABD ⋂平面BCD BD =, 过点M 作MN BD ⊥交BD 于点N ,如图392-所示,则MN ⊥平面BCD , 且1122MN AB ==. 又1,1,2BCDCD BD BD CD S ⊥==∴=. ∴三棱倠A MBC -的体积1133A MBC A BCD M BCD BCDV V V AB S MN ---=-=⋅-. 112BCDS=.三、易错警示【例】正方体容器1AC 中盛满水, ,,E F G 分别是1111,,A B BB B C 的中点,若 3 个小孔分别位于,,E F G 三点处,则正方体中的水最多会剩下原体积的( ).A.78B.1112C.56D.2324【错解】剩下的水的最大容积是截面EFG 以下几何体的体积,如 图393-所示,设1CC 的中点为11,M C D 的中点为N ,则截面EFG 在正方体1AC 的截面是EFMN , 设正方体1AC 的棱长为 1, 则三棱柱11B EF C MN -的体积 1111111.2228B EFC MN V =⨯⨯⨯=于是, 正方体的水最多会剩下原体积的17188-=, 故 选 A.【评析及正解】上迌解法是否正确,我们可认考查另一种情形.考虑由1,,B E C 确定的截面,如图394-所示.此时,另一个小孔在截面1BEC的上方,此时三棱锥11B BEC -的体积为1113B BEC V -=⨯ 111111.22128⎛⎫⨯⨯⨯=< ⎪⎝⎭于是, 正方体中的水最多会剩下原体 积的11111212-=, 故应选B . 1. 从选项看,还有2324, 那么,会不会是这个结果呢? 我们可以 考虑一般的情形.【正确的解法】如下:【解析】:我们注意到, 当正方体中剩下的水最多时,这时的水平面必定经过其中的两个小孔, 不妨设经过小孔,E G , 如图395-所示,另一个小孔F 在该平面的上方. 设过,E G 的平面与棱1111,,BB CC C D 的交点分别为,,H P Q , 则流出的水的最小体积是台体11B EH C QP -的体积.设正方体1AC 的棱长为 2 , 则11B E =, 设()112B H x x =, 则12C P x =-. 由11B EHC QP , 得12xC Q x-=. 于是, 台体11B EH C QP -的体积为112231(2) 31(2)14 2233121 222,3312B EHC QPx V x x x x x x x ⎡⎤-=+⎢⎥⎢⎥⎣⎦⎡⎤-⎛⎫=+=+-⎢⎥ ⎪⎝⎭⎣⎦⎛⎫⋅==⨯ ⎪ ⎪⎝⎭ 当且仅当4x x =, 即2x =时,台体11B EH C QP -的体积最小, 为正方体体积的112. 此 时,点H 与点B 重合, 即截面为1BEC , 故选 B.四,难题攻略【例】在三棱台111ABC A B C -中, 111,2A B G AB =为1CC 的中点,截面1A BG 将棱台分成上、下两部分,求这两部分体积之比.【分析】由于合成的两部分都是不规则的几何体,故需将其分割成几个锥体(特别是三棱锥)的组合体才便于计算体积之比,需要提醒的是这里有等面积、等高,等体积的运用,使问题的解答别开生面.【解析】如图396-所示, 联结11,BC A C , 则棱台被分割成 4 个三棱锥的组合体, 注意到 3 个三棱锥11111,A BC G A BC B --,1A BCG -都等高, 因而其体积之比为底面面积之比.又在梯形11BCC B 中, 由111112B C A B BC AB ==, 且G 为1C C 的 中点, 有11.BCCBOGBC B SSS ==即111111ΛBCC A BCC A BC B V V V V ---===, 从而111112A BCC A BC B V V V V --=+=上,在三棱雉111B A B C -与三棱雉1A ABC -中, 它们的高相等, 且1114ABCA B C S S=,则1111111444A ABC B A B c A BC B V V V V ---===.从而1155A ABC A BCC V V V V --=+=下, 故t :2:5V V =下为所求.五、强化训练1.如图397-所示,在直三棱柱111ABC A B C -中,12,,2AB BC AA ABC M π∠===是BC 中点.(1)求证:1//A B 平面1AMC ;(2)求直线1CC 与平面AMC 所成角的正弦值;(3)试问在棱11A B 上是否存在点N ,使得AN 与1MC 所成角为?3π若存在,确定点N 位置;若不存在,请说明理由.【解析】(1)如图①所示,联结,设与相交于点,则为中点,联结,则为的中位线,依据线面平行判定定理可得.(2)将图①补体为图②,设直线与平面所成角为,则.由题意,不1A C 1AC O O 1A C OM OM 1A BC 11111AB OM A B AMC A B AMC OM AMC //⎫⎪⊄⇒//⎬⎪⊂⎭平面平面平面1CC 1AMC α11sin C AMC h CC α-=11妨设,依据等体积法可得.(3)假设在棱上存在点,使得与成角,不妨设在棱上取点,使得,易得,如图③所示,故与成角.在中,由余弦定理可得.故在棱上存在点,且为棱的中点,使得与成角.122AB BC AA ===111111133C AMC C AMC AMC C AMC AMCC AMCV V Sh Sh ----=⇒=11122sin 33C AMC C AMC h h CC α--⇒=⇒==11A B N AN 1MC 3π1(02)A N t t =≤≤CD Q CQ t =1AN C Q //1C Q 1MC 3π1MQC 22222211112cos3MQ MC QC MC QC π=+-⇒=+1[0,2]t -=∈11A B N N 11A B AN 1MC 3π1213。
知识梳理:已知直角三角形ABC 中有一个正方形AEFD ,已知BF =20cm ,FC =16cm ,你能计算出图中阴影部分的面积吗?BC分析:阴影部分是两个直角三角形,斜边长分别是20cm 和16cm ,将三角形BEF 沿EF 边切开,再把三角形BEF 的EF 边和三角形DFC 的FD 边重合拼组,正好与三角形DFC 合并成一个大直角三角形,这个大直角三角形的两条直角边分别是20cm 和16cm ,一条为高,另一条就是底,这样就可以求出这个大直角三角形的面积,也就是阴影部分的面积。
解答:20×16÷2=160(cm ²)FBC割补法:把一个图形的某一部分割下来,填补在图形的另一部分,在原面积不变的情况下,使其转化为已经掌握的图形,便于问题的解答。
一个较复杂的图形, 通过恰当的分割,可以转化成简单的图形。
【规律总结】——割补法和分割法联系:割补法和分割法都是将图形进行切割,在保证面积不变的情况下,使其转化为已经掌握的图形,便于问题的解答。
区别:割补法要把切下来的图形移动到其他位置,而分割法把图形切开后并不需要移动。
例题1 求图中阴影部分的面积。
(单位:厘米)解答过程:利用割补法将阴影部分分割平移成一个长方形(如图所示),长是28,宽是20。
答案:28×20=560(cm²)例题2 在等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三部分,三角形的面积是120平方厘米。
你能求出阴影部分的面积吗?解答过程:从等腰三角形的顶点作底边上的高,得到两个完全一样的直角三角形,将左边的三角形倒过来与另一个三角形拼成一个长方形,由已知条件“将三角形的两条边等分成三部分”可知:长方形面积正好是阴影部分面积的3倍。
答案:120÷3=40(cm²)例题3 如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)解答过程:按照一般解法,首先求出梯形的面积,然后减去空白部分的面积即得所求面积。
割补法和分割法
什么叫做割补法和分割法?
割补法和分割法都是计算平面几何图形面积的推导方法,也是一种思考方法。
在面积和体积教学中,都有着广泛的应用。
割补法是指:把一个图形的某一部分割下来,填补在图形的另一部分,在原来面积不变的情况下,使其转化为已经掌握的旧的图形,以利于计算公式的推导。
平行四边形通过割补可转化为长方形(或正方形),梯形通过割补可转化为平行四边形,圆通过割补可转化为近似长方形等。
(1)平行四边形割补后转化为长方形:
(2)梯形割补后转化为平行四边形:
分割法是指:对一些不规则图形的面积,不能使用割补法,可以利用不规则图形的凹凸特点,将其分割成若干个可以计算的规则图形(如:长方形、三角形、梯形、……),先将各个规则图形的面积计算出来,然后再把这些规则图形的面积加在一起,总面积就是不规则图形的面积。
这种计算不规则图形的方法,叫做分割法。
下面两个图形就采用了分割法。
(1)
(2)
左图ABDE是一个不规则图形,用分割法可分成一个平行四边形ABDE,一个三角形BCD,把平行四边形和三角形的面积分别求出来,再把所得的结果加在一起,就是这个不规则图形的面积。