奇偶

6、 奇 偶 性1．函数的奇偶性(1)定义： ①奇函数：设函数y ＝f (x )的定义域为D ，如果对于D 内的任意一个x ，都有，则这个函数叫做奇函数．②偶函数：设函数y ＝g (x )的定义域为D ，如果对于D 内的任意一个x ，都有，则这个函数叫做偶函数．(2)性质如果一个函数是奇函数，则这个函数的图象是以 为对称中心的对称图形，反之，如果一个函数的图象是以为对称中心的中心对称图形，则这个函数是奇函数．如果一个函数是偶函数，则它的图象是以为对称轴的轴对称图形；反之，如果一个函数的图象关于 对称，则这个函数是偶函数． (3)判断奇偶性①f (x )＝|x |；②f (x )＝1－x 2＋x 2－1 ③f (x )＝x 2 (x ≥1)；④f (x )＝|x ＋1|－|x －1|.2．用定义判断函数奇偶性的步骤是：(1)求定义域，看定义域是否关于原点对称，若定义域关于原点不对称，则为非奇非偶函数．(2)定义域关于原点对称时，看f (－x )＝±f (x )(或f (x )±f (－x )＝0或f (－x )f (x )＝±1(用此式时，f (x )≠0对定义域内任意x 都成立))是否成立．如不成立，则为非奇非偶函数．(3)f (－x )＝－f (x )成立时为奇函数．f (－x )＝f (x )成立时为偶函数． 3．若一次函数y ＝kx ＋b 为奇函数，则b ＝ ，若二次函数y ＝ax 2＋bx ＋c 为偶函数则b ＝.反比例函数y ＝k x(k ≠0)是函数．对于函数奇偶性的讨论，学习时应把握下述几点：①函数的奇偶性讨论是在函数的整个定义域上进行的．考察一个函数y ＝f (x )是否具有奇偶性，不仅考察f (x )与f (－x )之间的关系，更应考察函数的定义域是否关于原点对称．③以函数的奇偶性作为划分标准，可将函数分为四类：偶函数，奇函数，既是奇函数又是偶函数，非奇非偶函数．既是奇函数又是偶函数的函数f (x )一定是常数函数f (x )＝0，但f (x )＝0不一定既是奇函数也是偶函数，须特别注意定义域是否关于原点对称这一限制条件．④奇函数y ＝f (x )若在x ＝0处有定义，则一定有f (0)＝0.⑤综合函数的单调性与奇偶性，可得以下常用的两个结论：奇函数在区间[a ，b ]和[－b ，－a ]上有相同的单调性；偶函数在区间[a ，b ]和[－b ，－a ]上有相反的单调性(ab >0)．⑥有时也用奇偶函数的性质来判断：偶函数的和、差、积、商(定义域符合要求)仍为偶函数．奇函数的和、差为奇函数，两个奇函数的积、商为偶函数．⑦有些判断奇偶性的题目，须先化简f (x )的表达式，观察其特点，然后再进行判断． [例1] 1、判断下列函数的奇偶性(1)f (x )＝x 3＋1x；(2)f (x )＝x 2＋1；(3)f (x )＝|x ＋1|＋|x －1|；(4)f (x )＝2x ＋1；(5)f (x )＝x －1＋1－x ；(6)f (x )＝1|x |－1.2、判断函数f(x)＝|x＋a|－|x－a|(a∈R)的奇偶性．[例2]已知函数y＝f(x)的图象关于原点对称，且当x＞0时，f(x)＝x2－2x＋3.试求f(x)在R上的表达式，并画出它的图象，根据图象写出它的单调区间．2、已知函数f(x)为偶函数，且当x<0时，f(x)＝x＋1，则x>0时，f(x)＝________.[例3]1、已知b＞a＞0，偶函数y＝f(x)在区间[－b，－a]上是增函数，问函数y＝f(x)在区间[a，b]上是增函数还是减函数？2、(1)已知函数y＝f(x)是定义在R上的偶函数，在[2,6]上是减函数，比较f(－5)与f(3)的大小结果为______．(2)如果奇函数f(x)在区间[1,6]上是增函数，且最大值为10，最小值为4，那么f(x)在[－6，－1]上是增函数还是减函数？求f(x)在[－6，－1]上的最大值和最小值．[例4]1、已知偶函数f(x)(图(1))和奇函数g(x)(图(2))在y轴右边的一部分图象，试根据偶函数和奇函数的性质，分别作出它们在y轴左边的图象．2、(1)如图①是奇函数y＝f(x)的部分图象，则f(－4)·f(－2)＝________.(2)如图②是偶函数y＝f(x)的部分图象，比较f(1)与f(3)的大小的结果为________．[例5] 判断下列函数的奇偶性： (1)f (x )＝(x －1)x ＋1x －1； (2)f (x )＝1－x 2|x ＋2|－2课堂练习一、选择题1．下列函数不具备奇偶性的是 ( )A ．y ＝－xB ．y ＝－1x C ．y ＝x －1x ＋1D ．y ＝x 2＋22．下列命题中真命题的个数为( )(1)对f (x )定义域内的任意x ，都有f (x )＋f (－x )＝0则f (x )是奇函数(2)对f (x )的定义域内的任意x ，都有f (x )－f (－x )＝0，则f (x )是偶函数(3)对f (x )的定义域内的任意x ，都有f (－x )f (x )＝－1，则f (x )是奇函数(4)对f (x )的定义域内的任意x ，都有f (－x )f (x )＝1，则f (x )是偶函数A ．1B ．2C ．3D ．43．若函数y ＝f (x )为奇函数，则下列坐标表示的点一定在函数f (x )的图象上的是 ( ) A ．(a ，－f (a )) B ．(－a ，－f (－a )) C ．(－a ，f (a )) D ．(－a ，－f (a ))4．已知y ＝f (x )是奇函数，且方程f (x )＝0有六个实根，则方程f (x )＝0的所有实根之和是 ( )A ．4B ．2C ．1D ．05．已知f (x )＝(m －1)x 2＋2mx ＋3为偶函数，则f (x )在(－5，－2)上是( ) A ．增函数 B ．减函数 C ．部分为增函数，部分为减函数 D ．无法确定增减性 6．偶函数y ＝f (x )在区间[－4，－1]是增函数，下列不等式成立的是( )A ．f (－2)<f (3)B ．f (－π)<f (π)C ．f (1)<f (－3)D ．f (－2)>f (3)二、解答题 7．判断下列函数的奇偶性．(1)f (x )＝⎩⎪⎨⎪⎧1 x 是有理数－1 x 是无理数. (2)f (x )＝|2x ＋1|－|2x －1|.(3)f (x )＝2|x |. (4)f (x )＝⎩⎪⎨⎪⎧x (x －2) x ≥0－x (x ＋2) x <0课后练习一、选择题 1．下列命题中错误的是( )①图象关于原点成中心对称的函数一定为奇函数 ②奇函数的图象一定过原点 ③偶函数的图象与y 轴一定相交 ④图象关于y 轴对称的函数一定为偶函数 A ．①② B ．③④ C ．①④ D ．②③2．如果奇函数f (x )在(0，＋∞)上是增函数，则f (x )在(－∞，0)上( )A ．减函数B ．增函数C ．既可能是减函数也可能是增函数D ．不一定具有单调性3．已知f (x )＝x 7＋ax 5＋bx －5，且f (－3)＝5，则f (3)＝( ) A ．－15B ．15C ．10D ．－104．若f (x )在[－5,5]上是奇函数，且f (3)<f (1)，则下列各式中一定成立的是( ) A ．f (－1)<f (－3) B ．f (0)>f (1) C ．f (2)>f (3) D ．f (－3)<f (5)5．设f (x )是定义在R 上的奇函数，且当x >0时，f (x )＝2x－3，则f (－2)的值等于( ) A ．－1B ．1 C.114D ．－1146．设f (x )在[－2，－1]上为减函数，最小值为3，且f (x )为偶函数，则f (x )在[1,2]上( )A ．为减函数，最大值为3B ．为减函数，最小值为－3C ．为增函数，最大值为－3D ．为增函数，最小值为37．(胶州三中高一模块测试)下列四个函数中，既是偶函数又在(0，＋∞)上为增函数的是( ) A ．y ＝x 3B ．y ＝－x 2＋1 C ．y ＝|x |＋1 D ．y ＝2－|x |8．(09·辽宁文)已知偶函数f (x )在区间[0，＋∞)单调递增，则满足f (2x －1)<f ⎝⎛⎭⎫13的x 取值范围是( )A.⎝⎛⎭⎫13，23 B.⎣⎡⎭⎫13，23 C.⎝⎛⎭⎫12，23 `D.⎣⎡⎭⎫12，23 9．若函数f (x )＝(x ＋1)(x ＋a )为偶函数，则a ＝( ) A ．1B ．－1C ．0D ．不存在10．奇函数f (x )当x ∈(－∞，0)时，f (x )＝－2x ＋3，则f (1)与f (2)的大小关系为( ) A ．f (1)<f (2) B ．f (1)＝f (2) C ．f (1)>f (2) D ．不能确定二、填空题11．若f (x )＝ax 2＋bx ＋c (a ≠0)为偶函数，则g (x )＝ax 3＋bx 2＋cx 的奇偶性为________． 12．偶函数y ＝f (x )的图象与x 轴有三个交点，则方程f (x )＝0的所有根之和为________． 三、解答题13．判断下列函数的奇偶性：(1)f (x )＝⎩⎪⎨⎪⎧－x 2＋x (x >0)x 2＋x (x ≤0)； (2)f (x )＝1x 2＋x .14．已知f (x )是偶函数，g (x )是奇函数，且f (x )＋g (x )＝x 2＋x －2，求f (x )，g (x )的表达式．15．函数f (x )＝ax ＋b 1＋x 2是定义在(－1,1)上的奇函数，且f ⎝⎛⎭⎫12＝25，求函数f (x )的解析式．16．定义在(－1,1)上的奇函数f (x )是减函数，且f (1－a )＋f (1－a 2)<0，求实数a 的取值范围．17．f (x )是奇函数，当x ≥0时，f (x )的图象是经过点(3，－6)，顶点为(1,2)的抛物线的一部分，求f (x )的解析式，并画出其图象．答案1．函数的奇偶性(1)定义： ①奇函数：－x ∈D ，且f (－x )＝－f (x ) ②偶函数：－x ∈D ，且g (－x )＝g (x ) (2)性质： 坐标原点 坐标原点 y 轴 y 轴 (3)[答案] ①偶 ②既是奇函数，又是偶函数 ③非奇非偶 ④奇 2．用定义判断函数奇偶性的步骤是：(1)求定义域，看定义域是否关于原点对称，若定义域关于原点不对称，则为非奇非偶函数．(2)定义域关于原点对称时，看f (－x )＝±f (x )(或f (x )±f (－x )＝0或f (－x )f (x )＝±1(用此式时，f (x )≠0对定义域内任意x 都成立))是否成立．如不成立，则为非奇非偶函数．(3)f (－x )＝－f (x )成立时为奇函数．f (－x )＝f (x )成立时为偶函数． 3． b ＝0， b ＝0 奇.对于函数奇偶性的讨论，学习时应把握下述几点：①函数的奇偶性讨论是在函数的整个定义域上进行的．考察一个函数y ＝f (x )是否具有奇偶性，不仅考察f (x )与f (－x )之间的关系，更应考察函数的定义域是否关于原点对称． ③以函数的奇偶性作为划分标准，可将函数分为四类：偶函数，奇函数，既是奇函数又是偶函数，非奇非偶函数．既是奇函数又是偶函数的函数f (x )一定是常数函数f (x )＝0，但f (x )＝0不一定既是奇函数也是偶函数，须特别注意定义域是否关于原点对称这一限制条件．④奇函数y ＝f (x )若在x ＝0处有定义，则一定有f (0)＝0.⑤综合函数的单调性与奇偶性，可得以下常用的两个结论：奇函数在区间[a ，b ]和[－b ，－a ]上有相同的单调性；偶函数在区间[a ，b ]和[－b ，－a ]上有相反的单调性(ab >0)．⑥有时也用奇偶函数的性质来判断：偶函数的和、差、积、商(定义域符合要求)仍为偶函数．奇函数的和、差为奇函数，两个奇函数的积、商为偶函数．⑦有些判断奇偶性的题目，须先化简f (x )的表达式，观察其特点，然后再进行判断．[例1] 1、 [分析] 利用函数奇偶性定义来判断． ∴f (x )为奇函数．(2)f (x )定义域为R ，且f (－x )＝(－x )2＋1＝x 2＋1＝f (x )，∴f (x )为偶函数．(3)定义域为(－∞，＋∞)，∵f (－x )＝|－x ＋1|＋|－x －1|＝|x －1|＋|x ＋1|＝f (x )，∴f (x )为偶函数． (4)定义域为(－∞，＋∞)，f (－x )＝－2x ＋1， ∵f (－x )≠－f (x )且f (－x )≠f (x )， ∴f (x )为非奇非偶函数． (5)定义域为{1}，∵定义域不关于原点对称，∴f (x )为非奇非偶函数．2、 [解析] f (x )的定义域为R ，当a ≠0时，f (－x )＝|－x ＋a |－|－x －a |＝|x －a |－|x ＋a |＝－f (x )， ∴f (x )为奇函数，当a ＝0时，有f (x )＝0，∴f (x )既是奇函数又是偶函数.[例2] 1、 [分析] 由函数图象关于原点对称可知y ＝f (x )是奇函数．利用奇函数性质可求得解析式． [解析] ∵函数f (x )的图象关于原点对称． ∴f (x )为奇函数，则f (0)＝0，设x ＜0，则－x ＞0，∵x >0时，f (x )＝x 2－2x ＋3， ∴f (x )＝－f (－x )＝－(x 2＋2x ＋3)＝－x 2－2x －3 于是有：f (x )＝⎩⎪⎨⎪⎧x 2－2x ＋3 (x ＞0)0 (x ＝0)－x 2－2x －3 (x ＜0)先画出函数在y 轴右边的图象，再根据对称性画出y 轴左边的图象．如下图．由图象可知函数f (x )的单调递增区间是(－∞，－1]、[1，＋∞)，单调递减区间是[－1,0)、(0,1]． 2、 [答案] －x ＋1[解析] x >0时，－x <0，∴f (－x )＝－x ＋1，又∵f (x )为偶函数，∴f (x )＝－x ＋1.[例3] 1、已知b ＞a ＞0，偶函数y ＝f (x )在区间[－b ，－a ]上是增函数，问函数y ＝f (x )在区间[a ，b ]上是增函数还是减函数？[分析] 由函数的奇偶性进行转化．[解析] 设a ≤x 1＜x 2≤b ，则－b ≤－x 2＜－x 1≤－a .∵f (x )在[－b ，－a ]上是增函数．∴f (－x 2)＜f (－x 1) 又f (x )是偶函数，∴f (－x 1)＝f (x 1)，f (－x 2)＝f (x 2) 于是 f (x 2)＜f (x 1)，故f (x )在[a ，b ]上是减函数．[点评] 由函数单调性和奇偶性的定义，可以证明在关于原点对称的两个区间上，偶函数的单调性恰是相反的，奇函数的单调性是相同的． 2、[答案] (1)f (－5)<f (3)[解析] (1)∵f (x )是偶函数，∴f (－5)＝f (5)，∵f (x )在[2,6]上是减函数， ∴f (5)<f (3)，∴f (－5)<f (3)．(2)设－6≤x 1<x 2≤－1，则1≤－x 2<－x 1≤6，∵f (x )在[1,6]上是增函数且最大值为10，最小值为4，∴4＝f (1)≤f (－x 2)<f (－x 1)≤f (6)＝10， 又∵f (x )为奇函数，∴4≤－f (x 2)<－f (x 1)≤10， ∴－10≤f (x 1)<f (x 2)≤－4，即f (x )在[－6，－1]上是增函数，且最小值为－10，最大值为－4.[例4] 1、[解析] (1)根据偶函数图象关于y 轴对称的性质，画出函数在y 轴左边的图象，如图(1)． (2)根据奇函数的图象关于原点对称的性质，画出函数在y 轴左边的图象，如图(2)．2、 [答案] (1)2 (2)f (3)>f (1)[解析] (1)∵奇函数的图象关于原点对称，且奇函数f (x )图象过点(2,1)和(4,2)， ∴必过点(－2，－1)和(－4，－2)， ∴f (－4)·f (－2)＝(－2)×(－1)＝2.(2)∵偶函数f (x )满足f (－3)>f (－1)， ∴f (3)>f (1)．[点评](1)可由奇函数的性质，先去掉函数记号¡°f ¡±内的负号，f (－4)·f (－2)＝－f (4)·[－f (2)]＝f (4)·f (2)＝2×1＝2.[辨析] 要判断函数的奇偶性，必须先求函数定义域(看定义域是否关于原点对称)．有时还需要在定义域制约条件下将f (x )进行变形，以利于判定其奇偶性．[例5] [正解] (1)由x ＋1x －1≥0得{x |x ＞1，或x ≤－1}，∵f (x )定义域关于原点不对称，∴f (x )为非奇非偶函数．(2)由⎩⎪⎨⎪⎧1－x 2≥0|x ＋2|－2≠0得－1≤x ≤1且x ≠0，定义域关于原点对称，又－1≤x ≤1且x ≠0时，f (x )＝1－x 2x ＋2－2＝1－x 2x ，∵f (－x )＝1－(－x )2－x ＝－1－x 2x ＝－f (x )，∴f (x )为奇函数． 课后练习答案 一、选择题1．[答案] C2．[答案] D[解析] 四个命题都正确，故选D.3．[答案] D[解析] ∵－f (a )＝f (－a )，∴点(－a ，－f (a ))在y ＝f (x )的图象上，故选D. 4．[答案] D[解析] 奇函数的图象关于原点对称，方程f (x )＝0的六个根，即f (x )图象与x 轴的六个交点横坐标，它们分布在原点两侧各三个，且分别关于原点对称， ∴和为0.5．[答案] A[解析] ∵f (x )＝(m －1)x 2＋2mx ＋3为偶函数，∴m ＝0，∴f (x )＝－x 2＋3，因此f (x )在(－5，－2)上为增函数，故选A.6．[答案] D二、解答题a7． [解析] (1)为偶函数．∵x ∈Q 时，－x ∈Q ， ∴f (－x )＝1＝f (x )．同理，x 为无理数时，－x 也为无理数． ∴f (－x )＝－1＝f (x )，∴f (x )为偶函数．(2)奇函数．∵f (－x )＝|－2x ＋1|－|－2x －1|aa ＝|2x －1|－|2x ＋1|＝－f (x )， ∴f (x )为奇函数．(3)偶函数．∵f (－x )＝2|－x |＝2|x |＝f (x )，∴f (x )为偶函数．(4)画出其图象如图，可见f (x )为奇函数．课后练习答案 一、选择题 1． [答案] D[解析] f (x )＝1x 为奇函数，其图象不过原点，故②错；y ＝⎩⎪⎨⎪⎧x －1 x ≥1－x －1 x ≤－1为偶函数，其图象与y 轴不相交，故③错． 2．[答案] B 3．[答案] A[解析] 解法1：f (－3)＝(－3)7＋a (－3)5＋(－3)b －5＝－(37＋a ·35＋3b －5)－10＝－f (3)－10＝5，∴f (3)＝－15. 解法2：设g (x )＝x 7＋ax 5＋bx ，则g (x )为奇函数，∵f (－3)＝g (－3)－5＝－g (3)－5＝5，∴g (3)＝－10，∴f (3)＝g (3)－5＝－15.4．[答案] A[解析] ∵f (3)<f (1)，∴－f (1)<－f (3)，∵f (x )是奇函数，∴f (－1)<f (－3)． 5．[答案] A[解析] ∵x >0时，f (x )＝2x－3，∴f (2)＝22－3＝1，又f (x )为奇函数，∴f (－2)＝－f (2)＝－1. 6．[答案] D[解析] ∵f (x )在[－2，－1]上为减函数，最大值为3，∴f (－1)＝3，又∵f (x )为偶函数，∴f (x )在[1,2]上为增函数，且最小值为f (1)＝f (－1)＝3.7．[答案] C[解析] 由偶函数，排除A ；由在(0，＋∞)上为增函数，排除B ，D ，故选C. 8．[答案] A[解析] 由题意得|2x －1|<13⇒－13<2x －1<13⇒23<2x <43⇒13x <23，∴选A.9．[答案] B[解析] 解法1：f (x )＝x 2＋(a ＋1)x ＋a 为偶函数，∴a ＋1＝0，∴a ＝－1. 解法2：∵f (x )＝(x ＋1)(x ＋a )为偶函数，∴对任意x ∈R ，有f (－x )＝f (x )恒成立，∴f (－1)＝f (1)，即0＝2(1＋a )，∴a ＝－1. 10．[答案] C [解析] 由条件知，f (x )在(－∞，0)上为减函数， ∴f (－1)<f (－2)，又f (x )为奇函数，∴f (1)>f (2)．[点评] 也可以先求出f (x )在(0，＋∞)上解析式后求值比较，或利用奇函数图象对称特征画图比较． 二、填空题11． [答案] 奇函数 [解析] 由f (x )＝ax 2＋bx ＋c (a ≠0)为偶函数得b ＝0，因此g (x )＝ax 3＋cx ，∴g (－x )＝－g (x )， ∴g (x )是奇函数． 12． [答案] 0[解析] 由于偶函数图象关于y 轴对称，且与x 轴有三个交点，因此一定过原点且另两个互为相反数，故其和为0. 三、解答题13．[解析] (1)f (－x )＝⎩⎪⎨⎪⎧x 2－x (x ≥0)－x 2－x (x <0)，∴f (－x )＝－f (x )，∴f (x )为奇函数．(2)f (－x )＝1x 2－x≠f (x )，f (－x )≠－f (x )，∴f (x )既不是奇函数，又不是偶函数．14． [解析] f (－x )＋g (－x )＝x 2－x －2，由f (x )是偶函数，g (x )是奇函数得，f (x )－g (x )＝x 2－x －2 又f (x )＋g (x )＝x 2＋x －2，两式联立得：f (x )＝x 2－2，g (x )＝x .15． [解析] 因为f (x )是奇函数且定义域为(－1,1)，所以f (0)＝0，即b ＝0. 又f ⎝⎛⎭⎫12＝25，所以12a1＋⎝⎛⎭⎫122＝25，所以a ＝1，所以f (x )＝x 1＋x 2. 16． [解析] 由f (1－a )＋f (1－a 2)<0及f (x )为奇函数得，f (1－a )<f (a 2－1)， ∵f (x )在(－1,1)上单调减，∴⎩⎪⎨⎪⎧－1<1－a <1－1<1－a 2<11－a >a 2－1解得0<a <1. 故a 的取值范围是{a |0<a <1}．17． [解析] 设x ≥0时，f (x )＝a (x －1)2＋2，∵过(3，－6)点，∴a (3－1)2＋2＝－6，∴a ＝－2.即f (x )＝－2(x －1)2＋2.当x <0时，－x >0，f (－x )＝－2(－x －1)2＋2＝－2(x ＋1)2＋2，∵f (x )为奇函数，∴f (－x )＝－f (x )，∴f (x )＝2(x ＋1)2－2，即f (x )＝⎩⎪⎨⎪⎧－2(x －1)2＋2 (x ≥0)2(x ＋1)2－2 (x <0)， 其图象如图所示．。

[难点正本 疑点清源] 1．函数奇偶性的判断
判断函数的奇偶性主要根据定义：一般地，如果对于 函数 f(x)的定义域内任意一个 x，都有 f(－x)＝f(x)(或 f(－x)＝－f(x))，那么函数 f(x)就叫做偶函数(或奇函 数)．其中包含两个必备条件： ①定义域关于原点对称，这是函数具有奇偶性的必要 不充分条件，所以首先考虑定义域有利于准确简捷地 解决问题； ②判断 f(x)与 f(－x)是否具有等量关系．在判断奇偶 性的运算中，可以转化为判断奇偶性的等价关系式 (f(x)＋f(－x)＝0(奇函数)或 f(x)－f(－x)＝0(偶函数)) 是否成立．
2．函数奇偶性的性质 (1)奇函数在关于原点对称的区间上若有单调性，则其单 调性完全相同；偶函数在关于原点对称的区间上若有单 调性，则其单调性恰恰相反． (2)若 f(x)为偶函数，则 f(－x)＝f(x)＝f(|x|)． (3)若奇函数 f(x)定义域中含有 0，则必有 f(0)＝0. f(0)＝0 是 f(x)为奇函数的既不充分也不必要条件． (4)定义在关于原点对称区间上的任意一个函数，都可表 示成“一个奇函数与一个偶函数的和(或差)”． (5)复合函数的奇偶性特点是：“内偶则偶，内奇同外”． (6)既奇又偶的函数有无穷多个(如 f(x)＝0，定义域是关 于原点对称的任意一个数集)．
∴f(x)为偶函数．
题型二 函数的奇偶性与单调性
例 2 (1)已知 f(x)是 R 上的奇函数，且当 x>0 时，f(x) ＝x2－x－1，求 f(x)的解析式； (2)设 a>0，f(x)＝eax＋eax是 R 上的偶函数，求实数 a 的值；
(3)已知奇函数 f(x)的定义域为[－2,2]，且在区间 [－2,0]内递减，求满足 f(1－m)＋f(1－m2)<0 的实 数 m 的取值范围． 思维启迪 (1)f(x)是一个分段函数，当 x<0 时，转化为

认识奇偶总结知识点一、奇偶数的定义1.1 整数的定义首先，我们来定义奇偶数。

在数学中，整数可以分为两类：奇数和偶数。

对于任意的整数n，如果它可以被2整除，那么这个整数就是偶数，记作n是偶数。

如果一个整数n不能被2整除，即n/2有余数，那么这个整数就是奇数，记作n是奇数。

换句话说，偶数是能被2整除的整数，而奇数是不能被2整除的整数。

1.2 奇偶数的性质奇偶数之间有许多有趣的性质，比如：1）奇数加偶数的和一定是奇数，因为奇数加偶数还是奇数；2）奇数加奇数的和一定是偶数，因为奇数加奇数是偶数；3）偶数加偶数的和一定是偶数，因为偶数加偶数还是偶数。

另外，还有一些规律，比如任何数乘以偶数都是偶数，奇数的整数倍还是奇数等等。

1.3 奇偶数的应用奇偶数的应用非常广泛。

在生活中，很多问题涉及到奇偶性质，比如排队时奇数位和偶数位的规律、奇数月和偶数月等。

在数学问题中，奇偶性质也起到了非常重要的作用，比如整数的性质、多项式的运算、图论等。

二、奇偶数的性质2.1 整数的性质奇偶数有许多重要的性质。

首先，我们来看整数的性质。

任何一个整数都可以表示为奇数或偶数。

当然，0是一个特殊的偶数，因为0是可以被2整除的。

对于任意的整数n，它有以下的性质：1）如果n是偶数，则-n也是偶数；2）如果n是奇数，则-n也是奇数；3）任意两个奇数的乘积一定是奇数；4）任意两个偶数的乘积一定是4的倍数，即偶数。

这些性质可以帮助我们更好地理解奇偶数的规律。

2.2 多项式的性质在代数中，奇偶数也有非常重要的应用。

我们知道，多项式是含有多个项的式子，而奇偶性质可以帮助我们判断多项式的性质。

具体来说，一个多项式的奇偶性与它的最高次项的指数有关。

如果一个多项式的最高次项为偶数，那么这个多项式就是偶函数。

如果一个多项式的最高次项为奇数，那么这个多项式就是奇函数。

对于一个奇函数，如果它的自变量x取负数，那么函数值与x取正数时的函数值互为相反数；对于一个偶函数，如果它的自变量x取负数，函数值与x取正数时的函数值相等。

判断下列函数的奇偶性： 判断下列函数的奇偶性： (1)f(x)=x( (ቤተ መጻሕፍቲ ባይዱ)f(x)=log2(x+ (3)f(x)= (4)f(x)= (5)f(x)=x2-|x-a|+2. [思路点拨 思路点拨] 思路点拨 ); ); ;
[课堂笔记 (1)函数定义域为 －∞，0)∪(0，＋ 课堂笔记] 函数定义域为(－ ， ∪ ，＋ ，＋∞). 课堂笔记 函数定义域为 ∵f(-x)=-x( )
2.奇偶函数的性质 奇偶函数的性质 (1)奇函数在关于原点对称的区间上的单调性 相同 ，偶函数 奇函数在关于原点对称的区间上的单调性 填 相同 相同”、 相反 相反”). 在关于原点对称的区间上的单调性 相反 (填“相同 、“相反 (2)在公共定义域内， 在公共定义域内， 在公共定义域内 ①两个奇函数的和函数是 奇函数 ，两个奇函数的积函数 是 偶函数 ； ②两个偶函数的和函数、积函数是 偶函数 . 两个偶函数的和函数、 ③一个奇函数，一个偶函数的积函数是 奇函数 . 一个奇函数， (3)若f(x)是奇函数且在 ＝0处有定义，则f(0)＝ 0 . 若 是奇函数且在 是奇函数且在x＝ 处有定义 处有定义， ＝
已知函数f(x)对一切 、 ∈ ，都有f(x＋ ＝ 已知函数 对一切x、y∈R，都有 ＋y)＝f(x) 对一切 ＋f(y). (1)试判断 的奇偶性； 试判断f(x)的奇偶性 试判断 的奇偶性； (2)若f(－3)＝a，用a表示 若 － ＝ ， 表示f(12). 表示 [思路点拨 思路点拨] 思路点拨
4.已知函数 ＝f(x)为奇函数，若f(3)－f(2)＝1，则f(－2)－ f(－3) 已知函数y＝ 为奇函数 为奇函数， 已知函数 － ＝ ， － － － ＝ .
解析：由题意得f(－2)－f(－3)＝－ ＋f(3) ＝－f(2)＋ 解析：由题意得 － － － ＝－ ＝f(3)－f(2)＝1. － ＝ 答案： 答案：1

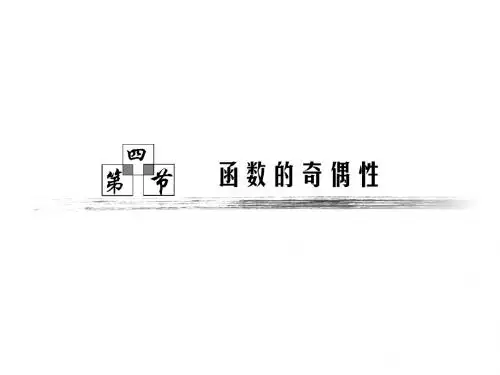
函数奇偶性知识点归纳考点分析配经典案例分析函数的奇偶性定义：1．偶函数：一般地，对于函数()f x 的定义域内的任意一个x ，都有()()f x f x -=，那么()f x 就叫做偶函数．2．奇函数：一般地，对于函数()f x 的定义域的任意一个x ，都有()()f x f x -=-，那么()f x 就叫做奇函数．二、函数的奇偶性的几个性质1、对称性：奇（偶）函数的定义域关于原点对称；2、整体性：奇偶性是函数的整体性质，对定义域内任意一个x 都必须成立；3、可逆性：)()(x f x f =-⇔)(x f 是偶函数；)()(x f x f -=-⇔)(x f 奇函数；4、等价性：)()(x f x f =-⇔0)()(=--x f x f (||)()f x f x ⇔=；)()(x f x f -=-⇔0)()(=+-x f x f ；5、奇函数的图像关于原点对称，偶函数的图像关于y 轴对称；6、可分性：根据函数奇偶性可将函数分类为四类：奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数。

7、判断或证明函数是否具有奇偶性的根据是定义。

8、如果一个奇函数f(x)在x=0处有意义，则这个函数在x=0处的函数值一定为0。

并且关于原点对称。

三、关于奇偶函数的图像特征 一般地：奇函数的图像关于原点对称，反过来，如果一个函数的图像关于原点对称，那么这个函数是奇函数； 即：f(x)为奇函数<=>f(x)的图像关于原点对称 点（x,y ）→（-x,-y ）偶函数的图像关于y 轴对称，反过来，如果一个函数的图像关于y 轴对称，那么这个函数是偶函数。

即： f(x)为偶函数<=>f(x)的图像关于Y 轴对称 点（x,y ）→（-x,y ）奇函数对称区间上的单调性相同（例：奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。

）偶函数对称区间上的单调性相反（例：偶函数在某一区间上单调递增，则在它的对称区间上单调递减）。

④若函数 具有奇偶性，则函数 和函数 的奇偶性相同。
①对于定义域内任意一个 ，若有 成立，则 是偶函数。若有 成立，则 为奇函数.
②任何一个非奇非偶函数均可写成一个奇函数与一个偶函数之和.
对称性
图像关于原点对称.
图像关于y轴对称
单调性
在关于原点对称的区间上具数的性质.
奇函数
偶函数
奇偶性函数
运算性质
奇函数的和、差仍为奇函数；奇（偶）数个奇函数的积、商（分母不为零）为奇（偶）函数。
偶函数的和、差、积、商（分母不为零）仍为偶函数。
定义域关于原点对称.
①一个奇函数与一个偶函数的积为奇函数.
②奇函数+偶函数=非奇非偶函数
③若 是不为0的常数，且函数 具有奇偶性，则函数 和函数 的奇偶性相同；
复合函数
内奇外奇为奇；内奇外偶为偶.
内偶为偶（即 为偶函数， 为偶函数。）
若 关于原点对称，则
若奇函数在原点处有意义，则 恒成立。
当 =0的定义域关于原点对称时， 既是奇函数，又是偶函数。

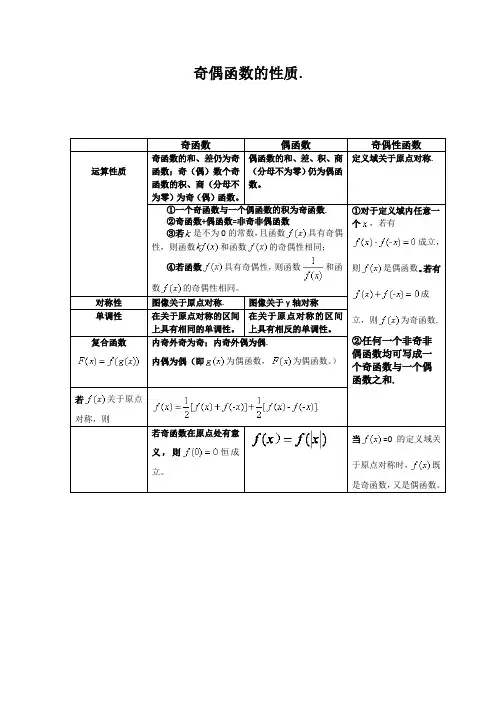
第13讲奇偶分析法把全体整数按被2除的余数分为两类：被2除余数为0整数的称为偶数，一般表示为2k(k为整数)，被2除余数为1整数的称为奇数，一般表示为2k+1(k为整数)．由于既不会有一个整数同时出现在奇数类和偶数类，也不会有一个整数既不在奇数类又在偶数类，因此，我们可以把对整数问题的研究转化为对奇数和偶数的研究．这种利用奇偶数分析问题的方法就可以使一些看起来比较困难的题目变得简单易解了.奇偶分析利用了奇数与偶数的一些性质：1、奇数不等于偶数；2、在自然数数列中，奇数与偶数是相间排列的；3、奇数±奇数=偶数，偶数±偶数=偶数，奇数±偶数=奇数；奇数个奇数的和是奇数，偶数个奇数的和是偶数，任意个偶数的和是偶数；4、奇数×奇数=奇数，偶数×偶数=4的倍数，偶数×整数=偶数；5、两个整数的和与这两个整数的差具有相同的奇偶性6、奇数的平方被4除余1，偶数平方为4的倍数；奇偶分析也常表现为染色，把一个图形染成黑白两色，往往可视为其中一色为奇数，另一色为偶数；也可视为用+1与-1(或1与0)标号，……总之，在分成两类对问题进行讨论时，常常可以看成是在进行奇偶分析．A类例题例1⑴证明：平面上的格点中，任取五点，必有两点，其连线中点是格点．⑵至多可以取出多少个格点，使这些点中任取三点为顶点的三角形面积都不是整数．⑴分析按横坐标与纵坐标的奇偶性把平面格点分类，用抽屉原理证明．证明按横坐标与纵坐标的奇偶性把平面上的所有格点分类，共有4类：(奇，奇)，(奇，偶)，(偶，奇)，(偶，偶)．任取5个格点，必有2点属于同一类，设A (x 1，y 1)，B (x 2，y 2)这二点是属于同一类的两点，则其连线的中点M (12(x 1＋x 2)，12(y 1＋y 2))即为格点．故得证．⑵ 分析 考虑三角形的面积如何计算．解 由三角形面积表达式S =12[(x 1－x 2)(y 2－y 3)－(x 2－x 3)(y 1－y 2)]知，如果三角形有某两个顶点属于同一类(上题中的分类)，则其面积为整数；如果三个顶点都不同类，则其面积不为整数．于是取分属于4个不同的类的4个格点，以这4点中的任三点为顶点的三角形面积都不为整数，但如果取5个格点，则必有某两点属于同一类，此时以这二个点及另外任一点为顶点的三角形面积为整数．故至多取4个点，且此四点应分属不同的4类．说明 把整数分成“奇数”与“偶数”这两类，就相当于构造了两个抽屉，从而奇偶分析常常用抽屉原理为工具解决问题．例2设a1，a2，…，a64是1，2，…，63，64的任意一种排列．令b1=|a1－a2|，b2=|a3－a4|，…，b32=|a63－a64|；c1=|b1－b2|，c2=|b3－b4|，…，c16=|b31－b32|；d1=|c1－c2|，d2=|c3－c4|，…，d8=|c15－c16|；………这样一直作下去，最后得到一个整数x．求证：x为偶数．分析可以从后向前推：若x为奇数，则其前一次运算时的两个数必一奇一偶，…，这样直到开始时的64个数的奇偶性．这就是证法一的思路；也可以从前向后推：第一次运算得到的32个数的奇偶性与原来各数的奇偶性有什么关联？第二次运算所得16个数又与第一次运算的32个数有什么关联？又与原来的64个数有何关联？…，这样直到最后一个数．这就是证法二的思路．证法一假定x为奇数，则上述计算过程中倒数第二步的两个数是一奇一偶，倒数第三步的四个数或者是三奇一偶或者是一奇三偶．仿此推知，计算过程中的每一步只能有奇数个奇数，那么在a1，a2，…，a64，中也该有奇数个奇数.但它们是1，2，…，64的某一排列，其中奇数有32个，这就产生了矛盾.所以最后一个数只能是偶数．证法二因为整数a与|a|的奇偶性一致，整数a、b的和a+b与其差a －b的奇偶性也一致，所以上述计算过程的第二步中的32个数：|a1－a2|，|a3－a4|，…，|a63－a64|，分别与a1+a2，a3+a4，…，a63+a64的奇偶性一致，于是，可改为考虑：第一步：a1，a2，…，a64；第二步：a1+a2，a3+a4，…，a63+a64；第三步：a1+a2+a3+a4，…，a61+a62+a63+a64；…………很明显，这样做最后所得的数是a1+a2+a3+a4+…+a63+a64．而x与它的奇偶性一致．由于a1，a2，…，a64是1，2，…，64的某一排列，因此，a1+a2+a3+a4+…+a63+a64＝1+2+……+64=32×65，这是一个偶数，故知x 为偶数．情景再现1．将某个17位数的数字顺序颠倒，再将得到的数与原来的数相加．证明：得到的和中至少有一个数字是偶数．(1970年第四届全苏数学奥林匹克8年级试题)2．若a，b，c都是整数，且a与b同为奇数或同为偶数，c为奇数，求证：找不到整数n，使an2+bn+c=0．B类例题例3有n×n(n＞3)的一张空白方格表，在它的每一个方格内任意的填入+1与-1这两个数中的一个，先将表内n个两两既不同行又不同列的方格中的数的乘积称为一个基本项．试证明：按上述方式所填成的每一个方格表，它的全部基本项之和总能被4整除(即总能表示成4k的形式，其中k∈Z)．(1989年全国数学联赛)分析一下子证明基本项之和总能被4整除较难，可以分两步走：先证明基本项的和能被2整除，再证其能被4整除．这样就较容易了．证明基本项共有n!个，n＞3，故基本项的个数为4的倍数，设基本项共有4m项．设第i行第j列的格子中填入了a ij(a ij=＋1或－1，1≢i，j≢n)，每个基本项都是由n个＋1或－1相乘而得，故每个基本项都等于＋1或－1．其次，每个数a ij都要在(n－1)!个基本项中出现，由于n＞3，故(n－1)!为偶数．所以，把所有基本项乘起来后，每个a ij都乘了(n－1)!次，于是所有基本项的乘积等于1．这说明等于－1的基本项有偶数个，同样，等于+1的基本项也有偶数个．若等于－1的基本项有4l个，则等于+1的基本项有4m－4l个，其和为4m－4l－4l=4(m－2l)为4的倍数；若等于－1的基本项有4l－2个，则等于+1的基本项有4m－4l+2个，例4设P(x)=a0x+a1x+…+a n-1x+a n是整系数多项式，如果P(0)与P(1)都是奇数，证明P(x)无整数根．(第3届加拿大数学奥林匹克) 分析奇数h与整数n积的奇偶性与n的奇偶性相同．要证P(x)没有整数根，只要证明P(x)既没有奇数根，又没有偶数根即可．证明P(0)＝a n，故a n为奇数；P(1)＝a0＋a1＋…＋a n－1＋a n为奇数，故a0＋a1＋…＋a n－1为偶数，从而a0，a1，…，a n－1中有偶数个奇数．任取一奇数k，则k i(i＝1，2，…，n)为奇数，从而a n－i k i(i＝1，2，…，n)的奇偶性与a n－i的奇偶性相同，于是，a0k n+a1k n-1+…+a n-1k的奇偶性与a0＋a1＋…＋a n－1的奇偶性相同，即a0k n+a1k n-1+…+a n-1k为偶数，从而P(k)=a0k n+a1k n-1+…+a n-1k+a n与a n的奇偶性相同，即P(k)为奇数．从而P(k)≠0，故k不是P(x)的根．任取一偶数h，则h i(i＝1，2，…，n)为偶数，从而a n－i h i(i＝1，2，…，n)为偶数，于是a0h n+a1h n-1+…+a n-1h为偶数，从而P(h)=a0h n+a1h n-1+…+a n-1h+a n与a n的奇偶性相同，即P(h)为奇数．从而P(h)≠0，故h不是P(x)的根．因为任何奇数与任何偶数都不是P(x)的根，所以P(x)没有整数根．例5在12，22，32，…，19892这1989个连续的完全平方数的每个数前都添“+”或“-”号，使其代数和为最小的非负数，并写出算式．(1989年第15届全俄数学奥林匹克)分析要求该和式的最小非负值，由于该和式为整数，而最小非负整数为0，所以首先考虑此和能否等于0？如果不能，应该证明和式不能等于0，再研究和式能否等于1？如果和能等于1，则也要证明和式不能等于1．……，这样依此类推，直到找出和式的最小值为止．要求这1989个完全平方数的和式的最小值，可以考虑找到某种规律，把这些数分成若干小段，每个小段的和为0，最后再处理少数几个数，这样就容易得出结果．为此可对照研究一个简单的问题：在1，2，…，1989这1989个连续整数的每个数前都添“+”或“-”号，使其代数和为最小的非负数．解这1989个数中有995个奇数，994个偶数，故其和为奇数，所以，这1989个平方数的和不可能等于0．而改变和式中任一个的符号(“＋”号改为“－”号)都不改变结果的奇偶性，所以，无论怎样安排各数前的“＋”、“－”号，都不可能使此代数和为0．故所求最小非负代数和≣1．由于n2－(n+1)2－(n+2)2+(n+3)2＝4．因此可以把连续8个整数取出，使其前4个的符号按此安排，其和为4，后4个的符号则与之相反，其和为－4，则此8个数的代数和为0．即n2－(n+1)2－(n+2)2+(n+3)2－(n＋4)2＋(n＋5)2＋(n＋6)2－(n＋7)2＝0．而1989=8×248+5．现从142开始，每连续8个完全平方数为一组，共得247组，每组的第1，4，6，7个数前取“+”号，第2，3，5，8个数前取“－”号，则这组8个数之和为0．按此安排，可以使从142起到19892止的数的代数和为0．又，12＋22＋32＋…＋132＝819，而⎣⎡⎦⎤8192＝409． 经试验知，42＋92＋122＋132＝16＋81＋144＋169＝410．故知－12－22－32＋42－52－62－72－82＋92－102－112＋122＋132＝1． 于是可得，所求最小非负代数和为1．说明 若只把前5个平方数留下，从62起，每8个数分成一组，按上述安排，可以使从62起到19892止的数的代数和为0．但12＋22＋32＋42＋52＝55，而这5个平方数中找不到其中几个，其和为⎣⎡⎦⎤552＝27．如果据此断言，此代数和不可能为1就错了．本解中继续取出62到132这8个数与前5个平方数在一起再加以考察，得出代数和可以等于1的最佳结果．试考虑下面问题：试研究把19892改成n 2后的一般结论？情景再现3．在国际象棋的棋盘上，放有8枚棋子，已知其中任意两枚不同行，也不同列．证明：黑格中的棋子数为偶数．4．在整个平面上有一个无限大的方格棋盘，上面摆好了一些棋子，它们恰好组成一个3k ⨯n 的矩形．按下述规则进行游戏：每一枚棋子都可以越过(沿水平方向或竖直方向)相邻的棋子而放入这枚棋子的相邻的空格里，并把相邻的这枚棋子从棋盘上取走．证明：不论怎样走，棋盘上都不会只剩下1枚棋子．(1982波兰数学竞赛题)5．设a 1，a 2，a 3，a 4，a 5和b 是满足关系式a 21+a 22+a 23+a 24+a 25＝b 2的整数，证明：所有这些数不可能全是奇数．6．设x 1，x 2，…，x n 是一组数，它们之间每一个都取+1或-1，并且x1x2x3x4+ x2x3x4x5+…+x n-3x n-2x n-1x n+x n-2x n-1x n x1+x n-1x n x1x2+x n x1x2x3=0．求证：n是4的倍数．(第26届IMO预选题)C类例题例6设E={1，2，3，…，200}，G={a1，a2，…，a100}是E的真子集，且G具有下列两条性质：1）对于任何1≢i＜j≢100，恒有a i+a j≠201；2）a1+a2+…+a100=10080．试证明：G中的奇数的个数是4的倍数，且G中所有数的平方和为一定数．(1990年全国数学联赛)分析要证G中奇数的个数是4的倍数，可以分两步走：先证G中有偶数个奇数，再进而证明G中的奇数个数是4的倍数．这可以通过考虑奇数与偶数的表示方法做到：偶数是所有被2整除的数，也可看成是被4除余0或2的数；奇数是被2除余1的数，也是被4除余1或3的数．要证明这100个数的平方和为定值，由于这100个数不确定，但E中200个数是确定的，因此应把G中的元与E中不是G的元的那100个元合起来一起考虑它们的平方和．⑴证明：把E中的200个数分成100组，每组两个数，且同组两个数的和为201：A i＝{i，201－i}(i＝1，2，…，100)．(即分成{1，200}，{2，199}，{3，198}，…，{100，101}这100个组)；于是同组的两个数不能都是G的元素，这说明G中的元素不能超过100个．又若某一组中的两个数都不是G的元素，则G中的元素个数将少于100．这说明上述分组中的每个组都必须有1个数且只能有1个数是G 的元素．设G的元素中，x1，x2，…，x i为奇数，y1，y2，…，y j为偶数，且i+j=100(x1，x2，…，x i，y1，y2，…y j是a1，a2，…，a100的一个排列)．x1+x2+…+x i +y1+y2+…+y j=10080．由于i个奇数的和为偶数，故i为偶数，令i=2p(p∈N)．又由于201≡1(mod 4)，故A i中两个数或被4除余0与1，或被4除余2与3．把Ai中两数被4除的余数把这100组再分两类：{4k+1，4(50－k)}型的组共有50个(即A1，A4，A5，A8，…，A97，A100这50组)，{4k+3，4(50－k)－2}型的组共有50个(即A2，A3，A6，A7，…，A98，A99这50组)．设G中4k+1型的奇数共有m个，则4k+3型的奇数共有2p－m个，4(50－k)型的偶数共有50－m个，4(50－k)－2型的数共有50－2p+m个．所以，和a1+a2+…+a100≡m×1＋(2p－m)×3＋(50－m)×0＋(50－2p+m)×2 (mod 4)．即2p＋100应能被4整除．所以，2|p，即4|i．即是：G中奇数的个数是4的倍数．⑵证明因{a1，a2，…，a100，201－a1，201－a2，…，201－a100}＝{1，2，3，…，200}．故a21+a22+…+a2 100+(201－a1)2+(201－a2)2+…+(201－a100)2=12+22+32+…+2002为定值(＝16×200×201×401＝2686700)．展开即是a21+a22+…+a2 100＋2012×100－2×201×(a1＋a2＋…＋a100)＋a21+a22+…+a2 100=2(a21+a22+…+a2 100)＋2012×100－2×201×10080为定值(＝2686700)．即a21+a22+…+a2 100为定值(＝1349380)．例7 设有一个顶点都是格点的100边形，它的边都与x轴或y轴平行，且边长都是奇数．求证：它的面积也是奇数．(1987年中国数学奥林匹克) 分析先研究这个100边形的形状，必定是凹的多边形；再研究如何求这个多边形的面积，由于其形状不能确定，但其边与坐标轴平行，故可以用向x轴作垂线的方法(如例2的链接中所用的方法)把该多边形面积转化为一批矩形的面积和．再研究各矩形面积的奇偶性．证明显然，这些边必是一横一竖相间．从而这100条边中有50条为横边，50条为竖边．如图，不妨把这个100边形放在第一象限的x轴上方，并设A1A2为横边，A2A3为竖边，分别过A1、A3、A5、…、A99作x轴的垂线A1B1、A3B3、A5B5、…、A99B99，垂足分别为B1、B3、B5、…、B99．则该100边形可以看作50个矩形A1A2B3B1、A3A4B5B3、A5A6B7B5、…，A99A100B1B99的面积的代数和．由于A3B3＝A1B1±A3B3，而A3B3的长度为奇数，故A1B1与A3B3的长度数值奇偶性相反，于是，A1B1、A3B3、…、A99B99这50条线段的长度数值奇偶性相间．但A1A2、A3A4、…、A99A100的长度数值都是奇数，从而这50个矩形的面积数值也是奇偶相间，故其中有25个奇数，25个偶数．所以，这50个矩形面积的代数和为25个奇数与25个偶数的代数和，必为奇数．故证．例8 能否把1，1，2，2，3，3，4，4，…1986，1986这些数排成一行，使得两个1之间夹着一个数，两个2之间夹着两个数，…，两个1986之间夹着1986个数？请你证明你的结论．(1986年中国数学奥林匹克) 分析把位置编号，再进行奇偶分析．证明把一行1986×2＝3972个位置从左向右编成1至3972号，如果能排列成，则每个数都应占据一个号码．设两个“1”分别占了第i1及第i1＋2这两号，两个“2”分别占了第i2及i2＋3号，…，一般的，两个数“k”(k＝1，2，…，1986)分别占了第i k及第i k＋k＋1号．证法一各数所占的号码的和为(i1＋i1＋2)＋(i2＋i2＋3)＋…＋(i1986＋i1986＋1987)＝2(i1＋i2＋…＋i1986)＋2＋3＋…＋1987＝2(i1＋i2＋…＋i1986)＋1989×993．⑴故此号码和是奇数．但此号码和也应等于1＋2＋3＋…＋1986×2＝3973×1986．⑵却是偶数．由⑴、⑵矛盾，知不能按要求排成．证法二若k为奇数，则两个“k”占的第i k及第i k＋k＋1号是奇偶性相同的两个号码；若k为偶数，则两个“k”占的第i k及第i k＋k＋1号是奇偶性不同的两个号码．从1到3972共有1986个奇数号码与1986个偶数号码．又，从1到1986共有993个奇数，993个偶数．其中993个偶数分别占了993个奇数号码与993个偶数号码．于是余下993个奇数号码与993个偶数号码，每个奇数或占两个奇数号码，或占两个偶数号码，故必占偶数个奇数号码及偶数个偶数号码，而余下的却是奇数奇数号码与奇数个偶数号码，从而这样的排列不能排成．链接本题有一般性的结论，这就是下述竞赛题：求所有具有下述性质的n ∈N *，能够把2n 个数1，1，2，2，3，3，…，n ，n 排成一行，使得当k =1，2，…，n 时，在两个k 之间恰有k 个数．(1982年前苏联数学竞赛题)解：设n ∈N *，a 1，a 2，…，a 2n 是满足要求的排列．设数k 排在第m k 及m k +k +1位，故这2n 个数的数位和(即{a i }的下标和)为k =1∑n (m k +m k +k +1)=2k =1∑nm k +12n (n +3)． 但这2n 个数的位的和又等于1+2+…+2n =n (2n +1)．∴ 2k =1∑nm k = n (2n +1)－12n (n +3)= 12n (3n －1)． 于是14n (3n －1)为整数，但n 与3n －1奇偶性不同，故当n =4l 或3n －1=4l '时，即n =4l 或n =4l '－1时14n (3n －1)为整数． ∴ 当n ≡1，2(mod 4)时，不存在满足要求的排列．当n ≡0(mod 4)时，可把这1~4l 这些数如下排列：l =1时：2，3，4，2，1，3，1，4．l =2时：4，6，1，7，1，4，8，5，6，2，3，7，2，5，3，8．一般的：4l －4，...，2l ，4l －2，2l －3，...，1，4l －1，1， (2)－3，2l ，…，4l －4，4l ，4l －3，…2l +1，4l －2，2l －2，…，2， 2l －1，4l －1，2，…2l －2，2l +1，…4l －3，2l －1，4l ．当n ≡－1(mod 4)时，可把这4l －1个数如下排列：l =1时：2，3，1，2，1，3；l =2时：4，6，1，7，1，4，3，5，6，2，3，7，2，5．一般的，4l －4，...，2l ，4l －2，2l －3，...，1，4l －1，1， (2)－3，2l ，…，4l －4，2l －1，4l －3，…2l +1，4l －2，2l －2，…，2， 2l －1，4l －1，2，…2l －2，2l +1，…4l －3．其中，“…”表示一个公差为2或－2的等差数列．情景再现7．在圆周上按任意顺序写上4个1与5个0，然后进行下面的运算：在相邻的相同数字之间写上0，而在不同的相邻数字之间写上1，并擦掉原来的数字．接着进行同样的运算，如此继续．证明：不管这种运算进行多少次，都不可能得到9个0．(1975年南斯拉夫数学竞赛)8．设d1，d2，…，d k是正整数n的所有因数，这里，1=d1＜d2＜…＜d k＝n，k≣4，求所有满足d21+d22+d23+d24=n的正整数n．(1989年巴尔干数学竞赛)习题131．一天，某旅游者乘火车来到某个城市游玩，他玩了一天后于晚上回到来时的火车站，试证明：他总可以沿着他当天走过奇数次的街道回到火车站．2．将正方形ABCD分割成n2个相等的小方格(n是正整数)，把相对的项点A、C染成红色，把B、D染成蓝色，其它交点任意染红、蓝两色中的一种颜色．证明：恰有三个顶点同色的小方格数目必是偶数．3．在黑板上写有若干个0、1和2，现在可以擦掉两个不同的数字，并用另一个数字代替它们(用2代替0与1，用1代替0与2，用0代替1与2)．证明如果这种做法，最后在黑板上只留下一个数字，那么，留下的数字与操作顺序无关．(1975年第9届全苏数学奥林匹克)4．在平面上画了一个由边长为1的正六边形组成的蜂窝形网格，如果沿网格线从一个网格点A用最短路程走到另一个网格点时共走的路程为100，试证：他走的全程的一半是走在同一个方向上．5．已知多项式x3+bx2+cx+d的系数都是整数，并且bd+cd是奇数，则这个多项式不能分解成为两个整系数多项式的乘积．(1963年北京市高中数学竞赛)6．是否存在整数a，b，c，d，使得对所有的整数x，等式x4+2x2+2000x+30＝(x2+ax+b)(x2+cx+d)成立．7．能否将1990×1990方格表中的每个小方格涂成黑色或白色，使得关于表的中心对称的方格涂有不同的颜色，并且任一行及任一列中黑格与白格都各占一半．(1990全苏第4届数学奥林匹克)8．在99枚外观相同的硬币中，要找出其中的某些假币．已知每枚假币与真币的重量相差奇数克，而所给硬币重量和恰等于真币的重量，现有带指针标明整克数的双盘天平，证明只要称一次就可辨别指定的硬币是否是假币．(1987年第13届全俄数学奥林匹克)9．从集{0，1，2，…，14}中选出不同的数，填入图中的10个小圆圈中，使得由线段连结的两个数的差的绝对值均不相等，这可能吗？证明你的结论．(1991年第23届加拿大数学奥林匹克)10．设正整数d不等于2、5、13，证明：在集合{2，5，13，d}中，可以找到两个不同元素的a，b，使ab-1不是完全平方数．（1986年第27届国际数学奥林匹克竞赛试题）11．设P0，P1，P2，…，P1993=P0为xy平面上不同的点，具有下列性质：⑴P i的坐标均为整数，i=0，1，2，3， (1992)⑵在线段P i P i+1上没有其他的点，坐标均为整数，i=0，1，2，3， (1992)求证：对某个i，0≢i≢1992，在线段P i P i+1上有一个点Q(q x，q y)使2q x，2q y，均为奇整数．(1993年亚太地区数学奥林匹克)12．设n≣2，a1，a2，…，a n都是正整数，且a k≢k（1≢k≢n）．试证明：当且仅当a1+a2+…+a n为偶数时，可适当选取“+”号与“-”号，使a1±a2±…±a n=0．(1990年中国数学奥林匹克)本节“情景再现”解答：1．证明取十七位数a17a16…a2a1，颠倒其数字顺序后，所得数为Array a1a2…a16a17，把两数相加，如果和的各位数字都是奇数，则末位的a1＋a17是奇数，但和的首位数字是a17＋a1或a17＋a1＋1(当计算第16位数字时，如果没有进位，则为a17＋a1，若有进位，则为a17＋a1＋1)的末位数字(如果此和≣10，则此和是一个18位数，其首位为1)，若计算第16位时有进位，则第17位数字将是偶数a17＋a1＋1(或a17＋a1－9)，故第16位在计算时没有进位．这说明第16位的a2＋a16没有进位，此时，若第二位计算时有进位，则只能进1且由a2＋a16＝9，a1＋a17≣10引起，此时，和的第二位数字为0，与假设矛盾．即a1＋a17与a2＋a16均不能有进位．去掉a1、a2、a16、a17这4个数字后余下13位数，又可仿上证明，再连续去掉4位数字三次，剩下a9＋a9，只能得偶数．与假设矛盾，从而可知，和的各位数字中至少有一个是偶数．2．证明⑴当n为奇数时，因a、b同奇偶，所以an2+bn为偶数，又c为奇数，故an2+bn+c为奇数，所以an2+bn+c 0．⑵当n为偶数时，an2+bn为偶数，c为奇数，故其和an2+bn+c 为奇数，不等于零．3．证明我们不妨设棋盘的左上角为白格，设从上至下的行号依次为1，2，…，8，从左向右的列号依次为1，2，…，8．这样，国际象棋棋盘的每个方格被赋予一个坐标(a，b)，容易看出，棋盘的每个白格的坐标的两个分量之和都是偶数；每一个黑格的坐标的分量之和都是奇数．由条件，我们考虑这8枚棋子所在的坐标的各分量之和的总和S，则S＝(1+2+…+8)×2＝72．于是S为偶数，若黑格中的棋子数为k，就有k个奇数的和为偶数，从而k为偶数，即.棋盘的黑格中的棋子的个数为偶数．4．解按右图把棋盘的每个格子编号，由于共有3k行放了棋子，故每种编号的中放的棋子数一样多．每走一步，有两种编号上放的棋子数减少1，而第三种编号中放的棋子数增加1．于是每种格子中的棋子数的奇偶性都改变了．即开始时，每种格子中棋子数奇偶性相同，以后每走一步，三种格子中棋子数的奇偶性仍相同．如果最后只剩下1枚棋子，则有两种编号的中的棋子数为0，而另一种编号中的棋子数为1．奇偶性不同．矛盾．故不可能．5．证明若这些数都是奇数，则由于a2i≡1(mod 8)(i＝1，2，3，4，5)．所以a21+a22+a23+a24+a25≡5(mod 8)．但b2≡1(mod 8)，故证．6．证明记y i＝x i x i＋1x i＋2x i＋3，(1，2，…，n)，且x n＋r＝x r(r＝1，2，3，4)．则y i＝＋1或－1．由于y1＋y2＋…＋y n＝0，故{y1，y2，…，y n}中＋1与－1的个数相等，故2|n，设n＝2k(k∈N*)．即{y1，y2，…，y n}中有k个＋1，k个－1．又y1y2…y n＝x41x42…x4n＝1，但y1y2…y n＝(＋1)k(－1)k．故(－1)k＝1，从而k为偶数，设k＝4h(h∈N*)所以，n＝4h，即n是4的倍数．7．解若经过k次操作，第一次出现9个0，(即前面k－1次操作都没有出现9个0的情况)．这说明，第k－1次应该出现9个相同的数字，但不是0，而应出现全部是1，于是第k－2次操作所得应是全部0，1相间．于是圆周上的标数个数应为偶数个．但原来只标出9个数字，是奇数个，而经过1次操作，并不改变标出数字的个数．8．证明若n为奇数，则其每个因数都是奇数，于是d21+d22+d23+d24=n为偶数，矛盾．故n为偶数．故d1=1，d2=2，且d3、必一奇一偶．若d3=3，则d4≢6且d4必为偶数．当d4=4时，d21+d22 +d23+d24=30，不满足d4=4；当d4=6时d21+d22+d23+d24=50，不满足d4=6．故d3>3．3 |/n．若d3=4，则4|n，且d4为奇．由于d21+d22+d23+d24=n≡0(mod 4)，而d21≡1(mod4)，d22≡0(mod4)，d23≡0(mod4)，d24=1，与d21+d22+d23+d24≡0(mod 4)矛盾．故d3>4．4 |/n．从而d3必为奇数，于是由d21+d22+d23+d24=n≡2(mod4)故d4为偶数，从而d4=2d3．故1+4+d23+4d23=5+5d23=5(1+d23)=n，即5|n，d3=5，d4=10，⇒n=130．“习题13”解答：1．解设他到达某路口后，准备回火车站，此时设他已经到过这个交叉路口k次，前k－1次都是到达此路口又离开的，只有最后一次是他刚到达此路口的，从而他走过了连接该路口的2(k－1)＋1＝2k－1条街道(某条街道走过几次就算几条)，于是他不可能超过其中的每一条街道都是偶数次，即至少有一条街道他以前走过奇数次．于是，他可以沿此街道走下去，到达另一个路口，同样的道理，他又可选择一条他走过奇数次的街道走下去，由于他前面经过的街道是有限条，从而他不可能这样一直走下去，必于某一时刻到达车站．2．证明用数字代表颜色，红色记为1，蓝色记为－1．将小方格编号为1，2，…，n2，并记每个小方格四顶点的乘积为A i （i=1，2，…，n2）.若恰有三顶点同色，A i＝－1，否则A i=1．现在考虑乘：对正方形内部的交点，各点相应的数重复出现4次；积A1×A2×…×An2正方形各边上不是端点的交点所相应的数各出现2次；A、B、C、D四点＝1．因相应的数的乘积为1×1×(－1)×(－1)＝1．于是，A1×A2×…×An2中－1的个数必为偶数，即恰有三个顶点同色的小方此，A1，A2，…，An2格必有偶数个．3．解设原来写了p个0，q个1，r个2，每次操作，每种数字或增加1个，或减少1个，于是，每次操作，这3种数字的个数的奇偶性都同时改变，即p、q、r这三个数的奇偶性如果原来相同，则经过操作，其奇偶性仍相同，若原来奇偶性不同，则经过操作后奇偶性仍不同．若最后只留下一个数字，该数字的个数为奇，其余两个数字的个数为0，是偶数．这说明，原来p、q、r按奇偶性分类，必有2个属于同一类，这两类数最后全部擦去；另一个则属于另一类，而最后留下的数就是后一类的数．4．解考虑他走过水平的两条路，若这两条路之间没有走水平的路，则在这两条路上前进的方向不能相反，否则不是最短路，即走此两条路时的方向相同．由此可见，他在水平路上的前进方向始终相同，而在相邻的两次水平路间一定走过奇数条其他方向的路．故这两条水平路的路程数奇偶性相同．同理，其余两个方向上走的路程数的奇偶性也分别相同，即总有某个方向走了全路程的一半．5．证明设多项式x3+bx2+cx+d可以分解成两个多项式的乘积，则必可分解成一个一次式与一个二次式的积．设3+bx2+cx+d=(x+p)(x2+qx+r)，其中p、q、r都是整数．于是比较此式两边的系数，得pr=d；①pq+r=c；②p+q=b．③因bd+cd=(b+c)d为奇数，故d与b+c都是奇数．所以b与c必一奇一偶．⑴若b为奇数，c 为偶数，则由①：pr=d为奇数，故p与r都为奇数，所以由②知q为奇数，由③知q为偶数，二者矛盾；⑵若b为偶数，c为奇数，则由①知p与r都是奇数，于是由②得q 为偶数，由③得q 为奇数，二者矛盾．故x 3+bx 2+cx +d 不能分解成为两个整系数多项式的乘积．6．解 如果已知等式成立，又右边=x 4+(a +c )x 3+(b +d +ac )x 2+(bc +ad )x +bd ，于是有等式 x 4+2x 2+2000x +30=x 4+(a +c )x 3+(b +d +ac )x 2+(bc +ad )x +bd比较等式两边的对应项的系数，则有⎩⎨⎧a +c ＝0， ①b +d +ac ＝2， ②bc +ad ＝2000， ③bd ＝30． ④由④知，b 和d 一个为奇数，一个为偶数，不妨设b 为奇数，d 为偶数．再考虑③式，由d 是偶数，则ad 为偶数，又因为2000为偶数，则bc 必为偶数，再由b 为奇数得，c 为偶数.根据这些结果考虑②式，由b 为奇数，d 和c 为偶数可知b +d +ac 为奇数，可是等式右边是2，2为偶数，这样②式不可能成立，因此题目要求的a ，b ，c ，d 不存在．7．解 若能涂成，把黑格记为数“＋1”，白格记为数“－1”，于是所有各格中数的和为0．现把此方格表分成4个995×995的小方格表A 1，A 2，A 3，A 4如图．由于每个995×995方格中方格数都是奇数，从而其各数的和不等于0，由对称性知A 1与A 4、A 2与A 3中各数和符号相反，不妨设A 1、A 2中各数和为正，A 4、A 3中各数和为负．由于原方格表的前995行的和都为正，这说明此995行中不可能每行的数的和都为0．即存在某些行，该行中各数和为正．即该行中黑格比白格多．矛盾．故不可能涂成．8．证明 所给的硬币除指定的一枚硬币外，把余下的98枚分成两组，每组49枚，将它们分别置于两边的盘子上．如果两边的重量相差偶数克，那么取出那一枚硬币为真币；如果两边的重量相差奇数克，那么取出的那枚硬币是伪币．事实上，由于假币的重量与真币的重量相差奇数克，故当假币有奇数个时，这些假币的重量和必与相同个数的真币重量和相差奇数克，从而相差的克数不可能为0．所以在这99枚硬币中，假币有偶数枚．如果指定的这枚硬币是假币，则余下98枚硬币中，有奇行行。

奇偶性的运算法则
奇偶性的运算法则:两个奇函数的乘积是偶函数，两个偶函数的乘积是偶函数，一个奇函数与一个偶函数的乘积是奇函数。

运算法则
(1) 两个偶函数相加所得的和为偶函数
(2)两个奇函数相加所得的和为奇函数
(3)一个偶函数与一个奇函数相加所得的和为非奇函数与非偶函数
(4) 两个偶函数相乘所得的积为偶函数。

(5) 两个奇函数相乘所得的积为偶函数
(6)一个偶函数与一个奇函数相乘所得的积为奇函数。

函数奇偶性常用结论
(1) 奇函数在对称的单调区间内有相同的单调性
偶函数在对称的单调区间内有相反的单调性
(2) 若f (x-a) 为奇函数，则f (x) 的图像关于点(a，0) 对称
若f (x-a) 为偶函数，则f (x) 的图像关于直线x=a对称
(3) 在f (x)，g (x) 的公共定义域上: 函数函数=奇函数
偶函数士偶函数=偶函数
奇函数X奇函数=偶函数。

f x
注：(1)在处理抽象函数问题上，一般常用赋值法；
Ex：定义在R上的函数y=f(x)，对任意x1， x2 ∈R都有f(x1+x2)=f(x1)+f(x2)，判断函 数y=f(x)的奇偶性并证明。奇函数
x2 2x 5 f x 2 x 2 x
x0 x0
奇
奇偶性的证明方法一般是定义法： ①.看定义域是否关于原点对称 ②.若满足①，再看f(x)与f(-x)的关系
对复杂函数的奇偶性判断，不要轻易下结论，应 先化简
Ex：判断下列函数的奇偶性
x x 1 f x 2 1 2x
-1 小 则 f x 在 , 0 上有最___值___. 例：定义在实数集上的函数f(x)，对任意x， y∈R有f(x+y)+f(x-y)=2f(x)· f(y)且f(0)≠0 ①求证：f(0)=1；②求证：y=f(x)是偶函数
(2)在判断奇偶性问题上，通过赋值产生 f x 与
Ex：定义在(-∞,+∞)上的任意函数f(x)都 可以表示成一个奇函数g(x)和一个偶函数 h(x)之和,如果 f x lg 10 x 1 , x R, 那 么（ C ）
1 x , h x 1 lg 10 x 1 x B . g x lg 10 1 x 2 2 x x x C . g x , h x lg 10 1 2 2 x x x D . g x , h x lg 10 1 2 2
①奇函数的图象关于原点 对称；反之亦然。 偶函数的图象关于 Y轴 对称；反之亦然。 ② 奇 函数在关于原点对称的两个区间上单调 性相同； 函数在关于对称轴对称的两个区 偶 间上单调性相反。

数的奇偶性奇数和偶数的特点奇数和偶数是我们在数学中经常遇到的两种数字类型。

它们有着不同的特点和性质，本文将深入探讨奇数和偶数的特点，并进一步说明它们在数学和现实生活中的应用。

一、奇数的特点奇数是不能被2整除的数，其特点如下：1. 奇数的个位数只能是1、3、5、7和9，十位数以上没有限制。

2. 任何一个奇数都可以用2n+1表示，其中n是任意整数。

3. 任何两个奇数相加的结果一定是一个偶数。

4. 奇数和奇数的乘积一定是奇数。

二、偶数的特点偶数是能够被2整除的数，其特点如下：1. 偶数的个位数可以是0、2、4、6和8，十位数以上没有限制。

2. 任何一个偶数都可以用2n表示，其中n是任意整数。

3. 任何两个偶数相加的结果一定是一个偶数。

4. 偶数和偶数的乘积一定是偶数。

奇数和偶数在数学中起着重要的作用，它们的特点和性质被广泛应用于各个领域：1. 在代数学中，奇数和偶数的性质被用于证明和推导各种数学定理和公式。

2. 在计算机科学中，奇偶校验被广泛应用于数据传输和错误检测。

3. 在统计学中，奇数和偶数的分布特点可用于分析和描述一组数据的结构和规律。

4. 在日常生活中，奇数和偶数的概念被广泛应用于周数、楼层数、座位排列等方面。

总结起来，奇数和偶数具有各自独特的特点和性质，它们在数学和现实生活中都扮演着重要的角色。

了解和理解奇数和偶数的特点有助于我们更好地应用它们，解决问题和推导结论。

正确理解奇偶性对于数学学习和科学研究都具有重要的意义。

无论是奇数还是偶数，它们都是数字世界中不可或缺的一部分。

通过本文的介绍，我们对奇数和偶数的特点有了更深入的了解。

希望读者能够从中获得知识和启发，并能在实际应用中灵活运用奇偶性的概念，进一步探索奇数和偶数所承载的更多数学奥秘。

让我们共同致力于数学的学习与研究，探索数字的无限魅力。

奇偶函数解题
奇偶函数是指在一个数轴上对称的函数。

一个函数f(x)是奇函数，如果对于任意实数x，有f(-x) = -f(x)；一个函数f(x)是偶
函数，如果对于任意实数x，有f(-x) = f(x)。

解奇偶函数的题目，一般有以下几种方法：
1. 验证函数关系式：根据函数关系式来判断函数的奇偶性质，即验证f(x)是否满足f(-x) = -f(x)或者f(-x) = f(x)。

2. 利用函数性质：奇函数的性质是在函数图像上关于原点对称，所以可以根据函数图像来判断函数的奇偶性。

3. 利用函数的导数：对于可导的函数，若f(x)是奇函数，则
f'(x)是偶函数；若f(x)是偶函数，则f'(x)是奇函数。

4. 利用函数的积分：对于可积的函数，若f(x)是奇函数，则
∫[a,-a] f(x) dx = 0；若f(x)是偶函数，则∫[a,-a] f(x) dx ≠ 0。

需要注意的是，对于非可导或非可积的函数，则不能直接利用导数或积分性质来判断函数的奇偶性。

奇偶知识点总结一、奇偶数的定义1. 自然数的分类在自然数中，我们可以将所有的数分为两类：奇数和偶数。

奇数是指能够被2整除，余数为1的自然数，如1、3、5、7等；偶数则是指能够被2整除，余数为0的自然数，如2、4、6、8等。

2. 奇偶数的表示奇偶数可以用数学符号来表示，通常用字母n表示一个任意的自然数，如果n是偶数，则可以表示为n=2k，其中k是一个整数；如果n是奇数，则可以表示为n=2k+1，其中k是一个整数。

3. 奇偶数的判断判断一个数是奇数还是偶数，可以通过对2取余来实现。

如果一个数除以2的余数为0，则它是偶数；如果余数为1，则它是奇数。

二、奇偶数的性质1. 奇数的性质奇数的平方是奇数，奇数与奇数相加得到的结果是偶数，奇数与偶数相乘得到的结果是偶数。

2. 偶数的性质偶数的平方是偶数，偶数与偶数相加得到的结果是偶数，偶数与奇数相乘得到的结果是偶数。

3. 奇偶数的运算在进行奇偶数的运算时，奇数与奇数相加得到的结果是偶数，奇数与偶数相加得到的结果是奇数，偶数与偶数相加得到的结果是偶数；奇偶数相乘得到的结果都是偶数。

4. 奇数的递增规律奇数具有递增的规律，即从1开始，依次加2，就可以得到所有的奇数。

5. 偶数的递增规律偶数也具有递增的规律，即从2开始，依次加2，就可以得到所有的偶数。

三、奇偶数的相关定理1. 奇数与奇数相加等于偶数定理：两个奇数相加得到的结果一定是偶数。

证明：假设有两个奇数a和b，可以表示为a=2m+1，b=2n+1，其中m和n都是整数。

那么a+b=2m+1+2n+1=2(m+n)+2=2(m+n+1)，得到的结果是偶数。

因此，两个奇数相加得到的结果一定是偶数。

2. 奇数与偶数相乘等于偶数定理：一个奇数乘以一个偶数得到的结果一定是偶数。

证明：假设有一个奇数a和一个偶数b，则可以表示为a=2m+1，b=2n，其中m和n都是整数。

那么a*b=(2m+1)*2n=2(m+1)2n，得到的结果是偶数。

又∵f(x)在(-1,1)上为减函数， ∴
1-a>a2-1 -1<1-a<1 -1<a2-1<1,解得0<a<1.
（2）因为函数g(x)在［-2,2］上是偶函数，则由g(1-m)<g(m)，可得g(|1m|)<g(|m|),
又当x≥0时，g(x)为减函数，得到
|1-m|≤2 |m|≤2
1 解之得-1≤m< 2
（4）f(x)= 1 x2 x2 1
.
x
11
(1)x x 定1 1
(x)2 1 x2 x2
义 域 为
x1 x
得x2 1
（
3 ）
函
数
的
定
义
域
为
A
=
{
学点二 由奇偶性求函数解析式 设f(x)是定义在R上的奇函数，当x>0时，f(x)= x2 +x+1,求 函数解析式. 【分析】由奇函数的图象关于原点对称，找x≥0和x<0时解析 式间的联系.
（2）如果一个函数的定义域关于原点不对称，那么这个 函数既不是奇函数，也不是偶函数.
（3）定义域关于原点对称，满足f(-x)=-f(x)=f(x)的函数， 既是奇函数，又是偶函数，如f(x)=0,x∈R.
判断下列函数的奇偶性：
1
1
（1）f(x)=x+ （3）f(x)=x+
xx
;
1
;
（2）f(x)=x2+ x2 ;
|1-m|>|m|,.
1.在函数的奇偶性中应注意什么问题？
（1）对于函数奇偶性的理解
①函数的奇偶性与单调性的差异:函数的奇偶性是相对于函数 的整个定义域来说的，这一点与函数的单调性不同.从这个意 义上来讲，函数的单调性是函数的“局部”性质，而奇偶性是 函数的“整体”性质，只有对函数定义域内的每一个值x，都 有f(-x)=-f(x)（或f(-x)=f(x)）,才能说f(x)是奇（或偶）函数.

奇偶函数运算⑴ 两个偶函数相加所得的和为偶函数。

⑵ 两个奇函数相加所得的和为奇函数。

⑶ 两个偶函数相乘所得的积为偶函数。

⑷ 两个奇函数相乘所得的积为偶函数。

⑸一个偶函数与一个奇函数相乘所得的积为奇函数。

⑹几个函数复合，只要有一个是偶函数，结果是偶函数；反之是奇函数。

⑺偶函数的和差积商是偶函数。

⑻奇函数的和差是奇函数。

⑼奇函数的偶数个积商是偶函数。

⑽奇函数的奇数个积商是奇函数。

一、定义原则及推理知识点首先要掌握奇偶特性的一些性质以及推论：1、奇偶运算基本法则奇数±奇数=偶数；偶数±偶数=偶数；偶数±奇数=奇数；奇数±偶数=奇数。

2、推论（1）任意两个数的和如果是奇数，那么差也是奇数；如果和是偶数，那么差也是偶数。

（2）任意两个数的和或差是奇数，则两数奇偶相反；和或差是偶数，则两数奇偶相同。

（3）奇数个奇数的和是奇数；偶数个奇数的和是偶数。

二、例题讲解例1、某地劳动部门租用甲、乙两个教室开展农村实用人才培训。

两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。

两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。

问甲教室当月共举办了多少次这项培训？（）（2010年国家公务员考试行测真题第48题）A、8B、10C、12D、15答案：D 解析：设甲教室共举办了x次，乙教室共举办了y次，50x+45y=1290X+y=2750x(偶数)+45y(偶数)=1290(偶数)，可推出y=偶数，X+y=27，可推出x=奇数15。

例2、甲购买3支签字笔、7支圆珠笔、1支铅笔共花费32元，乙购买同样价格的笔，其中签字笔4支，圆珠笔10支，铅笔1支，共用去43元，问：单独购买签字笔、圆珠笔、铅笔各一支共需多少钱?（）（2009年国家公务员考试行测真题第112题）A、21B、11C、10D、17答案：C解析：3x+7y+z=324y+10y+z=43由：4y(偶数)+10y(偶数)+z=43(奇数)，可推出z=奇数；3x+7y+z（奇数）=32（偶数），可推出3x+7y=奇数，3x为奇数时，则7y为偶数，反之一样，得到x,y为一奇一偶。

奇偶四则运算法则在数学中，奇偶性是一个非常重要的概念。

奇数是指不能被2整除的整数，而偶数则是可以被2整除的整数。

在四则运算中，奇偶性也有着自己的规则。

加法在加法中，奇数加偶数的结果一定是奇数，偶数加偶数的结果一定是偶数，奇数加奇数的结果则可能是奇数也可能是偶数。

这是因为奇数加偶数时，奇数的最后一位一定是1，而偶数的最后一位一定是0，所以相加后最后一位一定是1，即为奇数。

而偶数加偶数时，最后一位都是0，相加后最后一位仍然是0，即为偶数。

而奇数加奇数时，最后一位都是1，相加后最后一位为0，即为偶数，或者为1，即为奇数。

减法在减法中，奇数减偶数的结果一定是奇数，偶数减偶数的结果一定是偶数，奇数减奇数的结果则可能是奇数也可能是偶数。

这是因为奇数减偶数时，奇数的最后一位一定是1，而偶数的最后一位一定是0，所以相减后最后一位一定是1，即为奇数。

而偶数减偶数时，最后一位都是0，相减后最后一位仍然是0，即为偶数。

而奇数减奇数时，最后一位都是1，相减后最后一位可能为0，即为偶数，或者为1，即为奇数。

乘法在乘法中，奇数乘偶数的结果一定是偶数，偶数乘偶数的结果一定是偶数，奇数乘奇数的结果则一定是奇数。

这是因为奇数乘偶数时，偶数的最后一位一定是0，相乘后最后一位一定是0，即为偶数。

而偶数乘偶数时，最后一位都是0，相乘后最后一位仍然是0，即为偶数。

而奇数乘奇数时，最后一位都是1，相乘后最后一位仍然是1，即为奇数。

除法在除法中，奇数除以偶数的结果一定是奇数，偶数除以偶数的结果可能是奇数也可能是偶数，奇数除以奇数的结果则一定是奇数。

这是因为奇数除以偶数时，奇数的最后一位一定是1，而偶数的最后一位一定是0，所以相除后最后一位一定是1，即为奇数。

而偶数除以偶数时，最后一位都是0，相除后最后一位可能为0，即为偶数，或者为1，即为奇数。

而奇数除以奇数时，最后一位都是1，相除后最后一位仍然是1，即为奇数。

奇偶四则运算法则是数学中的一个重要概念，它可以帮助我们更好地理解数学运算的规律。

奇偶校验在实 际应用中的优 势和局限性： 介绍奇偶校验 在实际应用中 的优势和局限 性，包括其优 点和缺点等。
数学中的奇偶性应用
奇偶性在数学中的实际应用 案例
奇偶性在数学中的定义和性 质
奇偶性在数学中的意义和作 用
奇偶性在数学中的未来发展 前景
06
总结与回顾
总结奇偶数的概念和识别方法
奇偶数的定义：奇数和偶数是整数中的两个分类，奇数不能被2整除，偶数能被2整除。
通过个位数识 别：0、2、4、 6、8为偶数， 1、3、5、7、
9为奇数
通过十位数识 别：个位为奇 数，十位为偶 数为奇数；个 位为偶数，十 位为奇数为偶
数
通过百位数识 别：百位与个 位相同，十位 为偶数为奇数； 百位与个位相 反，十位为奇
数为偶数
通过千位数识 别：千位与个 位相同，百位 为偶数为奇数； 千位与个位相 反，百位为奇
数为偶数
通过计算识别
定义：奇数和偶数是根据数字除以2的余数来区分的 计算方法：通过除以2并取余数，可以确定一个数是奇数还是偶数 示例：例如，数字10除以2的余数是0，因此10是偶数 结论：通过计算可以快速准确地识别奇数和偶数
04
奇数和偶数的应用场景
数学中的奇偶性
奇偶数的定义：奇数和偶数是整数中按照除以2的余数来分类的两种数。
稻壳学院
奇偶数辨识
单击添加副标题
汇报人：MR.Z
目录
01
单击添加目录项标题
02
03
奇数和偶数的识别方法
04
05
奇偶性的实际应用案例
06
奇数和偶数的定义 奇数和偶数的应用场景
总结与回顾
01
添加章节标题
02