莫比乌斯带初探

莫比乌斯带平均分规律的初探榆林市第十二小学吴锦军北师大六年级数学下册中“神奇的莫比乌斯带”一课中，有一个剪纸环的活动，这个活动能发现“把莫比乌斯带沿平均分成2份剪开得到1个大环+0个小环”外，还能发现：“纸条分成3份，得到1个大环+1个小环”；“纸条分成4份，得到2个大环+0个小环”；“纸条分成5份，得到2个大环+1个小环”；“纸条分成6份，得到3个大环+0个小环”；“纸条分成7份，得到3个大环+1个小环”；“纸条分成8份，得到4个大环+0个小环”；规律是：纸条分的份数除以2，商是大环数，余数是小环数。

这个规律，用图也不难理解：把长方形纸条扭转180°后，两头再粘接起，沿原宽等分时，把左边接头记为①③⑤…奇数，右边接头记为②④⑥…偶数。

当两边接头连接形成环路时，说明形成一个圈。

二等分时，①接④，④和③，③接②，②和①，从①出发，回到①，说明形成一个圈。

此时四个接头已完结，所以是一个环，环长两个原莫比乌斯带的长。

如下图：三等分时，①接⑥，⑥和⑤，⑤接②，②和①，从①出发，回到①，说明形成一个圈。

此时四个接头已完结，还有③和④一个环。

所以是一个大环，一个小环。

大环长两个原莫比乌斯带的长，小环就是一个莫比乌斯带。

如下图：四等分时，①接⑧，⑧和⑦，⑦接②，②和①，从①出发，回到①，说明形成一个圈。

③接⑥，⑥和⑦，⑦接④，④和③，从③出发，回到③，说明形成一个圈。

此时八个接头已完结。

所以是二个大环。

如此继续等分五等分，等……假如分成n等分，①接2n，2n和2n-1，2n-1接②，②和①，从①出发，回到①，说明形成一个圈，所以从外开始，相邻两条接一个环。

所以，n等分后，环数=n除以2的商+余数。

如果把上述的等分带换成排线，又会怎么样呢？对于两条的排线,接好后撕开就是如下图的一个圈:对于三条的排线,接好后撕开就是如下图的两种情况:上图接线是按照同一方向①⑥、③④、⑤②接线，撕开就是两个套在一起的圈.因为③④形成的圈中只套住①⑥、⑤②的圈的一条线,所以这两个圈套在一起.上图的接线是按照同一方向①⑥、⑤②接线、然后再接③④、撕开就是两个分离的圈.因为③④形成的圈有两条另一个圈的线。

数学奥妙: 莫比乌斯带的奇妙性质1. 引言1.1 概述:随着科技的发展，数学作为一门基础学科，在日常生活和各个领域中扮演着重要的角色。

而莫比乌斯带作为数学中的一个神奇对象，具备非凡的特性和独特的结构，引起了许多人的兴趣与探索。

本文将深入探讨莫比乌斯带，并介绍它的奇妙性质以及在现实生活中的应用。

1.2 文章结构:本文分为五个部分来介绍莫比乌斯带。

首先是引言部分，概述整篇文章内容并指明目标。

接下来是莫比乌斯带的定义部分，介绍其几何形状、建模方法和常见应用领域。

然后是莫比乌斯带的特性与性质部分，涵盖单面性和非定向性、边界与表面积计算以及不可剪断和非平凡截面等方面。

紧接着是莫比乌斯带的数学推导与证明部分，重点讲解利用拓扑学、欧拉公式以及线性代数等方法研究莫比乌斯带的特性。

最后是本文的重点部分，探讨莫比乌斯带在现实生活中的应用，包括海洋科学、材料科学和计算机图形学等领域。

1.3 目的:本文旨在全面介绍莫比乌斯带的奇妙性质，并展示其在现实生活中的重要应用。

通过深入研究莫比乌斯带，读者可以了解到数学在解决实际问题中的作用，并体会到数学之美。

同时，本文也为对数学有兴趣的读者提供了一个拓展知识广度和深度的机会。

通过阅读本文，读者将能更好地理解和欣赏这个神奇又引人入胜的数学对象- 莫比乌斯带。

2. 莫比乌斯带的定义:2.1 几何形状莫比乌斯带是一种奇特的几何体，它具有一个非常有趣的性质：只有一个面和一个边。

在几何学上，通常我们所了解的物体都是有两个面的，例如长方体、球体等，但莫比乌斯带独特地只具有一个面。

莫比乌斯带由一个长而窄的长方形或正方形通过进行「莫比乌斯纸带」操作而得到。

这个操作是将纸带沿一侧旋转180度后再粘合起来，使得起初平行的两条边变为交叉相连。

通过这样的操作，我们就可以构造出一个莫比乌斯带，使得其呈现出令人着迷且难以直观理解的特性。

2.2 建模方法为了更好地描述和研究莫比乌斯带，数学家们开发了一种基于拓扑学的建模方法。

神奇的“莫比乌斯带”曾作过闻名数学家高斯助教的莫比乌斯在1858年与另一位数学家各自独立发觉了单侧的曲面，其中最闻名的是“莫比乌斯带”。

假如想制作这种曲面，只要取一片长方纸条，把一个短边扭转180°，然后把这边跟对边粘贴起来，就形成一条“莫比乌斯带”。

当用刷子油漆那个图形时，能连续不断地一次就刷遍整个曲面。

假如一个没有扭转过的带子一面刷遍了，要想把刷子挪到另一面，就必须把刷子移动跨过带子的一条边沿。

“莫比乌斯带”有点奇异，一时又派不上用场，然而人们依旧依照它的特性编出了一些故事，据说有一个小偷偷了一位专门老实农民的东西，并被当场捕捉，将小偷送到县衙，县官发觉小偷正是自己的亲小孩。

因此在一张纸条的正面写上：小偷应当放掉，而在纸的反面写了：农民应当关押。

县官将纸条交给执事官由他去办理。

聪慧的执事官将纸条扭了个弯，用手指将两端捏在一起。

然后向大伙儿宣布：依照县太爷的命令放掉农民，关押小偷。

县官听了大怒，责问执事官。

执事官将纸条捏在手上给县官看，从“应当”二字读起，确实没错。

认真观看字迹，也没有涂改，县官不知其中隐秘，只好自认倒霉。

县官明白执事官在纸条上做了手脚，怀恨在心，伺机报复。

一日，又拿了一张纸条，要执事官一笔将正反两面涂黑，否则就要将其拘役。

执事官不慌不忙地把纸条扭了一下，粘住两端，提笔在纸环上一划，又拆开两端，只见纸条正反面均涂上黑色。

县官的毒计又落空了。

现实可能全然可不能发生如此的故事，然而这两个故事却专门好地反映出“莫比乌斯带”的特点。

“莫比乌斯带”在生活和生产中差不多有了一些用途。

例如，用皮带传送的动力机械的皮带就能够做成“莫比乌斯带”状，如此皮带就可不能只磨损一面了。

假如把录音机的磁带做成“莫比乌斯带”状，就不存在正反两面的问题了，磁带就只有一个面了。

“师”之概念，大体是从先秦时期的“师长、师傅、先生”而来。

其中“师傅”更早则意指春秋时国君的老师。

《说文解字》中有注曰：“师教人以道者之称也”。

【日记】神奇的莫比乌斯带_650字今天我在课堂上学到了一个非常有趣的数学概念——莫比乌斯带。

莫比乌斯带是由德国数学家阿基米德·莫比乌斯于19世纪提出的，它是一种与众不同的立体形状。

莫比乌斯带的制作方法非常简单，只需要一个长方形的纸片，将两个相对的边缩进一定距离，然后将纸条的两端粘合在一起。

这样做出来的莫比乌斯带有一个很奇特的特点，就是只有一个面和一个边。

你可以拿一支笔描绘在上面，不管你走多远，只要你沿着带子的任意一侧走，就能回到出发点。

这就是莫比乌斯带的不可思议之处。

下课后，我做了一个莫比乌斯带，拿着一支笔在上面进行画画。

我发现，不管我怎么画，线条都是连续不断的，没有断开过。

感觉就好像是在一个无限循环的世界里一样，非常有趣。

我还发现，莫比乌斯带的面积是不变的。

我们可以把一个莫比乌斯带切开，得到一个带有两个边的环带，将这个环带再切开，就可以得到两个单独的边。

然后我们将这两个边接在一起，又得到了最初的莫比乌斯带。

这表明莫比乌斯带的表面积是恒定的，无论我们如何变化它的形状。

莫比乌斯带还有一些其他有趣的性质。

如果你用一把剪刀沿着莫比乌斯带的中心剪开，在不离开剪刀的情况下，剪刀会绕过整个带子一圈，最终剪开的结果是两个相互咬合的环。

这就是莫比乌斯带的“奇性”。

莫比乌斯带的独特性质深深吸引了我，让我对数学产生了更大的兴趣。

数学是一门非常有趣的学科，它可以揭示出许多隐藏在我们周围的神奇现象。

通过学习莫比乌斯带，我更加明白了数学与现实世界之间的联系，也更加欣赏了数学的美妙之处。

今天的课堂学习让我认识到了莫比乌斯带的神奇之处，它的独特性质让我着迷。

通过亲手制作莫比乌斯带，并进行一系列的实验，我对它有了更深的理解，并且对数学产生了更大的兴趣。

我相信，在未来的学习中，我会继续探索更多有趣的数学概念，享受数学带来的乐趣。

生活中莫比乌斯带的原理莫比乌斯带是一种非常有趣的几何形状，它的特点是具有一个面和一个边，而没有顶点。

莫比乌斯带的原理涉及到拓扑学和几何学的概念。

首先，我们需要了解一下拓扑学的基本概念。

拓扑学是数学中研究空间性质不受形状改变的学科。

在拓扑学中，物体的形状被忽略，只考虑其内部和边界之间的关系。

莫比乌斯带的构造方法是将一个长而细的长条形纸带的一端做一个180度的旋转，再与另一端粘合而形成的。

这个粘合的方式是先将一个端点旋转180度再与另一个端点粘合，从而形成了一个环面。

但是与一般的环面不同的是，莫比乌斯带只有一个面和一个边，而没有顶点。

莫比乌斯带的特殊之处在于它具有奇异性。

在几何学中，奇异性是指一个物体的性质与一般的对象不同。

莫比乌斯带的奇异性表现在它只有一个面和一个边上。

与此不同的是，一般的物体都有两个面和一些边。

这种特殊的性质使得莫比乌斯带成为了人们研究拓扑学和几何学的重要工具。

莫比乌斯带的奇异性可以通过以下实验来理解。

我们可以在莫比乌斯带的表面画上一条线，然后沿着这条线将莫比乌斯带剪开。

意想不到的是，当我们剪开莫比乌斯带时，得到的是一片更长的纸带，并没有得到两个分离的纸带。

这是因为莫比乌斯带只有一个面，所以我们无法将剪开的两端分离开来。

莫比乌斯带还有一个有趣的特性是它具有无法消除的旋转。

我们可以在莫比乌斯带的中间画上一个箭头，然后沿着莫比乌斯带的边缘将箭头移动一圈。

令人惊奇的是，当箭头移动一圈后，箭头的方向发生了改变。

这是因为在莫比乌斯带上边缘与面之间没有明显的分界线，所以当我们沿着边缘旋转时，箭头的方向也会发生旋转。

莫比乌斯带的应用并不仅仅局限于几何学和拓扑学的研究。

它也被广泛用于科学教育，可以用来解释一些抽象的数学概念和物理原理。

例如，在电磁学中，我们可以将莫比乌斯带作为一个模型来说明电流与磁场之间的关系。

由于莫比乌斯带上只有一个面和一个边，所以通过它可以直观地展示电流和磁场的奇特的相互作用。

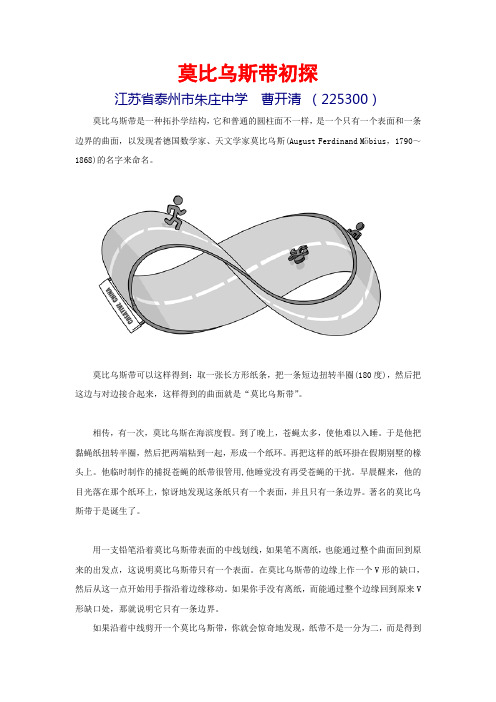
莫比乌斯带初探江苏省泰州市朱庄中学曹开清（225300）莫比乌斯带是一种拓扑学结构，它和普通的圆柱面不一样，是一个只有一个表面和一条边界的曲面，以发现者德国数学家、天文学家莫比乌斯(August Ferdinand Möbius，1790～1868)的名字来命名。

莫比乌斯带可以这样得到：取一张长方形纸条，把一条短边扭转半圈(180度)，然后把这边与对边接合起来，这样得到的曲面就是“莫比乌斯带”。

相传，有一次，莫比乌斯在海滨度假。

到了晚上，苍蝇太多，使他难以入睡。

于是他把黏蝇纸扭转半圈，然后把两端粘到一起，形成一个纸环。

再把这样的纸环掛在假期别墅的椽头上。

他临时制作的捕捉苍蝇的纸带很管用,他睡觉没有再受苍蝇的干扰。

早晨醒来，他的目光落在那个纸环上，惊讶地发现这条纸只有一个表面，并且只有一条边界。

著名的莫比乌斯带于是诞生了。

用一支铅笔沿着莫比乌斯带表面的中线划线，如果笔不离纸，也能通过整个曲面回到原来的出发点，这说明莫比乌斯带只有一个表面。

在莫比乌斯带的边缘上作一个V形的缺口，然后从这一点开始用手指沿着边缘移动。

如果你手没有离纸，而能通过整个边缘回到原来V 形缺口处，那就说明它只有一条边界。

如果沿着中线剪开一个莫比乌斯带，你就会惊奇地发现，纸带不是一分为二，而是得到一个两倍长的纸环，而且这个环相当于把纸带的端头两次扭转半圈后连接起来的双侧面环！再把刚才得到的那个纸环沿中线剪开，这回可真的一分为二了！如果把莫比乌斯带的纸面宽3等分，并沿着3等分线剪开，会得到两个环，一个是窄一些的莫比乌斯带，另一个则是两次扭转半圈后接合起来的双侧面环。

如果把莫比乌斯带的纸面宽4等分，并沿着4等分线剪开，会得到两个更窄一些的两次扭转半圈后连接起来的双侧面环。

一般地，如果把莫比乌斯带的纸面宽n等分，并沿着n等分线剪开，将会得到：当n为偶数时，得到n/2个双侧面环；当n为奇数时，得到(n-1)/2 个双侧面环和一个莫比乌斯带。

莫比乌斯带麦比乌斯圈(Möbius strip, Möbius band)是一种单侧、不可定向的曲面。

因A.F.麦比乌斯(August Ferdinand Möbius, 1790-1868)发现而得名。

将一个长方形纸条ABCD 的一端AB固定，另一端DC扭转半周后，把AB和CD粘合在一起，得到的曲面就是麦比乌斯圈，也称麦比乌斯带。

莫比乌斯带莫比乌斯带（Möbiusstrip或者Möbiusband），又译梅比斯环或麦比乌斯带，是一种拓扑学结构，它只有一个面（表面），和一个边界。

它是由德国数学家、天文学家莫比乌斯和约翰·李斯丁在1858年独立发现的。

这个结构可以用一个纸带旋转半圈再把两端粘上之后轻而易举地制作出来。

事实上有两种不同的莫比乌斯带镜像，他们相互对称。

如果把纸带顺时针旋转再粘贴，就会形成一个右手性的莫比乌斯带，反之亦类似。

莫比乌斯带本身具有很多奇妙的性质。

如果从中间剪开一个莫比乌斯带，不会得到两个窄的带子，而是会形成一个把纸带的端头扭转了两次再结合的环（并不是莫比乌斯带），再把刚刚做出那个把纸带的端头扭转了两次再结合的环从中间剪开，则变成两个环。

如果你把带子的宽度分为三分，并沿着分割线剪开的话，会得到两个环，一个是窄一些的莫比乌斯带，另一个则是一个旋转了两次再结合的环。

另外一个有趣的特性是将纸带旋转多次再粘贴末端而产生的。

比如旋转三个半圈的带子再剪开后会形成一个三叶结。

剪开带子之后再进行旋转，然后重新粘贴则会变成数个Paradromic。

莫比乌斯带常被认为是无穷大符号“∞”的创意来源，因为如果某个人站在一个巨大的莫比乌斯带的表面上沿着他能看到的“路”一直走下去，他就永远不会停下来。

但是这是一个不真实的传闻，因为“∞”的发明比莫比乌斯带还要早。

公元1858年，两位德国数学家莫比乌斯和Johann Benedict Listing分别发现，一个扭转180度后再两头粘接起来的纸条，具有魔术般的性质。

人教版数学四年级上册神奇的默比乌斯带说课（精选３篇）〖人教版数学四年级上册神奇的默比乌斯带说课第【1】篇〗《神奇的莫比乌斯带》教学设计【教材说明】莫比乌斯带是德国数学家莫比乌斯在1858年研究“四色定理”时偶然发现的一个副产品。

“莫比乌斯圈”已被作为“了解并欣赏的有趣的图形”之一写进了《数学课程标准》，编进了义务教育课程标准实验教科书《数学》。

【说教学内容】小学数学四上第77页数学实践活动课――神奇的莫比乌斯带【说教学目标】1、学会做莫比乌斯带，探究发现莫比乌斯带的特征。

2、经历大胆猜想、操作验证的过程，提高学生思维想象、动手操作的能力。

3、感受数学图形的神奇与美妙，拓宽数学视野，进一步激发学好数学的志趣。

【教具学具】（老师）一张双色纸条、一个2等分线的普通纸圈，剪刀（学生）每人四张双色纸条、剪刀、胶水【说教学过程】一、认识莫比乌斯带1、操作演示，铺垫引入师：（出示长方形纸条）同学们，谁能告诉我这张纸条有几个面？几条边？哪两个面，哪四条边，指给大家看看。

师：大家也拿出纸条，咱们一起来摸摸看跟他说的是不是一样的。

师：我能把它变成只剩下2个面2条边，你知道怎么做吗？（指名演示，提问：两个面在哪呢，边呢）师:咱们也一起来体验一下，（与生一起，边做边说）外圈一个面，内圈一个面，左边一条边，右边一条边。

2、情境创设，激发探索师：瞧，这个圈跑到电脑上了（课件动画播放：纸圈外有一蚂蚁，圈内有一块小蛋糕。

）师：猜猜看蚂蚁这时最想干什么？猜对了，饥饿的蚂蚁特别想吃蛋糕，可是有个要求：咱这只蚂蚁啊只能这样爬（边说边演示），不能沿着边缘翻到内圈也不能打洞到达内圈。

你们说它能吃到蛋糕吗？（不能）师：咱们还是请蚂蚁先生辛苦地爬一趟试试看吧（动画播放）师：唉呀，真的不能吃到啊，为什么呢？预设：（通过观察）学生可能会说因为蚂蚁只能在外圈爬，不能经过边缘它肯定爬不到内圈，所以就吃不到蛋糕。

师：也就是说要想吃到蛋糕，蚂蚁必须从外圈（生：爬到内圈）师：怎样才能让蚂蚁从外圈爬到内圈呢？咱们一起来想想办法，制作一个让蚂蚁能从外圈爬到内圈吃到蛋糕的纸圈。

神奇的“莫比乌斯带”教学目标:1、让学生认识“莫比乌斯带”，学会将长方形纸条制成莫比乌斯带。

2、引导学生通过思考操作发现并验证“莫比乌斯带”的特征，培养学生大胆猜测、勇于探究的求索精神。

3、在莫比乌斯带魔术般的变化中感受数学的无穷魅力，拓展数学视野，进一步激发学生学习数学的兴趣，培养学生良好的数学情感。

重点: 让学生认识“莫比乌斯带”，学会将长方形纸条制成莫比乌斯带。

难点: 引导学生通过思考操作发现并验证“莫比乌斯带”的特征，培养学生大胆猜测、勇于探究的求索精神。

教具:准备剪刀，双面胶、彩笔三条长方形纸条教学过程:活动一：蚂蚁能顺利吃到面包屑吗？如果蚂蚁爬在这样的一条纸带上，它不翻越纸条边缘也可以吃到粘在纸条另一面的面包屑，太神奇了。

今天我们就一起来认识这神奇的莫比乌斯带。

（课件显示）那么看了这个课题你们有什么想法吗？师问１：为什么叫莫比乌斯带？师问２：莫比乌斯带有什么神奇的地方？师问３：莫比乌斯带在生活中有哪些应用？师：同学们想知道的还真不少，要想知道这些问题还得从这张小小的纸条说起．活动二：做一做，认识莫比乌斯带1．每个同学拿出一根长方形纸条。

看，这是根普通的纸条，但也是一根神奇的纸条呢。

先说说它有几条边，几个面？（说：四条边两个面）2．同学们能将它两头对接起来吗？3．小组活动。

同学们拿出①号纸条试着做一做。

4．小组同学上台汇报。

师：说说你是怎样对接的？这样接起来纸条就成了一个环（圈）。

是这样接的同学把作品举起来。

摸一摸看一看，现在它有几条边，几个面？师投影：两条边两个面像这样有两条边两个面的纸环我们把它叫（双侧曲面）师：说到这，同学们可能会觉得，这也没什么神奇的呀！是呀，这点小把戏，地球人都知道．奇妙的是我还能把它变成一个面，一条边．（停顿，环视学生）．看，我变出来了是这样的．（学生看师做纸圈）师：这是怎么做出来的？你们能做吗？师：好请看，先把它做成一个普通的纸圈，然后将一端翻转180度，再把它粘好．（学生跟着一起做）现在同学们请拿出2号纸条出来开始做，同学之间可以互相帮助．这位同学做出来了，说说你是怎么做出来的？师：刚才我说它只有一个面，（那么它是不是一个面呢？）我们一起来动手验证一下，用笔在纸圈中间画一条线，笔尖不离开纸面一直画一圈，你会有什么发现？生：又回来了师：说明了什么？生：它只有一个面．师：我们用手指沿着纸圈的边走一圈，你又发现了什么？（同学们真的很会观察发现）师：你们知道这样的一个纸圈叫什么名字吗？（板书显示课题：神奇的莫比乌斯带）它是德国数学家莫比乌斯在1858年在偶然间发现的，所以就以他的名字命名叫“莫比乌斯带”，也有人叫它“莫比乌斯圈”，还有人管他叫“怪圈”。