2020届高中毕业年级第一次质量预测(含答案)
- 格式:doc
- 大小:3.48 MB
- 文档页数:10

2020年高中毕业年级第一次质量预测语文参考答案一、现代文阅读(36分)(一)论述类文本阅读(本题共3小题,9分)1.(3分)C(A.曲解文意。
“社会情绪是……非理性的”不当。
根据第一段的“在学者的论述和相关部门的报告中,社会情绪往往被描述为......流变的、非理性的”和第四段的“情绪作为一种非正式的社会控制方式显得......冲动、没有计划性,不需要复杂的技巧,但看似感性的情绪表达其实有其实践理性........,遵循着模糊的实践感”等语句可知,是某些学者和相关部门将社会情绪视为“非理性的”,但作者对此并不认同,他认为社会情绪的中有“实践理性”。
B.张冠李戴。
“其表现形式为法律、宗教戒律、习俗等”不是罗斯的观点,而是“人们通常”的看法。
D.说法绝对。
“社会情绪是建设性的”不当,原文为“它可以..是建设性的”,且“消极的”社会情绪就不是“建设性的”。
)2.(3分)B(曲解文意。
吉布斯的看法能论证观点,罗斯的看法则不能。
根据原文,罗斯的看法是传统的,而作者的看法与传统不同,所以作者引述罗斯的看法,是为了对它加以否定,进而表达自己的看法,即社会情绪也是一种社会控制的方式,而不是用罗斯的看法来证明自己的观点。
)3.(3分)D(“对社会治理而言,‘软控制’要优于‘硬控制’”于文无据。
)(二)实用类文本阅读(本题共3小题,12分)4.(3分)C(以偏概全。
“生产的安全窗口期非常短暂”只是迪拜特殊气候条件下海水稻的生产情况。
)5.(3分)B(概括不当。
“芽长、根长及根数下降的速度越快”有误,由图表可知,在浓度为9g/L的时候,芽长、根长及根数下降的速度最快。
)6.(6分)困难:①盐碱土壤影响水稻种子萌发和幼苗生长;②我国盐碱地类型多样复杂;③迪拜农业生态气候条件恶劣,不利于海水稻生产。
成果:①经过多年繁殖、筛选,育成有较好耐盐性的“海稻 86”;②亩产屡创新高,已达到国际先进水平;③试验区域逐年扩大;④海水稻品种越来越丰富;⑤海水稻种植走出国门,种植面积和单产均刷新了迪拜沙漠水稻种植纪录。

2020年高中毕业年级第一次质量预测数学(理科) 参考答案一、选择题1-12 BDACBCBCDB DA 二、填空题13. 10;x y -+= 14.4; 15.;53016.{}.66,2,0-- 三、解答题17.解析:(I)222(sin sin )()sin .R A B a c C -=-∴2222(sin sin )()sin 2,R R A B a c C R ⋅-=-⋅即:222.ac b ac +-= ……3分∴2221cos .22a cb B ac +-== 因为0,B π<<所以3B π∠=……6分(II)若12,8b c ==,由正弦定理,sin sin b cB C=, sin C =,由b c >,故C ∠为锐角,cos C =……9分 1sin sin()sin()32A B C C π=+=+=+=……12分 18. 解析:(I )如图所示:连接OM , 在ABC ∆中:2,AB BC AC ===90,ABC BO ∠=︒=OB AC ⊥.……2分在MAC ∆中:MA MC AC ===O 为AC 的中点,则OM AC ⊥,且OM = ……4分在MOB ∆中:BO OM MB ===222BO OM MB +=根据勾股定理逆定理得到OB OM ⊥ ,AC OM 相交于O , 故OB ⊥平面AMC ………………….6分CA(Ⅱ)因为,,OB OC OM两两垂直,建立空间直角坐标系O−xyz如图所示.因为MA MB MC AC====2ABBC==则(0,A B C M……8分由23BN BC=u u u r uu u r所以,(33N设平面MAN的法向量为(,,)m x y z=u r,则(,(,,)0,3333(,,)0AN n x y z x yAM n x y z⎧⋅=⋅=+=⎪⎨⎪⋅=⋅=+=⎩u u u r ru u u ur r令y=(1)m=--u r……10分因为BO⊥平面AMC,所以OB=u u u r为平面AMC的法向量,所以(1)m=--u r与OB=u u u r所成角的余弦为cos,m OB<>==u r u u u u r所以二面角的正弦值为2|sin,|m OB<>===u r u u u u r.……12分19.(I)由题意知1b=,2ca=.……1分又因为222ab c=+解得,a=3分所以椭圆方程为2212yx+=. ……4分(Ⅱ)设过点1(,0)3-直线为13x ty=-,设()11,A x y,()22,B x y由221312x tyxy⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160t tyy+--=,且>0∆.则12212212,918616,918yy ytytt⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分又因为()111,CA x y=-u u u r,()221,CB x y=-u u u r,()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++⎪⎪⎝⎭⎝⎭u u u r u u u r ()22216412161091839189t t t t t -=+-⋅+=++,……10分所以CA CB ⊥u u u ru u u r.因为线段AB 的中点为M ,所以||2||AB CM =.……12分 20. 解析:(I)该混合样本达标的概率是28()39=,……2分 所以根据对立事件原理,不达标的概率为81199-=.……4分 (II)(i )方案一:逐个检测,检测次数为4.方案二:由(1)知,每组两个样本检测时,若达标则检测次数为1,概率为89;若不达标则检测次数为3,概率为19.故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6.其分布列如下,可求得方案二的期望为26416119822()246818181819E ξ=⨯+⨯+⨯== 方案四:混在一起检测,记检测次数为ξ4,ξ4可取1,5. 其分布列如下,可求得方案四的期望为46417149()15818181E ξ=⨯+⨯=. 比较可得42()()4E E ξξ<<,故选择方案四最“优”.……9分 (ii)方案三:设化验次数为3η,3η可取2,5.333()25(1)53E p p p η=+-=-;方案四:设化验次数为4η,4η可取1,54444()5(1)54E p p p η=+-=-;由题意得34343()()53544E E p p p ηη<⇔-<-⇔<. 故当304p <<时,方案三比方案四更“优”.……12分 21解析:(I)()ln xe f x x x x=--,定义域(0,)+∞,221(1)(1)()()1x x e x x x e f x x x x ---'=--=, 由1x e x x ≥+>,()f x 在(0,1]增,在(1,)+∞减,max ()(1)1f x f e ==-……4分 (II)1()()e 1xf x x bx x++-≥ e e ln e 1x x xx x x bx x x⇔-+-++-≥ln e 10x x x x bx ⇔-++--≥e ln 1x x x xb x --+⇔≥min e ln 1(),x x x x b x --+⇔≥……6分令e ln 1()x x x x x x ϕ--+=,2ln ()x x e xx xϕ+'=令2()ln x h x x e x =+,()h x 在(0,)+∞单调递增,0,()x h x →→-∞,(1)0h e =>()h x 在(0,1)存在零点0x ,即02000()ln 0xh x x e x =+=001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=……9分由于x y xe =在(0,)+∞单调递增,故0001lnln ,x x x ==-即001x e x =()x ϕ在0(0,)x 减,在0(,)x +∞增,000000min00e ln 111()2x x x x x x x x x ϕ--++-+===所以2b ≤.……12分22.解析:(I)将点3(1,)2P 代入曲线E 的方程,得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =,……2分所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cossin )143ρθθ+=.……5分(Ⅱ)不妨设点,A B 的极坐标分别为1212()()00,2A B πρθρθρρ+>>,,,,,则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分2212111174312ρρ+=+=,即22117||||12OA OB +=……10分 23. 解:(I)由()f x m ≥,得,不等式两边同时平方,得221)(21)x x ≥(-+,……3分 即3(2)0x x +≤,解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤.……5分(Ⅱ)设g (x )=|x -1|-|2x +1|,……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==,(3)1,(4)2,(1) 3.g g g -=--=-=-又恰好存在4个不同的整数n ,使得()0f n ≥, 所以2 1.m -<-≤-故m 的取值范围为[1,2). ……10分12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。
2020年高中毕业年级第一次质量预测数学(理科) 参考答案一、选择题1-12 BDACB CBCDB DA二、填空题13. 10;x y -+= 14.4; 15.;530 16.{}.66,2,0-- 三、解答题17.解析:(I)222(sinsin )()sin .R A B a c C -=- ∴2222(sinsin )()sin 2,R R A B a c C R ×-=-× 即:222.a c b ac +-= ……3分 ∴2221cos .22a cb B ac +-== 因为0,B p <<所以3B p Ð=……6分 (II)若12,8b c ==,由正弦定理,sin sin b c BC =, sin 3C =, 由b c >,故C Ð为锐角,cos 3C =……9分1sin sin()sin()323236A B C C p +=+=+=×+×=……12分 18. 解析:(I )如图所示:连接OM , 在ABC D中:2,AB BC AC ===,则90,ABC BO Ð=°AC .……2分 在MAC D 中:M A M C A C ===,O 为AC AC ^,且O M ……4分 在MOB D 中:BO OM MB ==222OM MB += 根据勾股定理逆定理得到OB OM ^ ,AC OM 相交于O ,故OB ^平面AMC ………………….6分(Ⅱ)因为,,OB OC OM 两两垂直,建立空间直角坐标系 − 如图所示. 因为M A M B M C AC ====,2AB BC ==则(0,A B C M ……8分 由23BN BC =uuu r uuu r所以,(,,0)33N 设平面MAN 的法向量为(,,)m x y z =u r ,则(,0)(,,)0,3333(,,)0AN n x y z x y AM n x y z ì×=×=+=ïíï×=×==îuuu r r uuuu r r令y =,得(1)m =--u r ……10分因为BO ^平面AMC,所以OB =uuu r为平面AMC 的法向量,所以(1)m =--u r与OB =uuu r所成角的余弦为cos ,m OB <u ruuuu r所以二面角的正弦值为2|sin ,|79m OB <=u ruuuu r .……12分 19.(I )由题意知1b =,2c a =.……1分 又因为222a b c =+解得,a =……3分 所以椭圆方程为2212y x +=. ……4分 (Ⅱ) 设过点1(,0)3-直线为13x ty =-,设()11,A x y ,()22,B x y 由221312x ty x y ì=-ïïíï+=ïî得()2291812160t ty y +--=,且>0D . 则12212212,918616,918y y y t y t t ì+=ïï+¼¼íï=-ï+î分又因为()111,CA x y =-uuu r ,()221,CB x y =-uuu r , ()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y æöæö×=--+=--+=+-++ç÷ç÷èøèøuuu r uuu r ()22216412161091839189t t t t t -=+-×+=++,……10分 所以C A C B ^uuu r uuu r .因为线段AB 的中点为M ,所以||2||AB CM =.……12分20. 解析:(I)该混合样本达标的概率是28(39=,……2分 所以根据对立事件原理,不达标的概率为81199-=.……4分 (II)(i )方案一:逐个检测,检测次数为4. 方案二:由(1)知,每组两个样本检测时,若达标则检测次数为1,概率为89;若不达标则检测次数为3,概率为19.故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6.其分布列如下,可求得方案二的期望为26416119822()246818181819E x =´+´+´== 方案四:混在一起检测,记检测次数为ξ4,ξ4可取1,5. 其分布列如下,可求得方案四的期望为46417149()15818181E x =´+´=. 比较可得42()()4E E x x <<,故选择方案四最“优”.……9分 (ii)方案三:设化验次数为3h ,3h 可取2,5.3h2 5 p3p31p - 3333()25(1)53E p p p h =+-=-;方案四:设化验次数为4h ,4h 可取1,5 4h1 5 p4p 41p -4444()5(1)54E p p p h =+-=-;由题意得34343()()53544E E p p p h h <Û-<-Û<.故当304p <<时,方案三比方案四更“优”.……12分 21解析:(I)()ln x e f x x x x=--,定义域(0,)+¥, 221(1)(1)()()1x x e x x x e f x x x x---¢=--=, 由1x e x x ³+>,()f x 在(0,1]增,在(1,)+¥减,max ()(1)1f x f e ==-……4分 (II)1()()e 1x f x x bx x++-³ e e ln e 1x x x x x x bx x xÛ-+-++-³ ln e 10x x x x bx Û-++--³e ln 1x x x x b x --+Û³min e ln 1(,x x x x b x--+Û³……6分 令e ln 1()x x x x x x j --+=,2ln ()x x e x x xj +¢= 令2()ln x h x x e x =+,()h x 在(0,)+¥单调递增,0,()x h x ®®-¥,(1)0h e =>()h x 在(0,1)存在零点0x ,即02000()ln 0x h x x e x =+=0001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=Û=-=……9分 由于x y xe =在(0,)+¥单调递增,故0001ln ln ,x x x ==-即001x e x = ()x j 在0(0,)x 减,在0(,)x +¥增,000000min00e ln 111()2x x x x x x x x x j --++-+=== 所以2b £.……12分 22.解析:(I)将点3(1,)2P 代入曲线E 的方程,得1cos ,3,2a a a =ìïí=ïî解得24a =,……2分 所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cos sin )143r q q +=.……5分 (Ⅱ)不妨设点,A B 的极坐标分别为1212()(00,2A B p r q r q r r +>>,,,,, 则22221122222211(cos sin )1,4311(cos (sin ()1,4232r q r q p p r q r q ì+=ïïíï+++=ïî 即22212222111cos sin ,43111sin cos ,43q q r q q r ì=+ïïíï=+ïî……8分 2212111174312r r +=+=,即22117||||12OA OB +=……10分 23. 解:(I)由()f x m ³,得,不等式两边同时平方,得221)(21)x x ³(-+,……3分 即3(2)0x x +£,解得20x -££.所以不等式()f x m ³的解集为{|20}x x -££.……5分(Ⅱ)设g (x )=|x -1|-|2x +1|, ……8分()0()f n g n m ³Û³-因为(2)(0)0g g -==,(3)1,(4)2,(1) 3.g g g -=--=-=- 又恰好存在4个不同的整数n ,使得()0f n ³, 所以2 1.m -<-£-故m 的取值范围为[1,2). ……10分 12,,21()3,1,22,1,x x g x x x x x ì+£-ïïï=--<£íï-->ïïî。

2020年高中毕业年级第一次质量预测数学(文科) 参考答案一、选择题:1---12 BDACB BAADC DB 二、填空题:三、解答题:17.解: ...2分...4分...6分...8分...10分...12分 18.解:(1) ...1分...4分...5分...6分...8分313.2114.3515.42222(22)(23)(24)d d d +++=+(1)由题意知23440d d ∴--=223d d ∴==-或{}n a 为递增数列2d ∴={}2.n n a a n =故数列的通项公式为1111(2)()(21)(21)22121n b n n n n ==-+--+11111111[(1)()()...()]2335572121n S n n ∴=-+-+-++--+11(1)221n =-+21nn =+2AC BC AD BD CD =====由题知图(1)中∴111,A BCD A D BD AC BC -==在三棱锥中,1G A B 点是的中点11,DG A B CG A B ∴⊥⊥=DG CG G ⋂又1A B DGC∴⊥平面1M N AC BC 又点、分别是、的中点1//MN A B ∴MN DGC ∴⊥平面11,=,CD A D CD BD A D BD D ⊥⊥⋂(2)由图(1)知,且1CD A DG ∴⊥平面01160A DB A DB ∠=∴∆又为等边三角形分...12分19.解:(Ⅰ)根据频率分布直方图可知,样本中分数高于60的频率为,所以样本中分数高于60的概率为.故从总体的500名学生中随机抽取一人,其分数高于60的概率估计为0.8.3分(Ⅱ)根据题意,样本中分数不小于50的频率为,...5分分数在区间内的人数为. ...6分所以总体中分数在区间内的人数估计为. ...7分(Ⅲ),,则从这5名同学中选取2人的结果为:共10种情况. ...9分其中2人中男女同学各1人包含结果为:,共6种. ...10分,则所以,抽取的2人中男女同学各1人的概率是. ...12分20.解:(1)由抛物线定义得2+=3,...2分解得,所以曲线C方程为....4分(2). ...5分11111,2,1,2DG A B A B AG A B DG∴⊥====1111122A DGS A G DG∆∴=⨯=⨯=11111233G A DC C A DG A DGV V S CD--∆==⨯==(0.020.040.02)100.8++⨯=0.8(0.010.020.040.02)100.9+++⨯=[40,50)1001000.955-⨯-=[40,50)550025100⨯=123,,a a a设3名男生分别为12,b b2名女生分别为12131112212231322312{,},{,},{,},{,},{,},{,}{,},{,},{,},{,}a a a a ab a b a b a b a b a b a a b b,111221223132{,},{,},{,},{,}{,},{,}a b a b a b a b a b a b,{21}A=设事件抽取的人中男女同学各人63()105P A==352p2p=24x y=OPQ以为直径的圆过原点,OP OQ∴⊥设直线的方程为,与曲线C 方程联立,得解得 于是. ...7分 又直线的方程为,同理: .....9分 又直线斜率存在,即...12分20.解:(1)因为在点处的切线与直线平行,...4分...6分OP (0)y kx k =≠24x y =24x kx =0(4x x k ==舍去)或2(4,4)P k k OQ 1y x k =-244(,)Q k k-PQ 22244,44....1404y k x kPQ k k k k --∴=---的直线方程为分1() 4.y k x k=-+04.PQ ∴直线恒过定点(,)2()ln ,f x ax x x =-+'1()21.f x ax x ∴=-+'(1)2...1.k f a ∴==分()f x (1,(1))f 21y x =+...222, 1.a a ∴==即分(1)0,..1,.30f ∴=故切点坐标为().分2-2.y x ∴=切线方程为2'121(2)()21,ax x f x ax x x-+=-+=2122100,.ax x x x ∴-+=+∞由题知方程在(,)上有两个不等实根1212180,10,210,2a x x a x x a ⎧⎪∆=->⎪⎪∴+=>⎨⎪⎪=>⎪⎩10.8a ∴<<221212121222121212212121212()()()ln ln ()()ln()=[()2]()ln()11=ln1,24f x f x ax ax x x x x a x x x x x x a x x x x x x x x a a+=+-+++=+-+++--++--又...12分22.详细分析:(I)将点代入曲线E 的方程,得解得,……2分所以曲线的普通方程为, 极坐标方程为.……5分(Ⅱ)不妨设点的极坐标分别为则即……8分 ,即……10分 23. 详细分析:(I)由,得,1,2t a =令()ln 1,(4,),2tg t t t =--∈+∞'112..9(.)0,22t g t t t -=-=<则分()(4,)g t ∴+∞在上单调递减.()(4)ln 432ln 2 3.g t g ∴<=-=-12()()2ln 2 3.f x f x +<-即3(1,)2P 1cos ,3,2a αα=⎧⎪⎨=⎪⎩24a =E 22143x y +=22211(cossin )143ρθθ+=,A B 1212()()00,2A B πρθρθρρ+>>,,,,,22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩2212111174312ρρ+=+=22117||||12OA OB +=()f x m ≥不等式两边同时平方,得,……3分 即,解得.所以不等式的解集为.……5分 (Ⅱ)设g (x )=|x -1|-|2x +1|,……8分因为,又恰好存在4个不同的整数n ,使得, 所以故的取值范围为. ……10分221)(21)x x ≥(-+3(2)0x x +≤20x -≤≤()f x m ≥{|20}x x -≤≤()0()f n g n m ≥⇔≥-(2)(0)0g g -==(3)1,(4)2,(1) 3.g g g -=--=-=-()0f n ≥2 1.m -<-≤-m [1,2)12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。

河南省郑州市2020届高中毕业年级第一次质量预测数 学(文科)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上. 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回,一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合}4,3,2,1{=A ,}31|{<<-=x x B ,则B A A .}1{B .}2,1{C .}3,2,1{D .}4,3,2,1{2.复数iiz +=1在复平面内对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限3.设312=a ,32)41(=b ,21log 2=c ,则A .c b a >>B .b c a >>C .c a b >>D .a c b >>4.设α、β是两个不同的平面,l 、m 是两条不同的直线,且α⊂l ,β⊂m ,则 A .若β//a ,则m l // B .若α//m ,则βα// C .若α⊥m ,则βα⊥D .若βα⊥,则m l ⊥5.“纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样. 为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3 的正方形将其包含在内,并向该正方形内随机投掷2000个点,己知 恰有800个点落在阴影部分,据此可估计阴影部分的面积是A .516B .518 C .10 D .532 6.若变量x ,y 满足约束条件⎪⎩⎪⎨⎧≤-+≥-≥+.043,0,0y x y x y x 则x y 2-的最小值是A .-1B .-6C .-10D .-157.已知函数)(x f y =的图像由函数x x g cos )(=的图像经如下变换得到:先将)(x g 的图像向右平移6π个单位,再将图像上所有点的横坐标变为原来的一半,纵坐标不变,则函数)(x f y -的对称轴方程为 A .122ππ+=k x ,Z k ∈B .62ππ+=k x ,Z k ∈C .12ππ+=k x ,Z k ∈D .6ππ+=k x ,Z k ∈8.直线043=++m y x 与圆014222=++-+y x y x 相切,则m = A .-5或15B .5或-15C .-21或1D .-1或219.已知椭圆)0(12222>>=+b a b y a x 的离心率为53,直线0102=++y x 过椭圆的左顶点,则椭圆方程为A .14522=+y xB .192522=+y xC .191622=+y xD .1162522=+y x10.已知三棱锥ABC P -的四个顶点均在球面上,⊥PB 平面ABC .32=PB ,ABC ∆为直角三角形,BC AB ⊥,且1=AB ,2=BC ,则球的表面积为 A .π5B .π10C .π17D .π61717 11.关于函数|cos |||sin )(x x x f -=有下述四个结论:①)(x f 是偶函数②)(x f 在区间⎪⎭⎫⎝⎛ππ,2单调递减 ③)(x f 最大值为2④当)4,4(ππ-∈x 时,0)(<x f 恒成立 其中正确结论的编号是 A .①② B .①②③C .①③④D .①②④12.已知关于x 的方程为)3(23)3(2222-+=--x ee e x x x ,则其实根的个数为 A .2 B .3 C .4D .5二、填空题:本题共4小题,每小题5分,共20分. 13.已知0>a ,0>b ,42=+b a ,则ab3的最小值为 . 14.已知等比数列}{n a 的前n 项和为S n ,且83336=S s ,则=+4562a a a .15.已知双曲线)0,0(1:2222>>=-b a by a x C 的实轴长为8,右焦点为F ,M 是双曲线C 的一条渐近线上的点,且MF OM ⊥,O 为坐标原点,若6=∆OMF S ,则双曲线C 的离心率为 .16.在ABC ∆中,角A ,B ,C 所对应的边分别为a ,b ,c ,且)cos 2(cos 2C a A -=,2=c ,D 为AC 上一点,3:1:=DC AD ,则ABC ∆面积最大时,BD = .三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分.17.(12分)已知等差数列}{n a 为递增数列,且满足21=a ,252423a a a =+( I )求数列}{n a 的通项公式; (Ⅱ)令)()1)(1(1*1N n a a b n n n ∈++=-,S n 为数列}{n b 的前n 项和,求S n .如图(1)在等腰直角三角形ABC 中,︒=∠90ACB ,4=AB ,点D 为A B 中点,将ADC ∆沿DC 折叠得到三棱锥BCD A -1,如图(2),其中︒=∠601DB A ,点M ,N ,G 分别为A 1C , BC ,A 1B 的中点.( I )求证:⊥MN 平面DCG ; (Ⅱ)求三棱锥DC A G 1-的体积.19.(12分)2017年3月郑州市被国务院确定为全国46个生活垃圾分类处理试点城市之一,此后由郑州市城市管理局起草公开征求意见,经专家论证,多次组织修改完善,数易其稿,最终形成《郑州市城市生活垃圾分类管理办法》(以下简称《办法》).《办法》已于2019年9月26日被郑州市人民政府第35次常务会议审议通过,并于2019年12月1日开始施行.《办法》中将郑州市生活垃圾分为厨余垃圾、可回收垃圾、有害垃圾和其他垃圾4类.为了获悉高中学生对垃圾分类的了解情况,某中学设计了一份调查问卷,500名学生参加测试,从中随机抽取了100名学生问卷,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:( I )从总体的500名学生中随机抽取一人,估计其分数不低于60的概率;(Ⅱ)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的学生人数; (Ⅲ)学校环保志愿者协会决定组织同学们利用课余时间分批参加“垃圾分类,我在实践”活动,以增强学生的环保意识.首次活动从样本中问卷成绩低于40分的学生中随机抽取2人参加,已知样本中分数小于40的5名学生中,男生3人,女生2人,求抽取的2人中男女同学各1人的概率是多少?设曲线)0(2:2>=p Py x C 上一点)2,(m M 到焦点的距离为3.( I )求曲线C 方程;(Ⅱ)设P ,Q 为曲线C 上不同于原点O 的任意两点,且满足以线段PQ 为直径的圆过原点O ,试问直线PQ 是否恒过定点?若恒过定点,求出定点坐标;若不恒过定点,说明理由.21.(12分)已知函数xx ax x f 1ln)(2--= ( I )若,)(x f 在点))1(,1(f 处的切线与直线12+=x y 平行,求)(x f 在点))1(,1(f 的切线方程; (Ⅱ)若函数)(x f 在定义域内有两个极值点x l ,x 2,求证:32ln 2)()(21-<+x f x f .(二)选考题:共10分,请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题记分.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系xOy 中,已知曲线E 经过点)23,1(P ,其参数方程为⎩⎨⎧==,sin 3,cos ααy a x(α为参数),以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.( I )求曲线E 的极坐标方程; (Ⅱ)若直线l 交E 于点A ,B ,且OB OA ⊥,求证:22||1||1OB OA +为定值,并求出这个定值.23.[选修4-5不等式选讲](10分)已知函数m x x x f ++--=|12||1|)( ( I )求不等式m x f ≥)(的解集;(Ⅱ)若恰好存在4个不同的整数n ,使得0)(≥n f ,求m 的取值范围.数学(文科)参考答案一、选择题:1---12 BDACB BAADC DB 二、填空题:313.2 114.3515.42 三、解答题:17.解:222(22)(23)(24)d d d +++=+(1)由题意知 ...2分23440d d ∴--=223d d ∴==-或{}n a 为递增数列2d ∴= ...4分{}2.n n a a n =故数列的通项公式为 ...6分1111(2)()(21)(21)22121n b n n n n ==-+--+...8分11111111[(1)()()...()]2335572121n S n n ∴=-+-+-++--+...10分11(1)221n =-+ 21n n =+...12分18.解:(1)2AC BC AD BD CD =====由题知图(1)中 ...1分∴111,A BCD A D BD AC BC -==在三棱锥中, 1G A B 点是的中点11,DG A B CG A B ∴⊥⊥=DG CG G ⋂又1A B DGC∴⊥平面 ...4分1M N AC BC 又点、分别是、的中点1//MN A B ∴ ...5分MN DGC ∴⊥平面 ...6分11,=,CD A D CD BD A D BD D ⊥⊥⋂(2)由图(1)知,且1CD A DG ∴⊥平面...8分 01160A DB A DB ∠=∴∆又为等边三角形11111,2,1,2DG A B A B AG A B DG ∴⊥====1111122A DG S A G DG ∆∴=⨯=⨯= ...10分11111233G A DC C A DG A DG V V S CD --∆==⨯== ...12分19. 解:(Ⅰ)根据频率分布直方图可知,样本中分数高于60的频率为(0.020.040.02)100.8++⨯=,所以样本中分数高于60的概率为0.8.故从总体的500名学生中随机抽取一人,其分数高于60的概率估计为0.8.3分(Ⅱ)根据题意,样本中分数不小于50的频率为(0.010.020.040.02)100.9+++⨯=, ...5分分数在区间[40,50)内的人数为1001000.955-⨯-=. ...6分 所以总体中分数在区间[40,50)内的人数估计为550025100⨯=. ...7分 (Ⅲ)123,,a a a 设3名男生分别为,12,b b 2名女生分别为,则从这5名同学中选取2人的结果为:12131112212231322312{,},{,},{,},{,},{,},{,}{,},{,},{,},{,}a a a a a b a b a b a b a b a b a a b b ,共10种情况. ...9分 其中2人中男女同学各1人包含结果为:111221223132{,},{,},{,},{,}{,},{,}a b a b a b a b a b a b ,,共6种. ...10分{21}A =设事件抽取的人中男女同学各人,则63()105P A == 所以,抽取的2人中男女同学各1人的概率是35. ...12分 20.解:(1)由抛物线定义得2+2p=3, ...2分 解得2p =,所以曲线C 方程为24x y = ....4分(2)O PQ 以为直径的圆过原点,OP OQ ∴⊥. ...5分 设直线OP 的方程为(0)y kx k =≠,与曲线C 方程24x y =联立,得24x kx =解得0(4x x k ==舍去)或 于是2(4,4)P k k . ...7分 又直线OQ 的方程为1y x k=-,同理:244(,)Q k k - .....9分又直线PQ 斜率存在,22244,44....1404y k x kPQ k k k k --∴=---的直线方程为分即1() 4.y k x k=-+04.PQ ∴直线恒过定点(,) ...12分20.解:(1)2()ln ,f x ax x x =-+ '1()21.f x a x x ∴=-+'(1)2...1.k f a ∴==分因为()f x 在点(1,(1))f 处的切线与直线21y x =+平行, ...222, 1.a a ∴==即分(1)0,..1,.30f ∴=故切点坐标为().分2-2.y x ∴=切线方程为 ...4分 2'121(2)()21,ax x f x ax x x-+=-+=2122100,.ax x x x ∴-+=+∞由题知方程在(,)上有两个不等实根1212180,10,210,2a x x a x x a ⎧⎪∆=->⎪⎪∴+=>⎨⎪⎪=>⎪⎩10.8a ∴<< ...6分 221212121222121212212121212()()()ln ln ()()ln()=[()2]()ln()11=ln1,24f x f x ax ax x x x x a x x x x x x a x x x x x x x x a a+=+-+++=+-+++--++--又1,2t a =令()ln 1,(4,),2t g t t t =--∈+∞'112..9(.)0,22t g t t t-=-=<则分()(4,)g t ∴+∞在上单调递减.()(4)ln 432ln 2 3.g t g ∴<=-=-12()()2ln 2 3.f x f x +<-即 ...12分22.解析:(I)将点3(1,)2P 代入曲线E 的方程,得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =,……2分所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cossin )143ρθθ+=.……5分(Ⅱ)不妨设点,A B 的极坐标分别为1212()()00,2A B πρθρθρρ+>>,,,,,则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分2212111174312ρρ+=+=,即22117||||12OA OB +=……10分23. 解析:(I)由()f x m ≥,得,不等式两边同时平方,得221)(21)x x ≥(-+,……3分 即3(2)0x x +≤,解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤.……5分(Ⅱ)设g (x )=|x -1|-|2x +1|,……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==,(3)1,(4)2,(1) 3.g g g -=--=-=-又恰好存在4个不同的整数n ,使得()0f n ≥, 所以2 1.m -<-≤-故m 的取值范围为[1,2). ……10分12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。

2020届高中毕业年级第一次质量预测语文试题卷一、现代文阅读(36分)社会情绪及其治理是当前中国学界关注的重要议题之一。
在学者的论述和相关部门的报告中,社会情绪往往被描述为流变的、非理性的,因而需要对其进行监测、引导和规制。
从社会控制的角度审视如何有效认识和管控社会情绪,不仅是当前相关部门感到棘手的现实问题,也是学界研究社会情绪的基本出发点。
而笔者认为,社会情绪本身就是一种社会控制方式。
社会学家罗斯在《社会控制》中强调了社会控制的规范属性,即社会控制是对越轨行为的制裁。
在社会控制的传统定义下,人们通常将法律、宗教戒律、习俗、礼仪视为社会控制,并且习惯性地将社会控制与强制权力联系在一起。
事实上,在我们的日常生活中,社会控制远不只是人们所熟悉的权力机构实施的控制,诸如社会舆论、群体情感等也都是社会控制的有力方式。
前者属于正式的社会控制或者“硬控制”,后者属于非正式的社会控制或者“软控制”。
在社会互动中,人们善于利用情绪对他人施加影响,通过情绪控制他人,以使特定行为发生或得以避免。
正如杰克·吉布斯对社会控制的突破性定义所言,社会控制是一方相信公开的行为会增加或减少另一方行为改变的概率。
一方的情绪也会对另一方的行为产生影响,正是情绪作为一种非正式的社会控制方式的核心要义。
稚童通过哭泣让父母满足自己的要求、父母通过怒目让孩子停止错误的行为、妻子通过赌气让丈夫妥协,类似的情况在日常生活中比比皆是。
在群体行动中,行动者激昂的情绪可以帮助他们吸引社会组织和媒体的注意力,从而对后者施加影响,这同样是情绪作为非正式控制方式的一种体现。
当然,不管是消极的情绪还是积极的情绪,都是非正式的社会控制。
与正式的社会控制方式相比,情绪作为一种非正式的社会控制方式显得冲动、没有计划性、不需要复杂的技巧,但看似感性的情绪表达其实有其实践理性、遵循着模糊的实践感,比如情绪的持续时间、强烈程度与社会空间、社会时间、互动双方之间的社会距离(上下垂直距离、文化距离等)密切相关。

2020 届高中毕业年级第一次质量预测地理试题卷本试卷分选择题和非选择题两部分。
考试时间90 分钟,满分100 分。
考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。
交卷时只交答题卡。
、选择题:本题共25小题,每小题2分,共50分o 在每小题给出的四个选项中,只有一项是符合题目要求的。
暑假期间,小明前往墨尔本(37 ° 46'S) 旅行。
在墨尔本,小明发现很多建筑的布局并非严格的南北朝向,而是有一定的偏角。
图图。
据此完成1~2 题。
1 为墨尔本某街道上两栋方形大楼的俯视A.大楼甲的①墙面B.大楼甲的②墙面C.大楼乙的③墙面D.大楼乙的④墙面2.为使大楼乙的①墙面全年每天均有采光机会,墙面与街道的夹角α 最小可能是A. 14°B.32°C.45°D.59°图 2 为亚洲部分地区11 月17 日某时段三个不同时刻海平面气压分布图(单位:百帕)。
据此完成3~5 题。
1.建筑物的布局方位会影响墙面的采光条件。
小明旅行期间,全天都不能采光的墙面是高三地理试题卷第 1 页(共 8 页)3.①时刻, M 地盛行A .东南风B .东北风C .西南风D .西北风4.该时段,图示区域依次出现的气压场分布形势为A.①②③ B .③②① C .②①③ D.②③① 5.该时段, P 地经历的天气过程最可能是A.气温先上升后下降 B .气压持续升高C .由阴雨转为晴朗D .持续性雨雪天气6.砾岩由砾石沉积而成。
据图 3 推断其沉积环境为A .陆地B .滨海C .浅海D .深海 7.图 4 所示岩层剖面表明该地在地质历史时期经历了A.海侵过程 B .海退过程 C .先海侵后海退 D .先海退后海侵8.在地质演化过程中,形成界面 M 的地质作用最可能是 A.挤压 B .断裂 C .侵蚀 D .变质2019年 4 月,一张飘絮预警图(图 5)在朋友圈广为传播。

2020年高中毕业年级第一次质量预测数学(理科) 参考答案一、选择题1-12 BDACBCBCDB DA二、填空题13. 10;x y -+=14.4; 15.;53016.{}.66,2,0-- 三、解答题17.解析:(I)222(sinsin )()sin .R A B a c C -=- ∴2222(sinsin )()sin 2,R R A B a c C R ⋅-=-⋅ 即:222.a c b ac +-= ……3分∴2221cos .22a cb B ac +-== 因为0,B π<<所以3B π∠=……6分(II)若12,8b c ==,由正弦定理,sin sin b c B C=, sin C =, 由b c >,故C ∠为锐角,cos C =……9分 1sin sin()sin()32A B C C π=+=+=+=……12分 18. 解析:(I )如图所示:连接OM ,在ABC ∆中:2,AB BC AC ===90,ABC BO ∠=︒=OB AC ⊥.……2分在MAC ∆中:MA MC AC ===O 为AC 的中点,则OM AC ⊥,且OM = ……4分在MOB ∆中:BO OM MB ===222BO OM MB += 根据勾股定理逆定理得到OB OM ⊥ ,AC OM 相交于O ,故OB ⊥平面AMC ………………….6分CA(Ⅱ)因为,,OB OC OM两两垂直,建立空间直角坐标系如图所示.因为MA MB MC AC====2AB BC==则(0,A B C M……8分由23BN BC=所以,33N设平面MAN的法向量为(,,)m x y z=,则2(,(,,)0,3333(,,)0AN n x y z x yAM n x y z⎧⋅=⋅=+=⎪⎨⎪⋅=⋅=+=⎩令y=(1)m=--……10分因为BO⊥平面AMC,所以(2,0,0)OB=为平面AMC的法向量,所以(1)m =--与(2,0,0)OB=所成角的余弦为cos,m OB<>==.所以二面角的正弦值为2|sin,|m OB<>===分19.(I)由题意知1b=,2ca=.……1分又因为222a b c=+解得,a=3分所以椭圆方程为2212yx+=. ……4分(Ⅱ)设过点1(,0)3-直线为13x ty=-,设()11,A x y,()22,B x y由221312x tyxy⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160t tyy+--=,且>0∆.则12212212,918616,918yy ytytt⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分又因为()111,CA x y=-,()221,CB x y=-,()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++ ⎪⎪⎝⎭⎝⎭()22216412161091839189t t t t t -=+-⋅+=++,……10分 所以CA CB ⊥.因为线段AB 的中点为M ,所以||2||AB CM =.……12分20. 解析:(I)该混合样本达标的概率是28(39=,……2分 所以根据对立事件原理,不达标的概率为81199-=.……4分 (II)(i )方案一:逐个检测,检测次数为4. 方案二:由(1)知,每组两个样本检测时,若达标则检测次数为1,概率为89;若不达标则检测次数为3,概率为19.故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6. 其分布列如下,可求得方案二的期望为26416119822()246818181819E ξ=⨯+⨯+⨯== 方案四:混在一起检测,记检测次数为ξ4,ξ4可取1,5.其分布列如下,可求得方案四的期望为46417149()15818181E ξ=⨯+⨯=. 比较可得42()()4E E ξξ<<,故选择方案四最“优”.……9分(ii)方案三:设化验次数为3η,3η可取2,5.333()25(1)53E p p p η=+-=-;方案四:设化验次数为4η,4η可取1,54444()5(1)54E p p p η=+-=-;由题意得34343()()53544E E p p p ηη<⇔-<-⇔<. 故当304p <<时,方案三比方案四更“优”.……12分 21解析:(I)()ln xe f x x x x=--,定义域(0,)+∞, 221(1)(1)()()1x x e x x x e f x x x x ---'=--=, 由1x e x x ≥+>,()f x 在(0,1]增,在(1,)+∞减,max ()(1)1f x f e ==-……4分 (II)1()()e 1x f x x bx x++-≥ e e ln e 1x x x x x x bx x x⇔-+-++-≥ ln e 10x x x x bx ⇔-++--≥e ln 1x x x x b x --+⇔≥min e ln 1(),x x x x b x--+⇔≥……6分 令e ln 1()x x x x x x ϕ--+=,2ln ()x x e x x xϕ+'= 令2()ln x h x x e x =+,()h x 在(0,)+∞单调递增,0,()x h x →→-∞,(1)0h e =>()h x 在(0,1)存在零点0x ,即02000()ln 0x h x x e x =+=0001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=……9分 由于x y xe =在(0,)+∞单调递增,故0001ln ln ,x x x ==-即001x e x =()x ϕ在0(0,)x 减,在0(,)x +∞增,000000min00e ln 111()2x x x x x x x x x ϕ--++-+=== 所以2b ≤.……12分 22.解析:(I)将点3(1,)2P 代入曲线E 的方程,得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =,……2分 所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cos sin )143ρθθ+=.……5分 (Ⅱ)不妨设点,A B 的极坐标分别为1212()()00,2A B πρθρθρρ+>>,,,,, 则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩ 即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分2212111174312ρρ+=+=,即22117||||12OA OB +=……10分 23. 解:(I)由()f x m ≥,得,不等式两边同时平方,得221)(21)x x ≥(-+,……3分 即3(2)0x x +≤,解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤.……5分(Ⅱ)设g (x )=|x -1|-|2x +1|,……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==,(3)1,(4)2,(1) 3.g g g -=--=-=- 又恰好存在4个不同的整数n ,使得()0f n ≥, 所以2 1.m -<-≤-故m 的取值范围为[1,2). ……10分 12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。

2020年河南省郑州市高中毕业班第一次质量预测高中物理物理试题本试卷分第一卷〔选择题〕和第二卷〔非选择题〕两部分,考试时刻90min,总分值100分。
第一卷〔选择题共40分〕本卷须知:1.答第一卷前,考生务必将自己的姓名、考号、试题科目涂写在答题卡上。
2.请将第一卷的对应答案用铅笔把答题卡上对应题目的答案标号涂黑。
考试终止时,只交答题卡和答题卷。
选择题答案写在试卷上无效。
一、选择题〔此题共10个小题,每题4分,共40分。
在每题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确,全部选对的得4分,选对但不全的得2分,有选错或不答的得0分〕1.以下讲法正确的选项是〔〕A.某星球表面的温度为-300℃B.第二类永动机不可能制成的缘故是违抗了能量守恒定律C.热量不可能从低温物体传到高温物体D.从单一热源吸取的热量全部用来做功是可能的2.以下讲法正确的选项是〔〕A.假设声波波源向观看者靠近,那么观看者接收到的声波频率减小B.声波击碎玻璃杯的实验原理是共振C.超声波在水中传播的距离要比光波和无线电波远得多D.〝闻其声不见其人〞是声波的干涉现象3.如图1甲所示,在粗糙的水平面上,质量分不为m和M〔m :M=1:2〕的物块A、B 用轻弹簧相连,两物块与水平面间的动摩擦因数相同。
当用水平力F作用于B上且两物块共同向右加速运动时,弹簧的伸长量为x1当用同样大小的力F竖直加速提升两物块时〔如图l乙所示〕,弹簧的伸长量为x2,那么x1:x2等于〔〕A .1:1B .1:2C .2:1D .2:34.振源A 带动细绳振动,某时刻形成的横波波形如图2所示,从波传播到细绳上的一点P开始计时,图3中有四个图形,能表示P 点振动图象的是〔 〕5.正弦交变电源与电阻R 、交流电压表、交流电流表按照如图4所示的方式连接,R=200Ω,图5是交变电源输出电压u 随时刻t 变化的图象,那么〔 〕A .交流电压表的读数为311VB .交流电流表的读数是C .R 两端电压随时刻变化的规律是 u R =311cosπt VD .R 中流过的电流随时刻变化的规律是i R =1。

2020年高中毕业年级第一次质量预测数学(理科) 参考答案一、选择题1-12 BDACBCBCDB DA 二、填空题13. 10;x y -+=14.4; 15.;53016.{}.66,2,0-- 三、解答题17.解析:(I)222(sin sin )()sin .R A B a c C -=-∴2222(sin sin )()sin 2,R R A B a c C R ⋅-=-⋅即:222.ac b ac +-= ……3分∴2221cos .22a cb B ac +-== 因为0,B π<<所以3B π∠=……6分(II)若12,8b c ==,由正弦定理,sin sin b cB C=, sin C =,由b c >,故C ∠为锐角,cos C =……9分 1sin sin()sin()32A B C C π=+=+=+=……12分 18. 解析:(I )如图所示:连接OM , 在ABC ∆中:2,AB BC AC ===90,ABC BO ∠=︒=OB AC ⊥.……2分在MAC ∆中:MA MC AC ===O 为AC 的中点,则OM AC ⊥,且OM = ……4分在MOB ∆中:BO OM MB ===222BO OM MB +=根据勾股定理逆定理得到OB OM ⊥ ,AC OM 相交于O , 故OB ⊥平面AMC ………………….6分CA(Ⅱ)因为,,OB OC OM两两垂直,建立空间直角坐标系如图所示.因为MA MB MC AC====2AB BC==则(0,A B C M……8分由23BN BC=所以,33N设平面MAN的法向量为(,,)m x y z=,则2(,(,,)0,3333(,,)0AN n x y z x yAM n x y z⎧⋅=⋅=+=⎪⎨⎪⋅=⋅=+=⎩令y=(1)m=--……10分因为BO⊥平面AMC,所以(2,0,0)OB=为平面AMC的法向量,所以(1)m =--与(2,0,0)OB=所成角的余弦为cos,m OB<>==.所以二面角的正弦值为2|sin,|m OB<>===分19.(I)由题意知1b=,2ca=.……1分又因为222a b c=+解得,a=3分所以椭圆方程为2212yx+=. ……4分(Ⅱ)设过点1(,0)3-直线为13x ty=-,设()11,A x y,()22,B x y由221312x tyxy⎧=-⎪⎪⎨⎪+=⎪⎩得()2291812160t tyy+--=,且>0∆.则12212212,918616,918yy ytytt⎧+=⎪⎪+⋯⋯⎨⎪=-⎪+⎩分又因为()111,CA x y=-,()221,CB x y=-,()()212121212121244416(1)(1)13339CA CB x x y y ty ty y y t y y t y y ⎛⎫⎛⎫⋅=--+=--+=+-++⎪⎪⎝⎭⎝⎭()22216412161091839189t t t t t -=+-⋅+=++,……10分所以CA CB ⊥.因为线段AB 的中点为M ,所以||2||AB CM =.……12分20. 解析:(I)该混合样本达标的概率是28(39=,……2分 所以根据对立事件原理,不达标的概率为81199-=.……4分 (II)(i )方案一:逐个检测,检测次数为4.方案二:由(1)知,每组两个样本检测时,若达标则检测次数为1,概率为89;若不达标则检测次数为3,概率为19.故方案二的检测次数记为ξ2,ξ2的可能取值为2,4,6. 其分布列如下,可求得方案二的期望为26416119822()246818181819E ξ=⨯+⨯+⨯== 方案四:混在一起检测,记检测次数为ξ4,ξ4可取1,5. 其分布列如下,可求得方案四的期望为46417149()15818181E ξ=⨯+⨯=. 比较可得42()()4E E ξξ<<,故选择方案四最“优”.……9分 (ii)方案三:设化验次数为3η,3η可取2,5.333()25(1)53E p p p η=+-=-;方案四:设化验次数为4η,4η可取1,54444()5(1)54E p p p η=+-=-;由题意得34343()()53544E E p p p ηη<⇔-<-⇔<. 故当304p <<时,方案三比方案四更“优”.……12分 21解析:(I)()ln xe f x x x x=--,定义域(0,)+∞,221(1)(1)()()1x x e x x x e f x x x x---'=--=, 由1x e x x ≥+>,()f x 在(0,1]增,在(1,)+∞减,max ()(1)1f x f e ==-……4分 (II)1()()e 1xf x x bx x++-≥ e e ln e 1x x xx x x bx x x⇔-+-++-≥ln e 10x x x x bx ⇔-++--≥e ln 1x x x xb x --+⇔≥min e ln 1(),x x x x b x --+⇔≥……6分令e ln 1()x x x x x x ϕ--+=,2ln ()x x e xx xϕ+'=令2()ln x h x x e x =+,()h x 在(0,)+∞单调递增,0,()x h x →→-∞,(1)0h e =>()h x 在(0,1)存在零点0x ,即02000()ln 0xh x x e x =+=001ln 2000000ln 1ln 0(ln )()x x x x x e x x e e x x +=⇔=-=……9分由于x y xe =在(0,)+∞单调递增,故0001lnln ,x x x ==-即001x e x =()x ϕ在0(0,)x 减,在0(,)x +∞增,000000min00e ln 111()2x x x x x x x x x ϕ--++-+===所以2b ≤.……12分22.解析:(I)将点3(1,)2P 代入曲线E 的方程,得1cos ,3,2a αα=⎧⎪⎨=⎪⎩解得24a =,……2分所以曲线E 的普通方程为22143x y +=, 极坐标方程为22211(cossin )143ρθθ+=.……5分(Ⅱ)不妨设点,A B 的极坐标分别为1212()()00,2A B πρθρθρρ+>>,,,,,则22221122222211(cos sin )1,4311(cos ()sin ()1,4232ρθρθππρθρθ⎧+=⎪⎪⎨⎪+++=⎪⎩即22212222111cos sin ,43111sin cos ,43θθρθθρ⎧=+⎪⎪⎨⎪=+⎪⎩……8分 2212111174312ρρ+=+=,即22117||||12OA OB +=……10分 23. 解:(I)由()f x m ≥,得,不等式两边同时平方,得221)(21)x x ≥(-+,……3分 即3(2)0x x +≤,解得20x -≤≤.所以不等式()f x m ≥的解集为{|20}x x -≤≤.……5分(Ⅱ)设g (x )=|x -1|-|2x +1|,……8分()0()f n g n m ≥⇔≥-因为(2)(0)0g g -==,(3)1,(4)2,(1) 3.g g g -=--=-=-又恰好存在4个不同的整数n ,使得()0f n ≥, 所以2 1.m -<-≤-故m 的取值范围为[1,2). ……10分12,,21()3,1,22,1,x x g x x x x x ⎧+≤-⎪⎪⎪=--<≤⎨⎪-->⎪⎪⎩。

河南省郑州市2020年高中毕业班第一次质量预测数学文科试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟,第Ⅰ卷1至2页,第Ⅱ卷3至8页,考试结束后,将本试卷和答题卡一并交回。
注意事项:1. 答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,答在答卷上的无效。
参考公式: 如果事件A 、B 互斥,那么球的表面积公式()()()P A B P A P B +=+24S R π=如果事件A 、B 相互独立,那么球的体积公式()()()P A B P A P B =g g如果事件A 在一次实验中发生的概率是P343V R π=球那么n 次独立重复实验中恰好发生k 次概率其中R 表示球的半径()(1)k kn k n n P k C P P -=-第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.若全集U R =,集合2{|10},{|20}A x x B x x x =-<=-≤,则 ()A B ⋂= A .{|12}x x <<B .{|12}x x <≤C .{|12}x x x <≥或D .{|12}x x x ≤>或2.已知向量( 5.3),(2,)a x b x =--=,且a b ⊥,则由x =A . 2或3B .-1或6C .6D .23.已知双曲线的方程为22236x y -=,则此双曲线的离心率为A .32B C . D 4.已知2:231,:310p x q x x -<--<,则p 是q 的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.若数列{}n a 的通项公式为23n a n =+,则13599a a a a ++++=…A .5150B .2700C .9270D .48606.设e 为椭圆221(2)2x y m m-=>-的离心率,且,1)2e ∈,则实数m 的取值范围为A .(-1,0)B .(-2,-1)C .(-1,1)D .(-2,-12) 7.函数12()xy x R -=∈的反函数的解析式为A .21log (1)2xy x -=< B .22log (1)1y x x =<-C .22log (0)y x x=>D .2log (0)2xy x =>8.若log 3log 30a b <<,则下面结论成立的是 A .01a b <<< B .01a b <<<C .01b a <<<D .01b a <<<9.线段AB 长为2,两个端点A 、B 分别在一个直二面角的两个面上,A B 和两个面所成的角分别是045和030,那么A 、B 在则个二面角的棱上的射影C 、D 间的距离是A .1B .12C .2 D10.若直线2x y -=被圆22()4x a y -+=所截得的弦长为,则实数a 的值为A .-1B .1或3C .-2或6D .0或411.若以连续掷骰子分别得到的点数m 、n 作为点P 的横、纵坐标,则点P 的直线5x y +=下方的概率为A .16B .14C .112D .1912.若曲线2y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为 A .440x y -+= B .440x y --=B .4120x y --=D .440x y --=第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题4分,共16分)13.二项式251()x x+的展开式中4x 的系数为________ .(用数字作答) 14.在ABC ∆中,内角A 满足2sin 23A =,则sin cos A A +=_______。
2020届河南省郑州市高三第一次质量预测数学(理)试题一、单选题1.设集合A=(xeZ||x|<2},B={y\y=l-x1},则AcB的子集个数为()A. 4B.8C.16D.32【答案】C【解析】分析:求出集合A,B,得到AC8,可求AnB的子集个数详解:A={xeZ|国<2}={xg Z|-2<x<2}={-2,-1,0.1,2},B={y|y=l_J}={y|y〈l},An B={-2,-1,0,1},AoB的子集个数为24=16.故选C.点睛:本题考查集合的运算以及子集的个数,属基础题.2.复数z=——在复平面内对应的点位于()iA.第一象限B.第二象限C.第三象限D.第四象限【答案】D【解析】化简复数为z=。
+初的形式,求得复数对应点的坐标,由此判断所在的象限.【详解】。
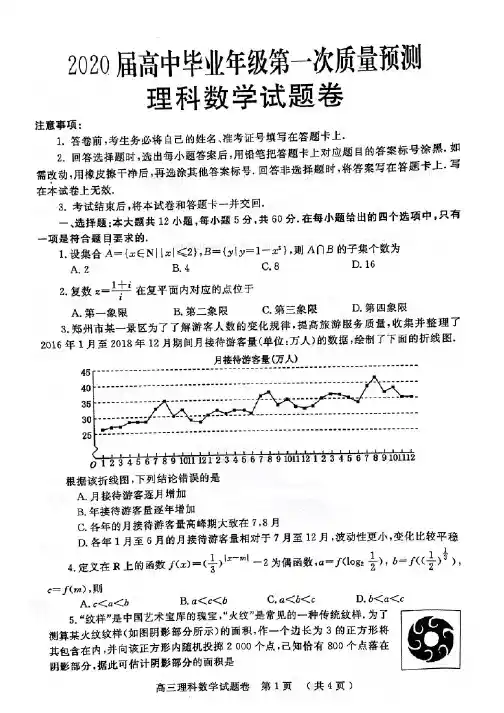
I.z=b=l-2Z,该复数对应的点为(1,一2),在第四象限.故选D.【点睛】本小题主要考查复数的运算,考查复数对应点的坐标所在象限.3.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图,根据该折线图,下列结论错误的是()A.各年的月接待游客量高峰期大致在7,8月份B.年接待游客量逐年增加C.月接待游客量逐月增加D.各年1月至6月的月接待游客量相对7月至12月,波动性更小,变化比较平稳【答案】C【解析】根据折线图依次判断各个选项,可通过反例得到。
错误.【详解】由折线图可知,每年游客量最多的月份为:7,8月份,可知A正确;年接待游客量呈现逐年递增的趋势,可知B正确;以2018年8月和9月为例,可得到月接待游客量并非逐月增加,可知C错误;每年1月至6月的月接待游客量相对于7月至12月的变化较小,数量更加稳定,可知。
正确.本题正确选项:C【点睛】本题考查根据统计中的折线图判断数据特征的问题,属于基础题.4.定义在R上的函数=偶函期«=/(log2|),Z,=/((l)3),c=f(m),贝ijA.c<a<bB.a<c<bC.a<b<cD.b<a<c【答案】C【解析】由偶函数得到m=0,明确函数的单调性,综合利用奇偶性与单调性比较大小即可.【详解】/■⑴=(<)E—2为偶函数,.•.m=0,即/(x)=(|)W-2,且其在[0,+8)上单调递减,11又0<(一)3<1,111c=/(m)=f(0)罚=/((-)3)〉a=/(log2-)=/(1)故选:C【点睛】本题考查函数的性质,考查函数的奇偶性与单调性,考查转化思想,属于中档题.5. “纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其包含在内,并向该正方 形内随机投掷2000个点,己知恰有800个点落在阴影部分,据此可估计阴影部分的面 积是16A,—5B.18C. 1032D,—5【答案】B【解析】边长为3的正方形的面积S 正您=9,设阴影部分的面积为S 网,由几何概型得S 阴 800了」=房而,由此能估计阴影部分的面积.'正方形【详解】解:为了测算某火纹纹样(如图阴影部分所示)的面积,作一个边长为3的正方形将其 包含在内,则边长为3的正方形的面积S 正",=9,设阴影部分的面积为S 耕..•该正方形内随机投掷2000个点,已知恰有800个点落在阴影部分,..S 阴 800S 正方形2000… 800 ° 800 八 18解得S 阴=-----x ‘中方形=------x 9 =——2000 正方形 2000 51 Q..•估计阴影部分的面积是;.故选:B.【点睛】本题考查阴影面积的求法,考查几何概型等基础知识,考查运算求解能力,考查函数与方程思想,是基础题.6.已知向量q与》夹角为;,且\a\=\,|2a-Z?|=V3,贝\\\b\=A.也B.y/2C.1D.亟2【答案】C【解析】对\2a-b\=yf3两边平方,结合数量积的定义与法则即可得到结果.【详解】I,向量a与Z?夹角为:,且|«|=1 >|2a—Z?|=^3,p*一外=3,即4a2-4a-b+b2=3••.4一2种+祥=3,所以\b\=l,故选:C【点睛】本题考查利用数量积求模,考查数量积定义与运算法则,考查运算能力.7.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题,松长三尺,竹长一尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输人的a,。
郑州市 2020 年高中毕业年级第一次质量预测数学(文科)参考答案一、选择题:1---12 BDACB BAADC DB二、填空题:13. 314.115.516. 6 2 3 4 2三、解答题:17. 解:(1) 由题意知 (2 2d )2 (2 3d) 2 (2 4d) 2分...23d 2 4d 4 0d 2或d 2 3{ a n }为递增数列d 2故数列 { a n}的通项公式为a n2n.(2) b n 11) 1 ( 1 1 )(2n 1)(2n 2 2n 1 2n 1S n 1[(1 1) (11 ) (11) ... ( 111 )]2 3 3 5 5 7 2n 2n 11(1 1 )2 2n 1...4分...6分...8分...10分n2n 1 ...12 分18. 解:( 1)由题知图(1)中 AC BC 2 2,AD BD CD 2...1分在三棱锥 1 中, 1BCA BCD A1D BD , AC点G是A1B的中点DG A1B,CG A1 B又 DG CG =G A1B 平面 DGC...4 分又点 M 、N分别是AC1 、 BC的中点MN //A1B ...5 分MN 平面 DGC ...6 分( 2)由图( 1)知 CD A1D, CD BD,且 A1D BD=D , CD 平面 A1 DG ...8 分又 A1DB 600 A1DB 为等边三角形DG A1 B, A1B 2, AG1 1A1 B 1,DG 3, 2S A1DG 1 1DG11 33...10 分2 AG 2 2VG ADC VC ADG1S ADG CD 1 3 2 3 ....12 分1 1 3 1 32 319. 解:(Ⅰ)根据频率分布直方图可知,样本中分数高于60 的频率为(0.02 0.04 0.02) 10 0.8 ,所以样本中分数高于60 的概率为0.8.故从总体的 500 名学生中随机抽取一人,其分数高于60 的概率估计为 0.8 .3 分(Ⅱ)根据题意,样本中分数不小于50 的频率为(0.01 0.02 0.04 0.02) 10 0.9 ,...5 分分数在区间 [40,50) 内的人数为100 100 0.9 5 5 ....6 分所以总体中分数在区间 [40,50) 内的人数估计为500 5 25 ....7 分100(Ⅲ)设 3名男生分别为 a1 , a2 , a3, 2名女生分别为 b1, b2,则从这5 名同学中选取 2 人的结果为:{ a1 , a2},{ a1 , a3 },{ a1, b1},{ a1,b2 },{ a2 , b1},{ a2 , b2}{,a3, b1},{ a3 , b2 },{ a2 , a3},{ b1, b2}共10种情况....9 分其中 2 人中男女同学各 1 人包含结果为:{ a1, b1},{ a1, b2 },{ a2 ,b1},{ a2 , b2}{,a3 ,b1},{ a3 , b2} ,共6种. ...10 分设事件 A { 抽取的 2人中男女同学各6 3 1人} ,则P( A)5 3 .10所以,抽取的 2 人中男女同学各 1 人的概率是...12 分5p=3,20. 解:( 1)由抛物线定义得 2+ ...2 分2解得 p 2 ,所以曲线C方程为 x2 4 y ....4 分( 2)以 PQ为直径的圆过原点O, OP OQ . ...5 分设直线 OP 的方程为y kx(k 0) ,与曲线C方程 x2 4 y 联立,得 x 2 4kx 解得 x 0(舍去)或 x 4k 于是 P(4 k,4 k 2 ) . ...7 分又直线 OQ 的方程为y 1x ,同理: Q( 4, 4) .....9 分k k k2又直线 PQ 斜率存在,PQ的直线方程为y 4k 2 x 4k4 4k 2 4,....10分4kk 2 k即 y ( k 1) x 4. k直线 PQ恒过定点( 0,4). ...12 分20. 解:(1)f ( x) ax2 x ln x, f ' ( x) 2ax 1 1 .xk f ' (1) 2a....1分因为 f ( x) 在点 (1, f (1))处的切线与直线 y 2x 1平行,2a 2,即a 1....2分f (1) 0, 故切点坐标为( 1,0) ....3分切线方程为 y 2x - 2. ...4 分(2) f ' ( x) 2ax 1 1 2ax2 x 1 ,x x由题知方程 2ax2 x 1 0在( 0,)上有两个不等实根 x1, x2.1 8a 0,x1 x210, 0 a 1 . (6)2a分8x1 x2 10, 2a又f (x1) f (x2 ) ax12 ax22 ( x1 x2 ) ln x1 ln x2a( x12 x22 ) (x1 x2 ) ln( x1 x2 )=a[( x1 x2 )2 2x1 x2 ] (x1 x2 ) ln( x1x2 )1 11,=ln4a2a令t 1 , g(t) ln t t 1,t (4, ), 则 g ' (t ) 11 2 t0, (9)分2a 2 t 2 2tg (t )在(4, )上单调递减 .g (t ) g(4) ln 4 3 2ln 2 3.即 f (x1) f (x2 ) 2ln 2 3. ...12 分22.解析: (I) 将点P(1,3)代入曲线E的方程,21 acos ,得 3 3sin ,2解得 a2 4,2分x2 y2,所以曲线 E 的普通方程为 14 3极坐标方程为 2 ( 1 cos2 1 s in2 ) 1 . 5分4 3( Ⅱ ) 不妨设点A, B 的极坐标分别为A( 1, ),B( 2,), 1 0, 2 0,21 2 2 1 2 2( 4 1 cos 3 1 sin ) 1,则1 12 2 2 2( 4 2 cos ( 2 ) 3 2 sin ( 2 ) 1,1 12 1 2,2 cos sin即 1 4 38 分1 1 12 2, 2 sin cos24 31 1 1 1 7, 即1 1 72 24 3 12 2 2 10 分1 2 |OA | |OB| 12 23. 解析: (I) 由 f x m ,得,不等式两边同时平方,得( x-1)2 (2 x+1)2 ,3分即 3x( x 2) 0 ,解得 2 x 0 .所以不等式 f x m 的解集为{ x | 2 x 0} . 5分( Ⅱ ) 设g( x) = | x- 1| - |2 x+ 1| ,x 2, x 1 ,2g( x) 3x, 1x 1,28 分x 2, x 1,f n 0g (n) m 因为 g( 2) g(0) 0 ,g( 3) 1, g ( 4) 2, g(1) 3.又恰好存在 4 个不同的整数n f n 0,,使得所以 2 m 1.故 m 的取值范围为 [1,2) .10 分。
32 1 2020 届郑州市高中毕业年级第一次质量预测理科数学试题卷一、选择题(本大题共 12 小题,每小题 5 分,共 60 分。
1. 设集合 A = {x ∈ N | x |≤ 2}, B = {y y = 1 - x 2 },则 A B 的子集个数为A.2B .4C.8D.162. 复数 z = 1 + i在复平面内对应的点位于iA.第一象限B.第二象限C.第三象限 D .第四象限3. 郑州市某一景区为了了解游客人数的变化规律,提高旅游服务质量,收集并整理了 2016 年 1 月至 2018 年 12 月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.根据该折线图,下列结论错误的是 A .月接待游客逐月增加 B.年接持游客量逐年增加C.各年的月接待游客量高峰期大致在 7,8 月D.各年 1 月至 6 月的月接待游客量相对于 7 月至 12 月,波动性更小,变化比较平稳4. 定义在 R 上的函数 f (x ) = ( )|x -m |- 2 为偶函數, a = f (log 2 31 ) , b = f ((2 1 )3 ) , c = f (m ) ,则 2 A. c < a < b B. a < c < b C. a < b < c D. b < a < c5. “纹样”是中国艺术宝库的瑰宝,“火纹”是常见的一种传统纹样,为了测算某火纹纹样(如图阴影部分所示)的面积, 作一个边长为 3 的正方形将其包含在内,并向该正方形内随机投掷 2000 个点,己知恰有 800 个点落在阴影部分,据此可估计阴影部分的面积是 A. 16 5 B. 18 5 C. 10D. 32 56. 已知向量 a 与b 夹角为,且| a |= 1 , | 2a - b |=3A. B. C .1,则| b |=D.3 27. 宋元时期数学名著《算学启蒙》中有关于“松竹并生"的问题,松长三尺,竹长一尺,松日自半,竹日自倍,松竹何日而长等,如图是源于其思想的一个程序框图,若输人的 a , b 分别为 3,1,则输出的 n 等于 А.5B .4 C.3 D.22x +1 8. 函数 f (x )=2x -1⋅ cos x 的图象大致是3 13 ⎨答案:C9. 第十一届全国少数民族传统体育运动会在河南郑州举行,某项目比赛期间需要安排3 名志愿者完成 5 项工作,每人至少完成一项,每项工作由一人完成,则不同的安排方式共有多少种A.60B.90C.120D .15010. 已知抛物线 y 2 = 2x 的焦点为 F ,准线为l , P 是l 上一点,直线 PF 与抛物线交于 M , N 两点,若 PF = 3MF ,则| MN | =A. 16 3B. 8 3C.2 D. 83 311. 已知三棱锥 P - ABC 内接于球 O , PA ⊥ 平面 ABC , ∆ABC 为等边三角形,且边长为 ,球O 的表面积为16,则直线 PC 与平面 PAB 所成的角的正弦值为A. 15 7B. 15 5C. 15 2D. 51012. f (x ) = ⎧ | 2x + 1|, x < 1 , g (x ) = 5 x 3 - 15x 2 + m + 2 ,若 y = f (g (x )) - m 有 9 个零点,则 m 的取值范围是A . (0,1)⎩log 2 (x - 1), x > 1B. (0,3) 4 4C. (1, 5) 3D. ( 5 3,3) 二、填空题:本大题共 4 小题,每小题 5 分,共 20 分.13. 曲线 y = xe x - 2x 2 + 1 在点(0,1) 处的切线方程为.答案: x - y +1 = 0;14. 若 S 是等差数列{a }的前 n 项和,若 a ≠ 0 , a = 3a , 则S 10=nn1215S6 3 ON2 - = > > 15. 已知双曲线C : x a 2 y 2b 21(a 0, b 0) 的右顶点为 A ,以 A 为圆心,6 为半径做圆,圆 A 与双曲线 C 的一条渐近线相交于 M ,N 两点,若OM = 3 ON ( O 为坐标原点),则双曲线 C 的离心率为 216. 已知数列{a n }满足:对任意 n ∈ N * 均有 a n +1 = pa n + 2 p - 2 (p 为常数, p ≠ 0 且 p ≠ 1 ),若.答案:30 ; 5a 2 , a 3 , a 4 , a 5 ∈{- 18,-6,-2,6,11,30},则 a 1 的所有可能取值的集合是.答案: {0,-2,-66}.三、解答题:共 70 分,解答应写出文字说明、证明过程或演算步骤.17.(12 分)已知∆ ABC 外接圆半径为 R ,其内角 A ,B ,C 的对边长分别为 a ,b ,c ,设2R (sin 2 A - sin 2 B ) = (a - c ) sin C .(1) 求角 B ;(Ⅱ)若 b =12,c =8,求 sin A 的值17. 【解析】(I) 2R (sin2A - sin 2B ) = (a - c ) sinC .∴2R ⋅ 2R (sin 2 A - sin 2 B ) = (a - c ) sin C ⋅ 2R , 即: a 2 + c 2 - b 2 = ac . ……3 分a 2 + c 2 -b 2 1 ∴c os B = = .2ac 2因为0 < B < , 所以∠B = ……6 分3(II)若b = 12, c = 8 ,由正弦定理,b sin B =c , sin C sin C = 3 ,3由b > c ,故∠C 为锐角, cos C = 6. ……9 分 3sin A = sin(B + C ) = sin( + C ) = 3 ⋅ + 1 ⋅ =3 2 + 3 . ……12 分 18.(12 分)3 2 3 2 3 6已知三棱锥 M -ABC 中,MA =MB =MC =AC = 2 证明:BO ⊥ 平面 AMC ; (2) 求二面角 N -AM -C 的正弦值.M,AB =BC =2,O 为 AC 的中点,点 N 在棱 BC 上,且 BN = 2BC .(1) 3ACB18. 【解析】(I )如图所示:连接OM , 在∆ABC 中: AB = BC = 2, AC = 2,则∠ABC = 90︒, BO =, OB ⊥ AC .2 分在∆MAC 中: MA = MC = AC = 2 , O 为 AC 的中点,则OM ⊥ AC ,且OM =6. ……4 分在∆MOB 中: BO =2,OM = 6, M B = 2 ,满足: BO 2 + OM 2 = MB 222 2 2 2-5 6 79 2 -5 379 79 2 79 ⎩< > =x 根据勾股定理逆定理得到OB ⊥ OM AC , OM 相交于O , 故OB ⊥ 平面 AMC ......................... 6 分(Ⅱ)因为OB , OC , OM 两两垂直,建立空间直角坐标系O ‒ xyz 如图所示. 因为 MA = MB = MC = AC = 2 , AB = BC = 2 则 A (0, - 2, 0), B ( 2, 0, 0), C (0, 2, 0), M (0, 0, 6) ……8 分 2 2 2 2由 BN = 3 BC 所以, N ( 3 , , 0)3设平面 MAN 的法向量为m = (x , y , z ) ,则⎧2 5 2 2 5 2⎪ AN ⋅ n = ( , ⎨ 3 , 0) ⋅ (x , y , z ) = x + 33 3 y = 0, ⎪ AM ⋅ n = (0, 2, 6) ⋅ (x , y , z ) =2 y + 6z = 0 令 y = ,得m = (-5 3, 3, -1) ……10 分因为 BO ⊥ 平面 AMC ,所以OB = ( 2, 0, 0) 为平面 AMC 的法向量,所以m = (-5 3, 3, -1) 与OB = ( 2, 0, 0) 所成角的余弦为cos < m , O B >= =.所以二面角的正弦值为| sin m , OB | 1- ( -5 3 )2= 792 = .……12 分 79A19.(12 分)y 2 x 2 E : + = > >2 C (1,0) 已知椭圆a 2b 2 1(a b 0) 的离心率为 ,且过点 . 2(1) 求椭圆 E 的方程; (2) 若过点(-1,0) 的任意直线与椭圆 E 相交于 A ,B 两点,线段 AB 的中点为 M ,求证,恒有| AB |= 2 | CM | .19. 【解析】(I )由题意知b = 1,c= a2 .……1 分2又因为 a 2 = b 2 + c 2 解得, a = . ……3 分所以椭圆方程为 y 2 + 22= 1 . ……4 分(Ⅱ) 设过点(- 1 , 0) 直线为 x = ty - 1,设 A( x , y ) , B ( x , y )3⎧x = ty - 1 3 1122⎪ 3 2 2 由⎨ y 2 得(9 +18t )y -12ty -16 = 0 ,且> 0 .⎪ + x 2 = 1⎪⎩ 22 3 MOC NB23 2CA ⊥ CB 则⎧ 12t ⎪ y 1 + y 2 = 9 +18t 2 , ⎨ ⎪ y y = - 16 ⋯⋯6分 , ⎩⎪ 1 2 9 +18t 2又因为CA = ( x 1 -1, y 1 ) , CB = ( x 2 -1, y 2 ) ,⎛ 4 ⎫⎛ 4 ⎫ 24 16 CA ⋅ C B = (x 1 -1)(x 2 -1) + y 1 y 2 = ty 1 - ⎝ ⎪ ty - ⎭⎝ ⎪ + y 1 y 2 = (1+ t 3 ⎭ )y 1 y 2 - t ( y 1 + y 2 ) + 3 9 = (1+ t 2 ) -16 - 4t ⋅12t + 16 = 0 ,……10 分 9 +18t 2 所以 .3 9 +18t 2 9因为线段 AB 的中点为M ,所以| AB |= 2 | CM |.……12 分20.(12)水污染现状与工业废水排放密切相关,某工厂深人贯彻科学发展观,努力提高污水收集处理水平,其污水处理程序如下:原始污水必先经过 A 系统处理,处理后的污水(A 级水)达到环保标准(简称达标)的概率为 p (0<p <1).经化验检测,若确认达标便可直接排放;若不达标则必须进行 B 系统处理后直接排放.某厂现有4 个标准水量的A 级水池,分别取样、检测,多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验,混合样本中只要有样本不达标,则混合样本的化验结果必不达标,若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放 现有以下四种方案: 方案一:逐个化验;方案二:平均分成两组化验;方案三;三个样本混在一起化验,剩下的一个单独化验; 方案四:四个样本混在一起化验.化验次数的期望值越小,则方案越"优".(1) 若 p = 2 2,求 2 个 A 级水样本混合化验结果不达标的概率;3 (2) ①若 p = 求 p 的取值范围.,现有 4 个 A 级水样本需要化验,请问:方案一、二、四中哪个最“优"?②若“方案三”比“方案四"更“优”, 20. 【解析】(I)该混合样本达标的概率是(2 2 )2 = 8,……2 分 3 9 所以根据对立事件原理,不达标的概率为1- 8 = 1.……4 分9 9(II)(i )方案一:逐个检测,检测次数为 4.8 1 方案二:由(1)知,每组两个样本检测时,若达标则检测次数为 1,概率为 ;若不达标则检测次数为 3,概率为 .99故方案二的检测次数记为 ξ2,ξ2 的可能取值为 2,4,6. 其分布列如下,22 4 6p64 8116 81 1 812 2334max x 可求得方案二的期望为 E () = 2 ⨯64 + 4 ⨯ 16 + 6 ⨯ 1= 198 =22 281 81 81 81 9方案四:混在一起检测,记检测次数为 ξ4,ξ4 可取 1,5.其分布列如下,1 564 81 17 81可求得方案四的期望为 E ( ) = 1⨯ 64 + 5⨯ 17 = 149.4 81 81 81比较可得 E (4 ) < E (2 ) < 4 ,故选择方案四最“优”.……9 分(ii)方案三:设化验次数为3 ,3 可取 2,5.51-E () = 2 p 3 + 5(1- p 3 ) = 5 - 3 p 3 ;方案四:设化验次数为4 ,4 可取1, 551-E () = p 4 + 5(1- p 4 ) = 5 - 4 p 4 ;由题意得 E () < E () ⇔ 5 - 3 p 3< 5 - 4 p 4⇔ p < 3.344故当0 < p < 3时,方案三比方案四更“优”.……12 分421.(12 分)已知函数 f (x ) = x - ln x - e.x(1) 求 f (x ) 的最大值;(2) 若 f (x ) + (x + 1)e x - bx ≥ 1恒成立,求实数 b 的取值范围.x 21.【解析】(I) f (x ) = - - e x,定义域(0, +∞)x ln x x 1 e x (x -1) (x -1)(x - e x)f '(x ) = 1- - =, x x 2 x 2由e x≥ x +1 > x , f (x ) 在(0,1] 增,在(1, +∞) 减, f (x ) = f (1) = 1- e ……4 分,0 0 0 0 0(II) f ( x ) + ( x + 1 )e x x- bx ≥ 1 ⇔ - l n x + x - e x + x e x+ e x x - b x ≥ 1 ⇔ -ln x + x + x e x - bx - 1 ≥ 0 ⇔ x e x - ln x - 1 + x ≥ b ⇔ x x e x- l n x -1+ x ( x )min ≥ b , ……6 分x e x- ln x -1+ x 'x 2e x + ln x令 (x ) =,(x ) = x x令h (x ) = x 2e x + ln x , h (x ) 在(0, +∞) 单调递增, x → 0, h (x ) → -∞ , h (1) = e > 0h (x ) 在(0,1) 存在零点 x ,即 h (x ) = x 2e x 0+ ln x = 0ln x 1ln 1 x 2e x 0 + ln x = 0 ⇔ x e x 0 = - 0 = (ln )(e x 0 ) ……9 分 0 0 0x 0 x 0由于 y = xe x在(0, +∞) 单调递增,故 x = ln 1 x 0 = -ln x , 即e x 0= 1 x 0x e x 0 - ln x -1+ x 1+ x -1+ x (x ) 在(0, x ) 减,在(x , +∞) 增,(x ) = 0 0 0 = 0 0 = 2 0所以b ≤ 2 .……12 分minx 0 x 00 x。
2020届高中毕业年级第一次质量预测地理试题卷本试卷分选择题和非选择题两部分。
考试时间90分钟,满分100分。
考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。
交卷时只交答题卡。
一、选择题:本题共25小题,每小题2分,共50分o在每小题给出的四个选项中,只有一项是符合题目要求的。
暑假期间,小明前往墨尔本(37°46'S)旅行。
在墨尔本,小明发现很多建筑的布局并非严格的南北朝向,而是有一定的偏角。
图1为墨尔本某街道上两栋方形大楼的俯视图。
据此完成1~2题。
1.建筑物的布局方位会影响墙面的采光条件。
小明旅行期间,全天都不能采光的墙面是A.大楼甲的①墙面B.大楼甲的②墙面C.大楼乙的③墙面D.大楼乙的④墙面2.为使大楼乙的①墙面全年每天均有采光机会,墙面与街道的夹角α最小可能是A. 14°B.32°C.45°D.59°图2为亚洲部分地区11月17日某时段三个不同时刻海平面气压分布图(单位:百帕)。
据此完成3~5题。
3.①时刻,M地盛行A.东南风B.东北风C.西南风D.西北风4.该时段,图示区域依次出现的气压场分布形势为A.①②③B.③②①C.②①③ D.②③①5.该时段,P地经历的天气过程最可能是A.气温先上升后下降B.气压持续升高C.由阴雨转为晴朗D.持续性雨雪天气不同沉积环境会形成不同的沉积岩。
图3为常见沉积岩与沉积环境对应关系示意图,图4为我国某山局地岩层垂直剖面示意图。
据此完成6~8题。
6.砾岩由砾石沉积而成。
据图3推断其沉积环境为A.陆地B.滨海C.浅海D.深海7.图4所示岩层剖面表明该地在地质历史时期经历了A.海侵过程B.海退过程C.先海侵后海退D.先海退后海侵8.在地质演化过程中,形成界面M的地质作用最可能是A.挤压B.断裂C.侵蚀D.变质2019年4月,一张飘絮预警图(图5)在朋友圈广为传播。
杨树适应性强,枝叶繁茂,绿化中应用较为广泛。
每年四五月份,杨树新叶吐露前后,产生的杨絮也会在各地如约而至,让人不胜其扰。
据此完成9~11题。
9.杨树所属的植被类型为A.亚热带常绿阔叶林B.亚热带常绿硬叶林C.温带落叶阔叶林D.亚寒带针叶林10.导致我国北方地区进入飘絮季时间差异的主导因素是A.光照B.热量C.水分D.昼夜温差11.与南方相比,华北地区春季飞絮问题严重的原因是A.风力小,不易扩散B.湿度小,不易沉降C.水域广,不易打扫D.温度低,不易产絮丁坝是一种坝基与大堤相连,坝头伸向水流的拦水建筑物,在平面上与岸线构成丁字形。
根据丁坝与水流方向的交角分为上挑、下挑和正挑三种丁坝(图6),不同种类的丁坝对水流的影响存在差异。
图7为某弯曲河段遥感影像图。
读图完成12~14题。
12.丁坝的主要作用是A.促进凸岸堆积B.促使河道变宽C.减缓河道中心流速D.减轻凹岸侵蚀13.根据图7中丁坝位置可判断该河段侵蚀最严重的部位是A.①B.②C.③D.④14.该河段A.河流自西向东流,丁坝为上挑丁坝B.河流自西向东流,丁坝为下挑丁坝C.河流自东向西流,丁坝为正挑丁坝D.河流自东向西流,丁坝为上挑丁坝图8为2019年10月1 9日我国某地区降水预报示意图。
据此完成15~17题。
15.导致该地区降水形式差异的主要因素是A.纬度位置B.海陆位置C.地形D.洋流16.图中山脉北侧河流的主要补给水源是A.大气降水B.高山冰雪融水C.季节性积雪融水D.地下水17.甲、乙两地发展农业的限制性因素分别是A.热量、水源B.水源、热量C.热量、土壤D.土壤、水源婴儿潮是一定时期内人口出生率大幅度提升的现象,其形成受战争、政策、经济等多方面因素影响。
图9为2015年德国和我国的人口金字塔。
据此完成18~20题。
18.与我国相比,德国A.老年人口更多C.劳动力充足C.新生儿性别差异明显D.婴儿潮传递明显衰减19. 1985~1995年,我国出现婴儿潮的主要原因是A.战争结束之后社会休养生息B.生活水平显著降低C.上一代婴儿潮进人生育高峰D.国家政策鼓励生育20.目前,1985~1995年出现的婴儿潮对我国产生的影响主要是A.增加社会养老压力B.加剧中学教育资源紧张C.提供丰富劳动力D.缓解就业竞争压力地下植物工厂是在封闭或者半封闭环境中,借助人工光照,使用营养液培育绿叶蔬菜的场所。
日本幕张地下植物工厂利用靠近东京的城市地下综合管廊种植蔬菜,该地下综合管廊闲置已久,温度常年保持在18~22℃。
植物工厂建成后,从菜苗盒送入地下到长好蔬菜送至地面,实现全程自动化。
据此完成21~22题。
21.城市出现地下植物工厂的主要原因是城市A.耕地资源相对缺乏B.综合管廊普遍闲置C.市民空余时间较多D.地下农业经验丰富22.与传统蔬菜种植方式相比,地下植物工厂蔬菜种植①距离市场近,储运费用低②地下温度稳定,采暖降温成本低③全程自动化,劳动力成本低④技术较成熟,开发成本低A.①②③B.①②④C.①③④D.②③④近年来,部分日本企业在我国的生产工厂开始迁回本土或迁往越南等国。
据此完成23~25题。
23.越南吸引日本企业迁入的主要原因是当地A.原料丰富B.市场广阔C.劳动力廉价D.交通便利24.日本企业将生产工厂迁回本土主要得益于本国A.市场需求的增加B.劳动力数量的增加C.交通运输的发展D.生产效率的提高25.日本企业将生产工厂迁回本土表明,我国A.制造业成本降低B.消费市场扩大C.制造业崛起D.贸易壁垒减小二、非选择题:共50分。
26.(13分)阅读图文材料,完成下列要求。
桑树喜温暖湿润气候,适宜生长的温度为25~30℃。
桑蚕以桑叶为主要食料,其适养的温度为20~30℃,生长周期约1个月。
蚕丝是重要的纺织原料。
我国有悠久的种桑养蚕历史,近年来,江浙地区种桑面积和蚕丝产量日益萎缩。
2006年,我国实施“东桑西移”工程,广西充分发挥优势,积极承接蚕桑“西移”,推动桑蚕产业快速发展。
目前广西桑蚕产业存在生产产业链较短、“大而不强”的现象,且市场以国内东部沿海地区为主。
图10为我国部分桑蚕业优势区分布示意图。
高三地理试题卷第5页(共8页)(1)与江浙地区相比,分析广西发展桑蚕产业的有利气候条件。
(5分)(2)推测江浙地区桑蚕业日益萎缩的主要原因。
(3分)(3)简述发展桑蚕业对广西发展的积极影响。
(3分)(4)针对桑蚕产业存在的问题,请为广西桑蚕产业进一步发展提出合理建议。
(2分)27.(11分)阅读图文材料,完成下列要求。
卡拉博加兹湾(图11)位于里海东岸,平均深度只有10米,海湾内含盐量高达35%,是普通海水的10倍。
卡拉博加兹湾被一条长约100公里、最窄不到1公里的沙石洲与里海主体分隔,沙石洲中部有一开口,里海湖水由此流向卡拉博加兹湾。
土库曼斯坦计划修建大桥连通该开口南北两侧。
2018’年当地政府在贝克达实建成卡拉博加兹尿素厂大型工业综合体项目,当年向西班牙、意大利等国家出口浓缩氮肥超过1.2万吨,出口产品通过码头向外运输。
(1)从水循环角度分析卡拉博加兹湾海水盐度高的主要原因。
(4分)(2)分析土库曼斯坦在卡拉博加兹湾大力发展化工业的优势条件。
(4分)(3)推测修建卡拉博加兹湾大桥需要克服的困难。
(3分)28.(12分)阅读图文材料,完成下列要求。
克里特岛(图12)是希腊著名的旅游目的地,西欧和北欧地区是其重要容源地。
岛上游客数量存在显著的季节差异,导致岛内电力需求量出现明显的季节性变化。
克里特岛是希腊最大的自主供电岛屿,电网尚未与希腊大陆联网,岛上电力供应主要来自进口石油发电。
高三地理试题卷第6页(共8页)2019年11月,我国企业与希腊签署协议,将利用我国的塔式熔盐储能光热发电技术建设太阳能电站,其工作原理见图13。
项目建成后,每年可提供相当于当地电力需求10%的稳定清洁电力。
同时,中国国家电网将投资建设连接希腊大陆和克里特岛的海底电缆项目,并逐步构建南欧电力输送通道。
(1)从气候角度,推测希腊旅游旺季的季节并说明理由。
(4分)(2)说出克里特岛可开发利用的清洁能源。
(3分)(3)简述建设塔式熔盐储能光热电站对克里特岛的有利影响。
(3分)(4)分析海底电缆项目对希腊能源安全的有利作用。
(2分)29.(14分)阅读图文材料,完成下列问题。
纳米布沙漠(图14)是世界上最古老的沙漠之一,年降水量不足lOmm,这里的生物经过长期进化具备了一定的适应干旱环境能力,为人类在干旱区的开发提供了借鉴意义。
纳米布沙漠沿海多雾,早晨时这里的甲虫常在沙丘上迎风而立,甲虫壳能将空气中水汽液化,为甲虫提供生存必需的水源。
受纳米布甲虫的启发,人类发明了“空中取水灌溉系统”,实现了干旱区的低能耗、低水耗供水,其工作原理见图15。
高三地理试题卷第7页(共8页)(1)分析纳米布沙漠降水较少的主要原因。
(3分)(2)解释纳米布沙漠海岸多雾的原因。
(3分)(3)说明“空中取水灌溉系统”低能耗、低水耗的原理。
(4分)(4)你是否同意“空中取水灌溉系统”在我国西北进行大规模应用,请表明态度并解释理由(4分)高三地理试题卷第8页(共8页)2020年高中毕业年级第一次质量预测地理参考答案1.A2.B3.D4.D5.A6.A7.A8.C9.C 10.B 11.B 12.D 13.B 14.B 15.C 16.B 17.B 18.D 19.C 20.C 21.A 22.A 23.C 24.D 25.C26.(13分)(1)(5分)广西纬度较低,(1分)气温高,(1分)高温期长。
(1分)受冬季风影响小,低温冻害少。
(1分)高温期湿度高(降水较多)。
(1分)(2)(3分)江浙地区工业化、城市化发展速度快,农业用地规模减小,土地价格升高,农村人口减少,劳动力成本提高,农业产业结构调整。
(任答3点得3分)(3)(3分)利于提供就业岗位,增加就业;(1分)增加经济收入,促进经济发展;(1分)提高植被覆盖率,改善生态环境。
(1分)(4)(2分)坚持桑蚕业产业化经营,延长产业链,提高产品附加值;加强桑蚕养殖及茧丝产品的科研投入;打造品牌,提高质量,拓宽国内外市场。
(任答2点得2分)27.(11分)(1)(4分)深居内陆,距海较远,降水少;缺少河流注入;里海湖水流向卡拉博加兹湾,带来大量盐分;卡拉博加兹湾水域较为封闭,水体交换不畅;卡拉博加兹湾水域浅,盐度升高快。
(任答4点得4分)(2)(4分)湖水盐度高,为化工业发展提供丰富的原料;油气资源丰富,为化工业发展提供充足的能源;位于里海沿岸,水陆交通便利;国际消费市场广阔;政府政策与资金的支持。
(任答4点得4分)(3)(3分)气候干旱,水资源短缺;多风沙;温差大,不利于工程建设;海水盐度高,对桥梁耐腐蚀标准要求高;基础设施落后。
(任答3点得3分)28.(12分)(1)(4分)夏季。