2010年广东高考热点题型聚焦(三)《立体几何》

2010年高考数学试题分类汇编——立体几何（2010浙江理数）（6）设，是两条不同的直线，是一个平面，则下列命题正确的是 （A ）若，，则 （B ）若，，则 （C ）若，，则 （D ）若，，则解析：选B ，可对选项进行逐个检查。

本题主要考察了立体几何中线面之间的位置关系及其中的公理和判定定理，也蕴含了对定理公理综合运用能力的考察，属中档题（2010全国卷2理数）（11）与正方体的三条棱、、所在直线的距离相等的点（A ）有且只有1个 （B ）有且只有2个 （C ）有且只有3个 （D ）有无数个 【答案】D 【解析】直线上取一点，分别作垂直于于则分别作，垂足分别为M ，N ，Q ，连PM ，PN ，PQ ，由三垂线定理可得，PN ⊥PM ⊥；PQ ⊥AB ，由于正方体中各个表面、对等角全等，所以，∴PM=PN=PQ ，即P 到三条棱AB 、CC 1、A 1D 1.所在直线的距离相等所以有无穷多点满足条件，故选D.（2010全国卷2理数）（9）已知正四棱锥中，，那么当该棱锥的体积最大时，它的高为（A ）1 （B（C ）2 （D ）3 【答案】C【命题意图】本试题主要考察椎体的体积，考察告辞函数的最值问题.【解析】设底面边长为a ，则高所以体积，l m αl m ⊥m α⊂l α⊥l α⊥l m //m α⊥l α//m α⊂l m //l α//m α//l m //1111ABCD A BC D -AB 1CC 11A D S ABCD -SA =设，则，当y 取最值时，，解得a=0或a=4时，体积最大，此时，故选C.（2010陕西文数） 8.若某空间几何体的三视图如图所示，则该几何体的体积是 [B]（A ）2 （B ）1（C ）（D ）解析：本题考查立体图形三视图及体积公式 如图，该立体图形为直三棱柱所以其体积为（2010辽宁文数）（11）已知是球表面上的点，，，，，则球的表面积等于（A ）4 （B ）3 （C ）2 （D ）解析：选A.由已知，球的直径为，表面积为（2010辽宁理数）(12) (12)有四根长都为2的直铁条，若再选两根长都为a 的直铁条，使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架，则a 的取值范围是(A)（）(B)（1,））(D) （0,）【答案】A【命题立意】本题考查了学生的空间想象能力以及灵活运用知识解决数学问题的能力。

2010年高考立体几何专题复习岱山中学 孙珊瑚 鲁纪伟高考立体几何试题一般有选择、填空题, 解答题,考查的知识点在20个以内. 选择填空题考核立几中的计算型问题, 而解答题着重考查立几中的逻辑推理型问题, 当然, 二者均应以正确的空间想象为前提. 随着新的课程改革的进一步实施,立体几何考题正朝着“多一点思考,少一点计算”的发展.从历年的考题变化看, 以简单几何体为载体的线面位置关系的论证,角与距离的探求是常考常新的热门话题. 一、知识整合1．有关平行与垂直(线线、线面及面面)的问题，是在解决立体几何问题的过程中，大量的、反复遇到的，而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容，因此在主体几何的总复习中，首先应从解决“平行与垂直”的有关问题着手，通过较为基本问题，熟悉公理、定理的内容和功能，通过对问题的分析与概括，掌握立体几何中解决问题的规律——充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想，以提高逻辑思维能力和空间想象能力． 2.判定两个平面平行的方法：（1）根据定义——证明两平面没有公共点；（2）判定定理——证明一个平面内的两条相交直线都平行于另一个平面； （3）证明两平面同垂直于一条直线。

3.两个平面平行的主要性质： ⑴由定义知：“两平行平面没有公共点”。

⑵由定义推得：“两个平面平行，其中一个平面内的直线必平行于另一个平面。

⑶两个平面平行的性质定理：“如果两个平行平面同时和第三个平面相交，那么它们的交线平行”。

⑷一条直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

⑸夹在两个平行平面间的平行线段相等。

⑹经过平面外一点只有一个平面和已知平面平行。

以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”，但在解题过程中均可直接作为性质定理引用。

4.空间的角和距离是空间图形中最基本的数量关系，空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等．解这类问题的基本思路是把空间问题转化为平面问题去解决．空间的角，是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念，由它们的定义，可得其取值范围，如两异面直线所成的角θ∈(0，2π]，直线与平面所成的角θ∈0,2π⎡⎤⎢⎥⎣⎦，二面角的大小，可用它们的平面角来度量，其平面角θ∈[0，π]．对于空间角的计算，总是通过一定的手段将其转化为一个平面内的角，并把它置于一个平面图形，而且是一个三角形的内角来解决，而这种转化就是利用直线与平面的平行与垂直来实现的，因此求这些角的过程也是直线、平面的平行与垂直的重要应用．通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力．如求异面直线所成的角常用平移法（转化为相交直线）与向量法；求直线与平面所成的角常利用射影转化为相交直线所成的角；而求二面角α－l －β的平面角（记作θ）通常有以下几种方法：(1) 根据定义；(2) 过棱l 上任一点O 作棱l 的垂面γ，设γ∩α＝OA ，γ∩β＝OB ，则∠AOB ＝θ ；(3) 利用三垂线定理或逆定理，过一个半平面α内一点A ，分别作另一个平面β的垂线AB (垂足为B ),或棱l 的垂线AC (垂足为C )，连结AC ，则∠ACB ＝θ 或∠ACB ＝π－θ；(4) 设A 为平面α外任一点，AB ⊥α，垂足为B ，AC ⊥β，垂足为C ，则∠BAC ＝θ或∠BAC ＝π－θ；(5) 利用面积射影定理，设平面α内的平面图形F 的面积为S ，F 在平面β内的射影图形的面积为S '，则cos θ＝SS '.5.空间的距离问题，主要是求空间两点之间、点到直线、点到平面、两条异面直线之间（限于给出公垂线段的）、平面和它的平行直线、以及两个平行平面之间的距离．求距离的一般方法和步骤是：一作——作出表示距离的线段；二证——证明它就是所要求的距离；三算——计算其值．此外，我们还常用体积法求点到平面的距离．6.棱柱的概念和性质⑴理解并掌握棱柱的定义及相关概念是学好这部分知识的关键，要明确“棱柱 直棱柱 正棱柱”这一系列中各类几何体的内在联系和区别。

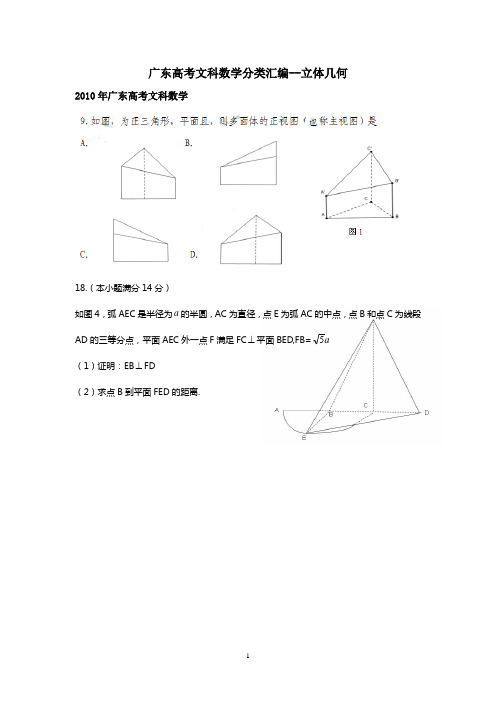
广东高考文科数学分类汇编--立体几何2010年广东高考文科数学18.（本小题满分14分）如图4，弧AEC是半径为a的半圆，AC为直径，点E为弧AC的中点，点B和点C为线段AD 的三等分点，平面AEC外一点F满足FC⊥平面BED,FB=a5（1）证明：EB⊥FD（2）求点B到平面FED的距离.2009年广东高考文科数学6.给定下列四个命题：①若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；②若一个平面经过另一个平面的垂线，那么这两个平面相互垂直；③垂直于同一直线的两条直线相互平行；④若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直. 其中，为真命题的是A．①和② B．②和③ C．③和④ D．②和④17.（本小题满分13分）某高速公路收费站入口处的安全标识墩如图4所示,墩的上半部分是正四棱锥P－EFGH,下半部分是长方体ABCD－EFGH.图5、图6分别是该标识墩的正(主)视图和俯视图.（1）请画出该安全标识墩的侧(左)视图（2）求该安全标识墩的体积（3）证明:直线BD 平面PEG2008年广东高考文科数学7．将正三棱柱截去三个角（如图1所示，A B C ，，分别是GHI △三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ ）18．（本小题满分14分）如图5所示，四棱锥P ABCD -的底面ABCD 是半径为R 的圆的内接四边形，其中B D 是圆的直径，60ABD ∠=，45BD C ∠=，ADP BAD △∽△． （1）求线段P D 的长；（2）若11PC R =，求三棱锥P ABC -的体积．E F DIA H GBC EF D AB C侧视 图1图2 BEA ．BEB ． BEC ．BED ．CPAB图5D2007年广东高考文科数学6．若l m n ，，是互不相同的空间直线，αβ，是不重合的平面，则下列命题中为真命题的是（ ）Ａ．若l n αβαβ⊂⊂，，∥，则l n ∥ Ｂ．若l αβα⊥⊂，，则l β⊥ Ｃ．若l n m n ⊥⊥，，则l m ∥Ｄ．若l l αβ⊥，∥，则αβ⊥17．（本小题满分12分）已知某几何体的俯视图是如图5所示的矩形，正视图（或称主视图）是一个底边长为8，高为4的等腰三角形，侧视图（或称左视图）是一个底边长为6，高为4的等腰三角形． （1）求该几何体的体积V ； （2）求该几何体的侧面积S ．8图562010年广东高考文科数学9.D10. 18.（1）证明： 点E 为弧AC 的中点2009年广东高考文科数学6.D7. 17.【解析】(1)侧视图同正视图,如右图所示.（２）该安全标识墩的体积为：P EFGH ABCD EFGH V V V --== 221406040203200032000640003=⨯⨯+⨯=+=()2cm（３）如图,连结EG,HF 及 BD ，EG 与HF 相交于O,连结PO.由正四棱锥的性质可知,PO ⊥平面EFGH , PO HF ∴⊥ 又EG HF ⊥ H F ∴⊥平面PEG 又B D H F P B D ∴⊥平面PEG ； 2008年广东高考文科数学7．A 18．解：（1）BD 是圆的直径ADP BAD △∽△90BAD ∴∠=，又ADP BAD △∽△，A D D PB AA D∴=，22234(sin 60)431(sin 30)22R ADBD D P R BABD R ⨯====⨯；（2）在Rt BCD △中，cos 452CD BD R ==2222229211PD C D R R R PC +=+==PD CD ∴⊥，又90P D A ∠=P D ∴⊥底面ABCD211321231sin(6045)22222224ABC S AB BC R R R ⎛⎫+=+=⨯+⨯= ⎪ ⎪⎝⎭△三棱锥P ABC -的体积为2311313133344P ABC ABC V S PD R R R -++===△2007年广东高考文科数学6．D17解: 由已知可得该几何体是一个底面为矩形，高为4，顶点在底面的射影是矩形中心的四棱锥V -ABCD ；(1) ()1864643V =⨯⨯⨯=(2) 该四棱锥有两个侧面VAD 、VBC 是全等的等腰三角形，且BC 边上的高为 22184422h ⎛⎫=+= ⎪⎝⎭， 另两个侧面V AB. VCD 也是全等的等腰三角形，AB 边上的高为 2226452h ⎛⎫=+= ⎪⎝⎭因此 112(64285)4024222S =⨯⨯+⨯⨯=+C PA B 图5D。

〔内部资料，请勿外传〕2010年广东高考热点题型聚焦（四）《解析几何》市教研室广东课标高考三年来风格特点（1）表现形式上是多曲线综合；（2）圆锥曲线重在定义、标准方程和几何性质；（3 ）核心是直线和圆的位置关系；（4）方法上强调：数形结合的思想方法、方程思想、待定系数法；（5）能力上要求：图形探究能力、逆向探究能力、运算求解能力、阅读理解能力参考题目：1.设动点P（x,y）（y 一0）到定点F （0,1）的距离比它到x轴的距离大1,记点P的轨迹为曲线C.（1）求点P的轨迹方程；（2）设圆M过A（0, 2），且圆心M在曲线C 上, EG是圆M在x轴上截得的弦，试探究当M运动时，弦长|EG是否为定值？为什么？解：（1）依题意知，动点P到定点F （0,1）的距离等于P到直线的距离，曲线C是以原点为顶点，F （0,1）为焦点的抛物线…P 11 …p = 22•••曲线C方程是x2=4y .......... 4分（2）解法1:过点M作X轴的垂线，垂足为D,则点D平分EG,设圆心为M（a, b），则2 2 22, 2 2 2 ,1 1 2| DG | =| MA | -1 MD | 二a (b -2) -b 二a -4b 4 a = 4b.q DG | = 2,| EG | = 4 ,即当M运动时，弦长EG为定值4.解法2：设圆的圆心为M（a,b）,•••圆M 过A (0, 2),•圆的方程为(x-a)2• (y -b)2=a2• (b -2)2令 y = 0 得：x 2 -2ax 4b -4 = 0 设圆与x 轴的两交点分别为(x 1,0) , (x 2,0)• % _x 2 仝4a 2「16b 16又•••点M (a,b)在抛物线x 2•••当M 运动时，弦长EG 为定值4 〔方法 2：v x-i x 2 = 2a , x-i x 2 =4b-4(X i -X 2)2 =(X i X 2)2 -4X 1 X 2 =(2a)2 -4(4b -4) =4a 2 -16b 16又•••点 M(a,b)在抛物线 x 2 =4y 上，• a 2=4b , •••当M 运动时，弦长EG 为定值4〕们的一个公共点.(1) 求G,C 2的方程； (2)过点 F 2且互相垂直的直线h,l 2与圆M| AB| ' |CD |的最大值，并求此时直线 l 1的方程.解：(1 )点 N('、2,1)是双曲线 G :x 2 - y 2 二 m(m • 0)上的点，.m=C ，2)2-1=1.•••双曲线 G :x 2 -y 2 =1，从而尺(-、.2,0), F 2C 、2,0) ,• a 2 b 2，且 a 2 -b 2 =2 .① 又点NG ，2,1)在椭圆上，则三2=1②a 2b 22 22 .已知双曲线C 1 :x - y 二m(m 0)与椭圆2 X C 2 二.a b2y2二1有公共焦点F 1,F 2，点N(习)是它方法1 ：不妨设x 1x 2，由求根公式得2a4a 2 匚 1613一16 X1 -2 ，X 22a - .'4a 2匚 1613一1610分X T —x 2 ==4，即 EG13 分14分(捲 _x 2)2 = 16:x 2 (y 1)2 = a 2分别相交于点 A,B 和C,D ，求2 2 由①②得a2 =4,b2 =2，所以椭圆的方程为—- 1.4 2(2)设圆M的圆心为M , h、丨2被圆M所截得弦的中点分别为2 2 2AECF是矩形，所以ME MF -F2M -3,即4® E,F，弦长分别为d1,d2，因为四边形” 2 "L _从而d1 d^ -.2 ■, d12d；=2.10，等号成立=二d?=3，化简得d12 d| -20(I )求动圆圆心的轨迹C 的方程;(II )若A 、B 是轨迹C 上的两不同动点，且 AN =^NB .分别以A 、B 为切点作轨迹 C 的切线,4 赳5 时，© d 2)max =2.10 ,即l i 、12被圆C 所截得弦长之和的最大值为2.10 .3•如图，F 是椭圆的右焦点，以 F 为圆心的圆过原点 O 和椭圆的右顶点，设 P 是椭圆的动点, 焦点距离之和等于 4.(I)求椭圆和圆的标准方程；P 到两(n)设直线I 的方程为X = 4,PM _ I ,垂足为M ,是否存在点使得 FPM 为等腰三角形？若存在，求出点 P 的坐标；若不存在，说 明理由•解：(I)由已知可得non2a =4,a =2c = a=2,c=1,b 二a -c =3•••椭圆的标准方程为22x y 221，圆的标准方程为(x-1) - y -143(n)设 P(x, y),则 M(4, y),F(1,0)•/ P(x, y)在椭圆上•22x y —21= y43=3 -3x 24= (x-1)2 3-3X 2 42 2 23 2| PM | =|x-4| = 9 y =12- —x4|PF|2= (X -1)2y 2冷(x —4)2• I PF I 二丄 I PM |,|PF 鬥PM |,2(1)若 | PF 冃 FM | 则 | PF | | FM 卜 PM |这与三角形两边之和大于第三边矛盾23 2 4(2)若 | PM |=| FM |,则(x -4) =12 x ,解得 x = 4或 x = — 4 7• y = 3 .15 • P(3,_3 .15)7 7 74 ••• |x| 乞 2 •••7综上可得存在两点e ,3严),& 315)使得△ PFM 为等腰三角形. 4.已知动圆过定点 N (0,2)，且与定直线y = -2相切.设其交点Q ,证明NQ AB 为定值.解：（I ）依题意，圆心的轨迹是以 N （0,2）为焦点，L: y - _2为准线的抛物线上因为抛物线焦点到准线距离等于 4 所以圆心的轨迹是 x 2=8y■ X1 — ' X211故 22i 2 - y1 =■ (y 2-2)且有 X 1X 2 - - 'X ； =_8，y 2 二-16.2,求导得y 丄1 x.所以过抛物线上 A 、B 两点的切线方程分别是41 1yxdx — xj y 1,y X 2(x —X 2) y ?, 442 1 2 1 1 2 即y^-^x x , y x 2x x 2. 4 8 4 8将（1）式两边平方并把 2 X 1—8 y i , X 2 — 8 y 2 ^代入彳得 y i =' y2(3)解（2）、（ 3）式得力=2显二， （II ）解法一：由已知 N(0,2),设A (心y) B(X 2,y 2)由ANV NB,即得(-心2 - yj Y.(X 2,y 2 -2),、、 1抛物线方程为y x8 解出两条切线的交点Q的坐标为（T 竽円宁,-2)111 x2 1 2 所以 NO AB =(— - ,-4)(X 2 - X 1,y 1 - y 2)(x ； 2 2X i21 2 -X 1)-4(齐所以NQ ・AB 为定值，其值为0. 13分解法二： 由已知N （0，2）设A （N ，yJ,B （X 2，y 2）由AN = • NB 知A,N,B 三点共线,；直线AB 与x 轴不垂直，设AB : ^kx 2.y 二 kx 2,由 1 2 可得 x 2-8kx T6 = 0 , x 1x^ -16厂8X.后面解法和解法一相同知圆O : x 2 y 2 =8交x 轴于A,B 两点，曲线C 是以AB 为长轴，直线：x =-4为准线的 已过定点E ，并求出点E 的坐标;C 交于G,H 两点，且EG =3HE ，试求此时弦PQ 的长.2解：（I ）设椭圆的标准方程为 召亠当=1* b 0，则:a ba=次2，故b = 2,所以椭圆的标准方程为I c = 2过定点E -2,0 。

专题09立体几何历年考题细目表历年高考真题汇编1．【2018年新课标1文科05】已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）A．12πB．12πC．8πD．10π【解答】解:设圆柱的底面直径为2R,则高为2R,圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，可得:4R2＝8，解得R，则该圆柱的表面积为：12π．故选：B．2．【2018年新课标1文科09】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中,最短路径的长度为（）A．2B．2C．3 D．2【解答】解：由题意可知几何体是圆柱，底面周长16，高为:2,直观图以及侧面展开图如图：圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上,从M到N的路径中,最短路径的长度：2．故选：B．3．【2018年新课标1文科10】在长方体ABCD﹣A1B1C1D1中，AB ＝BC＝2，AC1与平面BB1C1C所成的角为30°，则该长方体的体积为（）A．8 B．6C．8D．8【解答】解：长方体ABCD﹣A1B1C1D1中，AB＝BC＝2，AC1与平面BB1C1C所成的角为30°，即∠AC1B＝30°，可得BC12．可得BB12．所以该长方体的体积为:28．故选：C．4．【2017年新课标1文科06】如图，在下列四个正方体中，A,B为正方体的两个顶点，M，N,Q为所在棱的中点,则在这四个正方体中，直线AB与平面MNQ不平行的是( ）A．B．C．D．【解答】解：对于选项B，由于AB∥MQ，结合线面平行判定定理可知B不满足题意；对于选项C,由于AB∥MQ，结合线面平行判定定理可知C不满足题意；对于选项D,由于AB∥NQ，结合线面平行判定定理可知D不满足题意；所以选项A满足题意，故选：A．5．【2016年新课标1文科07】如图，某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径．若该几何体的体积是，则它的表面积是（)A．17πB．18πC．20πD．28π【解答】解：由题意可知三视图复原的几何体是一个球去掉后的几何体，如图：可得:，R＝2．它的表面积是:4π•2217π．故选:A．6．【2016年新课标1文科11】平面α过正方体ABCD﹣A1B1C1D1的顶点A，α∥平面CB1D1，α∩平面ABCD＝m,α∩平面ABB1A1＝n，则m、n所成角的正弦值为（）A．B．C．D．【解答】解:如图:α∥平面CB1D1，α∩平面ABCD＝m,α∩平面ABA1B1＝n，可知：n∥CD1，m∥B1D1，∵△CB1D1是正三角形．m、n所成角就是∠CD1B1＝60°．则m、n所成角的正弦值为：．故选：A．7．【2015年新课标1文科06】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题：“今有委米依垣内角，下周八尺,高五尺．问:积及为米几何？"其意思为：“在屋内墙角处堆放米（如图,米堆为一个圆锥的四分之一），米堆底部的弧长为8尺，米堆的高为5尺,问米堆的体积和堆放的米各为多少？”已知1斛米的体积约为1。

2010年高考数学考点解析：立体几何的题型与解法一、考试内容：直线、平面、简单几何体考试内容平面及其基本性质，平面图形直观图的画法。

平行直线，对应边分别平行的角，异面直线所成的角，异面直线的公垂线，异面直线的距离。

直线和平面平行的判定与性质，直线和平面垂直的判定与性质，点到平面的距离，斜线在平面上的射影，直线和平面所成的角，三垂线定理及其逆定理。

平行平面的判定与性质，平行平面间的距离，二面角及其平面角，两个平面垂直的判定与性质。

多面体、棱柱、棱锥、正多面体、球。

二、考试要求（1）掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图，能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想象它们的位置关系。

（2）了解空两条直线的位置关系，掌握两条直线平行与垂直的判定定理和性质定理，掌握两条直线所成的角和距离的概念（对于异面直线的距离，只要求会计算已给出公垂线时的距离）。

（3）了解空间直线和平面的位置关系，掌握直线和平面平行的判定定理和性质定理，理解直线和平面垂直的判定定理和性质定理，掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念，了解三垂线定理及其逆定理。

（4）了解平面与平面的位置关系，掌握两个平面平行的判定定理和性质定理。

掌握二面角、二面角的平面角、两个平面间的距离的概念，掌握两个平面垂直的判定定理和性质定理。

（5）会用反证法证明简单的问题。

（6）了解多面体的概念，了解凸多面体的概念。

（7）了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图。

（8）了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图。

（9）了解正多面体的概念，了解多面体的欧拉公式。

（10）了解球的概念，掌握球的性质，掌握球的表面积、体积公式。

三、复习目标1．在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的基础上，研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用；在有关问题的解决过程中，进一步了解和掌握相关公理、定理的内容和功能，并探索立体几何中论证问题的规律；在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用．2．在掌握空间角(两条异面直线所成的角，平面的斜线与平面所成的角及二面角)概念的基础上，掌握它们的求法(其基本方法是分别作出这些角，并将它们置于某个三角形内通过计算求出它们的大小)；在解决有关空间角的问题的过程中，进一步巩固关于直线和平面的平行垂直的性质与判定的应用，掌握作平行线(面)和垂直线(面)的技能；通过有关空间角的问题的解决，进一步提高学生的空间想象能力、逻辑推理能力及运算能力．3．通过复习，使学生更好地掌握多面体与旋转体的有关概念、性质，并能够灵活运用到解题过程中．通过教学使学生掌握基本的立体几何解题方法和常用解题技巧，发掘不同问题之间的内在联系，提高解题能力．4．在学生解答问题的过程中，注意培养他们的语言表述能力和“说话要有根据”的逻辑思维的习惯、提高思维品质．使学生掌握化归思想，特别是将立体几何问题转化为平面几何问题的思想意识和方法，并提高空间想象能力、推理能力和计算能力．5．使学生更好地理解多面体与旋转体的体积及其计算方法，能够熟练地使用分割与补形求体积，提高空间想象能力、推理能力和计算能力．。