《大学物理实验》准稳态法测量不良导体的导热系数和比热

准稳态法测不良导体的导热系数和比热预习报告实验目的1. 了解准稳态法测量不良导体的导热系数和比热的原理，并通过快速测量学习掌握该方法；2. 掌握使用温差电偶测量温度的方法。

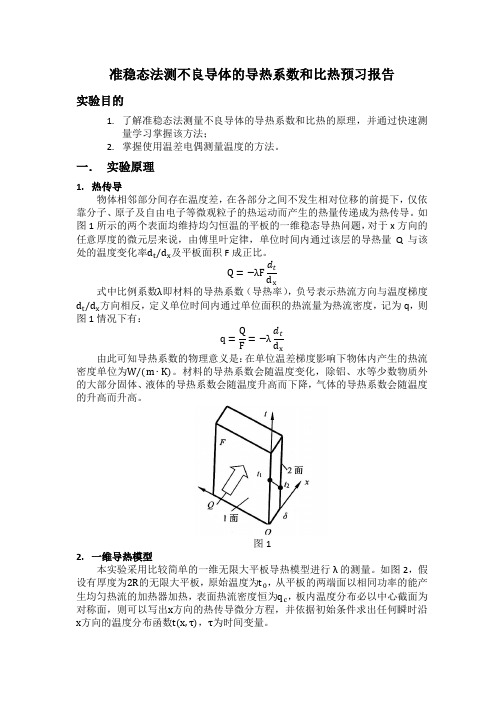
一． 实验原理1. 热传导物体相邻部分间存在温度差，在各部分之间不发生相对位移的前提下，仅依靠分子、原子及自由电子等微观粒子的热运动而产生的热量传递成为热传导。

如图1所示的两个表面均维持均匀恒温的平板的一维稳态导热问题，对于x 方向的任意厚度的微元层来说，由傅里叶定律，单位时间内通过该层的导热量Q 与该处的温度变化率d t /d x 及平板面积F 成正比。

Q =−λF d tx式中比例系数λ即材料的导热系数（导热率），负号表示热流方向与温度梯度d t /d x 方向相反，定义单位时间内通过单位面积的热流量为热流密度，记为q ，则图1情况下有：q =Q =−λd t x由此可知导热系数的物理意义是：在单位温差梯度影响下物体内产生的热流密度单位为W/(m ∙K)。

材料的导热系数会随温度变化，除铝、水等少数物质外的大部分固体、液体的导热系数会随温度升高而下降，气体的导热系数会随温度的升高而升高。

图12. 一维导热模型本实验采用比较简单的一维无限大平板导热模型进行λ的测量。

如图2，假设有厚度为2R 的无限大平板，原始温度为t 0，从平板的两端面以相同功率的能产生均匀热流的加热器加热，表面热流密度恒为q c ，板内温度分布必以中心截面为对称面，则可以写出x 方向的热传导微分方程，并依据初始条件求出任何瞬时沿x 方向的温度分布函数t(x,τ)，τ为时间变量。

3.热传导方程及求解∂t(x,τ)∂τ=a∂2t(x,τ)∂x(0<x<R,τ>0) （式4）初始条件t(x,τ)τ=0=t0（式5）边界条件q c=λ∂t(x,τ)∂x x=R（式6）λ∂t(x,τ)∂x x=0=0（式7）式中a=λ/cρ为热扩散率（或称热扩散系数），单位为m2/s，c为比热容，单位为J/(kg∙K)，ρ为密度，单位为kg/m3。

1实验目的1.了解准稳态法测量不良导体的导热系数和比热的原理，并通过快速测量学习掌握该方法。

2.掌握使用温差电偶测量温度的方法。

2实验数据记录与处理2.1数字万用表的练习使用实验中的交流信号是正弦波，有效值设为1V，频率设为1000Hz。

测量对象测量值量程精度不确定度完整测量结果交流电压有效值0.98058V2V0.2+0.050.00296V(0.98058±0.00296)F 交流信号频率999.96Hz20Hz-2kHz0.01+0.0030.16Hz(999.96±0.16)Hz电阻10.9289kΩ20kΩ0.020+0.0040.0023kΩ(10.9289±0.0023)kΩ电容1.046µF2µF1+0.50.020µF(1.046±0.020)µF二极管正向导通电压0.5826V0-2V0.06+0.0200.0007V(0.5829±0.0007)V表1:数字万用表的练习使用数据记录以电阻测量值为例计算，读数为10.9289kΩ，量程为20kΩ，精度为0.020+0.004，则∆R=0.020%×10.9289+0.004%×20.0000=0.0023kΩ最终得到R=(10.9289±0.0023)kΩ，其他测量值的不确定度计算过程类似。

3测导热系数和比热容3.1实验前的准备实验样品为有机玻璃，长宽L=W=90mm，厚度R=10mm，密度ρ=1196kgm3。

室温t0=19.9◦C。

中心面热电偶电阻为3.296Ω，加热面热电偶电阻为3.124Ω，冷端热电偶电阻为4.136Ω，并联而成的加热薄膜电阻r/2=55.071Ω。

加热前，测得加热面和中心面的温差U1(t2,t1)=4µV<10µV，故不必进行零位修正。

加热前，加热薄膜电压U前=17.9928V，∆U前=0.015%×17.9928+0.004%×20.0000=0.0035V；加热后，加热薄膜电压U后=17.9932V，∆U后=0.015%×17.9932+0.004%×20.0000=0.0035V。

准稳态法测量比热和导热系数
比热和导热系数是材料物理性质中的两个重要参数。

比热是指单位质量物质在温度变
化下吸收或释放的热量，而导热系数是指在温度梯度下单位面积材料所传导的热量。

准稳
态法是一种常用的测量比热和导热系数的方法。

准稳态法的原理是将材料置于热源和冷源之间，使其温度从热源端到冷源端逐渐降低。

在稳态时，材料的温度分布和热流分布达到了平衡状态，此时材料的导热系数和比热可通
过测量温度和热流来计算得到。

具体实验步骤如下：
1.在实验装置的热源端和冷源端分别接上热源和冷却器，并在中间加装被测材料。

2.启动热源和冷却器，使其保持恒定的温度。

3.通过热电偶等温度计测量被测材料的温度分布。

通常可以在材料表面粘贴一定数量
的热电偶，并通过微型电脑采集数据。

4.通过热流计测量热源和冷源之间传导的热流。

热流计是一种基于热电效应的电子仪器，可以测量电导率和温度梯度来计算热流。

5.通过实验数据计算被测材料的比热和导热系数。

根据热传导定律，可以将热流和导
热系数表示为以下关系：Q=λ×A×(T1-T2)/L，其中Q为热流，λ为导热系数，A为横截
面积，T1和T2分别为热源和冷源的温度，L为材料长度。

由于准稳态法测量过程中需要维持恒定的温度和热流，因此实验装置的设计和操作都
需要具备一定的技术水平。

此外，不同材料的比热和导热系数可能有很大的差异，因此在
实验计算中需要注意各项参数的精确度和精度。

用准稳态法测介质的导热系数和比热的实验报告实验目的本实验旨在通过准稳态法来测量介质的导热系数和比热。

实验原理介质热传导定律可以表示为:$\frac{dQ}{dt}=-kA\frac{dT}{dx}$其中$dQ$表示通过横截面$A$传导的热量、$dT/dx$表示温度梯度，$k$表示介质的导热系数。

考虑一根长为$L$、半径为$r$的柱形介质，将其放置在恒定温度$T_1$的热源上，使其与热源建立稳定热流，由于介质与外界的热交换可能会影响温度场的分布，但如果用温度计沿柱形介质的径向测量，可以保证温度场分布近似于径向对称的形态。

当恒定稳态建立后，热传导方程的解析解可以表示为:$T(r)=T_1+\frac{dQ}{2\pi kL}ln{\frac{r}{r_0}}$其中$r_0$表示温度计的距离。

同时根据恒定稳态条件，热流向是恒定的，可以通过测量温度差得到热流，即:$q=-k\frac{A}{\Delta x}(T_2-T_1)$其中$A$表示圆柱体的横截面积，$\Delta x$表示$\Delta T$的距离。

结合以上两式，可以得到介质的导热系数$k$为:$k=\frac{qd}{2\pi T_1 L ln{\frac{r_2}{r_1}}}$其中$d$为材料的直径，$T_1$为热源的温度，$r_1$和$r_2$为温度计的测量位置。

而比热则是通过热平衡条件给出的:$q_1t_1=q_2t_2$其中$q$为热流，$t$为温度，1和2表示两个状态。

在本实验中，温度上升了$\Delta T$，热流在某一时间间隔$t$内对介质的热量为$q=mC_p\Delta T$，其中$m$为穿过某一截面的质量，$C_p$为比热容。

因此可以得到比热:$C_p=\frac{q}{m\Delta T}$实验步骤1.准备材料：圆柱形样品和两台K型热电偶。

2.组装实验装置：将圆柱形样品嵌入加热炉中，将热电偶分别穿过样品并与数据采集仪相连。

在实际操作中要实现这样的条件比较困难，因而会导致测量的重复性、稳定性、一致性较差，误差也较大。

为了克服稳态法测量的这些弊端，本实验使用了一种新的测量方法——准稳态法，使用准稳态法只要求温差恒定和温升速率恒定，而不必通过长时间的加热达到稳态，就可以通过简单的计算得到导热系数和比热。

1.准稳态法测量原理考虑如图1 所示的一维无限大导热模型：一无限大不良导体平板厚度为２R，初始温度为t0，现在平板两侧同时施加均匀的指向中心面的热流密度q c，则平板各处的温度t(x, τ )将随加热时间τ 而变化。

以试样中心为坐标原点，上述模型的数学描述可表达如下：式中a = λ/ρc，λ为材料的导热系数，ρ为材料的密度，c 为材料的比热。

可以给出此方程的解为：考察t(x,τ )的解析式（2）可以看到，随加热时间的增加，样品各处的温度将发生变化，而且我们注意到式中的级数求和项由于指数衰减的原因，会随加热时间的增加而逐渐变小，直至所占份额可以忽略不计。

定量分析表明，当以后，上述级数求和项可以忽略。

这时式（2）可简写成：这时，在试件中心处有x = 0，因而有：在试件加热面处有x = R，因而有：由式（4）和（5）可见，当加热时间满足条件时，在试件中心面和加热面处温度和加热时间成线性关系，温升速率都为此值是一个和材料导热性能和实验条件有关的常数，此时加热面和中心面间的温度差为：由式（6）可以看出，此时加热面和中心面间的温度差↵t和加热时间⎜没有直接关系，保持恒定。

系统各处的温度和时间呈线性关系，温升速率也相同，我们称此种状态为准稳态。

当系统达到准稳态时，由式（6）得到根据式（7），只要测量进入准稳态后加热面和中心面间的温度差⊿t，并由实验条件确定相关参量q c和R ，则可以得到待测材料的导热系数λ。

另外在进入准稳态后，由比热的定义和能量守恒关系，可以得到下列关系式：比热为：式中为准稳态条件下试件中心面的温升速率（进入准稳态后各点的温升速率是相同的）。

用准稳态法测介质的导热系数和比热的实验报告实验报告：
本实验组进行了一系列实验，目的是测量介质的导热系数和比热。

为此，我们采用了准稳态法（Steady-State Method），通过测量系统的热流，温度和物理量来评估介质的热特性。

实验装置由两个金属块构成，它们之间以一定宽度填充介质。

两个金属块用热电偶连接，控制机械温度。

一个块由常温水浴恒温，使另一块保持稳定的温度，以产生恒定的热流。

然后，通过特殊测量仪器读取温度差。

通过改变被测物质的厚度，实验运行三次，同时测量温度。

在改变热流情况下，记录温度差随热导率的变化情况。

根据所得温度与热导率的关系，用分析技术计算出介质的导热系数和比热。

实验运行时，实验装置保持在常温水浴中，当热偶发出热量时，两个金属块之间的温差增大，测量装置会自动调整两个金属块的温度，以保持恒定的热流输出。

本实验的结果显示，随着介质的厚度的增加，介质的导热系数和比热值也随之增加。

未来，我们可以改进实验装置，看看它们是否可以产生更精确的结果。

实验1 测定不良导体的导热系数一 引语 (Introduction )热量的传输方式有多种，如辐射、对流、传导等。

对于固体材料而言，热传导是热量传输的方式之一，它是物体直接接触温度不均匀时而产生的。

导热系数是反映材料的导热性能的重要参数之一；在工程技术方面是不可缺少的。

如熔炼炉、传热管道、散热器、加热器，以及日常生活中水瓶、冰箱等都要考虑它们的导热程度大小。

所以，对导热系数的研究和测量就显得很有必要。

我们把导热系数大、导热性能较好的材料称为良导体；而把导热系数小，导热性能较差的材料称为不良导体。

一般说来，金属的导热系数比非金属的要大；固体的导热系数比液体的要大；气体的导热系数最小。

本实验仅介绍一种比较简单的利用稳态法测不良导体的导热系数的实验方法。

稳态法是通过热源在样品内部形成一稳定的温度分布后，用热电偶测出其温度的方法。

二 实验目的 (Purpose)1．掌握稳态法测不良导体的导热系数的方法。

2．了解物体散热速率和传热速率的关系。

3．理解温差热电偶特性。

三 实验仪器 (Instruments)红外灯、传热筒、杜瓦瓶、温差电偶、待测橡胶样品、调压器、数字电压表、硅油、停表。

图 1 导热系数测定仪装置图杜瓦瓶样品数字电压表热电偶四 实验原理 (principle)1. 热传导方程当物体内部各处的温度不均匀时，就会有热量从温度较高处传递到温度较低处，这种现象叫热传导现象。

测定导热系数的原理是法国数学、物理学家约瑟夫·傅立叶给出的导热方程式。

该方程式指出，在物体内部，垂直于导热方向上，二个相距为h ，面积为A ，温度分别为1θ、2θ的平行平面，在t ∆秒内，从一个平面传到另一平面的热量Q ∆，满足下述表达式：ht QA 21θθ∆∆λ-= (2-6-1)式中tQ ∆∆为传热速率，A 为样品面积，h 为样品厚度，1θ、2θ分别为样品上下表面温度，λ为该物体的导热系数，其值等于相距单位长度的两平面的温度相差一个单位时，在单位时间内，垂直通过单位面积所传递的热量。

补2 用准稳态法测介质的导热系数和比热热传导是热传递三种基本方式之一。

导热系数定义为单位温度梯度下每单位时间内由单位面积传递的热量，单位为W / (m · K)。

它表征物体导热能力的大小。

比热是单位质量物质的热容量。

单位质量的某种物质，在温度升高（或降低）1度时所吸收（或放出）的热量，叫做这种物质的比热,单位为J/（kg ·K ）。

测量导热系数和比热通常都用稳态法，使用稳态法要求温度和热流量均要稳定，但在实际操作中要实现这样的条件比较困难，因而会导致测量的重复性、稳定性、一致性较差，误差也较大。

为了克服稳态法测量的这些弊端，本实验使用了一种新的测量方法——准稳态法，使用准稳态法只要求温差恒定和温升速率恒定，而不必通过长时间的加热达到稳态，就可以通过简单的计算得到导热系数和比热。

【实验目的】1. 了解准稳态法测量导热系数和比热的原理；2. 学习热电偶测量温度的原理和使用方法；3. 用准稳态法测量不良导体的导热系数和比热。

【实验仪器】1. ZKY-BRDR 型准稳态法比热、导热系数测定仪2. 实验装置一个，实验样品两套（橡胶和有机玻璃，每套四块），加热板两块，热电偶两只，导线若干，保温杯一个【实验原理】1. 准稳态法测量原理考虑如图B2－１所示的一维无限大导热模型：一无限大不良导体平板厚度为R 2，初始温度为0t ，现在平板两侧同时施加均匀的指向中心面的热流密度c q ，则平板各处的温度),(τx t 将随加热时间τ而变化。

以试样中心为坐标原点，上述模型的数学描述可表达如下：⎪⎪⎪⎩⎪⎪⎪⎨⎧==∂∂=∂∂∂∂=∂∂022)0,(0),0(),(),(),(t x t x t q x R t x x t a x t c τλττττ式中c a ρλ/=，λ为材料的导热系数，ρ为材料的密度，c 为材料的比热。

可以给出此方程的解为（参见附录）：)cos)1(2621(),(222121220τπππτλτR an n n c e x Rn n R R x R R a q t x t -∞=+⋅∑-+-++=（B2－１）考察),(τx t 的解析式（B2－１）可以看到，随加热时间的增加，样品各处的温度将发生变化，而且我们注意到式中的级数求和项由于指数衰减的原因，会随加热时间的增加而逐渐变小，直至所图B2－1理想的无限大不良导体平板占份额可以忽略不计。

梧州学院数理系学生实验报告成绩：指导教师：专业：班别：实验时间：实验人：学号：同组实验人：盘，让散热盘在电扇作用下冷却，记录散热盘温度θ随时间t 的下降情况，求出散热盘在2θ时的冷却速率2θθθ=∆∆t，则散热盘P 在2θ时的散热速率为：2θθθ=∆∆=∆∆tmc t Q （3） 其中m 为散热盘P 的质量，c 为其比热容。

在达到稳态的过程中，P 盘的上表面并未暴露在空气中，而物体的冷却速率与它的散热表面积成正比，为此，稳态时铜盘P 的散热速率的表达式应作面积修正：()()PPPPP Ph R Rh R Rtmc t Q ππππθθθ222222++∆∆=∆∆= （4）其中p R 为散热盘P 的半径，p h 为其厚度。

由(2)式和(4)式可得：()()PPPPP PBBh R Rh R R tmcd h ππππθπθθλθθ2224222212++∆∆=-= （5）所以样品的导热系数λ为：()()()221142222B B P P P P d h h R h R tmcπθθθλθθ-++∆∆== （6）实验仪器F D －TC －B 型导热系数测定仪装置如图1．所示，它由电加热器、铜加热盘C 、橡皮样品圆盘B 、铜散热盘P 、支架及调节螺丝、温度传感器以及控温与测温器组成。

实验内容(1)取下固定螺丝，将橡皮样品放在加热盘与散热盘中间，橡皮样品要求与加热盘散热盘完全对准；要求上下绝热薄板对准加热和散热盘。

调节底部的三个微调螺丝，使样品与加热盘、散热盘接触良好，但注意不宜过紧或过松：(2)按照图1所示，插好加热盘的电源插头；再将2根连接线的一端与机壳相连，另一有传感器端插在加热盘和散热盘小孔中，要求传感器完全插入小孔中，并在传感器上抹一些硅油或者导热硅脂，以确保传感器与加热盘和散热盘接触良好。

在安放加热盘和散热盘时，还应注意使放置传感器的孔上下对齐 (注意：加热盘和散热盘两个传感器要一一对应，不可稳态时(1 0分钟内温度基本保持不变,样品上表面的温度示值1θ=℃，样品下表面温度示值2θ=℃。

准稳态法测不良导体的比热和导热系数一、实验任务1．了解准稳态法测量导热系数和比热的物理模型；2．掌握利用温差电偶测量温度和温差的原理和实验方法；3．掌握测量不良导体导热系数和比热的方法。

二、预习指导本实验能否获得满意的实验结果，主要取决于实验前的实验准备工作是否充分。

实验前应仔细阅读实验测量原理和了解实验装置，思考并能回答以下问题：1．本实验采用的是何种导热模型？在装置上是如何实现的？2．求解温度场的微分方程中各量的物理意义是什么？3．本实验对初始条件有何要求？实验时如何满足？4．何谓准稳态，如何判断系统是否达到准稳态？列出系统进入准稳态后的几个特征？5．热流密度的定义和单位是什么？在本实验中热流密度公式是如何得到的？6．本实验中是如何利用两只热电偶测量加热面和中心面的温差的？三、操作要点1．熟悉实验装置，了解实验样品和热电偶的装配方法。

检查热端和冷端是否连接正常，查热电偶的电阻是否为3～5Ω，按下图联接电路，检测并记录初始温差及初始温度。

调节加热器电压为21伏，预热二十分钟。

在加热样品前，须经教师检查许可后进行，以防损坏仪器或实验失误。

2．接通加热器电源，测t τΔ 及(0,)t ττ 曲线。

每隔三十秒测量一次t Δ和(0,)t τ（利用转换开关来实现，先测t Δ），准稳态出现后再测五组数据。

3．本实验分别对有机玻璃和橡胶各测一次。

四、注意事项在装卸样品和热电偶时，要带好手套以免造成样品初始温度不均匀和影响热电偶的输出。

另外热电偶极易损坏，装配时要小心，注意保护。

五、报告要求用坐标纸画出t τΔ 及(0,)t ττ 曲线（绘在一个坐标内），从图上判断准稳态并求出t Δ和/dt d τ；计算导热系数、比热。

六、讨论题1、2。

3．如果冷端槽不处于冰水中，而是处于恒定温度的空气中，是否影响本实验导热系数和比热的测量？。

准稳态法测不良导体的导热系数和比热实验报告一、实验目的（1）实验一：万用表使用测量：熟悉万用表的使用方法，学习量程的选择方法，以及根据量程得到数据精度并计算不确定度的方法。

（2）实验二：热导实验：1、了解准稳态法测量不良导体的导热系数和热比的方法；2、掌握热电偶测量温度法方法；3、加深对直线拟合处理数据方法的理解。

二、实验一：万用表使用测量计算过程：（2）交流电源有效值∆X读数精度% * 测量值+ 量程精度% * 量程= 0.2%*0.34474 + 0.05%*2 = 0.0017V =X=XX0.34474 ±0.0017V±=∆（3）交流信号的频率∆X读数精度% * 测量值+ 量程精度% * 量程= 0.01%*999.98 + 0.003%*2000 = 0.16Hz =XX999.98 ±0.16Hz=X∆=±（4）电阻∆X读数精度% * 测量值+ 量程精度% * 量程=0.020%*10.9457 + 0.004%*20 = 0.003kΩ=X==XX10.9457 ±0.003kΩ±∆（5）电容∆X读数精度% * 测量值+ 量程精度% * 量程=1%*0.930 + 0.5%*2=0.019uF ==XX0.930 ±0.019uFX±=∆（6）二极管∆X读数精度% * 测量值+ 量程精度% * 量程=0.06%*0.5735+0.020%*2 = 0.0007V =X=XX0.5736 ±0.0007V∆=±实验二：热导实验三、数据处理（2）U1(t2t1)~τ，U2(t1tc)~τ曲线分析：当样品进入准稳态时，样品内各点的温升速率相同并保持不变，且样品内两点间温差恒定。

对应的电压值变化趋势为：中心面和冷面温差U2(t1tc)线性增长，热面和中心面温差U1(t2t1)基本保持不变。

准稳态法比热与导热系数测定热传导是一种重要的物理现象，它在工程、物理、化学等领域都有着广泛的应用。

为了研究热传导现象，我们需要测定材料的比热和导热系数。

本文将介绍一种测定材料比热和导热系数的方法——准稳态法。

一、准稳态法的原理准稳态法是测定材料比热和导热系数的一种常用方法。

它的原理是基于热传导的基本方程式：frac{partial T}{partial t} = alphaabla^2 T其中，T是温度，t是时间，alpha是热扩散系数，abla^2是拉普拉斯算子。

在准稳态条件下，即当时间足够长时，温度分布不再随时间变化，即frac{partial T}{partial t} = 0因此，我们可以得到下面的方程：abla^2 T = 0根据边界条件，我们可以求出温度分布，从而计算出材料的比热和导热系数。

二、准稳态法的实验步骤1. 实验装置准稳态法的实验装置主要包括一个热源、一个热传导材料和一个温度传感器。

2. 实验步骤（1）将热源放置在热传导材料的一端，并加热。

（2）等待一段时间，使得温度分布达到准稳态。

（3）在热传导材料的另一端放置一个温度传感器，记录温度随时间的变化。

（4）根据温度分布和时间变化，计算出材料的比热和导热系数。

三、准稳态法的优缺点1. 优点准稳态法测定材料比热和导热系数的方法简单，实验装置也比较容易搭建。

2. 缺点准稳态法需要等待一段时间，使得温度分布达到准稳态，这会导致实验时间较长。

此外，准稳态法对实验环境的影响比较大，需要对实验环境进行控制。

四、结论准稳态法是一种测定材料比热和导热系数的有效方法，它基于热传导的基本方程式，通过测量温度随时间的变化来计算材料的比热和导热系数。

虽然准稳态法需要等待一段时间，但它的实验装置简单，对实验环境的要求也比较低，因此在实际应用中具有一定的优势。

稳态法测量不良导体的导热系数实验报告实验报告实验名称：稳态法测量不良导体的导热系数实验目的：本实验旨在通过稳态法测量不良导体的导热系数，进一步了解材料的导热性能，并提高实验操作能力。

实验原理：热传导是物质内能的传递，是由高温区向低温区传递热量的过程。

在导体中，热量的传导主要通过自由电子传导和晶格振动传导两种机制实现。

本实验通过稳态法测量不良导体的导热系数。

在稳态下，热量的输入和输出相等，即：Qin = Qout根据傅立叶热传导定律，稳态下热传导的热流密度Q与导热系数λ、导热面积A、温度差ΔT之间的关系为：Q = λAΔT / d其中，Q为单位时间内通过导体的热量，λ为导热系数，A为导热面积，ΔT为温度差，d为导体的厚度。

实验器材：1. 不良导体样品2. 直立式热传导仪3. 温度计实验步骤：1. 将热传导仪取出，并调整热电偶测温头至样品位置，并与温度计校准。

2. 将样品固定于热传导仪上，并调整加热电压至一定值，保持恒温。

3. 记录热电偶和温度计示数，计算温度差ΔT。

4. 根据所用材料的厚度测量所得，计算导热系数λ。

实验结果及数据处理：进样品的加热电压为V = 5V，测得的热电偶示数为T1 = 40℃，T2 = 30℃，沿导体厚度方向测得的样品厚度为d = 2cm。

由此可计算出温度差ΔT = T1 - T2 = 40℃ - 30℃ = 10℃。

代入傅立叶热传导定律公式Q = λAΔT / d，可得热流密度Q。

将实验中测得的其他参数代入公式，可计算得到不良导体的导热系数λ。

实验结论：通过稳态法测量不良导体的导热系数，可以得到材料的导热性能。

该实验结果为XX（具体结果），表明该不良导体具有较低的导热系数，其热传导能力较差。

实验过程中需注意：1. 实验开始前要确保热传导仪和温度计都已校准，并测得的数据准确可靠。

2. 在稳态状态下测量温度差，并注意尽量减小其他误差的影响。

3. 实验结束后及时关闭加热电源，并注意对实验器材的清理和归位。

稳态法测量不良导体的导热系数实验报告实验报告：稳态法测量不良导体的导热系数实验实验目的：本实验旨在通过稳态法测量不良导体的导热系数，了解不良导体的导热性能，并进一步分析材料的热传导特性。

实验仪器：1. 实验台2. 电热器3. 铜棒样品4. 温度计5. 计时器6. 多用电表7. 导热油实验原理：稳态法测量导热系数是通过测量材料的温度梯度和热流量来计算导热系数的。

在实验过程中，首先将导热油倒入实验台中，使其充满整个实验空间。

然后，在台面上放置热源和试样，热源通过导热油将热量传递给试样，试样将热量传递给周围环境。

通过测量试样两端的温度差和热流量，可以计算出导热系数。

实验步骤：1. 准备工作: 将实验台内充填导热油，并使其达到温度平衡。

2. 将导热棒和试样一起放置在实验台上，使其与实验台接触良好。

3. 将电流通入电热器中，通过导热油将热量传递给试样，使热量在试样内传递。

4. 同时使用温度计测量试样两端的温度差，并通过多用电表测量电热器的电流和电压，计算出热流量。

5. 记录不同时间间隔的试样温度和热流量数据，并绘制温度与热流量的关系曲线。

6. 根据数据计算出导热系数。

实验结果：根据实验得到的温度-热流量关系曲线，可以通过线性拟合得到试样的斜率，即热流量值。

通过计算不同时间间隔内的温度差，可以得到导热系数的数值。

实验结论：根据实验结果，可计算出不良导体的导热系数。

导热系数是衡量材料导热性能的重要参数，通过实验可以了解不良导体的导热性能，并为材料的热传导特性分析提供参考。

实验注意事项：1. 实验过程中要注意安全，避免触电或烫伤等意外情况。

2. 导热油的量要足够充填实验台，且温度均匀平衡。

3. 实验前要对实验仪器进行检查，确保正常工作。

4. 实验操作要严格按照实验步骤进行，尽量减小误差产生。

5. 实验完成后要对实验环境进行清理和整理，保持实验台的整洁。

实验三 准稳态法测材料的导热性能实验一、实验目的1. 测量绝热材料（不良导体）的导热系数和比热、掌握其测试原理和方法。

2. 掌握使用热电偶测量温差的方法。

二、实验原理本实验是根据第二类边界条件，无限大平板的导热问题来设计的。

设平板厚度为2δ，初始温度为t 0，平板两面受恒定的热流密度q c 均匀加热（见图1）。

求任何瞬间沿平板厚度方向的温度分布t (x ，τ)。

导热微分方程式、初始条件和第二类边界条件如下：22),(),(xx t a x t ∂∂=∂∂τττ 0=τ时, 0t t =0=x 处， 0=∂∂xtδ±=x 处， c q xt=∂∂-λ方程的解为：)]exp()cos(2)1(63[),(02211220F xx a q t x t n n n n c μδμμδδδδτλτ--+--=-+∞=∑式中：τ—— 时间，s ；λ—— 平板的导热系数，w/m ∙℃；a —— 平板的导温系数，a cλρ=m 2/s ； n μ——πn ，n=1，2，3，……；Fo —— 傅立叶准则，Fo ＝2a τδ ； t 0 —— 初始温度,℃；c q —— 沿x 方向从端面向平板加热的恒定热流密度，w/m 2。

随着时间τ的延长，F 0数变大，上式中级数和项愈小。

当F 0>0.5时，级数和项变得很小，可以忽略，上式变成：20221(,)()26c q at x t x t δτλδδ-=+- （1）由此可见，当F 0>0.5后，平板各处温度和时间成线性关系，温度随时间变化的速率是常数,并且到处相同。

这种状态称为准稳态。

在准稳态时，平板中心面x=0处的温度为：021(0,)()6c q a t t δττλδ-=- (2) 平板加热面x=δ处为：)31(),(20+=-δτλδτδa q t t c (3) 此两面的温差为：λδττδc q t t t ⋅=-=∆21),0(),( 如已知q c 和δ，再测出Δt ，就可以由式（3）求出导热系数： tq c ∆=2δλ （4） 实际上，无限大平板是无法实现的，实验总是用有限尺寸的试件。

稳态法测量不良导体的导热系数实验报告(一)稳态法测量不良导体的导热系数实验报告简介本报告介绍了使用稳态法测量不良导体的导热系数实验的方法和结果。

该实验采用了稳态法测量导热系数的方法，通过测量导体两端的温度差和导热长度，计算导热系数。

实验目的•测量不同材料的导热系数，了解不良导体的导热性能；•分析不良导体的导热差异，为后续材料选择和优化提供参考。

实验步骤1.准备实验所需材料和设备；2.温度测量：使用温度计测量导体的两端温度，并记录；3.确定导热长度：根据实验设计，测量导体的长度，并记录；4.安装导体：将导体安装在恒温水槽中，确保整个导体完全浸没在水中；5.稳定温度：打开恒温水槽，调节水温，使其稳定于所需温度；6.等待稳定态：在恒温水槽中放置一段时间，待温度稳定后进行下一步；7.测量数据记录：记录稳定温度下导体两端的温度差和导热长度；8.计算导热系数：根据测量数据，使用导热系数计算公式计算导体的导热系数；9.分析结果：对实验结果进行分析和比较，得出结论。

实验结果•实验所得数据：测量到的导体两端的温度差为ΔT，导热长度为L；•导热系数计算结果：根据导热系数计算公式，得出不同导体的导热系数；•数据分析：对比各种导体的导热系数，分析不良导体的导热性能。

结论通过稳态法测量不良导体的导热系数实验，我们得到了不同导体的导热系数数据，并进行了比较和分析。

根据实验结果，可以得出以下结论： 1. 不同材料的导热系数存在较大差异，不良导体的导热性能较差； 2. 在进行材料选择和优化时，需要考虑材料的导热性能；3. 导热系数可作为评价材料导热性能的重要指标之一。

参考文献[1] 张三, 李四, 稳态法测量导热系数实验方法研究, 物理实验杂志, 20XX.[2] 中国测绘科学研究院，导热系数测量技术方法，测绘标准化与质量保证，20XX。

实验条件和设备•实验条件：室温为25°C，相对湿度为50%；•实验设备：–温度计：使用数字温度计，具有高精度和稳定性；–恒温水槽：具有恒温控制功能，能够稳定控制水温；–导体样品：选择不同材料的导体样品，确保样品的尺寸一致；–数据记录器：记录实验数据，确保数据准确性；–恒温计时器：用于稳定时间的控制，确保温度稳定于所需状态。

稳态法测量不良导体导热系数学号：100441731 徐坦迪中欧106041A摘要：导热系数是反映材料导热性能的物理量，在加热器、散热器、导热管道、冰箱制造、建筑保温隔热设计等领域都涉及该设计参数。

材料的导热系数与材料的容量、空隙率、湿度、温度等因素有关，小于0.25W/m·K的材料为绝热材料。

导热系数的测量方法有稳态法和动态法两类，本实验采用稳态法。

关键词：稳态法导热系数热流量比热容冷却速率Steady method for measuring the poor conductor coefficient of thermal conductivityAbstract: the coefficient of thermal conductivity is reflect material thermal conductivity physical quantities, in the heater, radiator, thermal pipe, refrigerator manufacture, construction insulation design, and other fields involve the design parameters. The thermal conductivity of materials and the capacity of the materials, pore ratio and other factors, such as temperature, humidity, less than 0.25 W/m k. materials for insulation. Coefficient of thermal conductivity measurement method is steady method and dynamic method two kinds, this experiment used steady state law.Keywords: Steady state law Coefficient of thermal conductivity Heat flow Specific heat let Cooling rate【实验目的】1. 学习用稳态法测量不良导体的导热系数。