第11章 交流绕组的磁动势

交流绕组部分（感应电动势和磁动势）习题1.谐波电动势对电机运行有何影响？为什么同步发电机定子绕组采用星型接法？谐波电动势使电机的电动势波形非正弦，产生谐波转矩和附加损耗。

为了消除3次谐波，同步电机定子绕组采用星形接法。

（三相交流电流中，各相基波电动势相位差为120度，而各相的三次谐波电动势相位差为360度，即为同相。

同理，3的倍数的各奇次谐波也为同相位。

这样接成星形时，在线电动势中不可能出现3次和3的倍数奇次谐波电动势。

当三相绕组接成三角形，3次及3的倍数奇次谐波电动势在闭合的三角形电路中被短路而形成环流，引起附加铜损耗，虽然这时只残留微少的电压降，线电动势中仍不出现这类谐波。

因此多采用星形连接。

）2.为什么交流绕组的磁动势，既是时间函数又是空间函数？用单相绕组基波磁动势来说明。

交流绕组的电流是随时间而变化的正弦函数。

磁动势为空间函数，磁场在空间分布。

（见练习题书P.121）3.脉动磁动势和旋转磁动势有什么关系？脉动磁动势可以分解为两个旋转磁动势分量，每个旋转磁动势分量的振幅为脉动磁动势振幅的一半，旋转速度相同，但旋转方向相反。

（分解的表达式见笔记p.3）。

等式左边为脉动磁动势，等式右边第一项为正向旋转磁动势，在空间按正弦规律分布，幅值不变，幅值位置在wt-x=0处，随时间变化，磁动势波在空间移动，移动的速度为w，所以是旋转磁动势。

等式右边第二项为负向旋转磁动势。

4.产生圆形旋转磁动势和椭圆形旋转磁动势的条件有何不同？m相对称电流流入m相对称绕组时，产生圆形旋转磁动势。

m相不对称电流流入m相对称绕组，或者m相对称电流流入m相不对称绕组时，产生椭圆形旋转磁动势。

5.如果不考虑谐波分量，在任一瞬间，脉动磁动势的空间分布是怎样的？圆形旋转磁动势的空间分布是怎样的？椭圆形旋转磁动势在空间分布是怎样的？如果观察一瞬间，能否区别该磁动势是脉动磁动势、圆形旋转磁动势或椭圆形旋转磁动势？如果不考虑谐波分量，在任一瞬间，脉动磁动势、圆形旋转磁动势和椭圆形旋转磁动势在空间分布均为正弦波，故不能区别三种磁动势。

交流绕组的磁动势§9-2 一相绕组的磁动势(1)一相绕组的磁动势为一空间位置固定、幅值随时间变化的脉振磁动势，脉振的频率等于电流的频率，脉振磁动势的幅值位于相绕组的轴线上。

(2)一相绕组的基波(或谐波)脉振磁动势可以分解成两个幅值相等。

转速相同，转向相反的旋转磁动势。

旋转电角速度w 恰恰等于角频率每分钟转数同步速n1(3)一相绕组的 v 次谐波磁动势表达式为：f ϕν =Fϕν=Fϕmνcosναcosωt cosνα=0.9νIwkp wνcosωt cosνα交流绕组的磁动势§9-3 三相绕组的磁动势研究对象为研究方便，把三相绕组的每一相用一个等效的单层整距集中绕组来代替，该等效绕组的匝数等于实际一相串联匝数w 乘以绕组因数kw1, kw1w 称为一相的有效匝数，三相绕组在空间互差120度电角度。

这是一对极电机的三相等效绕组示意图。

电流正方向+B +AYC A XZ α=0 B+C三相绕组的基波磁动势结论：三相基波合成磁动势具有以下性质1）三相对称绕组通入三相对称电流产生的基波合成磁动势为一幅值不变的旋转磁动势。

由于基波磁动势矢量的端点轨迹是一个圆形，故又称为圆形旋转磁动势。

2）三相基波合成磁动势的幅值为一相基波脉振磁动势最大幅值的3/2 倍，即F 1 =32Fϕm1= 1.35Iwkp w1(安/ 极)3）三相基波合成磁动势的转向取决于电流的相序和三相绕组在空间上的排列次序。

基波合成磁动势总是从电流超前的相绕组向电流滞后的相绕组方向转动，例如电流相序为A－B－C，则基波合成磁动势按A轴－B轴－C轴方向旋转，改变三相绕组中电流相序可以改变旋转磁动势的转向。

4）三相基波合成磁动势的转速与电流频率保持严格不变的关系，即该转速即为同步速。

5）当某相电流达到最大值时，基波合成磁动势的波幅刚好转到该相绕组的轴线上，磁动势的方向与绕组中电流的方向符合右手螺旋定则。

分析方法如果三相等效绕组里通过三相对称电流，则每相均产生一脉振磁动势；把三个相绕组的磁动势进行合成，即得三相绕组的合成磁动势。

五、脉振磁动势的分解()()11111111cos cos cos cos 22m m m f F t F t f f F t φφφφφφωαωαωα==−++''+'=即：一个脉振磁动势可以分解为两个幅值为的磁动势。

121m F ϕ1）第一项：()αωϕϕ−='t F f m cos 2111即：旋转磁动势（行波）的角速度等于电流角频率，朝+α方向旋转。

在空间上向前运动的波形在物理学上叫行波。

因此该磁动势不再是一个脉振的磁动势，而是变为一个空间分布不变，但向前运动的旋转磁动势。

因其幅值不变，旋转矢量末端的轨迹是一个圆，所以也称为圆形旋转磁动势。

()1602d dft f n dt dtpαωωπ====取磁动势幅值为这一点进行研究121m F ϕ§9-2 一相绕组的磁动势（续）()αωϕϕ−='t F f m cos 2111对应的波形图选取波形幅值所在位置的点进行分析，令ωt-α=0，则α=ωt上图中从左到右的三个波形分别对应，α=0、α=π/2、α=π三个时刻的波形。

对应上述三个时刻的波形，可以看到幅值对应的点在向右移动，在电机表面就是在逆时针旋转。

旋转角速度d α/dt=ω（rad/s ）换算为电机转速为同步速2）第二项：即：旋转磁动势转速与的相同，但转向相反。

可见第二项和第一项都是圆形旋转磁动势，幅值、转速都相同，只是转向相反。

同样我们也可以用波形来分析第二项。

可以得到和第一项类似的结果。

()αωϕϕ+=''t F f m cos 21111602d f f n dt pαωπ=−=−=−1ϕf '对应的波形图选取波形幅值所在位置的点进行分析，令ωt+α=0，则α=-ωt上图中从左到右的三个波形分别对应，α=0、α=-π/2、α=-π三个时刻的波形。

对应上述三个时刻的波形，可以看到幅值对应的点在向左移动，在电机表面就是在顺时针旋转。

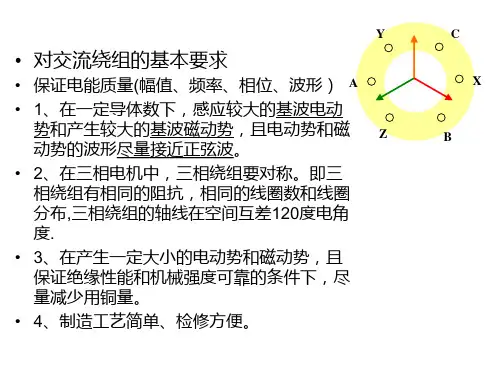
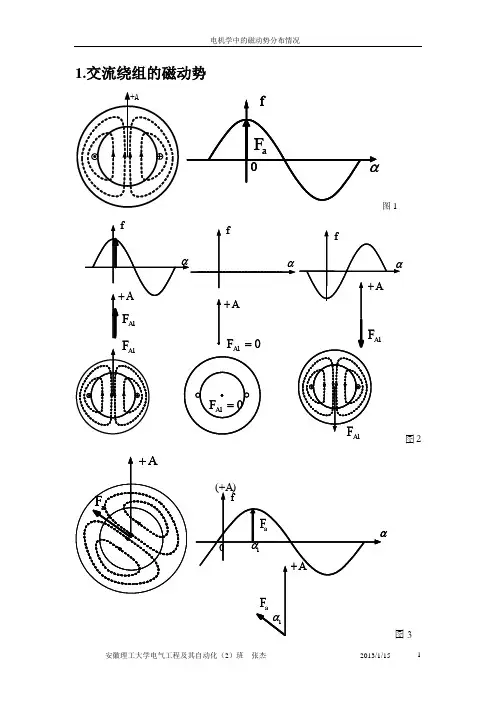
1.交流绕组的磁动势图1图2 图3从图中可以看出三相电流产生的总的磁场是随着转子的旋转而旋转的，设转子开始的位置就是A 相的轴线位置，也就是0α︒=时，此时a F 在轴线+A 轴上，当转子逆时针转动1α角时，a F 也转动1α角，这样最大的磁动势线就对应在1α，1α也就是t ω。

值得注意的是，上面的图是三相电流合成之后的磁动势，而对于每一相电流，他们产生的基波磁动势的表达式是11cos cos cos cos k k k f N I t F t ωαωα==，这个式子可以傅里叶变换为：'''1111111cos()cos()22k k k k k f F t F t f f αωαω=-++=+，可以发现，一个脉振磁动势可以分解为两个极对数和波长与脉振波完全一样，类比上面的合成磁动势，这里的cos()t αω-可以看成是振幅为112k F 的磁动势沿着逆时针转动，也就是转子的转动方向旋转，并且旋转的角速度为d d tdt dtαωω==，也就是说，这个行波是电角速度为ω，大小与转子转动的电角速度相等，也就是线圈中电流的电角速度相等。

另外，cos()t αω+部分可以看成振幅为112k F 的磁动势沿着顺时针转动，这个行波是电角速度为-ω，大小与转子转动的电角速度相等，也就是线圈中电流的电角速度相等。

这些都是电枢绕组上的电枢电流所产生的磁动势特征，分别通过对总的电枢磁动势a F 的旋转方向来过渡到单相电流产生的磁动势，由于转子是逆时针方向转动，所以电动势是逆时针转动，导致电枢电流逆时针转动，然后就有了a F 逆时针转动，可以形象的通过上面的图3看出随着α而转动。

1cos()f F αα=-2.图示说明分布、短距绕组的物理意义两槽单线圈磁场空间分布为矩形波，所以含有大量的谐波在里面，那么产生的电动势也就有大量的谐波。

图4 两槽单线圈磁力线分布6槽三相电机磁场空间分布为阶梯波，所以也含有大量的谐波。

§9-4 椭圆形旋转磁动势举例：已知三相交流绕组的电流：11111111cos cos cos()cos()22A m m A m A f F t F t F F F t φφφωαωαωα==+=+−+'"分析：111111AB AB F F F F F F +−''=+''''=+定义：12212111cos(120)cos(120)cos()cos(240)22B m m m B B f F t F t F t F F φφφωαωαωα=−−=−++=+−'"10C f =2cos 2cos(120)0A AB BC i I t i I t i ωω==−=选定任一时刻，在矢量图上找到对应的这四个圆形旋转磁动势的矢量。

然后合成正反转的两个圆形旋转磁动势如图所示。

此两个圆形旋转磁动势空间有相对运动，因此合成磁动势幅值是变化的，因此其变化轨迹是一个椭圆。

故称为椭圆形旋转磁动势。

−11F F 、＋椭圆形旋转磁动势βcos 21121211−+−+++=F F FFF 1）椭圆形旋转磁动势幅值：2）椭圆形旋转磁动势的转向：与磁动势强的转向一致。

3）椭圆形旋转磁动势的转速：短轴处转速最高，长轴处转速最低。

2211121F F n n F +−−'=1160f n r /minp=平均转速：旋转磁动势产生条件：只要电机两相以上绕组在空间上有相位差，通入时间上有相位差的电流，就能产生旋转磁动势。

−11F F 、＋110F F +−=≠10F +≠10F −≠11F F +−≠2）椭圆形旋转磁动势。

条件：且且。

1）圆形旋转磁动势。

条件：中一个为零；3）脉振磁动势。

条件：。

磁动势的三种状态及条件：11112111cos cos 11cos()cos()22cos(90)cos(90)11cos()cos(180)22A m m m A m m m f F t F t F t f F t F t F t φφφφφφωαωαωαωαωαωα==−++=−=−++++1cos I I tω=()02cos 90I I t ω=−1121cos()A A m f f f F t φωα=+=−磁动势性质及其产生条件可总结如下：1）两相以上的绕组在空间上对称，同时电流在时间上对称，则产生的基波合成磁动势为圆形旋转磁动势。

绕组电势磁势一、选择１设同步电机稳定运行时，定子电枢电流产生的旋转磁势相对定子的转速为ｎa ,转子励磁电流产生的旋转磁势相对定子的转速为ｎb ,则： ⑴ｎa ＞ｎb ； ⑵ｎa ＜ｎb ； ⑶ｎa ＝ｎb ; ⑷都有可能,与电机的运行状态有关.２当采用短距绕组同时削弱定子绕组中的五次和七次谐波磁势时，下列那一种绕组是我们应该选用的： ⑴绕组跨距为(４／５）τ； ⑵绕组跨距为（５／６）τ； ⑶绕组跨距为（６／７）τ； ⑷绕组跨距为（７／８）。

３交流绕组每相感应电势公式Ｅ1＝４．４４ｆＮｋw1φ1中的φ1是： ⑴磁通随时间交变的最大值； ⑵一台电机的基波磁通量; ⑶一个极的基波磁通量。

４公式Ｆ＝１．３５（Ｎｋw1／ｐ）Ｉ1是指: ⑴一相的磁势振幅；⑵三相一对极的合成磁势振幅； ⑶三相一个极的合成磁势振幅.５由三相定子绕组基波电流产生的五次空间磁势谐波，它的转速是： ⑴静止不动；⑵是基波磁场转速的１／５; ⑶等于基波磁场转速; ⑷五倍于基波磁场转速。

６由三相定子绕组基波电流产生的七次空间磁势谐波，它产生的磁通切割定子绕组感应电势的频率是：⑴等于零； ⑵等于基波频率； ⑶等于基频的１／７； ⑷等于基频的七倍。

７三相异步电动机定子绕组做成分布及短距以后，虽然感应电势的基波分量有所减少，但是它带来的优点主要是： ⑴改善了电势的波形; ⑵可以增加某次谐波电势; ⑶可以增加电机的额定转速；⑷可以改善磁势的波形。

８整数槽双层迭绕组最大并联支路数为ａｍ，极对数为ｐ,它们之间的关系是：①ａｍ＝２ｐ；②ａｍ＝ｐ;③ａｍ＝０．５ｐ.①（６０°相带）；②(１２０°相带）９整数槽单层绕组的最大并联之路数为ａｍ，极对数为ｐ，它们之间的关系是：①ａｍ＝２ｐ；②ａｍ＝ｐ;③ａｍ＝０．５ｐ.①（ｑ为偶数）；②(ｑ为奇数)１０整数槽双层波绕组的最大并联之路数为ａｍ，极对数为ｐ，最大并联支路数为：①２ｐ; ②ｐ；③２。

交流电机定子绕组内的磁动势谐波和反电动势谐波概述摘要：综合分析了交流电机定子绕组内的磁动势谐波和反电动势谐波这两类谐波的原理和性质。

从谐波转矩、谐波漏抗和谐波损耗三个方面分析了谐波对交流电机性能的影响，阐述了谐波的抑制及用途。

关键词：谐波；磁动势；分数槽；电动势；齿谐波0.引言交流电机中的谐波与电机的损耗、噪声、转矩、绕组电抗等密切相关[1-5]。

现有的文章多数仅专注于某一种特定谐波，而对交流电机定子绕组内谐波的综合概述还比较少。

本文综合考虑交流电机定子绕组内的磁动势谐波和反电动势谐波，对这两种谐波的产生机理、特性，以及对电机的影响等方面进行了分析和总结，并讨论了谐波的危害和谐波的一些有利的用途。

1.定子绕组磁动势谐波1.1 磁动势谐波的成因磁动势谐波是一种空间上的谐波，由于每相绕组都是由有限个产生方波的绕组线圈去逼近正弦分布，电机中不可避免地产生磁动势谐波。

整数槽绕组基波磁动势的极对数与电机的极对数相等，谐波磁动势的极对数则为基波极对数的整数倍。

分数槽绕组更复杂，绕组的特殊结构造成极数不明显，使绕组中明显包含多种极对数的谐波。

分数槽绕组磁动势中与电机转子极对数相同的谐波成分称为“基波”；多于转子极对数的谐波称为“高次谐波”；少于转子极对数的谐波称为“次谐波”；多于转子极对数但又不能被它整除的谐波叫做“分数次谐波”。

1.2磁动势谐波的性质定子绕组中的基波电流和谐波电流都会产生谐波磁动势，为得到普遍的多相绕组谐波合成磁动势表达式，需对文献[1]中通入正弦电流的三相绕组合成磁动势的公式加以修改。

2.定子绕组反电动势谐波2.1 反电动势谐波的成因反电动势谐波通常有两个成因：一方面，即使电机的气隙磁导均匀，气隙磁动势中的谐波成分仍会产生磁密谐波，感生出谐波电动势；另一方面，电机开有齿槽，导致磁导不均匀，磁动势与不均匀磁导作用，感应出齿谐波电动势。

2.2 反电动势谐波的性质γ次转子磁动势谐波感应出的谐波电动势的电角频率是γω；而无论的取值是多少，定子绕组次谐波磁动势感应出的谐波电动势的电角频率都为。

《电机技术》精编习题与答案变压器的工作原理和基本结构基础题1、 变压器是利用___________原理来工作的。

2、 变压器的主要结构有___________、___________。

3、 一台单相变压器，kVA S N 5000=，kV U U N N 3.6/10/21=，求一、二次侧的额定电流。

4、 一台三相变压器，kVA S N 5000=，kV U U N N 5.10/35/21=，Y ，d 接法，求一、二次侧的额定电流。

参考答案：1、电磁感应。

2、铁心、绕组。

3、115000500 ()10N N N S I A U ===225000794 ()6.3N N N S I A U === 4、182.5 ()N I A ===2275 ()N I A ===变压器空载运行1、变压器中空载电流的主要作用是 ，其性质为 ，其大小约为额定电流的 。

14、为什么变压器空载运行时的功率因数很低？参考答案：3、产生磁场、感性无功性质、2%~10%。

14、变压器空载运行时输入的空载电流主要用来产生主磁场，只有很小的部分产生有功损耗，所以空载电流属于感性无功性质，故此时变压器的功率因数低。

变压器负载运行1、随着变压器负载电流的增大，其主磁通幅值会__________。

A ．显著增大B ．显著减小C ．基本不变6、当变压器的负载增大时，变压器原边电流为什么会增大？参考答案1、C 。

2、当变压器副边电流增大，该电流所产生的磁场会对原边电流所产生的磁场有去磁作用，为了维持主磁通不变，所以原边电流必须相应增大。

变压器参数的测定3、通过变压器的空载试验，可测得_________。

A ．铜损耗B ．铁损耗C ．附加损耗4、通过变压器的短路试验，可测得_________。

A ．铜损耗B ．铁损耗C ．附加损耗6、为什么可以把变压器的空载损耗看作变压器的铁耗，短路损耗看作额定负载时的铜耗？ 参考答案3、B ．4、A ．6、变压器空载试验时，从电源输入的有功功率主要消耗在铁心上（磁路）；变压器短路试验时，从电源输入的有功功率主要消耗在绕组上（电路）。