季节指数预测法

第九章时间序列预测9.3季节指数法市场变化趋势除了直线变动外还有季节性变动、循环变动和不规则变动趋势。

其中季节性变动现象与我们的生活息息相关。

让我们来了解一下，怎样利用季节性变动规律进行市场预测。

一、季节指数法的含义与作用1、季节指数法的含义首先要指出的是，这里所说的季节，既不同于日历上讲的季度，也不同于气象上所讲的季节，他是用来描述任何重复出现额每小时。

每周。

每月或每季等相似间隔的时间段。

在市场预测中多指一年中经营活动的某一固定形态。

季节变动是以一年为周期，经济变量随季节变化而变化的周期性变动。

在社会经济活动中，这种变动是客观存在的而且是常见的，他与春夏秋冬自然季节和社会风俗相联系。

如服装、冷食、高档副食品、农药等，季节性需求变动非常明显。

掌握季节变动规律，就可以利用这种规律进行市场预测。

所谓季节系数法，是根据预测对象各个日历年度按月或按季编制的时间序列资料，以统计方法测定出反映季节变动规律的季节变动系数，并据以进行预测的一种预测方法。

季节系数(也称季节系数)是以相对数形式表现的季节变动指标，一般用百分数或系数表示。

利用季节系数法进行预测，一般要求时间序列的时间单位或是季或是月；要掌握至少三年以上的按月或按季编制的时间序列，因为仅靠一年或两年的统计资料来确定季节变动规律，可能会由于偶然因素的影响而造成较大误差。

所以，为保证预测的准确性，一般需要掌握多年的时间序列资料。

2、季节指数预测法的目的季节指数预测法的目的是要分析季节变动因素对预测对象发展趋势的影响作用，并以此来预测未来趋势。

季节指数预测法在生活中的应用非常广泛，许多经济现象和市场变化都能够利用该方法得到较准确的预测，因此受到人们的重视。

二、季节指数法的应用1、直线趋势比率平均法时间序列存在直线趋势的情况下，季节变动预测通常需要消除只直线趋势的影响。

直线趋势比率平均法能够很好滴消除这种影响，达到准确预测。

调查窗口 9—2 季节指数法季节指数法可分为两类：一类是不考虑长期趋势的季节系数法；另一类是考虑长期趋势的季节系数法。

季节变动预测法课件2023-10-29•季节变动预测法概述•季节变动预测法的基本原理•季节变动预测法的应用•季节变动预测法的实践案例•季节变动预测法的优缺点及改进方向目•相关软件工具介绍及操作演示录01季节变动预测法概述定义季节变动预测法是一种基于时间序列数据，识别和预测具有季节性特征的周期性变化的方法。

特点考虑了时间序列数据中季节性因素的影响，能够揭示数据的周期性变化规律，适用于具有明显季节性特征的时间序列数据的预测。

定义与特点适用范围适用于具有明显季节性特征的周期性变化的时间序列数据，如旅游客流量、能源消耗量、农产品产量等。

限制不适用于非周期性变化的数据，或者季节性特征不明显的数据。

此外，季节变动预测法通常需要较长的历史数据，对于较短的时间序列数据可能无法准确预测。

适用范围与限制方法比较与选择方法比较01季节变动预测法与其他预测方法相比，如线性回归、指数平滑等，具有更强的针对性，特别是对于具有明显季节性特征的数据，预测效果通常更佳。

方法选择02在选择季节变动预测法时，需要考虑数据的特征和预测需求。

对于周期性变化明显、季节性因素重要的数据，季节变动预测法是一种有效的预测方法。

注03以上内容仅为概括性的描述，实际应用中还需要根据具体数据特征和预测需求进行详细的分析和应用。

02季节变动预测法的基本原理时间序列分析时间序列的分类根据数据性质的不同，时间序列可分为定量数据和定性数据两大类。

时间序列分析的意义通过对时间序列数据的分析，可以揭示现象在时间上的变化规律，发现其发展变化的趋势，为预测未来走势提供依据。

时间序列的定义时间序列是指按时间顺序排列的一组数据，用于反映某一现象在时间上的变化和发展趋势。

1季节指数计算23季节指数是根据时间序列数据，通过计算特定时间段内数据的平均值或加权平均值，反映现象在该时间段内的变化规律。

季节指数的定义根据时间序列数据性质的不同，季节指数可分为日季节指数、月季节指数、季度季节指数等。

季节指数预测法运用实例假设公司经营多种产品，其中一种产品是每年销售量呈现明显的季节性变化。

我们已经收集到该产品过去5年（60个月）的销售数据，现在需要利用这些数据来预测未来12个月的销售情况。

首先，我们应该生成季节指数。

季节指数可以通过计算每个季度平均销售量占总年销售量的比例来得到。

然后，季度平均销售量除以季度指数，即可得到季度调整后的销售量。

假设我们选取第一年的数据作为基期计算季度指数，即将第一年的季度指数设为1、则可以按照以下步骤进行计算：1.计算每个季度的销售总量：季度1：(销售量1+销售量5+销售量9+销售量13+销售量17+销售量21+销售量25+销售量29+销售量33+销售量37+销售量41+销售量45+销售量49+销售量53+销售量57)=总销售量1季度2：(销售量2+销售量6+销售量10+销售量14+销售量18+销售量22+销售量26+销售量30+销售量34+销售量38+销售量42+销售量46+销售量50+销售量54+销售量58)=总销售量2季度3：(销售量3+销售量7+销售量11+销售量15+销售量19+销售量23+销售量27+销售量31+销售量35+销售量39+销售量43+销售量47+销售量51+销售量55+销售量59)=总销售量3季度4：(销售量4+销售量8+销售量12+销售量16+销售量20+销售量24+销售量28+销售量32+销售量36+销售量40+销售量44+销售量48+销售量52+销售量56+销售量60)=总销售量42.计算每个季度的季度指数：季度指数1=总销售量1/(总销售量1+总销售量2+总销售量3+总销售量4)季度指数2=总销售量2/(总销售量1+总销售量2+总销售量3+总销售量4)季度指数3=总销售量3/(总销售量1+总销售量2+总销售量3+总销售量4)季度指数4=总销售量4/(总销售量1+总销售量2+总销售量3+总销售量4)3.计算每个月的季度调整销售量：月度销售量1=销售量1/季度指数1月度销售量2=销售量2/季度指数2...月度销售量60=销售量60/当季季度指数接下来，我们可以利用计算得到的季度调整销售量进行预测。

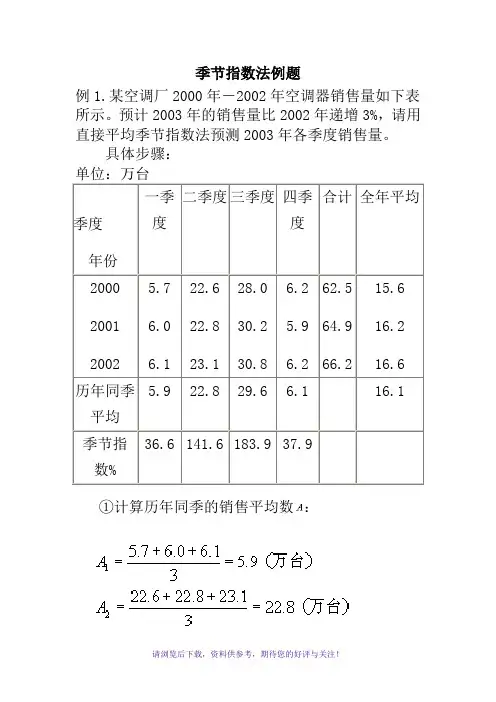
季节指数法例题
例1.某空调厂2000年－2002年空调器销售量如下表所示。

预计2003年的销售量比2002年递增3%，请用直接平均季节指数法预测2003年各季度销售量。

具体步骤：
季度
年份
一季
度
二季度三季度四季
度
合计全年平均
2000
2001
2002
5.7
6.0
6.1
22.6
22.8
23.1
28.0
30.2
30.8
6.2
5.9
6.2
62.5
64.9
66.2
15.6
16.2
16.6 历年同季
平均
5.9 22.8 29.6
6.1 16.1
季节指
数%
36.6 141.6 183.9 37.9
①计算历年同季的销售平均数：
同理，
②计算历年季度总平均数：
③计算季节指数：
同理有：
④计算2003年各季度预测值：
依据题意：
2003年销售预测值=（万台）
2003年第一季度预测值=（万台）
2003年第二季度预测值=（万台）
2003年第三季度预测值=（万台）
2003年第四季度预测值=（万台）。

季节指数法则
季节指数法是一种基于时间序列中季节性周期变动的预测方法。

它通过计算描述该变动的季节变动指数来预测目标未来的状况。

这种方法适用于具有明显季节性特征的数据，如销售、生产等。

季节指数的计算步骤如下：
1. 收集数据：收集时间序列数据，确保数据具有明显的季节性特征。

2. 求出各年同月或同季观察值的平均数（用A表示）。

3. 求历年间所有月份或季度的平均值（用B表示）。

4. 计算各月或各季度的季节指数，即C=A/B。

季节指数法的应用非常广泛，可以用于预测销售、库存、生产等领域的未来趋势。

通过计算季节指数，企业可以更好地了解市场需求和销售情况，从而制定更加合理的生产和销售计划。

需要注意的是，季节指数法只适用于具有明显季节性特征的数据，对于非季节性数据或季节性特征不明显的数据，这种方法可能不太适用。

同时，在进行季节指数预测时，还需要考虑其他因素的影响，如经济环境、市场竞争等。

因此，在使用季节指数法进行预测时，需要结合其他方法和数据来源进行综合分析。

第一节季节变动数据模式分析法及预测步骤一、数据模式的分析法1、叠加法2、乘积法二、预测步骤第一步：确定在不考虑季节变化因素影响下的年度预测值，也称水平/趋势预测值。

第二步：利用按季（月）度的各年历史值（3年以上）计算各季度的季节指标（季节指数、季节变差、季节比重。

第三步：运用步骤二中得到的季节指标和步骤一中得到的年度预测值，从而估算预测期各季（月）度的预测值。

第二节季节指数预测法一、季节指数的测算方法1、按季平均法例：某食品公司历年肉制品按季销售资料如表所示（单位：吨）：表8—1 按季平均法计算表年份第一季度第二季度第三季度第四季度2001 2150 1440 1485 17682002 2192 1500 1510 17952003 2089 1495 1504 17652004 2230 1530 1525 18102005 2285 1510 1579 1796历年同季的季度平均值见上表中所示。

表8—2 按季平均法计算表2、全年比率平均法分两步：二、实际预测1、情形一：已知年度预测值，估计各季度预测值2、情形二：已知某季度的实际值，估计其它各季预测值。

第三节季节变差预测法一、季节变差指标的测定方法某季的季节变差=历年同季的季节平均值－全时期季度平均值例题：上例中（见表8-1数据），要求利用季节变差估算各季度预测值。

二、实际预测1、情形一：已知年度预测值，预测其它各季度值。

某季的预测值=年度预测值/4+该季的季节变差例：数据同上，预计2006年该公司肉制品销售量比上年增加3%，估计其它各季度预测值，即2006年度预测值为：7170 ×（1+3%）=7385 （吨），预测各季度值。

2、情形二：已知某季的实际值，估计其它各季度预测值。

某季度预测值=已知季度的实际值—已知季度的季节变差+该季的季节变差例题：上例中，2004年一季度销售量为2400吨，要求预测其它各季销售量。

第二季度的预测值=2400-441.3+(-252.9)=1705.8（吨）第三季度的预测值=2400-441.3+(-229.1)=1729.6 （吨）第四季节的预测值=2400-441.3+38.9=1997.6 （吨）全年的预测值=(2400-441.3)×4=7834.8 （吨）第四节季节比重预测法一、季节比重指标的测定方法一年中各季的季节比重之和为100%，平均每季季节比重为25%，大于25%，高于平均水平，小于25%，低于平均水平。

四、季节变动预测法季节变动是指由于自然条件和社会条件的影响，事物现象在一年内随着季节的转换而引起的周期性变动。

例如，电力系统一天24小时的负荷和交通系统的客运量均呈现季节性的波动。

为了掌握季节性变动的规律，测算未来的需求，正确地进行各项经济管理决策，及时组织生产和交通运输、安排好市场供给，必须对季节变动进行预测。

季节变动预测就是根据以日、周、月、季为单位的时间序列资料，测定以年为周期、随季节转换而发生周期性变动的规律性方法。

进行季节变动分析和预测，首先要分析判断该时间序列是否呈现季节性变动。

通常，将3—5年的已知资料绘制历史曲线图，以其在一年内有无周期性波动作出判断。

然后，将各种影响因素结合起来，考虑它是否还受趋势变动和随机变动等其他因素的影响。

季节变动的预测方法有很多，最常用的方法是平均数趋势整理法。

它的基本思想是：通过对不同年份中同一时期数据平均，消除年随机变动，然后再利用所求出的平均数消除其中的趋势成分，得出季节指数，最后建立趋势季节模型进行预测。

下面以例5.5为例，介绍平均数趋势整理法的实际操作。

例5.5 已知某市2003年至2005年接待海外游客资料如表5.7所示，要求预测2006年第一季度各月该市接待海外游客的数量。

表5.7 某市2003-2005年接待海外游客资料单位：万人次[解] (1)求出各年的同月平均数，以消除年随机变动。

以n代表时间序列所包含的年数，i r表示各年第i个月的同月平均数，则：173191715...121111=++=+++=n y y y r n33.193212017...222122=++=+++=n y y y r n……253272523...1221211212=++=+++=n y y y r n求各年的月平均数，以消除月随机变动。

以)(t y -表示第t 年的月平均数，则：83.261223241715121121211)1(=++++=+++=-y y y y33.301225292017122122221)2(=++++=+++=-y y y y……5.321227302119121221)(=++++=+++=-n n n n y y y y建立趋势预测模型，求趋势值。

简单季节指数法的步骤[1]简单季节预测法的具体步骤如下：1.收集历年按季度记录的历史统计资料；2.计算出n年各相同季度的平均值(A)；3.计算出n年每一个季度的平均值(月)；4.计算季节指数，即用各季度的平均值除以所有季度的平均值：式中C=A/BC——季节指数。

5.利用季节指数(C),对预测值进行修正：Yt = (a + bT)C i式中Ci——第i季度的季节指数(i=1,2,3,4)；Yt——第t季度的销售量；a——待定系数；b——待定系数；T——预测期季度数，[编辑]简单季节指数法实例分析[1]例如，某公司从1996年到2001年，每一年各季度的纺织品销售量见下表。

预测2001年各季度纺织品的销售量。

1996 600 180 150 120 150 1997 660 210 160 130 160 1998 700 230 170 130 170 1999 750 250 180 140 180 2000 850 300 200 150 200 2001 1000 400 220 160 220 合计4560 1570 1080 830 1080 季节指数 1.38 0.95 0.73 0.95预测过程如下：1.六年各相同季节的平均销售量(Ai)A1=1970÷6≈262(单位)同理A_2=180，A_3≈138.3，A_4=180(单位)2.六年所有季度的平均销售量(B)(单位) M——6年销售量总和3.各季节销售指数(Ci)Ci=262÷19≈1.38同理C2≈0.95，C3≈0.73，C4≈0.954.修正2002年各季度预测值(1)建立时间序列线性回归预测模型由上表可得知各有关数据，利用公式(1)(2)y_t=190+1.90T式中T=-23,-21,…,-1,1,3,…,23(2)修正2002年各季度预测值第一季度预测值=(190+1.90×25)×1.38≈328(单位) 第二季度预测值=(190+1.90×27)×0.95≈229(单位) 第三季度预测值=(190+1.90×29)×0.73≈179(单位) 第三季度预测值=(190+1.90×31)×0.95≈236(单位)注意：如果n为奇数，例如n=9，则T=-4，-3，-2，1，0，1，2，3，4.季节销售指数也可以按月计算。