高考题分类线性规划

高考数学中的线性规划方法与应用随着社会的发展，人们的生活方式发生了改变，竞争压力也越
来越大。

在这样一个背景下，高考成为了每个学生追求的目标。

高考数学中，线性规划是一个重要的知识点，不仅在考试中会涉
及到，而且在现实生活中也有广泛的应用。

一、线性规划的概念与优化目标
线性规划是在一些约束条件下，寻求最大或最小值的一种优化
方法。

其优化目标是一种线性函数，约束条件可以是等式或不等式，且约束条件和目标函数都具有线性关系。

在高考数学中，线
性规划通常会考察如何列出约束条件和目标函数。

二、线性规划的解法
线性规划的解法有图像法、单纯形法和对偶理论法。

其中，单
纯形法是应用最广泛的一种解法，通过不断寻找相邻基的交点，
找出最优解。

三、线性规划在实际生活中的应用
线性规划在实际生活中有着广泛的应用。

比如，在物流领域中，通过线性规划可以优化物流路线和货物分配，从而降低成本和提
高效率。

在工业生产中，线性规划可以优化设备运行状态和员工
分配，实现生产效益的最大化。

在金融投资方面，线性规划可以
帮助投资者优化组合投资方案，最大化投资回报。

在航空运输方面，线性规划可以优化航线安排和机组人员分配，实现航空运输
的安全和效率。

以上仅是线性规划在实际生活中应用的一部分。

结语
高考数学中的线性规划知识点，虽然看起来有些枯燥，但是它
在实际生活中有着广泛的应用。

掌握线性规划的解法和应用场景，可以为学生的未来发展打下坚实的基础。

希望读者可以通过对线
性规划的学习，更好地了解这个领域的发展和应用。

高三数学线性规划试题1.变量、满足线性约束条件，则目标函数的最大值为 .【答案】【解析】作出不等式组所表示的可行域如图所示，联立得，作直线，则为直线在轴上的截距，当直线经过可行域上的点时，直线在轴上的截距最大，此时取最大值，即.【考点】线性规划.2.设，满足约束条件且的最小值为7，则A．-5B．3C．-5或3D．5或-3【答案】B【解析】根据题中约束条件可画出可行域如下图所示，两直线交点坐标为：，又由题中可知，当时，z有最小值：，则，解得：;当时，z无最小值．故选B【考点】线性规划的应用3.若、满足和，则的取值范围是________.【答案】【解析】不等式组表示的平面区域如图中，令，解方程组得，解方程组得，平移直线经过点使得取得最大值，即，当直线经过点使得取得最小值，即，故的取值范围是.【考点】不等式组表示的平面区域，求目标函数的最值，容易题.4.若变量、满足约束条件，则的最大值是（）A．2B．4C．7D．8【答案】C【解析】不等式组表示的平面区域如图的四变形（包括边界），解方程组得点，令，平移直线经过点使得取得最大值，即.选C.【考点】不等式组表示的平面区域，求目标函数的最大值，容易题.5.已知α，β是三次函数f(x)＝x3＋ax2＋2bx(a，b∈R)的两个极值点，且α∈(0,1)，β∈(1,2)，求动点(a，b)所在的区域面积S.【答案】【解析】解：由函数f(x)＝x3＋ax2＋2bx(a，b∈R)可得，f′(x)＝x2＋ax＋2b，由题意知α，β是方程x2＋ax＋2b＝0的两个根，且α∈(0,1)，β∈(1,2)，因此得到可行域即，画出可行域如图．∴动点(a，b)所在的区域面积S＝.6.设是不等式组表示的平面区域内的任意一点，向量，，若（为实数），则的最大值为（）A．4B．3C．-1D．-2【答案】A【解析】解：设点的坐标为，则，所以所以由得此不等式组对应的平面区域如下图中的阴影部分所示：设，则，当变化时，它表示一组与平行的直线，在轴上的截距为，当直线在轴上的截距最小时最大，由图可知，当直线经过点时，直线在轴上的截距最小，从面取得最大值故选A.【考点】1、向量的坐标表示与坐标运算；2、线性规划.7. [2013·陕西高考]若点(x ，y)位于曲线y ＝|x －1|与y ＝2所围成的封闭区域，则2x －y 的最小值为________．【答案】－4 【解析】由题意知y ＝，作出曲线y ＝|x －1|与y ＝2所围成的封闭区域，如图中阴影部分所示，即得过点A(－1,2)时，2x －y 取最小值－4．8. (2014·孝感模拟)已知实数x,y 满足若z=x 2+y 2,则z 的最大值为________.【答案】13【解析】画出可行域,z=x 2+y 2=()2,表示可行域内的点(x,y)和原点(0,0)距离的平方,可知点B(2,3)是最优解,z max =13.9. 已知函数在x 1处取得极大值,在x 2处取得极小值,且x 1∈（－1，1），x 2∈（1，2），则2a+b 的取值范围是（ ） A ．（－7，2） B ．（－7，3） C ．（2，3） D ．（－1，2）【答案】B【解析】∵f′(x)= x 2+bx －a, ∴据题意知, f′(x 1)= f′(x 2)=0,又据二次函数知, f′(－1) ＞0 且f′(1)＜0且f′(2)＞0 即如图为(a,b)之可行域,A(1,0),B(2,－1),(－2,－3)．把A,B,C 三点坐标代入2a+b 得2,3,－7所以2a+b 的范围为(－7,3)10.若，满足约束条件，则的最大值为．【答案】【解析】画出可行域，如图所示，将目标函数变形为，当直线经过点时，目标函数取到最大值为．【考点】线性规划.11.若变量满足约束条件，则目标函数z=2x+3y的最大值为________.【答案】14【解析】如图所示，画出可行域，目标函数变形为，当取最大值时，纵截距最大，故将直线向上平移到E时，目标函数z=2x+3y取到最大值，此时．【考点】线性规划.12.设z=kx+y，其中实数x、y满足，若z的最大值为12，则实数k= ．【答案】2【解析】由得.作出不等式组表示的区域如图所示.由图可知，若，则当或时最大，且最大值不超过4. 若，则当时最大，由得.【考点】线性规划.13.已知实数满足，则的最小值是.【答案】4【解析】因为实数满足，如图所示，令=k,所以.由于当k<0时抛物线的开口向下，所以不合条件.所以k>0，有两种情况当k取最小值即抛物线过点.所以的最小值是.当抛物线与直线相切的情况，，即的最小值是4.【考点】1.线性规划问题.2.抛物线的问题.3.分类归纳的思想.4.构建数形结合解题的思想.14.若实数满足，则的值域是 .【答案】[1,9]【解析】首先画出可行域（如图），直线，平移直线知，过时，最小值为0，过点时，的最大值为2；根据指数函数是单调增函数，即可得到的值域为[1,9].【考点】简单线性规划的应用，函数的值域.15.假设每天从甲地去乙地的旅客人数X是服从正态分布N(800,502)的随机变量．记一天中从甲.地去乙地的旅客人数不超过900的概率为p(1)求p的值；(参考数据：若X～N(μ，σ2)，有P(μ－σ＜X≤μ＋σ)＝0.682 6，P(μ－2σ＜X≤μ＋02σ)＝0.954 4，P(μ－3σ＜X≤μ＋3σ)＝0.997 4)(2)某客运公司用A、B两种型号的车辆承担甲、乙两地间的长途客运业务，每车每天往返一次．A、B两种车辆的载客量分别为36人和60人，从甲地去乙地的营运成本分别为1 600元/辆和2 400元/辆．公司拟组建一个不超过21辆车的客运车队，并要求B型车不多于A型车7的概率运完从甲地去乙地的旅客，且使公司从甲地去乙地的营运成本最辆．若每天要以不小于p小，那么应配备A型车、B型车各多少辆？【答案】(1) 0.977 2 (2)配备A型车5辆、B型车12辆【解析】解：(1)由于随机变量X服从正态分布N(800，502)，故有μ＝800，σ＝50，P(700<X≤900)＝0.954 4.由正态分布的对称性，可得p＝P(X≤900)＝P(X≤800)＋P(800<X≤900)＝＋P(700<X≤900)＝0.977 2. (2)设A型、B型车辆的数量分别为x，y辆，则相应的营运成本为1 600x＋2 400y. 依题意，x，y还需满足x＋y≤21，y≤x＋7，P(X≤36x＋60y)≥p.由(1)知，p0＝P(X≤900)，故P(X≤36x＋60y)≥p等价于36x＋60y≥900.于是原问题等价于求满足约束条件且使目标函数z＝1 600x＋2 400y达到最小的x，y.作可行域如图所示，可行域的三个顶点坐标分别为P(5,12)，Q(7,14)，R(15,6)．由图可知，当直线z＝1 600x＋2 400y经过可行域的点P时，直线z＝1 600x＋2 400y在y轴上截距最小，即z取得最小值．故应配备A型车5辆、B型车12辆．16.已知z="2x" +y，其中x，y满足且z的最大值是最小值的4倍，则a的值是【答案】【解析】画出可行域，可知目标函数在取最小值，在取最大值，故.【考点】线性规划.17.若函数图像上存在点满足约束条件,则实数的最大值为 .【答案】2【解析】作出不等式组表示的平面区域，得到如图所示的图形（阴影），为使函数图像上存在点在阴影部分内，由得，所以，实数的最大值为2.【考点】简单线性规划的应用18.已知中心为O的正方形ABCD的边长为2，点M，N分别为线段BC，CD上的两个不同点，且||=1，则的取值范围是．【答案】【解析】设M（2，b），N（a，2）．由，可得，即（a﹣2）2+（b﹣2）2=1．且1≤a≤2，1≤b≤2．如图所示，建立平面直角坐标系．又=（1，b﹣1）•（a﹣1，1）=a+b﹣2．作出可行域，即可得出答案．如图所示，建立平面直角坐标系．设M（2，b），N（a，2）．∵，∴，即（a﹣2）2+（b﹣2）2=1．且1≤a≤2，1≤b≤2．又O（1，1），∴=（1，b﹣1）•（a﹣1，1）=a+b﹣2．令a+b﹣2=t，则目标函数b=﹣a+2+t，作出可行域，如图2，其可行域是圆弧．①当目标函数与圆弧相切与点P时，，解得t=2﹣取得最小值；②当目标函数经过点EF时，t=2+1﹣2=1取得最大值．∴．即为的取值范围．故答案为．【考点】平面向量数量积的运算点评：本题综合考查了向量的模的计算公式、线性规划等基础知识，及数形结合思想方法．熟练掌握是解题的关键．19.已知x、y满足约束条件的取值范围为【答案】[-1，2]【解析】根据二元一次不等式组画出可行域，目标函数几何意义z为直线z=x-y的纵截距相反数，平移目标函数观察z取值范围解：①如图可行域，②令z=0得直线y=x平移直线可知当直线过（0，1）时，z有最小值z=0-1=-1，直线过（2，0）时，z有最大值z=2-0=2；所以z的取值范围为[-1，2]；故答案[-1，2]。

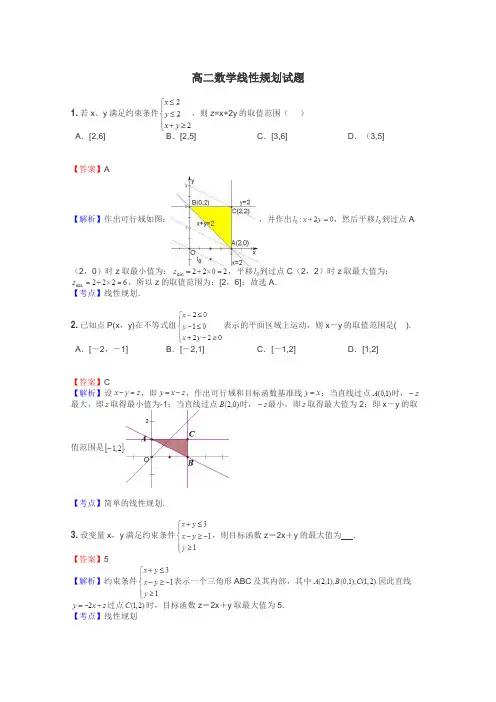
高二数学线性规划试题1.若x、y满足约束条件，则z=x+2y的取值范围（）A．[2,6]B．[2,5]C．[3,6]D．（3,5]【答案】A【解析】作出可行域如图：，并作出，然后平移到过点A（2，0）时z取最小值为：，平移到过点C（2，2）时z取最大值为：，所以z的取值范围为：[2，6]；故选A．【考点】线性规划．2.已知点P(x，y)在不等式组表示的平面区域上运动，则x－y的取值范围是( ). A．[－2，－1]B．[－2,1]C．[－1,2]D．[1,2]【答案】C【解析】设，即，作出可行域和目标函数基准线；当直线过点时，最大，即取得最小值为-1；当直线过点时，最小，即取得最大值为2；即x－y的取值范围是.【考点】简单的线性规划.3.设变量x，y满足约束条件，则目标函数z＝2x＋y的最大值为．【答案】5【解析】约束条件表示一个三角形ABC及其内部，其中因此直线过点时，目标函数z＝2x＋y取最大值为5.【考点】线性规划4.已知实数满足条件，则的最大值为．【答案】10【解析】作出满足约束条件下的平面区域，如图所示．由图可知点目标函数经过点时取得最大值，且最大值为．【考点】简单的线性规划．5.若实数满足不等式组，则的最小值为。

【答案】【解析】由不等式组作可行域如图，可行域内点的横纵坐标均为非负值，且不同时为0，可知在点C（0,1）处去最小值，将点C 代入，可知最小值为-1．【考点】简单线性规划．．6.若变量、满足约束条件，则的最大值为 .【答案】1【解析】可行域为如图所示三角形内部（包括边界）则【考点】线性规划问题7.某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨，供电至多450千瓦，问该厂如何安排生产，使得该厂日产值最大？最大日产值为多少?【答案】该厂每天安排生产甲产品5吨，乙产品7吨，则该厂日产值最大，最大日产值为124万元.【解析】根据已知条件列出线性约束条件，和目标函数。

高考数学常考题型：线性规划非线性目标函数---绝对值型典例1．已知实数,x y 满足：210210x y x x y -+≥⎧⎪<⎨⎪+-≥⎩，221z x y =--，则z 的取值范围是（ ） A ．5[,5]3B ．[0,5)C ．[0,5]D ．5[,5)31．B由约束条件作出可行域如图：()22,110x A x y =⎧⇒-⎨+-=⎩， 21012,1033x y B x y -+=⎧⎛⎫⇒⎨⎪+-=⎝⎭⎩． 令221u x y =--，变形可得12u y x +=-，平移目标函数线12u y x +=-使之经过可行域，当目标函数线过点()2,1A -时，纵截距最小，此时u 取得最大值，即()max 222115u =⨯-⨯--=．当目标函数线过点12,33B ⎛⎫ ⎪⎝⎭时，纵截距最大，此时u 取得最小值，即min 125221333u =⨯-⨯-=-． 因为点()2,1A -不在可行域内，所以553u -≤<，[)0,5z u ∴=∈．故B 正确．点评：有关线性规划的最值问题，数形结合是解决问题的关键。

求目标函数z ax by =+的最值，应先函数变为a z y x b b=-+，然后平移直线，求纵截距zb 的最值，进而可得z 的最值。

变式题1．若x,y 满足约束条件220130x y y x y -+≤⎧⎪≥⎨⎪+-≤⎩，则4312z x y =+-的最小值为（ ）A ．53B ．1C ．2D ．35典例2．已知点(),P x y 满足10100x y x y x -+≥⎧⎪+-≤⎨⎪≥⎩，2628x y y x +-+-+的取值范围是__________．4．画出不等式组表示的可行域如图阴影部分所示．∵2628x y y x +-+-+=+=，∴2628x y y x +-+-+表示可行域内的点到直线260x y +-=和280x y --=2628x y y x +-+-+无最大值．由28010x y x y --=⎧⎨+-=⎩解得32x y =⎧⎨=-⎩，所以点A 的坐标为()3,2-．此时26282x y y x +-+-+=．由26010x y x y +-=⎧⎨+-=⎩解得54x y =⎧⎨=-⎩，所以点A 的坐标为()5,4-． 此时26286x y y x +-+-+=． ∴2628x y y x +-+-+的最小值为2，故得2628x y y x +-+-+的取值范围为[)2,+∞．点评：线性规划中的目标函数中若含有绝对值，则解题时可根据点到直线的距离公式求解，在求解过程中需要注意对目标函数进行相应的变形，使之变为距离的形式，如ax by c ++=变式题2．变量,x y 满足约束条件220240,10x y x y x y +-≥⎧⎪+-≤⎨⎪-+≥⎩则目标函数231z x y =--的取值范围是___. 闯关题：1．已知221log 2()220xx f x x xx ⎧≤≤⎪=⎨⎪--≤⎩，若1111a b -≤≤⎧⎨-≤≤⎩，且方程2[()]()0f x af x b -+=有5________ 2．若实数,x y 满足方程228x y +=，则|2||6||6|x y x y x y +-++++--的最大值为( ) A ．12 B ．14C ．18D ．24参考答案变式题1．A将目标函数变形为431255x y z +-=⨯，即“目标函数表示可行域内的点到直线43120x y +-=的距离的5倍”.画出可行域如下图所示，由图可知，点A 到直线43120x y +-=最短，联立22030x y x y -+=⎧⎨+-=⎩，解得45,33A ⎛⎫⎪⎝⎭最短距离为16151213353+-=，乘以5得53，故选A.变式题2．[]1,3-不等式组对应的可行域如下图所示，当x≥0，0≤y≤1时，23(1)233z x y x y =--=+-，此时2333z y x +=-+，直线的纵截距越大，z 越大，纵截距越小，z 越小. 当直线经过点B(0,1)时，z 最小=0+3-3=0，当直线经过点D 3(,1)2时，z 最大=3+3-3=3，所以此时z 的范围为[0,3]当x≥0，y ＞1时，23(1)233z x y x y =--=-+，此时2333z z x -=+，直线的纵截距越大，z 越小，纵截距越小，z 越大. 当直线经过点A(1,2)时，z 最小=2-6+3=-1，当直线经过点D 3(,1)2时，z 最大=3-3+3=3，所以此时z 的范围为[-1,3]综合得z 的取值范围为：[]1,3-故答案为：[]1,3- 闯关题：1．作出函数()y f x =的图象如下图所示：设()t f x =，则方程()()20f x af x b -+=⎡⎤⎣⎦有5个不同根转化二次方程20t at b -+=的两根101t <<，20t <，构造函数()2g t t at b =-+，可得不等式()()0010g g ⎧<⎪⎨>⎪⎩，即010b a b <⎧⎨-+>⎩，结合1111a b -≤≤⎧⎨-≤≤⎩，作出图形如下图所示，不等式组1111a b -≤≤⎧⎨-≤≤⎩表示的平面区域为边长为2的正方形ABCD ，不等式组0101111b a b a b <⎧⎪-+>⎪⎨-≤≤⎪⎪-≤≤⎩表示的区域为下图中的阴影部分（不包括a 轴），视为可行域中的点(),a b 到直线210a b -+=的距离，当点(),a b 与点()1,0E==的取值范围是0,5⎡⎫⎪⎢⎪⎣⎭，故答案为：0,5⎡⎢⎣⎭. 2．C 令t x y =+，则4sin [4,4]4t πθθθ⎛⎫=+=+∈- ⎪⎝⎭， 于是|2|[0,6]t -∈，60t +>，60t ->，从而|2||6||6||2||6||6||2|12[12,18]x y x y x y t t t t +-++++--=-+++-=++∈，故选：C.。

高三数学线性规划试题答案及解析1.，满足约束条件，若取得最大值的最优解不唯一，则实数的值为（）A．或B．或C．或D．或【答案】D．【解析】如图，画出线性约束条件所表示的可行域，坐出直线，因此要使线性目标函数取得最大值的最优解不唯一，直线的斜率，要与直线或的斜率相等，∴或．【考点】线性规划．2.已知最小值是5，则z的最大值是（）A．10B．12C．14D．15【答案】A【解析】首先作出不等式组所表示的平面区域，如图中黄色区域，则直线-2x+y+c=0必过点B（2，-1），从而c=5,进而就可作出不等式组所表示的平面区域，如图部的蓝色区域：故知只有当直线经过点C（3，1）时，z取最大值为：，故选A．【考点】线性规划．3.执行如图1所示的程序框图，如果输入的，则输出的的最大值为（）A．B．C．D．【答案】C【解析】该程序执行以下运算：已知，求的最大值.作出表示的区域如图所示，由图可知，当时，最大，最大值为.选C.【考点】程序框图与线性规划.4.执行如图1所示的程序框图，如果输入的，则输出的的最大值为（）A．B．C．D．【答案】C【解析】该程序执行以下运算：已知，求的最大值.作出表示的区域如图所示，由图可知，当时，最大，最大值为.选C.【考点】程序框图与线性规划.5.设变量满足约束条件则目标函数的最小值为（）A．2B．3C．4D．5【答案】B【解析】作出可行域:oyxA(1，1)由图可知，当直线过点时，目标函数取最小值为3，选B.【考点】线性规划6.已知x，y满足条件，则目标函数的最大值为 .【答案】【解析】画出可行域，如下图所示，将目标函数变形为，当取到最大值时，直线的纵截距最大，故将直线向上平移到过点C时，目标函数取到最大值，，得，故．【考点】线性规划．7.若变量满足约束条件，则的最大值为_________.【答案】【解析】作出不等式组表示的区域如下,则根据线性规划的知识可得目标函数在点处取得最大值,故填.【考点】线性规划8.设x，y满足约束条件，则z＝(x＋1)2＋y2的最大值为()A．80B．4C．25D．【答案】A【解析】作出不等式组表示的平面区域，如图中阴影部分所示．(x＋1)2＋y2可看作点(x，y)到点P(－1,0)的距离的平方，由图可知可行域内的点A到点P(－1,0)的距离最大．解方程＝(3＋1)2＋82＝80.组，得A点的坐标为(3,8)，代入z＝(x＋1)2＋y2，得zmax9.已知实数满足，则目标函数的取值范围是．【答案】【解析】可行域表示一个三角形ABC，其中当直线过点A时取最大值4，过点B时取最小值2，因此的取值范围是.【考点】线性规划求取值范围10.设变量满足，则的最大值和最小值分别为（）A．1，-1B．2，-2C．1，-2D．2，-1【答案】B【解析】由约束条件，作出可行域如图，设，则，平移直线，当经过点时，取得最大值，当经过点时，取得最小值，故选．【考点】线性规划.11.（2011•浙江）设实数x、y满足不等式组，若x、y为整数，则3x+4y的最小值是（）A．14B．16C．17D．19【答案】B【解析】依题意作出可行性区域如图，目标函数z=3x+4y在点（4，1）处取到最小值z=16．故选B．12.若点(x,y)位于曲线y = |x|与y = 2所围成的封闭区域, 则2x－y的最小值为A．－6B．－2C．0D．2【答案】A【解析】的图像围成一个三角形区域，3个顶点的坐标分别是 (0,0),(-2,2),(2,2). 且当取点(-2,2)时，2x – y =" -" 6取最小值。

1．二元一次不等式(组)表示的平面区域满足二元一次不等式(组)的x和y的取值构成的有序数对(x，y)，叫做二元一次不等式(组)的解，所有这样的有序数对(x，y)构成的集合称为二元一次不等式(组)的解集．3．线性规划的有关概念1．画二元一次不等式表示的平面区域的直线定界，特殊点定域(1)直线定界：不等式中无等号时直线画成虚线，有等号时直线画成实线．(2)特殊点定域：若直线不过原点，特殊点常选原点；若直线过原点，则特殊点常选取(0，1)或(1，0)来验证．2．利用“同号上，异号下”判断二元一次不等式表示的平面区域对于Ax＋By＋C>0或Ax＋By＋C<0，则有(1)当B(Ax＋By＋C)>0时，区域为直线Ax＋By＋C＝0的上方；(2)当B(Ax＋By＋C)<0时，区域为直线Ax＋By＋C＝0的下方．3．平移规律当b >0时，直线z ＝ax ＋by 向上平移z 变大，向下平移z 变小；当b <0时，直线z ＝ax ＋by 向上平移z 变小，向下平移z 变大．一、思考辨析判断正误(正确的打“√”，错误的打“×”)(1)不等式Ax ＋By ＋C >0表示的平面区域一定在直线Ax ＋By ＋C ＝0的上方．( )(2)线性目标函数的最优解可能是不唯一的．( )(3)线性目标函数取得最值的点一定在可行域的顶点或边界上．( ) (4)在目标函数z ＝ax ＋by (b ≠0)中，z 的几何意义是直线ax ＋by －z ＝0在y 轴上的截距．( )答案：(1)× (2)√ (3)√ (4)× 二、易错纠偏常见误区| (1)不会用代点法判断平面区域； (2)不明确目标函数的最值与等值线截距的关系； (3)不理解目标函数的几何意义； (4)对“最优解有无数个”理解有误．1．若点(－2，t )在直线2x －3y ＋6＝0的上方，则t 的取值范围是__________． 解析：因为直线2x －3y ＋6＝0的上方区域可以用不等式2x －3y ＋6＜0表示，所以由点(－2，t )在直线2x －3y ＋6＝0的上方得－4－3t ＋6＜0，解得t ＞23.答案：⎝ ⎛⎭⎪⎫23，＋∞2．设x ，y 满足约束条件⎩⎨⎧y ＋2≥0，x －2≤0，2x －y ＋1≥0.则z ＝x ＋y 的最大值与最小值的比值为________．解析：不等式组所表示的平面区域如图中阴影部分所示，z ＝x ＋y 可化为y ＝－x ＋z ，当直线y ＝－x ＋z 经过A 点时，z 最大，联立⎩⎪⎨⎪⎧x －2＝0，2x －y ＋1＝0.得⎩⎪⎨⎪⎧x ＝2，y ＝5，故A (2，5)，此时z ＝7；当直线y ＝－x ＋z 经过B 点时，z 最小，联立⎩⎪⎨⎪⎧y ＋2＝0，2x －y ＋1＝0，得⎩⎨⎧x ＝－32，y ＝－2，故B ⎝ ⎛⎭⎪⎫－32，－2，此时z ＝－72，故最大值与最小值的比值为－2.答案：－23．已知x ，y 满足条件⎩⎨⎧x －y ＋5≥0，x ＋y ≥0，x ≤3，则z ＝y －1x ＋3的最大值为________．解析：作出可行域如图中阴影部分所示，问题转化为区域上哪一点与点M (－3，1)连线斜率最大，观察知点A ⎝ ⎛⎭⎪⎫－52，52，使k MA 最大，z max ＝k MA ＝52－1－52＋3＝3.答案：34．已知x ，y 满足⎩⎨⎧x －y ＋5≥0，x ＋y ≥0，x ≤3，若使得z ＝ax ＋y 取得最大值的点(x ，y )有无数个，则a 的值为________．解析：先根据约束条件画出可行域，如图中阴影部分所示，当直线z ＝ax ＋y 和直线AB 重合时，z 取得最大值的点(x ，y )有无数个，所以－a ＝k AB ＝1，所以a ＝－1.答案：－1二元一次不等式(组)表示的平面区域(多维探究) 角度一 平面区域的面积不等式组⎩⎨⎧x ≥0，x ＋3y ≥4，3x ＋y ≤4所表示的平面区域的面积等于()A ．32B ．23C ．43D ．34【解析】 由题意得不等式组表示的平面区域如图阴影部分所示，A ⎝ ⎛⎭⎪⎫0，43，B (1，1)，C (0，4)，则△ABC 的面积为12×1×83＝43.故选C ．【答案】 C角度二 平面区域的形状若不等式组⎩⎨⎧x －y ≥0，2x ＋y ≤2，y ≥0，x ＋y ≤a表示的平面区域是一个三角形，则a 的取值范围是________．【解析】不等式组⎩⎪⎨⎪⎧x －y ≥0，2x ＋y ≤2，y ≥0表示的平面区域如图所示(阴影部分)．解⎩⎪⎨⎪⎧y ＝x ，2x ＋y ＝2得A ⎝ ⎛⎭⎪⎫23，23；解⎩⎪⎨⎪⎧y ＝0，2x ＋y ＝2得B (1，0)．若原不等式组表示的平面区域是一个三角形，则直线x ＋y ＝a 中的a 的取值范围是0<a ≤1或a ≥43.【答案】 (0，1]∪⎣⎢⎡⎭⎪⎫43，＋∞(1)求平面区域面积的方法①首先画出不等式组表示的平面区域，若不能直接画出，应利用题目的已知条件转化为不等式组问题，从而再作出平面区域；②对平面区域进行分析，若为三角形应确定底与高，若为规则的四边形(如平行四边形或梯形)，可利用面积公式直接求解，若为不规则四边形，可分割成几个三角形分别求解再求和．(2)根据平面区域确定参数的方法在含有参数的二元一次不等式组所表示的平面区域问题中，首先把不含参数的平面区域确定好，然后用数形结合的方法根据参数的不同取值情况画图观察区域的形状，根据求解要求确定问题的答案．1．已知约束条件⎩⎨⎧x ≥1，x ＋y －4≤0，kx －y ≤0表示面积为1的直角三角形区域，则实数k的值为( )A ．1B ．－1C ．0D ．－2解析：选A ．作出约束条件表示的可行域如图中阴影部分所示，要使阴影部分为直角三角形，当k ＝0时，此三角形的面积为12×3×3＝92≠1，所以不成立，所以k ＞0，则必有BC ⊥AB ，因为x ＋y －4＝0的斜率为－1，所以直线kx －y ＝0的斜率为1，即k ＝1，满足题意，故选A ．2．设不等式组⎩⎨⎧x ≥1，x －y ≤0，x ＋y ≤4表示的平面区域为M ，若直线y ＝kx －2上存在M内的点，则实数k 的取值范围是( )A ．[1，3]B ．(－∞，1]∪[3，＋∞)C ．[2，5]D ．(－∞，2]∪[5，＋∞)解析：选C ．作出不等式组⎩⎪⎨⎪⎧x ≥1，x －y ≤0，x ＋y ≤4表示的平面区域，如图中阴影部分所示，因为直线l ：y ＝kx －2的图象过定点A (0，－2)，且斜率为k ，由图知，当直线l 过点B (1，3)时，k 取最大值3＋21－0＝5，当直线l 过点C (2，2)时，k 取最小值2＋22－0＝2，故实数k 的取值范围是[2，5]．求目标函数的最值(多维探究) 角度一 求线性目标函数的最值(2021·郑州第一次质量预测)若变量x ，y 满足约束条件⎩⎨⎧x ＋y ≥0，x －y ≥0，3x ＋y －4≤0，则y －2x 的最小值是( ) A ．－1 B ．－6 C ．－10D ．－15【解析】不等式组⎩⎪⎨⎪⎧x ＋y ≥0，x －y ≥0，3x ＋y －4≤0表示的平面区域如图中阴影部分所示．令z ＝y －2x ，作出直线y ＝2x ，并平移，当直线z ＝y －2x 过点B (2，－2)时，z 的值最小，最小值为－6，故选B ．【答案】 B(1)求目标函数的最值形如z ＝ax ＋by (b ≠0)的目标函数，可变形为斜截式y ＝－a b x ＋zb (b ≠0)． ①若b >0，当直线过可行域且在y 轴上的截距最大时，z 值最大，在y 轴上截距最小时，z 值最小；②若b <0，当直线过可行域且在y 轴上的截距最大时，z 值最小，在y 轴上的截距最小时，z 值最大．(2)求目标函数最优解的常用方法如果可行域是一个多边形，那么一般在某顶点处使目标函数取得最优解，到底哪个顶点为最优解，可有两种方法判断：①将可行域各顶点的坐标代入目标函数，通过比较各顶点函数值大小即可求得最优解；②将目标函数的直线平移，最先通过或最后通过的顶点便是最优解． 角度二 求非线性目标函数的最值(范围)实数x ，y 满足⎩⎨⎧x －y ＋1≤0，x ≥0，y ≤2.(1)若z ＝yx ，则z 的取值范围为________；(2)若z ＝x 2＋y 2，则z 的最大值为________，最小值为________．【解析】由⎩⎪⎨⎪⎧x －y ＋1≤0，x ≥0，y ≤2，作出可行域，如图中阴影部分所示．(1)z ＝yx 表示可行域内任一点与坐标原点连线的斜率，因此yx 的取值范围为直线OB 的斜率到直线OA 的斜率(直线OA 的斜率不存在，即z max 不存在)．由⎩⎪⎨⎪⎧x －y ＋1＝0，y ＝2，得B (1，2)， 所以k OB ＝21＝2，即z min ＝2， 所以z 的取值范围是[2，＋∞)．(2)z ＝x 2＋y 2表示可行域内的任意一点与坐标原点之间距离的平方． 因此x 2＋y 2的最小值为OA 2，最大值为OB 2. 由⎩⎪⎨⎪⎧x －y ＋1＝0，x ＝0，得A (0，1)， 所以OA 2＝(02＋12)2＝1，OB 2＝(12＋22)2＝5.【答案】 (1)[2，＋∞) (2)5 1【迁移探究1】 (变问法)本例条件不变，求目标函数z ＝y －1x －1的取值范围．解：z ＝y －1x －1可以看作过点P (1，1)及(x ，y )两点的直线的斜率．所以z 的取值范围是(－∞，0]．【迁移探究2】 (变问法)本例条件不变，求目标函数z ＝x 2＋y 2－2x －2y ＋3的最值．解：z ＝x 2＋y 2－2x －2y ＋3 ＝(x －1)2＋(y －1)2＋1，而(x －1)2＋(y －1)2表示点P (1，1)与Q (x ，y )的距离的平方PQ 2，PQ 2max ＝(0－1)2＋(2－1)2＝2，PQ 2min ＝⎝⎛⎭⎪⎪⎫|1－1＋1|12＋（－1）22＝12，所以z max ＝2＋1＝3，z min ＝12＋1＝32.常见两类非线性目标函数的几何意义(1)x 2＋y 2表示点(x ，y )与原点(0，0)间的距离，（x －a ）2＋（y －b ）2表示点(x ，y )与点(a ，b )间的距离；(2)yx 表示点(x ，y )与原点(0，0)连线的斜率，y －b x －a 表示点(x ，y )与点(a ，b )连线的斜率．角度三 求参数值或取值范围(2021·贵阳市第一学期监测考试)已知实数x ，y 满足⎩⎨⎧x ＋2≥y ，x ≤2，y －1≥0，若z＝x ＋ay (a >0)的最大值为10，则a ＝ ( )A ．1B ．2C ．3D ．4【解析】 不等式组表示的平面区域如图中阴影部分所示．由⎩⎪⎨⎪⎧x ＝2，x －y ＋2＝0， 解得⎩⎪⎨⎪⎧x ＝2，y ＝4，所以A (2，4)，由⎩⎪⎨⎪⎧x ＝2，y －1＝0，解得⎩⎪⎨⎪⎧x ＝2，y ＝1，所以B (2，1)，由⎩⎪⎨⎪⎧y －1＝0，x －y ＋2＝0，解得⎩⎪⎨⎪⎧x ＝－1，y ＝1，所以C (－1，1)．若(2，4)是最优解，则2＋4a ＝10，a ＝2，经检验符合题意；若(2，1)是最优解，则2＋a ＝10，a ＝8，经检验不符合题意；若(－1，1)是最优解，则－1＋a ＝10，a ＝11，经检验不符合题意．综上所述，a ＝2，故选B ．【答案】 B求解线性规划中含参数问题的基本方法有两种：一是把参数当成常数用，根据线性规划问题的求解方法求出最优解，代入目标函数确定最值，通过构造方程或不等式求解参数的值或取值范围；二是先分离含有参数的式子，通过观察的方法确定含参的式子所满足的条件，确定最优解的位置，从而求出参数．1．若x ，y 满足约束条件⎩⎨⎧x ＋y ≥1，x ＋2y ≤2，x ≤a ，目标函数z ＝2x ＋3y 的最小值为2，则a ＝________．解析：作出不等式组⎩⎪⎨⎪⎧x ＋y ≥1，x ＋2y ≤2，x ≤a 表示的平面区域如图中阴影部分所示，作出直线2x ＋3y ＝0，平移直线2x ＋3y ＝0，显然过A (a ，1－a )时，z ＝2x ＋3y 取得最小值，则2a ＋3(1－a )＝2，解得a ＝1.答案：12．(2021·开封市第一次模拟考试)已知点A (0，2)，动点P (x ，y )的坐标满足条件⎩⎨⎧x ≥0，y ≤x ，则|P A |的最小值是________．解析：依题意，画出不等式组⎩⎨⎧x ≥0，y ≤x 表示的平面区域，如图中阴影部分所示，结合图形可知，|P A |的最小值等于点A (0，2)到直线x －y ＝0的距离，即|0－2|2＝ 2.答案： 23．(2021·湖北八校第一次联考)已知实数x ，y 满足⎩⎨⎧2x －y ＋3≥0，2x ＋y －5≤0，y ≥1，则z ＝|x－y |的取值范围为________．解析：画出可行域如图中阴影部分所示，z ＝|x －y |＝|x －y |2·2表示可行域内的点(x ，y )到直线x －y ＝0的距离的2倍．作出直线x －y ＝0，由图可得可行域内的点(x ，y )到直线x －y ＝0的距离的最小值为0，最大值为直线2x －y ＋3＝0与2x ＋y －5＝0的交点C ⎝ ⎛⎭⎪⎫12，4到直线x －y ＝0的距离，即724，所以z 的取值范围为⎣⎢⎡⎦⎥⎤0，72.答案：⎣⎢⎡⎦⎥⎤0，72线性规划的实际应用(师生共研)某企业生产甲、乙两种产品均需用A ，B 两种原料，已知生产1吨每种产品所需原料及每天原料的限量如表所示．如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得的最大利润为( )甲 乙 原料限量 A /吨 3 2 12 B /吨128A ．16万元 C ．18万元D ．19万元【解析】 设该企业每天生产x 吨甲产品，y 吨乙产品，可获得利润为z 万元，则z ＝3x ＋4y ，且x ，y 满足不等式组⎩⎪⎨⎪⎧3x ＋2y ≤12，x ＋2y ≤8，x ≥0，y ≥0，作出不等式组表示的可行域如图中阴影部分所示，作出直线3x ＋4y ＝0并平移，可知当直线经过点(2，3)时，z 取得最大值，z max ＝3×2＋4×3＝18(万元)．故选C ．【答案】 C利用线性规划解决实际问题的五步曲某旅行社租用A ，B 两种型号的客车安排900名客人旅行，A ，B 两种车辆的载客量分别为36人和60人，租金分别为1 600元/辆和2 400元/辆，旅行社要求租车总数不超过21辆，且B 型车不多于A 型车7辆，则租金最少为________元．解析：设租用A 型车x 辆，B 型车y 辆，目标函数为z ＝1 600x ＋2 400y ，则约束条件为⎩⎪⎨⎪⎧36x ＋60y ≥900，x ＋y ≤21，y －x ≤7，x ，y ∈N ，作出可行域，如图中阴影部分所示，可知目标函数过点A (5，12)时，有最小值z min ＝36 800(元)．答案：36 800[A 级 基础练]1．不等式组⎩⎨⎧x －3y ＋6≤0，x －y ＋2>0表示的平面区域是( )解析：选C ．用特殊点代入，比如(0，0)，容易判断为C ． 2．设集合A ＝{(x ，y )|x －y ≥1，ax ＋y >4，x －ay ≤2}，则( ) A ．对任意实数a ，(2，1)∈A B ．对任意实数a ，(2，1)∉A C ．当且仅当a <0时，(2，1)∉A D ．当且仅当a ≤32时，(2，1)∉A解析：选D ．若(2，1)∈A ，则⎩⎪⎨⎪⎧2a ＋1>4，2－a ≤2，解得a >32，所以当且仅当a ≤32时，(2，1)∉A ，故选D ．3．(2020·高考浙江卷)若实数x ，y 满足约束条件⎩⎨⎧x －3y ＋1≤0，x ＋y －3≥0，则z ＝x ＋2y的取值范围是( )A ．(－∞，4]B ．[4，＋∞)C ．[5，＋∞)D ．(－∞，＋∞)解析：选B ．画出可行域如图中阴影部分所示，作出直线x ＋2y ＝0，平移该直线，易知当直线经过点A (2，1)时，z 取得最小值，z min ＝2＋2×1＝4，再数形结合可得z ＝x ＋2y 的取值范围是[4，＋∞)．故选B ．4．若M 为不等式组⎩⎨⎧x ≤0，y ≥0，y －x ≤2表示的平面区域，则当a 从－2 连续变化到1时，动直线x ＋y ＝a 扫过M 中的那部分区域的面积为( )A ．1B ．32C ．34D ．74解析：选D ．在平面直角坐标系中作出区域M 如图中阴影部分所示，当a 从－2连续变化到1时，动直线x ＋y ＝a 扫过M 中的那部分区域为图中的四边形AODE ，所以其面积S ＝S △AOC －S △DEC ＝12×2×2－12×1×12＝74，故选D ．5．若x ，y 满足约束条件⎩⎨⎧x －y ＋2≥0，x ＋y －m ≥0，x －3≤0，若z ＝2x －3y 的最大值为9，则正实数m 的值为( )A ．2B ．3C ．4D ．8解析：选A ．作出x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ＋2≥0，x ＋y －m ≥0，x －3≤0表示的可行域如图中阴影部分所示，由图可知z ＝2x －3y 在点A 处取得最大值， 由⎩⎪⎨⎪⎧x ＋y －m ＝0，x ＝3解得A (3，m －3)， 由z max ＝2×3－3(m －3)＝9，解得m ＝2. 故选A ．6．(2021·广州市阶段训练)设x ，y 满足约束条件⎩⎨⎧1≤x ≤3，0≤x ＋y ≤2，则z ＝x －2y的最小值为________．解析：依题意，在平面直角坐标系内作出不等式组表示的平面区域如图中阴影部分所示，作出直线x －2y ＝0，并平移，当平移到经过该平面区域内的点(1，1)时，相应直线在x 轴上的截距最小，此时z ＝x －2y 取得最小值，最小值为－1.答案：－17．(2021·合肥第一次教学检测)已知实数x ，y 满足⎩⎨⎧x ≥y ，x ≤2y ，x ＋y －6≤0，则z ＝2x＋y 取得最大值时的最优解为________．解析：方法一：作不等式组⎩⎪⎨⎪⎧x ≥y ，x ≤2y ，x ＋y －6≤0表示的平面区域，如图中阴影部分所示，作出直线2x ＋y ＝0，并平移，根据z 的几何意义，很容易看出当直线平移到点B 处时z 取得最大值，联立⎩⎪⎨⎪⎧x －2y ＝0，x ＋y －6＝0，得B (4，2)．方法二：易知目标函数z ＝2x ＋y 的最大值在交点处取得，只需求出两两相交的三个交点的坐标，代入z ＝2x ＋y ，即可求得最大值．联立⎩⎪⎨⎪⎧x ＝y ，x －2y ＝0，解得⎩⎪⎨⎪⎧x ＝0，y ＝0为原点，代入可得z ＝0；联立得⎩⎪⎨⎪⎧x ＝y ，x ＋y －6＝0，解得⎩⎪⎨⎪⎧x ＝3，y ＝3，将(3，3)代入可得z ＝9；联立⎩⎪⎨⎪⎧x －2y ＝0，x ＋y －6＝0，解得⎩⎪⎨⎪⎧x ＝4，y ＝2，将(4，2)代入可得z ＝10.通过比较可知，z 的最大值为10，故最优解为(4，2)．答案：(4，2)8．(2021·四省八校第二次质量检测)已知变量x ，y 满足约束条件⎩⎨⎧x －2≤0，x －2y ＋2≥0，x ＋y ＋1≥0，若－x ＋y ≥－m 2＋4m 恒成立，则实数m 的取值范围为________． 解析：设z ＝－x ＋y ，作出可行域如图中阴影部分所示，作出直线－x ＋y ＝0，并平移可知当直线过点B (2，－3)时z 取得最小值，所以z min ＝－5，所以－m 2＋4m ≤－5，m 2－4m －5≥0⇒m ≤－1或m ≥5，所以m 的取值范围为(－∞，－1]∪[5，＋∞)．答案：(－∞，－1]∪[5，＋∞)9.如图所示，已知D 是以点A (4，1)，B (－1，－6)，C (－3，2)为顶点的三角形区域(包括边界与内部)．(1)写出表示区域D 的不等式组；(2)设点B (－1，－6)，C (－3，2)在直线4x －3y －a ＝0的异侧，求a 的取值范围．解：(1)直线AB ，AC ，BC 的方程分别为7x －5y －23＝0，x ＋7y －11＝0，4x ＋y ＋10＝0.原点(0，0)在区域D 内，故表示区域D 的不等式组为⎩⎪⎨⎪⎧7x －5y －23≤0，x ＋7y －11≤0，4x ＋y ＋10≥0.(2)根据题意有[4×(－1)－3×(－6)－a ]·[4×(－3)－3×2－a ]<0，即(14－a )(－18－a )<0，解得－18<a <14.故a 的取值范围是(－18，14)．10．已知x ，y 满足⎩⎨⎧y ＞0，x ＋y ＋1＜0，3x ＋y ＋9＞0，记点(x ，y )对应的平面区域为P .(1)设z ＝y ＋1x ＋3，求z 的取值范围； (2)过点(－5，1)的一束光线，射到x 轴被反射后经过区域P ，当反射光线所在直线l 经过区域P 内的整点(即横纵坐标均是整数的点)时，求直线l 的方程．解：平面区域如图所示(阴影部分)，易得A ，B ，C 三点坐标分别为A (－4，3)，B (－3，0)，C (－1，0)．(1)由z ＝y ＋1x ＋3知z 的值即是定点M (－3，－1)与区域内的点Q (x ，y )连接的直线的斜率，当直线过A (－4，3)时，z ＝－4； 当直线过C (－1，0)时，z ＝12.故z 的取值范围是(－∞，－4)∪⎝ ⎛⎭⎪⎫12，＋∞.(2)过点(－5，1)的光线被x 轴反射后的光线所在直线必经过点(－5，－1)，由题设可得区域内坐标为整数点仅有点(－3，1)，故直线l 的方程是y －1（－1）－1＝x ＋3（－5）＋3，即x －y ＋4＝0.[B 级 综合练]11．已知点(x ，y )满足⎩⎨⎧x ＋y ≥1，x －y ≥－1，2x －y ≤2，目标函数z ＝ax ＋y 仅在点(1，0)处取得最小值，则a 的取值范围为( )A ．(－1，2)B ．(－2，1)C ．⎝ ⎛⎭⎪⎫12，＋∞D ．⎝ ⎛⎭⎪⎫－∞，－12解析：选B ．作出不等式组对应的平面区域，如图中阴影部分所示，由z ＝ax ＋y 可得y ＝－ax ＋z ，直线的斜率k ＝－a ， 因为k AC ＝2，k AB ＝－1，目标函数z ＝ax ＋y 仅在点A (1，0)处取得最小值，则有k AB <k <k AC ， 即－1<－a <2，所以－2<a <1，即实数a 的取值范围是(－2，1)．故选B ．12．若点M (x ，y )满足⎩⎨⎧x 2＋y 2－2x －2y ＋1＝0，1≤x ≤2，0≤y ≤2，则x ＋y 的取值集合是( )A ．[1，2＋2]B ．[1，3]C ．[2＋2，4]D ．[1，4]解析：选A ．x 2＋y 2－2x －2y ＋1＝(x －1)2＋(y －1)2＝1，根据约束条件画出可行域，如图中阴影部分所示，令z ＝x ＋y ，则y ＝－x ＋z ，根据图象得到当直线过点(1，0)时目标函数取得最小值，为1，当直线和半圆相切时，取得最大值，根据点到直线的距离等于半径得到|2－z |2＝1⇒z ＝2±2，易知2－2不符合题意，故z ＝2＋2，所以x ＋y 的取值范围为[1，2＋2]．故选A ．13．已知点A (2，1)，O 是坐标原点，P (x ，y )的坐标满足⎩⎨⎧2x －y ≤0x －2y ＋3≥0y ≥0，设z ＝OP →·OA→，则z 的最大值是________． 解析：方法一：由题意，作出可行域，如图中阴影部分所示．z ＝OP →·OA →＝2x ＋y ，作出直线2x ＋y ＝0并平移，可知当直线过点C 时，z 取得最大值，由⎩⎪⎨⎪⎧2x －y ＝0，x －2y ＋3＝0，得⎩⎪⎨⎪⎧x ＝1，y ＝2，即C (1，2)，则z 的最大值是4.方法二：由题意，作出可行域，如图中阴影部分所示，可知可行域是三角形封闭区域．z ＝OP →·OA →＝2x ＋y ，易知目标函数z ＝2x ＋y 的最大值在顶点处取得，求出三个顶点的坐标分别为(0，0)，(1，2)，(－3，0)，分别将(0，0)，(1，2)，(－3，0)代入z ＝2x ＋y ，对应z 的值为0，4，－6，故z 的最大值是4.答案：414．某化肥厂生产甲、乙两种混合肥料，需要A ，B ，C 三种主要原料．生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示：原料 肥料ABC甲 4 8 3 乙5510现有A 种原料200吨，B 种原料360吨，C 种原料300吨，在此基础上生产甲、乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元．分别用x ，y 表示计划生产甲、乙两种肥料的车皮数．(1)用x ，y 列出满足生产条件的数学关系式，并画出相应的平面区域； (2)问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．解：(1)由已知得，x ，y 满足的数学关系式为⎩⎪⎨⎪⎧4x ＋5y ≤200，8x ＋5y ≤360，3x ＋10y ≤300，x ≥0，y ≥0.二元一次不等式组所表示的平面区域为图1中的阴影部分．(2)设利润为z 万元，则目标函数为z ＝2x ＋3y .考虑z ＝2x ＋3y ，将它变形为y ＝－23x ＋z 3， 这是斜率为－23，随z 变化的一族平行直线.z 3为直线在y 轴上的截距，当z3取最大值时，z 的值最大．又因为x ，y 满足约束条件，所以由图2可知，当直线z ＝2x ＋3y 经过可行域上的点M 时，截距z3最大，即z 最大．解方程组⎩⎪⎨⎪⎧4x ＋5y ＝200，3x ＋10y ＝300，得点M 的坐标为(20，24)． 所以z max ＝2×20＋3×24＝112.即生产甲种肥料20车皮、乙种肥料24车皮时利润最大，且最大利润为112万元．[C 级 提升练]15．已知实数x ，y 满足⎩⎨⎧6x ＋y －1≥0，x －y －3≤0，y ≤0，则z ＝y －ln x 的取值范围为________．解析：作出可行域如图(阴影部分)，其中A (16，0)，B (3，0)，C (47，－177)．由图可知，当y ＝ln x ＋z 过点A (16，0)时z 取得最大值，z max ＝0－ln 16＝ln 6.设y ＝ln x ＋z 的图象与直线y ＝x －3相切于点M (x 0，y 0)，由y ＝ln x ＋z 得y ′＝1x ，令1x 0＝1得x 0＝1∈⎝ ⎛⎭⎪⎫47，3，故y ＝ln x ＋z 与y ＝x －3切于点M (1，－2)时，z 取得最小值，z min ＝－2－ln 1＝－2.所以z ＝y －ln x 的取值范围为[－2，ln 6]． 答案：[－2，ln 6]16．已知点A (53，5)，直线l ：x ＝my ＋n (n ＞0)过点A .若可行域⎩⎨⎧x ≤my ＋n ，x －3y ≥0，y ≥0的外接圆的直径为20，则n ＝________．解析：注意到直线l ′：x －3y ＝0也经过点A ，所以点A 为直线l 与l ′的交点． 画出不等式组⎩⎪⎨⎪⎧x ≤my ＋n ，x －3y ≥0，y ≥0表示的可行域，如图中阴影部分所示．设直线l 的倾斜角为α，则∠ABO ＝π－α. 在△OAB 中，OA ＝（53）2＋52＝10.根据正弦定理，得10sin （π－α）＝20，解得α＝5π6或π6.当α＝5π6时，1m ＝tan 5π6，得m ＝－ 3. 又直线l 过点A (53，5)， 所以53＝－3×5＋n ， 解得n ＝10 3.当α＝π6时，同理可得m ＝3，n ＝0(舍去)． 综上，n ＝10 3. 答案：10 3。

高考数学中的线性规划算法解题技巧高考数学中的线性规划是一种非常重要的问题类型，在考试中经常被考查，对于学生来说是必须掌握的一项技能。

而在线性规划中，解题的算法是关键，正确运用算法不仅能够提高解题效率，还能避免不必要的错误。

本文将介绍一些线性规划解题的算法和技巧，帮助学生在考试中取得更好的成绩。

一、线性规划的基本概念在解题之前，我们需要熟悉线性规划的一些基本概念。

线性规划是指在一定的限制条件下，求解一个线性函数的最大或最小值。

在这个过程中，我们需要确定目标函数、约束条件以及变量的取值范围。

通常情况下，我们可以将线性规划问题表示为标准型或非标准型。

标准型的形式如下：$$\max(z)=c_1x_1+c_2x_2+...+c_nx_n$$$$s.t.\begin{cases}a_{11}x_1+a_{12}x_2+...+a_{1n}x_n\le b_1\\a_{21}x_1+a_{22}x_2+...+a_{2n}x_n\le b_2\\...\\a_{m1}x_1+a_{m2}x_2+...+a_{mn}x_n\le b_m\\\end{cases}$$变量取值范围为$x_i\ge0(i=1,2,...,n)$而非标准型的形式则可以被转化为标准型。

二、单纯形法的原理和步骤单纯形法是解决线性规划问题的一种经典算法，其基本原理是通过不断地构造可行解和寻找可行解中的最优解来达到最终的优化目标。

其具体步骤如下：1、将标准型问题中的目标函数系数、约束条件系数和右端项系数分别组成一个矩阵。

2、选择其中一个非基变量（即取值为0的变量）作为入基变量，计算出使目标函数增大的最大步长。

3、选择其中一个基变量（即取值不为0的变量）作为出基变量，计算出使目标函数增大的最小步长。

4、通过第2步和第3步计算出的步长来更新目标函数和约束条件，得到一个新的可行解。

5、使用新的可行解重复进行第2-4步的计算，直到找到最优解。

需要注意的是，单纯形法有两种可能的结果：一是存在最优解，二是存在无穷多个最优解。

高考数学一轮复习《线性规划》复习练习题（含答案）一、单选题1．若x ，y 满足1010330x y x y x y +-⎧⎪--⎨⎪-+⎩，则4z x y =-的最小值为（ ）A ．-6B ．-5C ．-4D ．12．已知x ，y 满足不等式组240,3260,20,x y x y x y --≤⎧⎪--≤⎨⎪++≥⎩则23z x y =+的取值范围为（ ）A ．32,5⎡⎫-+∞⎪⎢⎣⎭B ．325,52⎡⎤--⎢⎥⎣⎦C ．[)6,-+∞D ．5,2⎡⎫-+∞⎪⎢⎣⎭3．设变量,x y 满足约束条件100240x y x y x y --≤⎧⎪+≥⎨⎪+-≥⎩，则2z x y =-的最大值为（ ）A ．0B ．32C ．3D ．44．已知实数,x y 满足2030330x y x y x y -+≥⎧⎪+-≤⎨⎪--≥⎩，则目标函数2z x y =+的最大值为（ ）A ．112B ．5C ．52D ．35．若实数x ，y 满足约束条件110x y x y x +≥⎧⎪-≤⎨⎪≥⎩，则2z x y =+的最小值是（ ）A ．-1B ．0C ．1D ．26．若,x y 满足约束条件310x y x y x +≤⎧⎪-≤-⎨⎪≥⎩，则2z x y =+的最小值为（ ）A ．1B ．2C ．3D ．47．不等式44x y +<表示的区域在直线440x y +-=的（ ） A ．左上方B ．左下方C ．右上方D ．右下方8．已知实数x ，y 满足210,10,2,x y x y x -+≥⎧⎪+-≥⎨⎪<⎩，则z =2x -y 的最小值是（ ）A ．5B ．52C ．0D ．-19．若实数x ，y 满足约束条件23023020x y x y x ++≥⎧⎪--≤⎨⎪+≥⎩，则3z x y =-的最大值是（ ）A ．6-B ．2C ．4D ．610．已知动点(),P m n 在不等式组400x y x y y +≤⎧⎪-≥⎨⎪≥⎩ 表示的平面区域内部及其边界上运动，则35n z m -=-的最小值（ ） A ．4 B ．13C ．53D ．311．甲、乙两艘轮船都要在某个泊位停靠6个小时，假定它们在一昼夜的时间中随机到达，若两船有一艘在停泊位时，另一艘船就必须等待，则这两艘轮船停靠泊位时都不需要等待的概率为（ ） A ．1116B ．916C ．716D ．51612．若实数,x y 满足约束条件10210y x y x y ≤⎧⎪-≤⎨⎪++≥⎩，则z ）A ．1BCD二、填空题13．已知x ，y 满足约束条件1000x y x y y +-≤⎧⎪-≥⎨⎪≥⎩则2z x y =-的最大值为_________．14．已知x 、y 满足2025020x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩，则21x y z x ++=+的最小值是__________．15．在等差数列{}n a 中，125024a a a ≤≥-≤，，，则4a 的取值范围是______． 16．若实数,x y 满足约束条件102310y x x x y ≥⎧⎪+≥⎨⎪+-≤⎩，则目标函数3z x y =+的取值范围是__________ .三、解答题17．制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目，根据预测，甲、乙两个项目可能的最大盈利率分别为100%和50%，可能的最大亏损率分别为30%和10%，投资人计划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元.(1)设投资人用x 万元、y 万元分别投资甲、乙两个项目，列出满足题意的不等关系式，并画出不等式组确定的平面区域图形；(2)求投资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？18．若变量x ，y 满足约束条件240101x y x y x +-≤⎧⎪--≤⎨⎪≥⎩(1)画出不等式组表示的平面区域； (2)求目标函数z =y +x 的最大值和最小值.19．已知点(),P x y 在圆()2211x y +-=上运动，(1)求12y x --的取值范围； (2)求2x ＋y 的取值范围．20．已知圆C ：222440x y x y +-+-=，直线l ：30mx y m -+-=()m R ∈与圆C 相交于A ､B 两点.(1)已知点(,)x y 在圆C 上，求34x y +的取值范围： (2)若O 为坐标原点，且2AB OC =，求实数m 的值.21．已知命题p ：0x ∃∈R ，()()2011(0)m x a a ++≤>，命题q ：x ∀，y 满足+1002x y x y -≤⎧⎪≥⎨⎪≤⎩，m .(1)若q 为真命题，求m 的取值范围.(2)判断p ⌝是q 的必要非充分条件，求a 的范围22．2021年6月17日9时22分，我国“神舟十二号”载人飞船发射升空，展开为期三个月的空间站研究工作，某研究所计划利用“神舟十二号”飞船进行新产品搭载试验，计划搭载若干件新产品,A B 、要根据产品的研制成本、产品重量、搭载试验费用和预计收益来决定具体安排，通过调查，搭载每件产品有关数据如表:（1）试用搭载,A B 产品的件数,x y 表示收益z (万元);（2）怎样分配,A B 产品的件数才能使本次搭载实验的利润最大，最大利润是多少?23．设函数(),()x f x e g x ax b ==+，其中, a b R ∈．（Ⅰ）若1,1a b ==-，当1x ≥时，求证：()()ln f x g x x ≥；（Ⅱ）若不等式()()f x g x ≥在[1,)+∞上恒成立，求()2223a e b -+的最小值．24．对于函数()f x 和()g x ，设集合(){}0,R A x f x x ==∈，(){}0,R B x g x x ==∈，若存在1x A ∈，2x B ∈，使得12(0)x x k k -≤≥，则称函数()f x 与()g x “具有性质()M k ”.(1)判断函数()sin f x x =与()cos g x x =是否“具有性质1()2M ”，并说明理由；(2)若函数1()22x f x x -=+-与2()(2)24g x x m x m =+--+“具有性质(2)M ”，求实数m 的最大值和最小值；(3)设0a >且1a ≠，1b >，若函数1()log x bf x a x=-+与()log x b g x a x=-+“具有性质(1)M ”，求1212x x -的取值范围。

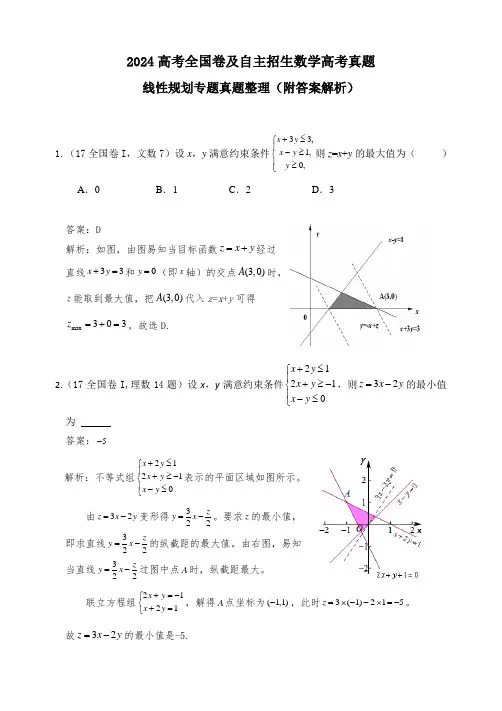
2024高考全国卷及自主招生数学高考真题线性规划专题真题整理（附答案解析）1.（17全国卷I ，文数7）设x ，y 满意约束条件33,1,0,x y x y y +≤⎧⎪-≥⎨⎪≥⎩则z =x +y 的最大值为（ ）A ．0B ．1C ．2D ．3 答案：D解析：如图，由图易知当目标函数z x y =+经过 直线33x y +=和0y =（即x 轴）的交点(3,0)A 时，z 能取到最大值，把(3,0)A 代入z =x +y 可得max 303z =+=，故选D.2.（17全国卷I,理数14题）设x ，y 满意约束条件21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩，则32z x y =-的最小值为 答案：5-解析：不等式组21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩表示的平面区域如图所示。

由32z x y =-变形得322z y x =-。

要求z 的最小值， 即求直线322z y x =-的纵截距的最大值。

由右图，易知 当直线322z y x =-过图中点A 时，纵截距最大。

联立方程组2121x y x y +=-⎧⎨+=⎩，解得A 点坐标为(1,1)-，此时3(1)215z =⨯--⨯=-。

故32z x y =-的最小值是-5.3.（17全国卷Ⅱ，文数7、理数5）设x 、y 满意约束条件2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩ .则2z x y =+ 的最小值是（ ）A. -15B.-9C. 1 D 9答案：A解析：不等式组2+330233030x y x y y -≤⎧⎪-+≥⎨⎪+≥⎩表示的可行域如图所示，易知当直线2z x y =+过到213y x =+与3y =-交点()63--，时，目标函数2z x y =+取到最小值，此时有()()min 26315z =⨯-+-=-，故所求z 最小值为15-．4.（17全国卷Ⅲ，文数5）设x ，y 满意约束条件326000x y x y +-≤⎧⎪≥⎨⎪≥⎩，则z =x -y 的取值范围是( )A.[-3,0]B.[-3,2]C.[0,2]D.[0,3] 答案：B解析：绘制不等式组表示的可行域，结合目标函数 的几何意义可得目标函数z =x -y 在直线3260x y +-=与 直线0x =（即x 轴）的交点()0,3A 处取得最小值， 此时min 033z =-=-。

高中必修5线性规划
简单的线性规划问题
一、知识梳理
1. 目标函数: Ｐ＝２ｘ＋ｙ是一个含有两个变量ｘ和ｙ的函数,称为目标函数．
2.可行域:约束条件所表示的平面区域称为可行域.
3. 整点:坐标为整数的点叫做整点．
4.线性规划问题:求线性目标函数在线性约束条件下的最大值或最小值的问题,通常称为线性规划问题．只含有两个变量的简单线性规划问题可用图解法来解决．
5. 整数线性规划:要求量取整数的线性规划称为整数线性规划．
二、疑难知识导析
1.对于不含边界的区域,要将边界画成虚线．
2.确定二元一次不等式所表示的平面区域有多种方法,常用的一种方法是“选点法”：任选一个不在直线上的点,检验它的坐标是否满足所给的不等式,若适合,则该点所在的一侧即为不等式所表示的平面区域；否则,直线的另一侧为所求的平面区域．若直线不过原点,通常选择原点代入检验．
3. 平移直线ｙ＝－kｘ＋Ｐ时,直线必须经过可行域．
4.对于有实际背景的线性规划问题,可行域通常是位于第一象限内的一个凸多边形区域,此时变动直线的最佳位置一般通过这个凸多边形的顶点．
5.简单线性规划问题就是求线性目标函数在线性约束条件下的最优解,无论此类题目是以什么实际问题提出,其求解的格式与步骤是不变的：1寻找线性约束条件,线性目标函数；2由二元一次不等式表示的平面区域做出可行域；3在可行域内求目标函数的最优解.
积储知识：。

线性规划高考试题精选（一）一•选择题（共15小题）f 2jt+3y-3<01•设x, y满足约束条件：：，/ '，则z=2x+y的最小值是（）[y+3>QA. - 15B.- 9C. 1D. 9X32 .若x, y满足、x^y》2,则x+2y的最大值为（）A. 1B. 3C. 5D. 9x+3y=C33. 设x, y满足约束条件* dl，则z=x+y的最大值为（）A. 0B. 1C. 2D. 3x-2y+5<04. 已知x, y 满足约束条件则z=x+2y的最大值是（）「y<2A.- 3B.- 1C. 1 D . 35. 若x、y满足约束条件r十y-3》0,则z=x+2y的取值范围是（）x-2y^0A . [0, 6]B . [0, 4] C. [6, +x） D . [4, +^）r3x+2y-6<06 .设x, y满足约束条件则z=x- y的取值范围是（）A . [ - 3, 0] B. [ - 3, 2] C. [0, 2] D . [0, 3]7.已知x, y满足约束条件3x+y+5<0，则z=x+2y的最大值是（）x+3^0kA . 0B . 2 C. 5 D . 6x-l-2y-2^08 .设变量x, y满足约束条件，则目标函数z=x+y的最大值为（A. ：：B. 1C. ；D. 33 29 .已知变量x, y满足约束条件迁^，则4x+2y的取值范围是（）A. [0, 10]B. [0, 12]C. [2, 10]D. [2, 12]2垃亨+6〉010. 不等式组5心0，表示的平面区域的面积为（）X<2LA. 48B. 24C. 16D. 12y-y+l^O11. 变量x、y满足条件y^Cl ，则（x- 2）2+y2的最小值为（）g>-1A. B.二C. 5 D.2 2yCx12. 若变量x, y满足约束条件x+y< 1且z=2x+y的最大值和最小值分别为m和n,贝U m- n等于（）A. 8B. 7C. 6 D . 513 .设x, y满足约束条件' x+y-2>0 ,当且仅当x=y=4时，z=ax- y取得最小值，x<4则实数a的取值范围是（）A . [ - 1, 1] B. （-X, 1）C. （0, 1）D. （-X, 1）u（1 , +x）x+y-3^0x^y-3^014 .实数x, y满足' 玫応珀，若z=2x+y的最大值为9,则实数m的值为（）A . 1B . 2 C. 3 D . 415 .平面区域的面积是（x2 + y2<2Lr B C -,-D. 上71~T~.选择题（共25小题）23.设实数x , y 满足约束条件- ,若目标函数 z=ax+by (a >0, b >0)\+2y<l16 •设x , y 满足约束条件2x+y>-l ，则z=3x- 2y 的最小值为 ____________L x-y^O17 .若x , y 满足约束条件* s+y-2<0,则z=3x- 4y 的最小值为 ___________ . \-y+l=C018 .已知x , y 满足约束条件r+y-9*C0,则z=5x+3y 的最大值为 ___________ .L x>l19. 若实数x , y 满足.- ■：，如果目标函数z=x- y 的最小值为-2,则实数I. x+y^nim= _____ .20. 已知a > 0, x , y 满足约束条件 5y<3 若z=2x+y 的最小值为1,则y^a(x-3)a= _____ .\+2y>021. ______________________________________________________________ 设z=x+y 其中x,y 满足rwVO ，若z 的最大值为6,则z 的最小值为______________ .L O^yCkfx>022.已知点x , y 满足不等式组' y>0 ，若ax+yw 3恒成立，则实数a 的取值L 2x+y^2范围是 _______ .的最大值为10,则a 2+b 2的最小值为_________ .x+y-l^O 24. _________________________________________________ 已知实数x , y 满足则二的最小值为 _________________________________________[y>-l Mx-y+2>0 x>0x+rC225. _________________________________________________ 若变量x, y满足* 2x-3穴9,则x2+y2的最大值是_______________________________ .x>0L.-；的取值范围是■：'的范围是 ------- %-y 亠26. 设变量x , y 满足约束条件s-2y+2>0 ,则L x+y-1^0f0<x<227. 在平面直角坐标系xOy 上的区域D 由不等式组，虫3 给定，若M （x , y ） 为D 上的动点，点A 的坐标为（2，1），则面•杰的最大值为r2x+y<428. 已知动点P （x ，y ）满足：宀 _，则x 2+y 2 - 6x 的最.h//+i+y ）>i小值为鼻>029. _______________________________________________ 已知实数x ，y 满足r+y<7，则艺的最小值是 __________________________________l 計 2<2y * X230. _______________________________________________ 设实数x ，y 满足* x+y>l ，则2y - x 的最大值为 ______________________________ .盂 031. ______________________________________________________________ 设x 、y 满足约束条件，则目标函数z=x 2+y 2的最大值为 ______________________ .QO, y>0s-y^O32. 已知x ，y 满足约束条件"时応2，若z=ax+y 的最大值为4，则a __________f x <2 ____33. 若x ，y 满足约束条件' x+y-2>0，则讥霉代的最小值是 ___________ .x-y+2^0 34.若x , y 满足约束条件r+y< 1 ,则 y>-L x-2y4-l>035.已知实数x ，y 满足：：x<2 ____________ ，z=2x- 2y - 1,则z 的取值范围是#+厂1>036. 若实数x，y满足不等式组' 2x-3y-8<0,目标函数z=kx- y的最大值为12,x>lL第4页（共35页）39.已知不等式组-表示的平面区域的面积为:,则实数k= _________3最小值为0,则实数k= _______ ."2x+y+2>037. 若实数x 、y 满足不等式组* x+y+mrC^O ，且z=y -2x 的最小值等于-2,则实数m 的值等于38. 设x , y 满足不等式组2x-y-l<0,若z=ax+y 的最大值为2a+4，最小值为 L 3x-y-2^0a+1，则实数a 的取值范围为 ________40.已知变量x , y 满足的约束条件' ，若x+2y >- 5恒成立，则实数aL x>a的取值范围为 _______线性规划高考试题精选（一）参考答案与试题解析一•选择题（共15小题）r2x+3y-3<01. （2017?新课标U ）设x , y 满足约束条件-2s-3y+3>0,则z=2x+y 的最小值是 y+3^0 （ ） A . - 15B .- 9 C. 1 D . 9r2x+3y-3<0【解答】解：x 、y 满足约束条件< 2x-3y+3>0的可行域如图：z=2x+y 经过可行域的A 时，目标函数取得最小值， 由 f 解得 A （- 6,- 3）, l2x-3y+3=0则z=2x+y 的最小值是：-15. 故选：A .\<32. （2017?北京）若x, y满足r+y>2,则x+2y的最大值为（）A. 1B. 3C. 5D. 9【解答】解：x, y满足x+y>2的可行域如图：由可行域可知目标函数z=x+2y经过可行域的A时，取得最大值，由. ,可得A (3, 3),目标函数的最大值为：3+2X 3=9.t+3y<33. （2017?新课标I）设x,y满足约束条件，则z=x+y的最大值为（）A. 0 B. 1 C. 2 D. 3x+3y=C3【解答】解：x, y满足约束条件rp>L的可行域如图：，则z=x+y经过可行域的A时，目标函数取得最大值，由（尸° 解得A （3, 0）,z+3y=3L所以z=x+y的最大值为：3.x^2y+5=C04. （2017?山东）已知x,y满足约束条件则z=x+2y的最大值是（）・虫2A.—3B.—1C. 1D. 3K^2y+5=C0【解答】解：x, y满足约束条件* X+3A0的可行域如图：目标函数z=x+2y经y<2L过可行域的A时，目标函数取得最大值，由:严解得A （—1, 2）,x-2y+5^0目标函数的最大值为：-1+2 X 2=3.故选：D.5. （2017?浙江）若x、y满足约束条件' x-hy-3^0,则z=x+2y的取值范围是（）A. [0, 6]B. [0, 4]C. [6, +x）D. [4, +^）^>0【解答】解：x、y满足约束条件r十,表示的可行域如图：x-2y^0目标函数z=x+2y经过C点时，函数取得最小值，由严金0解得c（2, 1）,x-2y-0目标函数的最小值为：4目标函数的范围是[4, +x）.故选：D.r3x+2y-6<06. (2017?新课标川)设x, y满足约束条件r>0则z=x- y的取值范围是( )A. [ - 3, 0]B. [ - 3, 2]C. [0, 2]D. [0, 3]r3i+2y-6<0【解答】解：x, y满足约束条件*心0的可行域如图：y>0L目标函数z=x- y,经过可行域的A, B时，目标函数取得最值，由’解得A (0, 3),(3x+2y-6=0(v=0 由厂解得B (2, 0),l3x+2y-6=0目标函数的最大值为：2,最小值为：-3,目标函数的取值范围：[-3, 2].故选：B.A J\-y+3=C07. (2 017?山东)已知x,y满足约束条件3x+y+5C0,则z=x+2y的最大值是( )A. 0B. 2C. 5D. 6【解答】解：画出约束条件宀計卩+5<0表示的平面区域，如图所示；忙+3>08. (2017?天津)设变量x , y 满足约束条件 ,则目标函数z=x+y 的最【解解: 变量 x , y 满足约束条件' 的可行域如由严口解得A (-3, 4),此时直线y=-丄x+ z 在y 轴上的截距最大,2 2 所以目标函数z=x+2y 的最大值为 Z max = - 3+2 X 4=5.故选：C.大值为（）9 3A .B. 1C. — D . 33 2目标函数z=x+y 结果可行域的A 点时，目标函数取得最大值, 由可得A (0, 3),目标函数z=x+y 的最大值为：3. (x=0 故选：D .yx+2y-2^0x+2y-2>0则4x+2y的取9. （2017?大庆三模）已知变量x, y满足约束条件（勺+厅, 值范围是（）A. [0, 10]B. [0, 12]C. [2, 10]D. [2, 12]【解答】解：法1:作出不等式组卩电表示的平面区域，l-Kx-Ki得到如图的四边形及其内部，其中A（2, 1）, B（0, 1）,设z=F（x, y）=4x+2y，将直线I: z=4x+2y进行平移，可得当I经过点A时，目标函数z达到最大值，z最大值=F（2, 1）=10, 当I经过点B时，目标函数z达到最小值，z最小值=F（0, 1）=2 因此，z=4x+2y的取值范围是[2, 10]. 法2:令4x+2y=u（x+y）+入（x- y）,贝叮"十[一°,解得卩=3入I卩-k二2故4x+2y=3 （x+y）+ （x- y）,又 1 w x+y< 3 ,故3< 3 （x+y）w 10 ,又-1 w x-y< 1,所以4x+2y€ [2 , 10].故选C.2x-y+6^=010. （2017?潮州二模）不等式组,表示的平面区域的面积为（）x<2A. 48B. 24C. 16D. 12‘2 垃-y+6〉0【解答】解：画出不等式组表示的平面区域如图阴影所示，X<2L则点 A （- 2, 2）、B （2,- 2）、C （2, 10）,所以平面区域面积为&ABC=丄|BC?h=, X（10+2）x（2+2）=24.x-y+l^O11. （2017?汉中二模）变量x、y满足条件' ¥<1 ，则（x-2）2+y2的最小值玄>-1为（）D (2, 0)的距离的平12. (2017?林芝县校级三模)若变量x , y 满足约束条件* 且 z=2x+y 的最大值和最小值分别为m 和n ,则m -n 等于( )A . 8 B. 7 C. 6 D . 5【解答】解：作出不等式组对应的平面区域如图： 由 z=2x+y ,得 y=- 2x+z ,平移直线y=- 2x+z ,由图象可知当直线y=-2x+z 经过点C 时,直线y=- 2x+z 的截距最大，此时 z 最大,由FT解得I.尸T A .B . ： C. 5 D. '2 2【解答】解：作出不等式组对应的平面区域， 设z= (x -2) 2+y 2,则z 的几何意义为区域内的点到定点 方， 由图象知CD 的距离最小，此时z 最小. 由严得严,即C (0, 1), t x-y+l=O (y=l此时 z= (x - 2) 2+y 2=4+1=5,即C (2,- 1),此时最大值z=2X 2-仁3, 当直线y=- 2x+z 经过点B 时,故选：C.直线y= - 2x+z的截距最小，此时z最小，由解得(尸T，即 B (- 1,- 1),I尸x 1尸1最小值为z=- 2- 1= -3,故最大值m=3，最小值为n= - 3,则m- n=3-( - 3) =6,故选：C\-y^013. (2017?瑞安市校级模拟)设x, y满足约束条件' x+y-2>0 ,当且仅当x=y=4时，z=ax- y取得最小值，则实数a的取值范围是( )A. [ - 1, 1]B. (-X, 1)C. (0, 1)D. (-X, 1)U( 1 , +x)【解答】解：作出约束条件' x+y-2>0所对应的可行域(如图阴影), x<4变形目标函数可得y=ax- z,其中直线斜率为a,截距为-z,••• z=ax- y取得最小值的最优解仅为点A (4, 4),•••直线的斜率a v 1,即实数a的取值范围为(-X, 1)故选：B.实数m 的值为（ ） A . 1B. 2C. 3D . 4【解答】解：作出不等式组对应的平面区域如图：（阴影部分）. 由 z=2x+y 得 y= - 2x+z , 平移直线y=- 2x+z ,由图象可知当直线y=- 2x+z 经过点B 时，直线y=- 2x+z 的截距最大, 此时z 最大，此时2x+y=9. 由严空，解得佗,即B （ 4, 1）, [x-y-3=0 ly=lT B 在直线y=m 上，••• m=1, 故选：A14. （2017?肇庆一模）实数 x . y 满足*&+卩-3〉0：2”迂° ,若z=2x+y 的最大值为9，则15. （2017?五模拟）平面区域V>W3x的面积是（.x2+y£C2A. B. C. D. 112 6 12 6【解答】解：作出不等式组对应的平面区域如图，则区域是圆心角是.是扇形, 5K~2F故面积是X K X 2=二.选择题（共25小题）\+2y<l16. （2017?新课标I）设x, y满足约束条件* ，则z=3x- 2y的最小值z-y^O\+2y<l【解答】解：由x, y满足约束条件2x+y>-l作出可行域如图,x-r<0L由图可知，目标函数的最优解为A,联立卩+T，解得人（—1,1）. i2x+y=-l••• z=3x- 2y 的最小值为-3X 1 - 2X 仁-5.故答案为：-5.A Jx-y>017. （2017?新课标川）若x, y满足约束条件r十y-2〈0,则z=3x- 4y的最小值y>0为 -1 .【解答】解：由z=3x- 4y,得y=；x-,作出不等式对应的可行域（阴影部分），4 4平移直线y=；x-王，由平移可知当直线y= x-王4 4 4 4经过点B （1, 1）时，直线y= x-的截距最大，此时z取得最小值，4 4将B的坐标代入z=3x- 4y=3 - 4= - 1,即目标函数z=3x- 4y的最小值为-1.故答案为：-1.平移直线y=-_二厶，则由图象可知当直线由1x+y-9= 0 解得x=4即 B (4, 5),\-y+l=C018. （2017?明山区校级学业考试）已知x, y满足约束条件r+y-gO ,则z=5x+3y 的最大值为35 .【解答】解：不等式组对应的平面区域如图:由z=5x+3y 得y=-3经过点B时直线y=-二-匸的截距最大,此时z最大,此时M=z=5X 4+3X 5=35,故答案为：35z=x— y的最小19. （2017?重庆模拟）若实数x, y满足*2x7，如果目标函数值为-2,则实数m= 8 .【解答】解：画出x，y满足的可行域如下图：可得直线y=2x- 1与直线x+y=m的交点使目标函数z=x- y取得最小值, y=2x-l故，,x+y=int解得x=… ,y=〃 ],3 3代入x —y=—2得…—叮-=—2? m=83 3xAi20. （2017?湖南三模）已知a>0, x, y满足约束条件5y<3若z=2x+y的最y>a（x-3）小值为1,则a= 「._z_【解答】解：先根据约束条件画出可行域，设z=2x+y,将最大值转化为y轴上的截距，当直线z=2x+y经过点B时，z最小，由卩" 得：，代入直线y=a （x—3）得，a#;[2x+y=l I 尸-1 2故答案为：Ix+2y>021. （2017?山东模拟）设z=x+y其中x, y满足rXO，若z的最大值为6，则O<y<kLz的最小值为 -3 .【解答】解：作出可行域如图：直线x+y=6过点A（k，k）时，z=x+y取最大，二k=3，z=x+y过点B处取得最小值，B点在直线x+2y=0上,•-B （- 6, 3），二z的最小值为=-6+3= - 3.故填：-3.垃>022. （2017?黄冈模拟）已知点x, y满足不等式组，若ax+y< 3恒成立, 则实数a的取值范围是（-%, 3].3x-y-6<0 x-y+2^0z 也最大.，即 A (4, 6).英>0【解答】解：满足不等式组的平面区域如右图所示,由于对任意的实数x 、y ,不等式ax+y w 3恒成立， 根据图形，可得斜率-a >0或-a >k AB = =- 3,解得：a w 3,则实数a 的取值范围是(-%, 3].故答案为：(-%, 3].23. (2017?惠州模拟)设实数x,y 满足约束条件，工〉°，若目标函数z=ax+by t y>0(a > 0, b > 0)的最大值为10，则a 2+b 2的最小值为 【解答】解：由z=a>+by (a >0, b >0)得y=—・•.， 作出可行域如图：I a > 0, b > 0,•••直线y=厂「的斜率为负，且截距最大时，z 也最大.b b即 2a+3b - 5=0,-1 >直线的截距最大，此时 此时z=4a+6b=10,24. （2017?历下区校级三模）已知实数x , y 满足7丁1》0 ,贝卩 1 —.「的最小值为【解答】解：作出不等式组对应的平面区域如图,的几何意义是区域内的点与点 E （3, 0）的斜率,K -3由图象知AE 的斜率最小，由严］弓得（日，丘-y+l 二 0 （y=l 即 A (0, 1),故答案为：1即（a , b ）在直线2x+3y -5=0上，a 2+b 2的几何意义为直线上点到原点的距离的平方, 则原点到直线的距离 则a 2+b 2的最小值为d 2=13故答案为：•此时「的最小值为联立厲爲,解得B （3，- 1），x 2+y 2的几何意义为可行域内动点与原点距离的平方,其最大值| OB| 2=于+ (- 1)=10,故答案为：r2x^r-2<026. （2017?遂宁模拟）设变量x , y 满足约束条件x-2y+2>0 ,则z+y-1^0【解答】解：不等式组 *2护2>0表示的区域如图,t x+y-1^0「的几何意义是可行域内的点与点（-1 ,-"构成的直线的斜率问题.25. （2017?平遥县模拟）若变量x,y 满足、加-3y<9 ,则x 2+y 2的最大值是 10L x>0x+y^2【解答】解：由约束条件' 2x-3y<9作出可行域如图，L x>0当取得点A (0, 1)时, 」取值为2,x+1当取得点C (1, 0)时, -取值为',x+1 2 故答案为：.匸27.(2017?渭南一模)在平面直角坐标系xOy 上的区域定，若M (x , y )为D 上的动点，点A 的坐标为(2, r0<x<2D 由不等式组' y<3 给 1),则丽顾的最大值为令 z= " " L =2x+y ，化为 y= - 2x+z ,作出可行域如图,第24页（共35页）由图可知，当直线y=-2x+z过B (2, 3)时，z有最大值为2X2+3=7.故答案为：7.r2x+y<428. (2017?湖北二模)已知动点P (x, y)满足：出工_ ___.(VZ^+1-J (Jy'+l+Q Ai 则x2+y - 6x的最小值为._!L一9 一【解答】解：由-V : -r- ■ 1 ,••• y+> y+|y|》°，丁• r s八...Vy +l+v，••函数f (x) =.,•■,•是减函数，••• x< y，r2x+y<4•••原不等式组化为' x>0 .该不等式组表示的平面区域如下图：I x2+y2- 6x= (x- 3) 2+y2- 9.由点到直线的距离公式可得，P (3, °)区域中A (〔• I )的距离最小，所以x2+y2- 6x的最小值为一^ .9故答案为：-「.9则：的最小值是_〔_.\>029. （2017?盐城一模）已知实数x , y 满足y+y<?, 2y 【解答】解：作出不等式组所表示的平面区域如图所示: 由于■■可以看做平面区域内的点与原点的连线的斜率,x 结合图形可知，当直线过 OA 时 斜率最小.由于露L 可得A （ 4,3），此时 故答案为：「. -2-330.(2017?和平区校级模拟)设实数x,y满足】r y<2x+y^>l，则2y- x的最大值为5f y<2【解答】解：画出,的可行域如图：将z=2y- x变形为y= x+ z作直线y= x将其平移至A时，直线的纵截距最大,2 2 2z最大，由(尸2可得A (- 1, 2),Lx+y=lz的最大值为：5.- 031. (2017?德州二模)设x、y满足约束条件x-y+2>0 ，贝阳标函数z=y+『QCh y>0的最大值为52 .【解答】解：作出不等式组表示的平面区域，得到如图的四边形OABC其中A (0, 2), B (4 , 6) , C (2 , 0) , O为原点设P (x , y)为区域内一个动点,贝U | OP| = , . J表示点P到原点O的距离z=>2+y2=| OP| 2,可得当P到原点距离最远时z达到最大值因此，运动点P使它与点B重合时，z达到最大值--z最大值=42+62=52故答案为：52s-y^O32. (2017?镇江模拟)已知x, y满足约束条件5y<2，若z=a)+y的最大值为4,贝U a= 2 .【解答】解：作出不等式组对应的平面区域如图：(阴影部分).则 A (2, 0), B (1,1),若z=ax^y过A时取得最大值为4,则2a=4,解得a=2,此时，目标函数为z=2x+y,即y=- 2x+z,平移直线y=- 2x+z，当直线经过A (2, 0)时，截距最大，此时z最大为4,满足条件，若z=ax^y过B时取得最大值为4,贝U a+仁4,解得a=3,此时，目标函数为z=3x+y,即y=- 3x+z,平移直线y= - 3x+z，当直线经过A (2, 0)时，截距最大，此时z最大为6,不满足条件，故a=2；故答案为：2.\<2 _______________33. （2017?南雄市二模）若x, y满足约束条件r+y-2>0 ,则厶2+ /的最小值是一二•\<2【解答】解：x, y满足约束条件0的可行域如图：x-y+2^0则，的几何意义是可行域的点到坐标原点距离，由图形可知OP的距离最小，直线x+y- 2=0的斜率为1,所以|OP|=「.故答案为：-.v34. （2017?青城区校级一模）若x, y满足约束条件r+y<l ,则工的范围y> 1 X+1z=2x- 2y-（阴影部分）.1+E 是：’..—____ 3^~【解答】解：作出不等式组-x+y<l对应的平面区域如图: 的几何意义是区域内的点到定点 D （- 1, 0）的斜率，由图象知CD的斜率最小，由卩：得C （斗冷），tx+y=l 2 2X则CD的斜率z=「—,2+1 3即z二"的取值范围是（0, 1 ],x+1 335. （2017?梅河口市校级一模）已知实数x, y满足：：x<2则z的取值范围是【一』【解答】解：不等式对应的平面区域如图：由z=2x- 2y- 1得y=x-匚一，平移直线由平移可知当直线y=x-——，经过点C时,故答案为：「.. 一-3由严y+m , 得(x+y-l=O 直线y=x -二的截距最小，此时z 取得最大值,2由(尸2 ，解得严，即C (2,- 1), b+y-l=O I 尸-1 此时 z=2x — 2y - 1=4+2 - 1=5, 可知当直线y=x-_l 二，经过点A 时，2 直线y=y=x-'■的截距最大，此时z 取得最小值, 2'：■，即 A (；「) y "3代入 z=2x- 2y - 1 得 z=2X 1 - 2X …-1 = -3 3 3故 z € [ - ], 5).故答案为：［-,5)g+y -36. (2017?深圳一模)若实数x , y 满足不等式组2x-3y-8<0, 目标函数z=kx -y 的最大值为12,最小值为0,则实数k= 3.K+y-4=C0【解答】解:实数x, y 满足不等式组2x-3y-S<0的可行域如图：得：A( 1,3),L QiB (1,- 2),C (4, 0).① 当k=0时，目标函数z=kx- y 的最大值为12,最小值为0，不满足题意.② 当k >0时，目标函数z=kx- y 的最大值为12,最小值为0,当直线z=kx- y 过 C (4, 0)时，Z 取得最大值12.当直线z=kx- y过A (1, 3)时，Z取得最小值0.可得k=3,满足题意.③当k v 0时，目标函数z=kx- y的最大值为12,最小值为0,当直线z=kx- y过C (4, 0)时，Z取得最大值12.可得k=- 3,当直线z=kx- y过，B (1,- 2)时，Z取得最小值0•可得k=- 2, 无解.综上k=3故答案为：3.2芨+y+戈>037. (2017?夏邑县校级模拟)若实数x、y满足不等式组-，且z=y-2x的最小值等于-2,则实数m的值等于 -1 .【解答】-1解：由z=y- 2x,得y=2x+z,作出不等式对应的可行域，平移直线y=2x+z,由平移可知当直线y=2x+z经过点A (1, 0)时，直线y=2x+z的截距最小，此时z取得最小值为-2,即y- 2x=- 2,点A也在直线x+y+m=0上，贝U m= - 1 ,l+y-尺038. (2017?阳山县校级一模)设x, y满足不等式组2x^-l<0 ,若z=ax+y的最大值为2a+4,最小值为a+1，贝U实数a的取值范围为[—2, 1].【解答】解：由z=ax+y得y=- ax+z,直线y= - ax+z是斜率为-a, y轴上的截距为z的直线，作出不等式组对应的平面区域如图：则 A (1 , 1), B (2, 4),••• z=ax^y的最大值为2a+4，最小值为a+1,•••直线z=ax^y过点B时，取得最大值为2a+4,经过点A时取得最小值为a+1,若a=0,则y=z,此时满足条件，若a>0,则目标函数斜率k=- a v0,要使目标函数在A处取得最小值，在B处取得最大值，则目标函数的斜率满足-a> k BC=- 1,即0v a< 1,若a v0,则目标函数斜率k=- a>0,要使目标函数在A处取得最小值，在B处取得最大值，则目标函数的斜率满足-a< k Ac=2,即-2< a v 0,）， 综上-2w a w 1, 故答案为：[-2, 1].39. （2017?许昌三模）已知不等式组 rXO 表示的平面区域的面积为寺，则y^x-k^O 实数k= 4.【解答】解：画出不等式组表示的平面区域, 如图所示, 由题意可知k >0,可行域的三个顶点为A （0, 0）,B （鱼上）c （些空 ••• AB 丄 BC, |AB 匸k , 2点C 到直线AB 的距离为 解得k=4, 故答案为：4.40. （2017?白银区校级一模）已知变量x, y满足的约束条件，若x+2y芷AnL>-5恒成立，则实数a的取值范围为[-1,1].【解答】解：由题意作出其平面区域，则实数a的取值范围为[-1,1].故答案为：[-1,1].。