下载文档原格式
有限差分法finite difference method用差分代替微分，是有限差分法的基本出发点。
是一种微分方程和积分微分方程数值解的方法。
把连续的定解区域用有限个离散点构成的网格来代替，这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似，积分用积分和来近似，于是原微分方程和定解条件就近似地代之以代数方程组，即有限差分方程组，解此方程组就可以得到原问题在离散点上的近似解。
然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解。
如何根据问题的特点将定解区域作网格剖分；如何把原微分方程离散化为差分方程组以及如何解此代数方程组。
此外为了保证计算过程的可行和计算结果的正确，还需从理论上分析差分方程组的性态，包括解的唯一性、存在性和差分格式的相容性、收敛性和稳定性。
对于一个微分方程建立的各种差分格式，为了有实用意义，一个基本要求是它们能够任意逼近微分方程，这就是相容性要求。
另外，一个差分格式是否有用，最终要看差分方程的精确解能否任意逼近微分方程的解，这就是收敛性的概念。
此外，还有一个重要的概念必须考虑，即差分格式的稳定性。
因为差分格式的计算过程是逐层推进的，在计算第n＋1层的近似值时要用到第n层的近似值，直到与初始值有关。
前面各层若有舍入误差，必然影响到后面各层的值，如果误差的影响越来越大，以致差分格式的精确解的面貌完全被掩盖，这种格式是不稳定的，相反如果误差的传播是可以控制的，就认为格式是稳定的。
只有在这种情形，差分格式在实际计算中的近似解才可能任意逼近差分方程的精确解。
最常用的方法是数值微分法，比如用差商代替微商等。
另一方法叫积分插值法，因为在实际问题中得出的微分方程常常反映物理上的某种守恒原理，一般可以通过积分形式来表示。
此外还可以用待定系数法构造一些精度较高的差分格式。
龙格库塔龙格-库塔(Runge-Kutta)方法是一种在工程上应用广泛的高精度单步算法。
有限差分法的原理与计算步骤有限差分法（Finite Difference Method）是一种常用的数值计算方法，用于求解偏微分方程的数值解。
其基本原理是将连续的偏微分方程转化为差分方程，通过逼近导数，使用离散的点代替连续的点，从而将问题转化为代数问题。
下面将详细介绍有限差分法的原理和计算步骤：一、基本原理：有限差分法基于Taylor级数展开，通过利用函数在其中一点附近的导数信息来逼近函数在该点处的值。
该方法将连续的偏微分方程转化为差分方程，使用离散的点代替连续的点，从而将问题转化为代数问题。
在有限差分法中，常用的差分逼近方式有前向差分、后向差分和中心差分。
二、计算步骤：1.网格划分：将求解区域划分为有限个离散点，并定义网格上的节点和网格尺寸。
通常使用等距离网格，即每个网格点之间的间距相等。
2.离散化：将偏微分方程中的各个导数项进行逼近，利用差分近似来替代和求解。
一般采用中心差分逼近方式，即通过函数值在两侧点的差来逼近导数。
3.代数方程系统：利用离散化的差分方程，将偏微分方程转化为代数方程系统。
根据问题的边界条件和初值条件，构建代数方程系统的系数矩阵和常数向量。
4. 求解代数方程：利用求解线性方程组的方法求解代数方程系统，常用的方法有直接法（如高斯消元法、LU分解法）和迭代法（如Jacobi迭代法、Gauss-Seidel迭代法）。
求解得到各个离散点的解。
5.后处理：根据求解结果进行后处理，包括结果的插值和可视化。
将离散点的解通过插值方法进行平滑处理，并进行可视化展示，以得到连续的函数解。
三、优缺点：1.直观：有限差分法基于网格划分，易于理解和实现。
2.精度可控：可通过调整网格大小和差分逼近方式来控制计算的精度。
3.广泛适用性：可用于求解各种偏微分方程，适用于不同的边界条件和初值条件。
然而，有限差分法也存在一些缺点：1.精度依赖网格：计算结果的精度受到网格划分的影响，因此需要谨慎选择网格大小。
2.限制条件：有限差分法适用于边界对应点处导数有定义的问题，不适用于奇异点和非线性问题。
有限差分法有限差分法是数学领域的一项最新成果，它在某些特定情况下能得到非常好的结果。
所谓有限差分方程就是利用积分和求差公式将差分方程化成为多个等价的偏微分方程组的组合形式，然后再应用最优化方法求解这种方程组，从而得出未知数的近似值。
当已知方程组的每个参数及其变量代入数据计算后的误差时，只要对其进行必要的调整或者修改后，就可获得满意的精度与效率的估计值。
此外，还可以通过有限差分方程的求解来了解其物理背景。
比如说在物体碰撞问题中，两个质点之间距离的测量往往涉及到很复杂的三维几何关系。
即使是一个小的距离误差也会引起很大的误差。
因此，对于碰撞问题中两个质点之间的相互位置误差测量，必须考虑它们之间的三维几何关系，并根据具体问题建立相应的坐标系统。
有限差分方程可以用来描述许多不同类型的实际问题，例如质量、压力、速度、温度、流动、热传导、声音和电磁场等。
但是由于数学模型本身的复杂性，使得有限差分方程在求解上遇到了困难。
因此，人们开始寻找一种更加直观的方法来解决问题。
有限差分法正是基于此原理提出的。
利用有限差分方程求解偏微分方程，我们首先要给出所求解的偏微分方程的数学表达式，这样才能够在有限差分方程的数学模型中寻找解析解。
有限差分方程的解析解，需要借助解析函数的理论来确定。
但是在自然科学和工程技术领域里，对于一般的实际问题，很少会存在着某种数学模型完全适合于所有的具体问题，那么对于任意一个偏微分方程，总是存在着一个解析解。
当把偏微分方程的解析解用适当的坐标表示出来后，有限差分方程的求解就转化为如何寻找与这个解相对应的函数值的问题。
通常，解析函数的形式是比较复杂的，因此需要运用数值方法进行拟合，从而得到符合实际的数学表达式。
然后通过对这个数学表达式的求解来确定所求偏微分方程的解析解。
这种数值求解方法称为数值积分法。
在研究有限元法和边界元法时都可以采用一些简单易行而且计算机可能很容易处理的函数作为边界条件，而这些函数本身又是很容易计算的。
有限差分法有限差分法（Finite Differential Method, FDM ）什么是有限差分法 有限差分法是指用泰勒技术展开式将变量的导数写成变量，在不同时间或空间点值的差分形式的方法。
按时间步长和空间步长将时间和空间区域剖分成若干网格，用未知函数在网格结(节)点上的值所构成的差分近似代替所用偏微分方程中出现的各阶导数，从而把表示变量连续变化关系的偏微分方程离散为有限个代数方程，然后解此线性代数方程组，以求出溶质在各网格结(节)点上不同时刻的浓度。
有限差分法的基本步骤（1）剖分渗流区，确定离散点。
将所研究的水动力弥散区域按某种几何形状(如矩形、任意多边形等)剖分成网络系统。
（2）建立水动力弥散问题的差分方程组。
（3）求解差分方程组。
采用各种迭代法，如点逐次超松驰方法(SOR)、线逐次超松驰方法(LSOR)、迭代的交替方向隐式方法(IADI)及强隐式方法(SID)等。
(1) 现在分别对时间（从0时刻到到期日）和股票价格（S max )为可达到的足够高的股票价格）进行分割，即\triangle S=S_{max}/M,\triangle T/N,这样就分别有N+1个时间段和M+1个股票价格，建立如图(所示的坐标方格，将定解区域网格化，坐标方格上的点（i,j ）对应时刻和股票价格，用变量f i ,j 表示（i,j ）点的期权价格。
2.建立差分格式（1）内含的有限差分方法其步骤可分为以下几步：(1)求前向差分近似:(2) 后向差分格式：(3)将(2),(3)式平均可更加对称地求出的近似，即(4)(2)求用前向差分近似：(5)(3)求(6)(4)将(4),(5),(6)式代入(1)式可得到内含有限差分公式：+ b j f i,j−c j f i,j + 1 = f i + 1,j(7)aj f i,j− 1其中：i=0,1,…，N-1。
j=0,1…，M-1针对看跌期权和看涨期权可分别求出方程的边界条件：看跌期权：看涨期权：(5)利用边界条件和(7)式可以给出M-1个联立方程组：+ b j f N− 1,j + c j f N− 1,j + 1j=1,2…，M-1aj f N− 1,j− 1求解这M-1个联立方程组即可以求出期权价格，但对美式看跌期权时我们必须考虑其提前执行的情况。
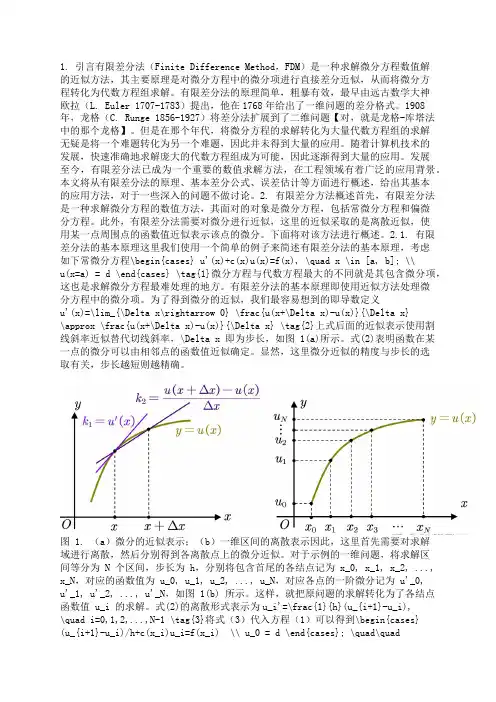
1. 引言有限差分法（Finite Difference Method，FDM）是一种求解微分方程数值解的近似方法，其主要原理是对微分方程中的微分项进行直接差分近似，从而将微分方程转化为代数方程组求解。
有限差分法的原理简单，粗暴有效，最早由远古数学大神欧拉（L. Euler 1707-1783）提出，他在1768年给出了一维问题的差分格式。
1908年，龙格（C. Runge 1856-1927）将差分法扩展到了二维问题【对，就是龙格-库塔法中的那个龙格】。
但是在那个年代，将微分方程的求解转化为大量代数方程组的求解无疑是将一个难题转化为另一个难题，因此并未得到大量的应用。
随着计算机技术的发展，快速准确地求解庞大的代数方程组成为可能，因此逐渐得到大量的应用。
发展至今，有限差分法已成为一个重要的数值求解方法，在工程领域有着广泛的应用背景。
本文将从有限差分法的原理、基本差分公式、误差估计等方面进行概述，给出其基本的应用方法，对于一些深入的问题不做讨论。
2. 有限差分方法概述首先，有限差分法是一种求解微分方程的数值方法，其面对的对象是微分方程，包括常微分方程和偏微分方程。
此外，有限差分法需要对微分进行近似，这里的近似采取的是离散近似，使用某一点周围点的函数值近似表示该点的微分。
下面将对该方法进行概述。
2.1. 有限差分法的基本原理这里我们使用一个简单的例子来简述有限差分法的基本原理，考虑如下常微分方程\begin{cases} u'(x)+c(x)u(x)=f(x), \quad x \in [a, b]; \\u(x=a) = d \end{cases} \tag{1}微分方程与代数方程最大的不同就是其包含微分项，这也是求解微分方程最难处理的地方。
有限差分法的基本原理即使用近似方法处理微分方程中的微分项。
为了得到微分的近似，我们最容易想到的即导数定义u'(x)=\lim_{\Delta x\rightarrow 0} \frac{u(x+\Delta x)-u(x)}{\Delta x}\approx \frac{u(x+\Delta x)-u(x)}{\Delta x} \tag{2}上式后面的近似表示使用割线斜率近似替代切线斜率，\Delta x 即为步长，如图 1(a)所示。
传热学有限差分法
传热学有限差分法是一种精确且高效的热分析方法。
它利用数学模型对传热过程进行模拟，能够准确地预测温度分布和热传导系数。
这种方法在工程领域被广泛应用，特别是在建筑、航空航天、电子和化学工业等领域。
有限差分法通过将连续的空间离散化为有限个网格，以解决偏微分方程的数值解问题。
在每个网格点上，有限差分法用差分方程近似代替偏微分方程，从而得到一组线性方程组。
然后，通过求解这组线性方程组，可以得到每个网格点的温度值，进而得到整个空间的温度分布。
这种方法具有高效性和精确性，因此在许多实际应用中都得到了广泛的应用。
例如，在建筑行业中，有限差分法可以用来模拟建筑物的热传导过程，从而预测建筑物的能耗和热舒适度。
在航空航天领域，有限差分法可以用来模拟飞机和火箭的热传导过程，从而预测其性能和安全性。
总的来说，传热学有限差分法是一种非常重要的工具，在解决复杂的传热问题时具有广泛的应用前景。
计算流体力学有限差分法流体力学有限差分法(Finite Difference Method，FDM)是一种常用的计算流体力学的方法。
它是基于流体力学基本方程对系统求解压力、速度和位置变化的一种近似数值方法，这些方程可以使用有限差分法求解得到准确结果。
一、流体力学有限差分法的概念1、端点条件：端点条件是差分方程组确定变量的边界条件，主要有边界条件和内部条件。
2、场变量定义：流动的物质可以用速度、压力和密度来描述，这种变量称为场变量。
3、有限差分法：有限差分法试图使描述精度在最小情况下得到一个可以接受的结果。
它将待求解区域划分为若干个小块，并且计算每一个小块上的变量。
4、边界条件：边界条件是用来描述物理事件发生的时候的物理量，如压力、流动量等。
二、流体力学有限差分法的基本步骤1、数学模型：开发有限差分方程，用来描述流体力学问题，这种模型可以由流体力学的基本方程得到。
2、网格划分：将区域网格划分成更小的网格，为了更准确的解决流体力学问题。
3、空间离散：将每一个网格按照有限差分公式空间离散，获得离散的压力方程式。
4、时间离散：在解决大规模动态流体力学问题时，通过一个更小的时间步骤进行求解。
5、求解：用适当的方法和算法求解有限差分方程式，获得求解结果。
三、流体力学有限差分法的优势1、高精度：使用此法，可以获得较高数值精度，从而准确描述流体力学过程。
2、计算效率：该方法可以快速找出有效的解决方案，并且计算效率更高。
3、计算能力：此方法可以处理复杂的物理问题，而且没有太多的硬件限制。
4、收敛性：当求解复杂的物理问题时，有限差分法不太容易出现"收敛"的情况。
5、可靠性：此方法可以快速、准确的求解出可靠的结果，相对于其他求解方法，其精度更高。
四、总结流体力学有限差分法是一种常用的计算流体力学的方法。
它易于实施，并且可以获得较高数值精度，从而准确描述流体力学过程。
处理复杂的物理问题时，它可以提供较快、较准确的结果，更能可靠性和可靠性更好。
第四章有限差分方法4.1引言有限差分法：数值求解常微分方程或偏微分方程的方法。
物理学和其他学科领域的许多问题在被分析研究之后, 往往可以归结为常微分方程或偏微分方程的求解问题。
一般说来，处理一个特定的物理问题，除了需要知道它满足的数学方程外，还应当同时知道这个问题的定解条件，然后才能设计出行之有效的计算方法来求解。
有限差分法以变量离散取值后对应的函数值来近似微分方程中独立变量的连续取值。
在有限差分方法中，我们放弃了微分方程中独立变量可以取连续值的特征，而关注独立变量离散取值后对应的函数值。
但是从原则上说，这种方法仍然可以达到任意满意的计算精度。
因为方程的连续数值解可以通过减小独立变量离散取值的间格，或者通过离散点上的函数值插值计算来近似得到。
这种方法是随着计算机的诞生和应用而发展起来的。
其计算格式和程序的设计都比较直观和简单，因而，它的实际应用已经构成了计算数学和计算物理的重要组成部分。
有限差分法的具体操作分为两个部分：(1)用差分代替微分方程中的微分，将连续变化的变量离散化，从而得到差分方程组的数学形式； (2)求解差分方程组。
在第一步中，我们通过所谓的网络分割法，将函数定义域分成大量相邻而不重合的子区域。
通常采用的是规则的分割方式。
这样可以便于计算机自动实现和减少计算的复杂性。
网络线划分的交点称为节点。
若与某个节点P 相邻的节点都是定义在场域内的节点，则P 点称为正则节点；反之，若节点P 有处在定义域外的相邻节点，则P 点称为非正则节点。
在第二步中，数值求解的关键就是要应用适当的计算方法，求得特定问题在所有这些节点上的离散近似值。
有限差分法的差分格式：一个函数在x 点上的一阶和二阶微商，可以近似地用它所临近的两点上的函数值的差分来表示。
如对一个单变量函数f(x)，x 为定义在区间[a,b]的连续变量。
以步长h=Δx 将[a,b]区间离散化，我们得到一系列节点x = a , x = x + h , x = x + h = a + 212132Δx , ..., x = x + h = b , 然后求出 f(x)在这些点上的近似值。
班级：通信13-4 姓名：学号：指导教师：**成绩：电子与信息工程学院信息与通信工程系求解金属槽的电位分布1.实验原理利用有限差分法和matlab软件解决电位在金属槽中的分布。
有限差分法基本思想是把连续的定解区域用有限个离散点构成的网格来代替,这些离散点称作网格的节点；把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似；把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解.然后再利用插值方法便可以从离散解得到定解问题在整个区域上的近似解.在采用数值计算方法求解偏微分方程时,若将每一处导数由有限差分近似公式替代,从而把求解偏微分方程的问题转换成求解代数方程的问题。
2.有限差分法方程的定解问题就是在满足某些定解条件下求微分方程的解。
在空间区域的边界上要满足的定解条件称为边值条件。
如果问题与时间有关，在初始时刻所要满足的定解条件，称为初值条件。
不含时间而只带边值条件的定解问题，称为边值问题。
与时间有关而只带初值条件的定解问题，称为初值问题。
同时带有两种定解条件的问题，称为初值边值混合问题。
定解问题往往不具有解析解，或者其解析解不易计算。
所以要采用可行的数值解法。
有限差分方法就是一种数值解法，它的基本思想是先把问题的定义域进行网格剖分，然后在网格点上，按适当的数值微分公式把定解问题中的微商换成差商，从而把原问题离散化为差分格式，进而求出数值解。
此外，还要研究差分格式的解的存在性和唯一性、解的求法、解法的数值稳定性、差分格式的解与原定解问题的真解的误差估计、差分格式的解当网格大小趋于零时是否趋于真解（即收敛性），等等。
有限差分方法具有简单、灵活以及通用性强等特点，容易在计算机上实现。
2.1有限差分法原理图1-1 有限差分法的网格划分导体槽中静电场的边值问题的拉普拉斯方程为：22220x y ϕϕ∂∂+=∂∂ (1-1) 为简单起见，将场域分成足够小的正方形网格，网格线之间的距离为h ，0h →。
节点0、1、2、3、4上的电位分别用0ϕ、1ϕ、2ϕ、3ϕ和4ϕ表示。
点1、点3在x 0处可微，沿x 方向在x 0处的泰勒级数展开式为2323100002311()()()()().2!3!h h h x x x ϕϕϕϕϕ∂∂∂=-+-+-+∂∂∂ (1-2)2323300002311()()()()().2!3!h h h x x xϕϕϕϕϕ∂∂∂=-+-+-+∂∂∂ (1-3)点2、点4在y 0处可微，沿y 方向在y 0处的泰勒级数展开式为2323200002311()()().2!3!h h h y y yϕϕϕϕϕ∂∂∂=++++∂∂∂ (1-4)2323400002311()()()()().2!3!h h h y y yϕϕϕϕϕ∂∂∂=-+-+-+∂∂∂ (1-5)忽略高次项22212340000224()()()4h xy ϕϕϕϕϕϕϕϕ⎡⎤∂∂+++=++=⎢⎥∂∂⎣⎦ (1-6)稍作变化得到拉普拉斯方程的五点差分格式：123404ϕϕϕϕϕ+++=(1-7)可通过迭代法求解以上差分方程。
2.2有限差分法步骤高斯—赛德尔迭代法图2-1网络下标标示1,,1,11,,4i j i j i j i ji j ϕϕϕϕϕ--+++++=(1-8)进行迭代时可写为 ,1,111,,11,14i j i j k k k k i j i j i j k ϕϕϕϕϕ-++-++++++=(1-9)1,2.......i M =,为行数，1,2.......j N =,为列数，k 为迭代次数，k ϕ为前次迭代的结果，1k ϕ+为当次迭代的结果，由于迭代从第一行、第一列开始，（1,i j -）、（,1i j -）点的迭代较（,i j ）点进行得早，顾可使用当次迭代的结果。
直到所有的点电位满足,,1i j i j k k ϕϕε+-<（ε为所设定精度）时迭代停止。
3.问题描述设有一个长直接地金属矩形槽，如图2-1所示，其侧壁与底面点位均为零，顶盖电位为100V （相对值），求槽内点位分布。
图3-1 金属槽4.程序设计4.1全场域问题对于问题（1）（2）（3）而言，以步距的正方形网格离散化场域。
每个网格对应于矩阵中的单个元素。
由此通过矩阵中的值的计算并指定相邻两次的迭代值误差不超过，应用matlab中的矩阵操作。
利用ones(x,y)建立一个且每个元素初值都为为1的矩阵A。
再对矩阵进行狄利克雷边界初始化，并且设置矩阵的左右边界为0，上下边界分别为100和0。
在保证精度的情况下以拉普拉斯差分式进行下一级的数值计算。
最终得到一个满足迭代要求的矩阵A。
具体程序实现见附录A。
4.2程序流程图图4-1 程序设计流程图通过函数contour(A)可以绘制出等电位分布图，这样可以观察出与理论情况的分布是否相同，分布图如图2-3所示：图4-2 金属槽等电位图4.3半场域问题对于问题（4），在程序设计中利用ones(x,y)建立一个且每个元素初值都为为1的矩阵A。
再对矩阵进行狄利克雷边界初始化，并且设置矩阵的左边界为0，左边界为初值为由式子100:-5:0产生的一个单位矩阵向量。
上下边界分别为100和0。
在保证精度的情况下以拉普拉斯差分式进行下一级的数值计算。
最终得到一个满足迭代要求的矩阵A。
具体程序实现见附录B 。
运行附录B 中的程序就可以得到半场域的数值解。
通过函数contour(A)可以绘制出等电位分布图，分布图如下：图4-3 半场域金属槽等电位图4.4中心点处的讨论对于问题（7），取中心点P()。
求解其电位的解析解，因为该点位置处于高度对称位置，所以该点所在的对称线上可视为匀强电场。
故有：E · L = φ (4-1)得：φ/2 = L/2 · E (4-2) 所以该点电位。
由附录A 中的程序运行得出该点的数值解为49.516V 。
由此可以得出误差范围为：0.4840V ，相对误差为：0.9700%。
5.收敛因子作用5.1超松弛迭代法为了加快收敛速度，常采用超松弛迭代法。
计算时，将某点的新老电位值之差乘以一个因子以后，再加到该点的新老电位值上，作为这一点的新电位值。
超松弛迭代法的表达式：,1,,,111,,11,1(4)4i j i j i ji jk k k k ki j i j i j k k ϕϕϕϕϕϕϕα-++-++++++-=+ (5-1)式中α称为松弛因子，其值介于1和2之间。
其中最佳收敛因子:21sin()o p απ=+ (5-2)其中p 为每边的节点数减去1。
其中M 、N 分别是x 、y 两个方向的内节点数。
对于本项目中，M=41、N=21，计算得：表4-1 最佳收敛因子迭代次数1.7516 迭代次数89取若干个收敛因子求得的迭代次数得表4-2和表4-3中的数据。
表4-2 收敛因子迭代次数和中心数值1.0 1.1 1.2 1.3 1.4 1.5 迭代次数 740 615 508 416 335 262 中心点电位值49.516749.516849.516949.517049.517149.5171表4-3 收敛因子迭代次数和中心数值1.6 1.7 1.74 1.78 1.8 1.9 迭代次数 196 133 106 73 80 161 中心点电位值49.517249.517249.517349.517349.517349.5173其中：中心点的解析解为50V 。
由收敛因子映射到中心电位值可以得到一个利用Excel 绘制的走势图。
如图：图4-1 中心点电势趋势图5.2关于收敛因子的结论5.2.1从迭代次数角度分析从迭代次数上看，收敛因子存在一个最佳值。
由表可以看出，当迭代因子从1开始趋近于最佳迭代因子时，收敛次数减少，进而使收敛速度较简单迭代法加快。
当收敛因子远离最佳收敛因子时，收敛次数又开始减少，进而使收敛速度较简单迭代法变慢。
即收敛因子影响收敛速度。
5.2.2从迭代次数角度分析从数值解的角度来说，由图3-7可知，随着加速收敛因子的增加，所得到的数值解就越接近于也随之增加。
到达一定的数值后，呈现出一种稳定的状态。
由此可知，收敛因子可以的增加会使数值解接近于解析解，而又不会等于解析解。
参考文献[1] 司守奎，孙玺箐.数学建模算法与应用.国防工业出版社，2015.2:411—424[2] 王家礼，朱满座，路宏敏.电磁场与电磁波.西安电子科技大学出版社，2009.8:118—122附录A：简单差分法求解电位分布%将待求区域化成20*40个边长为1的正方体% 顶板100V，左右底为0Vx=21;y=41;%网格节点数x行，y列A=ones(x,y);%设置21行，41列的矩阵A(1,:)=ones(1,y)*100;% 设置上基板的值A(x,:)=zeros(1,y);% 设置下基板的值A(:,1)=zeros(x,1);% 设置左基板的值A(:,y)=zeros(x,1);% 设置右基板的值disp(A);%命令行输出矩阵A瞅瞅A1=A;%初始化一级近似值A1max=1;%初始化最大绝对误差值，用于进入while循环k=0;%迭代次数while(max>1e-5)%由A迭代，算出·A1，迭代精度为1e-6k=k+1;%计算迭代次数max=0;%误差回归最小temp=0;%单次计算的前后两次迭代中的同元素的误差初始值for i=2:1:x-1 %从第2行到底20行for j=2:1:y-1 %从第2列到底40列A1(i,j)=( A(i,j+1)+A(i,j-1)+A(i+1,j)+A(i-1,j) )/4;%拉普拉斯方程差分式disp('A1(i,j)='),disp(A1(i,j));%log输出temp=abs(A1(i,j)-A(i,j));%相邻两次迭代解之间的误差disp('temp='),disp(temp);%log输出%控制精度的最大值，得到误差计算中的最大值if temp>maxmax=temp;endendendA=A1;%赋值给下次用enddisp('输出A1===='),disp(A);disp('输出迭代次数k===='),disp(k);附录B：收敛因子作用程序设计%比较最佳收敛因子和收敛因子的差异x=21;y=41;%网格节点数x行，y列A=ones(x,y);%设置21行，41列的矩阵A(1,:)=ones(1,y)*100;% 设置上基板的值A(x,:)=zeros(1,y);% 设置下基板的值A(:,1)=zeros(x,1);% 设置左基板的值A(:,y)=zeros(x,1);% 设置右基板的值disp(A);%命令行输出矩阵A瞅瞅A1=A;%初始化一级近似值A1max=1;%初始化最大绝对误差值，用于进入while循环k=0;%迭代次数a0=2-pi*sqrt((2/(41^2))+(2/(21^2)));%最佳收敛因子%------------------------------注意事项----------------------------%修改下面a的值就可以任意设定收敛因子%取值需要满足：1<=a<2%------------------------------注意事项----------------------------a=a0 ;% 收敛因子while(max>1e-5)%由A迭代，算出·A1，迭代精度为1e-6k=k+1;%计算迭代次数max=0;%误差回归最小temp=0;%单次计算的前后两次迭代中的同元素的误差初始值for i=2:1:x-1 %从第2行到底20行for j=2:1:y-1 %从第2列到底40列A1(i,j)=A(i,j)+( A(i,j+1)+A1(i,j-1)+A(i+1,j)+A1(i-1,j)-4*A(i,j) )*a/4;%超松弛迭代法表达式disp('A1(i,j)='),disp(A1(i,j));%log输出temp=abs(A1(i,j)-A(i,j));%相邻两次迭代解之间的误差disp('temp='),disp(temp);%log输出%控制精度的最大值，得到误差计算中的最大值if temp>maxmax=temp;endendendA=A1;%赋值给下次用enddisp('输出A1===='),disp(A1);disp('输出迭代次数k===='),disp(k);附录C：半场域程序设计%半场域的计算x=21;y=21;%网格节点数x行，y列A=ones(x,y);%设置21行，21列的矩阵A(1,:)=ones(1,y)*100;% 设置上基板的值A(x,:)=zeros(1,y);% 设置下基板的值A(:,1)=zeros(x,1);% 设置左基板的值right=100:-5:0;%建立一个100开头的行向量A(:,y)=right;% 设置右基板的值disp(A);%命令行输出矩阵A瞅瞅A1=A;%初始化一级近似值A1max=1;%初始化最大绝对误差值，用于进入while循环k=0;%迭代次数while(max>1e-5)%由A迭代，算出·A1，迭代精度为1e-6k=k+1;%计算迭代次数max=0;%误差回归最小temp=0;%单次计算的前后两次迭代中的同元素的误差初始值for i=2:1:x-1 %从第2行到底21行for j=2:1:y-1 %从第2列到底21列A1(i,j)=( A(i,j+1)+A(i,j-1)+A(i+1,j)+A(i-1,j) )/4;%拉普拉斯方程差分式disp('A1(i,j)='),disp(A1(i,j));%log输出temp=abs(A1(i,j)-A(i,j));%相邻两次迭代解之间的误差disp('temp='),disp(temp);%log输出%控制精度的最大值，得到误差计算中的最大值if temp>maxmax=temp;endendendA=A1;%赋值给下次用enddisp('输出A1===='),disp(A1);disp('输出迭代次数k===='),disp(k);。
