泊松分布与生灭过程

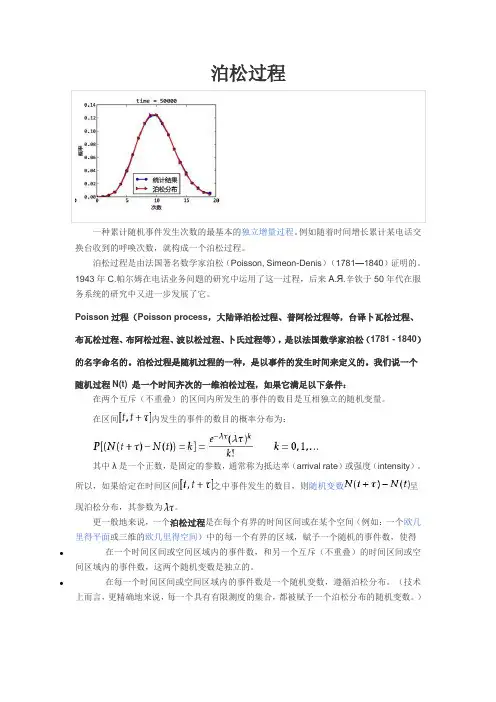
泊松过程一种累计随机事件发生次数的最基本的独立增量过程。

例如随着时间增长累计某电话交换台收到的呼唤次数，就构成一个泊松过程。

泊松过程是由法国著名数学家泊松（Poisson, Simeon-Denis）（1781—1840）证明的。

1943年C.帕尔姆在电话业务问题的研究中运用了这一过程，后来Α.Я.辛钦于50年代在服务系统的研究中又进一步发展了它。

Poisson过程（Poisson process，大陆译泊松过程、普阿松过程等，台译卜瓦松过程、布瓦松过程、布阿松过程、波以松过程、卜氏过程等），是以法国数学家泊松（1781 - 1840）的名字命名的。

泊松过程是随机过程的一种，是以事件的发生时间来定义的。

我们说一个随机过程N(t) 是一个时间齐次的一维泊松过程，如果它满足以下条件：在两个互斥（不重叠）的区间内所发生的事件的数目是互相独立的随机变量。

在区间内发生的事件的数目的概率分布为：其中λ是一个正数，是固定的参数，通常称为抵达率（arrival rate）或强度（intensity）。

所以，如果给定在时间区间之中事件发生的数目，则随机变数呈现泊松分布，其参数为。

更一般地来说，一个泊松过程是在每个有界的时间区间或在某个空间（例如：一个欧几里得平面或三维的欧几里得空间）中的每一个有界的区域，赋予一个随机的事件数，使得•在一个时间区间或空间区域内的事件数，和另一个互斥（不重叠）的时间区间或空间区域内的事件数，这两个随机变数是独立的。

•在每一个时间区间或空间区域内的事件数是一个随机变数，遵循泊松分布。

（技术上而言，更精确地来说，每一个具有有限测度的集合，都被赋予一个泊松分布的随机变数。

）泊松过程是莱维过程（Lévy process）中最有名的过程之一。

时间齐次的泊松过程也是时间齐次的连续时间Markov过程的例子。

一个时间齐次、一维的泊松过程是一个纯出生过程，是一个出生-死亡过程的最简单例子。

关于泊松分布与纯生过程【摘要】本文主要探讨了泊松分布与纯生过程的概念及特点，并着重介绍了它们之间的关系。

通过对泊松分布的定义和特点的分析，我们了解到泊松分布是一种描述事件在时间或空间上随机发生的概率分布。

纯生过程的概念和特点也被详细阐述，纯生过程是指在任意时间间隔内事件发生的次数是相互独立的。

通过比较泊松分布和纯生过程的特点和应用，我们发现它们在很多领域都有重要的应用价值，如通信网络、生态学等。

通过本文的阐述，读者能够更好地理解和应用泊松分布与纯生过程在实际问题中的作用。

【关键词】泊松分布、纯生过程、定义、特点、关系、应用1. 引言1.1 泊松分布与纯生过程概述泊松分布与纯生过程是概率论中重要的概念，常常在统计学、生态学、医学等领域得到广泛应用。

泊松分布是一种描述单位时间（或单位面积、单位体积等）内随机事件发生次数的概率分布，最早由法国数学家西蒙·丹尼·泊松提出，因而得名。

泊松分布的特点是事件的发生是相互独立、且各事件间的时间间隔是随机的。

纯生过程是一个不断进行、不断产生新事件的过程，其中每个事件的发生与之前的事件无关，且事件发生的概率在时间上保持不变。

纯生过程的特点是事件间的关联性很弱，每个事件的发生都是相互独立的，且事件的出现在时间上是随机的。

泊松分布与纯生过程有着密切的关系，泊松分布可以被看作是纯生过程的一种特例，即事件发生的概率为恒定值的情况。

泊松分布与纯生过程在实际应用中常常同时出现，例如在疫情爆发时，常常使用泊松分布来描述病例数量的分布，并假设病例的发生是一个纯生过程。

通过对泊松分布与纯生过程的深入研究，可以更好地理解随机事件的规律性，为实际问题的分析与解决提供重要参考。

2. 正文2.1 泊松分布的定义泊松分布是一种描述事件在一定时间或空间内发生次数的概率分布。

它通常用于描述在一个固定时间内事件发生的次数，比如单位时间内电话的拨打次数、一天内商店的顾客数量等。

泊松分布的定义为：若随机事件发生的次数服从泊松分布，那么该事件在任意两个不相交的区间上发生的次数是相互独立的，且在一个很小的时间段内发生的概率与时间段的长度成正比。

泊松过程总结
泊松过程是一种常见的随机过程，它在许多领域中都有重要的应用，如通信、金融、物流等。

以下是泊松过程的一些重要特性和总结： 1. 定义：泊松过程是一种离散时间、连续状态的计数过程，其状态变化是以固定时间间隔发生的独立事件的个数。

2. 独立增量性：泊松过程具有独立增量性，即在不重叠的时间间隔内，事件的发生个数是相互独立的。

3. 平稳性：泊松过程是平稳的，即其统计特性在时间上是不变的。

4. 无记忆性：泊松过程是无记忆的，即过去的事件发生情况对未来的事件发生情况没有影响。

5. 期望值和方差：泊松过程的期望值和方差均等于参数λ，即E[N(t)] = λt，Var[N(t)] = λt。

6. 泊松分布：泊松过程的时间间隔和事件发生个数都服从泊松分布，即P(X=k) = (λt)^k * e^(-λt) / k!，其中X表示在时间t 内发生k次事件的概率。

7. 事件发生率：泊松过程的事件发生率λ表示在单位时间内平均发生的事件个数。

8. 泊松过程的应用：泊松过程在实际中有广泛的应用，如电话呼叫中心中的呼叫到达、网络数据包到达、交通流量变化等。

总之，泊松过程是一种描述离散、独立、平稳的计数过程，它的统计特性和概率分布具有一些重要的性质，使得它在实际应用中具有
广泛的用途。

关于泊松分布与纯生过程作者：臧梓涵来源：《文理导航·教育研究与实践》2019年第02期【摘要】概率与随机过程作为数学理论的一部分，在实际生活中有着重大的意义，可以成为许多生活应用的理论基础。

本文以一种随机过程一泊松过程及其应用为切入点，进一步推广到纯生过程的性质，对于纯生过程爆炸的条件予以研究与推断。

【关键词】计数过程;独立增量过程;泊松分布;纯生过程;爆炸一、引言据美国人口普查局统计，2018年元旦全世界人口总数达到74，4444，3881人。

人口的不断增长不免使我们产生担心与好奇：世界的人口在未来的某一天会不会增长到地球无法容下，甚至于无穷，这是一个很难解决的问题。

本文将结合数学中的泊松分布等理论尝试给出解答。

先是由基础的随机变量等数学概念引入，随后转向一种特殊的独立增量过程一泊松过程。

熟悉其性质后，转向其一般化应用的一种跳过程：生灭过程。

再对一种特殊化的生灭过程：纯生过程进行研究，最终从纯生过程的性质分析中得到纯生过程爆炸的条件（即人口增至无穷的条件）。

二、泊松过程在引入泊松过程之前，我们先介绍随机变量并对其分布和期望的基本性质进行分析。

随机变量：随机变量X的概念，在高中的统计概率部分就已引入了，表示了随机试验各种结果的实值单值函数。

它在本质上是定义在样本空间上的一个或离散或连续的函数，对于R 的任意子集A，{X∈A}是事件。

通过将随机事件的结果用数量化的方式表示，可以更好地分析生活中的随机现象。

例如灯泡的寿命，病毒的分裂感染，公交汽车站等车乘客人数等。

概率分布：对于随机变量X称F（X）为X的分布函数。

分布函数是单调不减的右连续函数，如果X有离散的概率分布。

数学期望：假设离散随机变量X在点x j的概率为p j，如果E（X）=∑x j p j存在，则称其为X的数学期望，也就是概率加权平均值。

计数过程：用N（t）表示时间段[0，t]内某类事件发生的个数，N（t）是随机变量。

称{N （t）：t≥0}是计数过程。

关于泊松分布与纯生过程【摘要】泊松分布是概率论中重要的一种分布，描述了在一定时间或空间内事件发生的次数的概率分布。

本文首先介绍了泊松分布的定义与性质，以及其参数与应用。

接着讨论了纯生过程的概念与特点，以及泊松分布与纯生过程之间的关系。

探讨了泊松分布与纯生过程在实际应用中的重要性，并提出了未来研究方向。

通过对泊松分布与纯生过程的研究，我们能更好地理解事件发生的概率规律，为实际应用提供科学依据。

【关键词】泊松分布、纯生过程、定义、性质、参数、应用、概念、特点、关系、实际应用、重要性、未来研究方向、总结1. 引言1.1 泊松分布与纯生过程概述泊松分布与纯生过程是概率论中重要的概念，它们在不同领域中有着广泛的应用。

泊松分布是描述某个区间内随机事件发生次数的概率分布，它具有独立性和无记忆性的特点。

泊松分布的参数λ表示单位时间（或单位面积）内事件的平均发生次数。

而纯生过程则是指在一段无时间和空间相关性的随机事件序列中，任何两个事件之间的时间间隔是独立同分布的。

泊松分布与纯生过程之间存在着密切的关系，泊松分布可以看作是纯生过程中间隔时间为指数分布的特殊情况。

泊松分布在现实生活中有着广泛的应用，例如描述自然界中的地震次数、传染病的发生次数等。

而纯生过程在信号处理、通信系统等领域中也有着重要的作用。

泊松分布与纯生过程的研究不仅有着理论上的意义，也对实际问题的解决具有重要意义。

未来研究的方向可以在泊松分布参数λ的确定、纯生过程的进一步理解以及两者之间更深入的关联等方面进行探索。

泊松分布与纯生过程为我们理解随机事件发生规律提供了重要的工具，值得进一步研究和探索。

2. 正文2.1 泊松分布的定义与性质泊松分布是概率论中一种重要的离散型概率分布，它是由法国数学家西蒙·丹尼·泊松在1837年提出的。

泊松分布的定义如下：设随机变量X表示单位时间（或单位面积、单位体积等）内某一事件发生的次数，若事件在任意相互不重叠的时间段（或区域、体积等）内发生的概率近似相等，且相邻两个事件之间是独立的，则随机变量X服从参数为λ的泊松分布，记为X~P(λ)。