6教育统计学第六章
- 格式:ppt
- 大小:1.60 MB
- 文档页数:1
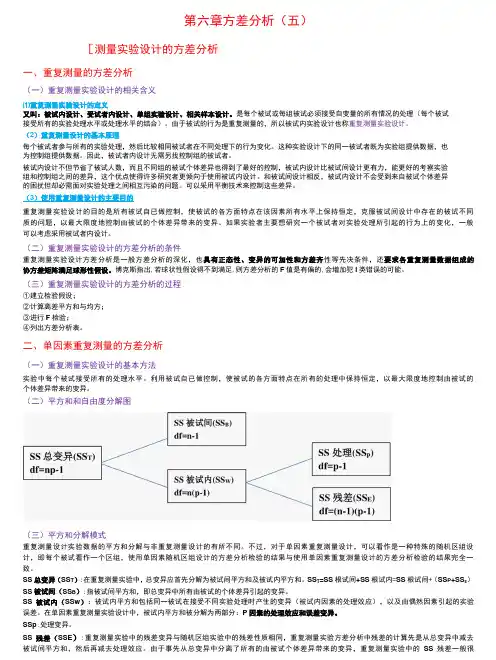
第六章方差分析(五)[测量实验设计的方差分析一、重复测量的方差分析(一)重复测量实验设计的相关含义⑴重复测量实验设计的定义又叫:被试内设计、受试者内设计、单组实验设计、相关样本设计。
是每个被试或每组被试必须接受自变量的所有情况的处理(每个被试接受所有的实验处理水平或处理水平的结合)。
由于被试的行为是重复测量的,所以被试内实验设计也称重复测量实验设计。
(2)重复测量设计的基本原理每个被试者参与所有的实验处理,然后比较相同被试者在不同处理下的行为变化。
这种实验设计下的同一被试者既为实验组提供数据,也为控制组提供数据。
因此,被试者内设计无需另找控制组的被试者。
被试内设计不但节省了被试人数,而且不同组的被试个体差异也得到了最好的控制,被试内设计比被试间设计更有力,能更好的考察实验组和控制组之间的差异,这个优点使得许多研究者更倾向于使用被试内设计。
和被试间设计相反,被试内设计不会受到来自被试个体差异的困扰但却必需面对实验处理之间相互污染的问题。
可以采用平衡技术来控制这些差异。
(3)使用重复测量设计的主要目的重复测量实验设计的目的是所有被试自已做控制,使被试的各方面特点在该因素所有水平上保持恒定,克服被试间设计中存在的被试不同质的问题,以最大限度地控制由被试的个体差异带来的变异。
如果实验者主要想研究一个被试者对实验处理所引起的行为上的变化,一般可以考虑采用被试者内设计。
(二)重复测量实验设计的方差分析的条件重复测量实验设计方差分析是一般方差分析的深化,也具有正态性、变异的可加性和方差齐性等先决条件,还要求各重复测量数据组成的协方差矩阵满足球形性假设。
博克斯指出,若球状性假设得不到满足,则方差分析的F值是有偏的,会增加犯I类错误的可能。
(三)重复测量实验设计的方差分析的过程①建立检验假设;②计算离差平方和与均方;③进行F检验;④列出方差分析表。
二、单因素重复测量的方差分析(一)重复测量实验设计的基本方法实验中每个被试接受所有的处理水平。


第一章绪论1,教育统计学是运用数理统计学的原理来研究教育问题的一门应用科学。
2,教育统计学分为描述统计、推断统计和实验设计三类。
(1)描述统计:计算集中量(算术平均数、中位数、众数、加权算术平均数、几何平均数、调和平均数)来反映集中趋势;计算差异量(全距、四分位距、百分位距、平均差、标准差、差异系数)反映离散程度;计算偏态量及峰态量反映分布形态;计算相关量(积差相关系数、等级、点二列、二列、四分、C相关系数、肯德尔和谐系数、多系列相关系数)反映一致性程度。
(2)推断统计包括总体参数估计和假设检验两部分。
3,随机现象三个特性:一,一次试验有多种可能的结果,其所有结果是已知的;二,试验之前不能预料那一种结果会出现;三,在相同条件下可以重复试验。
随机事件:随机现象的每一种结果。
随机变量:把能表示随机现象各种结果的变量称之4,总体:是我们研究的具有某种共同特性的个体的总和。
样本数目大于30称为大样本,小于等于30称为小样本。
第二章数据的初步整理1,教统资料来源有经常性资料和专题性资料。
专题性资料包括(1)教育调查。
按调查方法分为现情调查、回顾调查和追踪调查;按调查范围分全面调查和非全面调查(抽样调查和典型调查)。
(2)教育实验。
分为单组实验(指对同一实验对象先后实施两种实验处理)、等组实验(指在甲乙两组条件基本相同的情况下,对之实行不同的实验处理)和轮组实验(指在实验组和对照组分别进行两种实验处理,并且每种处理各重复一次,也即每个或多个单组实验的联合)2,数据的分类。
按来源分为点计数据和度量数据;按随机变量取值情况分为间断型随机变量(取值个数有限、独立的、两个单位之间不能再划分细小单位、一般用整数表示,如优劣程度、品德爱好打分)和连续性随机变量(个数无限、单位之间可以再划分、可以用小数表示如身高体重、完成作业的时间等)。
3,频数分布表制作步骤:求全距;决定组数和组距;决定组限;登记频数。
4,用累计频数表示的频数分布表称为累计频数分布表。


第六章方差分析第一节方差分析概述一.方差分析的定义[用途]定义:用途方差分析也称为变异数分析,是在教育与心理研究中最常用的变量分析方法,其主要功能在于分析测量或实验数据中不同来源的变异对总变异的贡献大小,从而确定测量或实验中因素对反应变量是否存在显著影响。
即用于置信度不变情况下的多组平均数之间的差异检验。
它既可以比较两个以上的样本平均数的差异检验,也可以应用于一个因素多种水平以及多个因素有多种水平的数据分析。
二.方差分析的作用方差分析主要应用于两种以上实验处理的数据分析,同时匕徽两个以上的样本平均数,推断多组资料的总体均数是否相同,也即检验多组数据之间的均数差异是否有统计意义。
在这个意义,也可以将其理解为平均数差异显著性检验的扩展。
当我们用多个t检验来完成这一过程时,相当于从t分布中随机抽取多个t值,这样落在临界范围之外的可能大大增加,从而增加了I型错误的概率,我们可以把方差分析看作t检验的增强版。
方差分析一次检验多组平均数的差异,降低了多次进行两组平均数检验所带来的误差。
在进行方差分析时,设定的假设是综合虚无假设,即假设样本所归属的所有总体的平均数都相等。
如果检验的结果是存在显著性差异,只能说明多组平均数之间存在显著性差异,但是无法确定究竟哪些组之间存在显著性差异,此时需要运用事后检验的方法来确定。
三.方差分析的相关概念一(一)数据的变异(1)变异:统计中的变异是普遍存在的7一般意义上的变异是指标志(包括品质标志和数量标志)在总体单位之间的不同表现。
可变标志的属性或数值表现在总体各单位之间存在的差异,统计上称之为变异,这是广义上的变异,即包括了品质标志和数量标志,有时仅指品质标志和在总体单位之间的不同表现。
注:随机性,即变异性。
(2)组间变异[组间差异]:组间变异表示处理间变异,主要指由于接受不同的实验处理(实验处理效应)而造成的各组之间的变异,可以用两个平均数之间的离差来表示,可将组间离差平方和记为SS AO组间差异可用组间方差来表征,用符号MS B表示。

第六章方差分析(六)第五节多因素方差分析一、多因素方差分析的定义多因素方差分析是用来研究两个及两个以上控制变量是否会对观测变量产生显著影响。
多因素方差分析不仅能够分析多个因素对观测变量 的独立影响,更能够分析多个控制因素的交互作用是否对观测变量的分布产生显著影响,进而最终找到利于观测变量的最优组合。
多因素 方差分析包括完全随机设出随机区组设计。
二、平均数差异检验、单因素方差分析、多因素方差分析比较当需要比较两个以上平均数的差异时,要使用单因素方差分析,而不进行多次平均数差异检验,这样就可以降低统计误差。
如果单次进行 平均数比较率,即显著性水平是a ,进行两两平均数比较的次数是N ,多次两两平均数差异的错误率:P N =l-(l-a)n o 同理多因素方差由于 同时进行两个因素以上的方差分析,亦能降低统计误差,同时,也能处理交互作用。
第六节事后检验(多个平均数之间的比较)一、事后检验[事后多重比较]事后检验的定义:方差分析所要检验的零假设是所有k 个处理的总体平均数没有显著性差异,相应的备择假设是k 个处理中至少有2个处 理的总体平均数之间存在显著差异。
但方差分析不拒绝零假设时,表明至少有2个处理的总体平均数不等,若方差分析F 检验的结果表明 差异显著就必须对各实验处理组的多对平均数进一步分析,做深入比较,判断究竟哪一对或哪几对的差异显著,确定两变量关系的本质。
事后检验也被称作事后多重比较,在这也叫做多个平均数之间的比较。
事后检验的目的:当方差分析表明一个主效应显著时,它只能提供几个变量之间是否存在显著差异的结果,又因为多重t 检验会使得I 型 错误发生的概率大大增加[吃1-Q :业L 因而我们只能采取事后检验。
二、事后检验的方法[1]N-K 法,也叫q 检验法;[2]HSD 检验(又叫Turkey 真实检验,更敏感,统计检验力更强,要求各组容量相等);[3]Scheffe 检验(匕啜保守,适用于样本容量不等,最大限降低了第一类误差a 水平,可能最安全);⑷费舍的最小显著差异法(LSD);一、协方差分析协方差分析的定义:协方差表示的是交互效应项,将处理引起的变异分解为处理在变量x 上引起的变异、在变量y 上引起的变异和在交互效应项xy 上引起的 变异。

第六章相关与回归分析习题一、填空题1.现象之间的相关关系按相关的程度分为、和;按相关的形式分为和;按影响因素的多少分为和。
2.两个相关现象之间,当一个现象的数量由小变大,另一个现象的数量,这种相关称为正相关;当一个现象的数量由小变大,另一个现象的数量,这种相关称为负相关。
3.相关系数的取值范围是。
4.完全相关即是关系,其相关系数为。
5.相关系数,用于反映条件下,两变量相关关系的密切程度和方向的统计指标。
6.直线相关系数等于零,说明两变量之间;直线相关系数等1,说明两变量之间;直线相关系数等于—1,说明两变量之间。
7.对现象之间变量的研究,统计是从两个方面进行的,一方面是研究变量之间关系的,这种研究称为相关关系;另一方面是研究关于自变量和因变量之间的变动关系,用数学方程式表达,称为。
8.回归方程y=a+bx中的参数a是,b是。
在统计中估计待定参数的常用方法是。
9. 分析要确定哪个是自变量哪个是因变量,在这点上它与不同。
10.求两个变量之间非线性关系的回归线比较复杂,在许多情况下,非线性回归问题可以通过化成来解决。
11.用来说明回归方程代表性大小的统计分析指标是。
二、单项选择题1.下面的函数关系是( )A销售人员测验成绩与销售额大小的关系B圆周的长度决定于它的半径C家庭的收入和消费的关系D数学成绩与统计学成绩的关系2.相关系数r的取值范围( )A -∞<r<+∞B -1≤r≤+1C -1<r<+1D 0≤r≤+13.年劳动生产率z(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均( )A增加70元B减少70元C增加80元D减少80元4.假设要证明两变量之间线性相关程度是高的,则计算出的相关系数应接近于( )A+1 B 0 C 0.5 D [1]5.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( )A线性相关还是非线性相关B正相关还是负相关C完全相关还是不完全相关D单相关还是复相关6.某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建立线性回归方程y =a+b x。


华东师大心理统计学大纲教材:《教育统计学》(王孝玲编著,修订版)华东师范大学出版社 1993年6月第一版第一章绪论第一节什么是统计学和心理统计学一、什么是统计学 统计学是研究统计原理和方法的科学。
具体地说,它是研究如何搜集、整理、分析反映事物总体信息的数字资料,并以此为依据,对总体特征进行推断的原理和方法。
统计学分为两大类。
一类是数理统计学。
它主要是以概率论为基础,对统计数据数量关系的模式加以解释,对统计原理和方法给予数学的证明。
它是数学的一个分支。
另一类是应用统计学。
它是数理统计原理和方法在各个领域中的应用,如数理统计的原理和方法应用到工业领域,称为工业统计学;应用到医学领域,称为医学统计学;应用到心理学领域,称为心理统计学,等等。
应用统计学是与研究对象密切结合的各科专门统计学。
二、统计学和心理统计学的内容 统计学和心理统计学的研究内容,从不同角度来分,可以分为不同的类型。
从具体应用的角度来分,可以分成描述统计,推断统计和实验设计三部分。
1.描述统计 对已获得的数据进行整理、概括,显示其分布特征的统计方法,称为描述统计。
2.推断统计 根据样本所提供的信息,运用概率的理论进行分析、论证,在一定可靠程度上,对总体分布特征进行估计、推测,这种统计方法称为推断统计。
推断统计的内容包括总体参数估计和假设检验两部分。
3.实验设计 实验者为了揭示试验中自变量和因变量的关系,在实验之前所制定的实验计划,称为实验设计。
其中包括选择怎样的抽样方式;如何计算样本容量;确定怎样的实验对照形式;如何实现实验组和对照组的等组化;如何安排实验因素和如何控制无关因素;用什么统计方法处理及分析实验结果,等等。
以上三部分内容,不是截然分开,而是相互联系的。
第二节统计学中的几个基本概念 一、随机变量 具有以下三个特性的现象,成为随机变量。
第一,一次试验有多中可能结果,其所有可能结果是已知的;第二,试验之前不能预料哪一种结果会出现;第三,在相同的条件下可以重复试验。

华东师大心理统计学大纲教材:《教育统计学》(王孝玲编著,修订版)华东师范大学出版社1993年6月第一版第一章绪论第一节什么是统计学和心理统计学一、什么是统计学统计学是研究统计原理和方法的科学。
具体地说,它是研究如何搜集、整理、分析反映事物总体信息的数字资料,并以此为依据,对总体特征进行推断的原理和方法。
统计学分为两大类。
一类是数理统计学。
它主要是以概率论为基础,对统计数据数量关系的模式加以解释,对统计原理和方法给予数学的证明。
它是数学的一个分支。
另一类是应用统计学。
它是数理统计原理和方法在各个领域中的应用,如数理统计的原理和方法应用到工业领域,称为工业统计学;应用到医学领域,称为医学统计学;应用到心理学领域,称为心理统计学,等等。
应用统计学是与研究对象密切结合的各科专门统计学。
二、统计学和心理统计学的内容统计学和心理统计学的研究内容,从不同角度来分,可以分为不同的类型。
从具体应用的角度来分,可以分成描述统计,推断统计和实验设计三部分。
1.描述统计对已获得的数据进行整理、概括,显示其分布特征的统计方法,称为描述统计。
2.推断统计根据样本所提供的信息,运用概率的理论进行分析、论证,在一定可靠程度上,对总体分布特征进行估计、推测,这种统计方法称为推断统计。
推断统计的内容包括总体参数估计和假设检验两部分。
3.实验设计实验者为了揭示试验中自变量和因变量的关系,在实验之前所制定的实验计划,称为实验设计。
其中包括选择怎样的抽样方式;如何计算样本容量;确定怎样的实验对照形式;如何实现实验组和对照组的等组化;如何安排实验因素和如何控制无关因素;用什么统计方法处理及分析实验结果,等等。
以上三部分内容,不是截然分开,而是相互联系的。
第二节统计学中的几个基本概念一、随机变量具有以下三个特性的现象,成为随机变量。
第一,一次试验有多中可能结果,其所有可能结果是已知的;第二,试验之前不能预料哪一种结果会出现;第三,在相同的条件下可以重复试验。

A+1 B 0 C 0.5 D [1]5.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( )A线性相关还是非线性相关B正相关还是负相关C完全相关还是不完全相关D单相关还是复相关6.某校经济管理类的学生学习统计学的时间()与考试成绩(y)之x间建立线性回归方程y c=a+b。
经计算,方程为y c=200—0.8x,该方程参数x的计算( )A a值是明显不对的B b值是明显不对的C a值和b值都是不对的 C a值和6值都是正确的7.在线性相关的条件下,自变量的均方差为2,因变量均方差为5,而相关系数为0.8时,则其回归系数为:( )A 8B 0.32C 2D 12.58.进行相关分析,要求相关的两个变量( )A都是随机的B都不是随机的C一个是随机的,一个不是随机的D随机或不随机都可以9.下列关系中,属于正相关关系的有( )A合理限度内,施肥量和平均单产量之间的关系B产品产量与单位产品成本之间的关系C商品的流通费用与销售利润之间的关系D流通费用率与商品销售量之间的关系10.相关分析是研究( )A变量之间的数量关系B变量之间的变动关系C变量之间的相互关系的密切程度D变量之间的因果关系11.在回归直线y c=a+bx,b<0,则x与y之间的相关系数( )A =0B =lC 0<<1D -1<<0r r r r12.在回归直线yc=a+bx中,b表示( )A当x增加一个单位,,y增加a的数量B当y增加一个单位时,x增加b的数量C当x增加一个单位时,y的均增加量D当y增加一个单位时,x的平均增加量13.当相关系数r=0时,表明( )A现象之间完全无关B相关程度较小C现象之间完全相关D无直线相关关系14.下列现象的相关密切程度最高的是( )A某商店的职工人数与商品销售额之间的相关系数0.87B流通费用水平与利润率之间的相关关系为-0.94C商品销售额与利润率之间的相关系数为0.51D商品销售额与流通费用水平的相关系数为-0.8115.估计标准误差是反映( )A平均数代表性的指标B相关关系的指标C回归直线的代表性指标D序时平均数代表性指标三、多项选择题1.下列哪些现象之间的关系为相关关系( )A家庭收入与消费支出关系B圆的面积与它的半径关系C广告支出与商品销售额关系D单位产品成本与利润关系E在价格固定情况下,销售量与商品销售额关系2.相关系数表明两个变量之间的( )A线性关系B因果关系C变异程度D相关方向E相关的密切程度3.对于一元线性回归分析来说( )A两变量之间必须明确哪个是自变量,哪个是因变量B回归方程是据以利用自变量的给定值来估计和预测因变量的平均可能值C可能存在着y依x和x依y的两个回归方程D回归系数只有正号E 确定回归方程时,尽管两个变量也都是随机的,但要求自变量是给定的。
第六章 抽样分布及总体平均数的推断教学目的:通过本章学习,同学们应理解抽样分布、小概率事件、显著性水平、统计推断的两类错误等基本概念,并熟练掌握总体参数估计和总体平均数的显著性检验的方法。
第一节 抽样分布一、抽样分布的基本概念三种不同性质的分布:1.总体分布:总体内数据的频数分布;2.样本分布:样本内数据的频数分布;3.抽样分布:某种统计量的概率分布。
平均数的抽样分布:从某一总体中抽出的,容量为n 的一切可能样本平均数的分布。
【如】:样本平均数的抽样分布、相关系数的抽样分布。
二、平均数抽样分布的几个定理1.从总体中随机抽出容量为n 的一切可能样本平均数之平均数等于总体平均数。
)()(1.6μ=X EE 表示平均的符号.2.容量为n 的样本平均数在其抽样分布上的标准差,与总体标准差成正比,与样本容量n 的方根成反比。
)(2.6nx σσ=x σ:是平均数抽样分布上的标准差(一般称作平均数的标准误)。
3.从正态总体中,随机抽取的容量为n 的一切可能样本平均数的分布也呈正态分布。
4.虽然总体不是正态分布,如果样本容量n 很大,平均数的抽样分布也近似正态分布。
※:标准误越小,表明统计量与参数值越接近。
三、样本平均数与总体平均数离差统计量的形态1.总体为正态分布,总体标准差σ已知时,平均数的离差统计量呈标准正态分布。
可写作)(3.6nX Z σμ-=2.总体为正态分布,但总体σ未知,平均数的离差统计量呈t 分布。
(1)总体标准差的估计量:)(14.6xn nS σ⋅-=。
:为贝塞尔氏校正系数.1-n n(2)平均数的标准误的估计量:)(1/15.6-=⋅-==n n n nnS S x x X σσ(3)平均数的离差统计量:)(16.6--=-=n X S X t x Xσμμ注:。
而变化和随着x X t σ(4)t 分布的特点① 单峰对称,曲线与基线永不相交; ② t 值有正有负,也可为零;③ t 分布是随d f =n -1而变化的一簇分布; 参看教材86页。
第六章时间数列分析(一) 填空题1、时间数列又称数列,一般由和两个基本要素构成。
2、动态数列按统计指标的表现形式可分为、和三大类,其中最基本的时间数列是。
3、编制动态数列最基本的原则是。
4、时间数列中的四种变动(构成因素)分别是:、、、和5、时间数列中的各项指标数值,就叫,通常用a表示。
6、平均发展水平是对时间数列的各指标求平均,反映经济现象在不同时间的平均水平或代表性水平,又称:平均数,或平均数。
7、增长量由于采用的基期不同,分为增长量和增长量,各增长量之和等于相应的增长量。
8、把报告期的发展水平除以基期的发展水平得到的相对数叫,亦称动态系数。
根据采用的基期不同,它又可分为发展速度和发展速度两种。
9、平均发展速度的计算方法有法和法两种。
10、某企业2000年的粮食产量比90年增长了2倍,比95年增长了0.8倍,则95年粮食产量比90年增长了倍。
11、把增长速度和增长量结合起来而计算出来的相对指标是:。
12、由一个时期数列各逐期增长量构成的动态数列,仍属时期数列;由一个时点数列各逐期增长量构成的动态数列,属数列。
13、在时间数列的变动影响因素中,最基本、最常见的因素是,举出三种常用的测定方法、、。
14、若原动态数列为月份资料,而且现象有季节变动,使用移动平均法对之修匀时,时距宜确定为项,但所得各项移动平均数,尚需,以扶正其位置。
15、使用最小平方法配合趋势直线时,求解 a、b参数值的那两个标准方程式为。
16、通常情况下,当时间数列的一级增长量大致相等时,可拟合趋势方程,而当时间数列中各二级增长量大致相等时,宜配合趋势方程。
17、用半数平均法求解直线趋势方程的参数时,先将时间数列分成的两部分,再分别计算出各部分指标平均数和的平均数,代入相应的联立方程求解即得。
18、分析和测定季节变动最常用、最简便的方法是。
这种方法是通过对若干年资料的数据,求出与全数列总平均水平,然后对比得出各月份的。
19、如果时间数列中既有长期趋势又有季节变动,则应用法来计算季节比率。
第六章数理统计的基本概念一、基本教学要求与主要内容(一)教学要求1.理解总体、个体、简单随机样本和统计量的概念,掌握样本均值、样本方差及样本矩的计算。
2.了解分布、t分布和F分布的定义和性质,了解分位数的概念并会查表计算。
3.掌握正态总体的某些常用统计量的分布。
4.了解最大次序统计量和最小次序统计量的分布。
本章重点:统计量的概念及其分布。
(二)主要内容1.总体、个体我们把研究对象的全体称为总体(或母体),把组成总体的每个成员称为个体。
在实际问题中,通常研究对象的某个或某几个数值指标,因而常把总体的数值指标称为总体。
设x为总体的某个数值指标,常称这个总体为总体X。
X的分布函数称为总体分布函数。
当X为离散型随机变量时,称X的概率函数为总体概率函数。
当X为连续型随机变量时,称X的密度函数为总体密度函数。
当X服从正态分布时,称总体X为正态总体。
正态总体有以下三种类型:(1)未知,但已知;(2)未知,但已知;(3)和均未知。
2.简单随机样本数理统计方法实质上是由局部来推断整体的方法,即通过一些个体的特征来推断总体的特征。
要作统计推断,首先要依照一定的规则抽取n个个体,然后对这些个体进行测试或观察得到一组数据,这一过程称为抽样。
由于抽样前无法知道得到的数据值,因而站在抽样前的立场上,设有可能得到的值为,n维随机向量()称为样本。
n称为样本容量。
()称为样本观测值。
如果样本()满足(1)相互独立;(2) 服从相同的分布,即总体分布;则称()为简单随机样本。
简称样本。
设总体X的概率函数(密度函数)为,则样本()的联合概率函数(联合密度函数为)3. 统计量完全由样本确定的量,是样本的函数。
即:设是来自总体X的一个样本,是一个n元函数,如果中不含任何总体的未知参数,则称为一个统计量,经过抽样后得到一组样本观测值,则称为统计量观测值或统计量值。
4. 常用统计量(1)样本均值:(2)样本方差:(3)样本标准差:它们的观察值分别为:这些观察值仍分别称为样本均值、样本方差和样本标准差。