电路分析 参考计算题题解 10-11

解得
对于第二个分解电路，由分流公式有
由叠加定理得
4-8 题4-8图所示电路中 ， ，当开关 在位置1时，毫安表的读数为 ；当开关 合向位置2时，毫安表的读数为 。如果把开关 合向位置3，则毫安表的读数为多少
题4-8图
解：将上图可知，产生毫安表所在支路电流的原因有电流源和电压源，电流源一直保持不变，只有电压源在变化，由齐次定理和叠加定理，可以将毫安表所在支路电流 表示为
题3-20图
解：选取参考节点如图所示，其节点电压方程为
整理得
因为
， ，
所以
，
故
3-21 用节点电压法求解题3-21图所示电路中电压 。
解：选取参考节点如图所示，其节点电压方程为
其中
解得 。
故
题3-21图
3-22 用节点电压法求解题3-13。
题3-22图
解：（1）选取参考节点如图（a）所示，其节点电压方程为
，
故电压源的功率为
（发出）
电流源的功率为
（发出）
电阻的功率为
（吸收）
1-8 试求题1-8图中各电路的电压 ，并分别讨论其功率平衡。
（b）解：标注电流如图（b）所示。
由 有
故
由于电流源的功率为
电阻的功率为
外电路的功率为
且
所以电路的功率是平衡的，及电路发出的功率之和等于吸收功率之和。
1-10 电路如题1-10图所示，试求：
1. 求电感电流初始值
由换路前电路可得
换路后，将电感开路，求其戴维宁等效电路
2.求开路电压
如下图所示，有
所以
3. 求等效电阻
如上图所示
因为
所以
故
4. 求电感电流终值 及时间常数

《电路分析基础》各章习题参考答案第1章习题参考答案1-1 (1) 50W；(2) 300 V、25V，200V、75 V；(3) R2=12.5Ω，R3=100Ω，R4=37.5Ω1-2 V A=8.5V，V m=6.5V，V B=0.5V，V C=−12V，V D=−19V，V p=−21.5V，U AB=8V，U BC=12.5，U DA=−27.5V1-3 电源（产生功率）：A、B元件；负载（吸收功率）：C、D元件；电路满足功率平衡条件。

1-4 (1) V A=100V，V B=99V，V C=97V，V D=7V，V E=5V，V F=1V，U AF=99V，U CE=92V，U BE=94V，U BF=98V，U CA=−3 V；(2) V C=90V，V B=92V，V A=93V，V E=−2V，V F=−6V，V G=−7V，U AF=99V，U CE=92V，U BE=94V，U BF=98V，U CA=−3 V1-5 I≈0.18A ，6度，2.7元1-6 I=4A，I1=11A，I2=19A1-7 (a) U=6V，(b) U=24 V，(c) R=5Ω，(d) I=23.5A1-8 (1) i6=−1A；(2) u4=10V，u6=3 V；(3) P1=−2W发出，P2 =6W吸收，P3 =16W吸收，P4=−10W发出，P5=−7W发出，P6=−3W发出1-9 I=1A，U S=134V，R≈7.8Ω1-10 S断开：U AB=−4.8V，U AO=−12V，U BO=−7.2V；S闭合：U AB=−12V，U AO=−12V，U BO=0V 1-11 支路3，节点2，网孔2，回路31-12 节点电流方程：(A) I1 +I3−I6=0，(B)I6−I5−I7=0，(C)I5 +I4−I3=0回路电压方程：①I6 R6+ U S5 +I5 R5−U S3 +I3 R3=0，②−I5 R5−U S5+ I7R7−U S4=0，③−I3 R3+ U S3 + U S4 + I1 R2+ I1 R1=01-13 U AB=11V，I2=0.5A，I3=4.5A，R3≈2.4Ω1-14 V A=60V，V C=140V，V D=90V，U AC=−80V，U AD=−30V，U CD=50V1-15I1=−2A，I2=3A，I3=−5A，I4=7A，I5=2A第2章习题参考答案2-1 2.4 Ω，5 A2-2 (1) 4 V，2 V，1 V；(2) 40 mA，20 mA，10 mA2-3 1.5 Ω，2 A，1/3 A2-4 6 Ω，36 Ω2-5 2 A，1 A2-6 1 A2-7 2 A2-8 1 A2-9 I1 = −1.4 A，I2 = 1.6 A，I3 = 0.2 A2-10 I1 = 0 A，I2 = −3 A，P1 = 0 W，P2 = −18 W2-11 I1 = −1 mA，I2 = −2 mA，E3 = 10 V2-12 I1 = 6 A，I2 = −3 A，I3 = 3 A2-13 I1 =2 A，I2 = 1A，I3 = 1 A，I4 =2 A，I5 = 1 A2-14 V a = 12 V ，I1 = −1 A，I2 = 2 A2-15 V a = 6 V，I1 = 1.5 A，I2 = −1 A，I3 = 0.5 A2-16 V a = 15 V，I1 = −1 A，I2 = 2 A，I3 = 3 A2-17 I1 = −1 A，I2 = 2 A2-18 I1 = 1.5 A，I2 = −1 A，I3 = 0.5 A2-19 I1 = 0.8 A，I2 = −0.75 A，I3 = 2 A，I4 = −2.75 A，I5 = 1.55 A2-20 I3 = 0.5 A2-21 U0 = 2 V，R0 = 4 Ω，I0 = 0.1 A2-22 I5 = −1 A2-23 (1) I5 = 0 A，U ab = 0 V；(2) I5 = 1 A，U ab = 11 V2-24 I L = 2 A2-25 I S =11 A，R0 = 2 Ω2-26 18 Ω，−2 Ω，12 Ω2-27 U＝5 V2-28 I =1 A2-29 U＝5 V2-30 I =1 A2-31 10 V，180 Ω2-32 U0 = 9 V，R0 = 6 Ω，U=15 V第3章习题参考答案3-1 50Hz，314rad/s，0.02s，141V，100V，120°3-2 200V，141.4V3-3 u=14.1sin (314t−60°) V3-4 (1) ψu1−ψu2＝120°；(2) ψ1＝−90°，ψ2＝−210°，ψu1−ψu2＝120°（不变）3-5 (1)150290VU=∠︒，25020VU=︒；(2) u3=1002ωt＋45°)V，u4=100ωt＋135°)V3-6 (1) i1=14.1 sin (ωt＋72°)A；(2) u2=300 sin (ωt－60°)V3-7 错误：(1) ，(3)，(4)，(5)3-8 (1) R；(2) L；(3) C；(4) R3-9 i=2.82 sin (10t−30°) A，Q≈40 var3-10 u=44.9sin (314t−135°) V，Q=3.18 var3-11 (1) I=20A；(2) P=4.4kW3-12 (1)I≈1.4A， 1.430AI≈∠-︒；(3)Q≈308 var，P=0W；(4) i≈0.98 sin (628t−30°) A3-13 (1)I=9.67A，9.67150AI=∠︒，i=13.7 sin (314t+150°) A；(3)Q=2127.4 var，P=0W；(4)I C=0A3-14 (1)C =20.3μF ；(2) I L ＝0.25A ，I C ＝16A第4章 习题参考答案4-1 (a) 536.87Z =∠︒Ω，0.236.87S Y =∠-︒；(b) 45Z =-︒Ω，45S Y =︒ 4-2 Y =(0.06-j0.08) S ，R ≈16.67 Ω，X L =12.5 Ω，L ≈0.04 H 4-3 R 600V U =∠︒，L 8090V U =∠︒，S 10053.13V U =∠︒ 4-4 2036.87A I =∠-︒4-5 100245Z =︒Ω，10A I =∠︒，R 1000V U =∠︒，L 12590V U =∠︒，C 2590V U =∠-︒ 4-645S Y =︒，420V U =∠︒，R 20A I =∠︒，L 0.2290A I =∠-︒，C 1.2290A I =∠︒ 4-7 10245A I =∠︒，S 10090V U =∠︒ 4-8 (a) 30 V ；(b) 2.24 A 4-9 (a) 10 V ；(b) 10 A 4-10 (a) 10 V ；(b) 10 V 4-11 U =14.1 V4-12 U L1 =15 V ，U C2 =8 V ，U S =15.65 V4-13 U X1 =100 V ，U 2 =600 V ，X 1=10 Ω，X 2=20 Ω，X 3=30 Ω4-14 45Z =︒Ω，245A I =∠-︒，120A I =∠︒，2290A I =∠-︒，ab 0V U =4-15 (1)A I =，RC 52Z =Ω，510Z =Ω；(2)10R =Ω，C 10X =Ω 4-16 P = 774.4 W ，Q = 580.8 var ，S = 968 V·A 4-17 I 1 = 5 A ，I 2 = 4 A4-18 I 1 = 1 A ，I 2 = 2 A ，526.565A I =∠︒，26.565V A 44.72S =∠-︒⋅4-19 10Z =Ω，190A I =∠︒，R252135V U =∠︒，10W P = 4-20 ω0 =5×106 rad/s ，ρ = 1000 Ω，Q = 100，I = 2 mA ，U R =20 mV ，U L = U C = 2 V 4-21 ω0 =104 rad/s ，ρ = 100 Ω，Q = 100，U = 10 V ，I R = 1 mA ，I L = I C = 100 mA 4-22 L 1 = 1 H ，L 2 ≈ 0.33 H第5章 习题参考答案5-3 M = 35.5 mH5-4 ω01 =1000 rad/s ，ω02 =2236 rad/s 5-5 Z 1 = j31.4 Ω，Z 2 = j6.28 Ω 5-6 Z r = 3+7.5 Ω 5-7 M = 130 mH 5-8 2245A I =∠︒ 5-9 U 1 = 44.8 V5-10 M 12 = 20 mH ，I 1 = 4 A 5-11 U 2 = 220 V ，I 1 = 4 A 5-12 n = 1.95-13 N 2 = 254匝，N 3 = 72匝 5-14 n = 10，P 2 = 31.25 mW第6章 习题参考答案6-1 (1) A 相灯泡电压为零，B 、C 相各位为220V6-3 I L = I p = 4.4 A ，U p = 220 V ，U L = 380 V ，P = 2.3 kW 6-4 (2) I p = 7.62 A ，I L = 13.2 A6-5 A 、C 相各为2.2A ，B 相为3.8A 6-6 U L = 404 V6-7 A N 20247U ''=∠-︒V6-8 cos φ = 0.961，Q = 5.75 kvar 6-9 33.428.4Z =∠︒Ω6-10 (1) I p = 11.26 A ，Z = 19.53∠42.3° Ω； (2) I p = I l = 11.26 A ，P = 5.5 kW 6-11 U l = 391 V6-12 A t 53.13)A i ω=-︒B t 173.13)A i ω=-︒C t 66.87)A i ω=+︒6-13 U V = 160 V6-14 (1) 负载以三角形方式接入三相电源(2) AB 3.8215A I =∠-︒，BC 3.82135A I =-︒，CA 3.82105A I =︒A 3.8645A I =∠-︒，B 3.86165A I =∠-︒，C 3.8675A I =∠︒6-15 L = 110 mH ，C = 91.9 mF第7章 习题参考答案7-1 P = 240 W ，Q = 360 var 7-2 P = 10.84 W7-3 (1)() 4.7sin(100)3sin3A i t t t ωω=+︒+ (2) I ≈3.94 A ，U ≈58.84 V ，P ≈93.02 W7-4 m12π()sin(arctan )V 2MU L u t t zRωωω=+-，z =7-5 直流电源中有交流，交流电源中无直流7-6 U 1=54.3 V ，R = 1 Ω，L = 11.4 mH ；约为8%，（L ’ = 12.33 mH ）7-7 使总阻抗或总导纳为实数（虚部为0）的条件为12X R R R ==7-8 19.39μF C =，275.13μF C = 7-9 L 1 = 1 H ，L 2 = 66.7 mH 7-10 C 1 = 10 μF ，C 2 = 1.25 μF第8章 习题参考答案8-6 i L (0+)＝1.5mA ，u L (0+)＝−15V8-7 i 1(0+)＝4A ，i 2(0+)＝1A ，u L (0+)＝2V ，i 1(∞)＝3A ，i 2(∞)＝0，u L (∞)＝0 8-8 i 1(0+)＝75mA ，i 2(0+)＝75mA ，i 3(0+)＝0，u L1(0+)＝0，u L2(0+)＝2.25V8-9 6110C ()2e A t i t -⨯= 8-10 4L ()6e V t u t -=8-11 6110C ()10(1e )V t u t -⨯=-，6110C ()5e A t i t -⨯= *8-12 500C ()115e sin(86660)V t u t -=+︒ 8-13 10L ()12e V t u t -=，10L ()2(1e )A t i t -=- 8-14 21R S ()eV t R Cu t U -=-，3R S (3)e V u U τ-=-8-15 (1) τ＝0.1s ，(2) 10C ()10e V t u t -=，(3) t ＝0.1s 8-16 510C ()109e V t u t -=-8-17 10L ()5e A t i t -=8-18 (a)00()1()1(2)f t t t t t =---；(b)00000()1()1()[1()1(2)]1()21()1(2)f t t t t t t t t t t t t t =------=-⨯-+- 8-19 0.50.5(1)C ()[5(1e )1()5(1e )1(-1)]V t t u t t t ---=--- 8-20 u o 为三角波，峰值为±0.05V*8-21 临界阻尼R ，欠阻尼R ，过阻尼R *8-22 12666L ()[(1e )1()(1e)1(1)2(1e)1(2)]t t ti t t t t -----=-+-----。

初三电路分析考试题及答案一、选择题（每题2分，共20分）1. 串联电路中，总电阻与各部分电阻的关系是：A. 总电阻等于各部分电阻之和B. 总电阻等于各部分电阻的倒数之和C. 总电阻小于各部分电阻中最小的一个D. 总电阻大于各部分电阻中最大的一个答案：A2. 并联电路中，总电阻的倒数等于各支路电阻倒数之和，这个规律适用于：A. 串联电路B. 并联电路C. 复杂电路D. 任何电路答案：B3. 欧姆定律表明电流与电压的关系是：A. 电流与电压成正比B. 电流与电压成反比C. 电流与电压无关D. 电流与电压的关系取决于电阻答案：A4. 以下哪个不是电路的基本组成部分：A. 电源B. 电阻C. 导线D. 电容器答案：D5. 电功率的公式是：A. P = IVB. P = I^2RC. P = V^2/RD. P = V/I答案：A6. 电流表的内阻应该是：A. 非常大B. 非常小C. 适中D. 没有内阻答案：B7. 电压表的内阻应该是：A. 非常大B. 非常小C. 适中D. 没有内阻答案：A8. 以下哪个不是电路的基本定律：A. 欧姆定律B. 基尔霍夫电流定律C. 基尔霍夫电压定律D. 法拉第定律答案：D9. 电路中的短路是指：A. 电路完全断开B. 电路中的电流非常小C. 电路中的电流非常大D. 电路中的电流为零答案：C10. 电容器在直流电路中的作用是：A. 储存电荷B. 阻止电流通过C. 允许电流通过D. 改变电流的方向答案：B二、填空题（每空1分，共10分）11. 当电路中的电阻增加时，电流将_______。

答案：减小12. 串联电路中，电流在各处是_______。

答案：相等13. 并联电路中，电压在各支路是_______。

答案：相等14. 电功率的单位是_______。

答案：瓦特（W）15. 电路的三种基本状态包括通路、开路和_______。

答案：短路三、简答题（每题5分，共10分）16. 解释什么是基尔霍夫电流定律，并给出一个应用实例。

返 回
电路分析基础
7、下图所示的交流电路中，电流表A1和A2的读数都是5A， 问： （1）若Z1=Z2，则A0的读数是多少？ （2）若Z1=R，Z2= jωL，则A0的读数是多少？ （3）若A0的读数是0，则Z1和Z2满足什么关系？ A0 Z0 Z Z
1 2
A1
A2
返 回
上一页
下一页
电路分析基础
电路分析基础
一、填空题
1、元件的特性主要由其（ ）所描述的。
2、电路中某元件的电压、电流取非关联参考方向，且已 知：Ｉ＝－50mＡ，该元件产生功率150mW，则端电压U= （ ）V。 3、直流电流源的电流值是IS，其两端的电压值由 （ ）决定。 a 2Ω 4、当一个二端网络与另一个二端网络 的伏安关系相同时，则称这两个二端网络 2Ω 在电路分析中对于外电路的作用（ ）。 1Ω 1Ω 2Ω 5、图示二端网络的等效电阻Rab为 b 1Ω （ ）。
返 回 上一页 下一页
电路分析基础
29、写出下图所示支路的伏安关系U＝（ I 3Ω - 12V + + U 30、RLC串联谐振电路，谐振频率0 =（ 数Q=100，若U= 4V，则UL=（ ）。
）。
）。品质因Βιβλιοθήκη 返 回上一页下一页
电路分析基础
二、计算题
1、求图示电路的I、U。 I 5Ω + + 20V 10V + U -
I 8Ω + 10V+ U 15、理想电流源在某一时刻可以给电路提供恒定不变的电 流，电流的大小与端电压无关，端电压由（ ）来决定。 16、已知i = 14.14cos(ωt+30°)A，其电流有效值为（ ） 安培，其等效有效值相量为（ ）A。

电路分析题库及详解答案1. 什么是基尔霍夫电流定律（KCL）？- 基尔霍夫电流定律指出，在任何电路的节点上，流入节点的电流之和等于流出节点的电流之和。

2. 基尔霍夫电压定律（KVL）的基本内容是什么？- 基尔霍夫电压定律表明，在任何闭合电路中，沿着闭合路径的电压降之和等于电压升之和。

3. 什么是欧姆定律？- 欧姆定律表明，通过导体的电流与导体两端的电压成正比，与导体的电阻成反比。

4. 如何计算串联电阻电路中的总电阻？- 串联电阻电路中的总电阻等于各个电阻值的和。

5. 并联电阻电路的总电阻如何计算？- 并联电阻电路的总电阻可以通过公式 \( \frac{1}{R_{total}} = \frac{1}{R_1} + \frac{1}{R_2} + \ldots + \frac{1}{R_n} \) 来计算。

6. 什么是戴维南定理？- 戴维南定理指出，任何线性双端网络都可以用一个单一的电压源和一个电阻来等效替代，该电压源的电压等于网络两端的开路电压，电阻等于网络短路时的输入电阻。

7. 什么是诺顿定理？- 诺顿定理是戴维南定理的对偶形式，它指出任何线性双端网络可以等效为一个电流源和电阻的并联组合。

8. 什么是叠加定理？- 叠加定理允许我们通过将独立电源分别作用于电路，然后求出各部分的响应，最后将这些响应相加来计算电路的总响应。

9. 什么是最大功率传输定理？- 最大功率传输定理指出，当负载电阻等于源电阻的复共轭时，负载上可以传输最大的功率。

10. 什么是节点分析法？- 节点分析法是一种解决电路问题的方法，它通过应用KCL在选定的节点上建立方程来求解未知节点电压。

11. 什么是网孔分析法？- 网孔分析法通过应用KVL在电路的独立回路中建立方程来求解未知电流。

12. 如何求解一个简单的RC电路的瞬态响应？- 一个简单的RC电路的瞬态响应可以通过求解RC电路的微分方程来获得，该方程描述了电容电压随时间的变化。

10-24 题图10-24所示电路中，已知电流i(t)=1cos(107t+90°)A。 求电压uR(t)、uL(t)、uC(t)、uS(t)的相量。
Im 3
400
（2）求电压与电流的相位差
u(t) 8sin(500t 50o) V i(t) 2sin(500t 140o)A
o o o
根据电流相位超前于电压90°，可确定该元件为电容 元件，其元件参数为
C Im 2 S 0.25S C 0.25S 0.25 F 5104 F 500 μF
10-1 已知正弦电压和电流为u(t)=311cos(314t-π/6)V， i(t)=0.2cos(2π×465×103t+π/3)A。（1）求正弦电压和电流的振 幅、角频率、频率和初相。（2）画出正弦电压和电流的波形
图。正弦电压和电流的波形如题图10-1所示
解：由电压和电流的瞬时值表达式得到以下结果：
Um 8
500
（3） 求电压与电流的相位差
u(t) 8cos(250t 60o) V i(t) 5sin(250t 150o)A 5cos(250t 60o)A
o o o
根据电压相位与电流同相，确定该元件为电阻元件，其元 件参数为
R Um 8 1.6 Im 5
10-23 题图10-23所示电路中，已知电压 us (t) 1.5 2 cos(105t 60o)V。 求电流iR(t)、iL(t)、iC(t)、i(t)的相量。
j2100I&m 200I&m 200 20o
求解代数方程得到电流振幅相量
I&m =
200 20o A j2100 200
200 200
20o A 1 45oA 245o

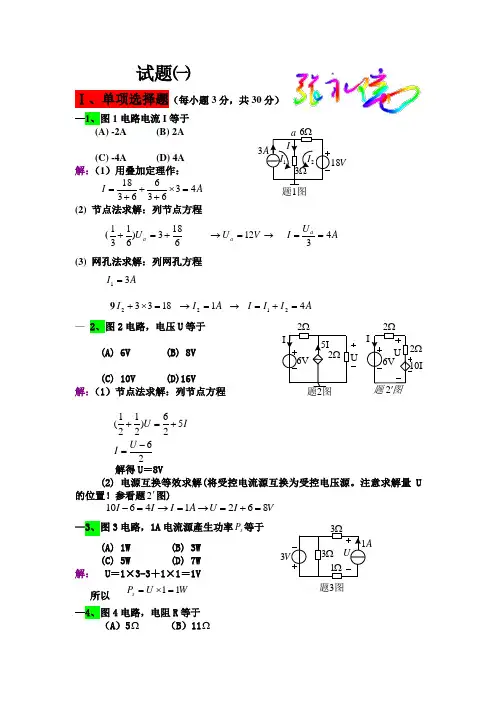
试题㈠Ⅰ、单项选择题（每小题3分，共30分）—1、图1电路电流I 等于(A) -2A (B) 2A(C) -4A (D) 4A 解：（1）用叠加定理作：A I 436366318=⨯+++=(2) 节点法求解：列节点方程(6183)6131+=+a U V U a 12=→→ A U I a 43==(3) 网孔法求解：列网孔方程 A I 31=918332=⨯+I A I 12=→ → A I I I 421=+=— 2、图2电路，电压U 等于 (A) 6V (B) 8V(C) 10V (D)16V解：（1）节点法求解：列节点方程解得U ＝8V(2) 电源互换等效求解(将受控电流源互换为受控电压源。

注意求解量U 的位置！参看题2'图)V I U A I I I 86214610=+=→=→=- —3、图3电路，1A 电流源產生功率s P 等于 (A) 1W (B) 3W (C) 5W (D) 7W 解： U ＝1×3-3＋1×1＝1V 所以W U P s 11=⨯=—4、图4电路，电阻R 等于 （A ）5Ω （B ）11Ω2Ω3V题1图26526)2121(-=+=+U I IU 3题3图（C ）15Ω （D ）20Ω 解： 30-18＝10I I=1.2AR=Ω=152.118—5、图5电路，电容ab C 等于 （A ）1F (B) 4F (C) 9F (D) 11F 解： F C ab 11263=++=—6、图6电路已处于稳态，t ＝0时S 闭合，则t ＝0时电容上的储能)0(C w 等于 (A) 13.5J (B) 18J解：—7、图7电路，节点1、2、3的电位分别为,,,321U U U 则节点1的节点电位方程为(A) 424321-=--U U U (B) 4427321-=--U U U (C) 424321=--U U U (D) 2.545.0321-=--U U U 解： S G 4115.015.05.0111=+++=S G 25.0112-=-=S G 15.05.0113-=+-= A I s 4165.05.0111-=-+-= 所以答案A 正确。

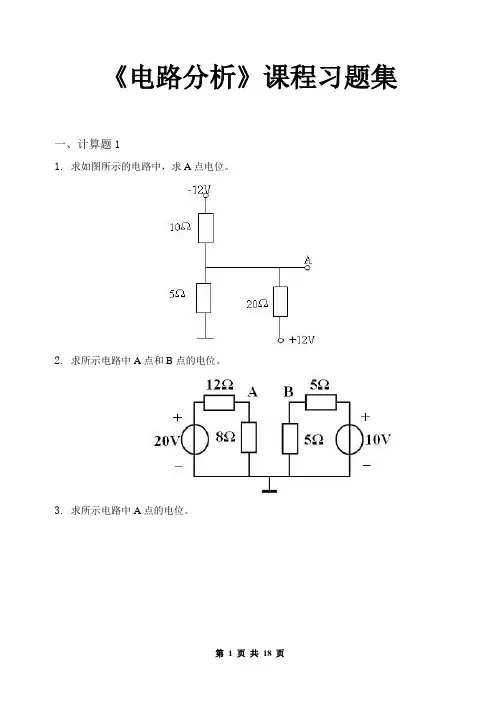
《电路分析》课程习题集一、计算题11.求如图所示的电路中，求A点电位。

2.求所示电路中A点和B点的电位。

3.求所示电路中A点的电位。

4.在下图中，V为直流电压表，其读数为3V，求I。

5.电路如图所示，其中R1＝R2=10Ω，Us =20V ，I S=1A，求电流源和电压源的功率，并说明元件是吸收还是发出功率。

6.试用源变换求下图中电流I。

7.用源变换求图示电路电压U。

8.利用电源的等效变换求Uo。

9.用源变换求U0。

10.用源变换求电流I。

二、计算题311.列出下图所示电路的网孔电流方程（只列方程不求解）。

12.用节点分析法计算图示电路的节点电压u1与u2（只列方程不求解）。

13.列出电路的节点电压方程，不用求解。

14.用支路电流法求各支路电流I1、I2、I3。

15.列出电路的网孔电流方程，不用求解。

16.用戴维南方法求图中电流I。

17. 求图示电路中负载电阻L R 获得的最大功率及此时的L R 值。

18. 电路图中，已知R=5Ω，若使电阻R 获得最大功率P max =7.2W,试求：g 和Us 的值。

19. 求图中端口ab 的戴维南等效电路及电阻R L 所获得的最大功率。

20. 已知U=32V ，R 1=R 2=16Ω，R 3=8Ω，R L =24Ω时，用诺顿定理R L 上流过的电流I L 。

21.对称负载接成三角形，已知电源线电压V U L 220=，电流表读数A I L 3.17=，三相功率P=4.5kW ，求每相负载的电阻和感抗。

22. 线电压U L =220 V 的三相电源上接有两组对称三相负载，一组是联接成三角形的感性负载，每相功率为4.84kW ，0.8cos =Φ，另一组是联接成星形的纯电阻负载，每相阻值为R=10Ω，求各组负载的相电流和总的线电流。

23. 电源电压为380/220V ，接有对称星形联结的白炽灯负载，其总功率为180W 。

在L 3相上接有额定电压为220V ，功率为40W ，功率因数cosφ=0.5的日光灯一支。

14
题4-12解答(c)：
求开路电压：
i1 (4 2i1) (8 2) 0.5A
uoc 8i1 4 0
求 Req
u
2i1 2

i1

i
u / i 2
Req u / i 2
Req Req 5 7
题4-17解答：
求图中负载电阻RL为何值时吸收的功率最大， 并求此功率。
已知u、I, 求阻抗Z和导纳Y
u 10 cos(10t 45)V i 2 cos(10t 90) A
答：
(3.54 j2.54) (0.14 j0.14)S
题9-5：
图中I2＝10A，Us＝10/root(2)，求电流I和电压U, 并画出电路的相量图。
题9-5解答：
ic (t) C
duc dt
3 e25t mA
题7-21：
题7-21解答：
题7-21解答：
R 2 L / C 2
题7-25：
题7-25解答：
题7-28：
图中电压U波形如图所示，求电流i(t)
题7-28解答(1)：
题7-28解答(2)：
题8-9：
题8-9解答：
求 R 的值及Q值和通带 BW
R Us I ( j0 ) 10 Q Uc ( j0 ) Us ) 100
BW 0 / Q 62.8103 rad / s
题11-10解答：
题11-19(1)：
作出下列网络函数的波特图
(1)H ( j) 1 10 j
(2)H ( j) 5( j 2) j( j 10)
题8-12：
题8-12解答：

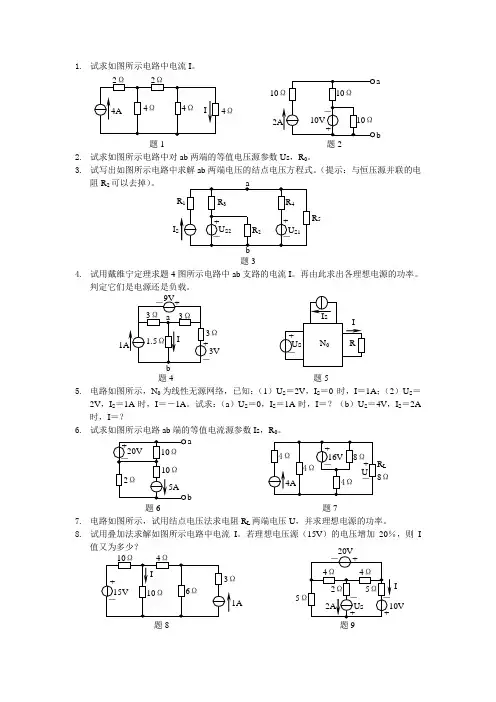
1. 试求如图所示电路中电流I 。

题1 题22. 试求如图所示电路中对ab 两端的等值电压源参数Us ，R 0。

3. 试写出如图所示电路中求解ab 两端电压的结点电压方程式。

（提示：与恒压源并联的电阻R 2可以去掉）。

题34. 试用戴维宁定理求题4图所示电路中ab 支路的电流I 。

再由此求出各理想电源的功率。

判定它们是电源还是负载。

题4 题55. 电路如图所示，N 0为线性无源网络，已知：（1）U S ＝2V ，I S ＝0时，I ＝1A ；（2）U S ＝2V ，I S ＝1A 时，I ＝－1A 。

试求：（a ）U S ＝0，I S ＝1A 时，I ＝？（b ）U S ＝4V ，I S ＝2A 时，I ＝？6. 试求如图所示电路ab 端的等值电流源参数Is ，R 0。

题6 题77. 电路如图所示，试用结点电压法求电阻R L 两端电压U ，并求理想电源的功率。

8. 试用叠加法求解如图所示电路中电流I 。

若理想电压源（15V ）的电压增加20％，则I值又为多少？题8 题94Ω10 IR 5Ω 3VL Ω5Ω I9. 试用戴维宁定理求如图所示电路中支路电流I 。

然后再求理想电流源端电压Us 。

10. 在下图所示的两个电路中，（1）R 1是不是电源的内阻？（2）R 2中的电流I 2及其两端电压U 2各等于多少？（3）改变R 1的阻值，对I 2和U 2有无影响？（4）理想电压源中的电流I 和理想电流源两端的电压U 各等于多少？（5）改变R 1的阻值，对（4）中的I 和U 有无影响？（a ） （b ）题1011. 计算下图所示两个电路中a ，b 间的等效电阻R ab 。

（b ）题1112. 有一无源二端电阻网络（题12图），通过实验测得：当U ＝10V 时，I ＝2A ；并已知该电阻网络由4个3Ω的电阻构成，试问这4个电阻是如何联接的？题12题1313. 在题13图中，R 1＝R 2＝R 3＝R 4＝300Ω，R 5＝600Ω，试求开关S 断开和闭合时a 和b之间的等效电阻。

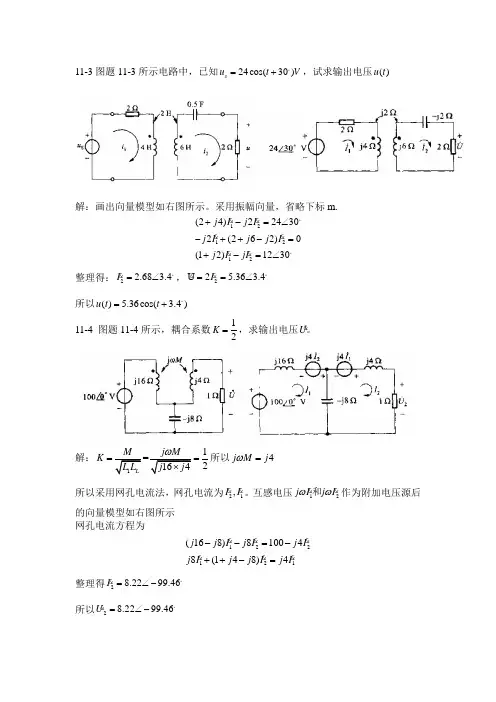
11-3图题11-3所示电路中，已知24cos(30)s u t V =+。

，试求输出电压()u t解：画出向量模型如右图所示。

采用振幅向量，省略下标m.121212(24)224302(262)0(12)1230j I j I j I j j I j I jI +-=∠-++-=+-=∠ 。

整理得：2 2.68 3.4I =∠ 。

，2U 2 5.36 3.4I ==∠ 。

所以() 5.36cos( 3.4)u t t =+。

11-4 图题11-4所示，耦合系数12K =，求输出电压U 。

解：12K ==所以4j M j ω= 所以采用网孔电流法，网孔电流为21,I I 。

互感电压12j I j I ωω 和作为附加电压源后的向量模型如右图所示网孔电流方程为122121(168)810048(148)4j j I j I j I j I j j I j I --=-++-= 整理得28.2299.46I =∠- 。

所以28.2299.46U =∠- 。

11-8电路图题11-8所示，试求对电源端的输入阻抗、电流12I I 和。

解：列网孔方程1212(24)21202(22)0j I j I j I j I +-=∠-++= 。

整理得12(22),2I j A I A =-= 所以12Z (33)22i j j =Ω=+Ω- 11-9 已知空心变压器的参数：1122L =9H,R =200,L =4H,R =1000.5.k ΩΩ=及所接负载为800Ω电阻和1F μ电容串联，所接正弦电压源频率为400rad/s, 电压有效值为300V ，内阻为500,Ω内电感为0.25H .试求传送给负载的功率P 和空心变压器的功率传输效率。

解：(1)可以画出电路如上图所示。

M=3H =做出向量模型后可以列出网孔方程为1212(500200100300)12003001200(10080016002500)0j j I j I j I j j I +++-=-+++-=整理得1271.56A 0.0596116.6A 50I I -==∠- 。

22
编辑ppt
练习题033：
列出图示电路的回路电流方程。
23
编辑ppt
练习题033解答：
补充： 整理得：
24
编辑ppt
练习题034：
列出图示电路的回路电流法方程。
25
编辑ppt
练习题034解答：
由图示回路有： 消去控制量： 整理得：
26
编辑ppt
练习题035：
图示电路已知，用回路电流法求各支路电流。
练习题018：
图示电路已知，求电压u3。
15
编辑ppt
练习题018解答：
由节点上的KCL方程依次可得
节点①： 节点②： 节点③： 再由回路l1的KVL方程得
16
编辑ppt
练习题021：
求图示电路运算放大器的输出功率。
17
练习题021解答：
编辑ppt
18
编辑ppt
练习题031：
图示电路已知，试列出支路电流法方程。
4
编辑ppt
练习题003：
电路如图所示，已知u1=2V，u2＝4V，u3=6V，u4＝8V。 (1)求以⑤为参考点的各节点电压。 (2)求以④为参考点的各节点电压。 (3)利用闭合回路上的KVL求未知支路电压。 (4)由节点电压求未知支路电压。
5
编辑ppt
练习题003解答：
（1）un1=u1=2V；un2=-u2+u1=-2V；un3=-u3+un2=-8V； un4=-u4+un3=-16V；un5=0； （2）u54=-un4=16V；u‘n1=un1+u54=18V； u’n2=un2+u54=14V；u‘n3=un3+u54=8V；u’n4=0； u‘n5=un5+u54=16V； （3）回路①③②①：u5=-u3-u2=-10V； 回路③①⑤③：u6=u5+u1=-8V； 回路②③④②：u7=u3+u4=14V； 回路④③⑤④：u8＝-u4+u6=-16V； （4）u5=un3-un1=u’n3-u‘n1=-10V；u6=un3-un5=u’n3u‘n5=-8V；u7=un2-un4=u’n2-u‘n4=14V；u8=un4un5=u’n4-u‘n5=-16V；

《电路分析基础》作业参考解答第一章（P26-31）1-5 试求题1-5图中各电路中电压源、电流源及电阻的功率（须说明是吸收还是发出）。

（a ）解：标注电压如图（a ）所示。

由KVL 有V U 52515=⨯-= 故电压源的功率为W P 302151-=⨯-=（发出）电流源的功率为W U P 105222=⨯=⨯=（吸收）电阻的功率为W P 20452523=⨯=⨯=（吸收）（b ）解：标注电流如图（b ）所示。

由欧姆定律及KCL 有A I 35152==，A I I 123221=-=-=故电压源的功率为W I P 151151511-=⨯-=⨯-=（发出）电流源的功率为W P 302152-=⨯-=（发出）电阻的功率为W I P 45953552223=⨯=⨯=⨯=（吸收）1-8 试求题1-8图中各电路的电压U ，并分别讨论其功率平衡。

（b ）解：标注电流如图（b ）所示。

由KCL 有A I 426=-= 故V I U 8422=⨯=⨯=由于电流源的功率为)(a)(bW U P 488661-=⨯-=⨯-=电阻的功率为W I P 32422222=⨯=⨯=外电路的功率为W U P 168223=⨯=⨯=且016324832131=++-=++=∑=P P P Pk k所以电路的功率是平衡的，及电路发出的功率之和等于吸收功率之和。

1-10 电路如题1-10图所示，试求： （1）图（a ）中，1i 与ab u ； 解：如下图（a ）所示。

因为19.02510i i ===所以A i 222.29209.021≈==V i i u ab 889.09829204)(41≈=⎪⎭⎫⎝⎛-⨯=-=1-19 试求题1-19图所示电路中控制量1I 及电压0U 。

解：如图题1-19图所示。

由KVL 及KCL 有⎪⎩⎪⎨⎧=+⎪⎭⎫ ⎝⎛-=+01010160050006000201000U I U I U I)(b)(a整理得⎩⎨⎧=-=+030002010000101U I U I 解得mA A I 510531=⨯=-，V U 150=。

《电路分析》试题（一）一、填空题（每小题4分，共40分）1.当取关联参考方向时，理想电容元件的电压与电流的一般关系式为。

2.对于具有n个结点b个支路的电路，可列出个独立的KCL方程，可列出个独立的KVL方程。

3.RLC串联谐振电路的谐振频率 = 。

4.对于二阶电路的零输入相应，当R<2时，电路为欠阻尼电路，放电过程为。

放电。

5.电感的电压相量于电流相量π/2，电容的电压相量于电流相量π/2。

6.正弦电压为u1=－10cos(100πt+3π/4),u2=10cos(100πt+π/4),则u1的相量为，u1＋u2= 。

7.额定值为220V、40W的灯泡，接在110V的电源上，其输出功率为 W。

8.RLC串联谐振电路品质因数Q=100，若U R=10V，则电源电压U= V，电容两端电压U C= 。

9.在采用三表法测量交流电路参数时，若功率表、电压表和电流表的读数均为已知（P、U、I），则阻抗角为φZ= 。

10.视在功率S=10KVA（输出电压220V）的交流电源，并联接上220V，40W，COSφ= 0.44的日光灯，满载可接只日光灯。

二、计算题（每小题10分，共60分）1、如图（1）所示，已知用网孔法求支路电流、。

2、如图（2）所示，试用戴维南定理求I。

3、如图（3）所示是一个相序指示器电路，由一个电容C和两个灯泡R组成设1/ωC=R1=R2=R，且线电压是对称的，试求两个灯泡的电压，并决定哪个灯泡比较亮。

4、已知电路如图（4）所示，R1=3Ω，R2=6Ω，R3=6Ω，U s1=12V，U s2=6V，L=1H，电路原已达到稳态，t = 0时开关S由a改合到b，用三要素法求：i L(t)，5、图（5）所示电路，已知L=0.25H, C=1F, R=0.2Ω，电源电压U S1=1V，U S2=5V，设开关S在位置1时电路已达稳态，t=0时将开关S合到位置2。

（1）做出运算电路；（2）用运算法求电容电压u c（t）6、电路如图所示，已知ω=1000rad/s, C=1μF, R=1Ω, L1=1H，，求：（1）u s(t)的有效值；（2）电阻电压；（3）电源发出的平均功率。

1-1 在图题1-1所示电路中。

元件A 吸收功率30W ，元件B 吸收功率15W ，元件C 产生功率30W ，分别求出三个元件中的电流I 1 、I 2 、I 3。

解 61=I A ，32-=I A ，63=I A1-5 在图题1-5所示电路中，求电流I 和电压U AB 。

解 1214=--=I A ，39442103=⨯+⨯+=AB U V1-6 在图题1-6所示电路中，求电压U 。

解 U +⨯-=253050，即有 30=U V1-8 在图题1-8所示电路中，求各元件的功率。

解 电阻功率：123223=⨯=ΩP W ，82/422==ΩP W电流源功率：0)6410(22=--=A P ，4141-=⨯-=A P W电压源功率：2021010-=⨯-=V P W ，4)221(44=-+=V P W2-7 电路如图题2-7所示。

求电路中的未知量。

解 1262=⨯=S U V349122==I A112/12/33===S U P I A 3/1313/420=++=I AΩ==121123RΩ2-+-+V50A3R U 3W123=PΩ===13363/13120I U R S eq2-9 电路如图题2-9所示。

求电路中的电流1I 。

解 从图中可知，2Ω与3Ω并联， 由分流公式，得1123553I I I =⨯=1113==I A所以，有131321+=+=I I I I 解得 5.01-=I A2-8 电路如图题2-8所示。

已知213I I =，求电路中的电阻R 。

解 KCL ：6021=+I I 213I I = 解得 451=I mA, 152=I mA. R 为6.615452.2=⨯=R k Ω解 (a)由于有短路线，Ω=6AB R , (b) 等效电阻为Ω=+=++=1.15.25.15.01//)1//11(1//1AB R2-12 电路如图题2-12所示。

求电路AB 间的等效电阻AB R 。

返 回 上一页 下一页
电路分析基础
（2）在非关联方向下，表示沿着电压方向移动 正电荷，电场力作负功，该元件发出能量，则为吸收 能量的负值，所以吸收功率为 d w( t ) p( t ) ui dt 功率的单位为瓦(W)，即1W = 1J/s。
若功率为正值，则表示该元件实际吸收功率；
返 回 上一页 下一页
电路分析基础
最简单的电路： 手电筒电路
S
它由 3 部分组成： ① ① 是电源。 干 ②灯泡 它的作用是将其他形 电 式的能量转换为电能。 池 ③导线 ② 是负载。 用电装臵。 它将电源供给的电能转换为其他形式的能量。 ③ 是连接电源与负载传输电能的金属导线。 图中干电池是电源，是将化学能转换为电能。 图中 S是为了节约电能所加的控制开关，需要照 图中灯泡是负载，是将电能转换为光和热能。 明时将开关S闭合，不需要照明时将S打开。
返 回 上一页 下一页
电路分析基础
u1i1 u2i2 u3i3 u4i1 u5回路 i3 u i1 0 16 中各支 i2 i1 i3 路电压的代数 和 (u1 u2 u4 u6 )i1 (u2 u3 u5 )i3 0
u1 u2 u4 u6 0 u2 u3 u5 0 u1 u4 u6 u5 u3 0
电压是矢量吗？
返 回
上一页
下一页
电路分析基础
R1 US R4
R5
R2
称为电桥电路
R3
请问：电阻R5的电流（电压）方向如何？ 在复杂电路中，电流（电压）的真实方向是难以 确定的； 或在交流电路中，电流（电压）的方向是交变的。
在电路中任意选定一个参考方向作为电流（电 压）的方向。规定电流（电压）的真实方向与参考方 向一致，电流（电压）为正值； 若两者相反，则电流 （电压）值小于零。

电路分析期末试题及答案第一题：简答题（20分）考察内容：电路分析基础知识答案：1. 什么是电路分析？电路分析是指通过分析和计算电路中各个元件之间的电流、电压和功率等关系，来研究电路的性质和特点。

2. 什么是欧姆定律？欧姆定律是指在电流通过某些导体时，电流与电压成正比例关系。

它可以用数学公式表示为V = IR，其中V表示电压，I表示电流，R表示电阻。

3. 什么是电压分压？电压分压是指在一个电路中，通过合理的串联或并联连接电阻，以降低或提高一部分电压。

4. 什么是电流分流？电流分流是指在一个电路中，通过合理的并联或串联连接电阻，以分配电流，使部分电流绕过某些元件。

5. 什么是戴维南定理？戴维南定理是指将电路中的各个电阻和电源转化为等效电动势和等效电阻，从而简化电路分析。

6. 什么是欧姆定律？欧姆定律是指在电流通过某些导体时，电流与电压成正比例关系。

它可以用数学公式表示为V = IR，其中V表示电压，I表示电流，R表示电阻。

7. 什么是电压分压？电压分压是指在一个电路中，通过合理的串联或并联连接电阻，以降低或提高一部分电压。

8. 什么是电流分流？电流分流是指在一个电路中，通过合理的并联或串联连接电阻，以分配电流，使部分电流绕过某些元件。

9. 什么是戴维南定理？戴维南定理是指将电路中的各个电阻和电源转化为等效电动势和等效电阻，从而简化电路分析。

10. 什么是电路节点？电路节点是指电路中的连接点或交叉点，常用符号表示为一个空心圆圈。

在节点处，电流可以自由地分流或汇聚。

第二题：计算题（40分）考察内容：串联和并联电路的计算答案：1. 已知电路中有三个电阻，分别为R1 = 20Ω，R2 = 30Ω和R3 =40Ω，求它们的串联电阻。

解：串联电阻的计算公式为RT = R1 + R2 + R3，代入数值得RT =20Ω + 30Ω + 40Ω = 90Ω。

2. 已知电路中有两个电阻，分别为R1 = 60Ω和R2 = 30Ω，求它们的并联电阻。