初一数学第五讲：一元一次方程

第五讲：一元一次方程与实际问题（二)1.设元方法①直接设元：即问什么设什么。

②间接设元：即所设的不是所求的，需要将要求的量以外的其他量设为未知数，便于找到符合题意的等量关系。

③辅助设元（设而不求）：有些应用题隐含了一些未知的常量，若不指明这些量的存在，则很难求其解，故需把这些未知的常量设出未知数，作为桥梁帮助分析。

2.行程问题基本量：速度、时间、路程。

路程=速度×时间（vt s =） 3.方案选择问题在阅读理解题意的基础上，可以借助表格分析题意，取舍题中信息。

要学会从不同的思维角度提出问题、分析问题，恰当地理解与应用数学知识。

一、设元技巧之设而不求。

例1、某音乐厅五月初决定在暑假期间举办学生专场音乐会，入场券分为团体票和零售票，其中团体票占总票数的32，若提前购票，则给予不同程度的优惠，在五月份内，团体票每张12元，共售出团体票的53；零售票每张16元，共售出零售票的一半。

如果在六月份内，团体票按每张16元出售，并计划在六月份内全部余票，那么零售票应按每张多少元定价才能使这两个月的票款收入持平？2832.19变形答案详见《全效学习》，元，最后算错，六月份每张解：设总票数P x x a =变式1、①一轮船从甲地到乙地顺流需航行4小时，从乙地到甲地逆流航行需6小时，有一木筏由甲地漂流至乙地，需_________小时。

小时24②某商场的电视机按原价九折销售，要使销售总收入不变，那么销量应增加______.（填写比例）91二、行程问题例2、甲骑自行车从A 地到B 地，乙骑自行车从B 到A 地，两人都匀速前进，已知两人在上午8时同时出发，到上午10时，两人还相距36千米，到中午12时，两人又相距36千米，求A 、B 两地间的路程。

千米，路程为以让学生上台展示方法此题解题方法较多，可108变式2：①、慢车车身长125米，车速17米/秒；快车车身长140米，车速22米/秒，快车车头与慢车车尾相距400米。

七年级数学（上）第 5 讲内容简介:5.1 认识一元一次方程 5.2 求解一元一次方程 5.3 等积变换问题 5.4 打折销售 5.5 “希望工程”义演 5.6 追赶小明(行程问题)主讲老师： 学生一元一次方程七年级数学 一元一次方程一、兴趣引导：用未知数表示数是数学史上一次伟大的进步。

通过对未知数的应用，人们的逻辑思维从特定发展到一般，从定量到发展到变量。

从而使数学的理论知识得以扩充到我们生活中的方方面面。

二、复习讲评：本章知识重点在于让同学们学会用方程解决实际问题，虽然中考中一般不会直接考一元一次方程的选择题或应用题，但是每年都考的二元一次方程的应用题中很大一部分解题思路却是在一元一次方程中学到的。

因此一元一次方程作为初中三年乃至高中三年将要学习的函数理论的基础，显然是十分重要的。

三、教学内容： 5.1 认识一元一次方程一元一次方程的三个特征： 1、分母中不含未知数； 2、只含一个未知数；3、未知数的次数的指数是1．三个条件必须同时具备，缺一不可．【基础达标】例1 判断下列各式是否为一元一次方程：(1)2223x x -=-；(2)73=-x y ；(3)213+=-xx ；(4)m m -=+523．随堂练习：1、下列式子中是一元一次方程的是( )A ．2348y x =+-B ．()225115x x -=-C ．5143-=-y y D ．)22(2)23(2x x x -=-2、若关于x 的方程04)62(2=+--m x m 是一元一次方程，则m = ．等式的性质全认识：1、对“两边”和“同一个”的理解：必须对两边所有项进行同一种运算，不能漏掉任何一项，乘数必须相同．2、如果两边同时除以同一个数时，这个数一定不能为0，等式两边才相等．例2 已知等式()()55-=-a c a 中1≠c ，求122--a a 的值．※例3 已知b a a b 23123-=--，试比较a 与b 的大小．随堂练习：1、(1)在等式23-=m m 的两边同时 ，得到22-=m ． (2)在等式427=-x 的两边同时 ，得到78-=x ．※2、已知()()a b b a -=-5，试比较a 与b 的大小．【易错分析】例4 下列说法正确的是( )A ．在等式ac ab =中，两边都除以a ,可得c b =B ．在等式b a =两边都除以12+c ，可得1122+=+c b c aC ．在等式ac a b =两边都除以a ，可得c b =D ．在等式b a x -=22两边都除以2，可得b a x -=1、请你依条件对方程进行变形．(1)由x x 526=-，两边都减去x 5；(2)由b a =-3两边都乘以n ；(3)由ayax =，两边都除以a ．【技巧提高】例5 已知4-是关于x 的方程52+=+x m x 的解，求m 的值．例6 当4=a 时，关于x 的方程0=-b ax 的解是2=x ，求方程0=+b ax 的解．随堂练习：1、已知3是关于x 的方程12=-a x 的解，则a 的值是( ) A ．5- B ．5 C ．7 D ．22、判断12,10==x x 是不是方程)]15(15[5.115x x -+⨯=+的解．3、已知关于x 的方程6)1(2++=x a ax ，求a 为何整数时，方程的解是正整数．【真题解析】例7 (浙江温州中考)方程314=-x 的解是( )A ．1-=xB ．1=xC ．2-=xD ．2=x例8 (贵州安顺中考)已知关于x 的方程234=-m x 的解是m x =，则m 的值是 ．随堂练习：1、(广西中考)方程042=-x 的解是( )A ．1=xB ．1-=xC ．2=xD ．2-=x2、(上海中考)如果2=x 是方程121-=+a x 的解，那么a 的值是( )A ．0B ．2C ．2-D ．6- 3、(四川泸州)若0132=-+m x 的解，则m 的值为( )A ．1-B ．0C ．1D ．315.2 求解一元一次方程解一元一次方程一般步骤为：去分母、去括号、移项、合并同类项、系数化为1．【基础达标】例9 解方程：56213102x x -=--．随堂练习：1、下列方程变形中的移项正确的是( )A ．由x x 475=+，得745=-x xB ．由532-=x x ，得523532=-=-=x x x xC ．由x x 24210-=-，得24210+=+x xD ．由128=+x ，得812+=x2、下列方程中，与方程21=-x 的解相同的是( )A ．62-=xB ．12-=+xC ．312=+xD ．93-=-x 3、方程131-=--xx 去分母后正确的结果是( )A ．11-=--x xB ．313-=--x xC ．313-=+-x xD ．113-=+-x x4、解方程：1.08.32.04.235.032xx x -=---【易错分析】例10 解方程：32213415-=+--x x x随堂练习： 1、方程4172755+-=+-x x 去分母得( )A ．()()177525+-=+-x xB ．()1775220+-=+-x xC ．()()1775220+-=+-x xD ．()17141020+-=+-x x2、由等式(m ＋3)x ＝m ＋3能得到x ＝１，则m 应满足的条件是__________．3、某同学解方程21133x x a -+=- ，在去分母时，方程右边的-1没有乘3,因而求得解为x=2 ,试求a 的值，并求出正确的解．【技巧提高】例11 解方程：81053314554-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-x ．例12 解方程：1.02.12.08.055.05.14x x x -=---．1、解下列方程： (1)12135225+=⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛-x x ； (2)168421x x x x x ++++=．2、解方程：759272911-=+z z ．【真题解析】例13 (湖北中考)已知关于x 的方程223=+a x 的解是1-a ，则a 的值为( )A ．1B ．53 C ．51D ．1-例14 (广东深圳中考)已知代数式3121y x a -与123---b y x 是同类项，那么ab 的值是 ．例15 (北京中考)()0122=+++n m ，则n m 2+的值为( )A ．4-B ．1-C ．0D ．4例16 (南宁中考)阅读下列材料：规定一种运算bc ad dc b a -=．例如2121043525432-=-=⨯-⨯=．根据这种运算求x 的值，使14233=--x x ．1、(江苏扬州中考)已知3=x 是方程()241133=⎥⎦⎤⎢⎣⎡-+⎪⎭⎫ ⎝⎛+x m x的解，且n 满足关系式12=+m n ，求n m +的值．2、(江苏宿迁)已知5是关于x 的方程723=-a x 的解，则a 的值为 ．3、(山东滨州中考)依据下列解方程3122.05.03.0-=+x x 的过程，请在前面的括号内填写变形步骤，在后面的括号内填写变形依据． 解：原方程可变形为312253-=+x x ；( )去分母，得()()122533-=+x x ；( ) 去括号，得24159-=+x x ；( )( )得21549--=-x x ；( ) 合并，得175-=x ．( ) ( )，得517-=x ．( )4、(北京中考变)已知125+a 与2)3(4-b 互为相反数，那么代数式2007)2(a a b += 。

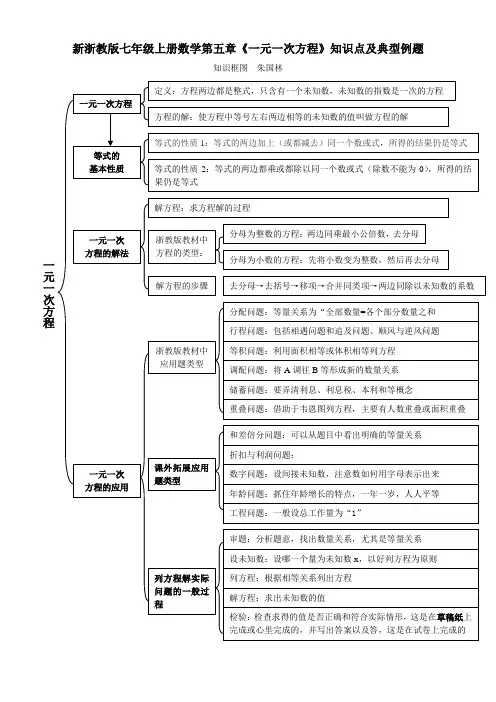
新浙教版七年级上册数学第五章《一元一次方程》知识点及典型例题知识框图朱国林关于一元一次方程概念的拓展教材中的概念：方程两边都是整式，只含有一个未知数，未知数的指数是一次的方程是一元一次方程，那么 x+2=x+3是一元一次方程吗？从概念上来看，是一元一次方程，但稍作变形，就是2=3，是不是觉得很可笑？因此，一元一次方程的概念应该是：方程两边都是整式，只含有一个未知数，未知数的指数是一次，并且能变形为ax=b （a ≠0，a 、b 均为常数）的方程是一元一次方程，也就是说，一元一次方程一定只有一个解。

关于用方程解应用题的秘诀：相关条件设未知数，剩余条件列方程考点一、判断方程是不是一元一次方程及一元一次方程概念的简单应用 考点二、关于在解方程过程中的某些变形问题，只能以选择题的形式出现 考点三、解一元一次方程考点四、列一元一次方程解与实际生活无关的题目（可以是选择题、填空题、解答题） 考点五、列一元一次方程解与实际生活有关的题目（可以是选择题、填空题、解答题）将考点与相应习题联系起来考点一、判断方程是不是一元一次方程及一元一次方程概念的简单应用 1、下列等式中是一元一次方程的是（ ）A ．3x=y-1B ．2(1)21x x -=+C ．3(x-1)= -2x-3D ．3x 2-2=3E ．11x x=+ 2、在方程23=-y x ，021=-+x x ，2121=x ，0322=--x x 中一元一次方程的个数为（ ） A ．1个 B ．2个 C ．3个 D ．4个 3、如果06312=+--a x是一元一次方程，那么=a ，方程的解为 。

（特别注意）考点二、关于在解方程过程中的某些变形问题，只能以选择题的形式出现 1、已知等式523+=b a ，则下列等式中不一定．．．成立的是（ ） （A ）;253b a =- （B ）;6213+=+b a （C ）;523+=bc ac （D ）.3532+=b a 2、解方程2631xx =+-，去分母，得（ ） （A ）133x x --= （B ）633x x --= （C ）633x x -+= （D ）133x x -+=3、下列方程变形中，正确的是（ ）（A ）方程1223+=-x x ，移项，得;2123+-=-x x （B ）方程()1523--=-x x ，去括号，得;1523--=-x x （C ）方程2332=t ，未知数系数化为1，得;1=t （D ）方程110.20.5x x --=化成101010125x x --= 考点三、解一元一次方程（1）x x 3.15.67.05.0-=-； （2；（3）1676352212--=+--x x x ； （4）4.06.0-x 3.011.0+x .考点四、列一元一次方程，解与实际生活无关的题目（可以是选择题、填空题、解答题） 1、方程432-=+x m x 与方程6)16(21-=-x 的解相同，则m 的值为__________. 2、已知5x+3=8x －3和65a x +=37这两个方程的解是互为相反数，则a= . 3、某数的4倍减去3比这个数的一半大4，则这个数为__________.4与互为相反数，则的值是 .5、一个两位数，个位上的数字是十位上的数字的3倍，它们的和是12，那么这个两位数是 .6、写出一个以x=－21为解的一元一次方程7、小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是：11222y y -=- 怎么办呢？小明想了一想，便翻看书后答案，此方程的解是53y =-，于是很快就补好了这个常数，你能补出这个常数吗？它应是（ ） A.1 B.2 C.3 D.48、已知21=x 是方程32142m x m x -=--的根，求代数式()⎪⎭⎫ ⎝⎛---+-121824412m m m 的值.★★★已知关于x 的一元一次方程b x x +=+2301121的解为2=x ，那么关于y 的一元一次方程b y y ++=++）（）（123101121的解为 ． 考点五、列一元一次方程解与实际生活有关的题目（可以是选择题、填空题、解答题） 1、日历上竖列相邻的三个数，它们的和是39，则第一个数是（ ）A.6B.12C.13D.142、有m 辆客车及n 个人，若每辆客车乘40人，则还有10人不能上车；若每辆客车乘43人，则还有1人不能上车．有下列四个等式：①4010431m m +=-；②1014043n n ++=；③1014043n n --=；④4010431m m +=+．其中正确的是（ ） A.①② B.②④ C.②③ D.③④ 3、某商店卖出两件衣服，每件60元，其中一件赚25%，另一件亏25%，那么这两件衣服卖出后，商店是 （ ） A.不赚不亏 B.赚8元 C.亏8元 D. 赚15元4、一件商品提价25%后发现销路不是很好，欲恢复原价，则应降价（ ） A.40% B.20% C.25% D.15%5、小强比他叔叔小30岁，而两年前，小强的年龄是他叔叔的41，则小强的叔叔今年____________岁. 6、一项工程甲独做10天完成，乙的工作效率是甲的2倍，两人合做了2天未完成，剩下的工作量由乙完成，还需的天数为 ( )(A)．1 天 (B)2 天 (C)3 天 (D)4天 7、小明存入100元人民币，存期一年，年利率为2％，到期应缴纳所获利息的20％的利息税，那么小明存款到期交利息税后共得款 （ ）A.106元B.102元C.111.6元D.101.6元8、银行教育储蓄的年利率如右下表：小明现正读七年级，今年7月他父母为他在银行存款30000元，以供3年后上高中使用. 要使3年后的收益最大，则小明的父母应该采用（ ） （A ）直接存一个3年期；（B ）先存一个1年期的，1年后将利息和自动转存一个2年期； （C ）先存一个1年期的，1年后将利息和自动转存两个1年期； （D ）先存一个2年期的，2年后将利息和自动转存一个1年期.9、某酒店为招揽生意，对消费者实施如下优惠：凡订餐5桌以上，多于5桌的部分按定价的7折收费.小叶集团公司组织工会活动，预定了10桌，缴纳现金2550元，那么每桌定价是 元.10、某商店将彩电按成本价提高50%，然后在广告上写“大酬宾，八折优惠”，结果每台彩电仍获利270元，那么每台彩电成本价是___________。

七年级数学一元一次方程一元一次方程是七年级数学中的重要内容。

它是数学中最基础也是最常用的代数表达式之一，在解决实际问题中起着重要的作用。

本文将介绍一元一次方程的定义、解法以及解决实际问题的应用。

一、一元一次方程的定义一元一次方程是指只含有一个未知数的一次方程。

一般形式为：ax + b = 0，其中a和b为常数，x为未知数。

解一元一次方程的目的是找到使等式成立的未知数的值。

二、解一元一次方程的方法1. 同加同减法原则同加同减法原则是解一元一次方程的基本方法之一。

根据同加同减法原则，可以将方程的左右两边同时加上或减去同一个数，使得方程的等式依然成立，从而消去方程中的某些项，简化计算。

2. 同乘同除法原则同乘同除法原则是解一元一次方程的另一个常用方法。

根据同乘同除法原则，可以将方程的左右两边同时乘以或除以同一个数，使得方程的等式依然成立，从而简化计算。

三、实际问题的应用一元一次方程在解决实际问题时起到了重要的作用。

下面以几个例子来说明一元一次方程在实际问题中的应用。

1. 问题一：班级花费账单李华和小明一起去超市购买了一些物品，总共花费了200元。

已知小明出了120元，而李华出的钱数是未知的。

根据此情况，我们可以列出如下的一元一次方程：x + 120 = 200通过解这个方程，我们可以得到李华出的钱数x是80元。

2. 问题二：速度问题某辆汽车从A地到B地的距离是120公里，已知汽车以每小时40公里的速度行驶。

现在要求计算汽车行驶的时间。

根据速度问题的公式：速度=距离/时间，我们可以列出如下的一元一次方程：40t = 120通过解这个方程，我们可以得到汽车行驶的时间t为3小时。

3. 问题三：年龄问题父亲的年龄是儿子年龄的3倍，而两人年龄之和是36岁。

现在要求计算父亲和儿子的年龄。

根据此情况，我们可以列出如下的一元一次方程：3x + x = 36通过解这个方程，我们可以得到父亲的年龄3x为27岁，儿子的年龄x为9岁。

七年级数学《一元一次方程》教案4篇七年级数学《一元一次方程》教案4篇七年级数学《一元一次方程》教案篇一2.自主探索、合作交流：先由学生独立思考求解，再小组合作交流，师生共同评价分析。

方法1：解：方程两边都加上2，得5x-2+2=8+2也就是5x=8+2合并同类项，得5x=10所以，x=23.理性归纳、得出结论（让学生通过观察、归纳，独立发现移项法则。

）比较方程5x=8+2与原方程5x-2=8，可以发现，这个变形相当于5x-2=85x=8+2即把原方程中的-2改变符号后，从方程的一边移到另一边，这种变形叫做移项。

教学建议：关于移项法则，不应只强调记忆，更应强调理解。

学生开始时也许仍习惯于利用逆运算而不利用移项法则来求解方程，可借助例题、练习题使相互逐步体会到移项的优越性）。

方法2；解：移项，得5x=8+2合并同类项，得5x=10方程两边都除以5，得x=24.运用反思、拓展创新[例1]解下列方程：(1)2x+6=1(2)3x+3=2x+7教学建议：先鼓励学生自己尝试求解方程，教师要注意发现学生可能出现的错误，然后组织学生进行讨论交流。

[例2]解方程:教学建议：①先放手让学生去做，学生可能采取多种方法，教学时，不要拘泥于教科书中的解法，只要学生的解法合理，就应给予鼓励。

②在移项时，学生常会犯一些错误，如移项忘记变号等。

这时，教士不要急于求成，而要引导学生反思自己的解题过程。

必要时，可让学生利用等式的性质和移项法则两种方法解例1、例2中的方程，并将两者加以对照，进而使学生加深对移项法则的理解，并自觉地改正错误。

5.小结回顾:学生谈本节课的收获与体会。

师强调：移项法则。

七年级数学《一元一次方程》教案篇二教学内容：人教版七年级上册3.1.1一元一次方程教学目标：知识与技能：1、理解一元一次方程，以及一元一次方程解的概念。

2、会从题目中找出包含题目意思的一个相等关系，列出简单的方程。

3、掌握检验某个数值是不是方程解的方法。