测试习题集-第二章 测试装置的基本特性

第二章 测试装置的基本特性一、知识要点及要求(1)了解测试装置的基本要求，掌握线性系统的主要性质；(2)掌握测试装置的静态特性，如线性度、灵敏度、回程误差和漂移等；(3)掌握测试装置的动态特性，如传递函数、频率响应函数、单位脉冲响应函数； (4)掌握一、二阶测试装置的动态特性及其测试。

二、重点内容及难点(一) 测试装置的基本要求1、测试装置又称为测试系统，既可指众多环节组成的复杂测试装置，也可指测试装置中的各组成环节。

2、测试装置的基本要求：(1)线性的，即输出与输入成线性关系。

但实际测试装置只能在一定工作范围和一定误差允许范围内满足该要求。

(2)定常的(时不变的)，即系统的传输特性是不随时间变化的。

但工程实际中，常把一些时变的线性系统当作时不变的线性系统。

3、线性系统的主要性质 (1)叠加原理：若)()()()(2211t y t x t y t x −→−−→−，则)()()()(2121t y t y t x t x ±−→−±(2)频率保持性：若输入为某一频率的简谐信号，则系统的稳态输出也是同频率的简谐信号。

*符合叠加原理和频率保持性，在测试工作中具有十分重要的作用。

因为，在第一章中已经指出，信号的频域函数实际上是用信号的各频率成分的叠加来描述的。

所以，根据叠加原理和频率保持性这两个性质，在研究复杂输入信号所引起的输出时，就可以转换到频域中去研究。

(二)不失真测试的条件 1、静态不失真条件在静态测量时，理想的定常线性系统Sx x a b y ==0，S 为灵敏度。

2、动态不失真条件在动态测量时，理想的定常线性系统)()(00t t x A t y -=，A 0为灵敏度，t 0为时间延迟。

(三)测试装置的静态特性静态特性：就是在静态测量时描述实际测试装置与理想定常线性系统的接近程度。

(1)线性度：指测试装置输出与输入之间保持线性比例关系的程度。

(2)灵敏度：指测试装置输出与输入之间的比例因子，即测试装置对输入量变化的反应能力。

测试装置基本特性习题1.线性定常系统有那些基本特性？简述同频性在动态测量中的重要意义。

2、.测量装置有哪些静态特性指标？3.待测压缩机转速为1000 r/min，现有1.0级精度，量程为1000 r/min及2.0级精度，量程为3000 r/min 的两个转速，请问使用哪一个转速表较好，并说明原因。

4.说明测量装置的幅频特性A(ω)和相频特性φ(ω)的物理意义。

为什么A(ω)=k(常数）和φ(ω)=-ωt。

时，可以作到理想的不失真测量？5.用时间常数为0.5秒的一阶测量装置进行测量，若被测参数按正弦规律变化，如果要求仪表指示值的幅值误差小于2%，问：被测参数变化的最高频率是多少？如果被测参数的周期是2秒和5秒，幅值误差是多少？6.求周期信号χ(t)=0.5cos10t+0.2cos(100t-45°)通过频率响应为Η（jω)=1/(1+0.005jω)的测量装置后得到的稳态响应。

7.用一个一阶测量装置测量100Hz的正弦信号，如果要求振幅的测量误差小于5%，问：此仪器的时间常数应不大于多少？若用具有该时间常数的测量仪器测量50Hz的正弦信号，相应的振幅误差和相位滞后是多少？8.试说明二阶测量装置的阻尼比的值多采用0.6～0.7的原因。

9.已知一个二阶测量装置，阻尼比ζ=0.65，fn=1200Hz,问：输入240Hz和480Hz的信号时A（ω）和φ(ω)是多少？若阻尼比ζ变为0.5和0.707，A（ω）和φ(ω)又各是多少？10.已知某一测力传感器为二阶测量装置，其动态参数为固有频率fn=1200Hz,ζ=0.707。

试求当测量信号χ(t)=sin2πft+sin6πft+sin10πft时其幅值、相位变化，其中f=600Hz。

最后请用幅频、相频图作出定性解释。

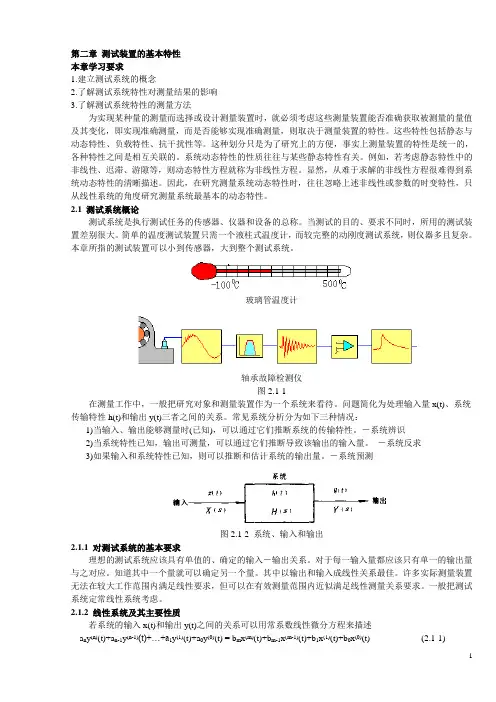
第二章测试装置的基本特性本章学习要求1.建立测试系统的概念2.了解测试系统特性对测量结果的影响3.了解测试系统特性的测量方法为实现某种量的测量而选择或设计测量装置时，就必须考虑这些测量装置能否准确获取被测量的量值及其变化，即实现准确测量，而是否能够实现准确测量，则取决于测量装置的特性。

这些特性包括静态与动态特性、负载特性、抗干扰性等。

这种划分只是为了研究上的方便，事实上测量装置的特性是统一的，各种特性之间是相互关联的。

系统动态特性的性质往往与某些静态特性有关。

例如，若考虑静态特性中的非线性、迟滞、游隙等，则动态特性方程就称为非线性方程。

显然，从难于求解的非线性方程很难得到系统动态特性的清晰描述。

因此，在研究测量系统动态特性时，往往忽略上述非线性或参数的时变特性，只从线性系统的角度研究测量系统最基本的动态特性。

2.1 测试系统概论测试系统是执行测试任务的传感器、仪器和设备的总称。

当测试的目的、要求不同时，所用的测试装置差别很大。

简单的温度测试装置只需一个液柱式温度计，而较完整的动刚度测试系统，则仪器多且复杂。

本章所指的测试装置可以小到传感器，大到整个测试系统。

玻璃管温度计轴承故障检测仪图2.1-1在测量工作中，一般把研究对象和测量装置作为一个系统来看待。

问题简化为处理输入量x(t)、系统传输特性h(t)和输出y(t)三者之间的关系。

常见系统分析分为如下三种情况：1)当输入、输出能够测量时(已知)，可以通过它们推断系统的传输特性。

－系统辨识2)当系统特性已知，输出可测量，可以通过它们推断导致该输出的输入量。

－系统反求3)如果输入和系统特性已知，则可以推断和估计系统的输出量。

－系统预测图2.1-2 系统、输入和输出2.1.1 对测试系统的基本要求理想的测试系统应该具有单值的、确定的输入－输出关系。

对于每一输入量都应该只有单一的输出量与之对应。

知道其中一个量就可以确定另一个量。

其中以输出和输入成线性关系最佳。

输入输出(响应)系统第二章 测试装置的基本特性第一节 概述测试是具有试验性质的测量，是从客观事物取得有关信息的过程。

在此过程中须借助测试装置。

为实现某种量的测量而选择或设计测量装置时，就必须考虑这些测量装置能否准确获取被测量的量值及其变化，即实现准确测量，而能否实现准确测量，则取决于测量装置的特性。

这些特性包括动态特性、静态特性、负载特性、抗干扰性等。

测量装置的特性是统一的，各种特性之间是相互关联的。

1、测试装置的基本要求通常工程测试问题总是处理输入量)(t x 、装置（系统）的传输特性)(t h 和输出量)(t y 三者之间的关系。

图2-1系统、输入和输出1)当输入、输出是可测量的(已知)，可以通过它们推断系统的传输特性。

(系统辨识)。

2)当系统特性已知，输出可测量，可以通过它们推断导致该输出的输入量。

(反求)。

3)如果输入和系统特性已知，则可以推断和估计系统的输出量。

(预测) 。

测试装置的基本特性主要讨论测试装置及其输入、输出的关系。

理想的测试装置应该具有单值的、确定的输入——输出关系。

即对应于某一输入量，都只有单一的输出量与之对应 。

知道其中的一个量就可以确定另一个量。

以输出和输入成线性关系为最佳。

一般测量装置只能在较小工作范围内和在一定误差允许范围内满足这项要求。

2、测量装置的静态特性测试系统的静态特性就是在静态测量情况下，描述实际测试装置与理想定常线性系统的接近程度。

测量装置的静态特性是通过某种意义的静态标定过程确定的。

静态标定是一个实验过程，这一过程是在只改变测量装置的一个输入量，而其他所有的可能输入严格保持为不变的情况下，测量对应得输出量，由此得到测量装置的输入输出关系。

3、测量装置的动态特性测量装置的动态特性是当被测量即输入量随时间快速变化时，测量输入与响应输出之间的动态关系得数学描述。

研究测量装置动态特性时，认为系统参数不变，并忽略迟滞、游隙等非线性因素，可用常系数线性微分方程描述测量装置输入与输出间的关系。

第二章测试装置的基本特性第一节概述一、对测试装置的基本要求1．工程测试问题通常的工程测试问题总是处理输入量x(t)、装置（系统）的传输特性h(t)和输出量y(t)三者之间的关系如图2－1，即：系统(响应)1）如果x(t)、y(t)可以观察(已知)的量，则可推断h(t)。

2）如果h(t)已知，y(t)可测，则可推断x(t)。

3）如果x(t)和h(t)已知，则可推断和估计y(t)。

2．理想的测试装置①输出和输入成线性关系。

即具有单值的、确定的输入-输出关系。

②系统为时不变线性系统。

3．实际的测试装置①只能在较小工作范围内和在一定误差允许范围内满足线性要求。

②很多物理系统是时变的。

在工程上，常可以以足够的精确度认为系统中的参数是时不变的常数。

二、线性系统及其主要性质1．线性方程方程中的所有变量的幂次不大于1的方程称为线性方程。

注意导数的阶次与幂次的区别，以及经过拉氏变换后所得到的相函数中，阶次与幂次的表现形式。

2．线性系统用线性方程来描述的系统就是线性系统。

线性系统符合叠加性和均匀性（齐次性）。

3．时不变线性系统当系统的输入x(t)和输出y(t)之间的关系可以用常系数线性微分方程)()(0)(1)(1)(0)(1)(1)(1111t x b bb b t y a a a a dtt dx dt t x d m dt t x d mdtt dy dtt y d n dtt y d n m m mm n n nn ++⋅⋅⋅++=++⋅⋅⋅++------ (2-1)来描述时，该系统称为时不变线性系统，也称定常线性系统。

式中t 为时间自变量。

系统的系数a n , a n-1, …,a 1, a 0和 b m , b m-1, …, b 1, b 0均为常数，既不随时间而变化，也不是自变量x 、因变量y 及它们各阶导数的函数。

4．时不变线性系统的性质如以x (t )→ y (t )表示上述系统的输入、输出的对应关系，则时不变线性系统具有以下一些主要性质。

2测试装置的基本特性第⼆章测试装置的基本特性测试是具有实验性质的测量，是从客观事物取得有关信息的过程。

本章知识要点及要求1、掌握线性系统及其主要特性。

2、掌握测试装置的动态特性及静态特性。

3、掌握⼀、⼆阶测试装置的频率响应特性。

4、掌握测试装置的不失真测试条件。

第⼀节概述⼀、重点内容1、测试装置的基本要求测试装置的基本特性主要讨论测试装置及其输⼊、输出的关系。

理想的测试装置应该具有单值的、确定的输⼊——输出关系。

即，对应于某⼀输⼊量，都只有单⼀的输出量与之对应。

知道其中的⼀个量就可以确定另⼀个量。

2、线性系统及其主要性质线性系统的输⼊x(t)与输出y(t)之间的关系可⽤下⾯的常系数线性微分⽅程来描述时，则称该系统为时不变线性系统，也称定常线性系统。

式中t为时间⾃变量，a n、a n 1、…、a1 、a 0 和b n 、b n 1、…、b1 、b0均为常数。

a n d n y(t)dt nbd m x(t)m dt m a n 1d n 1y(t)dt n 1d m 1x(t)m 1 midtady(t)1dtb1 b o x(t)dta°y(t)线性时不变系统的主要性质:1) 叠加原理特性若X i t y i t x2t y21X i t X2 y i t y22) ⽐例特性若xt ytax t ay t3）系统对输⼊导数的响应等于对原输⼊响应的导数dx t dy tdtdt4）如系统的初始状态均为零，则系统对输⼊积分的响应等同于对原输⼊响应的积分。

t0 0 xt dtty t dt5）频率保持性测试和测试装置的若⼲术语（⾃学）1、测量、计量和测试测量：是指以确定被测对象量值为⽬的的全部操作。

计量：是指实现单位统⼀和量值准确可靠的测量。

测试：具有试验性质的测量。

动态测量：确定量的瞬时值及其随时间变化的量所进⾏的测量。

静态测量：指测量期间被测量认为是恒定的。

2、测量装置的误差和准确度测量装置的误差：测量装置的⽰值和被测量的真值之间的差值称为测量装置的误差。

第二章 测试装置基本特性1、填空题1) 某一阶系统的频率响应函数为121)(+=ωωj j H ，输入信号2sin)(tt x =，则输出信号)(t y 的频率为=ω ，幅值=y ，相位=φ 。

2）当测试系统的输出)(t y 与输入)(t x 之间的关系为)()(00t t x A t y -=时，该系统能实现测试。

此时，系统的频率特性为=)(ωj H 。

3）传感器的灵敏度越高，就意味着传感器所感知的 越小。

4）一个理想的测试装置，其输入和输出之间应该具有 关系为最佳。

2、选择题 1）（ ）不属于测试系统的静特性。

（1）灵敏度 （2）线性度 （3）回程误差 （4）阻尼系数2）从时域上看，系统的输出是输入与该系统 响应的卷积。

（1）正弦 （2）阶跃 （3）脉冲 （4）斜坡3）两环节的相频特性各为)(1ωQ 和)(2ωQ ，则两环节串联组成的测试系统，其相频特性为（ ）。

（1）)()(21ωωQ Q （2）)()(21ωωQ Q + （3）)()()()(2121ωωωωQ Q Q Q +（4）)()(21ωωQ Q -4）一阶系统的阶跃响应中，超调量（ ）。

（1）存在，但<5％ （2）存在，但<1 （3）在时间常数很小时存在 （4）不存在5）忽略质量的单自由度振动系统是 系统。

（1）零阶 （2）一阶 （3）二阶 （4）高阶 6）一阶系统的动态特性参数是（ ）。

固有频率 （2）线性度 (3)时间常数 （4）阻尼比7）用阶跃响应法求一阶装置的动态特性参数，可取输出值达到稳态值（ ）倍所经过的时间作为时间常数。

（1）0.632 （2）0.865 （3）0.950 （4）0.982 3、判断题1）在线性时不变系统中，当初始条件为零时，系统的输出量与输入量之比的拉氏变换称为传递函数。

（ ） 2）当输入信号)(t x 一定时，系统的输出)(t y 将完全取决于传递函数)(s H ，而与该系统的物理模型无关。