均值标准差做方差分析

方差分析的实验报告方差分析的实验报告引言：方差分析是一种常用的统计方法，用于比较两个或多个组之间的均值差异是否显著。

在本次实验中，我们将运用方差分析来研究三种不同肥料对植物生长的影响。

通过对不同处理组的生长情况进行观察和数据分析，我们旨在探究不同肥料对植物生长的影响是否存在显著差异。

实验设计与方法：本实验采用了完全随机设计，共设置了四个处理组，分别为对照组和三个不同肥料处理组。

每个处理组设置了十个重复样本。

实验的主要步骤如下：1. 准备工作：选取相同品种的植物作为实验材料，并确保它们具有相似的生长状态和健康状况。

同时，为了消除外界因素的干扰，我们将植物放置在相同的环境条件下。

2. 分组处理：将植物随机分为四组，其中一组作为对照组，不施加任何肥料，另外三组分别施加三种不同的肥料。

3. 数据收集：在实验开始后的每个固定时间点，我们测量每个植物的生长指标，如株高、叶片数、根长等，并记录下来。

这些数据将用于后续的方差分析。

数据分析与结果：在实验结束后，我们对收集到的数据进行了方差分析。

通过计算各组的平均值、方差和标准差，我们得到了以下结果：1. 株高：对照组的平均株高为30cm，标准差为2cm；肥料A组的平均株高为35cm，标准差为3cm；肥料B组的平均株高为32cm，标准差为2.5cm；肥料C组的平均株高为33cm，标准差为2.8cm。

方差分析结果显示，不同处理组之间的株高差异是显著的（F=4.56, p<0.05）。

2. 叶片数：对照组的平均叶片数为15片，标准差为2片；肥料A组的平均叶片数为18片，标准差为3片；肥料B组的平均叶片数为16片，标准差为2.5片；肥料C组的平均叶片数为17片，标准差为2.8片。

方差分析结果显示，不同处理组之间的叶片数差异是显著的（F=3.21, p<0.05）。

3. 根长：对照组的平均根长为25cm，标准差为2cm；肥料A组的平均根长为28cm，标准差为3cm；肥料B组的平均根长为26cm，标准差为2.5cm；肥料C组的平均根长为27cm，标准差为2.8cm。

实验设计及数据分析-方差分析实验设计及数据分析方差分析一、方差分析的基本原理方差分析的核心思想是将观测值的总变异分解为不同来源的变异，然后通过比较不同来源变异的大小来判断因素对观测结果的影响是否显著。

总变异可以分解为组间变异和组内变异。

组间变异反映了不同组之间的差异，组内变异则反映了组内个体之间的随机误差。

如果组间变异显著大于组内变异，就说明不同组之间的均值存在显著差异，即所研究的因素对观测结果有显著影响。

二、实验设计要点1、确定研究因素和水平首先要明确研究的因素，以及每个因素的不同水平。

例如，研究不同肥料对作物产量的影响，肥料种类就是因素，不同的肥料品牌或配方就是水平。

2、选择合适的实验对象实验对象应具有代表性和随机性，以减少偏差。

3、控制无关变量在实验过程中，要尽量控制其他可能影响结果的无关变量，以确保结果的准确性。

4、确定样本量样本量的大小会影响统计检验的效力，一般来说，样本量越大，结果越可靠，但也要考虑实际操作的可行性和成本。

5、随机分组将实验对象随机分配到不同的组中，以保证各组之间的初始条件相似。

三、方差分析的类型1、单因素方差分析只考虑一个因素对观测结果的影响。

2、双因素方差分析同时考虑两个因素对观测结果的交互作用。

3、多因素方差分析涉及两个以上因素的情况。

四、数据分析步骤1、提出假设零假设（H0）：不同组之间的均值没有显著差异。

备择假设（H1）：不同组之间的均值存在显著差异。

2、计算统计量根据实验数据，计算出组间平方和、组内平方和、总平方和等，进而得到 F 统计量。

3、确定显著性水平通常选择 005 或 001 作为显著性水平。

4、查找临界值根据自由度和显著性水平，在 F 分布表中查找临界值。

5、做出决策如果计算得到的 F 统计量大于临界值，拒绝零假设，认为不同组之间的均值存在显著差异；否则，接受零假设。

五、结果解读1、查看 ANOVA 表ANOVA 表中会给出各项变异的来源、自由度、平方和、均方和 F 值等信息。

如何根据样本例数、均数、标准差进⾏T-Test和ANOVA⼤家看论⽂的时候经常看到的⼀些实验数据都是以例数、均数、标准差表⽰的。

如果想验证作者的统计结论，只有2组时还可以根据ttest的公式进⾏计算，2组以上进⾏⼿⼯计算就很⿇烦，⽽⼀些常⽤的统计软件好像也没提供这⼀功能。

⼀、⾸先强调⼀点，不管使⽤任何统计分析软件，如果不知道样本量，仅根据均值和标准差是没有办法进⾏T检验和⽅差分析的。

以⽅差分析为例，从最原始的⾓度给出详细理由如下：先看⽅差分析表，⼤家都很熟悉了吧，这⾥就不再介绍原理了。

1．假设共有k组数据，每组分别有n1，n2，n3，…，nk个数据点，每组均值分别为每组数据的标准差分别为S1，S2，S3，…，Sk。

（这⾥的n1，n2，n3，…，nk是不知道的，n总＝n1+n2+n3+，…，+nk当然也就不知道了）2．做⽅差分析的最后⼀步是计算F值：其中组间均⽅：组内均⽅：3．再其中组间离差平⽅和：，其中是第j组的组内均数，是总均数；组内离差平⽅和：总的离差平⽅和：SST＝SSA＋SSE4．对于单组数据标准差结合组内离差平⽅和：，我们尝试计算组内离差平⽅和SSE＝S12（n1-1）+ S22（n1-1）+…+ Sk2（nk-1），显然由于不知道n1，n2，n3，…，nk，所以SSE没有办法计算；因此组内均⽅：就更没有办法计算；5．再来看组间离差平⽅和：，⾸先是nj不知道，其次总均数也是不知道的，⽽仅仅根据每组数据的均值和组数k是绝对不可能推出总均数的,所以组间离差平⽅和：SSA就⽆法求得，更不⽤说组间均⽅：MSA了.6．那么是不是可以先捣⿎出总的离差平⽅和：SST＝SSA＋SSE呢？⼀看就知道了由于缺少总均数,这也是不可能算出来的。

7．更关键的是由于缺少每⼀组的数据个数n1，n2，n3，…，nk，⽅差分析的临界值F1-α就没有办法确定，因为这是与⾃由度有关的。

最后的结论：1. 仅根据均值和标准差是没有办法进⾏T检验和⽅差分析的。

化学实验数据的处理与分析平均值标准差与误差估计化学实验数据的处理与分析——平均值、标准差与误差估计在化学实验中，准确地处理和分析数据是非常重要的步骤。

通过合理的数据处理方法，我们可以得到可靠的实验结果，并进一步评估实验的准确性和可重复性。

在本文中，我们将详细介绍化学实验数据处理中的关键概念——平均值、标准差和误差估计，并分享一些常用的计算方法和注意事项。

一、平均值平均值是一组数据的总和除以数据个数得到的结果，常表示为x。

化学实验中，我们通常会进行多次实验，并记录下每次实验的结果，然后计算这些结果的平均值。

平均值能够反映一组数据的集中趋势，是数据处理的基础。

计算一组数据的平均值的方法很简单，只需要将所有数据相加，然后除以数据个数即可。

例如，我们进行了5次实验，分别得到了10、12、11、10.5和9.5的结果，那么这组数据的平均值为（10+12+11+10.5+9.5）/5 = 10.6。

二、标准差标准差是一组数据的离散程度的度量，常表示为σ。

标准差能够告诉我们数据的分散程度，即数据点相对于平均值的偏离程度。

标准差越大，表示数据点之间的差异越大，反之则表示差异较小。

计算一组数据的标准差需要进行一系列的步骤，包括计算每个数据点与平均值的差异，求平方，然后对这些平方值进行平均，并开方。

在实际操作中，我们通常使用计算机软件或者计算器来自动完成这些繁琐的计算。

有了标准差，我们可以通过比较不同数据集的标准差大小来评估它们的可靠性。

标准差较小的数据集表示数据点相对于平均值的偏离较小，数据较为集中，说明实验结果较为可靠。

三、误差估计在实际测量中，由于种种因素的影响，我们无法获得绝对准确的数据。

因此，我们需要对实验结果的误差进行估计。

误差估计是用来衡量数据的可信度和结果的精确度的方法。

常见的误差估计方法有两种，即绝对误差和相对误差。

1. 绝对误差绝对误差是每个数据点与对应平均值的差值的绝对值。

它可以用来表示每个数据点的测量误差的大小。

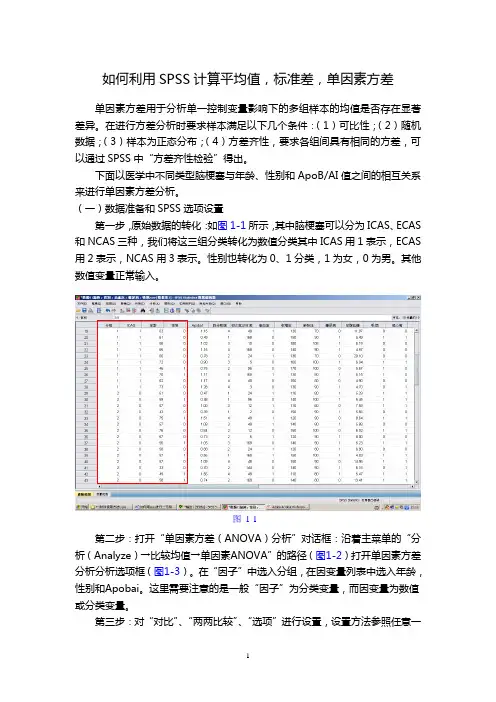
如何利用SPSS计算平均值，标准差，单因素方差单因素方差用于分析单一控制变量影响下的多组样本的均值是否存在显著差异。

在进行方差分析时要求样本满足以下几个条件：（1）可比性；（2）随机数据；（3）样本为正态分布；（4）方差齐性，要求各组间具有相同的方差，可以通过SPSS中“方差齐性检验”得出。

下面以医学中不同类型脑梗塞与年龄、性别和ApoB/AI值之间的相互关系来进行单因素方差分析。

（一）数据准备和SPSS选项设置第一步，原始数据的转化：如图1-1所示，其中脑梗塞可以分为ICAS、ECAS 和NCAS三种，我们将这三组分类转化为数值分类其中ICAS用1表示，ECAS 用2表示，NCAS用3表示。

性别也转化为0、1分类，1为女，0为男。

其他数值变量正常输入。

图1-1第二步：打开“单因素方差（ANOVA）分析”对话框：沿着主菜单的“分析（Analyze）→比较均值→单因素ANOVA”的路径（图1-2）打开单因素方差分析分析选项框（图1-3）。

在“因子”中选入分组，在因变量列表中选入年龄，性别和Apobai。

这里需要注意的是一般“因子”为分类变量，而因变量为数值或分类变量。

第三步：对“对比”、“两两比较”、“选项”进行设置，设置方法参照任意一本SPSS统计书籍中关于单因素方差分析的部分。

图1-2图1-3点击确定后输出数据，这里重点讲输出数据中各项所代表的意思。

我们经常会在其他文献中看到有关平均值（mean），标准差（SD）和标准误差（SE），即mean±SD或SE的情况。

如图1-4所示“描述图”中，在该图中我们很容易找到以上几项。

如图1-4所示“方差齐性检验”中，我们可以找到各组的显著性（即P值），也有软件表示为Sig.。

当该值大于0.05时说明各组间方差是齐性的，既满足前提的第四点。

可以进行后续分析。

一般我们需要的是多重比较的表格，如图1-5所示，该表中给出了年龄、性别和ApoB/AI值中各组间的显著性水平（P值），如年龄组中1、2组间显著性为0.972，差异不显著。

统计学中的标准差与方差分析一、引言统计学作为一门学科，在社会发展过程中扮演着越来越重要的角色。

随着科技的不断发展，数据量与精度的提高，统计学在各领域的应用越来越广泛。

本文将重点探讨统计学中的两个重要概念——标准差与方差分析，介绍它们的定义、性质、应用场景以及相关计算方法，希望能够对广大读者更好地理解和灵活运用这两个概念。

二、标准差1. 定义标准差是衡量一组数据的离散程度的一个指标，它是各个数据与均值偏差平方和的平均数的平方根。

标准差越小，意味着数据离散程度越小，反之亦然。

2. 性质标准差具有如下性质：（1）标准差为非负数；（2）当所有数据相等时，标准差为0；（3）标准差的值越大，表示数据的离散程度越大；（4）标准差的值受到极值（即离群值）的较大影响。

3. 应用场景标准差在统计分析中的应用非常广泛，特别是在概率分布、正态分布、抽样等方面。

例如，在投资领域中，标准差是指价格波动的大小和稳定性，是投资风险的重要度量。

4. 计算方法标准差的计算方法如下：（1）计算数据的均值；（2）将各个数据与均值的差值平方；（3）将差值平方求和并除以数据个数n；（4）将平均数的平方根即为标准差。

三、方差分析1. 定义方差分析是一种用于比较两个或多个总体均值是否相等的统计方法。

通过计算各组样本的方差、不同组间的方差和总体内部的方差，确定不同组之间的方差是否大于总体内部的方差。

2. 性质方差分析具有如下性质：（1）方差分析要求研究的总体是正态分布的；（2）方差分析所得的F统计量应该与其自由度一起考虑；（3）方差分析的显著性检验要根据选择的显著性水平进行处理。

3. 应用场景方差分析常用于生物学、医学、工程学、教育学等领域中的实验设计和比较分析。

例如，在医药研究中，方差分析可以用于评价新药物的疗效是否与传统疗法相同，确定不同治疗方案的疗效是否有显著差异。

4. 计算方法方差分析的计算方法分为单因素方差分析和双因素方差分析两种，其中单因素方差分析的计算方法如下：（1）计算各组数据的平均值；（2）计算总体平均值；（3）计算各组平均值与总体平均值之差的平方和；（4）计算组内偏差平方和；（5）计算组间偏差平方和；（6）计算组间偏差平方和与组内偏差平方和之比，得出F值和P值，进行显著性检验。

QC统计手法解析1. 引言在质量控制〔Quality Control，QC〕过程中，统计手法是一种重要的工具，它可以帮助我们分析数据并评估质量控制的效果。

本文将对常见的QC统计手法进行解析，包括均值、标准差、方差分析、控制图等。

2. 均值均值是一组数据的平均值，它可以用来判断样本数据是否稳定。

在质量控制中，我们通常使用控制图来监控均值的变化情况。

当均值超过控制限时，说明质量出现异常，需要进一步分析。

3. 标准差标准差是一组数据的离散程度的度量，表示数据的波动程度。

通过监控标准差的变化，我们可以判断质量控制的稳定性。

通常，标准差较大时，说明数据波动较大，需要注意质量问题。

4. 方差分析方差分析是一种常用的统计方法，用于比拟两个或多个样本均值之间的差异是否显著。

在质量控制中，我们可以使用方差分析来评估不同生产批次或不同工序之间的质量差异，并找出导致差异的原因。

5. 控制图控制图是一种用于监控质量数据变化的图表。

它通常包括上限、下限和中心线，用于标识正常质量范围和异常点。

常见的控制图有平均图〔X-Bar Chart〕、范围图〔R Chart〕和方差图〔S Chart〕等。

通过对控制图的监控，我们可以及时发现质量问题，并采取相应的措施进行改善。

6. 其他统计手法除了上述常见的统计手法外，还有许多其他的QC统计手法可以帮助我们进行质量控制。

例如，假设检验〔Hypothesis Test〕可以用来判断一个样本是否符合某个特定的分布；回归分析〔Regression Analysis〕可以用来建立质量数据与影响因素之间的关系模型。

这些统计手法在质量控制中扮演着重要的角色，帮助我们更好地分析和解决质量问题。

7. 总结QC统计手法是质量控制过程中必不可少的工具，它可以帮助我们分析数据、评估质量控制效果，并及时发现和解决质量问题。

了解和掌握这些统计手法，对于提高质量管理水平和生产效率具有重要意义。

通过合理运用QC统计手法，我们可以实现质量持续改良，提供更好的产品和效劳。

方差分析报告1. 引言方差分析是统计学中常用的一种假设检验方法，用于比较两个或多个样本均值之间的差异是否显著。

本报告旨在对某个实验数据集进行方差分析，并分析各组之间的差异。

2. 数据集描述本次实验收集了X个样本，每个样本包含了Y个观测值。

在进行方差分析之前，我们首先对数据集进行了基本统计分析，包括均值、标准差等指标。

3. 假设检验我们的研究问题是比较不同组之间的均值是否存在显著差异。

针对这个问题，我们建立了以下假设： - 原假设（H0）：不同组之间的均值没有显著差异。

- 备择假设（H1）：不同组之间的均值存在显著差异。

我们采用方差分析方法来检验上述假设。

4. 方差分析方法方差分析是一种基于方差的假设检验方法，通过比较组内变异与组间变异的大小，来判断组间均值是否存在显著差异。

在本次实验中，我们采用一元方差分析方法。

4.1 方差分析假设条件在应用方差分析之前，我们需要先检验一些假设条件的满足情况： 1. 独立性假设：各组别观测值之间应独立，即组内观测值间相互独立，组间观测值也相互独立。

2. 正态性假设：各组别的观测值应当服从正态分布。

3. 方差齐性假设：各组别的观测值方差应当相等。

4.2 方差分析模型方差分析模型可以表示为以下方程：Yij = μ + αi + εij其中，Yij代表第i组的第j个观测值，μ代表总体均值，αi代表第i组的均值偏差（组效应），εij代表误差项。

4.3 汇总平方和与均方值方差分析中，我们通过计算不同来源的平方和来评估组间和组内的变异程度。

•总平方和（SST）：反映了所有观测值与总体均值之间的差异总和。

•组间平方和（SSA）：反映了不同组均值与总体均值之间的差异总和。

•组内平方和（SSE）：反映了同一组别内观测值与该组均值之间的差异总和。

通过计算平方和，我们可以得到均方值（MS）： - 组间均方值（MSA）：SSA除以自由度（组别数-1）。

- 组内均方值（MSE）：SSE除以自由度（总观测数-组别数）。

采用均数和标准差进行方差分析的方法及SAS 实现广东省深圳市中医院 郭志武【摘要】目的 探讨采用均数和标准差进行方差分析的方法及SAS 程序。

方法 通过推导，得到基于均数和标准差的方差分析计算公式，并用简洁的SAS 程序实现。

结果 实现了有关算法及SAS 程序。

结论 采用均数和标准差进行方差分析是完全可行的，编制SAS 程序可以有效实现相关的计算，得到可靠的结果。

【关键词】均数 标准差 方差分析 SAS在实际工作中，通常会遇到一些研究资料只有均数和标准差而缺失原始数据的情况，比如年代久远的研究资料、期刊文献的资料等等。

对于这些资料，若需进行t 检验是很容易的，有现成的公式可用；但若需对多个样本资料做方差分析就不易了，现有的计算公式以及统计软件的算法都是基于原始数据的，因此有必要探讨基于均数和标准差的方差分析算法，以满足实际工作的需要。

1.算法的推导对于单因素方差分析，传统的算法是先计算总变异，然后分别算出组间变异和组内变异，最后求出F 值和对应的P 值。

这都是基于原始数据来计算的。

若只有均数和标准差，则需要通过推导得出计算组内变异和组间变异的公式。

组间变异组间SS 的理论公式为：∑=-=ki iiX Xn SS 12)(组间 （1）而∑∑===ki i ki i i n X n X 11/)(，因此：∑∑∑∑∑∑======-=-=ki i ki i i ki iiki ki i ki i i iin X n Xn n X n Xn SS 121121211/)()(]/)([组间 （2）组内变异组内SS 的理论公式为：∑∑==-=ki n i ijiX XSS 11j 2)(组内 （3）由于组内标准差)1/()(12--=∑=i n j i ij i n X X S i，因此)1()(22-=-i i i ij n S X X ，从而：∑=-=ki i in SSS 12)1(组内 （4）这样，通过（2）式和（4）式，可以很方便地计算出组间SS 和组内SS ，从而进一步计算出F 值。

只有均数和标准差情况下⽅差分析spss实现SPSS相关编程（Syntax语句）：data list free/x1 x2 x3 s1 s2 s3 .begin data17 13 16 7.4 8.8 3.2end data.compute ss1=s1**2*49+s2**2*57+s3**2*51.compute MS1=ss1/157.compute X=(x1*50+x2*58+x3*52)/160.compute ss2=50*(x1-X)**2+58*(x2-X)**2+52*(x3-X)**2.compute MS2=ss2/2.compute F=MS2/MS1.compute p=1-CDF.F(F,2,157).execute.举例：原始数据的统计描述：组别　例数　平均数 标准差 标准误1 50 17.0000 7.4000 1.04652 58 13.0000 8.8000 1.15553 52 16.0000 3.2000 0.4438参数统计应⽤条件检查：1) 正态性检验(矩法):样本含量⾜够⼤,不必进⾏正态性检验!2) ⽅差齐性检验:卡⽅值=46.4058, P=0.0000按α=0.0500⽔准，可认为该资料⽅差不齐!参数统计结果：⽅差分析:Ho:各个总体均数相等H1:各个总体均数不相等或不全相等α=0.0500⽅差分析结果=========================================变异来源 SS ν MS F P------------------------------------------------------------总 8095.4600　159组间 475.9000 2 237.9500 4.90　0.0086组内 7619.5600 157 48.5322============================================================结论:经过⽅差分析,得P=0.0086,按α=0.0500⽔准拒绝Ho,接受H1,故可认为各组总体均数不相等!3个样本均数两两⽐较的q检验(Newman-Keuls法)=============================================组别 两均数之差 组数 Q值 P值------------------------------------------------------------------第 1与第 2　4.0000 3 4.2077 <0.05第 1与第 3　1.0000 2 1.0249 >0.05第 2与第 3　3.0000 2 3.1889 <0.05=============================================平均住院⽇（天）原始数据的统计描述：组别　例数 平均数 标准差 标准误1 50 28.0000 6.1000 0.86272 58 22.0000 5.7000 0.74843 52 25.0000 1.7000 0.2357参数统计应⽤条件检查：1) 正态性检验(矩法):样本含量⾜够⼤,不必进⾏正态性检验!2) ⽅差齐性检验:卡⽅值=70.8595, P=0.0000按α=0.0500⽔准，可认为该资料⽅差不齐!参数统计结果：⽅差分析:Ho:各个总体均数相等H1:各个总体均数不相等或不全相等α=0.0500⽅差分析结果=============================================变异来源 SS ν MS F P------------------------------------------------------------总 4791.0100 159组间 968.4000 2 484.2000 19.89　0.0000组内 3822.6100 157 24.3478============================================================结论:经过⽅差分析,得P=0.0000,按α=0.0500⽔准拒绝Ho,接受H1,故可认为各组总体均数不相等! 3个样本均数两两⽐较的q检验(Newman-Keuls法)=======================================组　别 两均数之差 组数 Q值 P值------------------------------------------------------------------第 1与第 2 6.0000 3 8.9109 <0.01第 1与第 3 3.0000 2 4.3410 <0.01第 2与第 3 3.0000 2 4.5022 <0.01========================================如有基本统计量，可在如下站实现两两⽐较：/quickcalcs/index.cfm。

工艺验证与常用数理统计方法一、工艺验证的概念工艺验证是通过实验和测试，验证工艺过程是否能够满足产品质量要求的一系列活动。

其目的是为了验证工艺的可行性和稳定性，以确保产品在正常生产条件下能够稳定地满足质量要求。

工艺验证的步骤包括：确定验证目标和验证方法、制定验证计划、进行验证实验、分析验证结果、总结验证结论等。

在工艺验证过程中，为了分析验证结果和评估工艺稳定性，常会用到一些数理统计方法。

下面介绍几种常用的数理统计方法。

1.均值与标准差均值是一组数据平均值的统计量，可以用于评估工艺过程的中心趋势。

标准差则是一组数据离散程度的统计量，可以用于评估工艺过程的稳定性。

通过比较均值和标准差的大小，可以判断工艺过程的平均值和离散程度是否在允许范围内。

2.直方图与正态分布直方图是用来描述数据分布情况的一种图形表示方法。

通过绘制数据的频率分布图，可以直观地了解数据的分布情况。

如果数据呈现正态分布，即大部分数据集中在均值附近，呈钟形分布，则说明工艺过程稳定。

3.方差分析方差分析是一种用于比较两个或多个样本均值差异是否显著的统计方法。

在工艺验证中，可以通过方差分析来判断不同因素对工艺过程的影响是否显著，以确定优化工艺的方向。

4.回归分析回归分析是一种用于建立自变量与因变量之间关系的数学模型的统计方法。

在工艺验证中，可以通过回归分析建立工艺参数与产品质量之间的关系模型，用于预测和优化工艺参数。

5.其他方法除了以上常用的统计方法外，还有许多其他的数理统计方法可以用于工艺验证。

比如t检验、方差齐性检验、相关分析等。

根据实际情况选择合适的统计方法，并结合工程经验和专业知识进行分析和判断。

三、工艺验证的实践案例下面以企业的工艺验证为例，介绍工艺验证与常用数理统计方法的应用。

企业生产其中一种电子产品的工艺过程，需要验证其良品率是否能够满足质量要求。

首先确定验证目标为良品率，验证方法为收集一定数量的样本进行检测。

然后制定验证计划，包括确定样本数量、抽样方法、检测标准等。

土壤普查资料的平均值是指某一特定土壤参数在所有测量点处的测量值的平均数。

根据数学定义，土壤普查资料的平均值可以计算如下：
平均值= 所有测量值之和/ 测量点的数量
土壤普查资料的标准差是指土壤参数的测量值的离散程度。

根据数学定义，土壤普查资料的标准差可以计算如下：
标准差= √（（每个测量值-平均值）的平方的和/ 测量点的数量）
土壤普查资料的方差是指土壤参数的测量值的离散程度的平方。

根据数学定义，土壤普查资料的方差可以计算如下：
方差= （每个测量值-平均值）的平方的和/ 测量点的数量
对土壤普查资料进行平均值、标准差和方差分析可以帮助我们了解土壤参数的分布情况，从而为决策提供依据。

在计算平均值、标准差和方差时，可以使用计算机软件或统计软件来自动计算，也可以使用手算方法。

不过，在使用手算方法时需要注意，应确保数据的准确性，避免计算过程中的错误。

均数标准差方差分析均数、标准差和方差分析是统计学中常用的概念和方法，它们在数据分析和研究中起着重要的作用。

本文将对这三个概念进行详细的介绍和解释，希望能够帮助读者更好地理解和运用它们。

首先，我们来介绍一下均数。

均数，即平均数，是一组数据的总和除以数据的个数所得到的结果。

在统计学中，均数通常用来表示一组数据的集中趋势，它能够反映出数据的一般水平。

计算均数的方法非常简单，只需要将所有数据相加，然后除以数据的个数即可得到均数。

例如，如果我们有一组数据，2，4，6，8，10，那么这组数据的均数就是(2+4+6+8+10)/5=6。

接下来，让我们来了解一下标准差。

标准差是衡量一组数据的离散程度或者波动程度的指标。

它能够告诉我们数据点相对于均值的分散程度，标准差越大，表示数据的离散程度越高，反之则越低。

计算标准差的方法比较复杂，需要先计算每个数据点与均值的差的平方，然后将这些平方差值相加，再除以数据的个数，最后再取平方根即可得到标准差。

标准差的计算公式如下，σ=√(∑(X-μ)²/n)，其中σ表示标准差，∑表示求和，X表示每个数据点，μ表示均值，n表示数据的个数。

最后，让我们来讨论一下方差分析。

方差分析是一种用于比较两个或多个样本均值差异的统计方法。

它能够帮助我们判断不同组别之间的均值是否有显著差异。

方差分析通常用于实验设计和数据分析中，可以帮助我们确定影响因素对结果的影响程度。

在进行方差分析时，我们需要计算组内平方和、组间平方和以及总平方和，然后通过这些平方和的比较来判断均值之间的差异是否显著。

综上所述，均数、标准差和方差分析是统计学中非常重要的概念和方法。

它们能够帮助我们理解数据的分布特征、集中趋势以及不同组别之间的差异。

在实际应用中，我们可以根据这些方法来进行数据分析、决策和预测，从而更好地理解和利用数据。

希望本文的介绍能够帮助读者更好地掌握这些概念和方法，为实际工作和研究提供帮助。

数据分析公式数据分析是指通过收集、整理和分析各种数据，从中获取有价值的信息和洞察力。

在进行数据分析时，人们经常使用各种公式来计算和解释数据。

这些公式帮助数据分析人员理解数据的本质，并提供洞察数据背后的模式和趋势。

在本文中，我们将介绍一些常见的数据分析公式，以帮助读者更好地理解和应用数据分析。

1. 平均值平均值是最常见的数据分析公式之一。

平均值可以用来衡量一组数据的集中趋势。

计算平均值的公式如下：平均值 = 总和 / 数据个数2. 中位数中位数是将一组数据按大小排序后的中间值。

中位数可以作为数据集中趋势的替代指标，可以帮助排除数据中的异常值的影响。

计算中位数的公式如下：中位数 = 排序后的数据集中的值3. 众数众数是一组数据中出现次数最多的值。

计算众数的公式如下：众数 = 出现次数最多的值4. 标准差标准差是用来测量一组数据的离散程度的指标。

标准差越大，数据越分散；标准差越小，数据越集中。

计算标准差的公式如下：标准差 = √（（每个数据值 - 平均值）²的和 / 数据个数）5. 相关系数相关系数用于衡量两个变量之间的关联程度。

相关系数的取值范围为-1到1，其中-1表示负相关，0表示无相关，1表示正相关。

计算相关系数的公式可以根据具体的方法选择。

6. 百分位数百分位数可以帮助我们了解数据中某个特定百分比所处的位置。

例如，50%百分位数表示有一半的数据小于或等于该值。

计算百分位数的公式如下：百分位数 = （（百分位数位置 / 100） * 数据总数）四舍五入取整7. 回归分析公式回归分析是用来建立两个或多个变量之间关系的一种统计方法。

常见的回归分析公式有线性回归和多项式回归方程。

8. t检验t检验用于比较两组数据平均值之间是否存在显著差异。

t检验的公式需要根据具体的方法选择。

9. 方差分析方差分析是用于比较多个组别之间是否存在差异的统计方法。

方差分析的公式需要根据具体的方法选择。

10. 熵熵用于衡量数据集合的不确定度。