第三章[1].动力学和动量定理 第三部分 动量定理

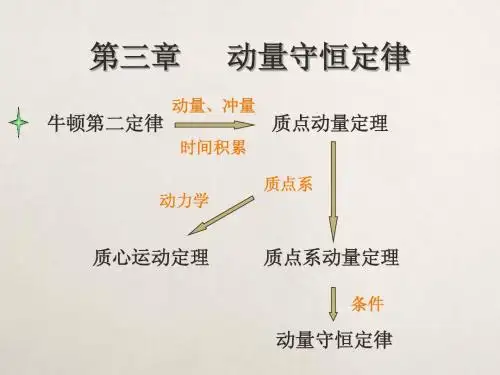
动量定理动量定理是力对时间的积累效应，使物体的动量发生改变，是高中物理学科学习的重点。

下面就为大家介绍动量定理，希望对大家有所帮助。

【动量定理知识点】1、动量定理:物体受到合外力的冲量等于物体动量的变化.Ft=mv/一mv或Ft=p/-p;该定理由牛顿第二定律推导出来:(质点m在短时间Δt内受合力为F合，合力的冲量是F合Δt;质点的初、未动量是mv0、mvt，动量的变化量是ΔP=Δ(mv)=mvt-mv0.根据动量定理得:F合=Δ(mv)/Δt)2.单位:牛·秒与千克米/秒统一:l千克米/秒=1千克米/秒2·秒=牛·秒;3.理解:(1)上式中F为研究对象所受的包括重力在内的所有外力的合力。

(2)动量定理中的冲量和动量都是矢量。

定理的表达式为一矢量式，等号的两边不但大小相同，而且方向相同，在高中阶段，动量定理的应用只限于一维的情况。

这时可规定一个正方向，注意力和速度的正负，这样就把大量运算转化为代数运算。

(3)动量定理的研究对象一般是单个质点。

求变力的冲量时，可借助动量定理求，不可直接用冲量定义式。

4.应用动量定理的思路:(1)明确研究对象和受力的时间(明确质量m和时间t);(2)分析对象受力和对象初、末速度(明确冲量I合，和初、未动量P0，Pt);(3)规定正方向，目的是将矢量运算转化为代数运算;(4)根据动量定理列方程(5)解方程。

【动量定理的内容】动量定理反应的是力在时间维度上的积累效果。

(1)基本概念描述:物体所受合外力的冲量，等于物体的动量变化量。

即F合t=I=Δp;(2)我们还可以这样来表述:对作用在物体上的各个力的冲量的代数和，等于动量的改变量。

在外力不恒定，或者各个力作用时间不同时，优先选择后者。

提醒:动量与冲量都是矢量，是有方向的，因此在解题时首先要规定好正方向。

【动量定理的表达式】基本表达式:F合t=I=Δp;当存在多个力做冲量时，还可以写成分力冲量代数和的形式: F1t1+F2t2+F3t3+……=I1+I2+I3+……=Δp【动量定理的表达式推广】当存在多个力做冲量时，动量定理的表达式还可以写成分力冲量代数和的形式:F1t1+F2t2+F3t3+……=I1+I2+I3+……=Δp这与动能定理的非常类似的。

第三章 动量定理及动量守恒定律（习题）3.5.1质量为2kg 的质点的运动学方程为 j ˆ)1t 3t 3(i ˆ)1t 6(r 22+++-=(t 为时间，单位为s ；长度单位为m).求证质点受恒力而运动，并求力的方向大小。

解，j ˆ)3t 6(i ˆt 12v ++= j ˆ6i ˆ12a +=jˆ12i ˆ24a m F +==（恒量）012257.262412tg )N (83.261224F ==θ=+=-3.5.2质量为m 的质点在oxy 平面内运动，质点的运动学方程为ωω+ω=b,a, ,j ˆt sin b i ˆt cos a r为正常数，证明作用于质点的合力总指向原点。

解， ,j ˆt cos b i ˆt sin a v ωω+ωω-= r,j ˆt sin b i ˆt cos a a 22 ω-=ωω-ωω-= r m a m F ω-==3.5.3在脱粒机中往往装有振动鱼鳞筛，一方面由筛孔漏出谷粒，一方面逐出秸杆，筛面微微倾斜，是为了从较底的一边将秸杆逐出，因角度很小，可近似看作水平，筛面与谷粒发生相对运动才可能将谷粒筛出，若谷粒与筛面静摩擦系数为0.4，问筛沿水平方向的加速度至少多大才能使谷物和筛面发生相对运动。

解答，以谷筛为参照系，发生相对运动的条件是,g a ,mg f a m 000μ≥'μ=≥'a ' 最小值为)s /m (92.38.94.0g a 20=⨯=μ='以地面为参照系：解答，静摩擦力使谷粒产生最大加速度为,mg ma 0max μ= ,g a 0max μ=发生相对运动的条件是筛的加速度g a a0max μ=≥'，a '最小值为)s /m (92.38.94.0g a20=⨯=μ='3.5.4桌面上叠放着两块木板，质量各为,m ,m 21如图所示。

2m 和桌面间的摩擦系数为2μ，1m 和2m 间的静摩擦系数为1μ。

动量和动量定理教案公开课第一章：动量的概念1.1 动量的定义向学生介绍动量的概念，即物体的质量与速度的乘积。

通过实际例子，让学生理解动量与物体的运动状态有关。

1.2 动量的表示解释动量的表示方式，即p = mv，其中p 表示动量，m 表示物体的质量，v 表示物体的速度。

让学生通过数学表达式理解动量的大小和方向。

1.3 动量与动能的关系向学生介绍动量与动能的关系，即动量是动能的量度。

通过示例和练习，让学生理解动量和动能之间的转换关系。

第二章：动量定理2.1 动量定理的表述向学生介绍动量定理，即物体的动量变化等于作用在物体上的合外力的冲量。

通过公式表达动量定理，即Δp = FΔt，其中Δp 表示动量的变化量，F 表示作用在物体上的合外力，Δt 表示作用时间。

2.2 动量定理的应用解释动量定理在实际问题中的应用，如碰撞、爆炸等。

通过示例和练习，让学生学会使用动量定理解决问题。

第三章：动量守恒定律3.1 动量守恒定律的表述向学生介绍动量守恒定律，即在没有外力作用的情况下，系统的总动量保持不变。

通过公式表达动量守恒定律，即Σp_initial = Σp_final，其中Σp_initial 表示系统初始总动量，Σp_final 表示系统最终总动量。

3.2 动量守恒定律的应用解释动量守恒定律在碰撞、弹性碰撞、非弹性碰撞等实际问题中的应用。

通过示例和练习，让学生学会使用动量守恒定律解决问题。

第四章：动量与动量定理的综合应用4.1 动量与动量定理的综合应用示例提供一些综合性的实际问题，让学生运用动量和动量定理进行解决。

通过示例和练习，让学生学会将动量和动量定理结合起来解决问题。

4.2 动量与动量定理的综合应用练习提供一些练习题，让学生自行运用动量和动量定理解决问题。

给予学生解答和指导，帮助学生巩固对动量和动量定理的理解和应用。

强调动量和动量定理在物理学中的重要性和实际意义。

5.2 动量和动量定理的复习提供一些复习题，让学生巩固对动量和动量定理的理解和应用。

动力学原理介绍
动力学是研究物体运动状态与时间的关系，以及力的作用效果与物体运动状态变化关系的科学。

动力学的基本原理包括牛顿第二定律、动量定理、动能定理等。

1.牛顿第二定律：
F=ma，其中F是力，m是质量，a是加速度。

这个定律描述了力与加速度之间的关系，即力的大小与物体的质量和加速度成正比。

2.动量定理：
Ft=mv，其中F是力，t是力的作用时间，m是质量，v是物体的速度。

这个定理描述了力的作用时间与物体的动量变化之间的关系，即力的作用时间与物体的动量变化成正比。

3.动能定理：
Fs=ΔE，其中Fs是力做的功，ΔE是物体动能的变化量。

这个定理描述了力做的功与物体动能变化之间的关系，即力做的功等于物体动能的变化量。

此外，动力学还涉及到一些复杂的概念，如动量守恒、能量守恒等。

这些概念在解决一些复杂的问题时非常有用。

例如，在研究天体运动时，牛顿运动定律和万有引力定律是解决天体运动问题的关键。

在研究碰撞问题时，动量定理和动能定理是解决碰撞问题的关键。

总之，动力学是物理学中的一个重要分支，它涉及到许多重要的概念和原理。

通过学习动力学，我们可以更好地理解物体的运动状态和力的作用效果，从而更好地解释自然现象并解决实际问题。

动能定理和动量定理动量定理是物体机械运动的一种量度．它是和物体运动速度相关的状态量．动量是矢量，其方向就是即时速度的方向，动量的大小等于物体的质量和物体即时速度的乘积，即p=mv．在国际单位制中，动量的单位是千克·米/秒．速度是相对的，动量也是相对的，我们一般取地面或相对地面静止的物体做参照物来确定动量的大小和方向．动能定理内容：力在一个过程中对物体所做的功等于在这个过程中动能的变化.合外力(物体所受的外力的总和,根据方向以及受力大小通过正交法能计算出物体最终的合力方向及大小)对物体所做的功等于物体动能的变化。

质点动能定理表达式：w1+w2+w3+w4…=△W=Ek2-Ek1（k2）（k1）为下标其中，Ek2表示物体的末动能，Ek1表示物体的初动能。

△W是动能的变化，又称动能的增量，也表示合外力对物体做的总功。

动能定理的表达式是标量式，当合外力对物体做正功时，Ek2>Ek1物体的动能增加；反之则，Ek1>Ek2,物体的动能减少。

动能定理中的位移，初末动能都应相对于同一参照系。

1能定理研究的对象式单一的物体，或者式可以堪称单一物体的物体系。

2动能定理的计算式式等式，一般以地面为参考系。

3动能定理适用于物体的直线运动，也适应于曲线运动；适用于恒力做功，也适用于变力做功；力可以式分段作用，也可以式同时作用，只要可以求出各个力的正负代数和即可，这就是动能定理的优越性。

组动能质点组动能定理质点系所有外力做功之和加上所有内力做功之和等于质点系总动能的改变量。

和质点动能定理一样，质点系动能定理只适用于惯性系，因为外力对质点系做功与参照系选择有关，而内力做功却与选择的参照系无关，因为力总是成对出现的，一对作用力和反作用力（内力）所做功代数和取决于相对位移，而相对位移与选择的参照系无关。

动能定理的内容：所有外力对物体总功，（也叫做合外力的功）等于物体的动能的变化。

动能定理的数学表达式：W总=1/2m(v2)的平方—1/2m(v1)的平方动能定理只适用于宏观低速的情况，而动量定理可适用于世界上任何情况。