当前位置：文档之家 › 第三章动量守恒定律

第三章动量守恒定律

  • 格式：ppt
  • 大小：6.52 MB
  • 文档页数：85

下载文档原格式

  / 85

合集下载

动量定理及动量守恒定律

动量定理及动量守恒定律

20
动量定理及动量守恒定律
oy N1 − m1g = 0 又f1max = N1μ1
以 m2 为隔离体，m2 受重力W = m2 g ;桌面的支持力 N2 ; m1 的压力 N1′ （大小与 N1 相等）; m1 作用在 m2 上的最大静摩擦力 f1max′（大小与 f1max 相等） ;桌面作用在 m2 上的
oA y A W3 − TA′ − TB′ = m3a3
(7)
因为不计滑轮及绳的质量，不计轴承摩擦. 且已知绳不可伸长.
∴ TA = TB = TA′ = TB′ = T
f A ,绳的拉力 TA , A 的动力学方程为

动量定理及动量守恒定律
W1 + N A + f A + TA = m1a1 建立如图 3.5.7（1）所示的坐标系 oA − xA y A .
oA xA TA − f A = m1a1
(1)
oA y A W1 − N A = 0
(2)
且 fA = NAμ
动量定理及动量守恒定律
第三章 动量定理及动量守恒定律
(Momentum and Conservation Law of Momentum)
一、内容简介（Abstract） 1．牛顿第一定律（Newton’s first law)
孤立质点静止或作等速直线运动，即质点在不受力或所受力的合力为零时，将保持静 止或匀速直线运动状态不变.（惯性定律） 2．牛顿第三定律（Newton’s third law）
g
y
x o
N
2
α m2
a2
W2
N1′
图3.5.（5 3）
y′
N1 f∗
m1

第3章动量守恒

第3章动量守恒

v = 2 gl
在其后的一小段时间dt内，对 在其后的一小段时间 内 的绳子， dm = λ dl = λ vdt 的绳子，忽略重力作 y 用，由动量定理可知 Fdt = 0 − dm ⋅ v − dm 2 ∴F = v = − λ v = − 2λ l g dt N = (m + dm) g + F ' ≈ 3λl g
L-l L
例题4 有一条单位长度质量为λ的匀质柔绳，开始 有一条单位长度质量为λ的匀质柔绳， 例题 时盘绕在光滑的水平桌面上，（ ，（1 时盘绕在光滑的水平桌面上，（1）若以恒定的加速 向上提起， 时作用于绳端的力； 度a向上提起，当提起的高度为 时作用于绳端的力； 向上提起 当提起的高度为y时作用于绳端的力 若以恒定的速度v向上提起 当提起的高度为y时 向上提起， （2）若以恒定的速度 向上提起，当提起的高度为 时 F 作用于绳端的力。 作用于绳端的力。 取竖直向上为正， 解 :(1)取竖直向上为正 ， 当绳加速上升 高度y 高度y时 v = 2ay a 其后一小段时间 dt 内 ,被提起的绳 被提起的绳 y 子将增加 dm = λ dy = λ vdt ，对提起 的绳子， 的绳子，由动量定理
0.2 × 10 = N + 0.2 × 9.8 N = 231N + 1.96 N ≈ 233 N 0 0.01× cos 30 由牛顿第三定律，小球对地面的平均冲力与F大 由牛顿第三定律 ， 小球对地面的平均冲力与 大 小相等，方向相反。 小相等，方向相反。 解法二：用分量式求解， 解法二：用分量式求解，选水平竖直平面内直角坐标 系0xy，写出动量定理的分量式： ，写出动量定理的分量式： x方向： 0 = mv sin β − mv0 sin α 方向： 方向 y方向： ( F − mg ) ⋅ ∆t = mv cos β − (− mv0 cos α ) 方向： 方向 两式联立，消去v得 两式联立，消去 得 mv0 ( F − mg ) ⋅ ∆t = sin(α + β ) sin β 因为 α + β = 900 ，故解得 mv0 F= + mg ∆t cos α

动量定理及动量守恒定律

动量定理及动量守恒定律

规定m0=1千克（kg），则有
m v 2 / v1 kg
2.动量 · 动量守恒定律 将气桌上两物体的碰撞抽象为两个质点m1和m2的相互作用， 则有
令 v10和v 20
m1v1 m2 v 2
分别表示两质点相互作用后的末速度，则
分别表示两质点相互作用前的初速度，v1和v 2
T cos d / 2 0 N T dT cos d / 2 0
因 d 很小 sin d / 2 d / 2, cos d / 2 1 得到 N Td , dT 0 N dT / T 0 d 4 , 0 0.5, T 积分得 dT / T 0 d ln T / T0 0 T0 5 N ,
d F 21 k m1 v1 dt


d , F 12 k m2 v 2 dt


式中k为常数。在SI中k=1，力的量纲为LMT-2，于是 d d F 21 m1 v1 , F 12 m2 v 2 dt dtFra bibliotek
d 或一般的可写作 F mv dt
r d Fi m dt ma 回旋加速器 （劳伦斯 1930） 2 动力学方程 qvB mv / r v qBr / m
Fin m
粒子运动半周的时间 t r / v m / qB 频率为 qB / 2 m 最早的回旋加速器
R 0.18m, B 1.7T , mD 3.35 1027 kg , q 1.6 1019 C 频率 1.3 107 H 速度 v 1.46 107 m / s z
yl 2
gt 2

第三章-动量守恒定律

第三章-动量守恒定律


cos d
R

2、求半径为 R 、顶角为 2 的均匀扇形薄板的质
心？
习题3-8
3、求质量均匀分布的半球体的质心？
解：

建立坐标系
计算 C z
dz z
由对称性可知，质心在 z 轴上 根据质心定义式 zC
设球体的体密度为
zdm dm
dm ( R 2 z 2 )dz

v10 v1 v2 v20 v10 v20 v2 v1
碰前相互接近的速度 = 碰后相互离开的速度
m1 m2 时 v1 v20 , v2 v10 m1 m2 2m1 v v , v v10 v20 0 时 1 10 2 m1 m2 m1 m2
根据质点动量定理：
t I Fdt p p0 mv mv0 0 mv0
根据平均冲力定义： F I mv0 t t m(v0 ) mv0 F t t
根据质点动能定理： mgh 1 mv 2 0
F
h
mg
m 2 gh F 3.1105 N t
2
v0 2 gh
方向向上
§ 3-2 质点系动量定理和质心运动定理
一、质点系动量定理
1、两个质点构成的质点系

研究对象 受力分析 内力：
F2
f12
2
f 21
F1
1
外力：

运动特点
t0 :
t:
分别对 应用质点动量定理
i
动量守恒定律
当外力矢量和为零时，质点系的总动量保持不变。
说明
分量守恒

第三章 动量守恒定律与能量守恒定律

第三章 动量守恒定律与能量守恒定律

第三章 动量守恒定律和能量守恒定律3-1 一架以12ms 100.3-⨯的速率水平飞行的飞机，与一只身长为0.20m 、质量为0.50kg 的飞鸟相碰。

设碰撞后飞鸟的尸体与飞机具有同样的速度，而原来飞鸟对于地面的速率很小，可以忽略不计。

估计飞鸟对飞机的冲击力，根据本题的计算结果，你对高速运动的物体与通常情况下不足以引起危害的物体相碰后产生后果的问题有什么体会？解：以飞鸟为研究对象，其初速为0，末速为飞机的速度，由动量定理。

vlt mv t =∆-=∆ ,0F 联立两式可得： N lmv F 521025.2⨯==飞鸟的平均冲力N F F 51025.2'⨯-=-=式中的负号表示飞机受到的冲击力与飞机的运动速度方向相反。

从计算结果可知N F F 51025.2'⨯-=-=大于鸟所受重力的4.5万倍。

可见，冲击力是相当大的。

因此告诉运动的物体与通常情况下不足以引起危险的物体相碰，可能造成严重的后果。

3-2 质量为m 的物体，由水平面上点O 以初速为0v 抛出，0v 与水平面成仰角α。

若不计空气阻力。

求：（1）物体从发射点O 到最高点的过程中，重力的冲量；（2）物体从发射点到落回至同一水平面的过程中，重力的冲量。

解：（1）在垂直方向上，物体m 到达最高点时的动量的变化量是：αsin 01mv P -=∆而重力的冲击力等于物体在垂直方向的动量变化量：ααsin sin 0011mv mv P I -=-=∆=（2）同理，物体从发射点到落回至同一水平面的过程中，重力的冲力等于物体竖直方向上的动量变化量αααsin 2sin sin 1222mv mv mv mv mv P I -=--=-=∆=负号表示冲量的方向向下。

3-3 高空作业时系安全带是非常必要的。

假如一质量为51.0kg 的人，在操作时不慎从高空跌落下来，由于安全带保护，最终使他悬挂起来。

已知此时人离原处的距离为 2.0m ，安全带弹性缓冲作用时间为0.50s 。

大学物理第三章动量守恒定律和能量守恒定律

大学物理第三章动量守恒定律和能量守恒定律

动量守恒定律的表述
总结词
动量守恒定律表述为系统不受外力或所 受外力之和为零时，系统总动量保持不 变。
VS
详细描述
动量守恒定律是自然界中最基本的定律之 一，它表述为在一个封闭系统中，如果没 有外力作用或者外力之和为零，则系统总 动量保持不变。也就是说，系统的初始动 量和最终动量是相等的。
动量守恒定律的适用条件
能量守恒定律可以通过电磁学 的基本公式推导出来。
能量守恒定律可以通过相对论 的质能方程推导出来。
能量守恒定律的应用实例
01
02
03
04
机械能守恒
在无外力作用的系统中，动能 和势能可以相互转化，但总和
保持不变。
热能守恒
在一个孤立系统中，热量只能 从高温物体传递到低温物体，
最终达到热平衡状态。
电磁能守恒
详细描述
根据牛顿第三定律，作用力和反作用力大小相等、方向相反。如果将一个物体施加一个力F，则该力会产生一个 加速度a，进而改变物体的速度v。由于力的作用是相互的，反作用力也会对另一个物体产生相同大小、相反方向 的加速度和速度变化。因此，在系统内力的相互作用下，系统总动量保持不变。
02
能量守恒定律
能量守恒定律的表述
感谢观看
01
能量守恒定律表述为：在一个封闭系统中，能量不能被创造或消灭， 只能从一种形式转化为另一种形式。
02
能量守恒定律是自然界的基本定律之一，适用于宇宙中的一切物理过 程。
03
能量守恒定律是定量的，可以用数学公式表示。
04
能量守恒定律是绝对的，不受任何物理定律的限制。
能量守恒定律的适用条件
能量守恒定律适用于孤立系统，即系统与外界没有能量 交换。

动量定理及动量守恒定律第三章

动量定理及动量守恒定律第三章

在直角坐标系中： ， ，
在自然坐标系中： ，
其中 是 、 在坐标轴上的投影，均为代数量，其正负由矢量和坐标轴方向间的夹角小于或大于 来定。方程的数目等于未知数的数目，有时要根据题目中的物理条件列出数字方程。
5解方程，对所得结果进行必要的讨论。
例题讲解：
1如图所示，在光滑的水平地面上放一质量为M的契块，契块底角为 ，斜边光滑，今在其斜边上放一质量为m的物体，求物体沿契块下滑时对契块和对地面的加速度。
解：参考系：地面
研究对象：契块和物体
m
mg
Nm
θ
受力分析： 契块 物体且N‘=-Nm
X
Y
θ
M
m
M
Mg
N
N’
一 章节小结
（一）． 惯性定律
1．惯性定律：自由粒子永远保持静止或匀速直线运动状态。
2．惯性参考系 对某一特定物体惯性定律成立的参考系。
其特性：（1）在惯性系中所有物体遵从惯性定律。
（2）一切相对惯性系作匀速直线运动的参考系都是惯性系。
3．相对性原理 对于牛顿动力学规律，一切惯性系都是等价的。
θ
坐标系：如图所示
β
设物体相对地面的加速度为 ，和水平面的夹角为 向下
物体相对契块的加速度为 ，沿斜面，和地面成角
契块相对地面的加速度为 ，沿水平方向后。
根据相对性： ，
例如，对阿特武德机，只能分别选两个物体为研究对象，而不能把两个物体作为一个研究对象来应用牛顿运动定律。
2分析研究对象的受力情况，画出受力图。
3建立坐标系：有了坐标系，才便于把力、加速度等矢量向坐标轴投影，使矢量运算化为标量运算，在动力学中坐标原点的位置可以任意。

大学物理 第三章 动量守恒定律和能量守恒定律 3-9 质心 质心运动定律

大学物理 第三章 动量守恒定律和能量守恒定律 3-9 质心 质心运动定律
物理学
第五版
3-9 质心 -
质心运动定律
一 质心
1 质心的概念
板上C点的运动轨迹是抛物线 板上 点的运动轨迹是抛物线 其余点的运动=随 点的平动+绕 点的 点的平动 点的转动 其余点的运动 随C点的平动 绕C点的转动
第三章 动量守恒和能量守恒
1
物理学
第五版
3-9 质心 -
质心运动定律
2 质心的位置 由n个质点组成 个质点组成 的质点系， 的质点系，其质心 的位置： 的位置：
13
物理学
第五版
3-9 质心 n n v v v m'vC = ∑ mi vi = ∑ pi = p i =1 i =1
质心运动定律
求一阶导数， 再对时间 t 求一阶导数，得
质心加速度
dp v m'aC = dt v v dp ex 根据质点系动量定理 = Fi dt
第三章 动量守恒和能量守恒
}⇒
x2 = 2 xC
17
第三章 动量守恒和能量守恒
物理学
第五版
3-9 质心 -
质心运动定律
例4 用质心运动定律 y F 来讨论以下问题． 来讨论以下问题． 一长为l 一长为 、密度均匀的 y 柔软链条， 柔软链条，其单位长度的质 c yC 量为 λ ．将其卷成一堆放在 地面． 若手提链条的一端， 地面． 若手提链条的一端， o 以匀速v 将其上提．当一端 以匀速 将其上提． 被提离地面高度为 y 时，求手的提力． 求手的提力．
竖直方向作用于链条的合外力为 F − λyg
第三章 动量守恒和能量守恒
20
物理学
第五版
3-9 质心 -
质心运动定律
v 得到 F − yλg = lλ ⋅ l

大学物理第三章动量守恒定律和能量守恒定律

大学物理第三章动量守恒定律和能量守恒定律
展望了未来在学习相对论和量子力学中，对动量守恒定律和能量守恒定律的更深入理解 和应用。
探索其他守恒定律
鼓励了对其他守恒定律的探索，如角动量守恒定律、电荷守恒定律等。
THANKS
感谢观看
探索性实验：动量与能量的关系研究
实验目的
研究动量与能量的关系，探索两者之间的联系和 区别。
实验步骤
选择合适的实验器材，如弹性碰撞器、非弹性碰 撞器等，设计不同的碰撞条件，记录实验数据。
实验原理
动量和能量是描述物体运动状态的物理量，两者 之间存在一定的关系。通过研究不同运动状态下 物体的动量和能量变化，可以深入理解两者之间 的关系。
05
实验验证与探索
动量守恒定律的实验验证
实验目的
通过实验验证动量守恒定律， 加深对动量守恒定律的理解。
实验原理
动量守恒定律指出，在没有外 力作用的情况下，系统的总动 量保持不变。
实验步骤
选择合适的实验器材，如滑轨、 滑块、碰撞器等，按照实验要求 进行操作，记录实验数据。
实验结果
通过分析实验数据，验证动量 守恒定律的正确性。
动量守恒定律的应用实例
总结词：举例说明
详细描述：应用动量守恒定律的实例包括行星运动、碰撞、火箭推进等。例如，在行星运动中，行星绕太阳旋转时动量守恒 ；在碰撞过程中，两物体相互作用时的动量变化遵循动量守恒定律；火箭推进则是通过燃料燃烧产生高速气体，利用反作用 力推动火箭升空，这一过程中动量守恒。
03
守恒定律的意义
强调了守恒定律在物理学中的重要地位，以及在解决实际问题中的应 用价值。
对动量守恒定律和能量守恒定律的思考
守恒的哲学思考
探讨了守恒定律在哲学上的意义，以及它们 对宇宙观的影响。

第三章 动量守恒定律

第三章 动量守恒定律

第三章 动量守恒定律3-1 用榔头击钉子，如果榔头的质量为500 g ，击钉子时的速率为18.0m s -⋅，作用时间为32.010s -⨯，求钉子所受的冲量和榔头对钉子的平均打击力。

已知：m=500g=0.50kg 0v =8.0m/s t v =032.010t s -=⨯求：tF dt ⎰F ，解：由动量定理：00tF dt mv mv =-⎰000.508.0 4.0tF dt mv N s ∴==⨯=⎰钉子冲量的方向竖直向下。

334.02.0102.010tF dt F N t-===⨯⨯⎰钉子受到的打击力的方向也是竖直向下的。

（以上计算忽略榔头的重力作用）3-2 质量为10 g 的子弹以1500m s -⋅ 的速度沿与板面垂直的方向射向木板，穿过木板，速度降为1400m s -⋅。

如果子弹穿过木板所需时间为51.010s -⨯，试分别利用动能定理和动量定理求木板对子弹的平均阻力。

已知：210 1.010m g kg -==⨯ 10500v ms -= 1400t v ms -= 51.0010t s -=⨯求：f解：（1）由动能定理：2201122f s mv mv -=- 而：02v v S t +=（看成是匀减速运动）()()()22200550 1.010500400 1.010() 1.0010m v v m v v f N v v t t ----+⨯⨯-∴====⨯-+⨯ （2）由动能定理：012f t mv mv -=-()2551.010500400 1.0101.0010f --⨯⨯-∴==⨯⨯ 3-3在无风的水面上行驶帆船，如果有人使用船上的鼓风机，对着帆鼓风，船将如何运动？为什么？答：如图示为鼓风机对蓬帆鼓风的示意图。

由动量守恒定理知，船运动的方向将与鼓风的方向一致。

3-4 质量为m 的小球与桌面相碰撞，碰撞前、后小球的速率都是v ，入射方向和出射方向与桌面法线的夹角都是α，如图所示。

第3章-动量动量守恒定律

第3章-动量动量守恒定律
牛顿对自己的成功有着清醒的认识， 他在一封信中写道：“ 如果 牛顿对自己的成功有着清醒的认识， 他在一封信中写道：
说我比别人看得更远一点的话， 说我比别人看得更远一点的话 ， 那是因为我站在 巨人们的肩膀上。 牛顿长期担任英国皇家学会会长一职， 巨人们的肩膀上 。 ”牛顿长期担任英国皇家学会会长一职，
第三章 动量、动量守恒定律 动量、
本章主要阐述三个问题： 本章主要阐述三个问题： 1）牛顿运动三定律及其应用。 牛顿运动三定律及其应用。 2）非惯性参照系。 非惯性参照系。 3）冲量、冲量定理（质点动量定理），动量、动量守恒 冲量、冲量定理（质点动量定理），动量、 ），动量 定律。 定律。
第三章 动量、动量守恒定律 动量、
第三章 动量、动量守恒定律 动量、
的小球在液体中由静止释放，竖直下沉。 【例题】质量为 m的小球在液体中由静止释放，竖直下沉。设液体相 例题】 对地面静止。液体对小球的浮力为F 对地面静止。液体对小球的浮力为F，粘滞阻力为 f = 6πη , η rV 是液体的粘滞系数， 为小球的下沉速度。求任意时刻小球的速度。 是液体的粘滞系数，V为小球的下沉速度。求任意时刻小球的速度。
r r r dp r 当质点以接近光速运动时， 为变量 为变量， 不成立， ④ 当质点以接近光速运动时，m为变量， F = m a不成立，但 F =
仍成立。 仍成立。
牛顿第二定律的表达式是矢量式； ③ 牛顿第二定律的表达式是矢量式；
dt
第三章 动量、动量守恒定律 动量、
3、牛顿第三定律
牛顿第三定律的内容可表述如下：作用力与反作用力大小相等， 牛顿第三定律的内容可表述如下：作用力与反作用力大小相等，
直到去世。牛顿终身未婚，把毕生的精力都贡献给了科学事业， 直到去世。牛顿终身未婚，把毕生的精力都贡献给了科学事业，他在 临终遗言中有这样一段话： 我不知道世人将如何看待我， 临终遗言中有这样一段话：“我不知道世人将如何看待我，

第3章-动量守恒定律和能量守恒定律

第3章-动量守恒定律和能量守恒定律

质点的位移在力方向的分量和力的大小的乘积。
dW
F
cos
dr
F cos
ds
dW F dr
B
*
0 90, dW 0 90 180 , dW 0
dr
*A
F
90 F dr dW 0
20
3-4 动能定理
• 变力的功
W
B F dr
B
F
cos
ds
A
A
dri
i
B
*
端 , 绳的上端固定在天花板上 . 起初把绳子放在与竖
直线成 30 角处, 然后放手使小球沿圆弧下落 . 试求
绳解与: 竖d直W线成F
10角时 小球 的速率 d s FT d s P d s
.
P d s mgl d cos
mgl sin d
W mgl sin d 0
mgl (cos cos0 )
I
t2 t1
Fdt
p2
p1
mv2
mv1
问：冲量是矢量，它的方向就是力的方向吗 ？
分量形 式 I Ixi Iy j Izk
单位和量纲 1N·s = 1kgm/s dimI = M·L-1·T-1
Ix
t2 t1
Fxdt
mv2 x
mv1x
I y
t2 t1
Fydt
mv2 y
mv1y
Iz
14
3-2 动量守恒定律
例 1 设有一静止的原子核, 衰变辐射出一个电子和一
个中微子后成为一个新的原子核. 已知电子和中微子的
运动方向互相垂直, 电子动量为1.210-22 kg·m·s-1,中微
子的动量为 6.410-23 kg·m·s-1 . 问新的原子核的动量的

第三章 动量定律及动量守恒定律1.

第三章 动量定律及动量守恒定律1.

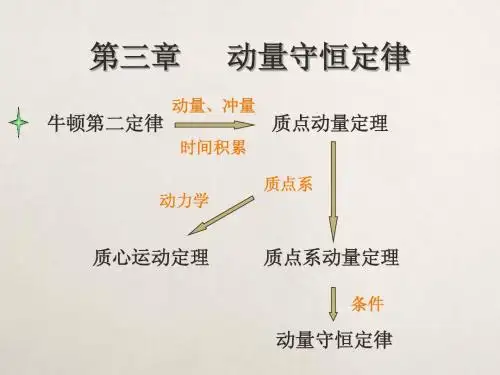
第三章 动量定律及动量守恒定律引言：本章开始研究动力学问题，即运动和物体间相互作用的关系。

意义：已知运动求力的各种问题仍然不断地摆在人们面前。

体系：纵观物理学，人们发现，动量的概念比力的概念更重要、更普遍、更基本。

本章从动量的概念入手，研究动力学，牛顿定律仍保持其应有的重要地位。

§3.1 牛顿第一定律和惯性参考系一、惯性定律：1．历史上对于运动和力的认识：亚里斯多德 2．伽利略的实验与结论 伽利略的理想实验3．牛顿第一定律：任何物体上只要没有外力改变它的运动状态，便会永远保持静止或匀速直线运动状态。

惯性：物体保持匀速直线运动或静止状态的特性。

所以牛顿第一定律——惯性定律4．第一定律表述中逻辑上的问题：力还没有定义孤立粒子（或自由粒子）（或孤立质点）：不受任何相互作用的质点。

理想模型，实际：粒子间相距非常远，可忽略其相互作用；或对该粒子的相互作用抵消。

孤立质点静止或作匀速直线运动。

二、惯性参考系举例说明：惯性定律在某些参考系是不成立的。

实验表明：在一个参考系中，只要某个物体符合惯性定律，则其它的物体都服从惯性定律。

惯性参考系：惯性定律成立的参考系惯性不是个别物体的性质，而是参考系、或者说是一种时空特性。

由于地球虽然也旋转，但很慢，研究范围不大（例大气环流范围太大）可近似为惯性系，即实验室参考系可视为惯性系。

讨论大范围、长时间的物理过程时，可另选惯性系，例：大气、海洋环流，人造卫星（地球卫星）运动，以地心——恒星为惯性系，讨论行星天体运动时，以日心——恒星参考系为惯性系。

若有一个参考系为惯性系，由伽利略变换知道，彼此间作匀速直线运动的其它参考系惯性定律都成立。

所以发现一个惯性系便有无穷多个惯性系。

v dt dxt d x d vtx x -=''-=' y y =' dtdydt y d ='t t ='dtdzdt z d =' （在一个惯性系静止或作匀速直线运动，在运动参考系内也作静止或匀速直线运动）§3.2 惯性质量、动量和动量守恒定律历史上对于质量概念的认识过程：17世纪提出质量，即“物质之量”—衡量物质之量的多少—从原子论角度看，原子数 牛顿：把“质量”与“物质之量”视为同意语使用19世纪下半叶：马赫提出质量概念的操作定义，定义了质量（即惯性质量），区分了质量与物质的量（mol ）。

大学物理-第三章-动量守恒定律和能量守恒定律

大学物理-第三章-动量守恒定律和能量守恒定律

20
★一对作用力与反作用力的功只与相对位移有关
f ji
ri

f ij

rij

rj
0


dW
jidWij

f
ji
dri
fij drj
f ji fij


fji f ji
(dd(rriidrrjj))

f ji
drij
S
S u
动量的相 对性和动量定 理的不变性
F(t)
t1 m
v1
光滑
v 2
m t2
参考系 t1 时刻 t2 时刻
动量定理
S系
S’系
mv1
mv2
m(v1 u) m(v2 u)
t2 t1
F (t )dt

mv2

mv1
5
例3-1: 作用在质量为1kg 的物体上的力 F=6t+3,如果物体在这
0＝m1(v1+v2)+m2v2
v2


m1v1 m1 m2
x
t 0
v2dt
m1 m1 m2
t 0
v1dt
L
t
0 v1dt
x m1L 0.8m m1 m2
负号表示船移动的方向与人前进的方向相反。
17
3-４ 动能定理
一、功的概念(work) 功率(power) 1、恒力的功
2、动能定理
2
1
或
F

dr
F

dr

1 2
mv22

第三章牛顿运动定律

第三章牛顿运动定律

第三章牛顿运动定律·动量守恒定律习题解答3.5.1质量为2kg的质点的运动方程为r=(6t2-10)i+(3t2+3t+10)j（t为时间，单位为s;长度单位为m）求证质点受恒力而运动，并求力的大小方向．解：运动学方程为恒矢量。

3.5.2质量为m的质点在Oxy平面内运动，质点的运动方程为r=acoswt i+bsinwt ja,b,w为正常数，证明作用于质点的合力总指向原点．解：运动学方程则与方向相反指向原点。

3.5.3在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷粒,一方面逐出秸杆,筛面微微倾斜,是为了从较低的一边将知杆逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才可能将谷粒筛出,若谷粒与得到面静摩擦系数为0.4,问得到沿水平方向的加速度至少多大才能使谷粒和得到面发生相对运动.解：摩擦力满足μmg ≤ ma则 a 至少为μg=0.4*9.8m/s2才能使它们发生相对运动。

3.5.4桌面上叠反放着两块木版，质量各为m1,m2,如图所示m2和桌面的摩察系数为μ2，m1和m2间的静摩察系数为μ1．沿水平方向用多大的力才能把下面的木版抽出来．解：研究对象分别为<m1><m2>坐标系：o-xy受力分析：m1: m2: 列方程坐标分量式①②③④联立解得：只有a2x≥ a1x 时,才能抽出。

3.5.5质量为m2的斜面可在光滑水平面上运动，斜面倾角为a，质量为m1的小球与斜面之间亦无摩察，求小球相对于斜面的加速度及其对斜面的压力．解：研究对象分别为<m1><m2>坐标系：o-xy受力分析：m1:m2:列方程坐标分量式①②③④由相对运动：投影：解得：3.5.6在图示的装置中两物体的质量各为m1,m2．物体之间及物体与桌面的间摩察系数都为μ．求在力F的作用下两物体加速度及其绳内张力．不计滑轮和绳的质量及轴承摩察，绳不可伸长．解：研究对象分别为<m1><m2>坐标系：o-x受力分析： m1:m2:列方程坐标分量式①②③3.5.7在图示的装置中,物体A,B,C 的质量各为m1,m2,m3且两两不相等,若物体A,B 与桌面间的摩擦系数均为μ,求三个物体的加速度及绳内的张力,不计绳和油轮质量,不计轴承摩擦.绳不可伸长.解：研究对象分别为<m1><m2><m3> 坐标系：o-xy 受力分析：m1:m2:m3:列方程T1= T1′= T2 = T2′= T 坐标分量式①②③辅助方程：（绳子的总长度一定）3.5.8天平左端挂一定滑轮,一轻绳跨过滑轮,绳的两端分别系上质量为m1,m2的物体(m1≠m2).天平右端的托盘内放有砝码.问天平托盘和砝码共重若干诸能保持天平平衡?不计滑轮和绳的质量及轴承摩擦,绳不伸长.解：研究对象分别为<m1><m2>坐标系：o-xm1:受力分析：m2:列方程坐标分量式①②绳不伸长，解得：于是天平左端受力大小为 2T右端的砝码和托盘重为：3.5.9跳伞运动员初张伞时的速度为,阻力大小与速度平方成正比:,人伞总质量为m,求的函数(提示:积分时可利用式.)解：,积分时变为则则则3.5.10一巨石与斜面因地震而分裂,脱离斜面下滑至水平石面之速度为v0,求在水平面上巨石速度与时间的关系,摩擦系数为(注:不必求v 作为t的显函数).解：在水平面上，t=0,则3.5.11棒球质量为0.14kg,用棒击棒球的力随时间的变化如图所示,设棒被击前后速度增量大小为70m/s.求力的最大值,打击时,不计重力.解：0 - 0.05s内：F=20Fmaxt0.05-0.08s内：F=Fmax（8-100t）冲量：=0.025Fmax+0.015Fmax=0.04 Fmax动量的增量：∴Fmax=245N3.5.12沿铅直向上发射玩具火箭的推力随时间变化如图所示．火箭的质量为2kg，t=0时处于静止．求火箭发射后的最大速率和最大高度（注意，推力＞重力时才起动）．解：由动量守恒：F > mg 时才起动，，t = 4 s 时F = mg时间应从t > 4 s 开始。

第三章 运动的守恒定律

第三章 运动的守恒定律

则
yg dyv
m2
O
dt
两边同乘以 y d y 则
m1
y
y2gdy ydy dyv yv dyv
dt
y
g y y2 d y yv yv dyv
0
0
1 gy 3 1 yv2
3
2
v
2
gy
1 2
3
3讨–1论质：点和质点系的动量定理 第三章动量守恒定律和能量守恒定律
仅对 y 长的m1而言：a g
例如人从高处跳下、飞机与鸟相撞、打桩等碰撞事件中，
作用时间很短，作用力的变化很大，这种力称为冲力。
mv
mv1
mv2
F
t2 t1
F Fdt
mv2
mv1
t2 t1
注意
在 t2p一t1定时，
F
Fm
F
o tt11
t
t2
t 越小，则 F 越大 .
3–1 质例点1和质一点质系量的为动0.0量5k定g、理速第率三为章动10量m守·恒s-1定的律钢和能球量,守以恒与定律
F m1g yg
T 0
因为 T 的反作用力（ –T）要拉动上面一段链条 dm ，
（-T ）的冲量等于dm 动量的增量。T
m2
F T m1a
O
yg T ya
m1 y
m1
y
ag
y F
3质–1点质系点动和量质定点理系的t动t0 量i 定F理i dt第三章动i 量守p恒i 定律和i 能量p守i0恒定律
(mv)
dt
（质点动量定理的微分形式）
t2
Fdt
t1
冲量 :
v2 v1
mdv
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

——质点系的总动量。 质点系动量定理的积分形式： t1 I Fi dt pi p0 i
t0 i i i
合外力的冲量等于质点系动量的增量，与 内力无关。
例 一辆装煤车以v =3m/s的速率从煤斗下面通过，每秒落入 车厢的煤为m=500kg。若使车厢的速率保持不变，应用多大 的力拉车厢？
物体相互碰撞时， 动量可以在物体间 相互传递，但必须 保持总动量守恒
牛顿摆--法国物理学家伊丹· 马略特
（3）动量守恒式的分量形式：
m v
i
ix
常量
if
if
if
F
i
i
ix
0
0
0
m v
i i
i i
i
iy
iz
常量
常量
F
i
iy
m v
F
iz
当系统在某一方向上合外力为零时，则此 方向上动量守恒。 此时总动量不一定守恒 （4）反冲运动中的动量守恒 （5）动量守恒律在近代物理学中的意义
第三章 动量守恒定律 和能量守恒定律
牛顿三定律给出了“力”的完整定义
力学图景：
力作用于物体，使其在时空中运动
力的时间瞬时效应
牛顿第二定律
三种效应：
力的空间累积效应
能量的概念
力的时间累积效应
动量的概念
§3.1 质点的动量定理
一、冲量和动量 1.力的冲量： 力和作用时间的乘积 ——力对时间的累积效应。
——航天先驱齐奥尔科夫斯基（K.E.
Tsiolkovsky, 1857-1935）
火箭最初质量为m0， 燃料烧完后 火箭的质量为m1 ，火箭最终速度决定 于两者的比值。 单级火箭不能使航天器的最终速度 达到第一宇宙速度. 所以，必须有多级 火箭技术和捆绑火箭技术.
神 舟 七 号 载 人 飞 船
万虎：明代官员，锦衣卫 都指挥使. 他是“第一个企图利用火箭 飞行的人。他用47只最大的火 箭绑在椅子背后，手拿两个大 风筝，想借助火箭的推力和风 筝上升的力量飞向空中。 1970年国际天文学会为了纪 念他，把月球背面的一个环行 山命名为“万虎环行山”。
生活中的碎花瓶理论
雅各布·博尔
丹麦
“雅各布· 博尔定律”：打碎后的物体的碎片按重量的数量 级分类，不同数量级间的表现为统一的倍数关系。花瓶或茶杯 状的物体倍数为16，棒状物约为11，球体则约为40。 约翰· 巴比克
美国
1935年成立了专门从事黏合剂研制生产的BBK公司。 如果用一个完整的玻璃瓶或瓷瓶做花瓶，它只能盛满一缕 缕花朵的芬芳和郁香。而一个人的心灵一旦摔不碎，什么样的 碎片都可能成为他生命的花瓣，飘逸出穿透岁月的清香。 苹果成全了牛顿，茶壶成全了瓦特，花瓶也同样成就了一些人 ；机遇只给那些有准备的人，世界也属于有心人的世界。
答：因为鸡蛋和薄板间的摩擦力很小，若棒打击 时间很短， Ff t 0, p 0 所以鸡蛋就 蛋 掉在杯中.
例 一质量m=140g的垒球，以v=40ms-1的速率沿水平 方向飞向击球手，被击后它以相同的速率沿° 的仰角飞出。求垒球受到的平均打击力。设球和棒 的接触时间t=1.2ms。
则平均冲力
mv 2
)θ
2mv cos 3 F 8 . 1 10 N 大小 t
方向
mv1
)
30
动量定理的应用
? 2、处理变质量物体的运动：
设某物体在 t 时刻质量为 m，速度为 另一质元 dm，以速度 u 运动，在 t+dt 时刻， dm与 m 合并，共同速度为 : v d v 并且在t~t+dt 时间内，有外力 F作用在系统上，求系统运动 规律?
F 1.5 10 ( N )
3
由动量定理：
动量守恒定律
若质点系所受的合外力 Fi 0
则 p mi vi const.
i
i
即：若质点系所受合外力为零，其动量守恒。 讨论 （1）内力不会影响系统的总动量，但可使系统内的 动量一个质点转移到另一个质点。 （2）动量守恒律是牛顿第二、三定律的直接结果； 是空间平移不变性的物理表现。
fdt 0 (vdt )v
地面受力
2m(l h) g f v v f' dt L m F f ' ml g (3l 2h) g L
2
vdt
§3.2 质点系的动量定理和动量守恒定律
质点系：由多个质点组成的系统。
内 外 力：系统内质点间的相互 作用力。 力：系统外物体对质点系的 作用力。 质点系 内力 外力 m1 m2 作用时间 f2 f 1 动量变化 F1 F2
可得： ( F1 F2 )dt d ( p1 p2 )
质点系动量定理的微分形式:
式中： F F1 F2 Fi
Fdt dP
——质点系所受的合外力。 P p1 p2 pi
v，
dm u
dt
u 和 v 分别为
m+dm
m
v
F
vd v
它们相对于地 面的速度
由动量定理：(m dm)(v dv) (mv udm) Fdt dv dm m ( v u) F dt dt
dv dm m vr F dt dt
3
Fy 4.0 103 N
F F F 8.1 10 N
3
arctan
Fy Fx
30
另解 由动量定理：
Ft mv 2 mv1
作矢量三角形如图，求出力的冲量
F t 。 F t
大小 Ft 2mv cos F t 30 方向 2
解 y 取坐标， 由动量定理的分量式：
v2 v1
x
2 x 2 y
F
Fx t mv 2 x mv1 x Fy t mv 2 y mv1 y
Fx t mv cos mv cos
o
Fy t mv sin mv sin
Fx 7.0 10 N
v r 为m相对于 dm的速度
[例1] 已知 M ，m， h，绳拉紧瞬间，绳与m、M 之 间的相互作用时间为t，求：绳子拉紧后，M 与 m 的共同的速度大小。(不计滑轮的质量) [解] 分析物体受力及运动情况：
T
v
M
x
T
m
v0
M
m
h
v
Mg
o
mg
M： (T Mg )t Mv 0 m：(T
mg )t mv (mv0 )
v 0 2 gh
m v 2 gh M m
M
m
h
[练习]一质点受合外力作用，外力为
2 F 10ti 2(2 t ) j 3t k (SI)
求此质点从静止开始在2s内所受合外力的冲量 和质点在2s末的动量。
解： 由冲量定义有 2 2 2 I Fdt 0 [10ti 2( 2 t ) j 3t k ]dt
说明
f1
m1
m2
f2
m1 v 1 m1 v 10 f1 t m2 v 2 m2 v 20 f 2 t
f1 f 2
m1 v 1 m1 v10 m2 v 2 m2 v 20
m1 v 1 m2 v 2 m1 v10 m2 v 20
2 2 2 10tdti 2(2 t )dtj 3t dtk 0 0 0 20i 4 j 8k N s 根据动量定理 I t t pt 2 p0 pt 2 pt 2 20i 4 j 8k N s
世界最强大的战列舰 “衣阿华”号9门主炮右 舷顺次射击，据称可导 致这艘排水量45000吨的 庞然大物侧移10米。
2011年在阿富汗南部坎大 哈省，美军野战队士兵在 前哨基地向本杰瓦尔地区 的火力基地发射榴炮弹 。
反冲运动：
当一个物体向某一方 向射出它的一部分时 ，这个物体的剩余部 分将向相反方向运动
dI Fdt
I

t2
t1
Fdt
2.质点的动量：质点的质量和速度的乘积
p mv
二、动量定理 设质点作任意曲线运动，有
Fdt dp ——动量定理的微分形式 t2 p2 对上式积分 Fdt dp 得：
t1 p1
dv dp F ma m dt dt
风 v1 Δv v2
F横 帆
F帆对风 Δ v
（2）F 方向变化时，I 一般不与其方向同。
F2 t 2
F1t1
I
n I Fi t i
i 1
Fn t n
（3）动量定理的分量形式：

t2
t1 t2
Fx dt mv 2 x mv 1 x
I x p2 x p1 x

t2
t1
Fdt mv 2 mv1 或
I p2 p1
质点的动量定理： 合外力对质点的冲量等于质点动量的增量。
讨论：
I p2 p1
（1）冲量与动量的改变量相联系， 而不是动量本身。
“好船家会 使八面风 ”
“逆风行舟”
演示
逆风行舟
F风对帆
F进
v1 v2
I F ( t )dt
t1
t2
----平均冲力
F ( t 2 t1 )