Eviews数据统计与分析VAR模型和VEC模型-Johansen协整检验
- 格式：ppt
- 大小：336.50 KB
- 文档页数：25
下载文档原格式
合集下载
Johanson协整检验与VEC模型
():原则差；[ ]：t统计量
因为VEC模型旳体现式仅仅合用于协整序列，所以应先运营 Johansen协整检验，并拟定协整关系数。需要提供协整信 息作为VEC对象定义旳一部分。
假如要建立一种VEC模型，在VAR对象设定框中，从 VAR Type 中 选 择 Vector Error Correction项 。在 VAR Specification栏中，除了特殊情况外，应该提供与无约束 旳VAR模型相同旳信息
将 yt 旳协整检验变成对矩阵 旳分析问题，这就是 Johansen协整检验旳基本原理。因为矩阵 旳秩等于它旳
非零特征根旳个数，所以能够经过对非零特征根个数旳检验
来检验协整关系和协整向量旳秩。略去有关 旳特征根旳 求解措施，设矩阵 旳特征根为 1 2 … k。
Johansen协整检验旳两种形式 特征根迹检验(trace检验)
估计成果往往因为一般滞后阶数，协整向量旳形式不同而非常敏感，实际 中可综合考虑做出联合选择； 信息准则AIC,SC，协整向量旳平稳性检验可辅助模型旳选择
能够根据模型实现脉冲响应函数和方差分解，并分析变量之 间旳影响关系(需要自己重新建立模型进行操作)
2. VEC系数旳取得
对于VEC模型，系数旳估计保存在三个不同旳二维数 组中：A，B和C。A包括调整参数矩阵 ；B包括协整矩阵； C包括短期参数矩阵 （一阶差方项滞后旳系数）。
Johanson协整检验：Var预测.wfl 考察中国GDP,宏观消费cons与基本建设投资inves旳协整关系
Step1:数据处理----价风格整后旳对数数据记为lngp,lncp,lnip—VAR01
11 10
9 8 7 6 5 4
55
60
65 70 LNIP
因为VEC模型旳体现式仅仅合用于协整序列，所以应先运营 Johansen协整检验，并拟定协整关系数。需要提供协整信 息作为VEC对象定义旳一部分。
假如要建立一种VEC模型，在VAR对象设定框中，从 VAR Type 中 选 择 Vector Error Correction项 。在 VAR Specification栏中，除了特殊情况外，应该提供与无约束 旳VAR模型相同旳信息
将 yt 旳协整检验变成对矩阵 旳分析问题，这就是 Johansen协整检验旳基本原理。因为矩阵 旳秩等于它旳
非零特征根旳个数，所以能够经过对非零特征根个数旳检验
来检验协整关系和协整向量旳秩。略去有关 旳特征根旳 求解措施，设矩阵 旳特征根为 1 2 … k。
Johansen协整检验旳两种形式 特征根迹检验(trace检验)
估计成果往往因为一般滞后阶数，协整向量旳形式不同而非常敏感，实际 中可综合考虑做出联合选择； 信息准则AIC,SC，协整向量旳平稳性检验可辅助模型旳选择
能够根据模型实现脉冲响应函数和方差分解，并分析变量之 间旳影响关系(需要自己重新建立模型进行操作)
2. VEC系数旳取得
对于VEC模型，系数旳估计保存在三个不同旳二维数 组中：A，B和C。A包括调整参数矩阵 ；B包括协整矩阵； C包括短期参数矩阵 （一阶差方项滞后旳系数）。
Johanson协整检验：Var预测.wfl 考察中国GDP,宏观消费cons与基本建设投资inves旳协整关系
Step1:数据处理----价风格整后旳对数数据记为lngp,lncp,lnip—VAR01
11 10
9 8 7 6 5 4
55
60
65 70 LNIP
JOHANSEN协整检验分析
JOHANSEN协整检验分析
一．Johansen协整检验
Johansen协整检验是一种用于分析多个时间序列之间存在长期均衡关系的检验方法，它可以用来分析货币、公債、股票等多种不同投资组合的关系，以确定它们之间的长期协整关系的强度，从而为投资者判断投资选择提供依据和建议。
Johansen协整检验基于多元线性回归，检验方法对于估计或分析长期关系非常有效。
Johansen协整检验是一种基于统计学方法的检验，检验的目标是使用VAR模型来确定两个时间序列之间是否存在长期均衡。
它使用滞后期和序列之间的协整回归，对长期协整关系的强度作出定量分析。
在这种检验方法中，使用的模型具有较强的可伸缩性，可应用于多元时间序列，并且可以适当地处理突发事件和时变性等变化。
从一般上来说，以下四个假设是检验协整关系的基本要求：
1）至少有两个时间序列的观测值。
2）时间序列的模型均属于线性范畴。
3）任意两个时间序列的关系应该是多元的。
4）所观测到的时间序列应该是非竞争性的。
Johansen协整检验的基本步骤是：首先，将多个时间序列分别标准化；其次，将标准化的时间序列皆转化为一阶差分模型；然后，运用VAR 模型对差分模型进行估计；随后。
Johansen协整与VECM模型
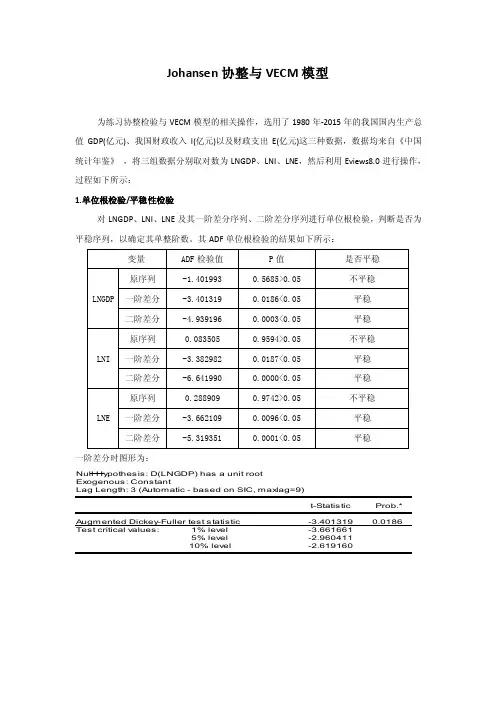
Johansen协整与VECM模型为练习协整检验与VECM模型的相关操作，选用了1980年-2015年的我国国内生产总值GDP(亿元)、我国财政收入I(亿元)以及财政支出E(亿元)这三种数据，数据均来自《中国统计年鉴》，将三组数据分别取对数为LNGDP、LNI、LNE，然后利用Eviews8.0进行操作，过程如下所示：1.单位根检验/平稳性检验对LNGDP、LNI、LNE及其一阶差分序列、二阶差分序列进行单位根检验，判断是否为平稳序列，以确定其单整阶数。
其ADF单位根检验的结果如下所示：一阶差分时图形为：从上述的检验结果中可以看出，原水平序列LNGDP 、LNI 和LNE的ADF 检验的P值都大于0.05，表现出非平稳特征。
而LNGDP 、LNI 和LNE一阶差分以及二阶差分的ADF检验的P值均小于0.05，表现出平稳特征，说明LNGDP 、LNI 和LNE的一阶差分就都已经是平稳序列，即LNGDP、LNI、LNE序列是一阶单整的，LNGDP~I(1)，LNI~I(1)，LNE~I(1)。
所以LNGDP序列、LNI序列和LNE序列是同阶单整的，因此具备了进行协整检验的条件。
2.Johansen协整（检验是否存在协整）（1）选择最优滞后期，则做VAR模型，而因为是年度数据，以3位最大滞后期数，进行实验，结果图如下：从上表打“*”处可知最优滞后期为3.（2）以最优滞后期3进行Johansen协整检验，结果如下由于当无协整时，p值为0.0004，小于0.05，拒绝原假设，所以看下一个；当有一个协整的时候，p值为0.0743，大于0.05，则接受原假设，所以存在一个协整关系。
3.VECM模型结果图如下：则最终结果为：(1)D(LNGDP t )=0.053123e t-1+1.050628DLNGDP t-1-0.373339DLNGDP t-2-0.527039DLNI t-1-0.378157DLNI t-2+ 0.457048DLNE t-1+0.372008DLNE t-2+ε1t(2)D(LNI t )=0.079927e t-1+0.260644DLNGDP t-1-0.386477DLNGDP t-2-0.064574DLNI t-1-0.566409DLNI t-2+ 0.812482DLNE t-1+0.373086DLNE t-2+ε2t(3)D(LNE t )=0.123095e t-1+0.158764DLNGDP t-1-0.422963DLNGDP t-2-0.129041DLNI t-1-0.410100DLNI t-2+ 0.872030DLNE t-1+0.100550DLNE t-2+ε3t4.补充内容VAR 模型的脉冲响应函数图Response of LNGDP to LNGDPResponse of LNGDP to LNIResponse of LNGDP to LNEResponse of LNI to LNGDPResponse of LNI to LNIResponse of LNI to LNEResponse of LNE to LNGDPResponse of LNE to LNIResponse of LNE to LNEResponse to Cholesky One S.D. Innovations ?2 S.E.以第一行第三图举例说明：Response of LNGDP to LNE 指来自于财政支出E 的一个标准差的冲击对国内生产总值的影响。
eviews协整检验协整方程
在EViews中进行协整检验和估计协整方程可以按照以下步骤进行：1. 导入数据：-打开EViews软件，选择"File" -> "Open"，导入需要进行协整检验的时间序列数据。
2. 创建VAR（向量自回归）模型：-选择"Quick/Estimation"或"Object/New Object"，然后选择"VAR"，创建一个新的VAR对象。
-在VAR对话框中，选择要包含在模型中的所有变量，并指定滞后阶数(lags)和其他选项。
-点击"OK"以创建VAR模型。
3. 进行协整检验：-在VAR对象上右键单击，选择"View/Residual Diagnostics"，打开模型诊断窗口。
-在模型诊断窗口中，选择"Tests"选项卡，在下拉菜单中选择"Engle-Granger Cointegration Test"。
-确定要检验的变量组合，点击"OK"进行协整检验。
结果将显示在输出窗口中。
4. 估计协整方程：-如果协整检验结果表明存在协整关系，可以进行协整向量估计。
-在VAR对象上右键单击，选择"View/Cointegrating Vectors"，打开协整向量窗口。
-在协整向量窗口中，选择所需的变量组合，并点击"OK"进行估计。
结果将显示在输出窗口中。
需要注意的是，以上步骤仅为一般性指导，具体操作可能因数据和研究目的而有所调整。
在使用EViews进行协整检验和估计协整方程时，建议参考EViews用户手册或相关教程以获取更详细的操作指导。
eviews操作实例-向量自回归模型VAR和VEC
-4.3194
-5.4324 -5.7557
5% 临界值
-2.9202 -2.9202 -2.9202
模型形式 （C t p）
(c 0 3) (c 0 0) (c 0 0)
DW值
1.6551 1.9493 1.8996
结论
LGDPt ～I(1) LCt ～I( 1)
LIt～I(1)
注 C为位移项， t为趋势，p为滞后阶数。
yNt
的最大p阶滞后变量为解释变量的方程组模型，方程组模 型中共有N个方程。显然，VAR模型是由单变量AR模型推广到 多变量组成的“向量”自回归模型。
对于两个变量（N=2），Yt ( yt xt )T 时，VAR(2)模型为
2
Yt iYti Ut 1Yt1 2Yt2 Ut i 1
6
用矩阵表示：
xt
121 yt1
122xt1
221yt2
222xt2
u2t
显然，方程组左侧是两个第t期内生变量；右侧分 别是两个1阶和两个2阶滞后应变量做为解释变量，且 各方程最大滞后阶数相同,都是2。这些滞后变量与随 机误差项不相关（假设要求）。
7
由于仅有内生变量的滞后变量出现在等式的 右侧，故不存在同期相关问题，用“LS”法估计 参数，估计量具有一致和有效性。而随机扰动列 向量的自相关问题可由增加作为解释应变量的滞 后阶数来解决。
3
政策分析。但实际中，这种模型的效果并不令人满 意。
联立方程组模型的主要问题：
（1）这种模型是在经济理论指导下建立起来的结构模型 。遗憾的是经济理论并不未明确的给出变量之间的动态关 系。
（2）内生、外生变量的划分问题较为复杂； （3）模型的识别问题，当模型不可识别时,为达到可识别 的目的，常要将不同的工具变量加到各方程中，通常这种 工具变量的解释能力很弱； （4）若变量是非平稳的（通常如此），则会违反假设， 带来更严重的伪回归问题。
-5.4324 -5.7557
5% 临界值
-2.9202 -2.9202 -2.9202
模型形式 （C t p）
(c 0 3) (c 0 0) (c 0 0)
DW值
1.6551 1.9493 1.8996
结论
LGDPt ～I(1) LCt ～I( 1)
LIt～I(1)
注 C为位移项， t为趋势，p为滞后阶数。
yNt
的最大p阶滞后变量为解释变量的方程组模型，方程组模 型中共有N个方程。显然，VAR模型是由单变量AR模型推广到 多变量组成的“向量”自回归模型。
对于两个变量（N=2），Yt ( yt xt )T 时，VAR(2)模型为
2
Yt iYti Ut 1Yt1 2Yt2 Ut i 1
6
用矩阵表示：
xt
121 yt1
122xt1
221yt2
222xt2
u2t
显然，方程组左侧是两个第t期内生变量；右侧分 别是两个1阶和两个2阶滞后应变量做为解释变量，且 各方程最大滞后阶数相同,都是2。这些滞后变量与随 机误差项不相关（假设要求）。
7
由于仅有内生变量的滞后变量出现在等式的 右侧，故不存在同期相关问题，用“LS”法估计 参数，估计量具有一致和有效性。而随机扰动列 向量的自相关问题可由增加作为解释应变量的滞 后阶数来解决。
3
政策分析。但实际中，这种模型的效果并不令人满 意。
联立方程组模型的主要问题：
（1）这种模型是在经济理论指导下建立起来的结构模型 。遗憾的是经济理论并不未明确的给出变量之间的动态关 系。
（2）内生、外生变量的划分问题较为复杂； （3）模型的识别问题，当模型不可识别时,为达到可识别 的目的，常要将不同的工具变量加到各方程中，通常这种 工具变量的解释能力很弱； （4）若变量是非平稳的（通常如此），则会违反假设， 带来更严重的伪回归问题。
Eviews数据统计与分析教程8章 时间序列模型-协整理论
EViews统计分析基础教程
三、随机过程
分类：
•白噪声（White Noise）过程
•随机游走（Random Walk）过程。
EViews统计分析基础教程
三、随机过程
分类： 白噪声过程 白噪声过程是指，对于随机过程{xt,t∈T}，如果 E (xt) = 0 Var(xt)= σ2< ∞ Cov (xt，xt+-s) =0 其中，t∈T，（t+s）∈T，s≠0，此时{xt}为白噪声过程。 白噪声过程是平稳的随机过程，其均值为0，方差为常数， 随机变量间不相关。白噪声源于物理学，指功率谱密度在整 个频域内均匀分布的噪声。
EViews统计分析基础教程
四、时间序列模型的分类
3、自回归移动平均（ARMA）模型
自回归移动平均模型是由自回归模型AR（p）和移动平均模 型MA（q）共同组成的随机过程，因而也被称为混合模型， 记作ARMA（p, q）。其表达式为 xt =c+1xt-1 + 2 xt-2 + …+p xt-p+ ut +β1 ut-1 +β2 ut-2 + …+βqut –q 其中，p和 q分别表示自回归模型和移动平均模型的最大阶 数。当p=0时，自回归移动平均模型ARMA（0, q）= MA （q）；当q=0时，自回归移动平均模型ARMA（p, 0）= AR （p）。
EViews统计分析基础教程
四、时间序列模型的分类
2、移动平均（MA）模型 时间序列{xt }的q阶移动平均（MA，Moving Average）模型 的表达式为 xt = c + ut +β1 ut -1 +β2 ut -2 + … +βq ut –q 其中，参数c为常数；β1，β2，…，βq为移动平均模型的系 数，是模型的待估参数；q为移动平均模型的阶数；ut为白 噪声序列，其均值为0，方差为σ2。称xt为q阶移动平均过程， 用MA（q）表示。 时间序列{xt }由1个ut和q个ut的滞后项加权的和组成， “移动”是指时间t的变化，“平均”指的是ut滞后项的加权 和。
Eviews11章VAR模型和VEC模型讲课讲稿
பைடு நூலகம்1.0
0.5
0.0
-0.5
-1.0
-1.5 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5
VAR模型中AR根的图
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立 VAR模型的滞后结构检验 （2）Granger因果检验 Granger因果检验的 原假设是 H0：变量x不能Granger引起变量y 备择假设是 H1：变量x能Granger引起变量y
EViews统计分析基础教程
一、向量自回归（VAR）模型
4. VAR模型的检验 VAR模型的滞后结构检验 （1）AR根的图与表 如果VAR模型所有根模的倒数都小于1，即都在单位圆内， 则该模型是稳定的；如果VAR模型所有根模的倒数都大于1， 即都在单位圆外，则该模型是不稳定的。如果被估计的VAR 模型不稳定，则得到的结果有些是无效的。
EViews统计分析基础教程
一、向量自回归（VAR）模型
2.结构VAR模型（SVAR）
结构VAR是指在模型中加入了内生变量的当期值，即解释变 量中含有当期变量，这是与VAR模型的不同之处。 下面以两变量SVAR模型为例进行说明。
xt=b10 + b12zt +γ11xt-1 +γ12 zt-1 + μxt zt=b20 + b21xt +γ21xt-1 +γ22 zt-1 + μzt 这是滞后阶数p=1的SVAR模型。其中，xt和zt均是平稳随机 过程；随机误差项μxt和μzt是白噪声序列，并且它们之间不相 关。系数b12表示变量的zt的变化对变量xt的影响；γ21表示xt-1 的变化对zt的滞后影响。该模型同样可以用如下向量形式表 达，即
0.5
0.0
-0.5
-1.0
-1.5 -1.5 -1.0 -0.5 0.0 0.5 1.0 1.5
VAR模型中AR根的图
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立 VAR模型的滞后结构检验 （2）Granger因果检验 Granger因果检验的 原假设是 H0：变量x不能Granger引起变量y 备择假设是 H1：变量x能Granger引起变量y
EViews统计分析基础教程
一、向量自回归（VAR）模型
4. VAR模型的检验 VAR模型的滞后结构检验 （1）AR根的图与表 如果VAR模型所有根模的倒数都小于1，即都在单位圆内， 则该模型是稳定的；如果VAR模型所有根模的倒数都大于1， 即都在单位圆外，则该模型是不稳定的。如果被估计的VAR 模型不稳定，则得到的结果有些是无效的。
EViews统计分析基础教程
一、向量自回归（VAR）模型
2.结构VAR模型（SVAR）
结构VAR是指在模型中加入了内生变量的当期值，即解释变 量中含有当期变量，这是与VAR模型的不同之处。 下面以两变量SVAR模型为例进行说明。
xt=b10 + b12zt +γ11xt-1 +γ12 zt-1 + μxt zt=b20 + b21xt +γ21xt-1 +γ22 zt-1 + μzt 这是滞后阶数p=1的SVAR模型。其中，xt和zt均是平稳随机 过程；随机误差项μxt和μzt是白噪声序列，并且它们之间不相 关。系数b12表示变量的zt的变化对变量xt的影响；γ21表示xt-1 的变化对zt的滞后影响。该模型同样可以用如下向量形式表 达，即
VAR模型、Johansen协整检验在eviews中的具体操作步骤及结果解释
式中，lnl(p)和 lnl(p+i)分别为VAR(p)和
VAR(p+i)模型的对数似然函数值；f为自由度。 用对数似然比统计量LR确定P的方法用案例说
明。
13
案例1 我国1953年～2004年支出法国内生产总
值（GDP）、最终消费（Ct）和固定资本形成总额（It） 的时序数据列于D8.1中。数据来源于《中国统计年鉴》 各期。
9
（2）VAR模型对参数不施加零约束 （如t检 验）；
（3）VAR模型的解释变量中不含t期变量，所 有与联立方程组模型有关的问题均不存在；
（4）VAR模型需估计的参数较多。如VAR模型 含3个变量（N=3），最大滞后期为p=2，则有 PN2=2×32=18个参数需要估计；
（5）当样本容量较小时，多数参数估计的精 度较差，故需大样本，一般n>50。
f=VAR(3) 估计参数个数-VAR(1)估计参数 个数 332 132 18 。
20
利用Genr命令可算得用于检验原假设是否 成立的伴随概率 P：
p=1-@cchisq(42.4250,18) =0.000964
故 P=0.000964< =0.05，应拒绝原假设
，建立VAR(3)模型。
3
政策分析。但实际中，这种模型的效果并不令人满 意。
联立方程组模型的主要问题：
（1）这种模型是在经济理论指导下建立起来的结构模型 。遗憾的是经济理论并不未明确的给出变量之间的动态关 系。
（2）内生、外生变量的划分问题较为复杂； （3）模型的识别问题，当模型不可识别时,为达到可识别 的目的，常要将不同的工具变量加到各方程中，通常这种 工具变量的解释能力很弱； （4）若变量是非平稳的（通常如此），则会违反假设， 带来更严重的伪回归问题。
VAR(p+i)模型的对数似然函数值；f为自由度。 用对数似然比统计量LR确定P的方法用案例说
明。
13
案例1 我国1953年～2004年支出法国内生产总
值（GDP）、最终消费（Ct）和固定资本形成总额（It） 的时序数据列于D8.1中。数据来源于《中国统计年鉴》 各期。
9
（2）VAR模型对参数不施加零约束 （如t检 验）；
（3）VAR模型的解释变量中不含t期变量，所 有与联立方程组模型有关的问题均不存在；
（4）VAR模型需估计的参数较多。如VAR模型 含3个变量（N=3），最大滞后期为p=2，则有 PN2=2×32=18个参数需要估计；
（5）当样本容量较小时，多数参数估计的精 度较差，故需大样本，一般n>50。
f=VAR(3) 估计参数个数-VAR(1)估计参数 个数 332 132 18 。
20
利用Genr命令可算得用于检验原假设是否 成立的伴随概率 P：
p=1-@cchisq(42.4250,18) =0.000964
故 P=0.000964< =0.05，应拒绝原假设
，建立VAR(3)模型。
3
政策分析。但实际中，这种模型的效果并不令人满 意。
联立方程组模型的主要问题：
（1）这种模型是在经济理论指导下建立起来的结构模型 。遗憾的是经济理论并不未明确的给出变量之间的动态关 系。
（2）内生、外生变量的划分问题较为复杂； （3）模型的识别问题，当模型不可识别时,为达到可识别 的目的，常要将不同的工具变量加到各方程中，通常这种 工具变量的解释能力很弱； （4）若变量是非平稳的（通常如此），则会违反假设， 带来更严重的伪回归问题。
第十一章 向量自回归(VAR)模型和向量误差修正(VEC)模型 理论及EVIEWS操作
1.格兰杰因果性定义 2.格兰杰因果性检验 案例 五、 建立VAR模型 案例 六、利用VAR模型进行预测 案例 七、脉冲响应函数与方差分解 案例 八、向量误差修正模型 案例
2
一、VAR模型及特点
1. VAR模型—向量自回归模型
经典计量经济学中，由线性方程构成的联立方程 组模型，由科普曼斯（poOKmans1950）和霍德－科普曼 斯（Hood-poOKmans1953）提出。联立方程组模型在20 世纪五、六十年代曾轰动一时，其优点主要在于对每个方 程的残差和解释变量的有关问题给予了充分考虑，提出了 工具变量法、两阶段最小二乘法、三阶段最小二乘法、有 限信息极大似然法和完全信息极大似然法等参数的估计方 法。这种建模方法用于研究复杂的宏观经济问题，有时多 达万余个内生变量。当时主要用于预测和
第十一章 向量自回归 ( VAR) 模型和向量误差 修正 (VEC)模型
本章的主要内容：
（1）VAR模型及特点； （2）VAR模型中滞后阶数p的确定方法； （3）变量间协整关系检验； （4）格兰杰因果关系检验； （5）VAR模型的建立方法； （6）用VAR模型预测； （7）脉冲响应与方差分解； （8）VECM的建立方法。
明。
13
我国1953年～2004年支出法国内生产总 值（GDP）、最终消费（Ct）和固定资本形成总额（It） 的时序数据列于D8.1中。数据来源于《中国统计年鉴》 各期。
用商品零售价格指数p90（1990年=100）对GDP、 Ct和It进行平减，以消除物价变动的影响，并进行自然 对数变换，以消除序列中可能存在的异方差，得到新序 列： LGDPt=LOG(GDPt/p90t)； LCt=LOG(Ct/p90t)； LIt=LOG(It/p90t)。 GDP、 Ct和 It与LGDPt、 LCt和LIt的时序图分别示于 图11-1和图11-2，由图11-2可以看出，三个对数序列的 14 变化趋势基本一致，可能存在协整关系。
2
一、VAR模型及特点
1. VAR模型—向量自回归模型
经典计量经济学中，由线性方程构成的联立方程 组模型，由科普曼斯（poOKmans1950）和霍德－科普曼 斯（Hood-poOKmans1953）提出。联立方程组模型在20 世纪五、六十年代曾轰动一时，其优点主要在于对每个方 程的残差和解释变量的有关问题给予了充分考虑，提出了 工具变量法、两阶段最小二乘法、三阶段最小二乘法、有 限信息极大似然法和完全信息极大似然法等参数的估计方 法。这种建模方法用于研究复杂的宏观经济问题，有时多 达万余个内生变量。当时主要用于预测和
第十一章 向量自回归 ( VAR) 模型和向量误差 修正 (VEC)模型
本章的主要内容：
（1）VAR模型及特点； （2）VAR模型中滞后阶数p的确定方法； （3）变量间协整关系检验； （4）格兰杰因果关系检验； （5）VAR模型的建立方法； （6）用VAR模型预测； （7）脉冲响应与方差分解； （8）VECM的建立方法。
明。
13
我国1953年～2004年支出法国内生产总 值（GDP）、最终消费（Ct）和固定资本形成总额（It） 的时序数据列于D8.1中。数据来源于《中国统计年鉴》 各期。
用商品零售价格指数p90（1990年=100）对GDP、 Ct和It进行平减，以消除物价变动的影响，并进行自然 对数变换，以消除序列中可能存在的异方差，得到新序 列： LGDPt=LOG(GDPt/p90t)； LCt=LOG(Ct/p90t)； LIt=LOG(It/p90t)。 GDP、 Ct和 It与LGDPt、 LCt和LIt的时序图分别示于 图11-1和图11-2，由图11-2可以看出，三个对数序列的 14 变化趋势基本一致，可能存在协整关系。
VAR模型和VEC模型Johansen协整检验
VAR模型和VEC模型Johansen协整 检验
一、向量自回归（VAR）模型
4. VAR模型的检验 VAR模型的滞后结构检验 （1）AR根的图与表 如果VAR模型所有根模的倒数都小于1，即都在单位圆内， 则该模型是稳定的；如果VAR模型所有根模的倒数都大于1， 即都在单位圆外，则该模型是不稳定的。如果被估计的VAR 模型不稳定，则得到的结果有些是无效的。
一、向量自回归（VAR）模型
3. VAR模型的建立
VAR模型的滞后结构检验 （3）滞后排除检验 滞后排除检验（Lag Exclusion Tests） 是对VAR模型中的每一阶数的 滞后进行排除检验。如右图所示。 第一列是滞后阶数， 第二列和第三列是方程的χ2统计 量， 最后一列是联合的χ2统计量。
四、 Johansen协整检验
EViews操作 在 EViews 软 件 操 作 中 ， 选 择 VAR01 对 象 工 具 栏 中 的 “View”|“Cointegration Test…”选项，打开下图所示的协整检 验设定对话框。
检验
一、向量自回归（VAR）模型
3. VAR模型的建立
选择“Quick”|“Estimate VAR…”选项，将会弹出下图所示的 对话框。 该对话框包括三个选项卡，分别是“Basics”、 “Cointegration”和“VEC Restrictions”， 后两个选项卡在VEC模型操 作中使用。系统默认是“Basics” 选项卡。。
VAR模型和VEC模型Johansen协整 检验
四、Johansen协整检验
2、Johansen协整检验 （1）特征根迹（Trace）检验 （2）最大特征值检验
VAR模型和VEC模型Johansen协整 检验
四、Johansen协整检验
一、向量自回归（VAR）模型
4. VAR模型的检验 VAR模型的滞后结构检验 （1）AR根的图与表 如果VAR模型所有根模的倒数都小于1，即都在单位圆内， 则该模型是稳定的；如果VAR模型所有根模的倒数都大于1， 即都在单位圆外，则该模型是不稳定的。如果被估计的VAR 模型不稳定，则得到的结果有些是无效的。
一、向量自回归（VAR）模型
3. VAR模型的建立
VAR模型的滞后结构检验 （3）滞后排除检验 滞后排除检验（Lag Exclusion Tests） 是对VAR模型中的每一阶数的 滞后进行排除检验。如右图所示。 第一列是滞后阶数， 第二列和第三列是方程的χ2统计 量， 最后一列是联合的χ2统计量。
四、 Johansen协整检验
EViews操作 在 EViews 软 件 操 作 中 ， 选 择 VAR01 对 象 工 具 栏 中 的 “View”|“Cointegration Test…”选项，打开下图所示的协整检 验设定对话框。
检验
一、向量自回归（VAR）模型
3. VAR模型的建立
选择“Quick”|“Estimate VAR…”选项，将会弹出下图所示的 对话框。 该对话框包括三个选项卡，分别是“Basics”、 “Cointegration”和“VEC Restrictions”， 后两个选项卡在VEC模型操 作中使用。系统默认是“Basics” 选项卡。。
VAR模型和VEC模型Johansen协整 检验
四、Johansen协整检验
2、Johansen协整检验 （1）特征根迹（Trace）检验 （2）最大特征值检验
VAR模型和VEC模型Johansen协整 检验
四、Johansen协整检验
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立
选择“Quick”|“Estimate VAR…”选项，将会弹出下图所示的 对话框。 该对话框包括三个选项卡，分别是“Basics”、 “Cointegration”和“VEC Restrictions”， 后两个选项卡在VEC模型操 作中使用。系统默认是“Basics” 选项卡。。
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立
VAR模型的滞后结构检验 （4）滞后阶数标准
选择VAR对象工具栏中的“View”|“Lag Structure”|“Lag Length Criteria”选项，在弹出的对话框中输入最大滞后 阶数，然后单击“OK”按钮即可得到检验结果。
EViews统计分析基础教程
四、Johansen协整检验
1、Johansen协整理论
设变量y1t， y2t，…，ykt均是非平稳的一阶单整序列，即 yt~I(1)。xt是d维外生向量，代表趋势项、常数项等， yt=A1 yt-1 +A2 yt-2 +…+ Ap yt-p+B xt + μt 变量y1t， y2t，…，ykt的一阶单整过程I(1)经过差分后变 为零阶单整过程I(0)
EViews统计分析基础教程
四、 Johansen协整检验
EViews操作
在 EViews 软 件 操 作 中 ， 选 择 VAR01 对 象 工 具 栏 中 的 “View”|“Cointegration Test…”选项，打开下图所示的协整检 验设定对话框。
EViews统计分析基础教程
-1.0
-0.5
0.0
0.5
1.0
1.5
VAR模型中AR根的图
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立 VAR模型的滞后结构检验 （2）Granger因果检验 Granger因果检验的 原假设是 H0：变量x不能Granger引起变量y 备择假设是 H1：变量x能Granger引起变量y
在VAR对象的工具栏中选择“View”|“Lag Structure”|“AR Roots Table/ AR Roots Graph”选项，得到AR根的表和图。
EViews统计分析基础教程
一、向量自回归（VAR）模型
4. VAR模型的检验
VAR模型的滞后结 构检验 （1）AR根的图与 表
Inverse Roots of AR Characteristic Polynomial 1.5 1.0 0.5 0.0 -0.5 -1.0 -1.5 -1.5
EViews统计分析基础教程
一、向量自回归（VAR）模型
4. VAR模型的检验 VAR模型的滞后结构检验 （1）AR根的图与表 如果VAR模型所有根模的倒数都小于1，即都在单位圆内， 则该模型是稳定的；如果VAR模型所有根模的倒数都大于1， 即都在单位圆外，则该模型是不稳定的。如果被估计的VAR 模型不稳定，则得到的结果有些是无效的。
其中，yt为k维内生变量向量；xt为d维外生变量向量；μt是k 维误差向量A1，A2，…，Ap，B是待估系数矩阵。
EViews统计分析基础教程
一、向量自回归（VAR）模型
1.向量自回归理论
滞后阶数为p的VAR模型表达式还可以表述为
即
上式称为非限制性向量自回归（Unrestricted VAR）模型， 是滞后算子L的k ╳ k 的参数矩阵。 当行列式det[A(L)]的根都在单位圆外时，不含外生变量的非 限制性向量自回归模型才满足平稳性条件。
EViews统计分析基础教程
四、Johansen协整检验
1、Johansen协整理论
在VAR(p)模型中，设变量y1t， y2t，…，ykt均是非平 稳的一阶单整序列，即yt~I(1)。xt是d维外生向量，代 表趋势项、常数项等， yt=A1 yt-1 +A2 yt-2 +…+ Ap yt-p+B xt + μt 变量y1t， y2t，…，ykt的一阶单整过程I(1)经过差分后 变为零阶单整过程I(0)
EViews统计分析基础教程
四、Johansen协整检验
2、Johansen协整检验
（2）最大特征值检验 原假设为 Hr0：λr+1=0 备择假设为 H r 1：λr+1>0， 检验统计量为 r = - n· ln(1-λr+1) 其中， r是最大特征根统计量。 当 0< 临界值时，接受H00，没有协整向量； 当 0> 临界值时，拒绝H00，至少有一个协整向量； 当 1< 临界值时，接受H10，只有一个协整向量； 当 1> 临界值时，拒绝H10，至少有两个协整向量； … 当 r< 临界值时，接受Hr0，只有r个协整向量。
EViews统计分析基础教程
四、Johansen协整检验
1、Johansen协整理论
其中，Δyt和Δyt-j（j=1，2，…，p）都是由I(0)变量构成 的向量，如果 yt-1是I(0)的向量，即y1t-1，y2t-1，…， ykt-1之间具有协整关系，则Δyt是平稳的。
EViews统计分析基础教程
EViews统计分析基础教程
一、向量自回归（VAR）模型
2.结构VAR模型（SVAR）
结构VAR是指在模型中加入了内生变量的当期值，即解释变 量中含有当期变量，这是与VAR模型的不同之处。 下面以两变量SVAR模型为例进行说明。 xt=b10 + b12zt +γ11xt-1 +γ12 zt-1 + μxt zt=b20 + b21xt +γ21xt-1 +γ22 zt-1 + μzt 这是滞后阶数p=1的SVAR模型。其中，xt和zt均是平稳随机 过程；随机误差项μxt和μzt是白噪声序列，并且它们之间不相 关。系数b12表示变量的zt的变化对变量xt的影响；γ21表示xt-1 的变化对zt的滞后影响。该模型同样可以用如下向量形式表 达，即 B0 yt= 0 + 1 yt-1 + μt
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立
VAR模型的滞后结构检验 （3）滞后排除检验 滞后排除检验（Lag Exclusion Tests） 是对VAR模型中的每一阶数的 滞后进行排除检验。如右图所示。 第一列是滞后阶数， 第二列和第三列是方程的χ2统计 量， 最后一列是联合的χ2统计量。
EViews统计分析基础教程
四、Johansen协整检验
2、Johansen协整检验 （1）特征根迹（Trace）检验
（2）最大特征值检验
EViews统计分析基础教程
四、Johansen协整检验
2、Johansen协整检验
（1）特征根迹（Trace）检验 原假设为 Hr0：λr>0，λr+1=0 备择假设为 H r1：λr+1>0， r=1，2，…，k-1 检验统计量为
EViews统计分析基础教程
二、脉冲响应函数
脉冲响应函数（IRF，Impulse Response Function）分 析方法可以用来描述一个内生变量对由误差项所带 来的冲击的反应，即在随机误差项上施加一个标准 差大小的冲击后，对内生变量的当期值和未来值所 产生的影响程度。 在 EViews 软 件 操 作 中 ， 选 择 VAR 对 象 工 具 栏 中 的 “ View”|“Impulse Response…” 选项，或者直接点击 VAR对象工具栏中的“Impulse”功能键即可得到脉冲 响应函数的设定对话框。。
EViews统计分析基础教程
二、脉冲响应函数
“Display Information”中输入冲击变量（Impulses）和 脉冲响应变量（ Responses ）。这里可以输入内生变 量的名称，也可以输入变量的序号。 在“ Periods” 中输入显示的最长时期。“ Accumlated Responses” 为累积响应。对于稳定的 VAR 模型，脉冲 响应函数应趋于0，累积响应趋于非0常数。
EViews统计分析基础教程
一、向量自回归（VAR）模型
3. VAR模型的建立
在“VAR Type”中有两个选项： •“Unrestricted VAR”建立的是无约束的向量自回归模型，即 VAR模型的简化式； •“Vector Error Correction”建立的是误差修正模型。 “Estimation Sample”的编辑框中输入的是样本区间，当工 作文件建立好后，系统会自动给出样本区间。 “Endogenous Variables”中输入的是内生变量。 “Exogenous Variables”中输入的是外生变量，系统默认情 况下将常数项c作为外生变量。 “Lag Intervals for Endogenous”中指定滞后区间
EViews统计分析基础教程
二、脉冲响应函数
在脉冲响应函数的设定对话框中有两个选项卡： 一个是“Display”， 一个是“Impulse Definition”。 系统默认下打开的是“Display”选项卡。 其中，“ Display Format” 包含三种显示形式，“ Table” 表 格 形 式 ， “ Multiple Graphs” 多 个 图 形 式 ， “ Combined Graphs” 组 合 图 形 式 。 系 统 默 认 下 是 “Multiple Graphs”选项。
其中， r是特征根迹统计量。
EViews统计分析基础教程
四、Johansen协整检验
2、Johansen协整检验
（1）特征根迹（Trace）检验 当 0< 临界值时，接受H00，没有协整向量； 当 1> 临界值时，接受H10，至少有一个协整向量； 当 1< 临界值时，接受H10，只有一个协整向量； 当 1> 临界值时，拒绝H10，至少有两个协整向量； … 当 r< 临界值时，接受Hr0，只有r个协整向量。