高考数学压轴专题2020-2021备战高考《算法与框图》图文答案

、选择题 新数学复习题?算法与框图?专题解析1.执行下边的程序框图,如果输人的 N 10,那么输出的S♦1A. 1 一 2 10 1B. 1 一 2!3! 10! C. 1 1 2【答案】B 【解析】 1 11,1 D. 1 - 2!13!1 11!试题分析：第一次循环,得 1,S 1,k 2；第二次循环,得 3; 第三次循环, 1 -- ,S 3 2 1 -,S 1 时退出, 输出 1 ---- ,k 2 14 ;第四次循环,得 …,由此可推出当k 111 ---------十 .•.+ ---- 4 32 1 10 L1 1 2! 1 3!1 一 ,应选B. 10! 考点：程序框图.［开帏〕~* A. m m 2 B. m m 1C. m m 1 【答案】A 【解析】 【分析】D. m m 2根据程序运行,将每一 【详解】 对选项A, S 2,m S 4,m 6,那么 S S 8,m 8,那么 S 对选项B, S 2,m S 4, m 5 ,那么 S S 4,m 6,那么 S S 8,m 7,那么 S 对选项C, S 2,m S 4,m 3,那么 S 对选项D, S 2,mS 4,m 2 ,那么 S ,个选项代入试运行,算出其输出结果,从而选出答案4,那么 S 2 4 2 4;4 6 488 8 8 0,所以输出结果S 0,所以正确. 4,那么 S 2 4 2 4;4 5 4 4 4 6 4 88 7 88 4,那么 S 2 4 3 4 4 4,那么 S 20 ,输出结果S4 24；0 ,输出结果S4 2 4; 0,所以输出结果 8,所以不正确4,所以不正确 4 2 4 8 应选：A 【点睛】 此题考查程序框图中循环,考查补全程序结构,属于中档题 S 8,所以不正确八卦■ . ■ ■■ ■ ■ .■ .■ .■■■ ■ 一… 二进制 000 001 010 011■■■A十进制 0123B3.我国古代 伏羲八卦图〞中的八卦与二进制、十进制的互化关系如表,依据表中规律, A, B 处应分别填写〔 〕 A. 110、 6 B. 110、 12 C. 101、 5 D. 101、 10【答案】A【解析】【分析】根据八卦图的规律求得A处所填,然后通过二进制转化为十进制的公式,计算出B处所填. 【详解】根据八卦图的规律得到用处填「10, 110田=0 + 1 x 2 + 1 X 2? = 2+ 4 = 处应填写6.应选A.【点睛】本小题主要考查二进制和十进制的相互转化,考查中国古代数学文化,属于根底题^ 4.执行如下图的程序框图,那么输出的5是〔〕A. -3B. -1C. 1D. 3【答案】B【解析】【分析】根据框图可得程序是求数列lg- 的前999项的和再加上2,由n 1a n lg —n— lg n lg n 1可得到答案. n 1【详解】根据框图的运行可得：程序是2加上数列lg- 的前999项的和.n 1又a n lg —n— lg n lg n 1 n 1所以S 2+ lg1 lg2 lg3 lg3 L L lg999 lg10002 lg1 lg1000 23 1应选：B【点睛】此题考查程序框图中的循环和裂项相消法求和,属于中档题 ^5,以下各数中,最小的是() A. 101 010(2)B. 111(5)C. 32(8)【答案】C 【解析】101010 2 1 25 0 24 1 23 0 22 42 21 01115 1 521 511 5031___1__0 ___32 83 812 8° 26一_ _1-0-54 6 5 64 6 34故最小的是328 故答案选C6 .某程序框图如下图,其中【解析】【分析】运行该程序,当n 的值为2021时,满足判断框内的条件；当 n 的值为2021时,不满足判 断框内的条件,退出循环,输出 S 的值,结合选项可选出答案 . 【详解】 由题意, g nj—1——产 J n 1 Vn , n 1 . n运行该程序,输入S 0,n 1,判断框成立； 那么S 0 g 1J2 1 , n 2,判断框成立；D. 54(6)J2021 1 ,那么判断A. n 2021?【答案】A B. n 2021? C. n 2021? D. n 2021?框内应填入的条件为〔那么S嫄1 g 2 73 1, n 3,判断框成立；那么Sj3lg3 6l,n4,判断框成立；…贝US J2021 1, n 2021,判断框成立；那么S J2021 1, n 2021,判断框不成立,输出S J2021 1.故判断框内应填入的条件为n 2021?.应选：A【点睛】此题考查程序框图,考查学生的推理水平,属于中档题^7 .执行如下图的程序框图,那么输出的结果为(ff B r /,।A. 4 B, 5 C, 6 D, 7【答案】B【解析】【分析】模拟执行程序框图,只要根据程序框图规定的运算方法逐次计算,直到到达输出条件即可得到输出的m的值. 【详解】第一次循环,n = = L4二5 ；第二次循环,■"二,,・■」二丁第三次循环,H = 3ml = 7K =37 + 27=2315 > 500 ,退出循环,输出讯=7-2 = 5,应选B.【点睛】此题主要考查程序框图的循环结构流程图,属于中档题.解决程序框图问题时一定注意以下几点：〔1〕不要混淆处理框和输入框；〔2〕注意区分程序框图是条件分支结构还是循环结构；〔3〕注意区分当型循环结构和直到型循环结构；〔4〕处理循环结构的问题时一定要正确限制循环次数；〔5〕要注意各个框的顺序,〔6〕在给出程序框图求解输出结果的试题中只要根据程序框图规定的运算方法逐次计算,直到到达输出条件即可^1 2i 1 2i应选：B.【点睛】此题考查利用程序框图计算输出结果,同时也考查了裂项求和法的应用, 属于中等题8.执行如下图的程序框图,输出的结果为〔 C.B.A.— 19 【答案】B 【解析】 【分析】 211920 D.—21根据程序框图得出 _£4 22 1_ 102,利用裂项相消法可求得输出的S 的值. 【详解】由程序框图可知,输出的 S 的值为 1 S2— 4 12114 221 1 19 2110 211 2i 1 2i考查计算水平,A. i 1B. i 5C. i 5D. i 7【答案】B 【解析】 【分析】根据框图,模拟程序的运算即可求解 .【详解】由程序框图得,S J 3, i 1,满足条件得S ,3 6,i 3,满足条件得 S 43 $3 后, i 5 ,满足条件S ,3 J 3 73 G , i 7,否,输出S 的值,结束程序, 因此判断框应该是i 5 ,应选：B. 【点睛】此题主要考查了算法的程序框图,根本逻辑结构中的循环结构,属中档题 ^10 .运行如下图的程序框图,假设输出的S 的值为1011,那么判断框中可以填〔〕/幅出A /A. i 2021?B. i 2021? C i 2022? D. i 2023?【答案】C 【解析】 【分析】利用程序框图的功能,进行模拟计算即可. 【详解】Fin 一程序的功能是计算S= 1sin —+3sin— +5sin+—•••= 1 —3+5—7+9+…土2 2 2那么1011 = 1+505X2= 1 - 3+5- 7+9+ --那么第1011个奇数为2X 1011- 1 =2021不成立,第1012个奇数为2X 1012- 1 = 2023成立,故条件为i>2022?,应选C.【点睛】此题主要考查程序框图的应用,利用程序框图的功能是解决此题的关键,属于根底题11 .阅读如下图的程序框图,运行相应的程序,输出的5的值等于()s=i v1 —*I占中Ifi=n+lA. 30B. 31C. 62D. 63【答案】B【解析】【分析】首先确定流程图的功能,然后计算其输出的结果即可^【详解】由流程图可知该算法的功能为计算S= 1+21+22+23+2A的值,1 X (1 ^2S) 即输出值为：二二二 _ 1 _ _ ：.1 -2应选：B.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构.(2)要识别、运行程序框图,理解框图所解决的实际问题.(3)根据题目的要求完成解答并验证.12.运行如下图的程序框图,设输出的数据构成集合A,从集合A中任取一个元素那么函数y x a 在〔0,〕上是增函数的概率为〔〕【答案】A 【解析】 【分析】根据程序框图运行程序即可得到集合能的取值,根据古典概型概率公式计算可得结果 【详解】根据程序框图运行程序,输入 i 1,满足i 3,那么y 1, i 0,满足i 3； 那么y 0, i 1 ,满足i3;那么y 3, i 2 ,满足i3 ;那么y8, i3,不满足i 3,框图运行结束, A 1,0,3,8.a -2 1当a 3或8时,y x 在0, 上是增函数, 所求概率p — —.4 2应选：A . 【点睛】此题以程序框图和备函数单调性为载体,考查了古典概型概率问题的求解；关键是能够熟 练掌握哥函数的解析式与该函数在第一象限内图象单调性之间的关系^C.-D.A ,根据哥函数单调性可确定满足条件的 a 的所有可13.执行如下图的程序框图,输出的值为〔A. 1B, - C. 2 D. 23 2【答案】A【解析】【分析】根据程序框图所示的意义可得a的值,构成周期数列,即可得答案；【详解】i 1, a 3；1i 2 , a 一；2. 0.1i 3, a —；3i 4, a 2；i 5, a 3,可以看出是周期为4的数列, 1i 55, a -. 31i 56,终止循环,输出a -. 3应选：A.【点睛】此题考查算法中程序框图的循环结构,考查函数与方程思想、转化与化归思想,考查逻辑推理水平、运算求解水平,求解时注意与数列的周期性相结合^14.执行如下图的程序框图,那么输出S的值为〔〕A.百 B §C. 0D. 3考点：循环结构流程图15.秦九韶是我国南宋时期的数学家,普州〔现四川省安岳县〕人,他在所著的?数书九章?中提出的多项式求值的秦九韶算法,至今仍是比拟先进的算法.如下图的程序框图给出了利用秦九韶算法求某多项式值的一个实例,假设输入 的值为v 1 2 2 4, i 2 1 1,i 0成立；v 4 2 1 9 , i 1 1 0,i 0 成立；v 9 2 0 18, i 0 11,i 0不成立,输出v 18.应选C.【解析】【分析】试题分析：第一次循环： a 13s2, 环：氏 0,S J3,第四次循环：a 4 六次循环：a 6 0,S 0,第七次循环: —,第二次循环：a 2 —,S #3,第三次循 2 2—,S 立,第五次循环：% —,S 0,第 2 22 a 7 ~~, S ,第八次循环： a 8 --, S J 3,2 2 2 第九次循环:0,S J3此时i 9 8,结束循环,输出 S J3,选A. n, x 的值分别为3, 2,那么输出v A. 35B. 20 【答案】C【解析】试题分析：模拟算法：开始：输入 C. 18 D. 9 n 3,x 2,v 1,i 3 1 2,i 0 成立;考点：1.数学文化；2.程序框图.所以a1或1 a 2或2 a 5 a 1或1 a 5,因此选D. 点睛：算法与流程图的考查,侧重于对流程图循环结构的考查概念,包括选择结构、循环结构、伪代码,其次要重视循环起点条件、循环次数、循环终 止条件,更要通过循环规律,明确流程图研究的数学问题,是求和还是求项 .17.执行如下图的程序框图,假设输出的 S 为154,那么输入的门为()f (x),假设f (a) 1 ,那么实数a 的取值范围是(A. ( ,2) (2,5]C ( ,2) (2,)【答案】D【解析】 B. ( , 1)U(1,) D. ( , 1) (1,5] 分析：先根据程序框图得 f X 解析式,再根据分段函数解三个不等式组,求并集得结果2 X ,x 详解：由于f(x)= 2x 3,2 1 ,x x 2x 5,所以由f a52 a 5T 或2a 3 1 .先明晰算法及流程图的相关 16.执行如下图的程序框图,令 y/ 输A、/ .I 七［3=| ^7L / ■加“ p-J-n 曲mt IA. 18B. 19C. 20D. 21 【答案】B 【解析】【分析】找到输出的S的规律为等差数列求和,即可算出i ,从而求出n.【详解】由框图可知,S 1 0 1 2 3 i 1 154 ,1 1 i即1 2 3 i 1 153,所以----------- 153,解得i 18,2故最后一次对条件进行判断时i 18 1 19,所以n 19.应选：B 【点睛】此题考查程序框图,要理解循环结构的程序框图的运行,考查学生的逻辑推理水平单题目.A. 120.属于简18.执行如下图的程序框图,如果输入n 6 , m 3,那么输出的P等于〔B. 360C. 840D. 1008【答案】A【解析】【分析】模拟执行程序框图,逐步写出各变量取值的变化,判断循环条件是否成立,最终可得答案【详解】执行程序框图,各变量的值依次变化如下：n 6, m 3,k 1, p 1;p 1 (6 3 1) 4, k m 成立；k 2, p 4 (6 3 2) 20, k m成立；k 3, p 20 (6 3 3) 120, k m 不成立,跳出循环,输出的p等于120.应选：A.【点睛】此题考查程序框图,解题的一般方法是模拟执行程序,依次写出各变量取值的变化,解题时要留意循环终止的条件.19.在如下图的程序框图中,假设输出的值是3,那么输入的x的取值范围是()A. (2, )B. (4,10] C (2,4] D, (4,)【答案】B【解析】【分析】由中的程序框图可知：该程序的功能是利用循环结构计算并输出变量i的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.x 3a 2, i 1 ,不满足退出循环的条件； x 9a 8, i 2 ,不满足退出循环的条件; x 27a 26, i 3,满足退出循环的条件; 故 9a 8, 82,且 27a 26 82 , 解得：a (4,10],应选：B.【点睛】此题考查的知识点是程序框图,当循环的次数不多,或有规律时,常采用模拟循环的方法 解答,属于中档题. 20.阅读如下图的程序框图,假设输入的 a b i 1,那么输出的a 的值为〔〕 ［申I〔州青〕A. 2021B. 1C. 2021 D, 2021【答案】B【解析】【分析】 根据程序框图进行运算即可 .【详解】将a,b,i 的值用表格表示如下：a 1 2 1 1 2 1 1… b 1 1 2 1 1 21 ••• i1 2 3 4 5 6 7 •••由表可知,a 的值以6为周期循环,2021 6 3363,i 3时对应的a 1. 应选：B【点睛】此题主要考查了程序框图的计算,考查了学生的运算求解水平 【详解】解：设输入x a, 第一次执行循环体后, 第二次执行循环体后, 第三次执行循环体后,口三晶］。

【高中数学】高考数学《算法与框图》解析一、选择题1．如图所示的一个算法的程序框图，则输出d的最大值为（）A．2B．2 C．12+D．122+【答案】C【解析】【分析】【详解】模拟程序的运行，可得程序框图的功能是求半圆y＝上的点到直线x﹣y﹣2＝0的距离的最大值，如图：可得：d的最大值为OP+r＝+1．故选：C．2．执行如图所示的程序框图，若输出S的值为43，则输入a的值可能为（）A ．4B ．10C ．79D ．93【答案】D 【解析】 【分析】由题中的程序框图知，该算法是一个以4为周期的函数，若输出S 的值为43，则得出相应的k 值，再由k a >输出，即可得出a 值，再判断选项得出 【详解】程序运行如下：3,1S k ==；4,23S k ==；1,32S k ==； 2,4S k =-=；3,5S k ==；…，此程序的S 值4个一循环.若输出S 的值为43，则相应k 的值为()1142k k N +∈， 因为k a >时，输出S ，则输入a 的值为()1141k k N +∈. 故选：D . 【点睛】本题考查了循环结构的程序框图，根据算法的功能确定S 值的周期规律及跳出循环的k 值是解答本题的关键，属于中档题．3．已知f （k ）＝k +（﹣1）k ，执行如图所示的程序框图，若输出k 的值为4，则判断框内可填入的条件是（ ）A ．s ＞3？B ．s ＞5？C ．s ＞10？D ．s ＞15？【答案】C 【解析】 【分析】根据程序框图依次计算得到答案. 【详解】模拟执行程序框图，可得：k ＝1，s ＝1，s ＝1，不满足判断框内的条件，执行循环体，k ＝2，s ＝4， 不满足判断框内的条件，执行循环体，k ＝3，s ＝6， 不满足判断框内的条件，执行循环体，k ＝4，s ＝11， 此时，应该满足判断框内的条件，退出循环，输出k 的值为4. 因此判断框内的条件可填：s ＞10？ 故选：C . 【点睛】本题考查了程序框图，意在考查学生的计算能力和理解能力.4．执行如图所示的程序框图，若输出的结果为126，则判断框内的条件可以为（ ）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤【答案】B【分析】根据框图，模拟程序运行即可求解. 【详解】根据框图，执行程序，12,2S n ==；1222,3S n =+=；⋯12222,1i S n i =++⋯+=+，令12222126i S =++⋯+=， 解得6i =，即7n =时结束程序， 所以6n ≤， 故选 ：B 【点睛】本题主要考查了程序框图，循环结构，条件分支结构，等比数列求和，属于中档题.genju5．我国古代名著《庄子·天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完.现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取20天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是（ ）A ．20i <，1S S i=-，2i i = B ．20i ≤，1S S i=-，2i i = C ．20i <，2SS =，1i i =+ D ．20i ≤，2SS =，1i i =+ 【答案】D 【解析】 【分析】先由第一天剩余的情况确定循环体，再由结束条件确定循环条件即可.根据题意可知，第一天12S =，所以满足2S S =，不满足1S S i=-，故排除AB ，由框图可知，计算第二十天的剩余时，有2SS =，且21i =，所以循环条件应该是20i ≤. 故选D. 【点睛】本题考查了程序框图的实际应用问题，把握好循环体与循环条件是解决此题的关键，属于中档题.6．执行如图所示的程序框图，若输入的,,a b c 依次为0.80.9，0.90.8，0.90.9，则输出的x 为（ ）A ．0.80.9B ．0.90.8C ．0.90.9D ．0.80.8【答案】A 【解析】 【分析】根据程序框图知：a 、b 、c 中最大的数用x 表示后输出，比较大小得到答案. 【详解】由题意可知a 、b 、c 中最大的数用x 表示后输出， 若输入的a ，b ，c 依次为0.80.90.90.9,0.8,0.9，利用指数函数的性质可得0.80.90.90.9>，0.90.90.80.9<，故最大的数x 为0.80.9， 故选：A . 【点睛】本题考查了程序框图，理解程序框图表示的意义是解题的关键.7．《周易》历来被人们视作儒家群经之首，它表现了古代中华民族对万事万物的深刻而又朴素的认识，是中华人文文化的基础，它反映出中国古代的二进制计数的思想方法.我们用近代术语解释为：把阳爻“”当作数字“1”，把阴爻“”当作数字“0”，则八卦所代表的数表示如下： 卦名 符号表示的二进制数 表示的十进制数 坤 000 0 震 001 1 坎 010 2 兑0113依此类推，则六十四卦中的“井”卦，符号“”表示的十进制数是（ ） A ．11 B ．18C ．22D ．26【答案】C 【解析】 【分析】根据题意井卦表示二进制数的010110，计算得到答案. 【详解】 六十四卦中符号“”表示二进制数的010110， 转化为十进制数的计算为01234502121202120222⨯+⨯+⨯+⨯+⨯+⨯=. 故选：C . 【点睛】本题考查了二进制，意在考查学生的计算能力和理解能力.8．执行如图所示的程序框图，若输出的值为，则判断框内可填入的条件是 （ ）A ．B ．C ．D ．【答案】A 【解析】本程序框图的主要功能是计算数列的前项和； 由于可知，数列的前项和为，由于输出的值为0.99，所以，因此 判断框内可填入的条件是，故选A.9．“二进制”来源于我国古代的《易经》，该书中有两类最基本的符号：“—”和“——”，其中“—”在二进制中记作“1”，“——”在二进制中记作“0”，例如二进制数(2)1011化为十进制的计算如下：321(2)(10)10111202121211=⨯+⨯+⨯+⨯=.若从两类符号中任取2个符号进行排列，则得到的二进制数所对应的十进制数大于2的概率为（ ） A ．0 B ．12C ．13D ．14【答案】D 【解析】 【分析】分类计算得到从两类符号中任取2个符号排列，则组成不同的十进制数为0，1，2，3，计算得到概率. 【详解】根据题意，不同符号可分为三类：第一类：由两个“—”组成，其二进制为(2)(10)113=； 第二类：由两个“——”组成，其二进制为(2)(10)000=；第三类：由一个“—”和一个“——”组成，其二进制为(2)(10)102=，(2)(10)011=， 所以从两类符号中任取2个符号排列，则组成不同的十进制数为0，1，2，3， 则得到的二进制数所对应的十进制数大于2的概率14P =， 故选：D. 【点睛】本题考查古典概型及进制转化的应用，意在考查学生的计算能力和应用能力.10．明代数学家程大位（1533~1606年），有感于当时筹算方法的不便，用其毕生心血写出《算法统宗》，可谓集成计算的鼻祖．如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题．执行该程序框图，若输出的y 的值为2，则输入的x 的值为（ ）A ．74B ．5627C ．2D ．16481【答案】C 【解析】 【分析】根据程序框图依次计算得到答案. 【详解】34y x =-，1i =；34916y y x =-=-，2i =；342752y y x =-=-，3i =；3481160y y x =-=-，4i =；34243484y y x =-=-，此时不满足3i ≤，跳出循环，输出结果为243484x -，由题意2434842y x =-=，得2x =． 故选:C 【点睛】本题考查了程序框图的计算，意在考查学生的理解能力和计算能力.11．执行如图所示的程序框图，若输入如下四个函数：①f （x ）＝sinx ②f （x ）＝cosx ③1()f x x= ④f （x ）＝x 2 则输出的函数是（ ） A ．f （x ）＝sinx B ．f （x ）＝cosxC ．1()f x x= D ．f （x ）＝x 2【答案】A 【解析】试题分析：对①()sin f x x =，显然满足()()0f x f x +-=，且存在零点.故选A. 考点：程序框图及函数的性质.12．德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家､天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P 表示π的近似值),若输入10n ＝,则输出的结果是( )A ．11114(1)35717P =-+-+⋅⋅⋅+B ．11114(1)35719P =-+-+⋅⋅⋅- C ．11114(1)35721P =-+-+⋅⋅⋅+ D ．11114(1)35721P =-+-+⋅⋅⋅- 【答案】B 【解析】 【分析】执行给定的程序框图，输入10n =，逐次循环，找到计算的规律，即可求解. 【详解】由题意，执行给定的程序框图，输入10n =，可得： 第1次循环：1,2S i ==； 第2次循环：11,33S i =-=； 第3次循环：111,435S i =-+=； L L第10次循环：11111,1135719S i =-+-+-=L ， 此时满足判定条件，输出结果111144(1)35719P S ==-+-+⋅⋅⋅-， 故选：B. 【点睛】本题主要考查了循环结构的程序框图的计算与输出，其中解答中认真审题，逐次计算，得到程序框图的计算功能是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.13．某程序框图如图所示，其中21()g n n n =+，若输出的20192020S =，则判断框内可以填入的条件为（ ）A ．2020?n <B ．2020?n …C ．2020?n >D ．2020?n … 【答案】A【解析】【分析】因为()()2111111g n n n n n n n ===-+++，此程序框图是对函数()g n 求和，利用裂项相消法求和，可知201912020n S n ==+，可知2019满足条件进入循环，2020不满足条件没有进入循环，根据选项得到正确结果.【详解】 由2221111111112019(1111222231112020n S n n n n n n ⎫⎛⎫⎛⎫=++⋯+=-+-+⋯+-=-==⎪ ⎪ ⎪++++++⎭⎝⎭⎝⎭，解得2019n =，可得n 的值为2019时.满足判断框内的条件，当n 的值为2020时，不满足判断框内的条件，退出循环，输出S 的值，故判断框内可以填人的条件为“2020n <？”.故选A.【点睛】本题考查根据循环框图的输出结果填写判断框的内容，关键是分析出满足输出结果时的n 值，再根据选项判断结果.14．执行如图所示的程序框图，则程序最后输出的结果为（ ）A ．15B ．25C ．35D ．45【答案】D【解析】【分析】模拟执行程序框图，读出程序框图实现的功能，即可求得输出结果.【详解】模拟执行程序框图，根据题意可知，11,5k a ==； 22,5k a ==； 43,5k a ==； 34,5k a ==； 15,5k a ==； 26,5k a ==； L 故归纳总结可得a 的取值周期为4，结合题中判断条件，2019k ≥，又201950443=⨯+可知： 输出的45a =. 故选：D.【点睛】本题考查求程序框图的输出结果，解题时，应模拟程序框图的运行结果得出结论，属中档题.15．为计算1234171834561920T =⨯⨯⨯⨯⋅⋅⋅⨯⨯，设计了下面的程序框图，则在空白框中应填入（ ）A ．W W i =⨯B ．()1W W i =⨯+C ．()2W W i =⨯+D ．()3W W i =⨯+【答案】C【解析】【分析】 根据程序的计算功能，寻找分子与分母之间的关系，即可求解．【详解】由题意，根据程序的计算功能，可得每个分式的分母比分子多2，即()2W W i =⨯+． 故选：C .【点睛】本题主要考查了程序框图的识别与应用，其中解答中根据程序框图，找出每个式子分子与分母的关系式解答的关键，着重考查分析问题和解答问题的能力．16．执行如图所示的程序框图，若输出的S 的值为2670，则判断框中的条件可以为（ ）A ．5?i <B ．6?i <C ．7?i <D ．8?i <【答案】B【解析】 阅读流程图，程序运行如下：第一次循环：1,2,12S S i S S i i i =⨯==+==+=；第二次循环：4,6,13S S i S S i i i =⨯==+==+=；第三次循环：18,21,14S S i S S i i i =⨯==+==+=；第四次循环：84,88,15S S i S S i i i =⨯==+==+=；第五次循环：440,445,16S S i S S i i i =⨯==+==+=；第六次循环：2670S S i =⨯=；由题意可知，此时程序应跳出循环，则判断框中的条件可以为6?i <本题选择B 选项.点睛：一是利用循环结构表示算法，一定要先确定是用当型循环结构，还是用直到型循环结构；当型循环结构的特点是先判断再循环，直到型循环结构的特点是先执行一次循环体，再判断；二是注意输入框、处理框、判断框的功能，不可混用；三是赋值语句赋值号左边只能是变量，不能是表达式，右边的表达式可以是一个常量、变量或含变量的运算式．17．鸡兔同笼，是中国古代著名的趣味题之一.《孙子算经》中就有这样的记载：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各有几何？设计如右图的算法来解决这个问题，则判断框中应填入的是（ ）A ．94m >B ．94m =C ．35m =D ．35m ≤【答案】B【解析】【分析】 由题意知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意可得出判断条件.【详解】由题意可知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意知，在程序框图中，当计算足的数量为94时，算法结束，因此，判断条件应填入“94m =”.故选B.【点睛】本题考查算法程序框图中判断条件的填写，考查分析问题和解决问题的能力，属于中等题.18．元朝著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒，携着游春走，遇店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中，当原多少酒?”用程序框图表达如图所示，即最终输出的0x =，则一开始输入的x 的值为( )A ．34B ．78C ．1516D ．3132【答案】B【解析】【分析】由已知中的程序语句可知：该程序的功能是利用循环结构计算输入时变量x 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得到答案.【详解】本题由于已知输出时x 的值，因此可以逆向求解：输出0x =,此时4i =；上一步：1210,2x x -==,此时3i =； 上一步：1321,24x x -==,此时2i =； 上一步：3721,48x x -==,此时1i =； 故选：B .【点睛】本题考查了程序框图的循环结构，考查了学生逻辑推理和数学运算的能力，属于基础题.19．如图所示的程序框图，则输出的,,x y z 的值分别是（ ）A ．13009，600，11203B ．1200，500，300C ．1100，400，600D ．300，500，1200 【答案】B【解析】【分析】根据程序框图依次计算得到答案.【详解】根据程序框图得：①300,1y i ==，满足3i <；②400,2y i ==，满足3i <； ③500,300y z ==，1200,3x i ==，不满足3i <.故输出的1200,500,300x y z ===. 故选：B .【点睛】本题考查了程序框图，意在考查学生的理解能力.20．《九章算术》卷第七——盈不足中有如下问题：“今有垣高九尺.瓜生其上，蔓日长七寸. 瓠生其下，蔓日长一尺.问几何日相逢.”翻译为“今有墙高9尺.瓜生在墙的上方，瓜蔓每天向下长7寸.葫芦生在墙的下方，葫芦蔓每天向上长1尺.问需要多少日两蔓相遇.”其中1尺=10寸.为了解决这一问题，设计程序框图如下所示，则输出的k 的值为（ ）A ．8B ．7C ．6D ．5【答案】C【解析】【分析】 模拟执行程序，依次写出每次循环得到的a,n,S 的值，当S=-1.2时满足条件S 0£ 退出循环输出n 的值从而得解【详解】运行该程序，第一次，9 1.77.3S =-=，2k =；第二次，7.3 1.7 5.6S =-=，3k =；第三次， 5.6 1.7 3.9S =-=，4k =；第四次， 3.9 1.7 2.2S =-=，5k =；第五次，2.2 1.70.5S =-=，6k =；第六次，0.5 1.7 1.2S =-=-，此时输出的k 的值为6 故选：C【点睛】本题考查数学文化、算法与程序框图，考查推理论证能力以及化归与转化思想.。

【高中数学】数学高考《算法与框图》试题含答案一、选择题1．运行如图所示的程序框图，若输出的s 值为10-，则判断框内的条件应该是( )A ．3k <？B ．4k <？C ．5k <？D ．6k <？【答案】C【解析】当1,1k s ==时，应满足继续循环的条件，故1,2s k ==；当2,1k s ==时，应满足继续循环的条件，故0,3s k ==；当3,0k s ==时，应满足继续循环的条件，故3,4s k =-=；当4,3k s ==-时，应满足继续循环的条件，故10,5s k =-=；当5,10k s ==-时，应不满足继续循环的条件，故判断框内的条件应该是5?k <，故选C ．【名师点睛】本题主要考查程序框图的循环结构流程图，属于中档题.解决程序框图问题时一定注意以下几点：(1)不要混淆处理框和输入框；(2)注意区分程序框图是条件分支结构还是循环结构；(3)注意区分当型循环结构和直到型循环结构；(4)处理循环结构的问题时，一定要正确控制循环次数；(5)要注意各个框的顺序；(6)在给出程序框图求解输出结果的试题中，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.2．执行如下的程序框图，则输出的S 是（ ）A ．36B ．45C ．36-D ．45-【答案】A【解析】【分析】 列出每一步算法循环，可得出输出结果S 的值.【详解】18i =≤满足，执行第一次循环，()120111S =+-⨯=-，112i =+=；28i =≤成立，执行第二次循环，()221123S =-+-⨯=，213i =+=；38i =≤成立，执行第三次循环，()323136S =+-⨯=-，314i =+=；48i =≤成立，执行第四次循环，()4261410S =-+-⨯=，415i =+=；58i =≤成立，执行第五次循环，()52101515S =+-⨯=-，516i =+=；68i =≤成立，执行第六次循环，()62151621S =-+-⨯=，617i =+=；78i =≤成立，执行第七次循环，()72211728S =+-⨯=-，718i =+=； 88i =≤成立，执行第八次循环，()82281836S =-+-⨯=，819i =+=；98i =≤不成立，跳出循环体，输出S 的值为36，故选：A.【点睛】本题考查算法与程序框图的计算，解题时要根据算法框图计算出算法的每一步，考查分析问题和计算能力，属于中等题.3．下列各数中，最小的是( )A ．101 010(2)B ．111(5)C ．32(8)D ．54(6)【答案】C【解析】()543221010101202120242=⨯+⨯+⨯+⨯=()210511115151531=⨯+⨯+⨯=()10832382826=⨯+⨯=()10654564634=⨯+⨯=故最小的是()832故答案选C4．某程序框图如图所示，若输出S ＝3，则判断框中M 为（ ）A ．k ＜14？B ．k≤14？C ．k≤15？D ．k ＞15？ 【答案】B【解析】【分析】 由框图程序可知12231S k k =++++L 可得解【详解】 由框图程序可知12231S k k =++++L 11n n n n =+++ 所以213243111S n n n =++=+L 所以113S n =+=，解得15n =，即当15n =时程序退出，故选B ．【点睛】 算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.5．程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作．卷八中第33问：“今有三角果一垛，底阔每面七个．问该若干？”如图是解决该问题的程序框图．执行该程序框图，求得该垛果子的总数S 为（ ）A ．28B ．56C ．84D ．120【答案】C【解析】【分析】 由已知中的程序可知：该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序运行过程，分析循环中各变量值的变化情况，即可求解.【详解】模拟程序的运行，可得：0,0,0i n S ===执行循环体，1,1,1i n S ===；不满足判断条件7i ≥，执行循环体，2,3,4i n S ===；不满足判断条件7i ≥，执行循环体，3,6,10i n S ===；不满足判断条件7i ≥，执行循环体，4,10,20i n S ===；不满足判断条件7i ≥，执行循环体，5,15,35i n S ===；不满足判断条件7i ≥，执行循环体，6,21,56i n S ===；不满足判断条件7i ≥，执行循环体，7,28,84i n S ===；满足判断条件7i ≥，退出循环，输出S 的值为84.故选：C.【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中模拟程序运行的过程，通过逐次计算和找出计算的规律是解答的关键，着重考查了推理与计算能力，属于基础题.6．阅读如图的程序框图，运行相应的程序，则输出的a 的值为（ ）A ．2-3B ．3-2C ．52D ．25【答案】C【解析】【分析】 根据给定的程序框图，计算前几次的运算规律，得出运算的周期性，确定跳出循环时的n 的值，进而求解a 的值，得到答案.【详解】 由题意，3,15a n ==， 第1次循环，2,23a n =-=，满足判断条件； 第2次循环，5,32a n ==，满足判断条件； 第3次循环，3,45a n ==，满足判断条件； L L可得a 的值满足以3项为周期的计算规律，所以当2019n =时，跳出循环，此时n 和3n =时的值对应的a 相同，即52a =. 故选：C.【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中认真审题，得出程序运行时的计算规律是解答的关键，着重考查了推理与计算能力.7．执行如图所示的程序框图，如果输入n=3，输出的S=（ ）A．67B．37C．89D．49【答案】B【解析】【分析】【详解】试题分析：由题意得，输出的为数列的前三项和，而，∴，故选B.考点：1程序框图；2.裂项相消法求数列的和.【名师点睛】本题主要考查了数列求和背景下的程序框图问题，属于容易题，解题过程中首先要弄清程序框图所表达的含义，解决循环结构的程序框图问题关键是列出每次循环后的变量取值情况，循环次数较多时，需总结规律，若循环次数较少可以全部列出.8．我国古代数学著作《九章算术》中有如下问题：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升(注：一斗为十升).问，米几何？”下图是解决该问题的程序框图，执行该程序框图，若输出的S=15(单位：升)，则输入的k的值为（）A ．45B ．60C ．75D ．100【答案】B【解析】【分析】根据程序框图中程序的功能，可以列方程计算．【详解】 由题意12315234S ⨯⨯⨯=，60S =．故选：B.【点睛】本题考查程序框图，读懂程序的功能是解题关键．9．如图所示的程序框图是求3333---的值的程序，则判断框中应填入（）A ．1i ≥B ．5i ≤C ．5i >D ．7i ≤【答案】B【解析】【分析】根据框图，模拟程序的运算即可求解.【详解】由程序框图得，3S =1i =，满足条件得33S =-3i =，满足条件得333S =--，5i =，满足条件3333S =---，7i =，否，输出S 的值，结束程序，因此判断框应该是5i ≤，故选：B ．【点睛】本题主要考查了算法的程序框图，基本逻辑结构中的循环结构，属中档题.10．执行如图所示的程序框图，输出的结果为（ ）A ．919B ．1021C ．1819D ．2021【答案】B【解析】【分析】根据程序框图得出2221114114214101S =+++⨯-⨯-⨯-L ，利用裂项相消法可求得输出的S 的值.【详解】 ()()21111141212122121i i i i i ⎛⎫==- ⎪--+-+⎝⎭Q ， 由程序框图可知，输出的S 的值为2221114114214101S =+++⨯-⨯-⨯-L 1111111012335192121⎛⎫=-+-++-= ⎪⎝⎭L . 故选：B.【点睛】本题考查利用程序框图计算输出结果，同时也考查了裂项求和法的应用，考查计算能力，属于中等题.11．执行如图所示的程序框图，则输出的n 值是（ ）A ．5B ．7C ．9D ．11【答案】C【解析】【分析】 根据程序框图列出算法循环的每一步，结合判断条件得出输出的n 的值.【详解】执行如图所示的程序框图如下：409S =≥不成立，11S 133==⨯，123n =+=； 1439S =≥不成立，1123355S =+=⨯，325n =+=； 2459S =≥不成立，2135577S =+=⨯，527n =+=； 3479S =≥不成立，3147799S =+=⨯，729n =+=. 4499S =≥成立，跳出循环体，输出n 的值为9，故选C. 【点睛】本题考查利用程序框图计算输出结果，对于这类问题，通常利用框图列出算法的每一步，考查计算能力，属于中等题.12．运行如图所示的程序框图，若输出的S 的值为1011，则判断框中可以填（ ）A ．2020?i >B ．2021?i ≥C ．2022?i >D ．2023?i >【答案】C【解析】【分析】 利用程序框图的功能，进行模拟计算即可．【详解】程序的功能是计算S ＝1sin2π+3sin 32π+5sin+52π…＝1﹣3+5﹣7+9+…+， 则1011＝1+505×2＝1﹣3+5﹣7+9+…则第1011个奇数为2×1011﹣1＝2021不成立，第1012个奇数为2×1012﹣1＝2023成立，故条件为i ＞2022？，故选C ．【点睛】 本题主要考查程序框图的应用，利用程序框图的功能是解决本题的关键，属于基础题.13．我国古代名著《庄子g 天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完.现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位：尺)，则①②③处可分别填入的是( )A．17?,,+1i s s i ii≤=-=B．1128?,,2i s s i ii≤=-=C．17?,,+12i s s i ii≤=-=D．1128?,,22i s s i ii≤=-=【答案】B【解析】【分析】分析程序中各变量的作用，再根据流程图所示的顺序，可得该程序的作用是累加并输出S 的值，由此可得到结论.【详解】由题意，执行程序框图，可得：第1次循环：11,42S i=-=；第2次循环：111,824S i=--=；第3次循环：1111,16248S i=--==；依次类推，第7次循环：11111,256241288S i=----==L，此时不满足条件，推出循环，其中判断框①应填入的条件为：128?i≤，执行框②应填入：1S Si=-，③应填入：2i i=.故选：B.【点睛】本题主要考查了循环结构的程序框图的应用，其中解答中正确理解程序框图的含义是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.14．如图所示的程序框图是为了求出满足2228n n ->的最小偶数n ，那么在X空白框中填入及最后输出的n 值分别是（ ）A ．1=+n n 和6B ．2=+n n 和6C ．1=+n n 和8D ．2=+n n 和8【答案】D 【解析】空白框中n 依次加2可保证其为偶数，排除A ，C6n =时，622664362628-=-=≤，8n =时，1282282566428-=-> 所以D 选项满足要求． 故选：D ．15．执行如图所示的程序框图，输出的值为（ ）A ．13B ．12C ．2D ．2-【答案】A【解析】 【分析】根据程序框图所示的意义可得a 的值，构成周期数列，即可得答案； 【详解】1i =，3a =-；2i =，12a =-；3i =，13a =；4i =，2a =；5i =，3a =-，可以看出是周期为4的数列，55i =，13a =.56i =，终止循环，输出13a =.故选：A. 【点睛】本题考查算法中程序框图的循环结构，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意与数列的周期性相结合.16．德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家､天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P 表示π的近似值),若输入10n ＝,则输出的结果是( )A ．11114(1)35717P =-+-+⋅⋅⋅+B ．11114(1)35719P =-+-+⋅⋅⋅- C ．11114(1)35721P =-+-+⋅⋅⋅+ D ．11114(1)35721P =-+-+⋅⋅⋅- 【答案】B 【解析】 【分析】执行给定的程序框图，输入10n =，逐次循环，找到计算的规律，即可求解. 【详解】由题意，执行给定的程序框图，输入10n =，可得： 第1次循环：1,2S i ==； 第2次循环：11,33S i =-=； 第3次循环：111,435S i =-+=； L L第10次循环：11111,1135719S i =-+-+-=L ， 此时满足判定条件，输出结果111144(1)35719P S ==-+-+⋅⋅⋅-， 故选：B. 【点睛】本题主要考查了循环结构的程序框图的计算与输出，其中解答中认真审题，逐次计算，得到程序框图的计算功能是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.17．执行如图所示的程序框图，则输出的a =（ ）A ．32-B ．13-C ．2D ．2-【答案】A 【解析】 【分析】根据循环程序框图，一次循环后，可知本题循环程序是求一个以3为周期的数列：2，13-，32-，2，13-，32-…，所以当2019i =时，输出结果，根据周期性，即可得出结果.【详解】解：根据程序框图，执行程序得： 2,1a i ==，否，11,2213a i =-=-=+，否， 13,31213a i =-=-=-+，否， 12,4312a i =-==-+，否， 11,5213a i =-=-=+，否， 13,61213a i =-=-=-+，否， L可知本题循环程序是一个以3为周期的数列：2，13-，32-，2，13-，32-…， 当2019i =时，输出结果，则20193673÷=，即循环673个周期， 所以输出结果为32-． 故选：A. 【点睛】本题考查由循环程序框图计算输出结果，理解循环结构框图是关键.18．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n ，x 的值分别为3，2，则输出v 的值为A ．35B ．20C ．18D ．9【答案】C 【解析】试题分析：模拟算法：开始：输入3,2,1,312,0n x v i i ====-=≥成立； 1224v =⨯+=，211,0i i =-=≥成立； 4219v =⨯+=，110,0i i =-=≥成立；92018v =⨯+=，011,0i i =-=-≥不成立，输出18v =.故选C.考点：1.数学文化；2.程序框图.19．阅读如图所示的程序框图，运行相应的程序，输出的的值等于（ ）A ．30B ．31C ．62D ．63【答案】B 【解析】 【分析】首先确定流程图的功能，然后计算其输出的结果即可.【详解】由流程图可知该算法的功能为计算的值，即输出值为：.故选：B.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．20．执行如图所示的程序框图，若输出的值为，则判断框内可填入的条件是（）A． B． C． D．【答案】A【解析】本程序框图的主要功能是计算数列的前项和；由于可知，数列的前项和为，由于输出的值为0.99，所以，因此判断框内可填入的条件是，故选A.。

新《算法与框图》专题解析一、选择题1．运行如图所示的程序框图，若输出的s 值为10-，则判断框内的条件应该是( )A ．3k <？B ．4k <？C ．5k <？D ．6k <？ 【答案】C 【解析】当1,1k s ==时，应满足继续循环的条件，故1,2s k ==； 当2,1k s ==时，应满足继续循环的条件，故0,3s k ==； 当3,0k s ==时，应满足继续循环的条件，故3,4s k =-=； 当4,3k s ==-时，应满足继续循环的条件，故10,5s k =-=； 当5,10k s ==-时，应不满足继续循环的条件， 故判断框内的条件应该是5?k <，故选C ．【名师点睛】本题主要考查程序框图的循环结构流程图，属于中档题.解决程序框图问题时一定注意以下几点： (1)不要混淆处理框和输入框；(2)注意区分程序框图是条件分支结构还是循环结构； (3)注意区分当型循环结构和直到型循环结构； (4)处理循环结构的问题时，一定要正确控制循环次数； (5)要注意各个框的顺序；(6)在给出程序框图求解输出结果的试题中，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.2．如图是求112122++的程序框图，图中空白框中应填入A ．A =12A + B ．A =12A+C ．A =112A+D ．A =112A+【答案】A 【解析】 【分析】本题主要考查算法中的程序框图，渗透阅读、分析与解决问题等素养，认真分析式子结构特征与程序框图结构，即可找出作出选择． 【详解】执行第1次，1,122A k ==≤是，因为第一次应该计算1122+=12A +，1k k =+=2，循环，执行第2次，22k =≤，是，因为第二次应该计算112122++=12A+，1k k =+=3，32k =≤，否，输出，故循环体为12A A=+，故选A ． 【点睛】秒杀速解 认真观察计算式子的结构特点，可知循环体为12A A=+．3．执行下面的程序框图，若输入的1A =，则输出的A 的值为（ ）A．7 B．-17 C．31 D．-65【答案】C【解析】【分析】根据程序框图依次计算得到答案.【详解】==；17,4A kA k==.=-=；31,5A k1,1A k==；5,2=-=；7,3A k结束，输出答案31故选C【点睛】本题考查了程序框图，根据程序框图依次计算是一种常用的方法，需要同学们熟练掌握. 4．明朝数学家程大位将“孙子定理”（也称“中国剩余定理”）编成易于上口的《孙子歌诀》：三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五便得知．已知正整数n被3除余2,被5除余3，被7除余4，求n的最小值．按此歌诀得算法如图，则输出n 的结果为（）A ．53B ．54C ．158D ．263【答案】A 【解析】按程序框图知n 的初值为263，代入循环结构，第一次循环158n =，第二次循环53,53105n =<，推出循环，n 的输出值为53 ，故选A.5．若执行下面的程序框图，输出的值为3，则判断框中应填入的条件是（ ）A ．7?k <B ．6?k <C ．9?k <D ．8?k <【答案】D 【解析】 【分析】根据程序框图，写出运行结果，根据程序输出的结果是S=3，可得判断框内应填入的条件． 【详解】根据程序框图，运行结果如下： S k 第一次循环 log 23 3 第二次循环 log 23•log 34 4 第三次循环 log 23•log 34•log 45 5 第四次循环 log 23•log 34•log 45•log 56 6 第五次循环 log 23•log 34•log 45•log 56•log 67 7第六次循环 log 23•log 34•log 45•log 56•log 67•log 78=log 28=3 8故如果输出S=3，那么只能进行六次循环，故判断框内应填入的条件是k ＜8． 故答案为：D ． 【点睛】本题考查程序框图，尤其考查循环结构，对循环体每次循环需要进行分析并找出内在规律是解题关键.6．程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作．卷八中第33问：“今有三角果一垛，底阔每面七个．问该若干？”如图是解决该问题的程序框图．执行该程序框图，求得该垛果子的总数S 为（ ）A ．28B ．56C ．84D ．120【答案】C 【解析】 【分析】由已知中的程序可知：该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序运行过程，分析循环中各变量值的变化情况，即可求解. 【详解】模拟程序的运行，可得：0,0,0i n S === 执行循环体，1,1,1i n S ===；不满足判断条件7i ≥，执行循环体，2,3,4i n S ===； 不满足判断条件7i ≥，执行循环体，3,6,10i n S ===； 不满足判断条件7i ≥，执行循环体，4,10,20i n S ===； 不满足判断条件7i ≥，执行循环体，5,15,35i n S ===； 不满足判断条件7i ≥，执行循环体，6,21,56i n S ===； 不满足判断条件7i ≥，执行循环体，7,28,84i n S ===； 满足判断条件7i ≥，退出循环，输出S 的值为84.故选：C. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中模拟程序运行的过程，通过逐次计算和找出计算的规律是解答的关键，着重考查了推理与计算能力，属于基础题.7．利用如图算法在平面直角坐标系上打印一系列点，则打印的点在圆2225x y +=内的个数为（ ）A ．2B ．3C ．4D ．5【答案】C 【解析】3,6x y =-= 时，打印点()3,6-不在圆内，2,5x y =-= ，50i => 是；打印点()2,5- 不在圆内，1,4x y =-= ，40i => 是；打印点()1,4-在圆内，0,3x y == ，30i => 是；打印点()0,3 在圆内，1,2x y == ，20i =>是；打印点()1,2在圆内，2,1x y == ，10i =>是；打印点()2,1在圆内，3,0x y == ，00i =>否，结束，所以()()()()1,40,31,22,1-共4个点在圆内，故选C.8．执行下面程序框图，若输入的的值分别为0和44，则输出的值为（ ）A．4 B．7 C．10 D．13【答案】C【解析】【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的的值.【详解】第一次循环：，，；第二次循环：，，；第三次循环：，，；第四次循环：，，刚好满足条件，结束循环，此时输出.故选.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.9．我国古代“伏羲八卦图”中的八卦与二进制、十进制的互化关系如表，依据表中规律，A，B处应分别填写八卦二进制000001010011A十进制0123BA ．110、6B ．110、12C ．101、5D ．101、10【答案】A 【解析】 【分析】根据八卦图的规律求得处所填，然后通过二进制转化为十进制的公式，计算出处所填. 【详解】根据八卦图的规律得到处填，处应填写6． 故选A ． 【点睛】本小题主要考查二进制和十进制的相互转化，考查中国古代数学文化，属于基础题.10．明代数学家程大位（1533~1606年），有感于当时筹算方法的不便，用其毕生心血写出《算法统宗》，可谓集成计算的鼻祖．如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题．执行该程序框图，若输出的y 的值为2，则输入的x 的值为（ ）A ．74B ．5627C ．2D ．16481【答案】C 【解析】 【分析】根据程序框图依次计算得到答案. 【详解】34y x =-，1i =；34916y y x =-=-，2i =；342752y y x =-=-，3i =；3481160y y x =-=-，4i =；34243484y y x =-=-，此时不满足3i ≤，跳出循环，输出结果为243484x -，由题意2434842y x =-=，得2x =． 故选:C 【点睛】本题考查了程序框图的计算，意在考查学生的理解能力和计算能力.11．某公司的财务报销流程图如图所示，则2019年初，采购人员为公司购进了一批办公用品，现准备报销此次所购的办公用品的经费，根据下面的流程图，则需要签字的次数为（）A．5 B．4 C．3 D．2【答案】B【解析】【分析】首先从流程图中得到报销此次所购的办公用品的经费，需要采购整理票据并签字、后勤部门审核签字、财务总监审核签字、总经理审核签字共四道签字过程，从而得到答案.【详解】根据题意，观察流程图，可知报销办公用品的经费，流程走右边的分支，需要采购整理票据并签字、后勤部门审核签字、财务总监审核签字、总经理审核签字共四道签字过程，所以需要签字的次数为4次，故选B.【点睛】该题考查的是有关流程图的问题，属于简单题目.N=,那么输出的S=（）12．执行下边的程序框图，如果输人的10A ．1111 (2310)++++ B ．1111......2!3!10!++++ C ．1111......2311++++ D ．1111......2!3!11!++++ 【答案】B 【解析】试题分析：第一次循环，得1,1,2T S k ===；第二次循环，得11,1,32121T S k ==+=⨯⨯；第三次循环，得111,1,432121321T S k ==++=⨯⨯⨯⨯⨯；第四次循环，得111,1432121321T S ==++⨯⨯⨯⨯⨯⨯＋14321⨯⨯⨯，5k =；…，由此可推出当11k =时退出，输出11121321S =++⨯⨯⨯＋14321⨯⨯⨯＋…＋110321⨯⨯⨯⨯L ，即输出11112!3!10!+++⋯⋯+，故选B ． 考点：程序框图．13．如图所示的一个算法的程序框图，则输出d 的最大值为（ ）A ．2B ．2C ．12+D ．122+【答案】C【解析】【分析】【详解】 模拟程序的运行，可得程序框图的功能是求半圆y ＝上的点到直线x ﹣y ﹣2＝0的距离的最大值，如图：可得：d 的最大值为OP +r ＝+1．故选：C ．14．已知二进制数(2)1010化为十进制数为n ，若()n x a +的展开式中，7x 的系数为15，则实数a 的值为（ ）A ．12B ．15C ．1D ．2【答案】A【解析】【分析】先利用进制转化求出n 的值,再利用二项展开式的通项公式,结合题意列式求得a 的值.【详解】根据进制转换法可得:31(2)1010121210=⨯+⨯=,所以10n =,设10()x a +展开式的通项为10110C k k k k T xa -+=, 令107k -=,∴3k =,∴7x 的系数为3310C 15a =,∴318a =,∴12a =, 故选:A.【点睛】本题考查二项式,考查进制转换,需要学生对基础知识牢固掌握且灵活运用.15．定义某种运算:S m n ⊗=⊗的运算原理如右边的流程图所示，则6547⊗-⊗=（ ）A ．3B ．1C ．4D ．0【答案】A【解析】【分析】 根据流程图知运算为分段函数，根据分段函数进行计算.【详解】由流程图得656(51)24,477(41)21,⊗=⨯-=⊗=⨯-=所以654724213⊗-⊗=-=,选A.【点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.16．执行如图所示的程序框图，则输出的a =（ ）A ．32-B ．13- C ．2 D ．2-【答案】A【解析】【分析】根据循环程序框图，一次循环后，可知本题循环程序是求一个以3为周期的数列：2，13-，32-，2，13-，32-…，所以当2019i =时，输出结果，根据周期性，即可得出结果.【详解】解：根据程序框图，执行程序得：2,1a i ==，否，11,2213a i =-=-=+，否， 13,31213a i =-=-=-+，否， 12,4312a i =-==-+，否， 11,5213a i =-=-=+，否， 13,61213a i =-=-=-+，否， L 可知本题循环程序是一个以3为周期的数列：2，13-，32-，2，13-，32-…， 当2019i =时，输出结果，则20193673÷=，即循环673个周期，所以输出结果为32-． 故选：A. 【点睛】 本题考查由循环程序框图计算输出结果，理解循环结构框图是关键.17．如图所示是为了求出满足122222018n +++>L 的最小整数n ，和两个空白框中，可以分别填入（ ）A ．2018S >？，输出1n -B ．2018S >？，输出nC ．2018S ≤？，输出1n -D ．2018S ≤？，输出n【答案】A【解析】【分析】 通过要求122222018n +++>L 时输出且框图中在“是”时输出确定“”内应填内容；再通过循环体确定输出框的内容．【详解】因为要求122222018n +++>L 时输出，且框图中在“是”时输出，所以“”内输入“2018S >？”， 又要求n 为最小整数，所以“”中可以填入输出1n -，故选：A ．【点睛】本题考查了程序框图的应用问题，是基础题．18．我国古代数学名著《九章算术》里有一道关于玉石的问题：“今有玉方一寸，重七两；石方一寸，重六两.今有石方三寸，中有玉，并重十一斤（176两）.问玉、石重各几何？”如图所示的程序框图反映了对此题的一个求解算法，运行该程序框图，则输出的x ，y 分别为（ ）A ．90，86B ．94，82C ．98，78D ．102，74【答案】C【解析】 执行程序框图，86,90,27x y s ==≠；90,86,27x y s ==≠；94,82,27x y s ==≠；98,78,27x y s ===，结束循环，输出的,x y 分别为98,78，故选C.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.19．根据下面的程序框图，输出的S 的值为（ ）A．1007 B．1009 C．0 D．-1【答案】A【解析】【分析】按照程序框图模拟运行即可得解.【详解】1 i=，1112x==--，0(1)1S=+-=-；2i=，111(1)2x==--，11122S=-+=-；3i=，12112x==-，13222S=-+=；4i=，1112x==--，31(1)22S=+-=，…，由此可知，运行程序过程中，x呈周期性变化，且周期为3，所以输出112672110072S⎛⎫=-++⨯-=⎪⎝⎭.故选A【点睛】本题主要考查程序框图和数列的周期性，意在考查学生对这些知识的理解掌握水平和分析推理能力.20．已知实数[]1,10x∈，执行如图所示的流程图，则输出的x不小于63的概率为（）A．49B．13C．25D．310【答案】B【解析】试题分析：运行该程序框图，第一次循环21,2x x n =+=；第二次循环()221+1=43,3x x x n =++=；第三次循环2187,4x x x n =+=+=；推出循环输出87x +，由8763x +≥得7x ≥，由几何概型概率公式可得输出的x 不小于63的概率为1071103-=，故选B. 考点：1、程序框图及循环结构；2、几何概型概率公式.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1)不要混淆处理框和输入框；(2)注意区分程序框图是条件分支结构还是循环结构；(3)注意区分当型循环结构和直到型循环结构；(4)处理循环结构的问题时一定要正确控制循环次数；(5)要注意各个框的顺序；（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.。

新《算法与框图》专题解析(1)一、选择题1．执行如图所示的程序框图，则程序最后输出的结果为（ ）A ．15B ．25C ．35D ．45【答案】D 【解析】 【分析】模拟执行程序框图，读出程序框图实现的功能，即可求得输出结果. 【详解】模拟执行程序框图，根据题意可知，11,5k a ==； 22,5k a ==； 43,5k a ==； 34,5k a ==； 15,5k a ==； 26,5k a ==； L故归纳总结可得a 的取值周期为4，结合题中判断条件，2019k ≥，又201950443=⨯+可知： 输出的45a =. 故选：D. 【点睛】本题考查求程序框图的输出结果，解题时，应模拟程序框图的运行结果得出结论，属中档题.2．如图所示的程序框图是求3333---的值的程序，则判断框中应填入（ ）A ．1i ≥B ．5i ≤C ．5i >D ．7i ≤【答案】B 【解析】 【分析】根据框图，模拟程序的运算即可求解. 【详解】 由程序框图得，3S =，1i =，满足条件得33S =-，3i =，满足条件得333S =--， 5i =，满足条件3333S =---， 7i =，否，输出S 的值，结束程序， 因此判断框应该是5i ≤， 故选：B ． 【点睛】本题主要考查了算法的程序框图，基本逻辑结构中的循环结构，属中档题.3．执行如图所示的程序框图，则输出的S 是（ ）A ．-3B ．-1C ．1D ．3【解析】 【分析】根据框图可得程序是求数列lg1n n ⎧⎫⎨⎬+⎩⎭的前999项的和再加上2，由()lglg lg 11n na n n n ==-++可得到答案. 【详解】 根据框图的运行可得：程序是2加上数列lg 1n n ⎧⎫⎨⎬+⎩⎭的前999项的和. 又()lglg lg 11n na n n n ==-++ 所以()()()2+lg1lg2lg3lg3lg999lg1000S =-+-++-L L2lg1lg1000231=+-=-=-故选：B 【点睛】本题考查程序框图中的循环和裂项相消法求和，属于中档题.4．若执行下面的程序框图，输出的值为3，则判断框中应填入的条件是（ ）A ．7?k <B ．6?k <C ．9?k <D ．8?k <【答案】D 【解析】 【分析】根据程序框图，写出运行结果，根据程序输出的结果是S=3，可得判断框内应填入的条件． 【详解】根据程序框图，运行结果如下： S k 第一次循环 log 23 3 第二次循环 log 23•log 34 4 第三次循环 log 23•log 34•log 45 5 第四次循环 log 23•log 34•log 45•log 56 6 第五次循环 log 23•log 34•log 45•log 56•log 67 7第六次循环 log 23•log 34•log 45•log 56•log 67•log 78=log 28=3 8故如果输出S=3，那么只能进行六次循环，故判断框内应填入的条件是k ＜8． 故答案为：D ．本题考查程序框图，尤其考查循环结构，对循环体每次循环需要进行分析并找出内在规律是解题关键.5．某程序框图如图所示，若输出的S=57，则判断框内为 A ．k ＞4? B ．k ＞5? C ．k ＞6? D ．k ＞7?【答案】A 【解析】试题分析：由程序框图知第一次运行112,224k S =+==+=，第二次运行213,8311k S =+==+=，第三次运行314,22426k S =+==+=，第四次运行4154,52557k S =+=>=+=，输出57S =，所以判断框内为4?k >，故选C.考点：程序框图.6．我国古代名著《庄子·天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完.现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取20天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是（ ）A ．20i <，1S S i=-，2i i = B ．20i ≤，1S S i=-，2i i = C ．20i <，2SS =，1i i =+ D ．20i ≤，2SS =，1i i =+ 【答案】D 【解析】 【分析】先由第一天剩余的情况确定循环体，再由结束条件确定循环条件即可. 【详解】根据题意可知，第一天12S =，所以满足2S S =，不满足1S S i=-，故排除AB ，由框图可知，计算第二十天的剩余时，有2SS =，且21i =，所以循环条件应该是20i ≤. 故选D. 【点睛】本题考查了程序框图的实际应用问题，把握好循环体与循环条件是解决此题的关键，属于中档题.7．《九章算术》卷第七——盈不足中有如下问题：“今有垣高九尺.瓜生其上，蔓日长七寸. 瓠生其下，蔓日长一尺.问几何日相逢.”翻译为“今有墙高9尺.瓜生在墙的上方，瓜蔓每天向下长7寸.葫芦生在墙的下方，葫芦蔓每天向上长1尺.问需要多少日两蔓相遇.”其中1尺=10寸.为了解决这一问题，设计程序框图如下所示，则输出的k 的值为（ ）A ．8B ．7C ．6D ．5【答案】C 【解析】 【分析】模拟执行程序，依次写出每次循环得到的a,n,S 的值，当S=-1.2时满足条件S 0£ 退出循环输出n 的值从而得解 【详解】运行该程序，第一次，9 1.77.3S =-=，2k =；第二次，7.3 1.7 5.6S =-=，3k =；第三次， 5.6 1.7 3.9S =-=，4k =；第四次， 3.9 1.7 2.2S =-=，5k =；第五次，2.2 1.70.5S =-=，6k =；第六次，0.5 1.7 1.2S =-=-，此时输出的k 的值为6 故选：C 【点睛】本题考查数学文化、算法与程序框图，考查推理论证能力以及化归与转化思想.8．执行如图所示的程序框图，若输人的[]1,1x ∈-，则输出的y 的取值范围为（ ）A ．(][),01,e -∞UB ．(]1,0,1e ⎡-∞⎤⎢⎥⎣⎦UC ．[)11,0,e⎡⎤⎢-⎥⎦∞⎣-+UD ．[][),10,e --+∞U【答案】B 【解析】 【分析】由程序框图，确定函数()f x 的解析式，然后可求得值域． 【详解】由程序框图可知，,10,ln ,01x e x y x x ⎧-≤≤=⎨<≤⎩，函数xy e =在区间[]1,0-上单调递增，值域为1,1e ⎡⎤⎢⎥⎣⎦；函数ln y x =在区间(]0,1上也单调递增，值域为(],0-∞，所以当[]1,1x ∈-时，y 的取值范围为(]1,0,1e ⎡-∞⎤⎢⎥⎣⎦U .故选：B ． 【点睛】本题考查程序框图及分段函数的值域. 本题可以画出分段函数,10,ln ,01x e x y x x ⎧-≤≤=⎨<≤⎩的图象，借助函数的图象求分段函数的值域.函数的值域为函数图象上所有点的纵坐标组成的集合.分段函数的值域为各段上函数值域的并集.9．某程序框图如图所示，若分别输入如下四个函数：1()f x x=，2()f x x =，2()f x e =，()sin f x x =，则可以输出的函数是（ ）A ．2()f x x =B ．1()f x x=C ．2()f x e =D ．()sin f x x =【答案】D 【解析】 【分析】分析程序框图中语言要求，得出输入函数()f x 具有的性质，然后针对四个选项一一分析即可得出答案. 【详解】由程序框图可得，当输入函数()f x ，并且输出函数()f x 本身时，则函数()f x 需满足两个条件：1、()()0f x f x +-=即得函数为奇函数；2、函数()f x 存在零点.则由函数2()f x x =和2()f x e =为偶函数故排除，函数1()f x x=不存在零点故排除，函数()sin f x x =为奇函数且存在零点满足题意. 故选：D. 【点睛】本题考查了程序框图的运用，考查了基本函数图象性质的运用，属于一般难度的题.10．执行如图所示的程序框图，则输出的a =（ ）A ．32-B ．13-C ．2D ．2-【答案】A 【解析】 【分析】根据循环程序框图，一次循环后，可知本题循环程序是求一个以3为周期的数列：2，13-，32-，2，13-，32-…，所以当2019i =时，输出结果，根据周期性，即可得出结果.【详解】解：根据程序框图，执行程序得： 2,1a i ==，否， 11,2213a i =-=-=+，否， 13,31213a i =-=-=-+，否， 12,4312a i =-==-+，否， 11,5213a i =-=-=+，否， 13,61213a i =-=-=-+，否， L可知本题循环程序是一个以3为周期的数列：2，13-，32-，2，13-，32-…， 当2019i =时，输出结果，则20193673÷=，即循环673个周期，所以输出结果为32-． 故选：A. 【点睛】本题考查由循环程序框图计算输出结果，理解循环结构框图是关键.11．某公司的财务报销流程图如图所示，则2019年初，采购人员为公司购进了一批办公用品，现准备报销此次所购的办公用品的经费，根据下面的流程图，则需要签字的次数为（ ）A ．5B ．4C ．3D ．2【答案】B 【解析】 【分析】首先从流程图中得到报销此次所购的办公用品的经费，需要采购整理票据并签字、后勤部门审核签字、财务总监审核签字、总经理审核签字共四道签字过程，从而得到答案. 【详解】根据题意，观察流程图，可知报销办公用品的经费，流程走右边的分支，需要采购整理票据并签字、后勤部门审核签字、财务总监审核签字、总经理审核签字共四道签字过程，所以需要签字的次数为4次， 故选B. 【点睛】该题考查的是有关流程图的问题，属于简单题目.12．如图所示是为了求出满足122222018n +++>L 的最小整数n ，和两个空白框中，可以分别填入（ ）A ．2018S >？，输出1n -B ．2018S >？，输出nC ．2018S ≤？，输出1n -D ．2018S ≤？，输出n【答案】A【解析】【分析】 通过要求122222018n +++>L 时输出且框图中在“是”时输出确定“”内应填内容；再通过循环体确定输出框的内容．【详解】因为要求122222018n +++>L 时输出，且框图中在“是”时输出，所以“”内输入“2018S >？”， 又要求n 为最小整数，所以“”中可以填入输出1n -，故选：A ．【点睛】本题考查了程序框图的应用问题，是基础题．13．执行如图所示的程序框图，令()y f x =，若()1f a >，则实数a 的取值范围是（ ）A ．(,2)(2,5]-∞⋃B ．(,1)(1,)-∞-+∞UC ．(,2)(2,)-∞⋃+∞D ．(,1)(1,5]-∞-⋃【答案】D【解析】 分析：先根据程序框图得()f x 解析式，再根据分段函数解三个不等式组，求并集得结果. 详解：因为2,2()=23,251,5x x f x x x x x⎧⎪≤⎪-<≤⎨⎪⎪>⎩，所以由()1f a >得25225112311a a a a a a >⎧≤<≤⎧⎧⎪⎨⎨⎨>->>⎩⎩⎪⎩或或 所以11225115a a a a a <-<≤<≤∴<-<≤或或或，因此选D.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.14．若框图所给的程序运行结果为，那么判断框中应填入的关于k 的条件是A ．？B ．？C ．？D ．？【答案】A【解析】【分析】根据所给的程序运行结果为，执行循环语句，当计算结果S 为20时，不满足判断框的条件，退出循环，从而到结论．【详解】 由题意可知输出结果为， 第1次循环，，， 第2次循环，，， 此时S 满足输出结果，退出循环，所以判断框中的条件为． 故选：A ．【点睛】本题主要考查了循环结构，是当型循环，当满足条件，执行循环，同时考查了推理能力，属于基础题．15．执行如图所示的程序框图，若输入如下四个函数：①f （x ）＝sinx ②f （x ）＝cosx ③1()f x x =④f （x ）＝x 2 则输出的函数是（ ）A ．f （x ）＝sinxB ．f （x ）＝cosxC ．1()f x x =D ．f （x ）＝x 2【答案】A【解析】 试题分析：对①()sin f x x =，显然满足()()0f x f x +-=，且存在零点.故选A. 考点：程序框图及函数的性质.16．执行如图所示的程序框图，若输出的S 为154，则输入的n 为（ ）A ．18B ．19C ．20D ．21【答案】B【解析】【分析】 找到输出的S 的规律为等差数列求和，即可算出i ，从而求出n .【详解】由框图可知，()101231154S i =+++++⋯+-= ，即()1231153i +++⋯+-=，所以()11532i i -=，解得18i =， 故最后一次对条件进行判断时18119i =+=，所以19n =.故选：B【点睛】本题考查程序框图，要理解循环结构的程序框图的运行，考查学生的逻辑推理能力.属于简单题目.17．在如图所示的程序框图中，若输出的值是3，则输入的x 的取值范围是（ ）A ．(2,)+∞B ．(4,10]C ．(2,4]D ．(4,)+∞【答案】B【解析】【分析】 由已知中的程序框图可知：该程序的功能是利用循环结构计算并输出变量i 的值，模拟程序的运行过程，分析循环中各变量值的变化情况，可得答案．【详解】解：设输入x a =，第一次执行循环体后，32x a =-，1i =，不满足退出循环的条件；第二次执行循环体后，98x a =-，2i =，不满足退出循环的条件；第三次执行循环体后，2726x a =-，3i =，满足退出循环的条件；故9882a -…，且272682a ->，解得：(4,10]a ∈，故选：B ．【点睛】本题考查的知识点是程序框图，当循环的次数不多，或有规律时，常采用模拟循环的方法解答，属于中档题．18．阅读如图所示的程序框图，运行相应的程序，输出的的值等于（ ）A ．30B ．31C ．62D ．63【答案】B【解析】【分析】 首先确定流程图的功能，然后计算其输出的结果即可.【详解】 由流程图可知该算法的功能为计算的值， 即输出值为：.故选：B.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．19．运行该程序框图，若输出的x 的值为16，则判断框中不可能填（ ）A ．5k ≥B ．4k >C ．9k ≥D ．7k >【答案】D运行该程序，第一次，1,k2x==,第二次，2,k3x==，第三次，4,k4x==，第四次，16,k5x==，第五次，4,k6x==，第六次，16,k7x==，第七次，4,k8x==，第八次，16,k9x==，观察可知，若判断框中为5k≥．，则第四次结束，输出x的值为16，满足；若判断框中为4k>．，则第四次结束，输出x的值为16，满足；若判断框中为9k≥．，则第八次结束，输出x的值为16，满足；若判断框中为7k>．，则第七次结束，输出x的值为4，不满足；故选D.20．我国古代名著《庄子g天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完.现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取7天后所剩木棍的长度(单位：尺)，则①②③处可分别填入的是( )A．17?,,+1i s s i ii≤=-=B．1128?,,2i s s i ii≤=-=C．17?,,+12i s s i ii≤=-=D．1128?,,22i s s i ii≤=-=【答案】B【分析】分析程序中各变量的作用，再根据流程图所示的顺序，可得该程序的作用是累加并输出S 的值，由此可得到结论.【详解】由题意，执行程序框图，可得：第1次循环：11,42S i=-=；第2次循环：111,824S i=--=；第3次循环：1111,16248S i=--==；依次类推，第7次循环：11111,256241288S i=----==L，此时不满足条件，推出循环，其中判断框①应填入的条件为：128?i≤，执行框②应填入：1S Si=-，③应填入：2i i=.故选：B.【点睛】本题主要考查了循环结构的程序框图的应用，其中解答中正确理解程序框图的含义是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.。

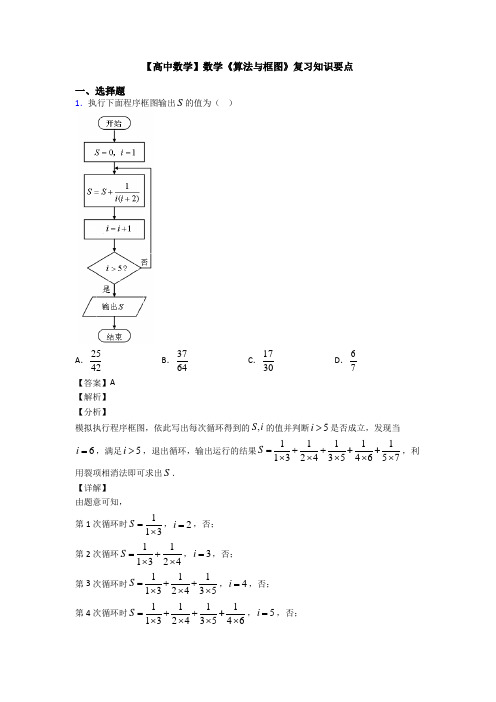
【高中数学】数学《算法与框图》复习知识要点一、选择题1．执行下面程序框图输出S 的值为（ ）A ．2542B ．3764C ．1730D ．67【答案】A【解析】【分析】模拟执行程序框图，依此写出每次循环得到的,S i 的值并判断5i >是否成立，发现当6i =，满足5i >，退出循环，输出运行的结果111111324354657S =++⨯⨯⨯⨯⨯++，利用裂项相消法即可求出S ．【详解】由题意可知，第1次循环时113S =⨯，2i =，否； 第2次循环111324S =+⨯⨯，3i =，否； 第3次循环时111132435S =++⨯⨯⨯，4i =，否； 第4次循环时111113243546S =++⨯⨯⨯⨯+，5i =，否；第5次循环时111111324354657S =+++⨯⨯⨯⨯⨯+，6i =，是； 故输出111111324354657S =++⨯⨯⨯⨯⨯++111111111112324354657⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫-+-+-+-+- ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦= 1111251226742⎛⎫=+--= ⎪⎝⎭ 故选：A.【点睛】本题主要考查程序框图中的循环结构，同时考查裂项相消法求和，属于基础题．2．若执行下面的程序框图，输出的值为3，则判断框中应填入的条件是（ ）A ．7?k <B ．6?k <C ．9?k <D ．8?k <【答案】D【解析】【分析】根据程序框图，写出运行结果，根据程序输出的结果是S=3，可得判断框内应填入的条件．【详解】根据程序框图，运行结果如下：S k第一次循环 log 23 3第二次循环 log 23•log 34 4第三次循环 log 23•log 34•log 45 5第四次循环 log 23•log 34•log 45•log 56 6第五次循环 log 23•l og 34•log 45•log 56•log 67 7第六次循环 log 23•log 34•log 45•log 56•log 67•log 78=log 28=3 8故如果输出S=3，那么只能进行六次循环，故判断框内应填入的条件是k ＜8． 故答案为：D ．【点睛】本题考查程序框图，尤其考查循环结构，对循环体每次循环需要进行分析并找出内在规律是解题关键.3．某程序框图如图所示，若输出的S=57，则判断框内为A ．k ＞4?B ．k ＞5?C ．k ＞6?D ．k ＞7?【答案】A【解析】试题分析：由程序框图知第一次运行112,224k S =+==+=，第二次运行213,8311k S =+==+=，第三次运行314,22426k S =+==+=，第四次运行4154,52557k S =+=>=+=，输出57S =，所以判断框内为4?k >，故选C. 考点：程序框图.4．执行如图所示的程序框图，如果输入n=3，输出的S=（ ）A．67B．37C．89D．49【答案】B【解析】【分析】【详解】试题分析：由题意得，输出的为数列的前三项和，而，∴，故选B.考点：1程序框图；2.裂项相消法求数列的和.【名师点睛】本题主要考查了数列求和背景下的程序框图问题，属于容易题，解题过程中首先要弄清程序框图所表达的含义，解决循环结构的程序框图问题关键是列出每次循环后的变量取值情况，循环次数较多时，需总结规律，若循环次数较少可以全部列出.5．我国古代数学著作《九章算术》中有如下问题：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米一斗五升(注：一斗为十升).问，米几何？”下图是解决该问题的程序框图，执行该程序框图，若输出的S=15(单位：升)，则输入的k的值为（）A．45 B．60 C．75 D．100【答案】B【解析】【分析】根据程序框图中程序的功能，可以列方程计算．【详解】由题意12315234S⨯⨯⨯=，60S=．故选：B.【点睛】本题考查程序框图，读懂程序的功能是解题关键．6．执行如图所示的程序框图，输出的结果为（）A ．919B ．1021C ．1819D ．2021【答案】B【解析】【分析】 根据程序框图得出2221114114214101S =+++⨯-⨯-⨯-L ，利用裂项相消法可求得输出的S 的值.【详解】 ()()21111141212122121i i i i i ⎛⎫==- ⎪--+-+⎝⎭Q ， 由程序框图可知，输出的S 的值为2221114114214101S =+++⨯-⨯-⨯-L 1111111012335192121⎛⎫=-+-++-= ⎪⎝⎭L . 故选：B.【点睛】本题考查利用程序框图计算输出结果，同时也考查了裂项求和法的应用，考查计算能力，属于中等题.7．运行如图所示的程序框图，若输入的a 的值为2时，输出的S 的值为20-，则判断框中可以填（ ）A ．3?k <B ．4?k <C ．5?k <D ．6?k <【答案】C【解析】【分析】 模拟执行程序框图的运行过程，即可得出程序运行后输出20S =-时判断框中可以填的条件.【详解】运行该程序：第一次循环，2,2,2S a k ==-=；第二次循环6,2,3S a k =-==；第三次循环，12,2,4S a k ==-=；第四次循环，20,2,5S a k =-==，此时输出S 的值，观察可知，仅选项C 符合题意.故选:C【点睛】本题主要考查含有当型循环结构的程序框图；考查学生的逻辑推理能力和运算求解能力；熟练掌握含有循环结构的程序框图的运行方法是求解本题的关键；属于中档题、常考题型.8．运行如图所示的程序框图，若输出z 是值为13，则判断框中可以填（ ）A ．3?z <B ．5?z <C ．8?z <D ．10?z <【答案】D【解析】【分析】 根据给定的程序框图，逐次计算，结合判断条件，即可求解，得到答案.【详解】由题意，运行该程序框图，可得，第一次3,2,3z x y ===；第二次5,3,5z x y ===；第三次8,5,8z x y ===；第四次13z =，此时需要输出z 的值，所以10?z <.故选：D .【点睛】算法与程序框图是高考的高频考点，试题往往依托循环结构进行考查，可以考查求值问题，也可以考查判断框中可以填写的条件，处理此类问题时，可以采用两种方法，一是列举法，二是归纳法，涉及项数较多的问题时，需要使用归纳法，看清算法本质.9．下列各数中，最小的是( )A ．101 010(2)B ．111(5)C ．32(8)D ．54(6)【答案】C【解析】 ()543221010101202120242=⨯+⨯+⨯+⨯=()210511115151531=⨯+⨯+⨯=()10832382826=⨯+⨯=()10654564634=⨯+⨯=故最小的是()832故答案选C10．执行如图所示的程序框图，则程序最后输出的结果为（ ）A ．15B ．25C ．35D ．45【答案】D【解析】【分析】模拟执行程序框图，读出程序框图实现的功能，即可求得输出结果.【详解】模拟执行程序框图，根据题意可知， 11,5k a ==； 22,5k a ==； 43,5k a ==； 34,5k a ==； 15,5k a ==； 26,5k a ==； L 故归纳总结可得a 的取值周期为4，结合题中判断条件，2019k ≥，又201950443=⨯+可知：输出的45a =. 故选：D.【点睛】本题考查求程序框图的输出结果，解题时，应模拟程序框图的运行结果得出结论，属中档题.11．执行如图所示的程序框图，若输入n 的值为13，输出S 的值是46，则a 的取值范围是（ ）A ．910a ≤<B ．910a <≤C ．1011a <≤D ．89a <≤【答案】B【解析】 分析：模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出46S =，即可得到输出条件.详解：输入13,0n S ==，第一次循环13,12S n ==；第二次循环25,11S n ==；第三次循环36,10S n ==；第四次循环46,9S n ==，输出46S =，此时应满足退出循环的条件，故a 的取值范围是9010<≤，故选B.点睛：本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.12．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例，若输入n ，x 的值分别为3，2，则输出v 的值为A ．35B ．20C ．18D ．9 【答案】C【解析】试题分析：模拟算法：开始：输入3,2,1,312,0n x v i i ====-=≥成立；1224v =⨯+=，211,0i i =-=≥成立；4219v =⨯+=，110,0i i =-=≥成立；92018v =⨯+=，011,0i i =-=-≥不成立，输出18v =.故选C.考点：1.数学文化；2.程序框图.13．执行如图所示的程序框图，若输出的结果为48，则输入k 的值可以为A ．6B ．10C ．8D ．4【答案】C【解析】【分析】 执行如图所示的程序框图，逐次循环，计算其运算的结果，根据选项即可得到答案.【详解】由题意可知，执行如图所示的程序框图，可知：第一循环：134,2146n S =+==⨯+=；第二循环：437,26719n S =+==⨯+=；第三循环：7310,2191048n S =+==⨯+=，要使的输出的结果为48，根据选项可知8k =，故选C.【点睛】本题主要考查了循环结构的计算与输出问题，其中解答中正确理解循环结构的程序框图的计算功能，逐次准确计算是解答的关键，着重考查了运算与求解能力，属于基础题.14．我国古代数学名著《九章算术》里有一道关于玉石的问题：“今有玉方一寸，重七两；石方一寸，重六两.今有石方三寸，中有玉，并重十一斤（176两）.问玉、石重各几何？”如图所示的程序框图反映了对此题的一个求解算法，运行该程序框图，则输出的x ，y 分别为（ ）A ．90，86B ．94，82C ．98，78D ．102，74【答案】C【解析】 执行程序框图，86,90,27x y s ==≠；90,86,27x y s ==≠；94,82,27x y s ==≠；98,78,27x y s ===，结束循环，输出的,x y 分别为98,78，故选C.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.15．如图所示的程序框图，则输出的,,x y z 的值分别是（ ）A ．13009，600，11203B ．1200，500，300C ．1100，400，600D ．300，500，1200 【答案】B【解析】【分析】根据程序框图依次计算得到答案.【详解】根据程序框图得：①300,1y i ==，满足3i <；②400,2y i ==，满足3i <； ③500,300y z ==，1200,3x i ==，不满足3i <.故输出的1200,500,300x y z ===. 故选：B .【点睛】本题考查了程序框图，意在考查学生的理解能力.16．鸡兔同笼，是中国古代著名的趣味题之一，《孙子算经》中就有这样的记载：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各有几何？设计如图的算法来解决这个问题，则判断框中应填入的是（ ）A ．94m >？B ．94m =？C ．35m =？D ．35m <？【答案】B【解析】【分析】 设鸡的数量为i ，兔子数量为j ,则腿的数量共有24m i j =+，判断m 是否为94即可得解.【详解】i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意，35j i =-从0i =开始，依次检验，只需判断足24m i j =+是否为94即可，故框中应填入“94m =？”.故选：B【点睛】本题主要考查了程序框图，循环结构，条件分支结构，属于中档题.17．阅读如图所示的程序框图，运行相应的程序，输出的的值等于（ ）A．30 B．31 C．62 D．63【答案】B【解析】【分析】首先确定流程图的功能，然后计算其输出的结果即可.【详解】由流程图可知该算法的功能为计算的值，即输出值为：.故选：B.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．18．根据下面的程序框图，输出的S的值为（）A．1007 B．1009 C．0 D．-1【答案】A【解析】【分析】按照程序框图模拟运行即可得解.【详解】1 i=，1112x==--，0(1)1S=+-=-；2i=，111(1)2x==--，11122S=-+=-；3i=，12112x==-，13222S=-+=；4i=，1112x==--，31(1)22S=+-=，…，由此可知，运行程序过程中，x呈周期性变化，且周期为3，所以输出112672110072S⎛⎫=-++⨯-=⎪⎝⎭.故选A【点睛】本题主要考查程序框图和数列的周期性，意在考查学生对这些知识的理解掌握水平和分析推理能力.19．执行如图的程序框图，那么输出S的值是( )A．-1 B．12C．2 D．1【答案】C【解析】判断2014<2017,执行1120141201512S k==-=+=-，；判断2015<2017,执行11201512016112S k，（）===+=--；判断2016<2017,执行12201612017112S k===+=-，；判断2017<2017,执行输出S,S=2；故选C点睛：本题考查的是算法与流程图，侧重于对流程图循环结构的考查.解决问题要先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.20．执行如图所示的程序框图，则输出的a=（）A．32-B．13-C．2 D．2-【答案】A【解析】【分析】根据循环程序框图，一次循环后，可知本题循环程序是求一个以3为周期的数列：2，13-，32-，2，13-，32-…，所以当2019i=时，输出结果，根据周期性，即可得出结果.【详解】解：根据程序框图，执行程序得：2,1a i==，否，11,2213a i=-=-=+，否，13,31213a i =-=-=-+，否， 12,4312a i =-==-+，否， 11,5213a i =-=-=+，否， 13,61213a i =-=-=-+，否， L 可知本题循环程序是一个以3为周期的数列：2，13-，32-，2，13-，32-…， 当2019i =时，输出结果，则20193673÷=，即循环673个周期， 所以输出结果为32-． 故选：A.【点睛】本题考查由循环程序框图计算输出结果，理解循环结构框图是关键.。

新《算法与框图》专题解析一、选择题1．阅读下侧程序框图，为使输出的数据为，则①处应填的数字为A．B．C．D．【答案】B【解析】考点：程序框图．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环求S的值，我们用表格列出程序运行过程中各变量的值的变化情况，不难给出答案．解：程序在运行过程中各变量的值如下表示：S i 是否继续循环循环前 1 1/第一圈3 2 是第二圈7 3 是第三圈15 4 是第四圈31 5 否故最后当i＜5时退出，故选B．2．明朝数学家程大位将“孙子定理”（也称“中国剩余定理”）编成易于上口的《孙子歌诀》：三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五便得知．已知正整数n被3除余2,被5除余3，被7除余4，求n的最小值．按此歌诀得算法如图，则输出n 的结果为（）A．53 B．54 C．158 D．263【答案】A【解析】按程序框图知n的初值为263，代入循环结构，第一次循环158n=，第二次循环53,53105n=<，推出循环，n的输出值为53，故选A.3．执行如图所示的程序框图，若输出S的值为43，则输入a的值可能为（）A．4 B．10 C．79 D．93【答案】D【解析】【分析】由题中的程序框图知，该算法是一个以4为周期的函数，若输出S的值为43，则得出相应的k值，再由k a>输出，即可得出a值，再判断选项得出【详解】程序运行如下：3,1S k ==；4,23S k ==；1,32S k ==； 2,4S k =-=；3,5S k ==；…，此程序的S 值4个一循环.若输出S 的值为43，则相应k 的值为()1142k k N +∈， 因为k a >时，输出S ，则输入a 的值为()1141k k N +∈.故选：D .【点睛】本题考查了循环结构的程序框图，根据算法的功能确定S 值的周期规律及跳出循环的k 值是解答本题的关键，属于中档题．4．程大位是明代著名数学家，他的《新编直指算法统宗》是中国历史上一部影响巨大的著作．卷八中第33问：“今有三角果一垛，底阔每面七个．问该若干？”如图是解决该问题的程序框图．执行该程序框图，求得该垛果子的总数S 为（ ）A ．28B ．56C ．84D ．120【答案】C【解析】【分析】 由已知中的程序可知：该程序的功能是利用循环结构计算并输出变量S 的值，模拟程序运行过程，分析循环中各变量值的变化情况，即可求解.【详解】模拟程序的运行，可得：0,0,0i n S ===执行循环体，1,1,1i n S ===；不满足判断条件7i ≥，执行循环体，2,3,4i n S ===；不满足判断条件7i ≥，执行循环体，3,6,10i n S ===；不满足判断条件7i ≥，执行循环体，4,10,20i n S ===；不满足判断条件7i ≥，执行循环体，5,15,35i n S ===；不满足判断条件7i ≥，执行循环体，6,21,56i n S ===；不满足判断条件7i ≥，执行循环体，7,28,84i n S ===；满足判断条件7i ≥，退出循环，输出S 的值为84.故选：C.【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中模拟程序运行的过程，通过逐次计算和找出计算的规律是解答的关键，着重考查了推理与计算能力，属于基础题.5．如图所示的程序框图，若输出的结果为4，则输入的实数的取值范围是（ ）A ．B ．C ．D ． 【答案】A 【解析】，，否，； ，否，； ，否，； ，，是，即； 解不等式，，且满足，，综上所述，若输出的结果为4，则输入的实数的取值范围是，故选． 点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.6．某程序框图如图所示，其中()1g n n n=++，若输出的20201S =，则判断框内应填入的条件为（ ）A ．2020?n <B ．2020?n ≤C ．2020?n >D ．2020?n ≥【答案】A【解析】【分析】 运行该程序，当n 的值为2019时，满足判断框内的条件；当n 的值为2020时，不满足判断框内的条件，退出循环，输出S 的值，结合选项可选出答案.【详解】由题意，()11g n n n n n ==+++， 运行该程序，输入0,1S n ==，判断框成立；则()0121S g =+=，2n =，判断框成立； 则()21231S g =+=，3n =，判断框成立； 则()31341S g +=，4n =，判断框成立；… 则20191S =，2019n =，判断框成立； 则20201S =，2020n =，判断框不成立，输出20201S =.故判断框内应填入的条件为2020?n <.故选：A【点睛】本题考查程序框图，考查学生的推理能力，属于中档题.7．执行如图所示的程序框图，则输出的结果为A．4 B．5 C．6 D．7【答案】B【解析】【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的的值.【详解】第一次循环，；第二次循环，；第三次循环，，退出循环，输出，故选B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.8．执行如图所示的程序框图，则输出的S （）A ．5050B ．5151C ．2500D ．2601【答案】C【解析】【分析】 模拟程序的运行，依次写出每次循环得到的S ，i 的值，可得当101i =时，不满足条件100i ≤，退出循环，输出S 的值．【详解】解：模拟程序的运行，可得：1,0,100i S i ==≤，是，0+1=13,100S i i ==≤，，是，1+35,100S i i ==≤，，是，1+3+57,100S i i ==≤，，是，1+3+5+79,100S i i ==≤，，是，L由题可知：当99i =时，100i ≤，是，135799,101,100S i i =+++++=≤L ，否，输出135799S =+++++L ，即()50199505025002S +==⨯=. 故选：C.【点睛】 本题考查循环结构的程序框图的应用，当循环的次数不多或有规律时，常采用模拟执行程序的方法解决．9．中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的，，依次输入的为2，2，5，则输出的（ ）A ．7B ．12C ．17D ．34【答案】C【解析】 第一次循环：2,2,1a s k === ；第二次循环：2,6,2a s k === ；第三次循环：5,17,32a s k ===> ；结束循环，输出17s = ，选C.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.10．执行如图所示的程序框图，输出的结果为（ ）A ．919B ．1021C ．1819D ．2021【答案】B【解析】【分析】 根据程序框图得出2221114114214101S =+++⨯-⨯-⨯-L ，利用裂项相消法可求得输出的S 的值.【详解】 ()()21111141212122121i i i i i ⎛⎫==- ⎪--+-+⎝⎭Q ， 由程序框图可知，输出的S 的值为2221114114214101S =+++⨯-⨯-⨯-L 1111111012335192121⎛⎫=-+-++-= ⎪⎝⎭L . 故选：B.【点睛】本题考查利用程序框图计算输出结果，同时也考查了裂项求和法的应用，考查计算能力，属于中等题.11．执行如图的程序框图，那么输出S 的值是( )A．-1 B．12C．2 D．1【答案】C【解析】判断2014<2017,执行1120141201512S k==-=+=-，；判断2015<2017,执行11201512016112S k，（）===+=--；判断2016<2017,执行12201612017112S k===+=-，；判断2017<2017,执行输出S,S=2；故选C点睛：本题考查的是算法与流程图，侧重于对流程图循环结构的考查.解决问题要先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.12．阅读下边程序框图，为使输出的数据为31，则①处应填的数字为（）A．3 B．4 C．5 D．6【答案】C【解析】【分析】根据程序框图知，表示求和2122...221n n S +=+++=-，解得答案. 【详解】程序框图表示求和2122...221n n S +=+++=-，取13121n S +==-，解得4n =. 故① 处应填的数字为5. 故选：C . 【点睛】本题考查了程序框图，意在考查学生的计算能力和理解能力.13．运行如图所示的程序框图，若输出的S 的值为1011，则判断框中可以填（ ）A ．2020?i >B ．2021?i ≥C ．2022?i >D ．2023?i >【答案】C 【解析】 【分析】利用程序框图的功能，进行模拟计算即可． 【详解】程序的功能是计算S ＝1sin2π+3sin 32π+5sin+52π…＝1﹣3+5﹣7+9+…+，则1011＝1+505×2＝1﹣3+5﹣7+9+…则第1011个奇数为2×1011﹣1＝2021不成立， 第1012个奇数为2×1012﹣1＝2023成立， 故条件为i ＞2022？， 故选C ． 【点睛】本题主要考查程序框图的应用，利用程序框图的功能是解决本题的关键，属于基础题.14．已知二进制数(2)1010化为十进制数为n ，若()n x a +的展开式中，7x 的系数为15，则实数a 的值为（ ）A ．12B ．15C ．1D ．2【答案】A 【解析】 【分析】先利用进制转化求出n 的值,再利用二项展开式的通项公式,结合题意列式求得a 的值. 【详解】根据进制转换法可得:31(2)1010121210=⨯+⨯=, 所以10n =,设10()x a +展开式的通项为10110C kkk k T x a -+=,令107k -=,∴3k =,∴7x 的系数为3310C 15a =,∴318a =,∴12a =,故选:A. 【点睛】本题考查二项式,考查进制转换,需要学生对基础知识牢固掌握且灵活运用.15．执行如图所示的程序框图，若输出的结果为11，则图中的判断条件可以为（ ）A ．1?S >-B ．0?S <C ．–1?S <D ．0?S >【答案】B 【解析】 【分析】根据程序框图知当11=i 时，循环终止，此时1lg110S =-<，即可得答案. 【详解】1i =，1S =.运行第一次，11lg 1lg30,33S i =+=->=，不成立，运行第二次，131lg lg 1lg50,535S i =++=->=，不成立，运行第三次，1351lg lg lg 1lg70,7357S i =+++=->=，不成立，运行第四次，13571lg lg lg lg 1lg90,93579S i =++++=->=，不成立，运行第五次，135791lg lg lg lg lg 1lg110,11357911S i =+++++=-<=，成立，输出i 的值为11，结束. 故选：B. 【点睛】本题考查补充程序框图判断框的条件，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意模拟程序一步一步执行的求解策略.16．执行如图所示的程序框图，令()y f x =，若()1f a >，则实数a 的取值范围是（ ）A ．(,2)(2,5]-∞⋃B ．(,1)(1,)-∞-+∞UC ．(,2)(2,)-∞⋃+∞D ．(,1)(1,5]-∞-⋃【答案】D 【解析】分析：先根据程序框图得()f x 解析式，再根据分段函数解三个不等式组，求并集得结果.详解：因为2,2()=23,251,5x x f x x x x x ⎧⎪≤⎪-<≤⎨⎪⎪>⎩，所以由()1f a >得25225112311a a a a a a >⎧≤<≤⎧⎧⎪⎨⎨⎨>->>⎩⎩⎪⎩或或 所以11225115a a a a a <-<≤<≤∴<-<≤或或或， 因此选D.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.17．若框图所给的程序运行结果为，那么判断框中应填入的关于k 的条件是A ．？B ．？C ．？D ．？【答案】A 【解析】 【分析】根据所给的程序运行结果为，执行循环语句，当计算结果S 为20时，不满足判断框的条件，退出循环，从而到结论．【详解】由题意可知输出结果为， 第1次循环，，， 第2次循环，，，此时S 满足输出结果，退出循环，所以判断框中的条件为．故选：A ． 【点睛】本题主要考查了循环结构，是当型循环，当满足条件，执行循环，同时考查了推理能力，属于基础题．18．执行如图所示的程序框图，若输出的120S =，则判断框内应填入的条件是( )A ．4k >B ．5k >C ．6k >D ．7k >【答案】B 【解析】 【分析】分析程序中两个变量和流程图可知，该算法为先计算后判断的直到型循环，模拟执行程序，即可得到答案. 【详解】 程序执行如下k2S S k =+终止条件判断 0否 1011+= 否 2 2224⨯+=否 324311⨯+= 否 4 211426⨯+= 否 5 226557⨯+=否6 2576120⨯+= 是故当6k =时120S =，程序终止，所以判断框内应填入的条件应为5k >. 故选：B. 【点睛】本题考查了循环结构的程序框图，正确判断循环的类型和终止循环的条件是解题关键19．执行如图所示的程序框图，若输入，则输出的S 的值是A ．B ．C ．D ．【答案】B 【解析】 【分析】本题首先可以通过程序框图明确输入的数值以及程序框图中所包含的关系式，然后按照程序框图所包含的关系式进行循环运算，即可得出结果． 【详解】由程序框图可知，输入，，，第一次运算：，；第二次运算：，；第三次运算：，；第四次运算：，；第五次运算：，；第六次运算：，；第七次运算：，；第八次运算：，；第九次运算：，；第十次运算：，，综上所述，输出的结果为，故选B．【点睛】本题考查程序框图的相关性质，主要考查程序框图的循环结构以及裂项相消法的使用，考查推理能力，提高了学生从题目中获取信息的能力，体现了综合性，提升了学生的逻辑推理、数学运算等核心素养，是中档题．20．《九章算术》卷第七——盈不足中有如下问题：“今有垣高九尺.瓜生其上，蔓日长七寸. 瓠生其下，蔓日长一尺.问几何日相逢.”翻译为“今有墙高9尺.瓜生在墙的上方，瓜蔓每天向下长7寸.葫芦生在墙的下方，葫芦蔓每天向上长1尺.问需要多少日两蔓相遇.”其中1尺=10寸.为了解决这一问题，设计程序框图如下所示，则输出的k的值为（）A ．8B ．7C ．6D ．5【答案】C 【解析】 【分析】模拟执行程序，依次写出每次循环得到的a,n,S 的值，当S=-1.2时满足条件S 0£ 退出循环输出n 的值从而得解 【详解】运行该程序，第一次，9 1.77.3S =-=，2k =；第二次，7.3 1.7 5.6S =-=，3k =；第三次， 5.6 1.7 3.9S =-=，4k =；第四次， 3.9 1.7 2.2S =-=，5k =；第五次，2.2 1.70.5S =-=，6k =；第六次，0.5 1.7 1.2S =-=-，此时输出的k 的值为6 故选：C 【点睛】本题考查数学文化、算法与程序框图，考查推理论证能力以及化归与转化思想.。

数学《算法与框图》试卷含答案一、选择题1．执行如图所示的程序框图，若输出的结果为11，则图中的判断条件可以为（ ）A ．1?S >-B ．0?S <C ．–1?S <D ．0?S >【答案】B【解析】【分析】 根据程序框图知当11=i 时，循环终止，此时1lg110S =-<，即可得答案.【详解】1i =，1S =.运行第一次，11lg 1lg30,33S i =+=->=，不成立，运行第二次， 131lg lg 1lg50,535S i =++=->=，不成立，运行第三次， 1351lg lg lg 1lg70,7357S i =+++=->=，不成立，运行第四次， 13571lg lg lg lg 1lg90,93579S i =++++=->=，不成立，运行第五次， 135791lg lg lg lg lg 1lg110,11357911S i =+++++=-<=，成立， 输出i 的值为11，结束.故选：B.【点睛】本题考查补充程序框图判断框的条件，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意模拟程序一步一步执行的求解策略.2．某程序框图如图所示，若输出S ＝3，则判断框中M 为（ ）A ．k ＜14？B ．k≤14？C ．k≤15？D ．k ＞15？ 【答案】B【解析】【分析】 由框图程序可知12231S k k =++++L 可得解【详解】 由框图程序可知12231S k k =++++L 11n n n n =+++ 所以213243111S n n n =++=+L 所以113S n =+=，解得15n =，即当15n =时程序退出，故选B ．【点睛】 算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.3．某程序框图如图所示，若输出的S=57，则判断框内为A ．k ＞4?B ．k ＞5?C ．k ＞6?D ．k ＞7?【答案】A【解析】试题分析：由程序框图知第一次运行112,224k S =+==+=，第二次运行213,8311k S =+==+=，第三次运行314,22426k S =+==+=，第四次运行4154,52557k S =+=>=+=，输出57S =，所以判断框内为4?k >，故选C. 考点：程序框图.4．我国古代名著《庄子·天下篇》中有一句名言“一尺之棰，日取其半，万世不竭”，其意思为：一尺的木棍，每天截取一半，永远都截不完.现将该木棍依此规律截取，如图所示的程序框图的功能就是计算截取20天后所剩木棍的长度（单位：尺），则①②③处可分别填入的是（ ）A ．20i <，1S S i =-，2i i =B ．20i ≤，1S S i =-，2i i =C ．20i <，2S S =，1i i =+ D ．20i ≤，2S S =，1i i =+ 【答案】D【解析】【分析】 先由第一天剩余的情况确定循环体，再由结束条件确定循环条件即可.【详解】根据题意可知，第一天12S =，所以满足2S S =，不满足1S S i=-，故排除AB ， 由框图可知，计算第二十天的剩余时，有2S S =，且21i =，所以循环条件应该是20i ≤. 故选D.【点睛】 本题考查了程序框图的实际应用问题，把握好循环体与循环条件是解决此题的关键，属于中档题.5．执行如图所示的程序框图，则输出的结果为A ．4B ．5C ．6D ．7【答案】B【解析】【分析】 模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的的值.【详解】第一次循环，； 第二次循环，； 第三次循环，，退出循环，输出，故选B.本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.6．执行如图所示的程序框图，输出的结果为（ ）A ．919B ．1021C ．1819D ．2021【答案】B【解析】【分析】 根据程序框图得出2221114114214101S =+++⨯-⨯-⨯-L ，利用裂项相消法可求得输出的S 的值.【详解】 ()()21111141212122121i i i i i ⎛⎫==- ⎪--+-+⎝⎭Q ， 由程序框图可知，输出的S 的值为2221114114214101S =+++⨯-⨯-⨯-L 1111111012335192121⎛⎫=-+-++-= ⎪⎝⎭L . 故选：B.本题考查利用程序框图计算输出结果，同时也考查了裂项求和法的应用，考查计算能力，属于中等题.7．阅读如图所示的程序框图，若输入的1a b i ===，则输出的a 的值为( )A ．2019B ．1C ．2018D ．2016【答案】B【解析】【分析】 根据程序框图进行运算即可.【详解】将,,a b i 的值用表格表示如下： a 1 2 1 1- 2- 1- 1 …b 1 1- 2- 1- 1 21 (i)1 2 3 4 56 7 … 由表可知，a 的值以6为周期循环，201963363,3i ÷=⋅⋅⋅⋅⋅⋅=时对应的1a =. 故选：B【点睛】本题主要考查了程序框图的计算，考查了学生的运算求解能力.8．阅读下侧程序框图，为使输出的数据为，则①处应填的数字为A．B．C．D．【答案】B【解析】考点：程序框图．分析：分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是利用循环求S的值，我们用表格列出程序运行过程中各变量的值的变化情况，不难给出答案．解：程序在运行过程中各变量的值如下表示：S i 是否继续循环循环前 1 1/第一圈3 2 是第二圈7 3 是第三圈15 4 是第四圈31 5 否故最后当i＜5时退出，故选B．9．明朝数学家程大位将“孙子定理”（也称“中国剩余定理”）编成易于上口的《孙子歌诀》：三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五便得知．已知正整数n被3除余2,被5除余3，被7除余4，求n的最小值．按此歌诀得算法如图，则输出n 的结果为（）A．53 B．54 C．158 D．263【答案】A【解析】n=，第二次循环按程序框图知n的初值为263，代入循环结构，第一次循环15853,53105n=<，推出循环，n的输出值为53，故选A.10．我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争.小僧三人分一个，大小和尚各几丁？”.如右图所示的程序框图反映了对此问题的一个求解算法，则输出n的值为（）A ．20B ．25C ．30D ．35【答案】B【解析】【分析】 模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的n 的值.【详解】输出20,80,100n m s ==≠；21,79,100n m s ==≠；22,78,100n m s ==≠；23,77,100n m s ==≠；24,76,100n m s ==≠；25,75,100n m s ===，退出循环，输出25n =，故选B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.11．执行如图所示的程序框图，则输出的结果是（ ）A ．5B ．7C ．9D ．11【答案】C【解析】循环依次为123,123;S K =+==+=369,325;S K =+==+=91019,527;S K =+==+=191433,729;S K =+==+=结束循环,输出9;K =选C.12．执行如图所示的程序框图，若输出的S 的值为2670，则判断框中的条件可以为（）A ．5?i <B ．6?i <C ．7?i <D ．8?i <【答案】B【解析】阅读流程图，程序运行如下：第一次循环：1,2,12S S i S S i i i =⨯==+==+=；第二次循环：4,6,13S S i S S i i i =⨯==+==+=；第三次循环：18,21,14S S i S S i i i =⨯==+==+=；第四次循环：84,88,15S S i S S i i i =⨯==+==+=；第五次循环：440,445,16S S i S S i i i =⨯==+==+=；第六次循环：2670S S i =⨯=；由题意可知，此时程序应跳出循环，则判断框中的条件可以为6?i <本题选择B选项.点睛：一是利用循环结构表示算法，一定要先确定是用当型循环结构，还是用直到型循环结构；当型循环结构的特点是先判断再循环，直到型循环结构的特点是先执行一次循环体，再判断；二是注意输入框、处理框、判断框的功能，不可混用；三是赋值语句赋值号左边只能是变量，不能是表达式，右边的表达式可以是一个常量、变量或含变量的运算式．13．（北京师范大学附中2018届高三下学期第二次模拟）习总书记在十九大报告中指出：坚定文化自信，推动社会主义文化繁荣兴盛．如图，“大衍数列”：0，2，4，8，12来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和．如图是求大衍数列前n项和的程序框图．执行该程序框图，输入8m=，则输出的S=A．44 B．68C．100 D．140【答案】C【解析】第1次运行，211,0,0002nn a S-====+=，不符合n m≥，继续运行；第2次运行，22,2,0222nn a S====+=，不符合n m≥，继续运行；第3次运行，213,4,4262nn a S-====+=，不符合n m≥，继续运行；第4次运行，24,8,86142nn a S====+=，不符合n m≥，继续运行；第5次运行，215,12,1412262nn a S-====+=，不符合n m≥，继续运行；第6次运行，26,18,2618442nna S====+=，不符合n m≥，继续运行；第7次运行，217,24,2444682nn a S-====+=，不符合n m≥，继续运行；第8次运行，28,32,68321002nn a S====+=，符合n m≥，推出运行，输出100S=；故选C14．执行如图所示的程序框图，令()y f x=，若()1f a>，则实数a的取值范围是（）A．(,2)(2,5]-∞⋃B．(,1)(1,)-∞-+∞UC．(,2)(2,)-∞⋃+∞D．(,1)(1,5]-∞-⋃【答案】D【解析】分析：先根据程序框图得()f x解析式，再根据分段函数解三个不等式组，求并集得结果.详解：因为2,2()=23,251,5x xf x x xxx⎧⎪≤⎪-<≤⎨⎪⎪>⎩，所以由()1f a>得25225112311aa aa aa>⎧≤<≤⎧⎧⎪⎨⎨⎨>->>⎩⎩⎪⎩或或所以11225115a a a a a<-<≤<≤∴<-<≤或或或，因此选D.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.15．下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图，若输入a 、b 、i 的值分别为6、8、0，则输出a 和i 的值分别为（ ）A ．0，3B ．0，4C ．2，3D ．2，4【答案】C【解析】【分析】 执行循环，直至a b =终止循环输出结果.【详解】执行循环，得1,2;2,4;3,2i b i a i a ======，结束循环，输出2,2a b ==，此时3i =,选C.【点睛】算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.16．若框图所给的程序运行结果为，那么判断框中应填入的关于k 的条件是A ．？B ．？C ．？D ．？【答案】A【解析】【分析】 根据所给的程序运行结果为，执行循环语句，当计算结果S 为20时，不满足判断框的条件，退出循环，从而到结论． 【详解】 由题意可知输出结果为， 第1次循环，，， 第2次循环，，，此时S 满足输出结果，退出循环，所以判断框中的条件为．故选：A ．【点睛】本题主要考查了循环结构，是当型循环，当满足条件，执行循环，同时考查了推理能力，属于基础题．17．执行如图所示的程序框图，若输入如下四个函数：①f （x ）＝sinx ②f （x ）＝cosx ③1()f x x =④f （x ）＝x 2 则输出的函数是（ ）A ．f （x ）＝sinxB ．f （x ）＝cosxC ．1()f x x =D ．f （x ）＝x 2【答案】A【解析】 试题分析：对①()sin f x x =，显然满足()()0f x f x +-=，且存在零点.故选A. 考点：程序框图及函数的性质.18．执行如图所示的程序框图，若输出的S 为154，则输入的n 为（ ）A ．18B ．19C ．20D ．21【答案】B【解析】【分析】 找到输出的S 的规律为等差数列求和，即可算出i ，从而求出n .【详解】由框图可知，()101231154S i =+++++⋯+-= ，即()1231153i +++⋯+-=，所以()11532i i -=，解得18i =， 故最后一次对条件进行判断时18119i =+=，所以19n =.故选：B【点睛】本题考查程序框图，要理解循环结构的程序框图的运行，考查学生的逻辑推理能力.属于简单题目.19．根据下面的程序框图，输出的S 的值为（ ）A ．1007B ．1009C ．0D ．-1【答案】A【解析】【分析】按照程序框图模拟运行即可得解.【详解】1 i=，1112x==--，0(1)1S=+-=-；2i=，111(1)2x==--，11122S=-+=-；3i=，12112x==-，13222S=-+=；4i=，1112x==--，31(1)22S=+-=，…，由此可知，运行程序过程中，x呈周期性变化，且周期为3，所以输出112672110072S⎛⎫=-++⨯-=⎪⎝⎭.故选A【点睛】本题主要考查程序框图和数列的周期性，意在考查学生对这些知识的理解掌握水平和分析推理能力.20．《九章算术》是中国古代第一部数学专著，是《算经十书》中最重要的一种，成于公元一世纪左右，它是一本综合性的历史著作，是当时世界上最简练有效的应用数学．“更相减损术”便是《九章算术》中记录的一种求最大公约数的算法，按其算理流程有如下流程框图，若输入的a b、分别为96、36，则输出的i为( )A．4 B．5 C．6 D．7【答案】A【解析】解：由程序框图可知：当a=96，b=36时，满足a＞b，则a=96-36=60，i=1由a＞b，则a=60-36=24，i=2由a＜b，则b=36-24=12，i=3由a>b，则b=24-12=12，i=4由a=b=12，输出i=4．故选A．。

新数学《算法与框图》试卷含答案一、选择题1．执行如图所示的程序框图，则输出的S =（ ）A ．5050B ．5151C ．2500D ．2601【答案】C 【解析】 【分析】模拟程序的运行，依次写出每次循环得到的S ，i 的值，可得当101i =时，不满足条件100i ≤，退出循环，输出S 的值． 【详解】解：模拟程序的运行，可得： 1,0,100i S i ==≤，是， 0+1=13,100S i i ==≤，，是， 1+35,100S i i ==≤，，是， 1+3+57,100S i i ==≤，，是，1+3+5+79,100S i i ==≤，，是，L由题可知：当99i =时，100i ≤，是，135799,101,100S i i =+++++=≤L ，否，输出135799S =+++++L ，即()50199505025002S +==⨯=.故选：C. 【点睛】本题考查循环结构的程序框图的应用，当循环的次数不多或有规律时，常采用模拟执行程序的方法解决．2．某程序框图如图所示，若分别输入如下四个函数：1()f x x=，2()f x x =，2()f x e =，()sin f x x =，则可以输出的函数是（ ）A ．2()f x x =B ．1()f x x=C ．2()f x e =D ．()sin f x x =【答案】D 【解析】 【分析】分析程序框图中语言要求，得出输入函数()f x 具有的性质，然后针对四个选项一一分析即可得出答案. 【详解】由程序框图可得，当输入函数()f x ，并且输出函数()f x 本身时，则函数()f x 需满足两个条件：1、()()0f x f x +-=即得函数为奇函数；2、函数()f x 存在零点.则由函数2()f x x =和2()f x e =为偶函数故排除，函数1()f x x=不存在零点故排除，函数()sin f x x =为奇函数且存在零点满足题意. 故选：D. 【点睛】本题考查了程序框图的运用，考查了基本函数图象性质的运用，属于一般难度的题.3．执行如图所示的程序框图，若输出的S 的值为0，则中可填入( )A ．2m m =+B ．1=+m mC ．1m m =-D ．2m m =-【答案】A 【解析】 【分析】根据程序运行，将每一个选项代入试运行，算出其输出结果，从而选出答案. 【详解】对选项A ，2,4S m ==，则()2424S =⨯-=;4,6S m ==,则()4648S =⨯-=8,8S m ==,则()8880S =⨯-=,所以输出结果0S =,所以正确.对选项B ，2,4S m ==，则()2424S =⨯-=;4,5S m ==,则()4544S =⨯-=4,6S m ==,则()4648S =⨯-=8,7S m ==,则()87880S =⨯-=-<，输出结果8S =-,所以不正确.对选项C ，2,4S m ==，则()2424S =⨯-=;4,3S m ==,则()43440S =⨯-=-<，输出结果4S =-,所以不正确.对选项D ，2,4S m ==，则()2424S =⨯-=;4,2S m ==,则()42480S =⨯-=-<,所以输出结果8S =-,所以不正确.故选：A 【点睛】本题考查程序框图中循环，考查补全程序结构，属于中档题.4．某程序框图如图所示，若该程序运行后输出的结果为86，则正整数k 的最小值为（ ）A ．1 806B ．43C ．48D ．42【答案】B 【解析】 【分析】根据已知中的程序框图，模拟程序的执行过程，可得答案． 【详解】解：开始，n ＝1，S ＝1，故S ＝2×1＋1＝3，n ＝1×(1＋1)＝2， S 与输出的结果不符，故2≥k 不成立． S ＝2×3＋2＝8，n ＝2×(2＋1)＝6， S 与输出的结果不符，故6≥k 不成立． S ＝2×8＋6＝22，n ＝6×(6＋1)＝42， S 与输出的结果不相符，故42≥k 不成立． S ＝2×22＋42＝86，n ＝42×(42＋1)＝1 806. S 与输出的结果相符，故1 806≥k 成立． 所以k 的最小值为43. 故选：B. 【点睛】本题考查的知识点是程序框图，难度不大，属于基础题．5．下列各数中，最小的是( ) A ．101 010(2) B ．111(5)C ．32(8)D ．54(6)【答案】C 【解析】()543221010101202120242=⨯+⨯+⨯+⨯=()210511115151531=⨯+⨯+⨯= ()10832382826=⨯+⨯= ()10654564634=⨯+⨯=故最小的是()832 故答案选C6．阅读如图的程序框图，运行相应的程序，则输出的a 的值为（ ）A ．2-3B ．3-2C ．52D ．25【答案】C 【解析】 【分析】根据给定的程序框图，计算前几次的运算规律，得出运算的周期性，确定跳出循环时的n 的值，进而求解a 的值，得到答案. 【详解】 由题意，3,15a n ==， 第1次循环，2,23a n =-=，满足判断条件； 第2次循环，5,32a n ==，满足判断条件； 第3次循环，3,45a n ==，满足判断条件； L L可得a 的值满足以3项为周期的计算规律，所以当2019n =时，跳出循环，此时n 和3n =时的值对应的a 相同，即52a =.【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中认真审题，得出程序运行时的计算规律是解答的关键，着重考查了推理与计算能力.7．利用如图算法在平面直角坐标系上打印一系列点，则打印的点在圆2225x y +=内的个数为（ ）A ．2B ．3C ．4D ．5【答案】C 【解析】3,6x y =-= 时，打印点()3,6-不在圆内，2,5x y =-= ，50i => 是；打印点()2,5- 不在圆内，1,4x y =-= ，40i => 是；打印点()1,4-在圆内，0,3x y == ，30i => 是；打印点()0,3 在圆内，1,2x y == ，20i =>是；打印点()1,2在圆内，2,1x y == ，10i =>是；打印点()2,1在圆内，3,0x y == ，00i =>否，结束，所以()()()()1,40,31,22,1-共4个点在圆内，故选C.8．执行如图所示的程序框图，若输出的结果为126，则判断框内的条件可以为（ ）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤【答案】B【分析】根据框图，模拟程序运行即可求解. 【详解】根据框图，执行程序，12,2S n ==；1222,3S n =+=；⋯12222,1i S n i =++⋯+=+，令12222126i S =++⋯+=， 解得6i =，即7n =时结束程序， 所以6n ≤， 故选 ：B 【点睛】本题主要考查了程序框图，循环结构，条件分支结构，等比数列求和，属于中档题.genju9．中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的，，依次输入的为2，2，5，则输出的（ ）A ．7B ．12C ．17D ．34【答案】C 【解析】第一次循环：2,2,1a s k === ；第二次循环：2,6,2a s k === ；第三次循环：5,17,32a s k ===> ；结束循环，输出17s = ，选C.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.10．执行如图所示的程序框图，则输出的结果为A．4 B．5 C．6 D．7【答案】B【解析】【分析】模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的的值.【详解】第一次循环，；第二次循环，；第三次循环，，退出循环，输出，故选B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.11．执行如图所示的程序框图，若输入，则输出的S的值是A．B．C．D．【答案】B【解析】【分析】本题首先可以通过程序框图明确输入的数值以及程序框图中所包含的关系式，然后按照程序框图所包含的关系式进行循环运算，即可得出结果．【详解】由程序框图可知，输入，，，第一次运算：，；第二次运算：，；第三次运算：，；第四次运算：，；第五次运算：，；第六次运算：，；第七次运算：，；第八次运算：，；第九次运算：，；第十次运算：，，综上所述，输出的结果为，故选B．【点睛】本题考查程序框图的相关性质，主要考查程序框图的循环结构以及裂项相消法的使用，考查推理能力，提高了学生从题目中获取信息的能力，体现了综合性，提升了学生的逻辑推理、数学运算等核心素养，是中档题．12．已知实数[]1,10x ∈，执行如图所示的流程图，则输出的x 不小于63的概率为（ ）A ．49 B ．13 C ．25 D ．310 【答案】B 【解析】试题分析：运行该程序框图，第一次循环21,2x x n =+=；第二次循环()221+1=43,3x x x n =++=；第三次循环2187,4x x x n =+=+=；推出循环输出87x +，由8763x +≥得7x ≥，由几何概型概率公式可得输出的x 不小于63的概率为1071103-=，故选B. 考点：1、程序框图及循环结构；2、几何概型概率公式.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1)不要混淆处理框和输入框；(2)注意区分程序框图是条件分支结构还是循环结构；(3)注意区分当型循环结构和直到型循环结构；(4)处理循环结构的问题时一定要正确控制循环次数；(5)要注意各个框的顺序；（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.13．如图所示的一个算法的程序框图，则输出d 的最大值为（ ）A．2B．2 C．12++D．122【答案】C【解析】【分析】【详解】模拟程序的运行，可得程序框图的功能是求半圆y＝上的点到直线x﹣y﹣2＝0的距离的最大值，如图：可得：d的最大值为OP+r＝+1．故选：C．14．执行如图所示的程序框图，输出的值为（）A．13B．12C．2 D．2-【答案】A【解析】【分析】根据程序框图所示的意义可得a的值，构成周期数列，即可得答案；【详解】1i=，3a=-；2 i=，12a=-；3 i=，13 a=；4i=，2a=；5i=，3a=-，可以看出是周期为4的数列，55 i=，13 a=.56i=，终止循环，输出13 a=.故选：A.【点睛】本题考查算法中程序框图的循环结构，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力，求解时注意与数列的周期性相结合.15．德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家､天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P表示π的近似值),若输入10n＝,则输出的结果是( )A ．11114(1)35717P =-+-+⋅⋅⋅+ B ．11114(1)35719P =-+-+⋅⋅⋅- C ．11114(1)35721P =-+-+⋅⋅⋅+ D ．11114(1)35721P =-+-+⋅⋅⋅- 【答案】B【解析】【分析】 执行给定的程序框图，输入10n =，逐次循环，找到计算的规律，即可求解.【详解】由题意，执行给定的程序框图，输入10n =，可得：第1次循环：1,2S i ==；第2次循环：11,33S i =-=；第3次循环：111,435S i =-+=； L L 第10次循环：11111,1135719S i =-+-+-=L ， 此时满足判定条件，输出结果111144(1)35719P S ==-+-+⋅⋅⋅-， 故选：B.【点睛】本题主要考查了循环结构的程序框图的计算与输出，其中解答中认真审题，逐次计算，得到程序框图的计算功能是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.16．秦九韶是我国南宋时期的数学家，普州（现四川省安岳县）人，他在所著的《数书九章》中提出的多项式求值的秦九韶算法，至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例.若输入n ，x 的值分别为4，2，则输出v 的值为( )A ．5B ．12C ．25D ．50【答案】D【解析】【分析】 根据程序框图依次运行，直到0i <，结束循环，输出v 的值，得出结果.【详解】由题意，运行该程序，输入4n =，2x =，则1v =，4130i =-=≥，判断框成立；则1235v =⨯+=，3120i =-=≥，判断框成立；则52212v =⨯+=，2110i =-=≥，判断框成立；则122125v =⨯+=，1100i =-=≥，判断框成立；则252050v =⨯+=，0110i =-=-<，判断框不成立，输出50v =.故选：D.【点睛】本题考查程序框图，关键在于准确识别循环结构和判断框语句，属于基础题.17．我国古代数学名著《九章算术》里有一道关于玉石的问题：“今有玉方一寸，重七两；石方一寸，重六两.今有石方三寸，中有玉，并重十一斤（176两）.问玉、石重各几何？”如图所示的程序框图反映了对此题的一个求解算法，运行该程序框图，则输出的x ，y 分别为（ ）A ．90，86B ．94，82C ．98，78D ．102，74【答案】C【解析】 执行程序框图，86,90,27x y s ==≠；90,86,27x y s ==≠；94,82,27x y s ==≠；98,78,27x y s ===，结束循环，输出的,x y 分别为98,78，故选C.【方法点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.18．如图所示的程序框图，则输出的,,x y z 的值分别是（ ）A ．13009，600，11203B ．1200，500，300C ．1100，400，600D ．300，500，1200 【答案】B【解析】【分析】根据程序框图依次计算得到答案.【详解】根据程序框图得：①300,1y i ==，满足3i <；②400,2y i ==，满足3i <； ③500,300y z ==，1200,3x i ==，不满足3i <.故输出的1200,500,300x y z ===. 故选：B .【点睛】本题考查了程序框图，意在考查学生的理解能力.19．执行如图所示的程序框图，如果输入6n =，3m =，则输出的p 等于（ ）A ．120B ．360C ．840D ．1008【答案】A【解析】【分析】 模拟执行程序框图，逐步写出各变量取值的变化，判断循环条件是否成立，最终可得答案.【详解】执行程序框图，各变量的值依次变化如下：6,3,1,1;n m k p ====1(631)4,p =⨯-+=k m <成立；2,4(632)20k p ==⨯-+=，k m <成立；3,20(633)120k p ==⨯-+=，k m <不成立，跳出循环，输出的p 等于120.故选：A.【点睛】本题考查程序框图，解题的一般方法是模拟执行程序，依次写出各变量取值的变化，解题时要留意循环终止的条件.20．执行如图所示的程序框图，若输出的值为，则判断框内可填入的条件是 （ ）A． B． C． D．【答案】A【解析】本程序框图的主要功能是计算数列的前项和；由于可知，数列的前项和为，由于输出的值为0.99，所以，因此判断框内可填入的条件是，故选A.。

新单元《算法与框图》专题解析一、选择题1．运行如图所示的程序框图，若输出的S 的值为1011，则判断框中可以填（ ）A ．2020?i >B ．2021?i ≥C ．2022?i >D ．2023?i >【答案】C 【解析】 【分析】利用程序框图的功能，进行模拟计算即可． 【详解】程序的功能是计算S ＝1sin2π+3sin 32π+5sin+52π…＝1﹣3+5﹣7+9+…+，则1011＝1+505×2＝1﹣3+5﹣7+9+…则第1011个奇数为2×1011﹣1＝2021不成立， 第1012个奇数为2×1012﹣1＝2023成立， 故条件为i ＞2022？， 故选C ． 【点睛】本题主要考查程序框图的应用，利用程序框图的功能是解决本题的关键，属于基础题.2．“二进制”来源于我国古代的《易经》，该书中有两类最基本的符号：“—”和“——”，其中“—”在二进制中记作“1”，“——”在二进制中记作“0”，例如二进制数(2)1011化为十进制的计算如下：321(2)(10)10111202121211=⨯+⨯+⨯+⨯=.若从两类符号中任取2个符号进行排列，则得到的二进制数所对应的十进制数大于2的概率为（ ） A ．0 B ．12C ．13D ．14【答案】D 【解析】 【分析】分类计算得到从两类符号中任取2个符号排列，则组成不同的十进制数为0，1，2，3，计算得到概率. 【详解】根据题意，不同符号可分为三类：第一类：由两个“—”组成，其二进制为(2)(10)113=； 第二类：由两个“——”组成，其二进制为(2)(10)000=；第三类：由一个“—”和一个“——”组成，其二进制为(2)(10)102=，(2)(10)011=， 所以从两类符号中任取2个符号排列，则组成不同的十进制数为0，1，2，3， 则得到的二进制数所对应的十进制数大于2的概率14P =， 故选：D. 【点睛】本题考查古典概型及进制转化的应用，意在考查学生的计算能力和应用能力.3．如图是求112122++的程序框图，图中空白框中应填入A ．A =12A + B ．A =12A+C ．A =112A+D ．A =112A+【答案】A 【解析】 【分析】本题主要考查算法中的程序框图，渗透阅读、分析与解决问题等素养，认真分析式子结构特征与程序框图结构，即可找出作出选择． 【详解】执行第1次，1,122A k==≤是，因为第一次应该计算1122+=12A+，1k k=+=2，循环，执行第2次，22k=≤，是，因为第二次应该计算112122++=12A+，1k k=+=3，32k=≤，否，输出，故循环体为12AA=+，故选A．【点睛】秒杀速解认真观察计算式子的结构特点，可知循环体为12AA=+．4．如图是计算11111++++246810值的一个程序框图，其中判断框内应填入的条件是( ) A．5k≥B．5k<C．5k>D．6k≤【答案】B【解析】【分析】根据计算结果，可知该循环结构循环了5次；输出S前循环体的n的值为12，k的值为6，进而可得判断框内的不等式．【详解】因为该程序图是计算11111246810++++值的一个程序框圈所以共循环了5次所以输出S前循环体的n的值为12，k的值为6，即判断框内的不等式应为6k≥或5k>所以选C【点睛】本题考查了程序框图的简单应用，根据结果填写判断框，属于基础题．5．阅读如图的程序框图，运行相应的程序，则输出的a 的值为（ ）A ．2-3B ．3-2C ．52D ．25【答案】C 【解析】 【分析】根据给定的程序框图，计算前几次的运算规律，得出运算的周期性，确定跳出循环时的n 的值，进而求解a 的值，得到答案. 【详解】 由题意，3,15a n ==， 第1次循环，2,23a n =-=，满足判断条件； 第2次循环，5,32a n ==，满足判断条件； 第3次循环，3,45a n ==，满足判断条件； L L可得a 的值满足以3项为周期的计算规律，所以当2019n =时，跳出循环，此时n 和3n =时的值对应的a 相同，即52a =. 故选：C. 【点睛】本题主要考查了循环结构的程序框图的计算与输出问题，其中解答中认真审题，得出程序运行时的计算规律是解答的关键，着重考查了推理与计算能力.6．如图所示的程序框图，若输出的结果为4，则输入的实数的取值范围是（ ）A ．B ．C ．D ．【答案】A 【解析】，，否，； ，否，； ，否，；，，是，即；解不等式，，且满足，，综上所述，若输出的结果为4，则输入的实数的取值范围是，故选．点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.7．阅读如图所示的程序框图，若输入的1a b i ===，则输出的a 的值为( )A ．2019B ．1C ．2018D ．2016【答案】B【解析】 【分析】根据程序框图进行运算即可. 【详解】将,,a b i 的值用表格表示如下：a 1 211- 2- 1- 1 …b 1 1- 2- 1- 1 2 1 … i 1 234567 …由表可知，a 的值以6为周期循环，201963363,3i ÷=⋅⋅⋅⋅⋅⋅=时对应的1a =. 故选：B 【点睛】本题主要考查了程序框图的计算，考查了学生的运算求解能力.8．明代数学家程大位（1533~1606年），有感于当时筹算方法的不便，用其毕生心血写出《算法统宗》，可谓集成计算的鼻祖．如图所示的程序框图的算法思路源于其著作中的“李白沽酒”问题．执行该程序框图，若输出的y 的值为2，则输入的x 的值为（ ）A ．74B ．5627C ．2D ．16481【答案】C 【解析】 【分析】根据程序框图依次计算得到答案. 【详解】34y x =-，1i =；34916y y x =-=-，2i =；342752y y x =-=-，3i =；3481160y y x =-=-，4i =；34243484y y x =-=-，此时不满足3i ≤，跳出循环，输出结果为243484x -，由题意2434842y x =-=，得2x =． 故选:C 【点睛】本题考查了程序框图的计算，意在考查学生的理解能力和计算能力.9．中国古代有计算多项式值的秦九韶算法，右图是实现该算法的程序框图.执行该程序框图，若输入的，，依次输入的为2，2，5，则输出的（ ）A ．7B ．12C ．17D ．34【答案】C 【解析】第一次循环：2,2,1a s k === ；第二次循环：2,6,2a s k === ；第三次循环：5,17,32a s k ===> ；结束循环，输出17s = ，选C.点睛：算法与流程图的考查，侧重于对流程图循环结构的考查.先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项.10．运行如图所示的程序框图，若输出的s 值为10-，则判断框内的条件应该是( )A ．3k <？B ．4k <？C ．5k <？D ．6k <？ 【答案】C 【解析】当1,1k s ==时，应满足继续循环的条件，故1,2s k ==； 当2,1k s ==时，应满足继续循环的条件，故0,3s k ==； 当3,0k s ==时，应满足继续循环的条件，故3,4s k =-=； 当4,3k s ==-时，应满足继续循环的条件，故10,5s k =-=； 当5,10k s ==-时，应不满足继续循环的条件， 故判断框内的条件应该是5?k <，故选C ．【名师点睛】本题主要考查程序框图的循环结构流程图，属于中档题.解决程序框图问题时一定注意以下几点： (1)不要混淆处理框和输入框；(2)注意区分程序框图是条件分支结构还是循环结构； (3)注意区分当型循环结构和直到型循环结构； (4)处理循环结构的问题时，一定要正确控制循环次数； (5)要注意各个框的顺序；(6)在给出程序框图求解输出结果的试题中，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.11．根据下面的程序框图，输出的S 的值为（ ）A ．1007B ．1009C ．0D ．-1【答案】A 【解析】 【分析】按照程序框图模拟运行即可得解. 【详解】1i =，1112x ==--，0(1)1S =+-=-；2i =，111(1)2x ==--， 11122S =-+=-；3i =，12112x ==-，13222S =-+=；4i =，1112x ==--，31(1)22S =+-=，…， 由此可知，运行程序过程中，x 呈周期性变化，且周期为3， 所以输出112672110072S ⎛⎫=-++⨯-= ⎪⎝⎭. 故选A 【点睛】本题主要考查程序框图和数列的周期性，意在考查学生对这些知识的理解掌握水平和分析推理能力.12．已知二进制数(2)1010化为十进制数为n ，若()n x a +的展开式中，7x 的系数为15，则实数a 的值为（ ） A ．12B ．15C ．1D ．2【答案】A【解析】 【分析】先利用进制转化求出n 的值,再利用二项展开式的通项公式,结合题意列式求得a 的值. 【详解】根据进制转换法可得:31(2)1010121210=⨯+⨯=, 所以10n =,设10()x a +展开式的通项为10110C kkk k T x a -+=,令107k -=,∴3k =,∴7x 的系数为3310C 15a =,∴318a =,∴12a =,故选:A. 【点睛】本题考查二项式,考查进制转换,需要学生对基础知识牢固掌握且灵活运用.13．执行如图所示的程序框图，则输出S 的值为（ ）A 3B 3C ．0D ．3-【答案】A 【解析】 【分析】 【详解】试题分析：第一次循环：133,22a S ==,第二次循环：2332a S ==环：30,3a S =,第四次循环：43322a S =-=,第五次循环：5302a S =-=,第六次循环：60,0a S ==,第七次循环：733,22a S ==,第八次循环：83,32a S ==,第九次循环：90,3a S ==此时98i =>，结束循环，输出3S =，选A.考点：循环结构流程图14．德国数学家莱布尼兹(1646年-1716年)于1674年得到了第一个关于π的级数展开式,该公式于明朝初年传入我国.在我国科技水平业已落后的情况下,我国数学家､天文学家明安图(1692年-1765年)为提高我国的数学研究水平,从乾隆初年(1736年)开始,历时近30年,证明了包括这个公式在内的三个公式,同时求得了展开三角函数和反三角函数的6个新级数公式,著有《割圆密率捷法》一书,为我国用级数计算π开创了先河.如图所示的程序框图可以用莱布尼兹“关于π的级数展开式”计算π的近似值(其中P 表示π的近似值),若输入10n ＝,则输出的结果是( )A ．11114(1)35717P =-+-+⋅⋅⋅+ B ．11114(1)35719P =-+-+⋅⋅⋅- C ．11114(1)35721P =-+-+⋅⋅⋅+ D ．11114(1)35721P =-+-+⋅⋅⋅- 【答案】B【解析】【分析】 执行给定的程序框图，输入10n =，逐次循环，找到计算的规律，即可求解.【详解】由题意，执行给定的程序框图，输入10n =，可得：第1次循环：1,2S i ==；第2次循环：11,33S i =-=；第3次循环：111,435S i =-+=；L L第10次循环：11111,1135719S i =-+-+-=L ， 此时满足判定条件，输出结果111144(1)35719P S ==-+-+⋅⋅⋅-， 故选：B.【点睛】本题主要考查了循环结构的程序框图的计算与输出，其中解答中认真审题，逐次计算，得到程序框图的计算功能是解答的关键，着重考查了分析问题和解答问题的能力，属于基础题.15．执行如图所示的程序框图，若输出的结果为11，则图中的判断条件可以为（ ）A ．1?S >-B ．0?S <C ．–1?S <D ．0?S >【答案】B【解析】【分析】 根据程序框图知当11=i 时，循环终止，此时1lg110S =-<，即可得答案.【详解】1i =，1S =.运行第一次，11lg 1lg30,33S i =+=->=，不成立，运行第二次， 131lg lg 1lg50,535S i =++=->=，不成立，运行第三次， 1351lg lg lg 1lg70,7357S i =+++=->=，不成立，运行第四次， 13571lg lg lg lg 1lg90,93579S i =++++=->=，不成立，运行第五次， 135791lg lg lg lg lg 1lg110,11357911S i =+++++=-<=，成立， 输出i 的值为11，结束.故选：B.本题考查补充程序框图判断框的条件，考查函数与方程思想、转化与化归思想，考查逻辑推理能力和运算求解能力，求解时注意模拟程序一步一步执行的求解策略.16．执行如图所示的程序框图，则程序最后输出的结果为（ ）A ．15B ．25C ．35D ．45【答案】D【解析】【分析】模拟执行程序框图，读出程序框图实现的功能，即可求得输出结果.【详解】模拟执行程序框图，根据题意可知，11,5k a ==； 22,5k a ==； 43,5k a ==； 34,5k a ==； 15,5k a ==； 26,5k a ==； L 故归纳总结可得a 的取值周期为4，结合题中判断条件，2019k ≥，又201950443=⨯+可知： 输出的45a =. 故选：D.本题考查求程序框图的输出结果，解题时，应模拟程序框图的运行结果得出结论，属中档题.17．为计算1234171834561920T =⨯⨯⨯⨯⋅⋅⋅⨯⨯，设计了下面的程序框图，则在空白框中应填入（ ）A ．W W i =⨯B ．()1W W i =⨯+C ．()2W W i =⨯+D ．()3W W i =⨯+【答案】C【解析】【分析】 根据程序的计算功能，寻找分子与分母之间的关系，即可求解．【详解】由题意，根据程序的计算功能，可得每个分式的分母比分子多2，即()2W W i =⨯+． 故选：C .【点睛】本题主要考查了程序框图的识别与应用，其中解答中根据程序框图，找出每个式子分子与分母的关系式解答的关键，着重考查分析问题和解答问题的能力．18．鸡兔同笼，是中国古代著名的趣味题之一.《孙子算经》中就有这样的记载：今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各有几何？设计如右图的算法来解决这个问题，则判断框中应填入的是（ ）A ．94m >B ．94m =C ．35m =D ．35m ≤【答案】B【解析】【分析】 由题意知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意可得出判断条件.【详解】由题意可知i 为鸡的数量，j 为兔的数量，m 为足的数量，根据题意知，在程序框图中，当计算足的数量为94时，算法结束，因此，判断条件应填入“94m =”.故选B.【点睛】本题考查算法程序框图中判断条件的填写，考查分析问题和解决问题的能力，属于中等题.19．阅读如图所示的程序框图，运行相应的程序，输出的的值等于（ ）A．30 B．31 C．62 D．63【答案】B【解析】【分析】首先确定流程图的功能，然后计算其输出的结果即可.【详解】由流程图可知该算法的功能为计算的值，即输出值为：.故选：B.【点睛】识别、运行程序框图和完善程序框图的思路：(1)要明确程序框图的顺序结构、条件结构和循环结构．(2)要识别、运行程序框图，理解框图所解决的实际问题．(3)按照题目的要求完成解答并验证．20．我国明朝数学家程大位著的《算法统宗》里有一道闻名世界的题目：“一百馒头一百僧，大僧三个更无争.小僧三人分一个，大小和尚各几丁？”.如右图所示的程序框图反映了对此问题的一个求解算法，则输出n的值为（）A ．20B ．25C ．30D ．35【答案】B【解析】【分析】 模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可得到输出的n 的值.【详解】输出20,80,100n m s ==≠；21,79,100n m s ==≠；22,78,100n m s ==≠；23,77,100n m s ==≠；24,76,100n m s ==≠；25,75,100n m s ===，退出循环，输出25n =，故选B.【点睛】本题主要考查程序框图的循环结构流程图，属于中档题. 解决程序框图问题时一定注意以下几点：(1) 不要混淆处理框和输入框；(2) 注意区分程序框图是条件分支结构还是循环结构；(3) 注意区分当型循环结构和直到型循环结构；(4) 处理循环结构的问题时一定要正确控制循环次数；(5) 要注意各个框的顺序,（6）在给出程序框图求解输出结果的试题中只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可.。